The Cluster Computation-Based Hybrid FEM–Analytical Model of Induction Motor for Fault Diagnostics
Abstract
:1. Introduction
2. The Motor’s Model
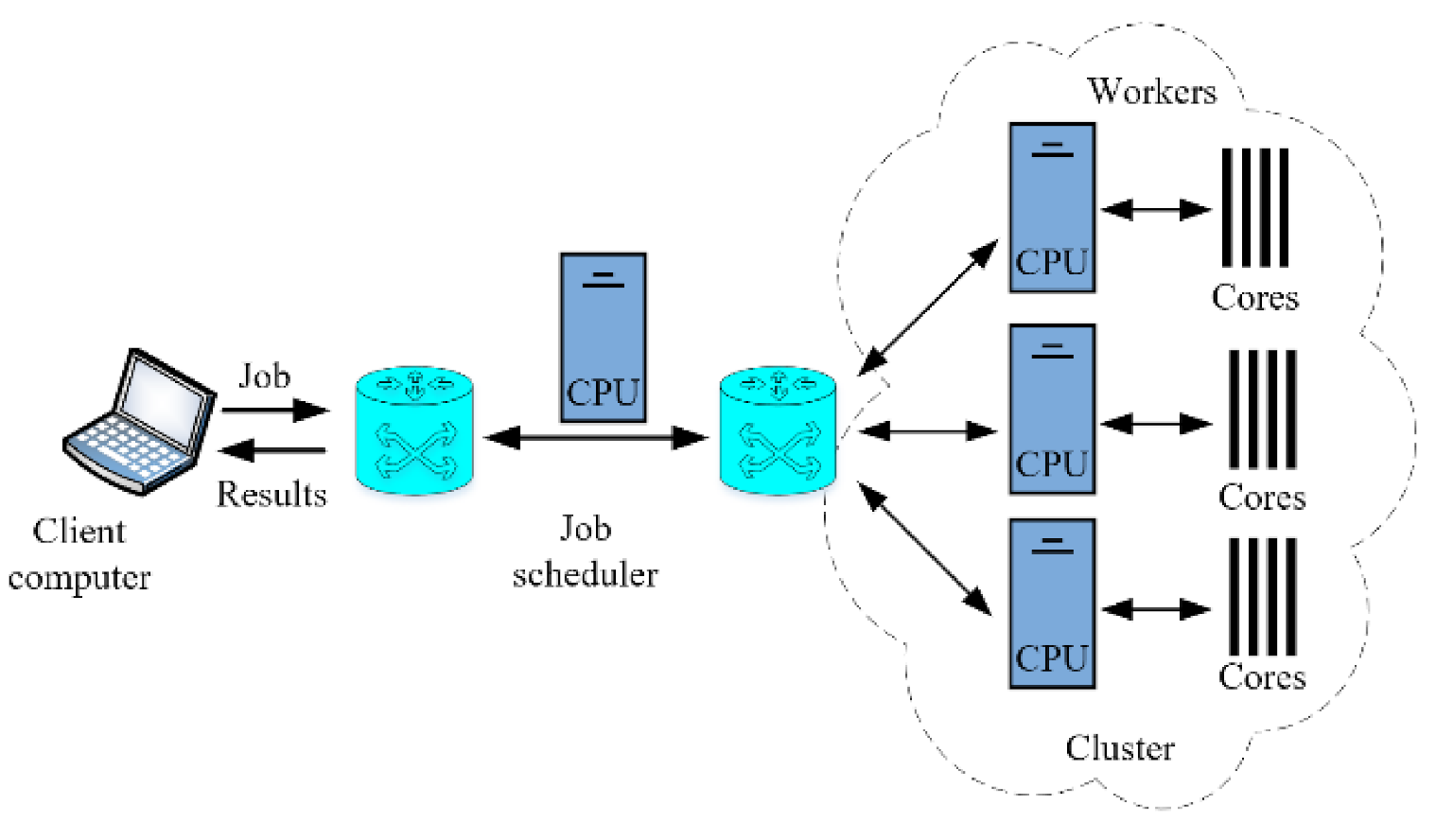
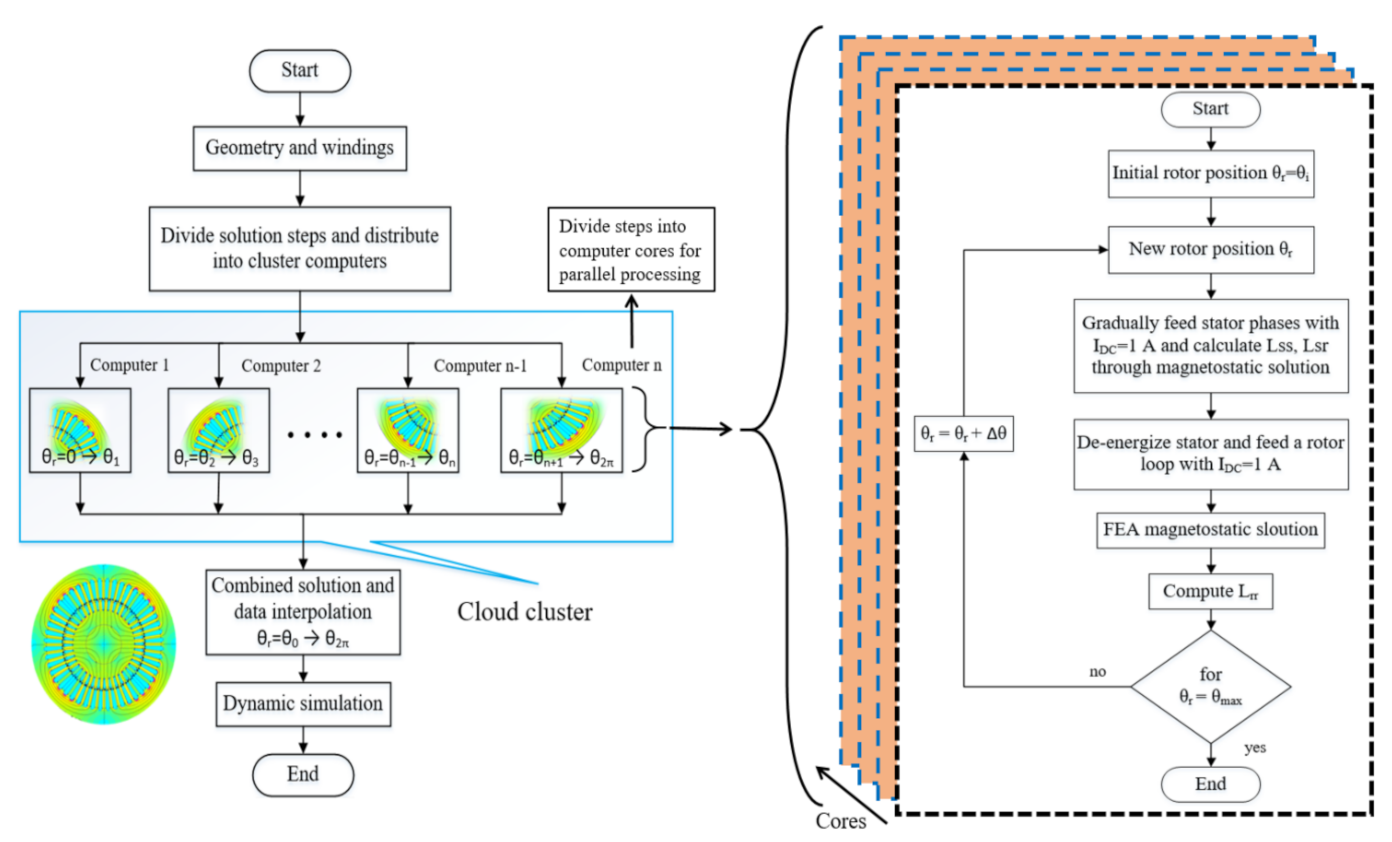
3. LAN Network for Cluster Formation
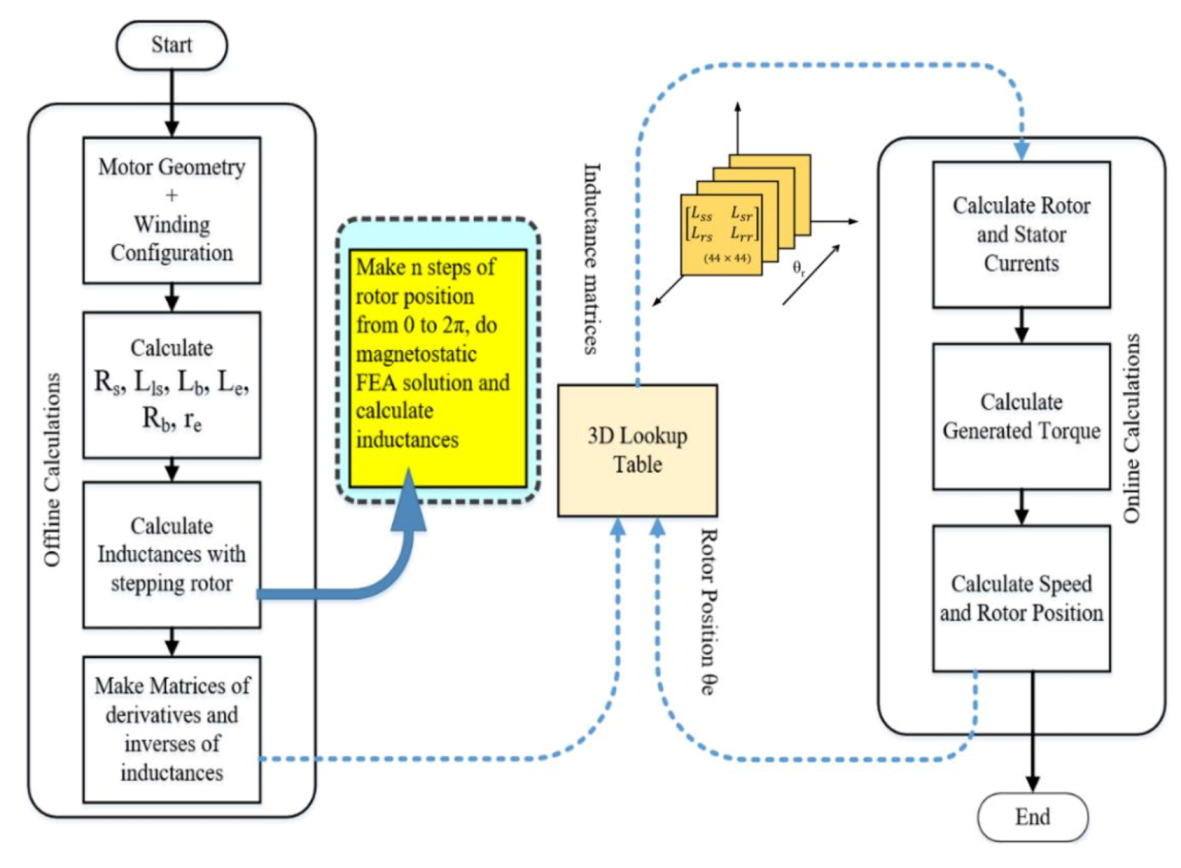
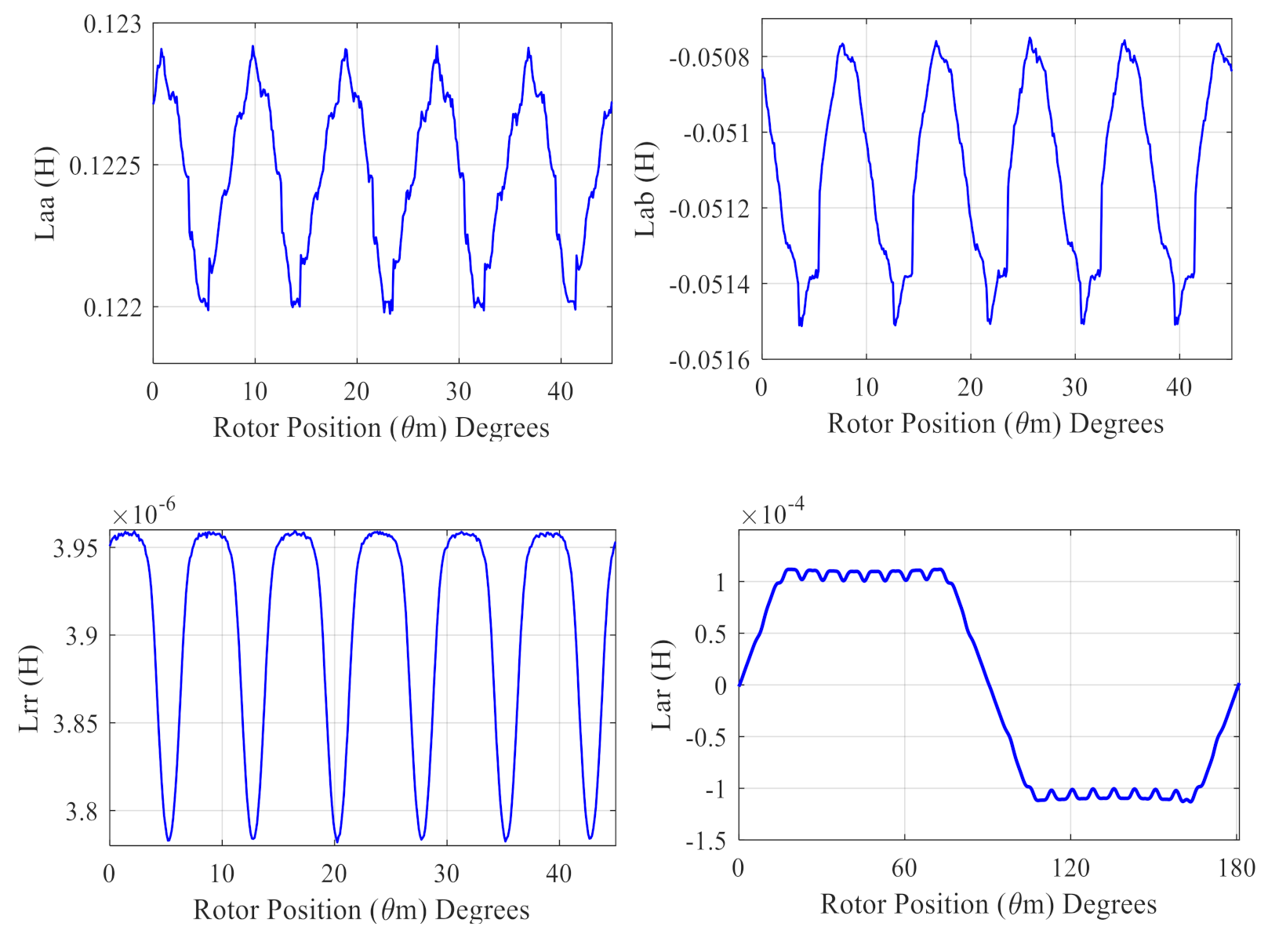
4. Inductances Calculations
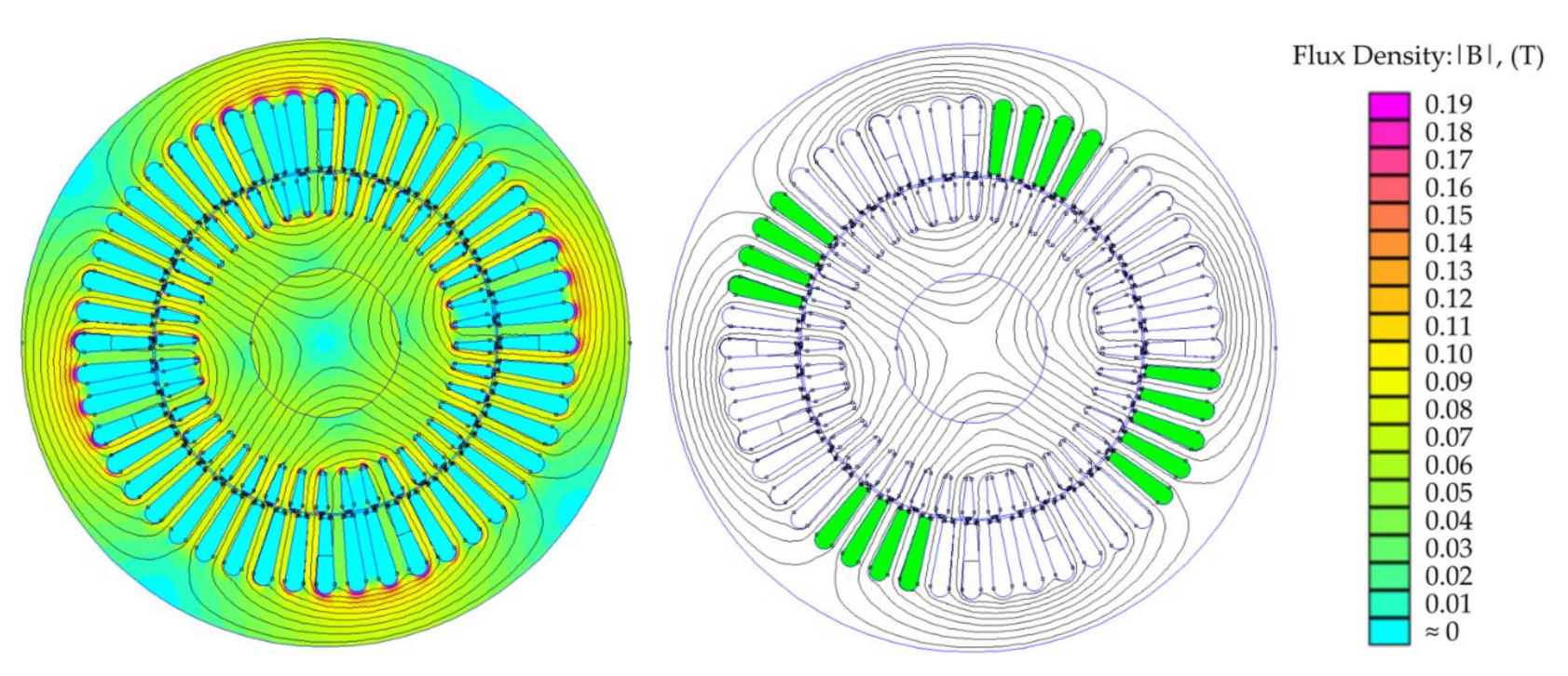
5. The Simulation Results
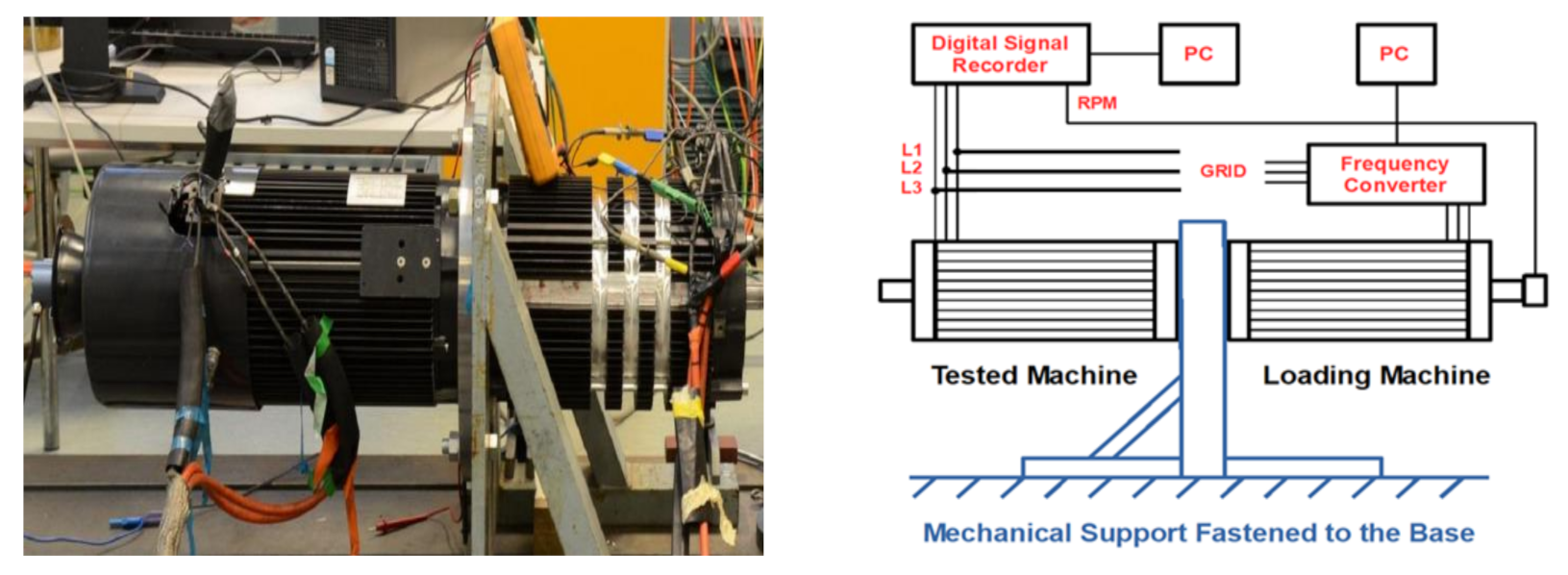
6. Test Setup
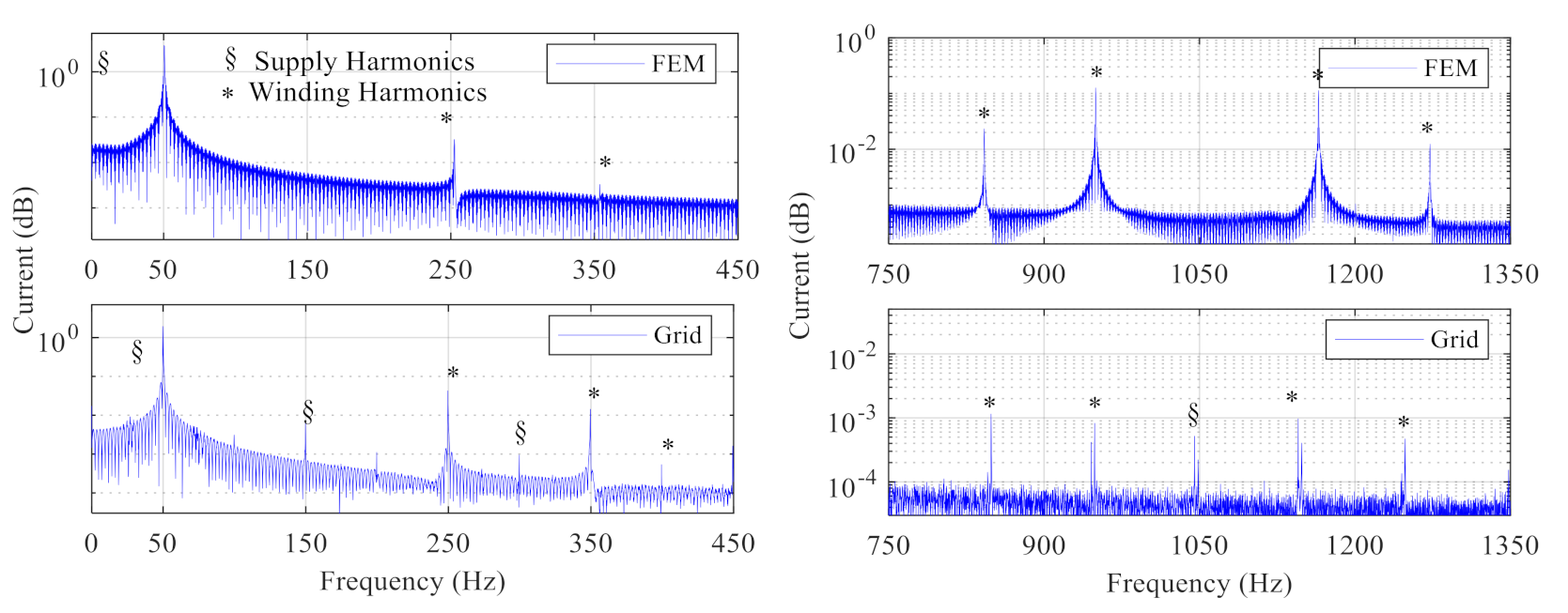
7. Results and Discussion
7.1. Stator Current Spectrum under Healthy and Broken Rotor Bar Cases
7.2. Time Comparison
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saidur, R. A review on electrical motors energy use and energy savings. Renew. Sustain. Energy Rev. 2010, 14, 877–898. [Google Scholar] [CrossRef]
- Sahraoui, M.; Cardoso, A.J.M.; Ghoggal, A. The use of a modified prony method to track the broken rotor bar characteristic frequencies and amplitudes in three-phase induction motors. IEEE Trans. Ind. Appl. 2015, 51, 2136–2147. [Google Scholar] [CrossRef]
- Naha, A.; Samanta, A.K.; Routray, A.; Deb, A.K. Low Complexity Motor Current Signature Analysis Using Sub-Nyquist Strategy with Reduced Data Length. IEEE Trans. Instrum. Meas. 2017, 66, 3249–3259. [Google Scholar] [CrossRef]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassõlkin, A.; Iqbal, M.N. Broken rotor bar fault detection of the grid and inverter-fed induction motor by effective attenuation of the fundamental component. IET Electr. Power Appl. 2019, 13, 2005–2014. [Google Scholar] [CrossRef]
- Zhen, D.; Wang, T.; Gu, F.; Ball, A. Fault diagnosis of motor drives using stator current signal analysis based on dynamic time warping. Mech. Syst. Signal Process. 2013, 34, 191–202. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Ramirez, A.G.; Morales-Hernandez, L.A.; Osornio-Rios, R.A.; García-Pérez, A.; Romero-Troncoso, R.D.J. Thermographic Technique as a Complement for MCSA in Induction Motor Fault Detection. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), ICEM 2014, Berlin, Germany, 2–5 September 2014; pp. 1940–1945. [Google Scholar]
- Taheri-Garavand, A.; Ahmadi, H.; Omid, M.; Mohtasebi, S.S.; Mollazade, K.; Smith, A.J.R.; Carlomagno, G.M. An intelligent approach for cooling radiator fault diagnosis based on infrared thermal image processing technique. Appl. Therm. Eng. 2015, 87, 434–443. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, Z. Diagnostics of stator faults of the single-phase induction motor using thermal images, MoASoS and selected classifiers. Measurement 2016, 93, 86–93. [Google Scholar] [CrossRef]
- Luong, P.; Wang, W. Smart Sensor-Based Synergistic Analysis for Rotor Bar Fault Detection of Induction Motors. IEEE/ASME Trans. Mechatronics 2020, 25, 1067–1075. [Google Scholar] [CrossRef]
- Caesarendra, W.; Kosasih, B.; Tieu, A.K.; Zhu, H.; Moodie, C.A.; Zhu, Q. Acoustic emission-based condition monitoring methods: Review and application for low speed slew bearing. Mech. Syst. Signal Process. 2016, 72–73, 134–159. [Google Scholar] [CrossRef]
- Vaimann, T.; Sobra, J.; Belahcen, A.; Rassõlkin, A.; Rolak, M.; Kallaste, A. Induction machine fault detection using smartphone recorded audible noise. IET Sci. Meas. Technol. 2018, 12, 554–560. [Google Scholar] [CrossRef] [Green Version]
- Henao, H.; Demian, C.; Capolino, G.-A. A frequency-domain detection of stator winding faults in induction machines using an external flux sensor. IEEE Trans. Ind. Appl. 2003, 39, 1272–1279. [Google Scholar] [CrossRef]
- Frosini, L.; Harlisca, C.; Szabo, L. Induction Machine Bearing Fault Detection by Means of Statistical Processing of the Stray Flux Measurement. IEEE Trans. Ind. Electron. 2015, 62, 1846–1854. [Google Scholar] [CrossRef]
- Stone, G.C.; Sedding, H.G.; Chan, C. Experience With Online Partial-Discharge Measurement in High-Voltage Inverter-Fed Motors. IEEE Trans. Ind. Appl. 2018, 54, 866–872. [Google Scholar] [CrossRef]
- Mirzaeva, G.; Saad, K.I.; Jahromi, M.G. Comprehensive Diagnostics of Induction Motor Faults Based on Measurement of Space and Time Dependencies of Air Gap Flux. IEEE Trans. Ind. Appl. 2017, 53, 2657–2666. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Konar, P.; Chattopadhyay, P. Bearing fault detection of induction motor using wavelet and Support Vector Machines (SVMs). Appl. Soft Comput. 2011, 11, 4203–4211. [Google Scholar] [CrossRef]
- Li, X.; Wang, K.; Jiang, L. The Application of AE Signal in Early Cracked Rotor Fault Diagnosis with PWVD and SVM. J. Softw. 2011, 6, 1969–1976. [Google Scholar] [CrossRef]
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing Health Monitoring Based on Hilbert–Huang Transform, Support Vector Machine, and Regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Sadeghian, A.; Ye, Z.; Wu, B. Online Detection of Broken Rotor Bars in Induction Motors by Wavelet Packet Decomposition and Artificial Neural Networks. IEEE Trans. Instrum. Meas. 2009, 58, 2253–2263. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Prieto, M.D.; Cirrincione, G.; Espinosa, A.G.; Ortega, J.A.; Henao, H. Bearing Fault Detection by a Novel Condition-Monitoring Scheme Based on Statistical-Time Features and Neural Networks. IEEE Trans. Ind. Electron. 2013, 60, 3398–3407. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Gao, R.X.; Yan, R. Current envelope analysis for defect identification and diagnosis in induction motors. J. Manuf. Syst. 2012, 31, 380–387. [Google Scholar] [CrossRef]
- Palácios, R.H.C.; Da Silva, I.N.; Goedtel, A.; Godoy, W.F. A comprehensive evaluation of intelligent classifiers for fault identification in three-phase induction motors. Electr. Power Syst. Res. 2015, 127, 249–258. [Google Scholar] [CrossRef]
- Wan, X.; Wang, D.; Tse, P.W.; Xu, G.; Zhang, Q. A critical study of different dimensionality reduction methods for gear crack degradation assessment under different operating conditions. Measurement 2016, 78, 138–150. [Google Scholar] [CrossRef]
- Ali, M.Z.; Shabbir, N.S.K.; Zaman, S.M.K.; Liang, X. Single- and Multi-Fault Diagnosis Using Machine Learning for Variable Frequency Drive-Fed Induction Motors. IEEE Trans. Ind. Appl. 2020, 56, 2324–2337. [Google Scholar] [CrossRef]
- Shao, S.; Yan, R.; Lu, Y.; Wang, P.; Gao, R.X. DCNN-Based Multi-Signal Induction Motor Fault Diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 2658–2669. [Google Scholar] [CrossRef]
- Jung, U.; Koh, B.-H. Wavelet energy-based visualization and classification of high-dimensional signal for bearing fault detection. Knowl. Inf. Syst. 2015, 44, 197–215. [Google Scholar] [CrossRef]
- Pandya, D.H.; Upadhyay, S.H.; Harsha, S.P. Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN. Expert Syst. Appl. 2013, 40, 4137–4145. [Google Scholar] [CrossRef]
- He, D.; Li, R.; Zhu, J. Plastic Bearing Fault Diagnosis Based on a Two-Step Data Mining Approach. IEEE Trans. Ind. Electron. 2013, 60, 3429–3440. [Google Scholar] [CrossRef]
- Baccarini, L.M.R.; De Menezes, B.R.; Caminhas, W.M. Fault induction dynamic model, suitable for computer simulation: Simulation results and experimental validation. Mech. Syst. Signal Process. 2010, 24, 300–311. [Google Scholar] [CrossRef]
- Cunha, C.C.M.; Oliveira, P.; Lyra, R.; Filho, B.C. Simulation and analysis of induction machines with rotor asymmetries. IEEE Trans. Ind. Appl. 2005, 41, 18–24. [Google Scholar]
- Liang, J.; Qiu, Y.; Zhao, M.; Kang, S.; Lu, H. The modeling and numerical simulations of wind turbine generation system with free vortex method and simulink. Energy Convers. Manag. 2015, 103, 762–777. [Google Scholar]
- Lubin, T.; Hamiti, T.; Razik, H.; Rezzoug, A. Comparison Between Finite-Element Analysis and Winding Function Theory for Inductances and Torque Calculation of a Synchronous Reluctance Machine. IEEE Trans. Magn. 2007, 43, 3406–3410. [Google Scholar]
- Raziee, S.M.; Misir, O.; Ponick, B. Winding Function Approach for Winding Analysis. IEEE Trans. Magn. 2017, 53, 1–9. [Google Scholar]
- Nandi, S. A Detailed Model of Induction Machines With Saturation Extendable for Fault Analysis. IEEE Trans. Ind. Appl. 2004, 40, 1302–1309. [Google Scholar]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassõlkin, A.; Iqbal, M.N. Modified winding function-based model of squirrel cage induction motor for fault diagnostics. IET Electr. Power Appl. 2020, 14, 1722–1734. [Google Scholar]
- Sudhoff, S.D.; Kuhn, B.T.; Corzine, K.A.; Branecky, B.T. Magnetic Equivalent Circuit Modeling of Induction Motors. IEEE Trans. Energy Convers. 2007, 22, 259–270. [Google Scholar]
- Apsley, J.M.; Williamson, S. Analysis of Multi-Phase Induction Machines with Winding Faults. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 249–255. [Google Scholar]
- Wang, L.; Jatskevich, J.; Pekarek, S.D. Modeling of induction machines using a voltage-behind-reactance formulation. IEEE Trans. Energy Convers. 2008, 23, 382–392. [Google Scholar]
- Sapena-Bano, A.; Martinez-Roman, J.; Puche-Panadero, R.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. Induction machine model with space harmonics for fault diagnosis based on the convolution theorem. Int. J. Electr. Power Energy Syst. 2018, 100, 463–481. [Google Scholar]
- Ding, Q.; Yang, Z.; Sun, X.; Zhao, Q.; Zhu, H. Analysis of rotor slot width influence on a bearingless induction motor. Comput. Electr. Eng. 2020, 81, 106534. [Google Scholar]
- Belahcen, A.; Rasilo, P.; Arkkio, A. Segregation of Iron Losses From Rotational Field Measurements and Application to Electrical Machine. IEEE Trans. Magn. 2014, 50, 893–896. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H. Online Thermal Monitoring Models for Induction Machines. IEEE Trans. Energy Convers. 2015, 30, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y.; Ruan, J.; Huang, T.; Yang, X.; Zhu, H.; Yang, G. Calculation of Temperature Rise in Air-cooled Induction Motors Through 3-D Coupled Electromagnetic Fluid-Dynamical and Thermal Finite-Element Analysis. IEEE Trans. Magn. 2012, 48, 1047–1050. [Google Scholar] [CrossRef]
- Bourchas, K.; Stening, A.; Soulard, J.; Broddefalk, A.; Lindenmo, M.; Dahlen, M.; Gyllensten, F. Quantifying Effects of Cutting and Welding on Magnetic Properties of Electrical Steels. IEEE Trans. Ind. Appl. 2017, 53, 4269–4278. [Google Scholar] [CrossRef] [Green Version]
- Sapena-Bano, A.; Chinesta, F.; Pineda-Sanchez, M.; Aguado, J.; Borzacchiello, D.; Puche-Panadero, R. Induction machine model with finite element accuracy for condition monitoring running in real time using hardware in the loop system. Int. J. Electr. Power Energy Syst. 2019, 111, 315–324. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.S.; Belahcen, A.; Kallaste, A.; Vaimann, T.; Gerokov, L.; Rassolkin, A. Thermal Analysis of a SynRM Using a Thermal Network and a Hybrid Model. In Proceedings of the 2018 23rd International Conference on Electrical Machines, ICEM 2018, Alexandroupoli, Greece, 3–6 September 2018; pp. 2682–2688. [Google Scholar]
- Mukhrejee, V.; Far, M.F.; Martin, F.; Belahcen, A. Constrained Algorithm for the Selection of Uneven Snapshots in Model Order Reduction of a Bearingless Motor. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Far, M.F.; Martin, F.; Belahcen, A.; Rasilo, P.; Awan, H.A.A. Real-Time Control of an IPMSM Using Model Order Reduction. IEEE Trans. Ind. Electron. 2020, 1. [Google Scholar] [CrossRef]
- Far, M.F.; Martin, F.; Belahcen, A.; Montier, L.; Henneron, T. Orthogonal Interpolation Method for Order Reduction of a Synchronous Machine Model. IEEE Trans. Magn. 2018, 54, 1–6. [Google Scholar]
- Borzacchiello, D.; Aguado, J.V.; Chinesta, F. Non-intrusive Sparse Subspace Learning for Parametrized Problems. Arch. Comput. Methods Eng. 2019, 26, 303–326. [Google Scholar] [CrossRef]
- Villalonga, A.; Beruvides, G.; Castano, F.; Haber, R.E. Cloud-Based Industrial Cyber–Physical System for Data-Driven Reasoning: A Review and Use Case on an Industry 4.0 Pilot Line. IEEE Trans. Ind. Informatics 2020, 16, 5975–5984. [Google Scholar] [CrossRef]
- Chen, Z.; Quan, W.; Wen, M.; Fang, J.; Yu, J.; Zhang, C.; Luo, L. Deep Learning Research and Development Platform: Characterizing and Scheduling with QoS Guarantees on GPU Clusters. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 34–50. [Google Scholar] [CrossRef]
- Gao, Y.; Ai, Y.; Tian, B.; Chen, L.; Wang, J.; Cao, D.; Wang, F.-Y. Parallel End-to-End Autonomous Mining: An IoT-Oriented Approach. IEEE Internet Things J. 2020, 7, 1011–1023. [Google Scholar] [CrossRef]
- Bandyopadhyay, I.; Purkait, P.; Koley, C. A combined image processing and Nearest Neighbor Algorithm tool for classification of incipient faults in induction motor drives. Comput. Electr. Eng. 2016, 54, 296–312. [Google Scholar] [CrossRef]
- Guesmi, H.; Ben Salem, S.; Bacha, K. Smart wireless sensor networks for online faults diagnosis in induction machine. Comput. Electr. Eng. 2015, 41, 226–239. [Google Scholar] [CrossRef]
- Chen, J.; Li, K.; Bilal, K.; Zhou, X.; Li, K.; Yu, P.S. A Bi-layered Parallel Training Architecture for Large-Scale Convolutional Neural Networks. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 965–976. [Google Scholar] [CrossRef] [Green Version]
- You, Y.; Zhang, Z.; Hsieh, C.-J.; Demmel, J.; Keutzer, K. Fast Deep Neural Network Training on Distributed Systems and Cloud TPUs. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2449–2462. [Google Scholar] [CrossRef]
- Huang, S.-R.; Huang, K.-H.; Chao, K.-H.; Chiang, W.-T. Fault analysis and diagnosis system for induction motors. Comput. Electr. Eng. 2016, 54, 195–209. [Google Scholar] [CrossRef]



| Sr. No. | Parameter | Symbol | Value |
|---|---|---|---|
| 1 | Rated speed | Nr | 1400 rpm@50 Hz |
| 2 | Rated power | Pr | 18 kW@50 Hz |
| 3 | Connection | Y, Δ | Star (Y) |
| 4 | Power factor | cosφ | 0.860 |
| 5 | Number of poles | P | 4 |
| 6 | Number of rotor bars | Nrb | 40 |
| 7 | Number of stator slots | Ns | 48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassõlkin, A.; Iqbal, M.N. The Cluster Computation-Based Hybrid FEM–Analytical Model of Induction Motor for Fault Diagnostics. Appl. Sci. 2020, 10, 7572. https://doi.org/10.3390/app10217572
Asad B, Vaimann T, Belahcen A, Kallaste A, Rassõlkin A, Iqbal MN. The Cluster Computation-Based Hybrid FEM–Analytical Model of Induction Motor for Fault Diagnostics. Applied Sciences. 2020; 10(21):7572. https://doi.org/10.3390/app10217572
Chicago/Turabian StyleAsad, Bilal, Toomas Vaimann, Anouar Belahcen, Ants Kallaste, Anton Rassõlkin, and M. Naveed Iqbal. 2020. "The Cluster Computation-Based Hybrid FEM–Analytical Model of Induction Motor for Fault Diagnostics" Applied Sciences 10, no. 21: 7572. https://doi.org/10.3390/app10217572
APA StyleAsad, B., Vaimann, T., Belahcen, A., Kallaste, A., Rassõlkin, A., & Iqbal, M. N. (2020). The Cluster Computation-Based Hybrid FEM–Analytical Model of Induction Motor for Fault Diagnostics. Applied Sciences, 10(21), 7572. https://doi.org/10.3390/app10217572










