A Multilevel Road Alignment Model for Spatial-Query-by-Sketch
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
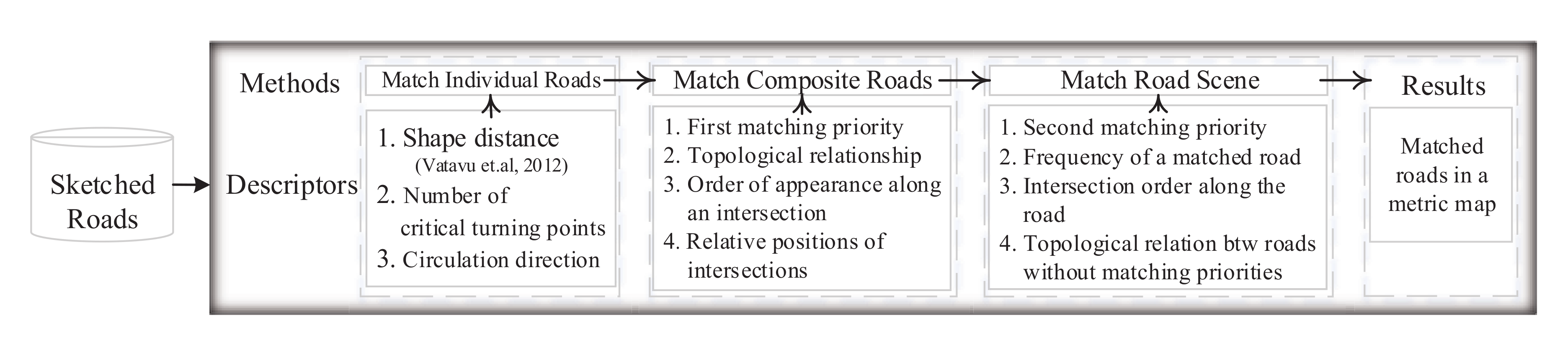
3.1. Multilevel Road Classification
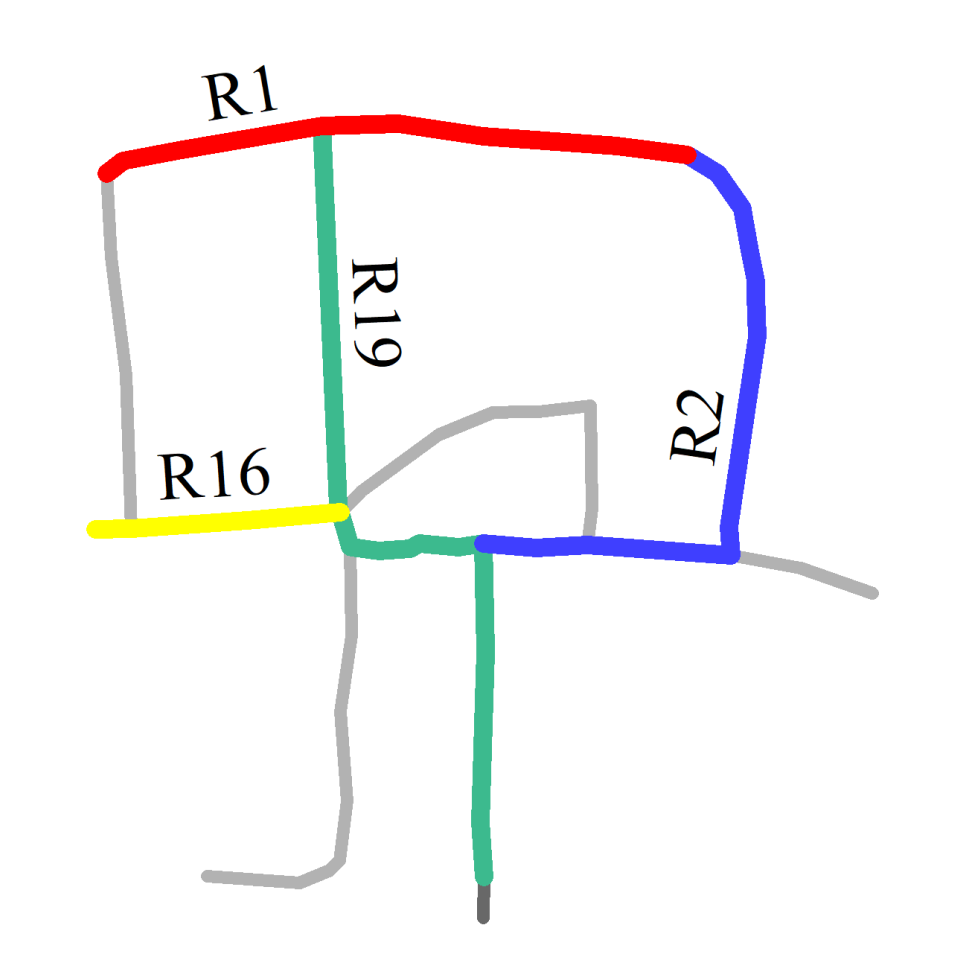
- A individual road refers to a road in a given location. For example, R0’, R1’, R2’, and R3’ are individual roads in the road network shown in Figure 1a.
- A composite road contains two individual and intersected roads. For example, the yellow line composed of R0’ and R1’ is a composite road in the road network shown in Figure 1a.
- A road scene represents the combination of all the roads in a given location. The green line composed of R0’, R1’, R2’, and R3’ in Figure 1a represents a road scene.
3.2. Characteristics and Matching Approach for Individual Roads
3.2.1. Extraction of Main Roads
- The degree centrality (), also known as the connectivity, indicates the number of roads connected to a certain road. A given road is considered more important if a larger number of roads are connected to it. In Figure 1a, R2’ has three roads connected to it (R0’, R1’, and R3’); therefore, the of R2’ is 3. R3’ has only one road (R2’) connected to it, and therefore, the corresponding is 1. Consequently, R2’ is more important than R3’ in terms of .
- The betweenness centrality () is a measure of the frequency at which a certain road is passed in all the shortest paths of a given location. A higher frequency indicates a greater connectivity of a road. In the proposed approach, is determined by calculating the shortest path from one endpoint of a certain road to the endpoints of all the other roads and considering the occurrence frequency of a road in all the shortest paths as the in that road in a given location. According to Figure 1b, the occurrence frequencies for each road that appeared in all the shortest paths are 4 (R0’), 4 (R1’), 6 (R2’), and 4 (R3’). This demonstrates that R2’ is more important than the other roads in this location, in terms of the .
- The closeness centrality (), in graph theory, is based on the degree to which a point is close to all the other points. In terms of roads, the indicates the shortest distance from a given road to all the other roads. Because the objective of this study is to determine the main roads in a given location, this factor is not calculated when extracting the main roads.
3.2.2. Shape Distance
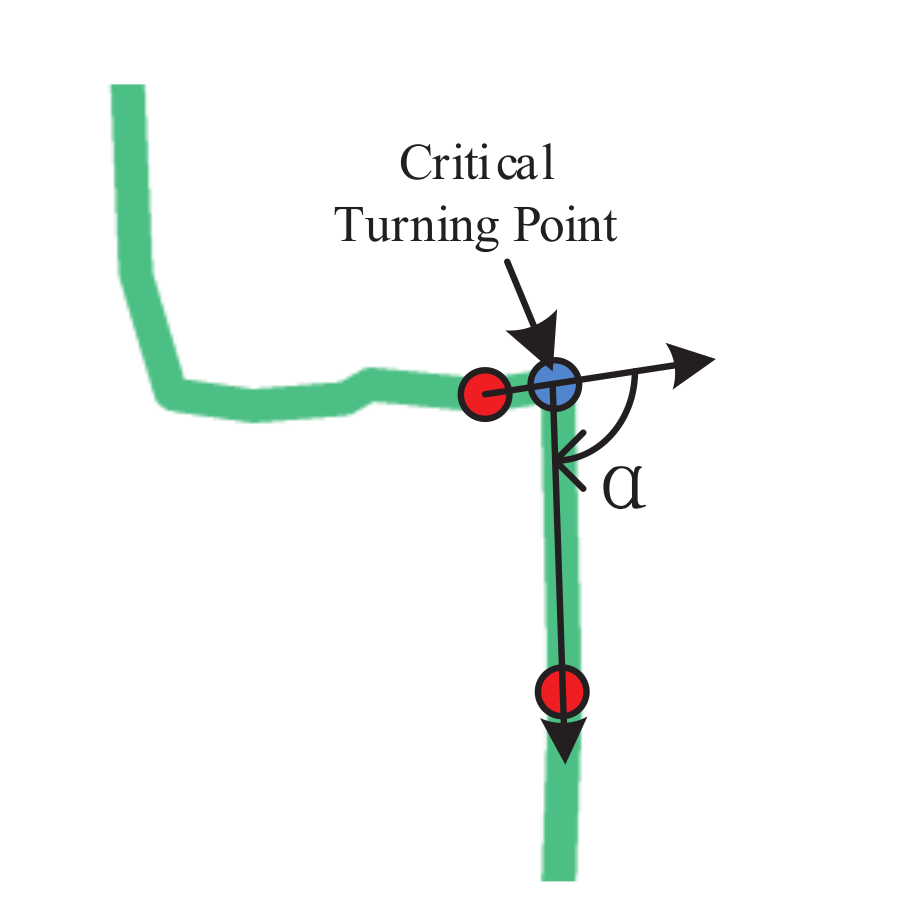
3.2.3. Number of Critical Turning Points
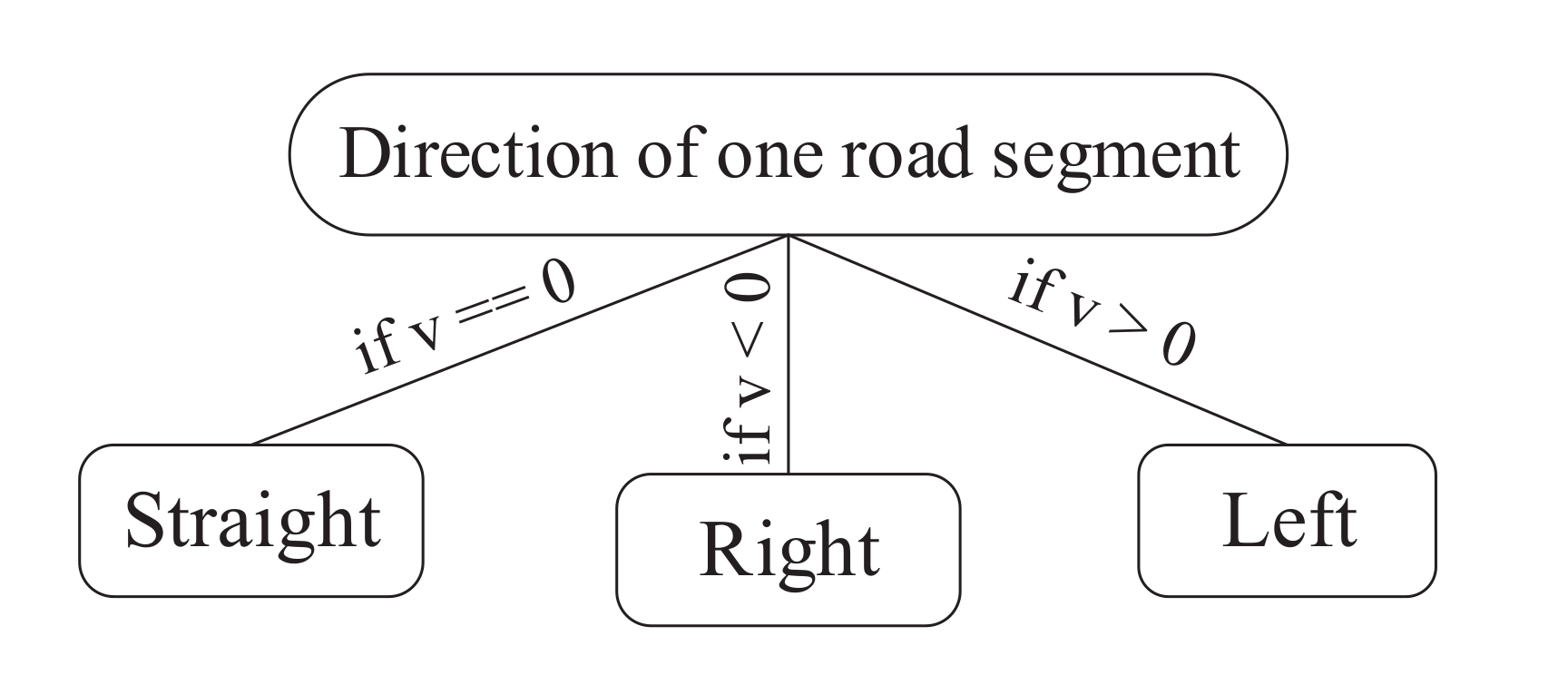
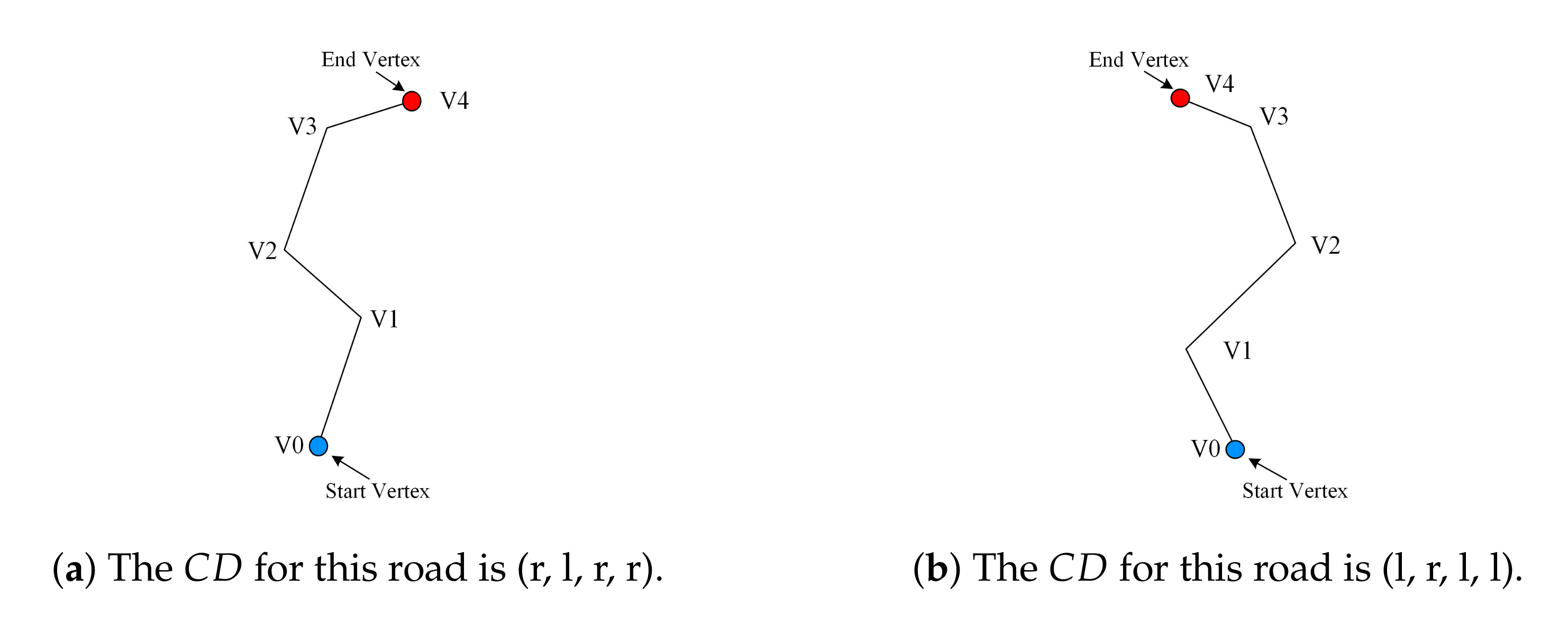
3.2.4. Circulation Direction
3.2.5. Computation of Similarity between Individual Roads
3.3. Characteristics and Matching Approach for Composite Roads
3.3.1. First Matching Priority
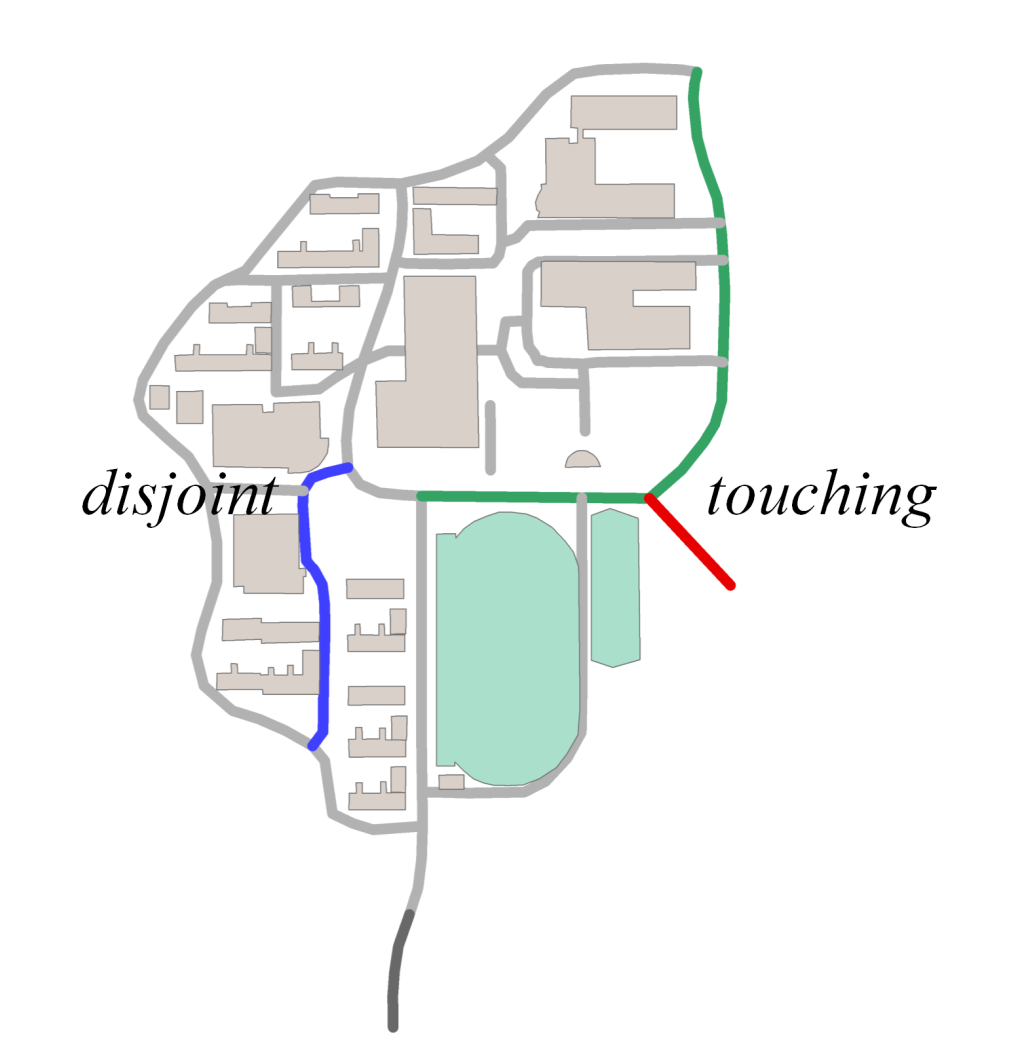
3.3.2. Topological Relationship of Composite Roads
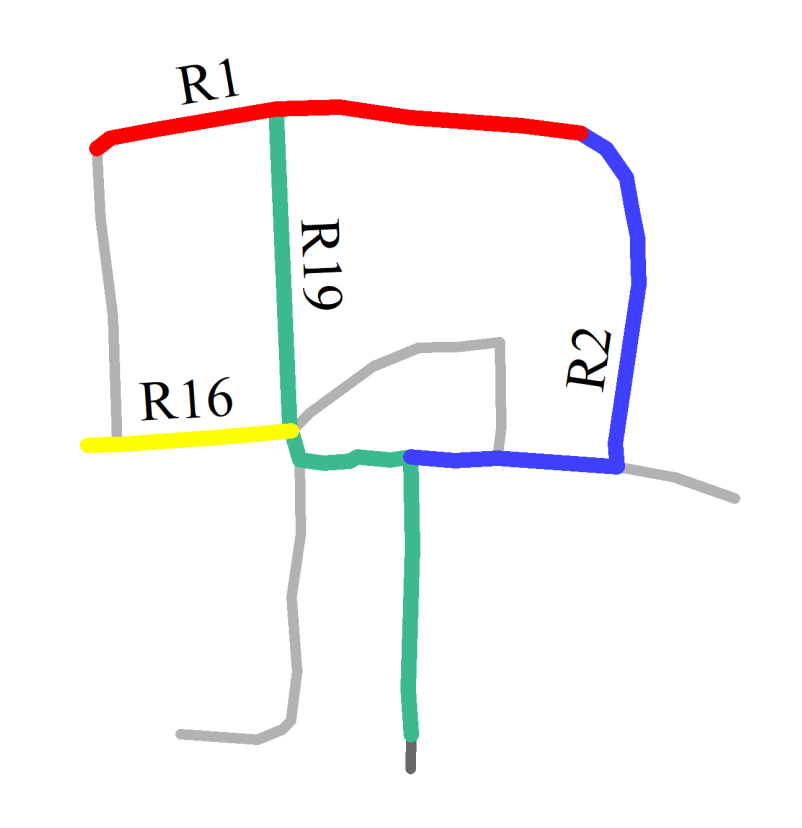
3.3.3. Order of Appearance of Roads along an Intersection
3.3.4. Relative Positions of Intersections
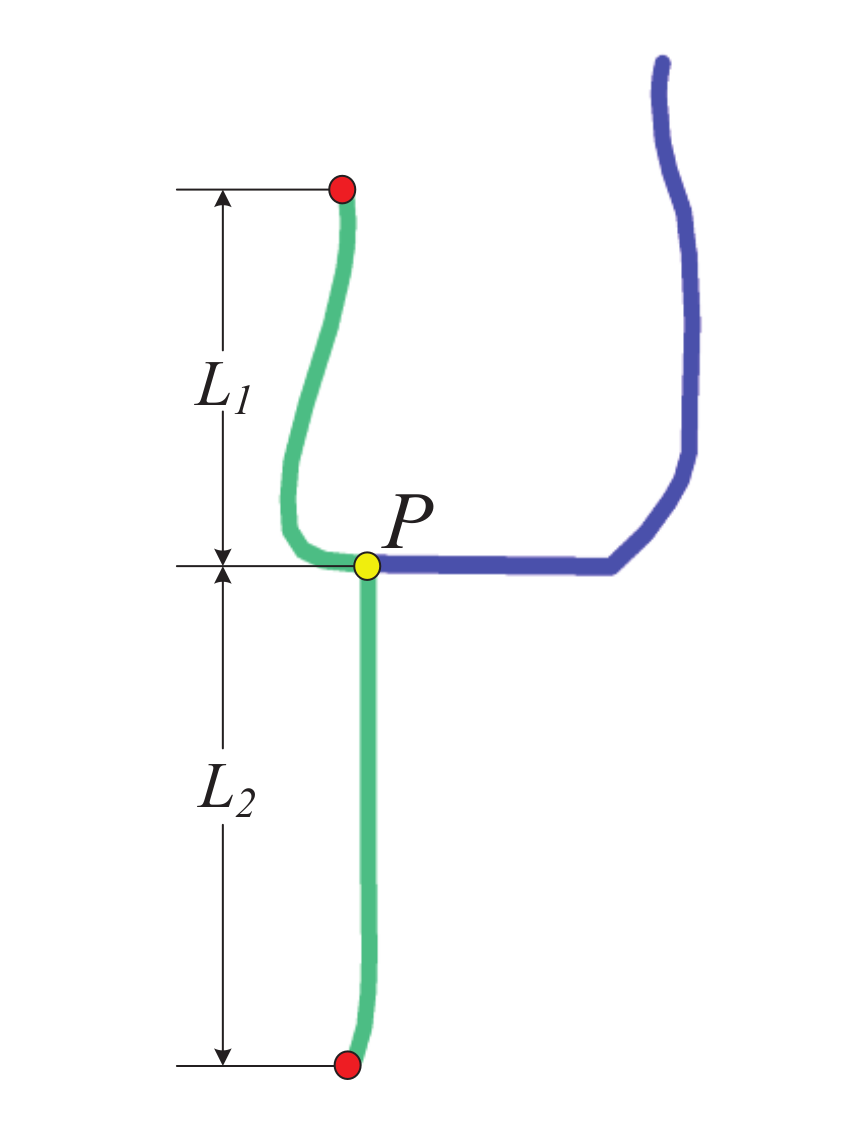
- The lengths of two parts of a road separated by P are computed for both the sketch and OSM aspects to obtain , , , and ;
- The distance between and is compared to obtain in terms of the . If is smaller than or equal to , the composite roads from a sketch and OSM are considered similar, as expressed in (12) and (13):where represents the similarity between two composite roads from the sketch and OSM, in terms of the , and is the threshold defined to compare the similarity in terms of the .
3.3.5. Computation of Similarity between Composite Roads
3.4. Characteristics and Matching Approach for Road Scenes
3.4.1. Second Matching Priority
3.4.2. Frequency of a Matched Road
3.4.3. Intersection Order of Roads along One Main Road
3.4.4. Topological Relationship between Roads without Matching Priorities
3.4.5. Computation of Similarity between Road Scenes
4. Results and Discussion
4.1. Extracting Main Roads
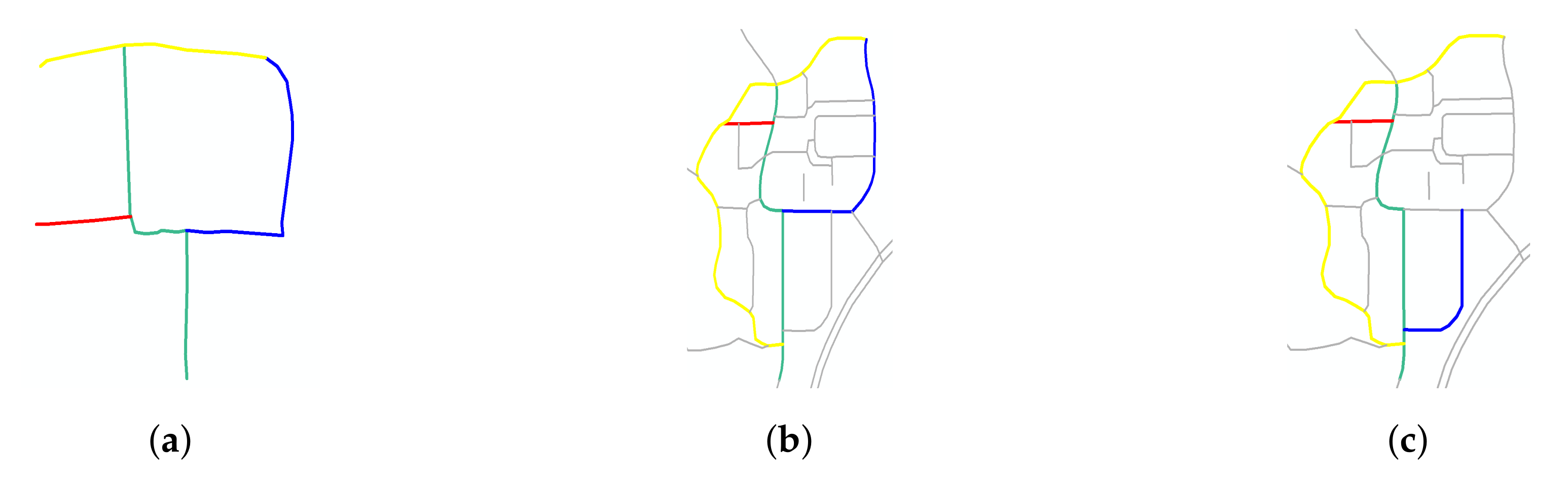
- R2 and R19 were most frequently extracted as the main roads. These roads are consistent with the main roads in OSM, as shown in Figure 16d. The same ID was assigned to the same roads in each sketch to facilitate the analysis.
- The number of main roads extracted from each sketch was different, as shown in the lower part of the second column in Table 4. The maximum number was 6 (S5), and the minimum number was 2 (S7); however, almost half the roads in each sketch were extracted as the main roads.
- In sketches S3, S4, and S7, all the roads were extracted as the main roads. In S3, the and values were the same for R2 and R19 and for R0 and R21. In S4, all the roads except for R19 had the same and . In S7, only two roads were drawn.
- In S5, R0, R1, R2, R3, R6, and R19 were selected as the main roads as they had the same values of and . In S9, although R1, R2, R3, R6, and R15 had similar values, R1 was not chosen as a main road owing to its lower . This aspect also holds for R0 and R16 in S8.
4.2. Road Scene Matching
- Each row in Table 5 shows the main roads extracted from each sketch, the matching parameters, and the matching results from OSM.
- The second column lists the main roads extracted from the sketches. In addition, the matching parameters are listed, including MaxMN, which represents the maximum number of roads from OSM involved in the matching of the road from one sketch with the first matching priority (, see Section 3.3.1), and ThresholdCon, which represents the threshold of the direction difference for comparing the circulation direction (, see Section 3.2.4) values.
- The remaining columns show the top-ranked matching results from the database based on the main roads extracted from each sketch. The similarity between each road scene from OSM and that from each sketch is also presented. The greater the similarity, the more similar are the roads between the sketch and OSM.
- matching of sketch S9 costs the shortest time, because the quantity of main roads extracted in sketch S9 is the least (3), and also two main sketched roads in scene S9 are curved. Note that there are only two sketched roads in sketch S7, so the time cost for matching of sketch S7 is just used for composite road matching.
- matching of sketch S6 costs the longest time. As it can be seen from Table 4, sketch S6 has only one curved main road, and the remaining main roads in sketch S6 are all nearly straight. Moreover, there were five roads extracted as main roads in sketch S6 for matching, which correspondingly increased the matching time.
4.3. Discussion
5. Conclusions and Future Work
- Comparison of the spatial relationship between roads and buildings, such as the orientation relationship, topological relationship, and ordering relationship. In particular, in some sketches, only a few roads are drawn, which makes it challenging to match these roads. Combining the sketched roads with buildings may improve the accuracy of matching.
- Development of a method to match the sketched places with discrete sketched roads. Discrete sketched roads are road segments generated during the process of digitization. Specifically, in this work, the roads in the sketch maps were digitized manually and the road integrity was guaranteed. In future work, the digitization will be conducted automatically, by decomposing the roads in the sketch maps into several line segments. Note that the shape of a discrete sketched road may be different from that of a completely sketched road, and the topological relationship between such roads may also be different. Therefore, in future work, we intend to realize matching between discrete sketched roads and complete roads in the metric map.
- Application of the proposed model to an unknown experimental area. In this study, the road similarity was examined considering roads in familiar places. An objective of future work is to study the characteristics and consistency of roads in unfamiliar scenes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| VGI | Volunteer Geographic Information |
| GIS | Geographic Information System |
| SQbS | Spatial-Query-by-Sketch |
| SSQbS | Shape-based Spatial-Query-by-Sketch |
| DCE | Discrete Curve Evolution |
| QSD | Qualitative Shape Description |
| DC | Degree Centrality |
| BC | Betweenness Centrality |
| CC | Closeness Centrality |
| OSM | OpenStreetMap |
| SD | Shape Distance |
| NCTP | Number of Critical Turning Points |
| CD | Circulation Direction |
| FMP | First Matching Priority |
| TR | Topological Relationship |
| OD | Order of Appearance of connected roads along one intersection |
| RPI | Relative Positions of Intersections |
| SMP | Second Matching Priority |
| FMR | Frequency of a Matched Road |
| IO | Intersection Order |
| TRMP | Topological Relationship between roads without Matching Priorities |
References
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Guo, D. Geospatial Analysis Based on Spatial Scene Similarity; China Science Publishing & Media Ltd. (CSPM): Beijing, China, 2016. [Google Scholar]
- Tolman, E.C. Cognitive maps in rats and men. Psychol. Rev. 1948, 55, 189. [Google Scholar] [CrossRef] [PubMed]
- Freksa, C.; Moratz, R.; Barkowsky, T. Schematic maps for robot navigation. In Spatial Cognition II; Springer: Berlin/Heidelberg, Germany, 2000; pp. 100–114. [Google Scholar] [CrossRef]
- Egenhofer, M.J. Spatial-query-by-sketch. In Proceedings of the 1996 IEEE Symposium on Visual Languages, Boulder, CO, USA, 3–6 September 1996; pp. 60–67. [Google Scholar] [CrossRef]
- Egenhofer, M.J. Query processing in spatial-query-by-sketch. J. Vis. Lang. Comput. 1997, 8, 403–424. [Google Scholar] [CrossRef]
- Schwering, A.; Wang, J.; Chipofya, M.; Jan, S.; Li, R.; Broelemann, K. SketchMapia: Qualitative representations for the alignment of sketch and metric maps. Spat. Cogn. Comput. 2014, 14, 220–254. [Google Scholar] [CrossRef]
- Chipofya, M.C.; Schultz, C.; Schwering, A. A metaheuristic approach for efficient and effective sketch-to-metric map alignment. Int. J. Geogr. Inf. Sci. 2016, 30, 405–425. [Google Scholar] [CrossRef]
- Jan, S.; Schwering, A.; Schultz, C.; Chipofya, M. Cognitively plausible representations for the alignment of sketch and geo-referenced maps. J. Spat. Inf. Sci. 2017, 2017, 31–59. [Google Scholar] [CrossRef]
- Jia Wang, R.L. An Empirical Study on Pertinent Aspects of Sketch Maps for Navigation. Int. J. Cogn. Inform. Nat. Intell. 2013, 7, 26–43. [Google Scholar] [CrossRef]
- Wang, F.; Kang, L.; Li, Y. Sketch-based 3D shape retrieval using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1875–1883. [Google Scholar] [CrossRef]
- Dutelle, A.W. An Introduction to Crime Scene Investigation; Jones and Bartlett Learning: Burlington, MA, USA, 2016. [Google Scholar]
- Blaser, A.D. Sketching Spatial Queries. Ph.D. Thesis, Spatial Information Science and Engineering, University of Maine, Orono, ME, USA, 2000. [Google Scholar]
- Davies, C.; Peebles, D. Spaces or scenes: Map-based orientation in urban environments. Spat. Cogn. Comput. 2010, 10, 135–156. [Google Scholar] [CrossRef]
- Meilinger, T.; Riecke, B.E.; Bülthoff, H.H. Local and global reference frames for environmental spaces. Q. J. Exp. Psychol. 2014, 67, 542–569. [Google Scholar] [CrossRef]
- Gergelóvá, M.B.; Kuzevičová, Ž.; Labant, S.; Gašinec, J.; Kuzevič, Š.; Unucka, J.; Liptai, P. Evaluation of Selected Sub-Elements of Spatial Data Quality on 3D Flood Event Modeling: Case Study of Prešov City. Appl. Sci. 2020, 10, 820. [Google Scholar] [CrossRef]
- Ślusarski, M.; Jurkiewicz, M. Visualisation of Spatial Data Uncertainty. A Case Study of a Database of Topographic Objects. Int. J. Geo-Inf. 2020, 9, 16. [Google Scholar] [CrossRef]
- Hátlová, K.; Hanus, M. A Systematic Review into Factors Influencing Sketch Map Quality. Int. J. Geo-Inf. 2020, 9, 271. [Google Scholar] [CrossRef]
- Nedas, K.A.; Egenhofer, M.J. Spatial-scene similarity queries. Trans. GIS 2008, 12, 661–681. [Google Scholar] [CrossRef]
- Kurata, Y.; Egenhofer, M.J. The head-body-tail intersection for spatial relations between directed line segments. In International Conference on Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 269–286. [Google Scholar] [CrossRef]
- Kurata, Y. The 9+-intersection: A universal framework for modeling topological relations. In International Conference on Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2008; pp. 181–198. [Google Scholar] [CrossRef]
- Nedas, K.A.; Egenhofer, M.J.; Wilmsen, D. Metric details of topological line-line relations. Int. J. Geogr. Inf. Sci. 2007, 21, 21–48. [Google Scholar] [CrossRef]
- Lewis, J.A.; Egenhofer, M.J. Oriented regions for linearly conceptualized features. In International Conference on Geographic Information Science; Springer: Cham, Switzerland, 2014; pp. 333–348. [Google Scholar] [CrossRef]
- Tang, M.; Falomir, Z.; Freksa, C.; Sheng, Y.; Lyu, H. Extracting invariant characteristics of sketch maps: Towards Place Query-by-Sketch. Trans. GIS 2020, 24, 903–943. [Google Scholar] [CrossRef]
- Timpf, S.; Volta, G.; Pollock, D.; Frank, A.; Egenhofer, M. A Conceptual Model of Wayfinding Using Multiple Levels of Abstraction. In Theories and Methods of Spatio-Temporal Reasoning in Geographic Space; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1992; Volume 639. [Google Scholar] [CrossRef]
- Gottfried, B. Shape from Positional-Contrast: Characterising Sketches with Qualitative Line Arrangements; Deutscher Universitäts-Verlag: Wiesbaden, Germany, 2007. [Google Scholar] [CrossRef]
- Gottfried, B. Global Feature Schemes for Qualitative Shape Descriptions. In IJCAI-05 Workshop Notes on Spatial and Temporal Reasoning; 2005; Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.73.634&rep=rep1&type=pdf (accessed on 26 October 2020).
- Gottfried, B. Querying for silhouettes by qualitative feature schemes. In Proceedings of the 2nd International Conference on Document Image Analysis for Libraries (DIAL’06), Lyon, France, 27–28 April 2006; pp. 281–290. [Google Scholar] [CrossRef]
- Gottfried, B. Qualitative similarity measures-the case of two-dimensional outlines. Comput. Vis. Image Underst. 2008, 110, 117–133. [Google Scholar] [CrossRef]
- Bai, X.; Yang, X.; Latecki, L.J. Detection and recognition of contour parts based on shape similarity. Pattern Recognit. 2008, 41, 2189–2199. [Google Scholar] [CrossRef]
- Latecki, L.J.; Lakämper, R. Convexity rule for shape decomposition based on discrete contour evolution. Comput. Vis. Image Underst. 1999, 73, 441–454. [Google Scholar] [CrossRef]
- Falomir, Z.; Gonzalez-Abril, L.; Museros, L.; Ortega, J.A. Measures of similarity between objects based on qualitative shape descriptions. Spat. Cogn. Comput. 2013, 13, 181–218. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, H.; Wang, C.; Li, Z.; Zhang, L.; Zhang, L. Mindfinder: Interactive sketch-based image search on millions of images. In Proceedings of the 18th ACM International Conference on Multimedia, Firenze, Italy, 25–29 October 2010; ACM: New York, NY, USA, 2010; pp. 1605–1608. [Google Scholar] [CrossRef]
- Xiao, C.; Wang, C.; Zhang, L.; Zhang, L. Sketch-based image retrieval via shape words. In Proceedings of the 5th ACM on International Conference on Multimedia Retrieval, Shanghai, China, 23–26 June 2015; ACM: New York, NY, USA, 2015; pp. 571–574. [Google Scholar] [CrossRef]
- Borgefors, G. Hierarchical chamfer matching: A parametric edge matching algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 849–865. [Google Scholar] [CrossRef]
- Zhang, M. Methods and Implementations of Road-Network Matching. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2009. [Google Scholar]
- Touya, G.; Coupé, A.; Jollec, J.L.; Dorie, O.; Fuchs, F. Conflation optimized by least squares to maintain geographic shapes. ISPRS Int. J. Geo-Inf. 2013, 2, 621–644. [Google Scholar] [CrossRef]
- Harrie, L.E. The constraint method for solving spatial conflicts in cartographic generalization. Cartogr. Geogr. Inf. Sci. 1999, 26, 55–69. [Google Scholar] [CrossRef]
- Sester, M. Optimization approaches for generalization and data abstraction. Int. J. Geogr. Inf. Sci. 2005, 19, 871–897. [Google Scholar] [CrossRef]
- Tong, X.; Liang, D.; Jin, Y. A linear road object matching method for conflation based on optimization and logistic regression. Int. J. Geogr. Inf. Sci. 2014, 28, 824–846. [Google Scholar] [CrossRef]
- Kim, I.H.; Feng, C.C.; Wang, Y.C. A simplified linear feature matching method using decision tree analysis, weighted linear directional mean, and topological relationships. Int. J. Geogr. Inf. Sci. 2017, 31, 1042–1060. [Google Scholar] [CrossRef]
- Ali Abbaspour, R.; Chehreghan, A.; Karimi, A. Assessing the efficiency of shape-based functions and descriptors in multi-scale matching of linear objects. Geocarto Int. 2018, 33, 879–892. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. A structural approach to the model generalization of an urban street network. GeoInformatica 2004, 8, 157–171. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Vatavu, R.D.; Anthony, L.; Wobbrock, J.O. Gestures as point clouds: A $P recognizer for user interface prototypes. In Proceedings of the 14th ACM international conference on Multimodal interaction, Santa Monica, CA, USA, 22–26 October 2012; ACM: New York, NY, USA, 2012; pp. 273–280. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Egenhofer, M.J.; Herring, J.R. Categorizing Binary Topological Relations between Regions, Lines, and Points in Geographic Databases; Technical Report; Department of Surveying Engineering, University of Maine: Orono, ME, USA, 1990. [Google Scholar]
- Herring, J. The mathematical modeling of spatial and non-spatial information in geographic information systems. In Cognitive and Linguistic Aspects of Geographic Space; Springer: Dordrecht, The Netherlands, 1991; pp. 313–350. [Google Scholar] [CrossRef]
- Eden, C. On the nature of cognitive maps. J. Manag. Stud. 1992, 29, 261–265. [Google Scholar] [CrossRef]

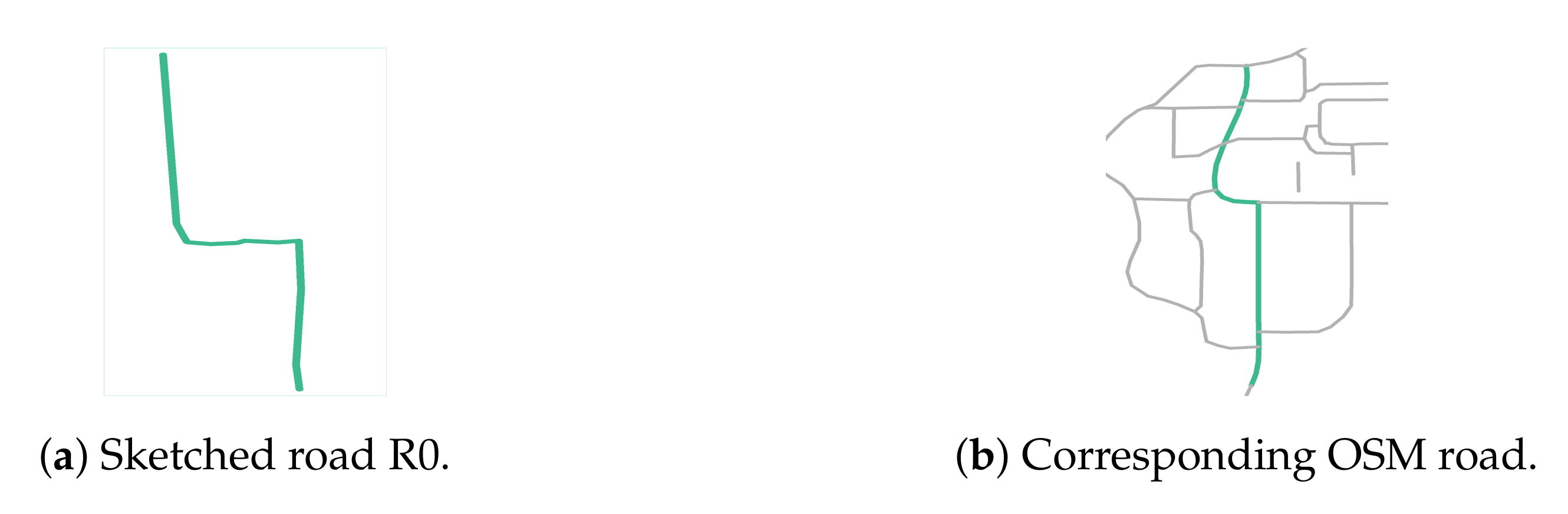






| Road ID | R1 | R2 | R3 | R4 | R5 |
|---|---|---|---|---|---|
| btw the sketched road (R0) and roads from OSM | 6.94 | 7.58 | 4.21 | 4.74 | 5.00 |
| Road from a Sketch | Roads from OSM | |||||
|---|---|---|---|---|---|---|
| Road ID | R0 | R1 | R2 | R3 | R4 | R5 |
| 2 | 0 | 1 | 2 | 4 | 3 | |
| - | No | No | Yes | Yes | Yes | |
| A Road in a Sketch | Roads from OSM | |||||
|---|---|---|---|---|---|---|
| Road ID | R0 | R1 | R2 | R3 | R4 | R5 |
| l, r | - | r | l,r | l,r | r,l,r | |
| - | No | No | Yes | Yes | Yes | |
| Roads in each sketch | 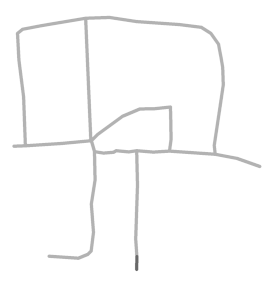 S1 | 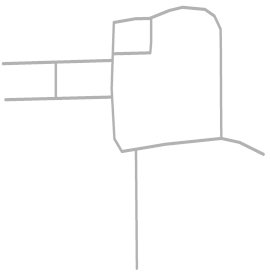 S2 | 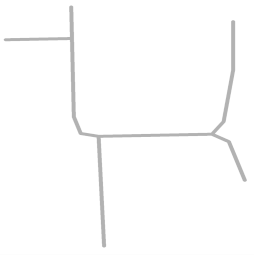 S3 |  S4 |  S5 | 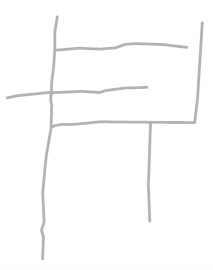 S6 | 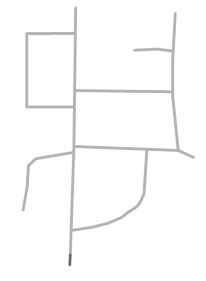 S8 |  S9 |
| DC and BC |  Roads extracted: 4/10 | 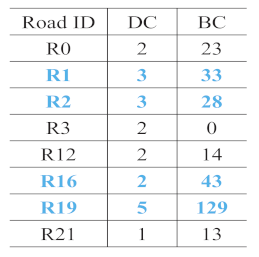 Roads extracted: 4/8 | 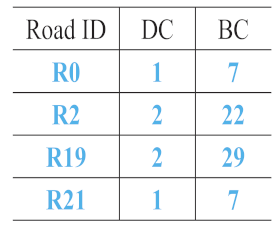 Roads extracted: 4/4 | 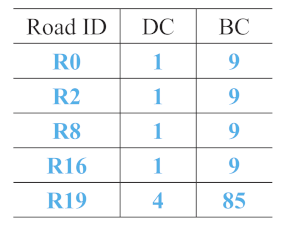 Roads extracted: 5/5 | 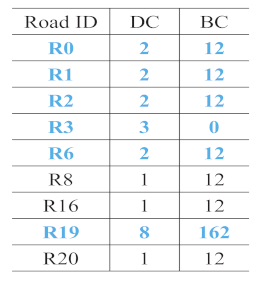 Roads extracted: 6/9 | 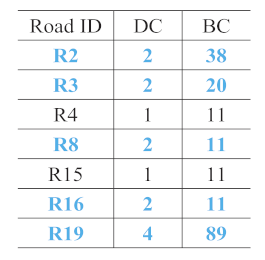 Roads extracted: 5/7 | 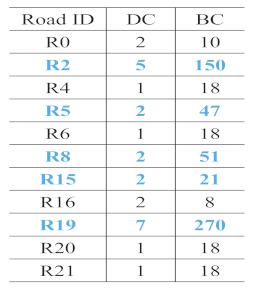 Roads extracted: 5/10 | 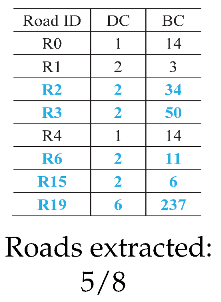 Roads extracted: 5/8 |
| Main roads (in color) Extracted | 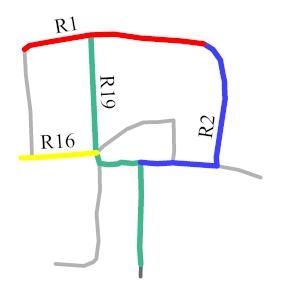 |  | 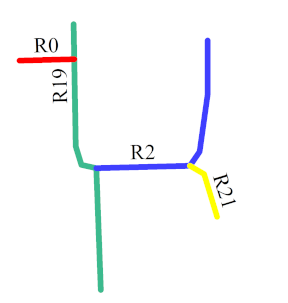 | 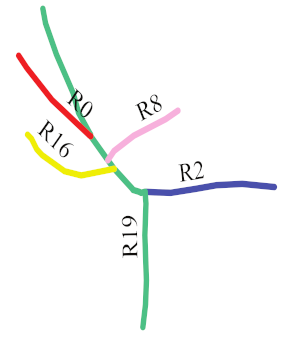 | 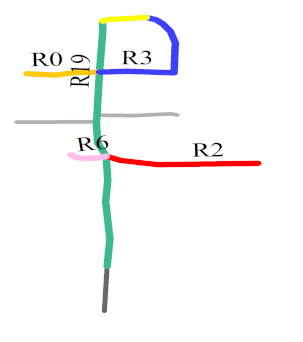 | 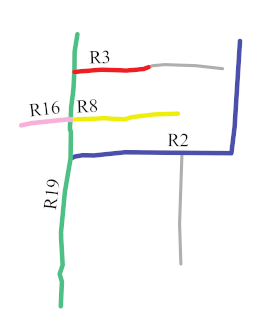 |  | 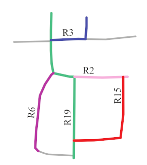 |
| Sketch ID | Main Roads Extracted and Matching Parameters | Top Three Matching Results from the Roads of Nanjing, China, in OSM and Their Similarities | ||
|---|---|---|---|---|
| S1 | 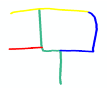 MaxMN = 30 ThresholdCon = 36 |  146.899 | 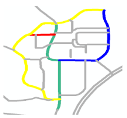 145.066 | 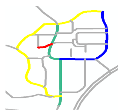 144.987 |
| S2 | 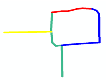 MaxMN = 30 ThresholdCon = 36 | 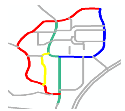 141.254 |  141.216 | 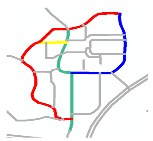 134.499 |
| S3 | 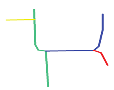 MaxMN = 10 ThresholdCon = 37 | 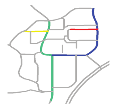 143.231 |  143.039 | 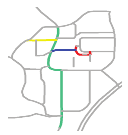 141.137 |
| S4 |  MaxMN = 50 ThresholdCon = 20 | 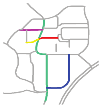 152.982 |  152.933 |  152.751 |
| S5 |  MaxMN = 50 ThresholdCon = 16 | 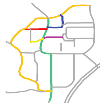 201.744 | 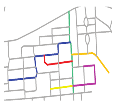 195.268 | 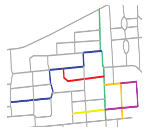 195.061 |
| S5 |  MaxMN = 50 ThresholdCon = 16 |  166.823 | 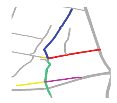 153.623 | 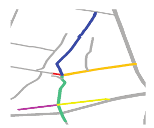 140.423 |
| S6 |  MaxMN = 70 ThresholdCon = 8 |  177.137 | 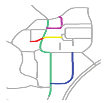 172.321 | 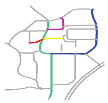 172.296 |
| S7 |  MaxMN = 200 ThresholdCon = 32 |  82.505 |  82.479 |  76.577 |
| S8 |  MaxMN = 10 ThresholdCon = 15 | 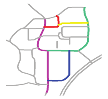 165.756 |  145.922 | 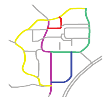 145.640 |
| S9 |  MaxMN = 5 ThresholdCon = 22 | 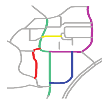 160.303 | 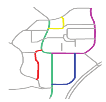 153.783 | 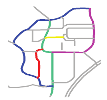 153.652 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Falomir, Z.; Sheng, Y. A Multilevel Road Alignment Model for Spatial-Query-by-Sketch. Appl. Sci. 2020, 10, 7685. https://doi.org/10.3390/app10217685
Tang M, Falomir Z, Sheng Y. A Multilevel Road Alignment Model for Spatial-Query-by-Sketch. Applied Sciences. 2020; 10(21):7685. https://doi.org/10.3390/app10217685
Chicago/Turabian StyleTang, Ming, Zoe Falomir, and Yehua Sheng. 2020. "A Multilevel Road Alignment Model for Spatial-Query-by-Sketch" Applied Sciences 10, no. 21: 7685. https://doi.org/10.3390/app10217685
APA StyleTang, M., Falomir, Z., & Sheng, Y. (2020). A Multilevel Road Alignment Model for Spatial-Query-by-Sketch. Applied Sciences, 10(21), 7685. https://doi.org/10.3390/app10217685






