Practical Security Bounds against Trojan Horse Attacks in Continuous-Variable Quantum Key Distribution
Abstract
1. Introduction
2. Theoratical Description
3. Trojan Horsse Attacks
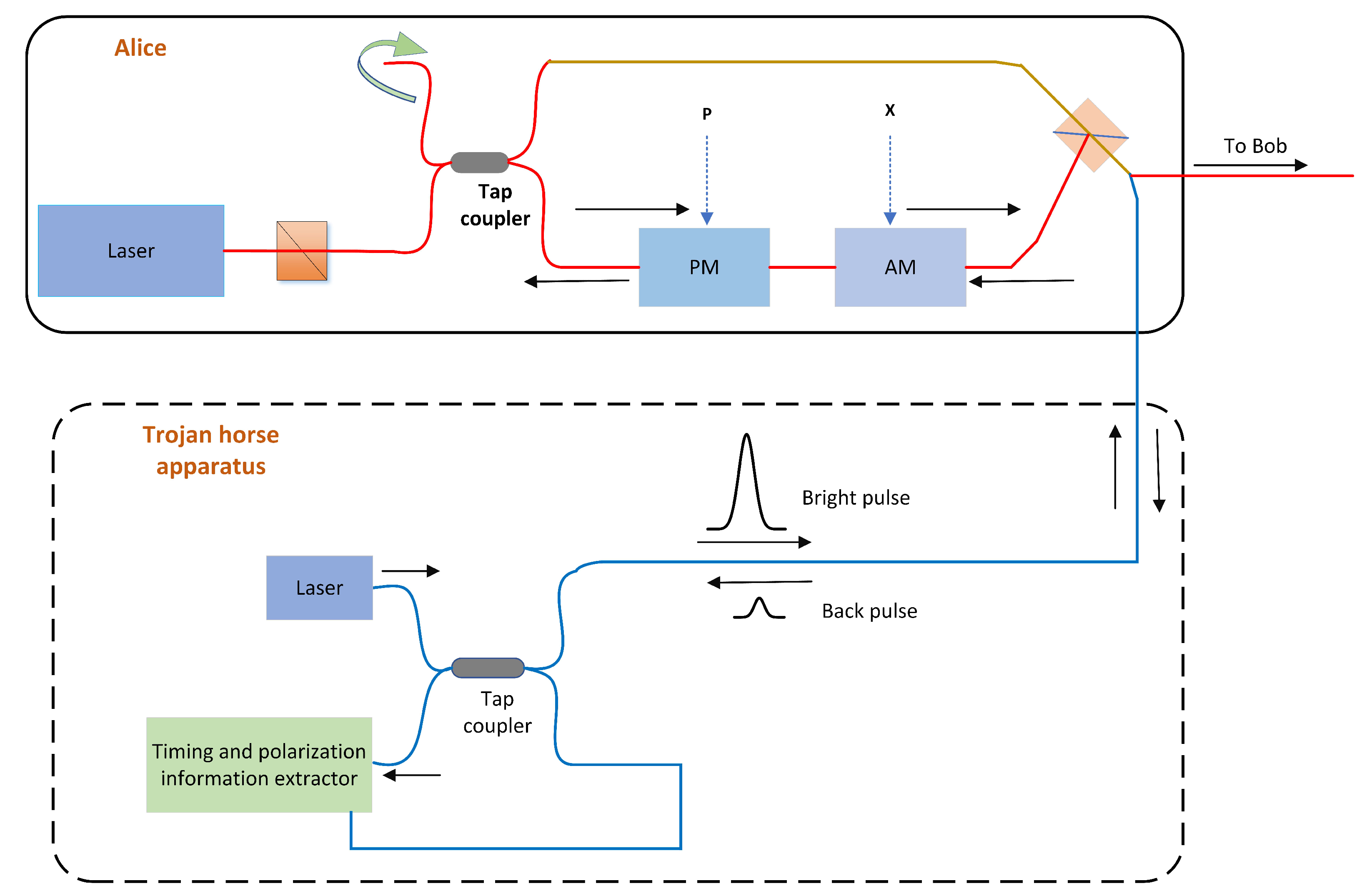
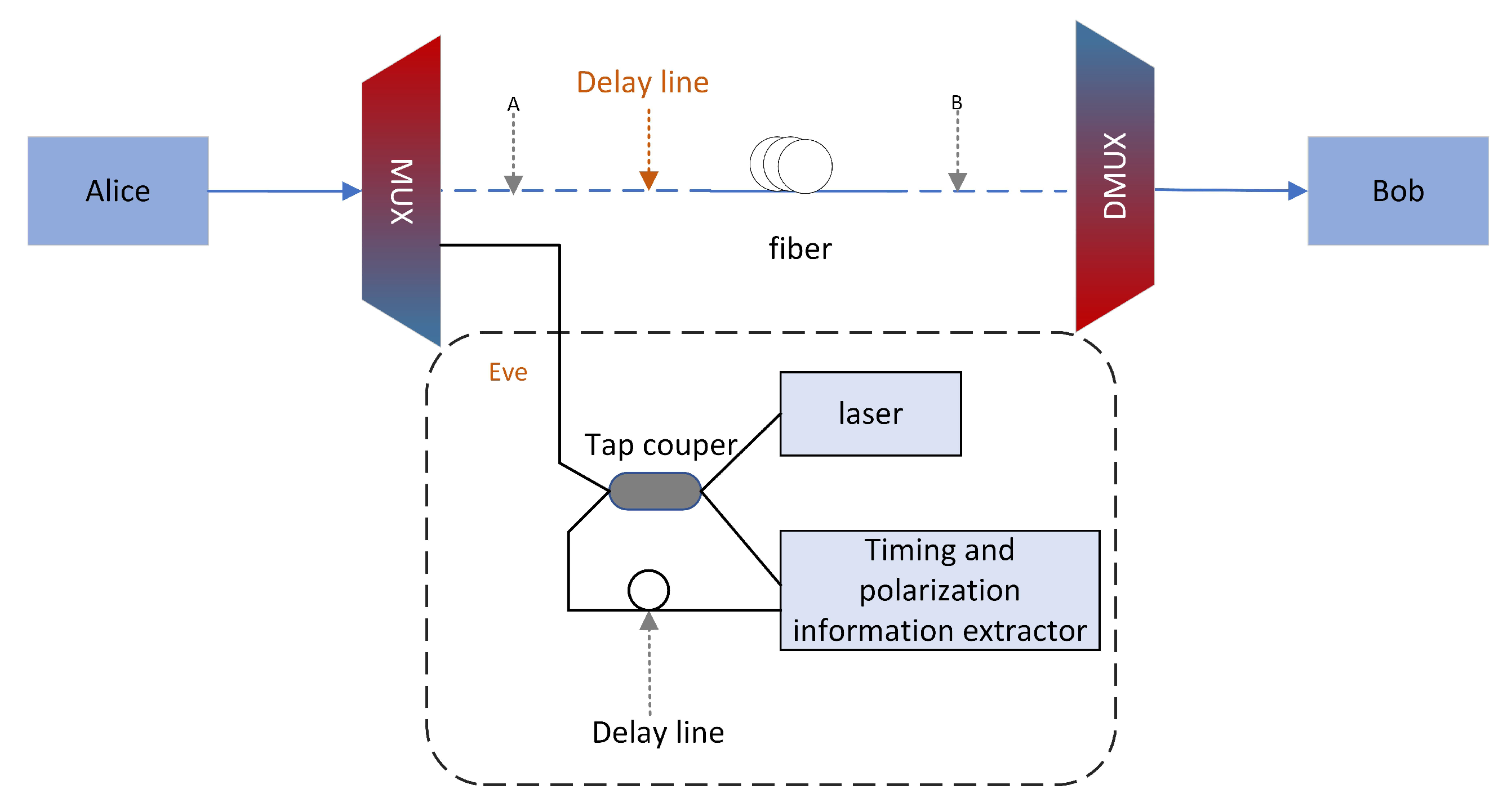
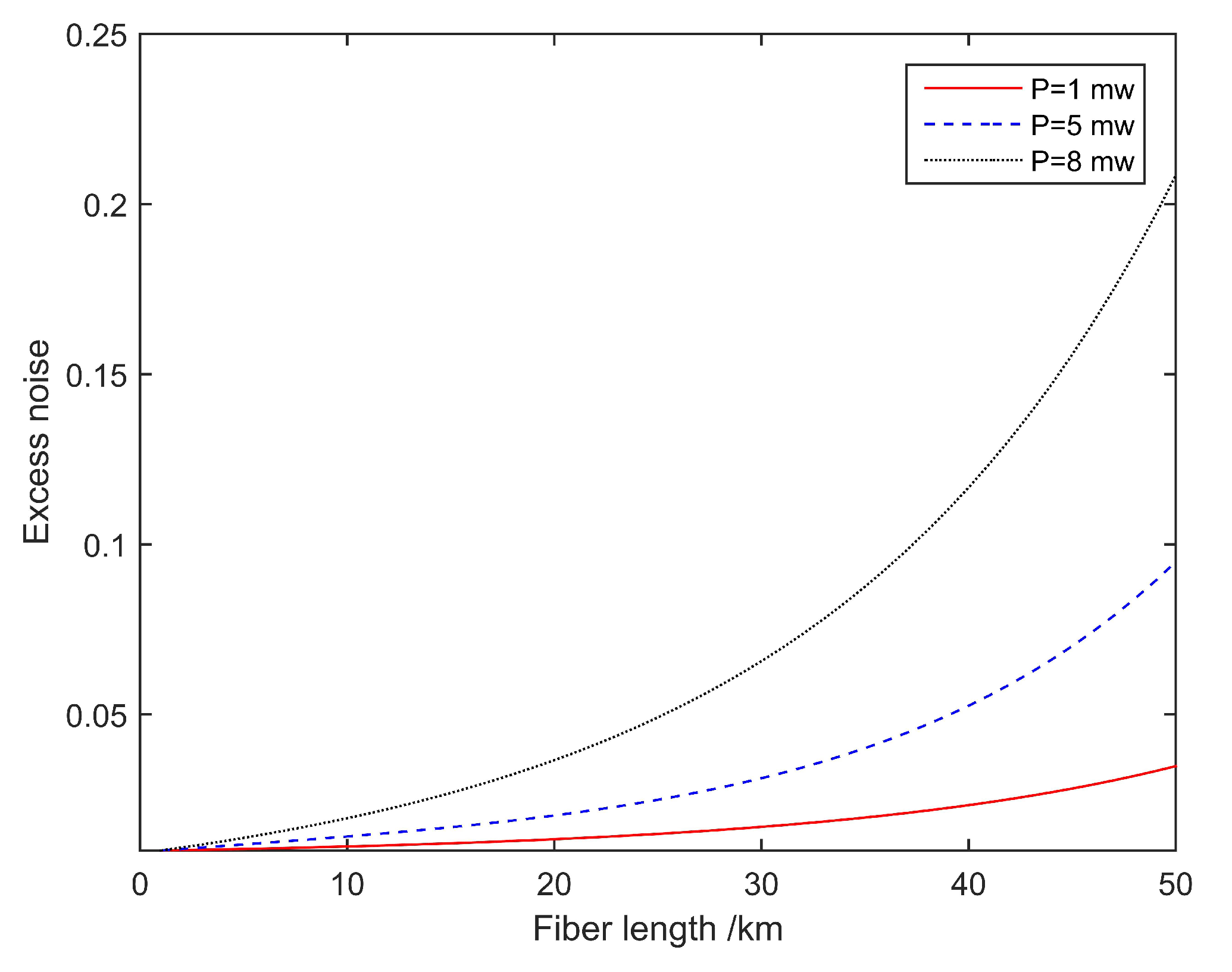
3.1. Attacks at the Same Wavelength as the Original Pulses
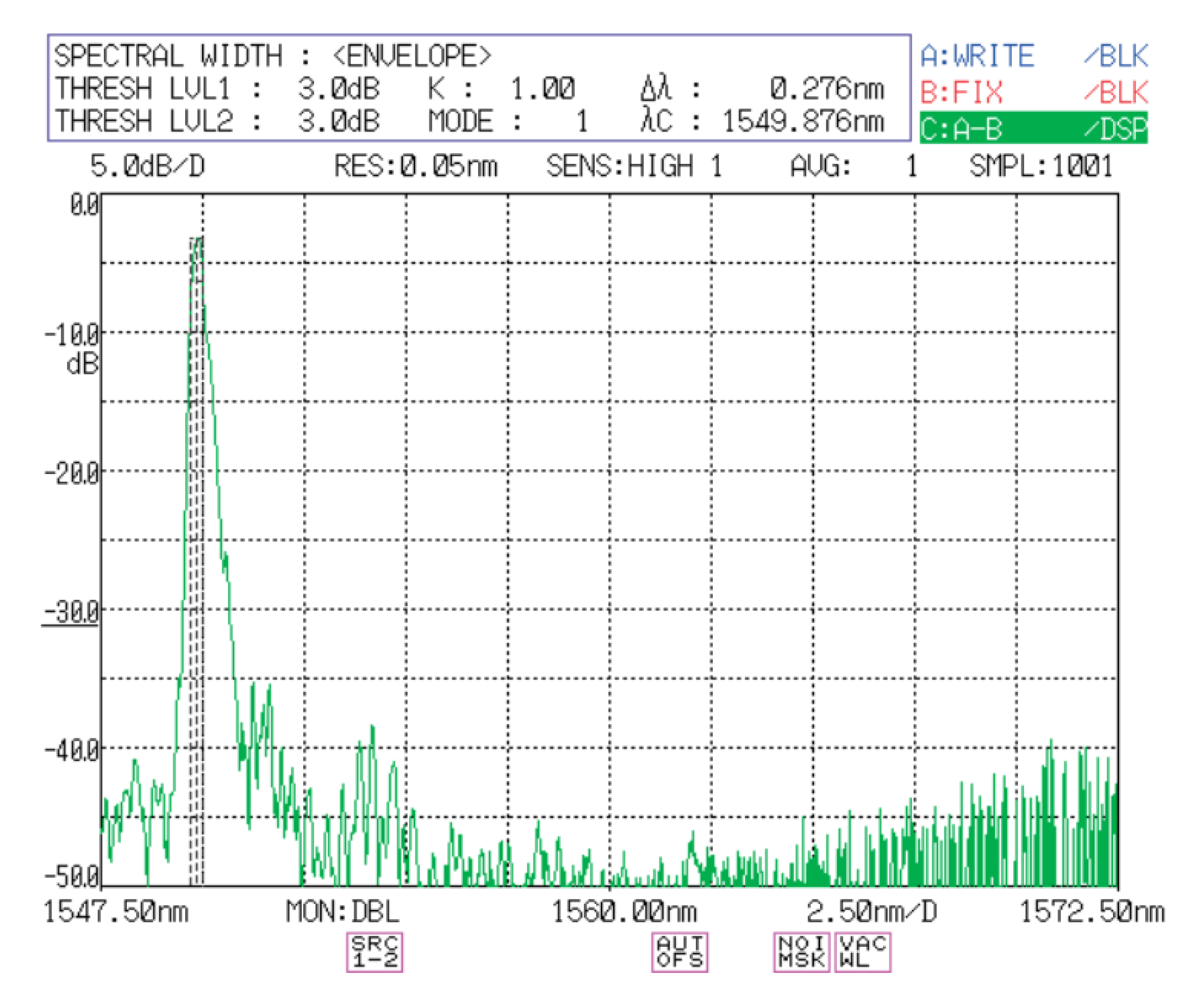
3.2. Attacks with Different Wavelengths from the Original Pulses
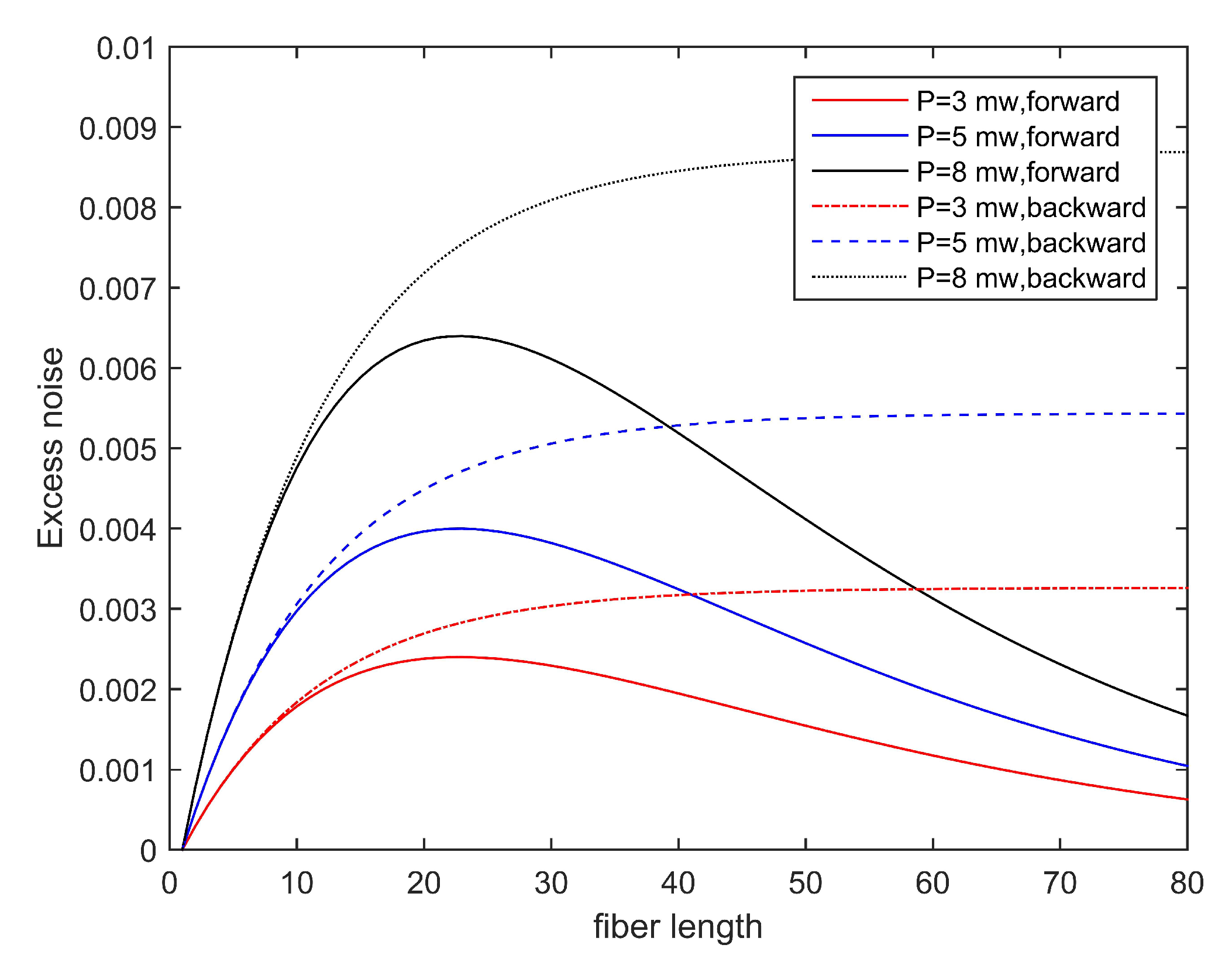
4. Bounds on Excess Noise
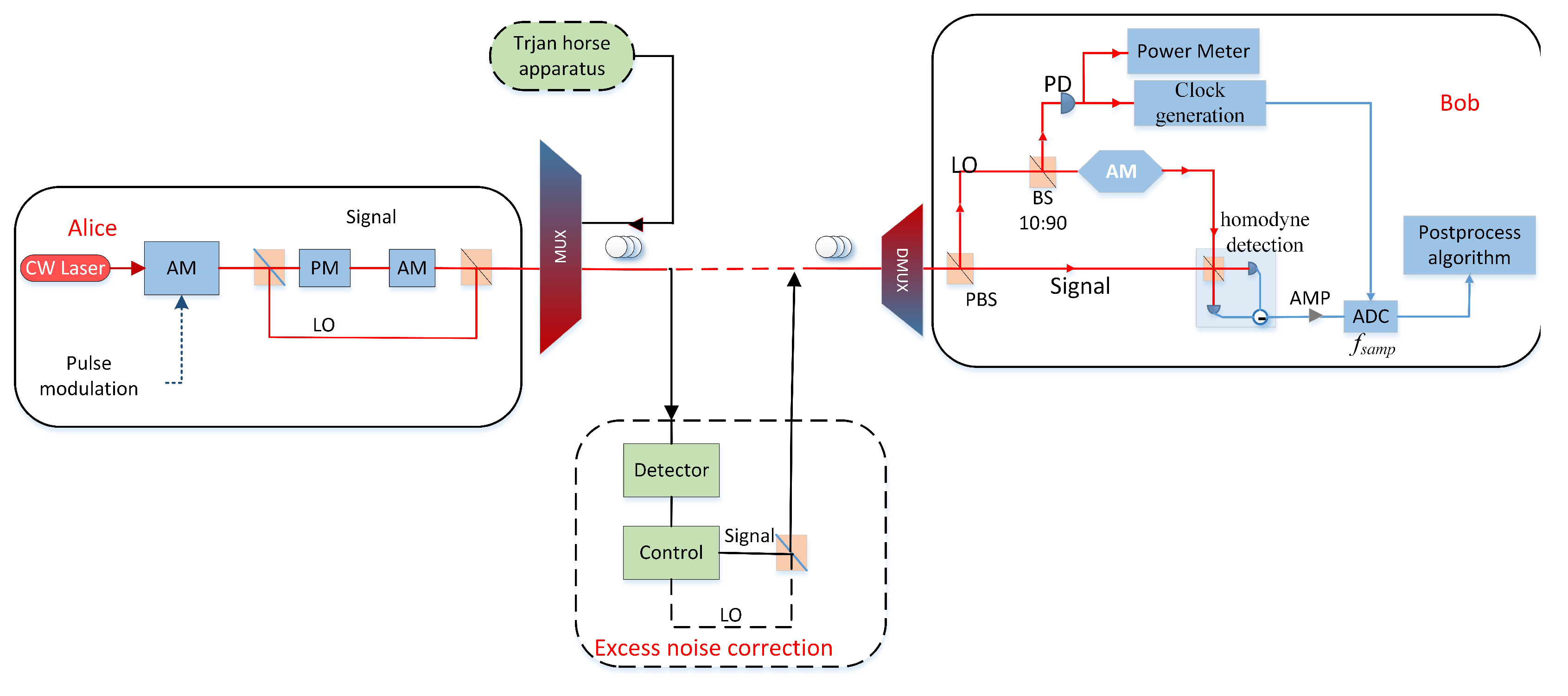
4.1. Excess Noise Correction
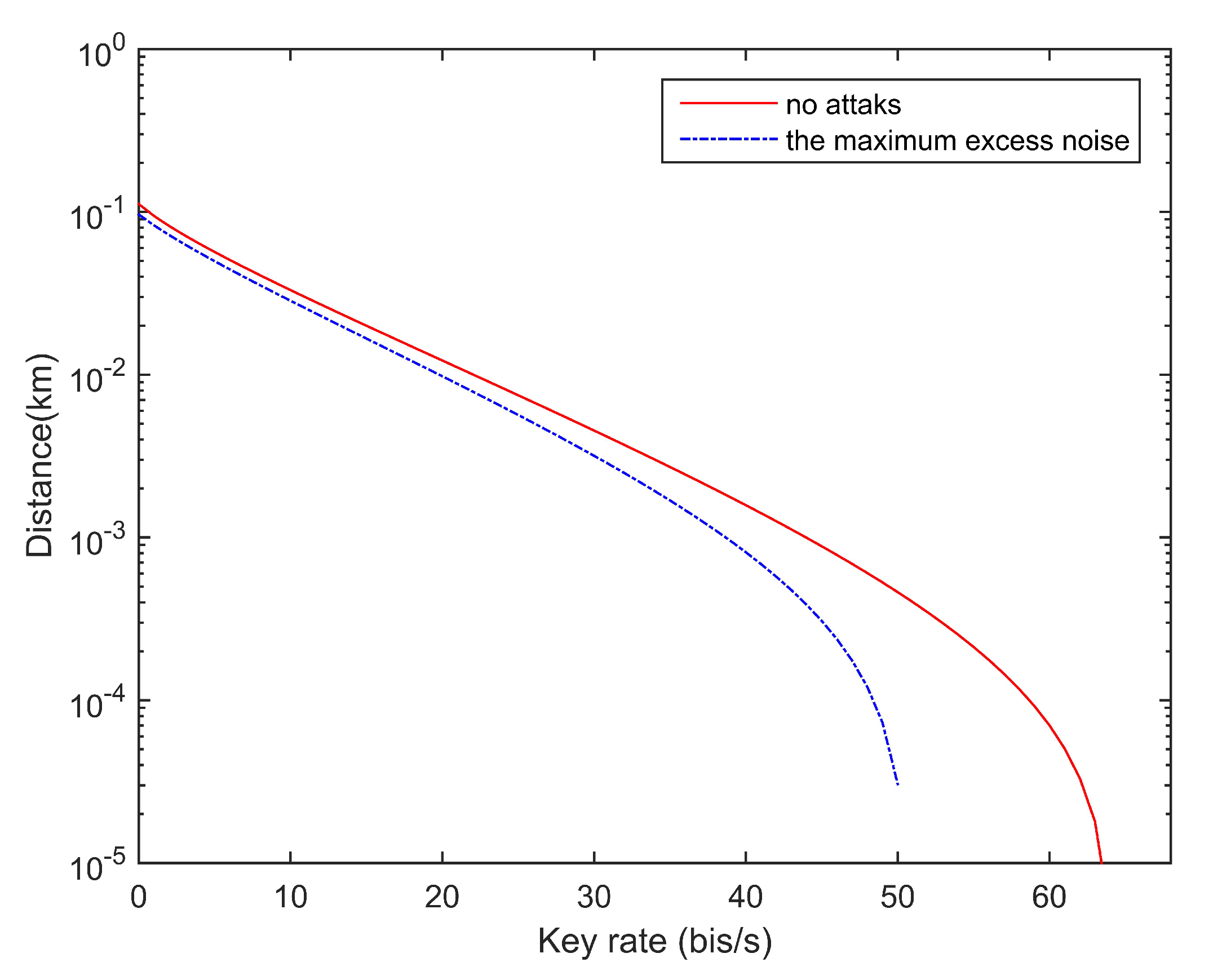
4.2. Threshold of Excess Noise
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CV-QKD | Continuous-variable quantum key distribution |
| QKD | Quantum key distribution |
| LO | Local oscillator |
| BS | Beam splitter |
| GMCS | Gaussian modulation coherent state |
| OTDR | Optical time-domain reflectometry |
| WDM | Wavelength division multiplexing |
| DEMUX | Demultiplxer |
| SARA | Spontaneous anti-Stokes Raman scattering |
| FM | Faraday mirrors |
| PBS | Polarizing beam splitter |
| AM | Amplitude modulation |
Appendix A
References
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Qi, B.; Qian, L.; Lo, H.K. A brief introduction of quantum cryptography for engineers. arXiv 2010, arXiv:1002.1237. [Google Scholar]
- Zeng, G. Quantum Private Communication, 1st ed.; Springer Publishing Company, Incorporated: Berlin, Germany, 2010. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Wehner, S.; Winter, A. Entropic uncertainty relations—A survey. New J. Phys 2010, 12, 025009. [Google Scholar] [CrossRef]
- Eleni, D.; Anthony, L. Distributing Secret Keys with Quantum Continuous Variables: Principle, Security and Implementations. Entropy 2015, 17, 6072–6092. [Google Scholar]
- Gottesman, D.; Preskill, J. Secure quantum key distribution using squeezed states. Phys. Rev. A 2001, 63, 022309. [Google Scholar] [CrossRef]
- Vladyslav, U.; Radim, F. Trusted Noise in Continuous-Variable Quantum Key Distribution: A Threat and a Defense. Entropy 2016, 18, 20. [Google Scholar]
- Grosshans, F.; Cerf, N.J. Continuous-variable quantum cryptography is secure against non-gaussian attacks. Phys. Rev. Lett. 2004, 92, 047905. [Google Scholar] [CrossRef]
- Renner, R.; Cirac, J.I. De Finetti Representation Theorem for Infinite-Dimensional Quantum Systems and Applications to Quantum Cryptography. Phys. Rev. Lett. 2009, 102, 110504. [Google Scholar] [CrossRef]
- García-Patrón, R.; Cerf, N.J. Unconditional Optimality of Gaussian Attacks against Continuous-Variable Quantum Key Distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar] [CrossRef] [PubMed]
- Navascués, M.; Grosshans, F.; Acín, A. Optimality of Gaussian Attacks in Continuous-Variable Quantum Cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar] [CrossRef] [PubMed]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Tualle-Brouri, R.; Grangier, P. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. B-AT. Mol. Opt. 2009, 42, 114014. [Google Scholar] [CrossRef]
- Leverrier, A.; Grosshans, F.; Grangier, P. Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 2010, 81, 36–43. [Google Scholar] [CrossRef]
- Leverrier, A. Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 2015, 114, 070501. [Google Scholar] [CrossRef] [PubMed]
- Ikuta, T.; Inoue, K. Intensity modulation and direct detection quantum key distribution based on quantum noise. New J. Phys. 2016, 18, 013018. [Google Scholar] [CrossRef]
- Lodewyck, J.; Debuisschert, T.; García-Patrón, R.; Tualle-Brouri, R.; Cerf, N.J.; Grangier, P. Experimental Implementation of Non-Gaussian Attacks on a Continuous-Variable Quantum-Key-Distribution System. Phys. Rev. Lett. 2007, 98, 030503. [Google Scholar] [CrossRef]
- Huang, P.; Huang, J.; Wang, T.; Li, H.; Huang, D.; Zeng, G. Robust continuous-variable quantum key distribution against practical attacks. Phys. Rev. A 2017, 95, 052302. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, Y.; Huang, W.; Qin, H.; Huang, D.; Guo, Y. Hidden-Markov-model-based calibration-attack recognition for continuous-variable quantum key distribution. Phys. Rev. A 2020, 101, 062320. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef]
- Qin, H.; Kumar, R.; Alléaume, R. Quantum hacking: Saturation attack on practical continuous-variable quantum key distribution. Phys. Rev. A 2016, 94, 012325. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Wavelength attack on practical continuous-variable quantum-key-distribution system with a heterodyne protocol. Phys. Rev. A 2013, 87, 052309. [Google Scholar] [CrossRef]
- Huang, J.Z.; Weedbrook, C.; Yin, Z.Q.; Wang, S.; Li, H.W.; Chen, W.; Guo, G.C.; Han, Z.F. Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 2013, 87, 062329. [Google Scholar] [CrossRef]
- Pljonkin, A.P. Vulnerability of the Synchronization Process in the Quantum Key Distribution System. Int. J. Cloud Appl. Comput. 2019, 9, 50–58. [Google Scholar] [CrossRef]
- Vakhitov, A.; Makarov, V.; Hjelme, D.R. Large pulse attack as a method of conventional optical eavesdropping in quantum cryptography. J. Mod. Opt. 2001, 48, 2023–2038. [Google Scholar] [CrossRef]
- Gisin, N.; Fasel, S.; Kraus, B.; Zbinden, H.; Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 2006, 73, 022320. [Google Scholar] [CrossRef]
- Lucamarini, M.; Choi, I.; Ward, M.B.; Dynes, J.F.; Shields, A.J. Practical Security Bounds Against the Trojan-Horse Attack in Quantum Key Distribution. Phys. Rev. X 2015, 5, 031030. [Google Scholar] [CrossRef]
- Jain, N.; Anisimova, E.; Khan, I.; Makarov, V.; Marquardt, C.; Leuchs, G. Trojan-horse attacks threaten the security of practical quantum cryptography. New J. Phys 2014, 16, 123030. [Google Scholar] [CrossRef]
- Jain, N.; Stiller, B.; Khan, I.; Makarov, V.; Marquardt, C.; Leuchs, G. Risk Analysis of Trojan-Horse Attacks on Practical Quantum Key Distribution Systems. IEEE J. Sel. Top. Quant. 2015, 21, 168–177. [Google Scholar] [CrossRef]
- Sajeed, S.; Radchenko, I.; Kaiser, S.; Bourgoin, J.P.; Pappa, A.; Monat, L.; Legré, M.; Makarov, V. Attacks exploiting deviation of mean photon number in quantum key distribution and coin tossing. Phys. Rev. A 2015, 91, 032326. [Google Scholar] [CrossRef]
- Khan, I.; Jain, N.; Stiller, B.; Jouguet, P.; Kunz-Jacques, S.; Diamanti, E.; Marquardt, C.; Leuchs, G. Trojan horse attacks on practical continuous-variables quantum key distribution systems. In Proceedings of the Conference on Quantum Cryptography (QCRYPT), Paris, France, 1–5 September 2014. [Google Scholar]
- Li, H.W.; Wang, S.; Huang, J.Z.; Chen, W.; Yin, Z.Q.; Li, F.Y.; Zhou, Z.; Liu, D.; Zhang, Y.; Guo, G.C.; et al. Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources. Phys. Rev. A 2011, 84, 062308. [Google Scholar] [CrossRef]
- Huang, J.Z.; Kunz-Jacques, S.; Jouguet, P.; Weedbrook, C.; Yin, Z.Q.; Wang, S.; Chen, W.; Guo, G.C.; Han, Z.F. Quantum hacking on quantum key distribution using homodyne detection. Phys. Rev. A 2014, 89, 032304. [Google Scholar] [CrossRef]
- Kunz-Jacques, S.; Jouguet, P. Robust shot-noise measurement for continuous-variable quantum key distribution. Phys. Rev. A 2015, 91, 022307. [Google Scholar] [CrossRef]
- Scarani, V.; Kurtsiefer, C. The black paper of quantum cryptography: Real implementation problems. Theor. Comput. Sci. 2014, 560, 27–32. [Google Scholar] [CrossRef]
- Wang, C.; Huang, P.; Huang, D.; Lin, D.; Zeng, G. Practical security of continuous-variable quantum key distribution with finite sampling bandwidth effects. Phys. Rev. A 2016, 93, 022315. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Huang, P.; Huang, D.; Wang, T.; Zeng, G. Practical continuous-variable quantum key distribution without finite sampling bandwidth effects. Opt. Express 2016, 24, 20481–20493. [Google Scholar] [CrossRef]
- Neumann, E.G. Single-Mode Fibers: Springer Series in Optical Sciences; Springer: Berlin, Germany, 1988. [Google Scholar]
- Wegmuller, M.; Scholder, F.; Gisin, N. Photon-Counting OTDR for Local Birefringence and Fault Analysis in the Metro Environment. J. Light. Technol. 2004, 22, 390. [Google Scholar] [CrossRef]
- Qi, B.; Zhu, W.; Qian, L.; Lo, H.K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 2010, 12, 103042. [Google Scholar] [CrossRef]
- Kumar, R.; Qin, H.; Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 2015, 17, 043027. [Google Scholar] [CrossRef]
- Chapuran, T.E.; Toliver, P.; Peters, N.A.; Jackel, J.; Goodman, M.S.; Runser, R.J.; McNown, S.R.; Dallmann, N.; Hughes, R.J.; McCabe, K.P.; et al. Optical networking for quantum key distribution and quantum communications. New J. Phys. 2009, 11, 105001. [Google Scholar] [CrossRef]
- Eraerds, P.; Walenta, N.; Legré, M.; Gisin, N.; Zbinden, H. Quantum key distribution and 1Gbps data encryption over a single fibre. New J. Phys. 2010, 12, 063027. [Google Scholar] [CrossRef]

| 0 | 0.1 | 0.2 | 0.3 | 0.4 | |
|---|---|---|---|---|---|
| 0.01 | 0.0147 | 0.0194 | 0.0241 | 0.0288 |
| 1545 | 1545.4 | 1546.2 | 1547 | 1547.6 | 1548.4 | 1548.6 | 1549.2 | 1546.4 | 1550 | |
| T | 0.4936 | 0.4941 | 0.4951 | 0.4962 | 0.4969 | 0.4979 | 0.4982 | 0.4989 | 0.4992 | 0.5 |
| 1551 | 1551.4 | 1552.2 | 1553 | 1553.6 | 1554.4 | 1554.6 | 1555.2 | 1555.4 | 1556 | |
| T | 0.5012 | 0.5017 | 0.5027 | 0.50380 | 0.5045 | 0.5055 | 0.5058 | 0.5066 | 0.5068 | 0.5076 |
| 1304 | 1304.2 | 1305 | 1305.6 | 1306.2 | 1306.8 | 1307.4 | 1308 | 1308.6 | 1308.8 | |
| T | 0.4910 | 0.4913 | 0.4925 | 0.4934 | 0.4943 | 0.4952 | 0.4961 | 0.4970 | 0.4979 | 0.4982 |
| 1311 | 1311.2 | 1312 | 1312.6 | 1313.2 | 1313.8 | 1314.4 | 1315 | 1315.6 | 1315.8 | |
| T | 0.5014 | 0.5017 | 0.5030 | 0.5039 | 0.5048 | 0.5057 | 0.5066 | 0.5075 | 0.5084 | 0.5087 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Zhang, L.; Huang, D. Practical Security Bounds against Trojan Horse Attacks in Continuous-Variable Quantum Key Distribution. Appl. Sci. 2020, 10, 7788. https://doi.org/10.3390/app10217788
Pan Y, Zhang L, Huang D. Practical Security Bounds against Trojan Horse Attacks in Continuous-Variable Quantum Key Distribution. Applied Sciences. 2020; 10(21):7788. https://doi.org/10.3390/app10217788
Chicago/Turabian StylePan, Yaxi, Ling Zhang, and Duan Huang. 2020. "Practical Security Bounds against Trojan Horse Attacks in Continuous-Variable Quantum Key Distribution" Applied Sciences 10, no. 21: 7788. https://doi.org/10.3390/app10217788
APA StylePan, Y., Zhang, L., & Huang, D. (2020). Practical Security Bounds against Trojan Horse Attacks in Continuous-Variable Quantum Key Distribution. Applied Sciences, 10(21), 7788. https://doi.org/10.3390/app10217788






