Finite Element Analysis of Reinforced Concrete Bridge Piers Including a Flexure-Shear Interaction Model
Abstract
:1. Introduction
2. Objectives and Methods
3. Numerical Model
3.1. Model Outline
3.2. Flexural Behavior
3.3. Slipage Behavior
3.4. Shear Behavior
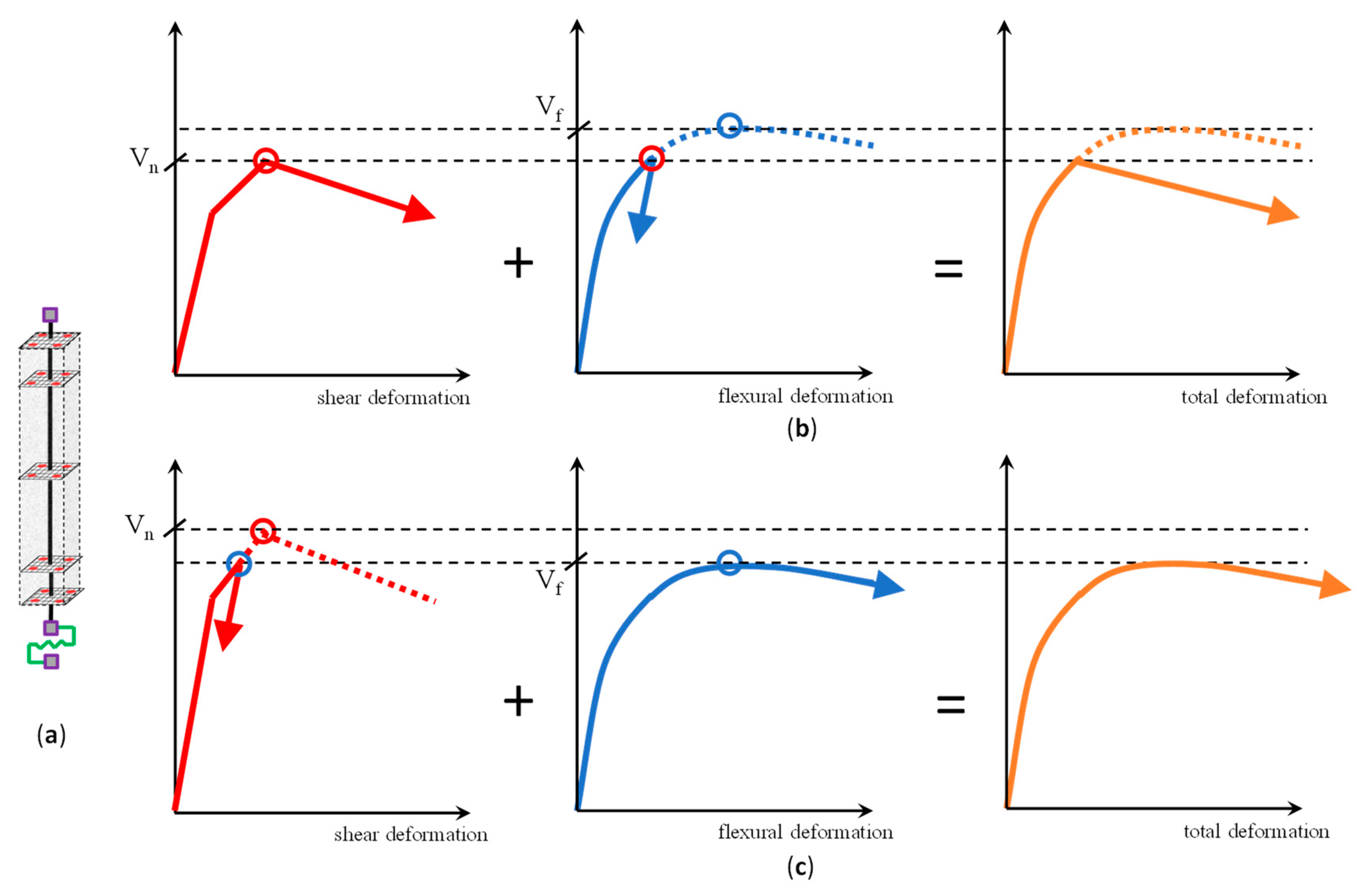
3.5. Interaction Model
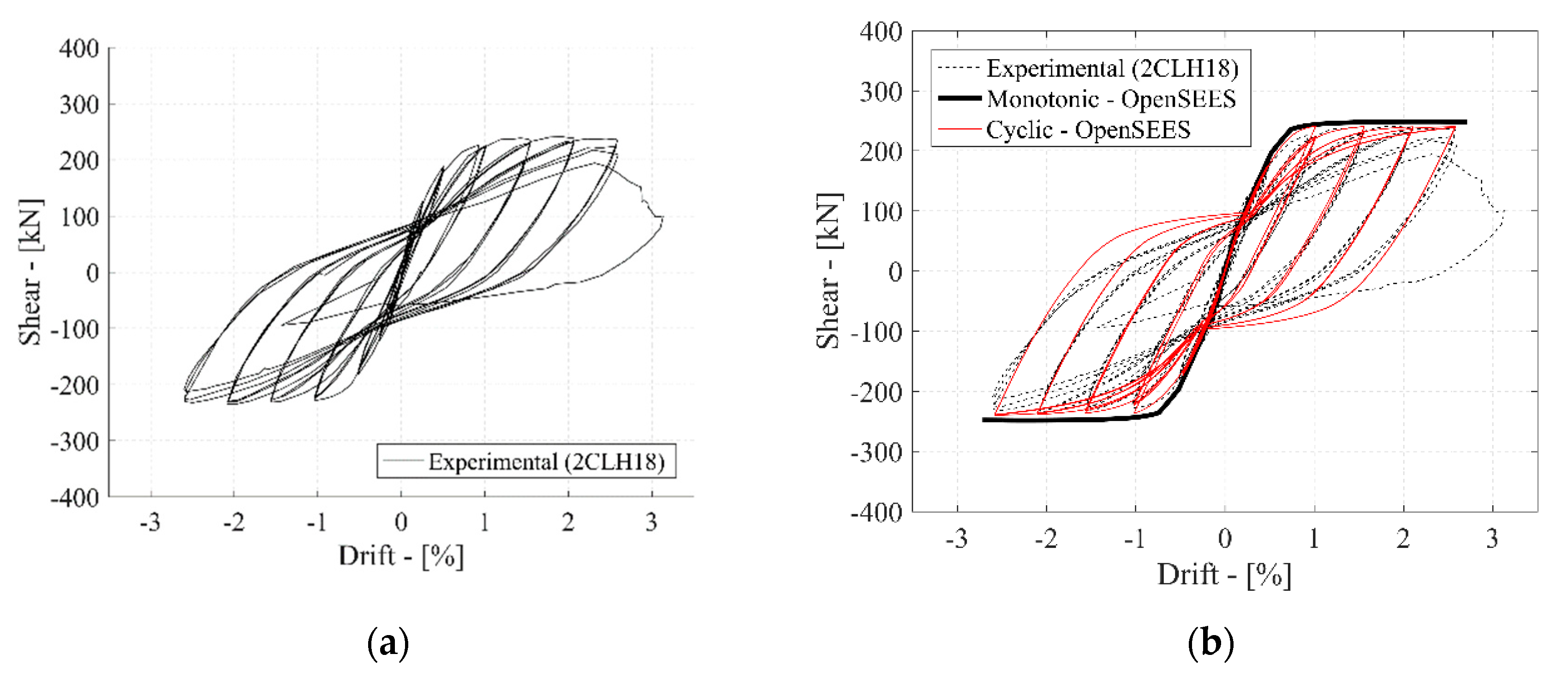
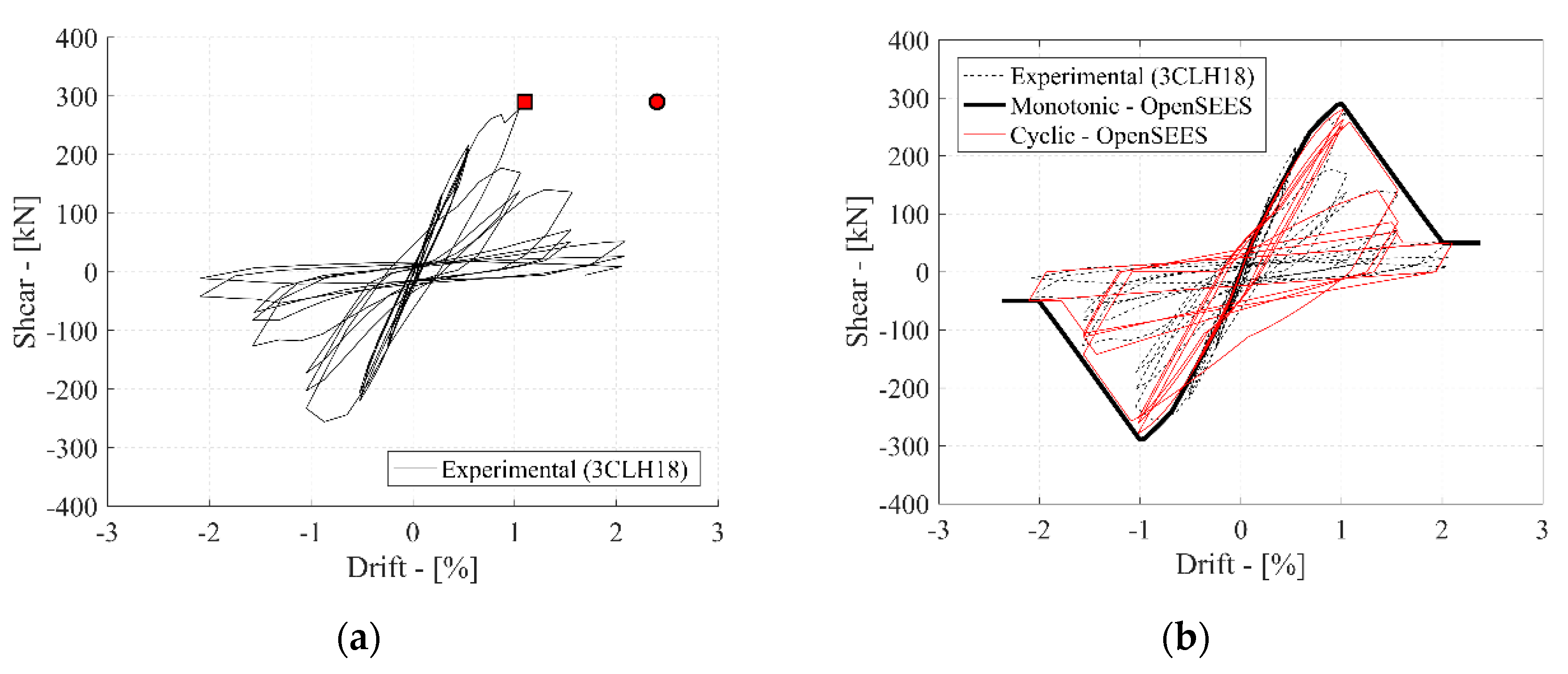
4. Numerical Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nuti, C.; Rasulo, A.; Vanzi, I. Seismic assessment of utility systems: Application to water, electric power and transportation networks. In Proceedings of the Safety, Reliability and Risk Analysis: Theory, Methods and Applications Proceedings of the Joint ESREL and SRA-Europe Conference, Valencia, Spain, 22–25 September 2008; Volume 3, pp. 2519–2529. [Google Scholar]
- Nuti, C.; Rasulo, A.; Vanzi, I. Seismic safety of network structures and infrastructures. Struct. Infrastruct. Eng. 2010, 6, 95–110. [Google Scholar] [CrossRef]
- Rasulo, A.; Testa, C.; Borzi, B. Seismic risk analysis at urban scale in Italy. Lect. Notes Comput. Sci. 2015, 9157, 403–414. [Google Scholar] [CrossRef]
- Rasulo, A.; Fortuna, M.A.; Borzi, B. Seismic risk analysis at urban scale in Italy. Lect. Notes Comput. Sci. 2016, 9788, 198–213. [Google Scholar] [CrossRef]
- Lavorato, D.; Pelle, A.; Fiorentino, G.; Nuti, C.; Rasulo, A. A nonlinear material model of corroded rebars for seismic response of bridges, COMPDYN 2019. In Proceedings of the 7th ECOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Grecee, 24–26 June 2019. [Google Scholar]
- Lavorato, D.; Fiorentino, G.; Pelle, A.; Rasulo, A.; Bergami, A.V.; Briseghella, B.; Nuti, C. A corrosion model for the interpretation of cyclic behavior of reinforced concrete sections. Struct. Concr. 2019. [Google Scholar] [CrossRef]
- Lynn, A.C.; Moehle, J.P.; Mahin, S.A.; Holmes, W.T. Seismic evaluation of existing reinforced concrete building columns. Earthq. Spectra 1996, 12, 715–739. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Seible, F.; Verma, R.; Xiao, Y. Seismic shear strength of reinforced concrete columns. In Structural Systems Research Project Report No. SSRP 93/06; University of California: San Diego, CA, USA, 1993. [Google Scholar]
- Sezen, H.; Moehle, J.P. Shear strength model for lightly reinforced concrete columns. J. Struct. Eng. 2004, 130, 1692–1703. [Google Scholar] [CrossRef]
- Filippou, F.C.; D’Ambrisi, A.; Issa, A. Nonlinear static and dynamic analysis of reinforced concrete subassemblages. In Earthquake Engineering Research Center Report No. UCB/EERC-92/08; University of California: Berkeley, CA, USA, 1992. [Google Scholar]
- Cassese, P.; De Risi, M.T.; Verderame, G.M. A degrading shear strength model for RC columns with hol-low circular cross-section. Int. J. Civ. Eng. 2019, 17, 1241–1259. [Google Scholar] [CrossRef]
- Cassese, P.; De Risi, M.T.; Verderame, G.M. A modelling approach for existing shear-critical RC bridge piers with hollow rectangular cross section under lateral loads. Bull. Earthq. Eng. 2019, 17, 237–270. [Google Scholar] [CrossRef]
- Guedes, J.; Pinto, A.V. A numerical model for shear dominated bridge piers. In Proceedings of the Second Italy–Japan Workshop on Seismic Design and Retrofit of Bridges, Rome, Italy, 27–28 February 1997. [Google Scholar]
- Ranzo, G.; Petrangeli, M. A fibre finite beam element with section shear modelling for seismic analysis of RC structures. J. Earthq. Eng. 1998, 2, 443–473. [Google Scholar] [CrossRef]
- Petrangeli, M. Fiber element for cyclic bending and shear of RC structures. II: Verification. J. Eng. Mech. 1999, 125, 1002–1009. [Google Scholar] [CrossRef]
- Marini, A.; Spacone, E. Analysis of reinforced concrete elements including shear effects. ACI Struct. J. 2006, 103, 645–655. [Google Scholar]
- Ceresa, P.; Petrini, L.; Pinho, R.; Sousa, R. A fibre flexure-shear model for seismic analysis of RC-framed structures. Earthq. Eng. Struct. Dyn. 2009, 38, 565–586. [Google Scholar] [CrossRef]
- McKenna, F.; Fenves, G.L.; Scott, M.H.; Jeremic, B. Open System for Earthquake Engineering Simulation (OpenSEES); University of California: Berkeley, CA, USA, 2000. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of Analysis of Cyclically Loaded RC Plane Frames including Changes in Geometry and Non-Elastic Behavior of Elements under Normal Force and Bending; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1973; pp. 15–22. [Google Scholar]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Eligehausen, R.; Bertero, V.V.; Popov, E.P. Local bond stress-slip relationships of deformed bars under generalized excitations: Tests and analytical model. In Report No EERC; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983; pp. 1–169. [Google Scholar]
- Sezen, H.; Setzler, E.J. Reinforcement slip in reinforced concrete columns. ACI Struct. J. 2008, 105, 280. [Google Scholar]
- CEB-FIB. Model Code 2010-Final Draft; The International Federation for Structural Concrete (FIB CEB-FIP): Lausanne, Switzerland, 2010. [Google Scholar]
- Elwood, K.J. Shake Table Tests and Analytical Studies on the Gravity Load Collapse of Reinforced Concrete Frames. Level of. Ph.D. Thesis, University of California, Berkeley, CA, USA, January 2002. [Google Scholar]
- Elwood, K.J.; Eberhard, M.O. Effective Stiffness of Reinforced Concrete Columns. In Research Digest No 2006-1. ACI Struct. J. 2009, 106, 476–484. [Google Scholar]
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Biskinis, D.E.; Roupakias, G.K.; Fardis, M.N. Degradation of Shear Strength of Reinforced Concrete Members with Inelastic Cyclic Displacements. ACI Struct. J. 2004, 101, 773–783. [Google Scholar]
- Elwood, K.J.; Moehle, J.P. Drift Capacity of Reinforced Concrete Columns with Light Transverse Reinforcement. Earthq. Spectra 2005, 21, 71–89. [Google Scholar] [CrossRef]
- Kowalsky, M.J.; Priestley, M.J.N. Improved Analytical Model for Shear Strength of Circular Reinforced Concrete Columns in Seismic Regions. ACI Struct. J. 2000, 97, 388–396. [Google Scholar]
- Lynn, A. Seismic Evaluation of Existing Reinforced Concrete Building Column. Ph.D. Thesis, University of California at Berkeley, Berkeley, CA, USA, 2001. [Google Scholar]
- Saatcioglu, M.; Ozcebe, G. Response of reinforced concrete columns to simulated seismic loading. Struct. J. 1989, 86, 3–12. [Google Scholar]
- Calvi, G.M.; Pavese, A.; Rasulo, A.; Bolognini, D. Experimental and numerical studies on the seismic response of R.C. hollow bridge piers. Bull. Earthq. Eng. 2005, 3, 267–297. [Google Scholar] [CrossRef]










| Rectangular Section | ||||||||||||
| Reference | Specimen | b (mm) | h (mm) | s (mm) | a/d (---) | ρl (---) | ρw (---) | f’c (MPa) | fyl (MPa) | fyw (MPa) | ν (---) | Test Type |
| Lynn A.C. [31] | 2CLH18 | 457.2 | 457.2 | 457.2 | 3.74 | 0.02 | 0.0007 | 26.8 | 330.7 | 399.6 | 0.09 | DC |
| 3CLH18 | 457.2 | 457.2 | 457.2 | 3.74 | 0.03 | 0.0007 | 26.8 | 330.7 | 399.6 | 0.09 | DC | |
| 3SLH18 | 457.2 | 457.2 | 457.2 | 3.74 | 0.03 | 0.0007 | 26.8 | 330.7 | 399.6 | 0.09 | DC | |
| 2SLH18 | 457.2 | 457.2 | 457.2 | 3.71 | 0.02 | 0.0007 | 27.5 | 330.7 | 399.6 | 0.07 | DC | |
| 3CMH18 | 457.2 | 457.2 | 457.2 | 3.74 | 0.03 | 0.0007 | 25.4 | 330.7 | 399.6 | 0.28 | DC | |
| 3CMD12 | 457.2 | 457.2 | 457.2 | 3.74 | 0.03 | 0.0017 | 25.4 | 330.7 | 399.6 | 0.28 | DC | |
| Saatcioglu Ozcebe [32] | U1 | 350.0 | 350.0 | 150.0 | 3.28 | 0.03 | 0.0085 | 43.6 | 430.0 | 470.0 | 0.00 | SC |
| U2 | 350.0 | 350.0 | 150.0 | 3.28 | 0.03 | 0.0085 | 30.2 | 453.0 | 470.0 | 0.16 | SC | |
| U3 | 350.0 | 350.0 | 75.0 | 3.28 | 0.03 | 0.0169 | 34.8 | 430.0 | 470.0 | 0.16 | SC | |
| Hollow Rectangular Section | ||||||||||||
| Reference | Specimen | b (mm) | h (mm) | s (mm) | a/d (---) | ρl (---) | ρw (---) | f’c (MPa) | fyl (MPa) | fyw (MPa) | ν (---) | Test Type |
| Calvi et al. [33] | T250 | 450.0 | 450.0 | 75.0 | 3.00 | 0.0177 | 0.0025 | 30.3 | 550.0 | 550.0 | 0.07 | SC |
| T500A | 450.0 | 450.0 | 75.0 | 3.00 | 0.0177 | 0.0025 | 29.7 | 550.0 | 550.0 | 0.15 | SC | |
| T500B | 450.0 | 450.0 | 75.0 | 3.00 | 0.0177 | 0.0025 | 32.7 | 550.0 | 550.0 | 0.15 | SC | |
| T750 | 450.0 | 450.0 | 75.0 | 3.00 | 0.0177 | 0.0025 | 30.8 | 550.0 | 550.0 | 0.21 | SC | |
| Rectangular Section | |||||
| Reference | Specimen | Δs/L (---) | Ks,deg (kN/mm) | Vs (kN) | Vres (kN) |
| Lynn A.C. (2001) [31] | 3CLH18 | 0.0100 | −7.5 | 277.0 | 50.0 |
| 3SLH18 | 0.0077 | −4.4 | 270.0 | 48.7 | |
| 2SLH18 | 0.0088 | −6.2 | 231.6 | − | |
| 3CMH18 | 0.0100 | −12.4 | 324.4 | 94.3 | |
| 3CMD12 | 0.0085 | −4.1 | 355.8 | − | |
| Saatcioglu, Ozcebe [32] | U1 | 0.044 | −2.8 | 273.0 | 70.0 |
| U2 | 0.021 | −6.0 | 280.0 | 90.0 | |
| U3 | 0.044 | −3.7 | 255.0 | − | |
| Hollow Rectangular Section | |||||
| Reference | Specimen | Δs/L (---) | Ktdeg (kN/mm) | Vs (kN) | Vres (kN) |
| Calvi et al. [33] | T250 | 0.022 | −8.9 | 217.2 | 47.9 |
| T500A | 0.010 | −6.3 | 209.0 | − | |
| T500B | 0.022 | −7.8 | 228.0 | − | |
| T750 | 0.020 | − | 257.9 | − | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasulo, A.; Pelle, A.; Lavorato, D.; Fiorentino, G.; Nuti, C.; Briseghella, B. Finite Element Analysis of Reinforced Concrete Bridge Piers Including a Flexure-Shear Interaction Model. Appl. Sci. 2020, 10, 2209. https://doi.org/10.3390/app10072209
Rasulo A, Pelle A, Lavorato D, Fiorentino G, Nuti C, Briseghella B. Finite Element Analysis of Reinforced Concrete Bridge Piers Including a Flexure-Shear Interaction Model. Applied Sciences. 2020; 10(7):2209. https://doi.org/10.3390/app10072209
Chicago/Turabian StyleRasulo, Alessandro, Angelo Pelle, Davide Lavorato, Gabriele Fiorentino, Camillo Nuti, and Bruno Briseghella. 2020. "Finite Element Analysis of Reinforced Concrete Bridge Piers Including a Flexure-Shear Interaction Model" Applied Sciences 10, no. 7: 2209. https://doi.org/10.3390/app10072209








