Systematically Investigating the Structural Variety of Crystalline and Kaleidoscopic Vortex Lattices by Using Laser Beam Arrays
Abstract
:1. Introduction
2. Theoretical Analysis
3. Experimental Setup
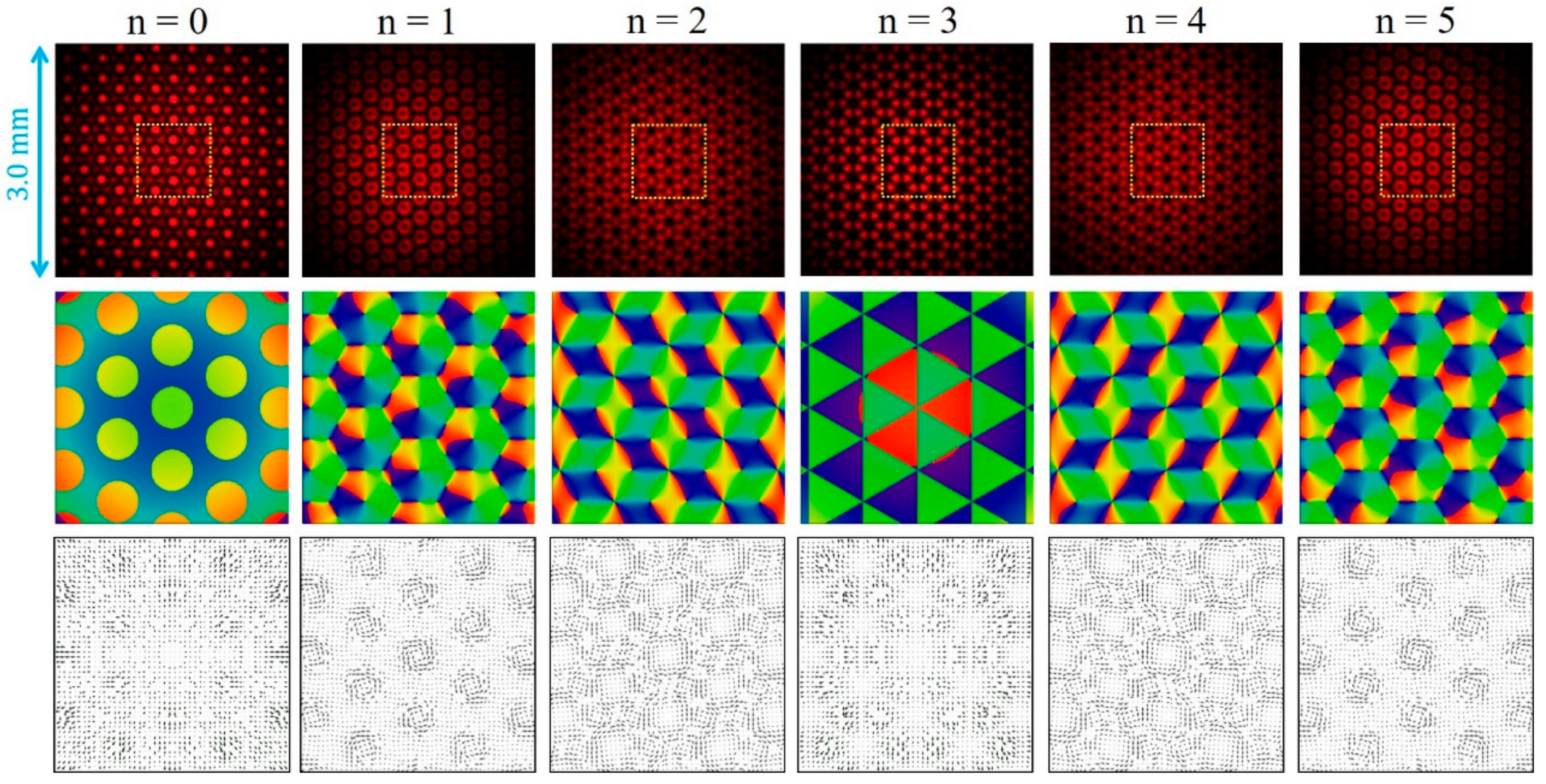
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Woerdemann, M.; Alpmann, C.; Esseling, M.; Denz, C. Advanced optical trapping by complex beam shaping. Laser Photon-Rev. 2013, 7, 839–854. [Google Scholar] [CrossRef]
- Padgett, M.J.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Shvedov, V.G.; Rode, A.V.; Izdebskaya, Y.V.; Desyatnikov, A.S.; Krolikowski, W.; Kivshar, Y.S. Giant Optical Manipulation. Phys. Rev. Lett. 2010, 105, 118103. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, X.; Kim, K.; Jhe, W.; Kwon, N. Efficient optical guiding of trapped cold atoms by a hollow laser beam. Phys. Rev. A 2001, 63, 063401. [Google Scholar] [CrossRef]
- Molina-Terriza, G.; Torres, J.P.; Torner, L. Twisted photons. Nat. Phys. 2007, 3, 305–310. [Google Scholar] [CrossRef]
- Toyoda, K.; Takahashi, F.; Takizawa, S.; Tokizane, Y.; Miyamoto, K.; Morita, R.; Omatsu, T. Transfer of Light Helicity to Nanostructures. Phys. Rev. Lett. 2013, 110, 143603. [Google Scholar] [CrossRef]
- Lu, C.; Lipson, R.H. Interference lithography: A powerful tool for fabricating periodic structures. Laser Photon-Rev. 2009, 4, 568–580. [Google Scholar] [CrossRef]
- Masajada, J. Small-angle rotations measurement using optical vortex interferometer. Opt. Commun. 2004, 239, 373–381. [Google Scholar] [CrossRef]
- Ladavac, K.; Grier, D.G. Microoptomechanical pumps assembled and driven by holographic optical vortex arrays. Opt. Express 2004, 12, 1144–1149. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.F.; Lan, Y.P. Transverse pattern formation of optical vortices in a microchip laser with a large Fresnel number. Phys. Rev. A 2001, 65, 013802. [Google Scholar] [CrossRef]
- Chen, Y.-F.; Ke, H.T.; Tseng, Y.C.; Hsieh, M.X.; Tung, J.-C.; Hsieh, Y.H.; Liang, H.-C.; Huang, K.F. High-power structured laser modes: Direct generation of a vortex array. Opt. Lett. 2020, 45, 4096–4099. [Google Scholar] [CrossRef]
- Chen, Y.F.; Lee, C.C.; Wang, C.H.; Hsieh, M.X. Laser transverse modes of spherical resonators: A review. Chin. Opt. Lett. 2020, 18, 091404. [Google Scholar] [CrossRef]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic holographic optical tweezers. Opt. Commun. 2002, 207, 169–175. [Google Scholar] [CrossRef]
- Grier, D.G.; Roichman, Y. Holographic optical trapping. Appl. Opt. 2006, 45, 880–887. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.C.; Lu, T.H.; Huang, K.F.; Chen, Y.F. Generation of optical vortex array with transformation of standing-wave La-guerre-Gaussian mode. Opt. Express 2011, 19, 10293–10303. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.H.; Huang, T.D.; Chiou, G.Y. Kaleidoscope vortex lasers generated from astigmatic cavities with longitudinal-transverse coupling. Opt. Express 2018, 26, 31464–31473. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.F.; Chang, C.C.; Lee, C.Y.; Tung, J.C.; Liang, H.C.; Huang, K.F. Characterizing the propagation evolution of wave patterns and vortex structures in astigmatic transformations of Hermite–Gaussian beams. Laser Phys. 2017, 28, 015002. [Google Scholar] [CrossRef]
- Li, L.; Chang, C.; Yuan, X.; Yuan, C.; Feng, S.; Nie, S.; Ding, J. Generation of optical vortex array along arbitrary curvilinear arrangement. Opt. Express 2018, 26, 9798–9812. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A. Structured light from lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Huang, T.D.; Lu, T.H. Controlling an optical vortex array form a vortex plate, mode converter, and spatial light modulator. Opt. Lett. 2019, 44, 3917–3920. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Z.; Dong, X. Multi-beams engineered to increase patterns of vortex lattices by employing zero lines of the coherent non-diffracting filed. Opt. Express 2019, 27, 21652–21666. [Google Scholar] [CrossRef] [PubMed]
- Masajada, J.; Dubik, B. Optical vortex generation by three plane wave interference. Opt. Commun. 2001, 198, 21–27. [Google Scholar] [CrossRef]
- Wang, L.G.; Wang, L.Q.; Zhu, S.Y. Formation of optical vortices using coherent laser beam arrays. Opt. Commun. 2009, 282, 1088–1094. [Google Scholar] [CrossRef] [Green Version]
- Xavier, J.; Vyas, S.; Senthilkumaran, P.; Joseph, J. Tailored complex 3D vortex lattice structures by perturbed multiples of three-plane waves. Appl. Opt. 2012, 51, 1872–1878. [Google Scholar] [CrossRef] [PubMed]
- Boguslawski, M.; Rose, P.; Denz, C. Increasing the structural variety of discrete nondiffracting wave fields. Phys. Rev. A 2011, 84, 013832. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.F.; Liang, H.C.; Lin, Y.C.; Tzeng, Y.S.; Su, K.W.; Huang, K.F. Generation of optical crystals and quasicrystal beams: Kaleidoscopic patterns and phase singularity. Phys. Rev. A 2011, 83, 053813. [Google Scholar] [CrossRef]
- Tsou, C.H.; Wu, T.W.; Tung, J.C.; Liang, H.C.; Tuan, P.H.; Chen, Y.F. Generation of pseudonondiffracting optical beams with superlattice structures. Opt. Express 2013, 21, 23441–23449. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-F.; Tu, Y.C.; Li, S.-C.; Hsieh, M.X.; Yu, Y.T.; Liang, H.-C.; Huang, K.F. Propagation-dependent evolution of interfering multiple beams and kaleidoscopic vortex lattices. Opt. Lett. 2021, 46, 102–105. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Fang, Y.; Jang, C.; Chen, W.; Lin, H.-C.; Liang, H. Systematically Investigating the Structural Variety of Crystalline and Kaleidoscopic Vortex Lattices by Using Laser Beam Arrays. Appl. Sci. 2021, 11, 8018. https://doi.org/10.3390/app11178018
Chen C, Fang Y, Jang C, Chen W, Lin H-C, Liang H. Systematically Investigating the Structural Variety of Crystalline and Kaleidoscopic Vortex Lattices by Using Laser Beam Arrays. Applied Sciences. 2021; 11(17):8018. https://doi.org/10.3390/app11178018
Chicago/Turabian StyleChen, Chengshang, Yuhan Fang, Chichen Jang, Wenchi Chen, Hui-Chi Lin, and Hsingchih Liang. 2021. "Systematically Investigating the Structural Variety of Crystalline and Kaleidoscopic Vortex Lattices by Using Laser Beam Arrays" Applied Sciences 11, no. 17: 8018. https://doi.org/10.3390/app11178018
APA StyleChen, C., Fang, Y., Jang, C., Chen, W., Lin, H.-C., & Liang, H. (2021). Systematically Investigating the Structural Variety of Crystalline and Kaleidoscopic Vortex Lattices by Using Laser Beam Arrays. Applied Sciences, 11(17), 8018. https://doi.org/10.3390/app11178018





