1. Introduction
The simulation of in-flight structural vibrations of an aeronautical vehicle requires modeling pressure fluctuations on its bounding surface and modeling the vehicle. The first diagram in
Figure 1 represents the target simulation process. In-flight experiments are rare, and the ability of the simulation process to reproduce the measured dynamic behavior depends on:
the Computational Fluid Dynamics (CFD) simulation of the flow around the vehicle,
the pressure fluctuation dimensionless model, and
the vehicle vibroacoustic model.
These three steps must be validated separately. The CFD simulation and the Turbulent Boundary Layer (TBL) pressure-fluctuation models are usually validated using wind tunnel experiments. The development of pressure-fluctuation models started in the 1960s with, in particular, works by Corcos [
1] and Bull [
2]. Many improvements have been proposed since then.
For subsonic flows without a pressure gradient, Goody’s model has proven to be one of the most relevant models to date, fitting with several wind tunnel experiments [
3]. Dedicated experiments have also focused on high Mach numbers for the modeling of ballistic vehicles. Houbolt [
4] and Lowson [
5] proposed the first models in the 1960s; Laganelli and Howe [
6] proposed improvements in the 1980s; and, more recently, these models have been challenged by new experiments (see [
7,
8] for example).
These models have all been validated using wind tunnel experiments, which is the second process shown in
Figure 1. The alternate validation process is the direct measurement of in-flight pressure fluctuations. Such data during hypersonic flight have been measured during the HI-FIRE experiment [
9]. However, this type of measurement is extremely rare.
Once the pressure-fluctuation model was chosen and the turbulent boundary layer simulated using dedicated CFD simulation, the surface dynamic load was defined in terms of the Power Spectral Density (PSD) level and surface correlation laws as a function of frequency. The response of a vibroacoustic model to this input can be computed. The full-frequency modeling of the vehicle must then be performed.
In the low-frequency range, the most widely used modeling methods are based on the Finite Element Method (FEM). Once the vehicle has been modeled using structural finite elements, applying a distributed random dynamic pressure—which is correlated in space and frequency—is not trivial. A few articles have tackled this issue. Among them, Hong and Shin proposed an equivalent uncorrelated random pressure field [
10], and Bonness et al. investigated several approaches to perform the computation efficiently [
11].
The most widely used method for applying an acoustic loading to a structural finite element model is the modeling of the air volume surrounding the structure using the Boundary Element Method (BEM). Many examples may be found for automotive or aeronautical applications (see for example [
12,
13,
14]). The combination with turbulent boundary layer pressure fluctuation loading has been studied, in particular, by Mongomery for an aeronautical application [
15] and by Li et al. with several correlation models applied on a plate [
16].
At higher frequencies, the relevance of a finite element model decreases as the size of the elements cannot be considered small in comparison to the wavelengths of the vibration modes. Statistical Energy Analysis (SEA) [
17] enables the prediction of high-frequency averaged vibration responses with a low computational cost. The response of an SEA model to turbulent boundary layer noise is often computed for the prediction of internal aircraft noise. For example, a recent SEA modeling of an aircraft fuselage was developed in [
18].
Combining a Finite Element model and a SEA model may result in a full-frequency model of the structure. However, between high and low-frequency ranges, there may be a range where neither finite elements nor SEA are relevant. Many “mid-frequency” methods have been proposed to bridge this gap. Most of them are described in the workbook [
19]. Various full-frequency modeling methods may be chosen.
Certain wave-based methods, such as the variational theory of complex rays [
20] proposed a unique full-frequency framework. Industrial studies often prefer a combination of a FE model with a SEA model and may use a hybrid FE–SEA model [
21] for mid-frequencies.
An example of such full-frequency modeling of an aircraft fuselage is described in [
22]. In this article, a FEM–BEM model and a SEA model of a ballistic re-entry aeroshell are developed. The final aim of such modeling is the computation of in-flight vibrations, which is the first process shown in
Figure 1. The simulation results depend both on the modeling of the structure and the modeling of the in-flight pressure fluctuations. In this article, a process for validating the structure model alone is deployed—the third process shown in
Figure 1.
The ground experiment chosen is diffuse acoustic testing. As well as turbulent boundary layer noise, diffuse acoustic noise is a dynamic pressure load correlated in space and frequency. Using a dedicated test facility, this load can be precisely controlled. Such experiments are widely used for the modeling of plates and panels [
23,
24]. Fewer test–simulation comparisons have been published on industrial structures (see [
25] for example).
The vibroacoustic response of a hypersonic aircraft external shape to a diffuse acoustic field has recently been studied by Pr. Yunjun Yan’s team. A FEM–BEM model [
26], a SEA model [
27] and a hybrid FE–SEA model [
28] of the structure have been developed. Simulations have been compared with diffuse acoustic testing experiments.
The approach deployed here uses diffuse field experimentation as a validation tool. The study focuses on the understanding, modeling and simulation of vibroacoustic phenomena. The aim is to simulate and interpret resonances in the low-frequency range on the one hand, and to simulate average responses at higher frequencies on the other. The experimental setup (test structure, diffuse acoustic testing facility and measurement tools) is described in the first section of this article. The second and third sections describe the model and the results obtained by FEM–BEM and SEA, respectively. Finally, the results obtained with the two models are combined to perform a full-frequency test–simulation comparison.
4. SEA Modeling
In the low-frequency range, the FEM–BEM modeling described previously proven to be relevant to predict vibroacoustic responses. At high frequencies, this ability is limited by the modal truncation. As modal density increases at high frequencies, a modal truncation at a significantly higher frequency (≫2500 Hz) would greatly increase the computational cost of the method. At these frequencies, the main expected engineering result is only the overall root mean square acceleration level.
Thus, a complementary method was used to evaluate the vibroacoustic response levels until 16 kHz with a low computational cost: Statistical Energy Analysis (SEA). The theory of the method is quickly introduced in the next section. The setup of the SEA model is then described, including dedicated experiments for the identification of key parameters. Finally, the simulation results are compared with diffuse acoustic field measurements.
4.1. SEA Equations and Hybrid FE–SEA Periodic Theory
In SEA, a complex vibroacoustic structure is represented as an assembly of coupled subsystems that can receive, store, dissipate and transfer energy. By adopting a statistical description of the local dynamic properties of each subsystem, it is possible to predict the overall average response of a complex system across a broad frequency range.
The basic SEA equations express the energy balance in the dynamic response model, which comprises a set of subsystems described by their gross geometric form and dynamic material properties. For a structure made of
n subsystems, for every subsystem
i, the energy conservation can be written as [
17]:
is the input power in subsystem
i that is known. The dissipated power in subsystem
i (
) and the power transferred from subsystem
i to subsystem
j (
) are modeled as:
where
is the damping loss factor (DLF) (or internal loss factor) and
is the coupling loss factor (CLF) between subsystem
i and subsystem
j. The brackets
denote spatial the average of the energies and will be omitted hereafter for simplicity. The coupling loss factors
and
are related by the expression:
where
is the modal density of subsystems
. Equation (
7) can then be written as:
By substituting Equations (
6) and (
9) in the energy conservation Equation (
5), the following set of linear equations is obtained:
Therefore, knowing the injected power and the loss factors, the energies of the subsystems can be determined.
The traditional approach to SEA modeling typically involves the description of a complex system in terms of a number of simpler connected subsystems. These SEA subsystems are usually chosen in a fixed formulation library, in order to fit the real geometry as closely as possible. However, traditional SEA codes often have somewhat limited libraries of subsystems that are based on analytical derivations of wave propagation and scattering in simplified cross-section. Such cross-sections are adequate for simple systems; however, they are often not general enough to rigorously describe the vibroacoustic behavior of complex structures.
The results presented in this article were obtained with Wave6 software, where a statistical energy analysis formulation using finite element and periodic structure theory, called hybrid FE–SEA periodic theory, was implemented [
21,
30,
32]. One of the main advantages of this formulation is the ability to compute some of the parameters involved in the SEA method, such as the coupling loss factors and modal density for complex structures. These parameters are usually calculated analytically only for simple structures [
17,
33] or need the development of experimental techniques [
34,
35].
The hybrid FE–SEA method offers a way to use deterministic and statistical subsystems in the same model by coupling them at their boundaries. Each 2D SEA subsystem is described by a unit cell modeled with structural finite elements. Periodic boundary conditions are then applied to the edges and corners of the cell, and phase constant surfaces are obtained by solving an algebraic eigenvalue problem. The SEA parameters can then be related to certain properties of the phase surfaces of the unit cell [
32]. The approach enables an arbitrary amount of details to be included in the cross-section of each subsystem, such as curvature or stress stiffening [
36].
The first task when setting up a SEA model is to define the subsystem partitioning and the damping loss factors of each subsystem. This is done here using experimental measurements.
4.2. Definition of SEA Subsystems and Estimation of Damping Loss Factors
One of the main difficulties of SEA modeling is the definition of the subsystems in such a way that the conditions of applicability of SEA theory are respected. These conditions are the following [
17]:
an adequate modal density for each subsystem (at least three modes per frequency band),
a spatial mode covering (the modes used to calculate the modal density must affect all the subsystem), and
a weak coupling between subsystems.
The experimental measurements presented here make it possible to determine the SEA subsystems of the HB–2 structure in order that the conditions mentioned above should be respected. Furthermore, the damping loss factor of each subsystem, which is a key parameter of the model, is measured.
The test setup is illustrated in
Figure 14a. The entire structure was freely suspended and driven sequentially at 11 points, denoted
in
Figure 14b, using a shaker attached to the excitation point. Analogously to the experimental setup for the vibrometry measurement shown in
Figure 3 and
Figure 5, the structure is suspended horizontally for an excitation point on the bottom, and vertically for an excitation point on the envelope. For each excitation, the resulting vibration responses were recorded with 21 accelerometers, denoted as
in
Figure 14b at randomly selected locations so that the spatial average could be estimated. The structure was excited with a white noise from 500 Hz to 16 kHz.
The first clear division of the structure into subsystems is the separation of the bottom and the envelope. Then, the analysis of the FRF measurements at different locations enables the determination of the envelope’s subsystems. The envelope is not homogeneous with stiffened zones and zones of different curvature. First, analysis of the measurements is performed by splitting the envelope where its curvature changes. As depicted in
Figure 14b, three zones, designated ENV1, ENV2, ENV3, are defined.
All the signals recorded by the accelerometers located in each zone are averaged together.
Figure 15 shows the absolute value of the average point mobility
obtained in each zone. The mobility measured in the two zones ENV1 and ENV2 appear to be similar, thereby, revealing strong coupling between these two zones. The ENV3 zone appears to be less coupled to the others. Indeed, the envelope in this zone possesses more stiffeners.
Therefore, the best choice of SEA subsystems for the HB–2 structure is the following: two subsystems for the envelope, designated SEA 2D 1 (for the ENV3 zone) and SEA 2D2 (for the ENV1-ENV2 zones grouped together), and one subsystem for the bottom, designated SEA 2D 3 (see
Figure 14b).
The second objective of the experiments is the determination of the damping loss factors. The DLF of each subsystem are calculated with the decay-rate method [
17]. They are related to the decay rate (
) by:
For each accelerometer, the impulsive time response is measured using a fast process involving correlated time sequences with a low crest factor. One impulsive time response is plotted in
Figure 16b. The signals obtained are time filtered for each third octave band. Then, as depicted in
Figure 16a, the Energy Time Curve (ETC) is plotted as well as the Schroeder integration [
37]. The Decay Rate (
DR) is deduced from this integration. The
DR corresponds to the time after which the residual integration dropped by −10 dB.
As illustrated in
Figure 16a, the chosen starting point is when the integration drops by 0.1 dB. For each frequency band and each measured point, the ETC is plotted, the
DR is calculated, and the DLF is deduced using Equation (
11). This allows, for each SEA subsystem, a statistical determination of the damping loss factors with a spatial average over various excitation points.
The DLFs obtained for each subsystem are represented in
Figure 17 by the mean, minimum and maximum estimated values. The values range from 0.25% to 1% for the envelope and from 1% to 3% for the bottom.
4.3. SEA Model
Figure 18 illustrates the SEA model in Wave6. Three 2D SEA subsystems are created for the bottom and the two envelope parts. They consist of a double curved shell with an aluminum cross section of 1 mm. The cross-section of the subsystems is described by a unit cell with a single QUAD8 shell element. The mean value of the damping loss factors obtained by experiments (see
Figure 17) are defined in each subsystem.
The external air volume and the internal air cavity are modeled with 3D SEA subsystems. The excitation source is a diffuse acoustic field as defined in
Section 2.2. Junctions between all the 2D and 3D SEA subsystems and the source are then created.
Line junctions are created between the 2D SEA subsystems, and area junctions are created between the source and the 2D and 3D SEA subsystems, with particular area junctions through the holes of the bottom between the external and internal air volumes. A SEA model is usually valid when there are at least three modes per frequency band. This criterion is estimated from modal analysis at low frequencies and is confirmed with the observed experimental resonances. We achieved above 1250 Hz for the envelope subsystems and above 1600 Hz for the bottom subsystem.
4.4. Test–Simulation Comparison
Figure 19 shows the mean RMS acceleration of each subsystem in the third octave bands. The simulated results (blue lines) are compared with experimental data obtained by laser vibrometry measurements (black lines with stars). The time acceleration response is measured at several points of each subsystem (46 and 20 measurements on a line along the
x-axis for the subsystems SEA 2D 1 and SEA 2D 2, and 175 measurements covering all the surface for the bottom subsystem SEA 2D 3).
The Power Spectral Density is then computed for each point. Then, for each subsystem, a spatial average of the PSD of all points belonging to the subsystem is performed. As explained in
Section 2.3, with scanning laser vibrometry, the measurements at different points are not synchronous but sequential, allowing only the computation of the PSD
and not the cross power spectral densities
between two points
.
Thus, the experimental results shown in
Figure 19 correspond to the average of the PSD (equal to
), which would be overestimated compared to the real average value, which accounts for cross spectral densities (
). Finally, the averaged PSD value of each subsystem is converted to RMS acceleration in each third octave band. The results shown in
Figure 19 show good test–simulation correlation. In subsystem SEA 2D 1, an averaged difference of −1.9 dB between the mean simulation results and measurements is observed.
In subsystem SEA 2D 2, this difference reaches −3.8 dB, revealing a slight underestimation of levels by SEA simulation or a slight overestimation of the experimental averaged PSD because of the lack of cross-spectral PSD data. In subsystem SEA 2D 3, simulation underestimates levels below 2.8 kHz; however, above 2.8 kHz, the averaged difference between simulation and experiments is only −1.1 dB.
5. Full-Frequency Test–Simulation Comparison
The FEM–BEM and SEA results are combined together to obtain full-frequency simulation results. The boundary between the two methods has to be set strictly beyond the validity criterion of the SEA model (>1600 Hz) and strictly below the limit of the modal truncation of the FEM model (2500 Hz). This boundary was set at 2200 Hz in order to include the second bottom resonance (around 2100 Hz) in the low-frequency range. FEM–BEM simulation provides the response acceleration PSD for every mesh point, with a fine frequency resolution, whereas SEA simulation provides a mean acceleration level per frequency band.
From an industrial perspective, the first expected output of a full-frequency simulation tool is the overall root mean square acceleration level at every point of the structure. For this purpose, for every point studied, the RMS level computed below 2200 Hz using FEM–BEM can be summed with the mean RMS level beyond 2200 Hz of the SEA subsystem to which the point belongs (using a quadratic sum). The second level of analysis is the frequency content of the simulated response.
For this analysis, the one-twelfth-octave band representation is chosen. The acceleration PSD measured is integrated in every one-twelfth-octave band to obtain the proper representation, and the FEM–BEM results are processed in the same way. The SEA simulation shown in
Section 4 is carried out again choosing the one-twelfth-octave band discretization. When working in one-twelfth-octave band, the SEA criteria (at least three modes per frequency band) is validated above 1600 Hz for the envelope subsystems and above 2000 Hz for the bottom.
Yet, in this last simulation, the DLF that were defined based on one-third-octave band measurement remain the same so that they are constant along each one-third-octave band. The results obtained are shown at three points located in the three SEA subsystems:
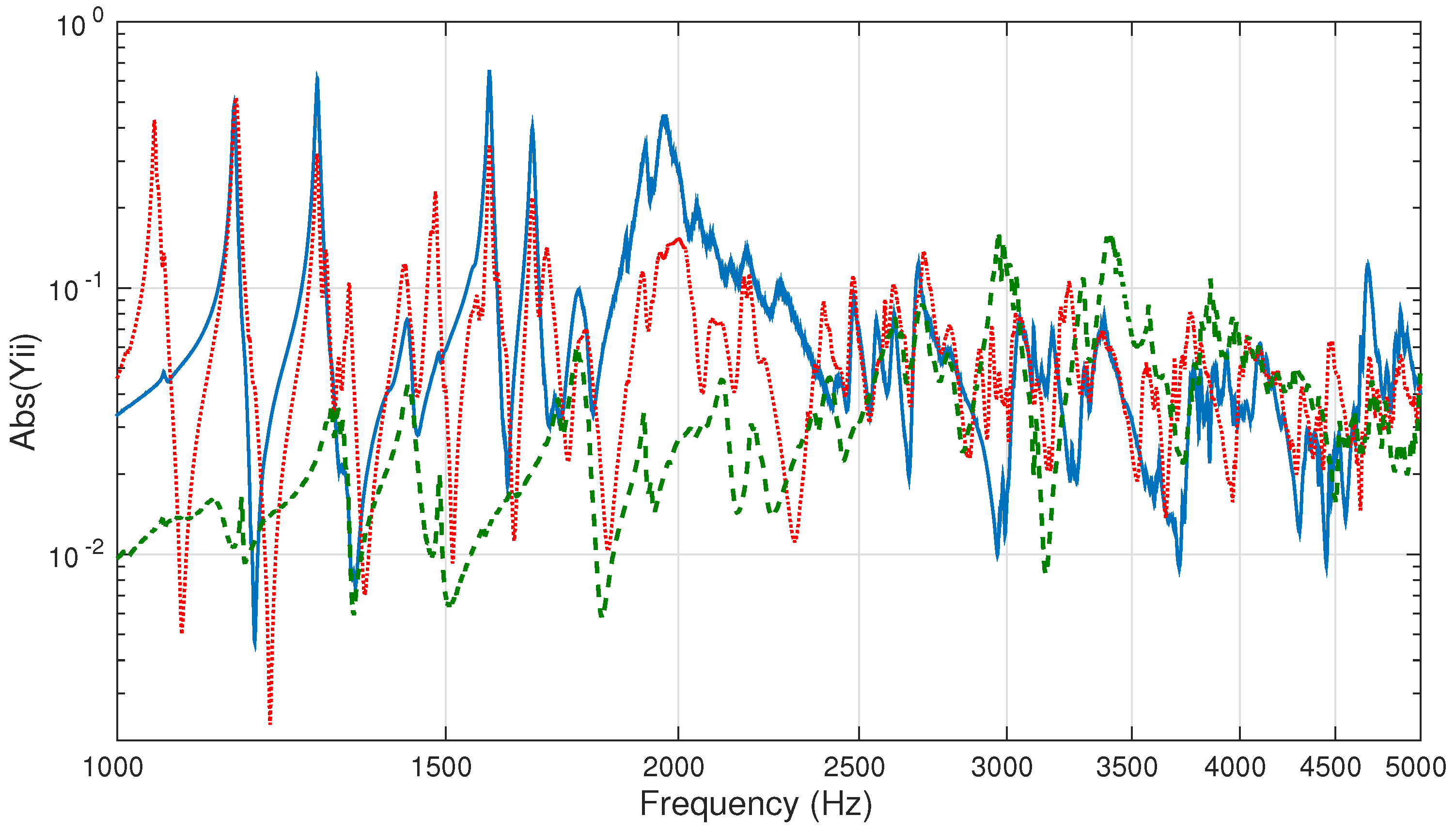
point (a) at the center of the envelope, located in SEA 2D 2, see
Figure 20,
point (b) located on the envelope, in SEA 2D 1 subsystem, see
Figure 21, and
point (c) on the bottom, located in SEA 2D 3, see
Figure 22.
A very good test–simulation agreement is observed in the full-frequency range, which proves the complementarity between the FEM–BEM and SEA methods. The corresponding RMS levels are presented in
Table 3.
6. Conclusions
This work is a step towards the simulation of the vibroacoustic response of a ballistic vehicle during flight. Beyond the difficulties of characterizing in-flight pressure fluctuations, which are not addressed in this study, a detailed vibroacoustic model of the vehicle is needed. A test structure representing an aeroshell was modeled using finite elements and Statistical Energy Analysis. This model was validated through diffuse acoustic field testing.
A dedicated experimental setup in a reverberant chamber was developed. In the low-frequency range, the test–simulation comparison highlights the need to model the air volume surrounding the structure to consider internal acoustic resonances and scattering effects. With BEM modeling of the surrounding air volumes, the simulation results are close to the experimental data, with a maximum 6 dB difference.
In the high-frequency range, two key steps were necessary to set up the SEA model: experimental identification of the Damping Loss Factor using a dedicated ground experiment and the use of a periodic FE–SEA method for the modeling of each subsystem and the computation of the Coupling Loss Factors. The results obtained with this model are in accordance with the mean responses in each subsystem.
A slight underestimation of the response level in the upper side of the envelope was observed (−3.8 dB); yet, this simulation–test agreement is sufficient to validate the model. The FEM–BEM and SEA results are complementary to obtain the full-frequency vibroacoustic response. For each simulation point studied, the estimated high-frequency response is the average value in the subsystem to which the point belongs, calculated using the SEA.
Good test–simulation agreement was observed with a maximum difference of −4.1 dB. For the particular structure under study, the boundary between the FE-BEM and SEA frequency domains was set at 2200 Hz. The full-frequency test–simulation comparison shows that this boundary is well-suited for the envelope and is slightly low considering the bottom of the structure.
The model could thus be improved by including more modes in the FEM–BEM analysis and by shifting the boundary with the SEA domain towards high frequencies. Another improvement could be the introduction of an additional mid-frequency model, such as an FE–SEA model. Regarding the industrial application, the full-frequency model described meets the need to forecast dynamic responses.