Long-Term Thermal Stress Analysis and Optimization of Contraction Joint Distance of Concrete Gravity Dams
Abstract
:1. Introduction
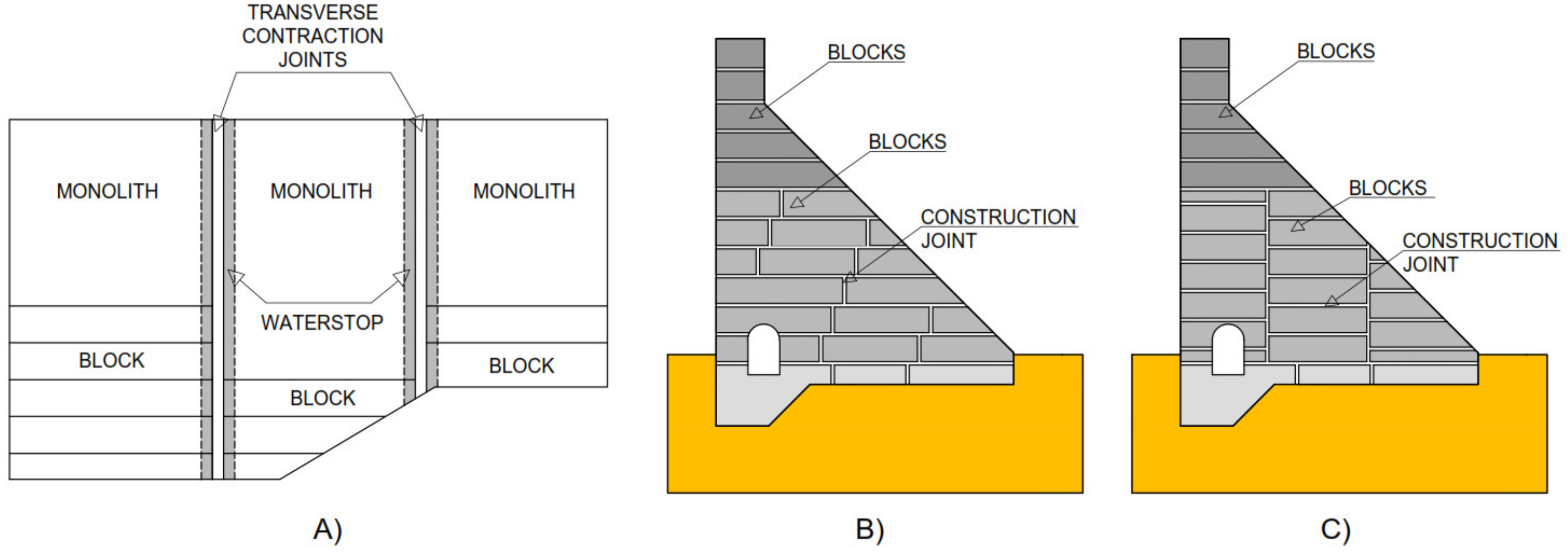
2. Thermal Stress Control and Prevention of Crack Formation
3. Theoretical Basis of Thermal Stress Processes
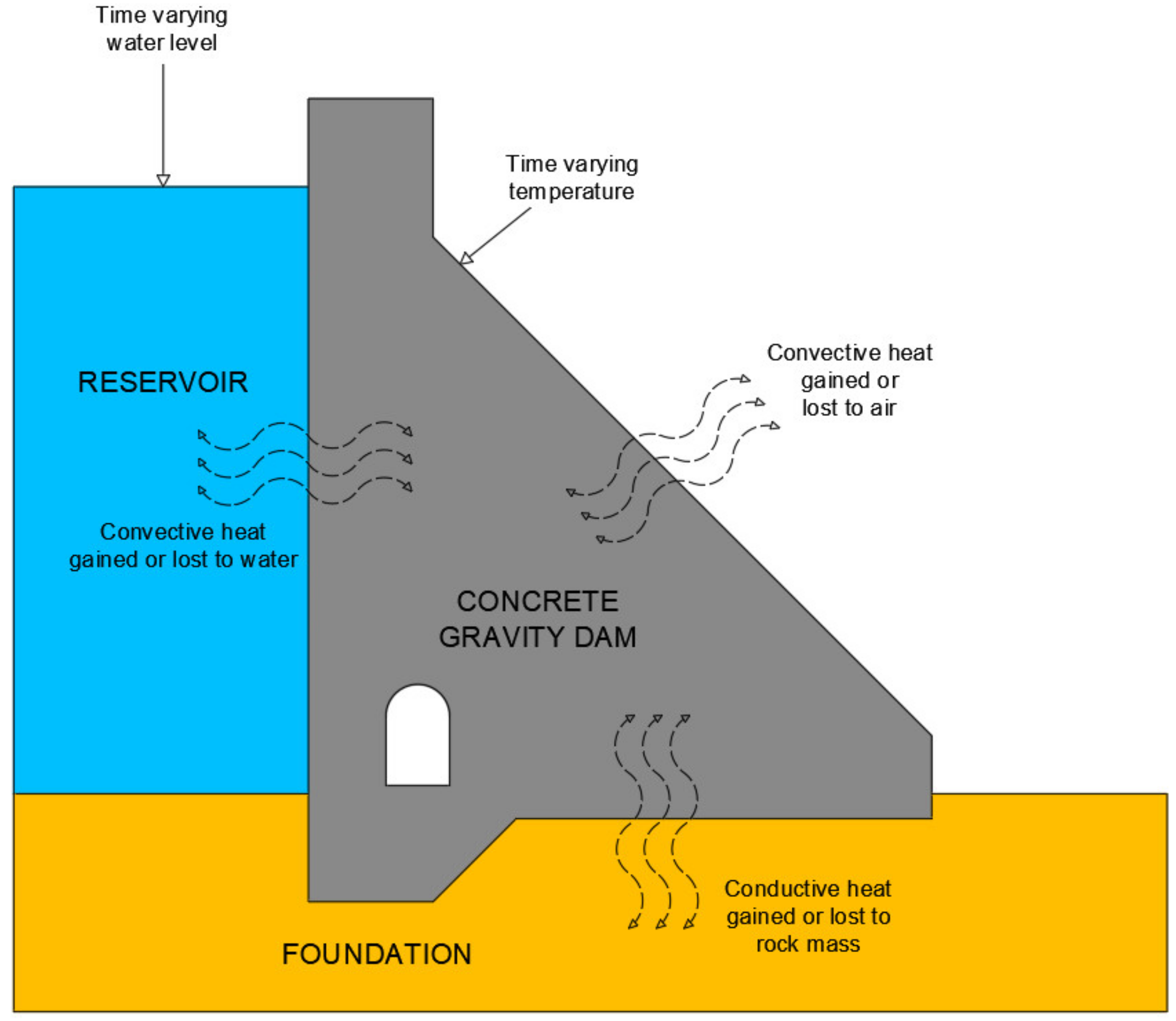
3.1. Fundamental Heat Transfer Equations
3.2. The Release of Heat from Concrete
3.3. Thermal Tensile Stress
4. Thermal Stress Analysis and Optimization of Contraction Joint Distance
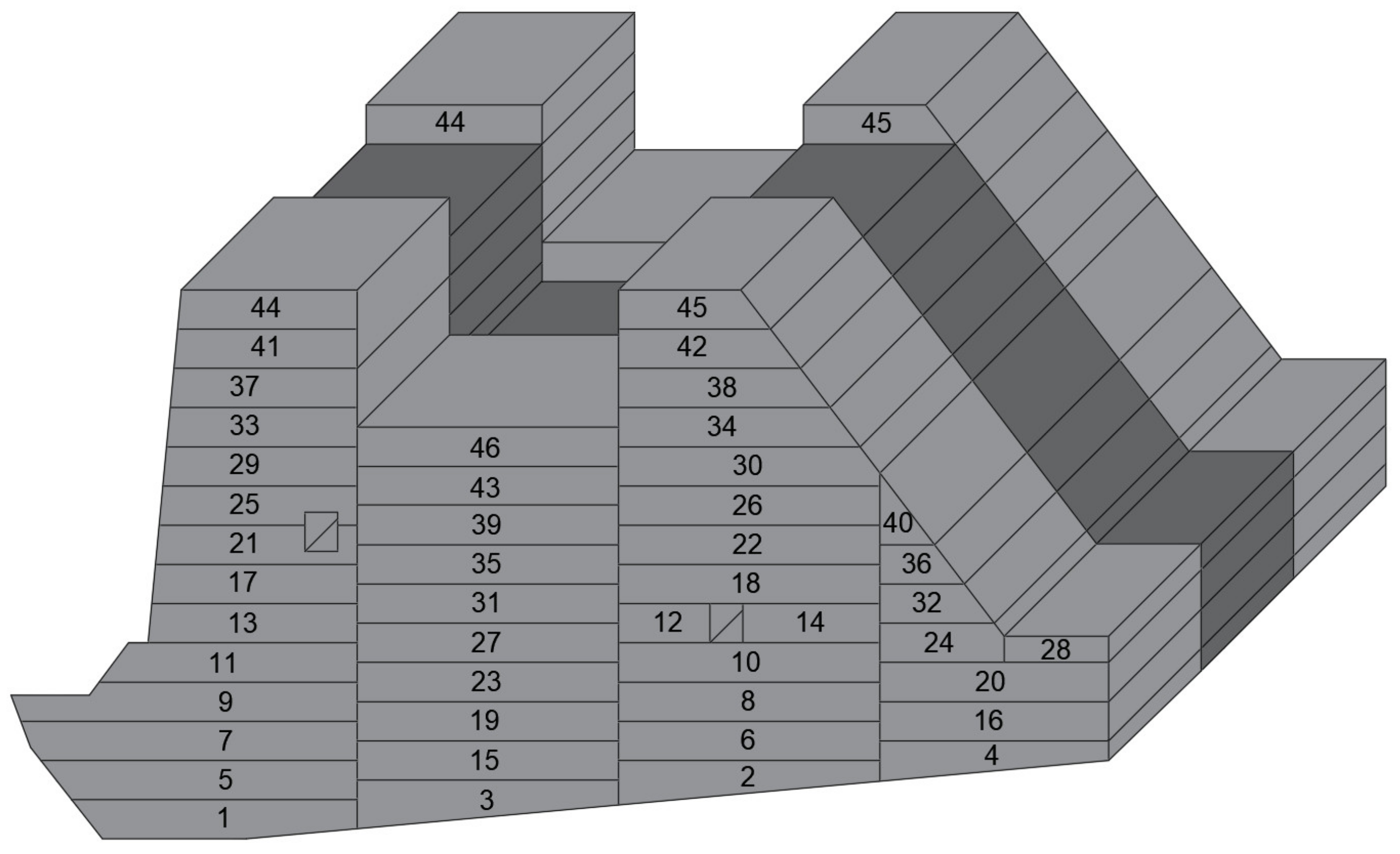
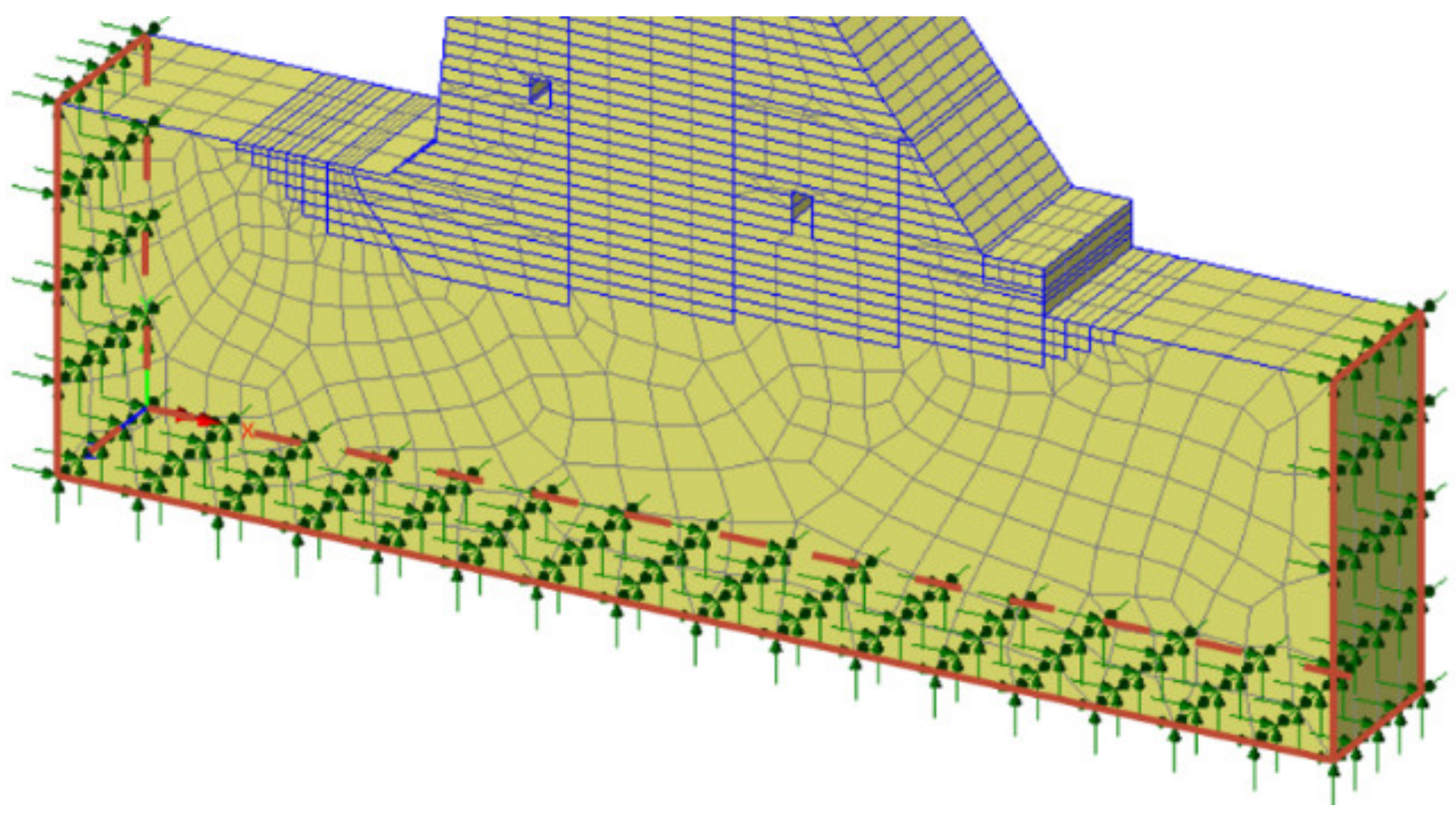
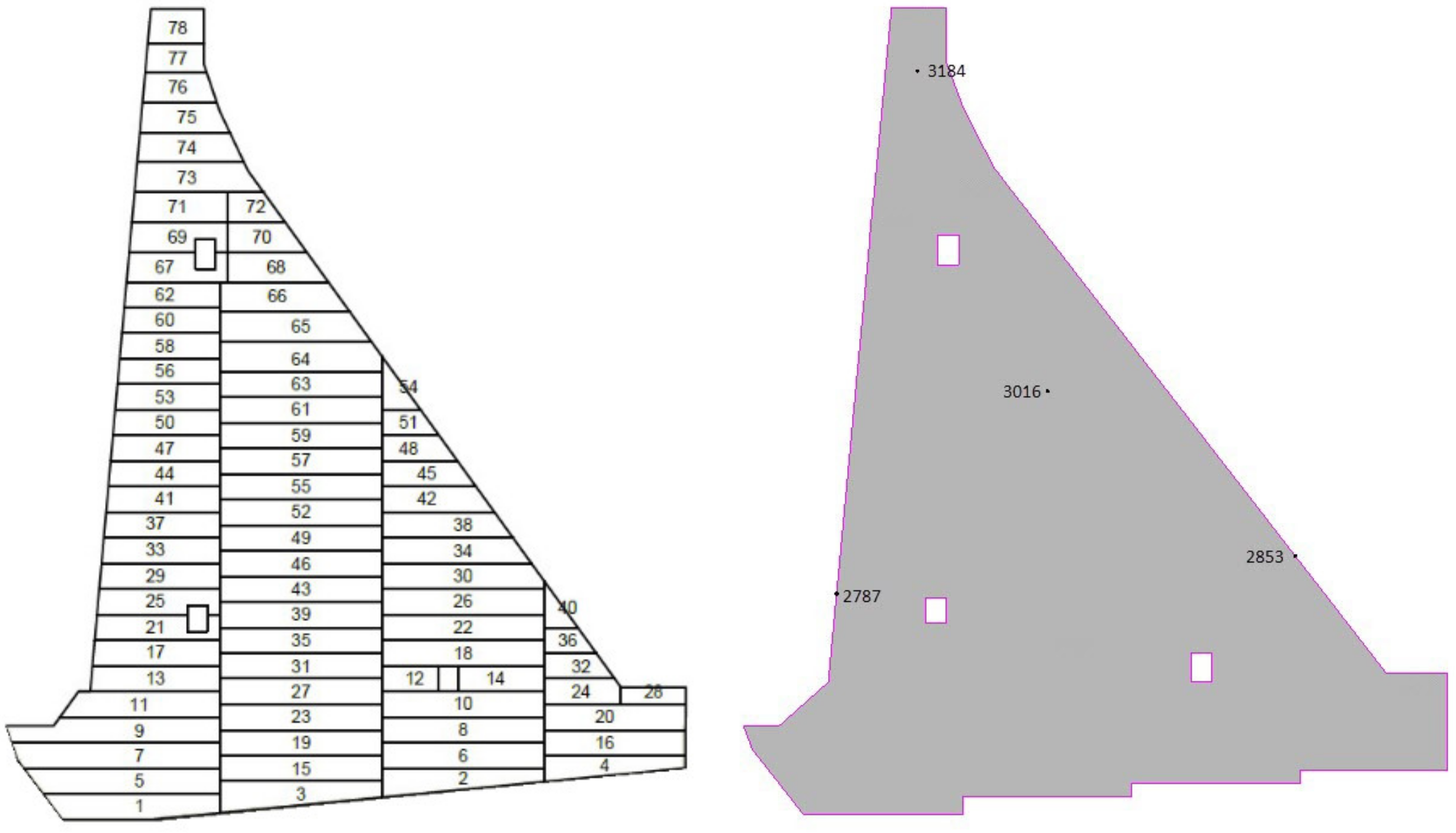
4.1. Description of the Calculation Model
4.2. Boundary Conditions and Actions
4.3. Material Parameters for Thermal Stress Analysis
4.4. Phases of Analysis and Distinctive Dates
- Beginning of the construction—18 October. Of the first year (the year in which the construction commenced);
- The first (winter) break of 12 days in the period from 15–27 December in the first year;
- The second (summer) break of 135 days in the period from 20 June–2 November in the second year;
- The third (winter) break of 12 days in the period from 15–27 December in the second year;
- The reservoir filling in the period from 27 May–20 November in the fourth year.
4.5. Optimization of Contraction Joint Distance
5. Results and Discussion
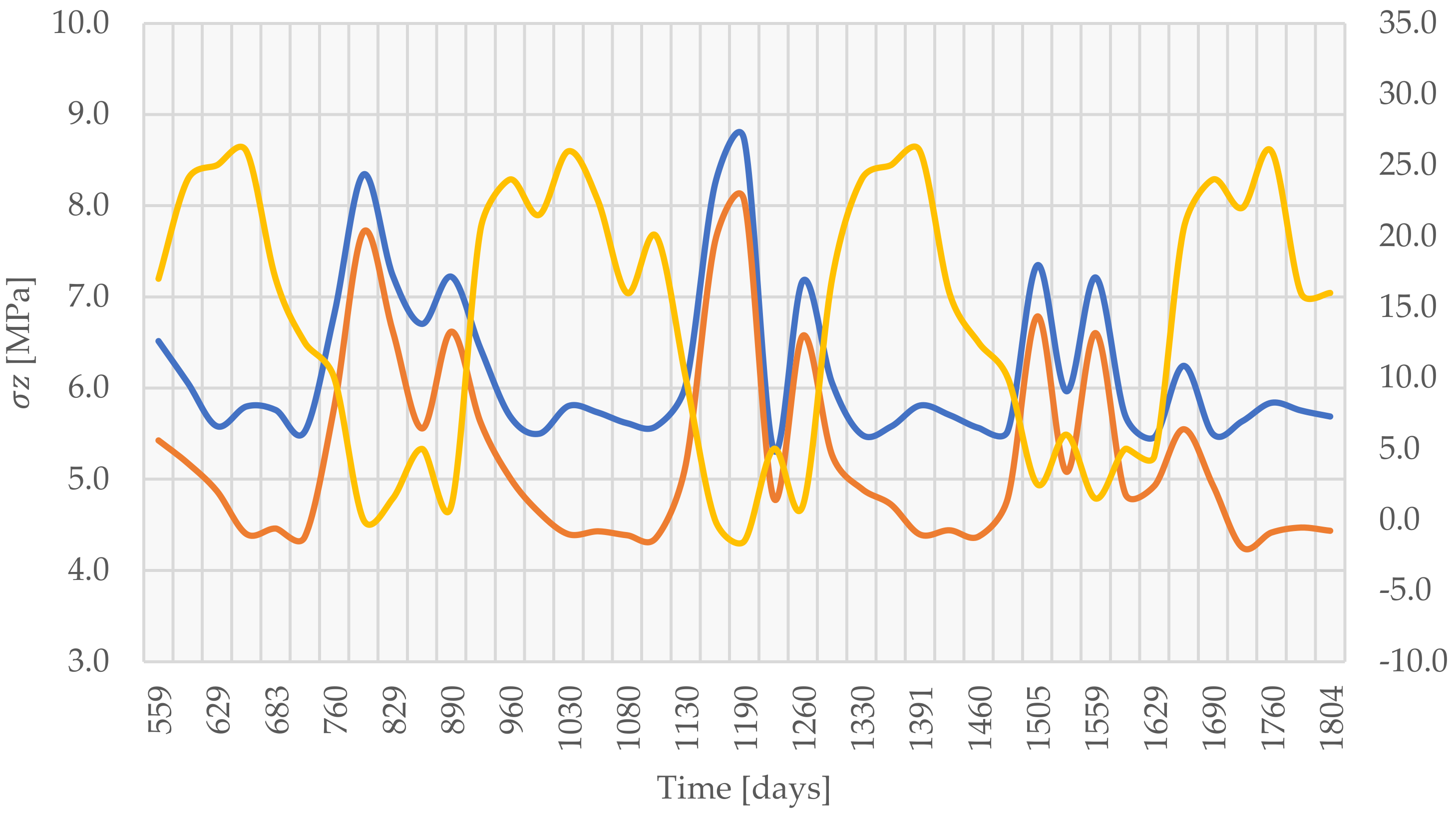
5.1. Validation of the Analysis Model concerning the Assigned Boundary Conditions
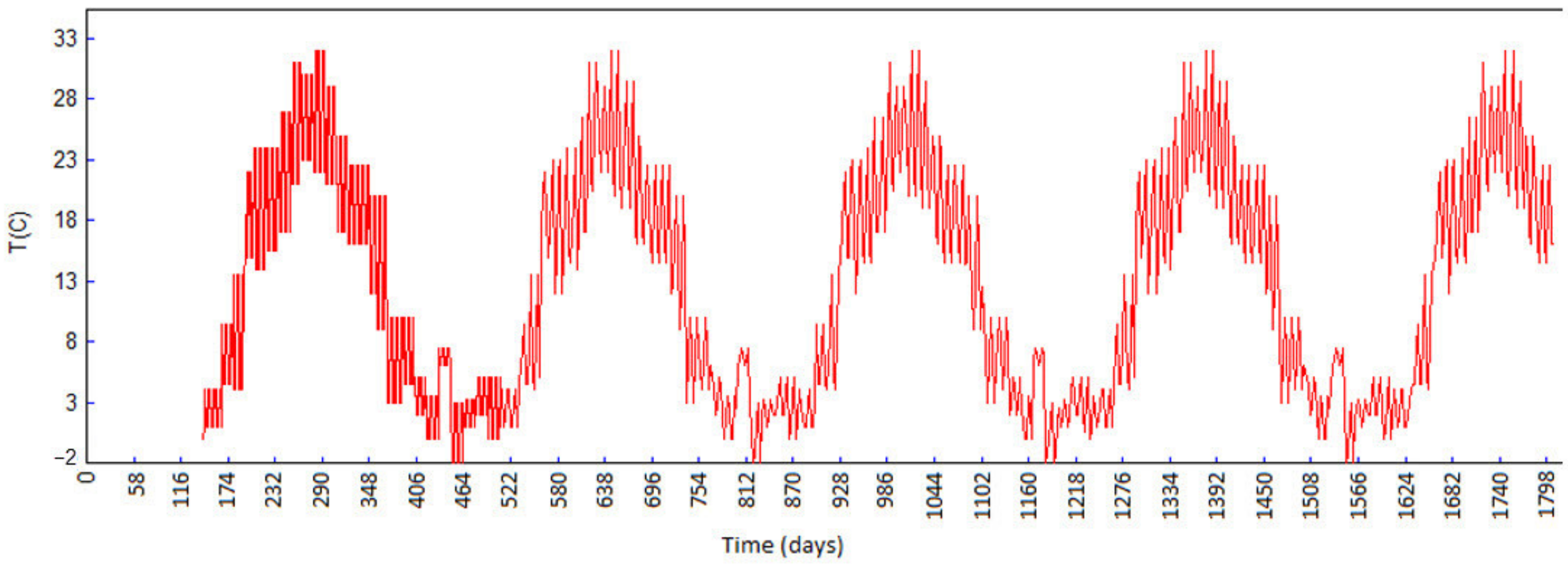
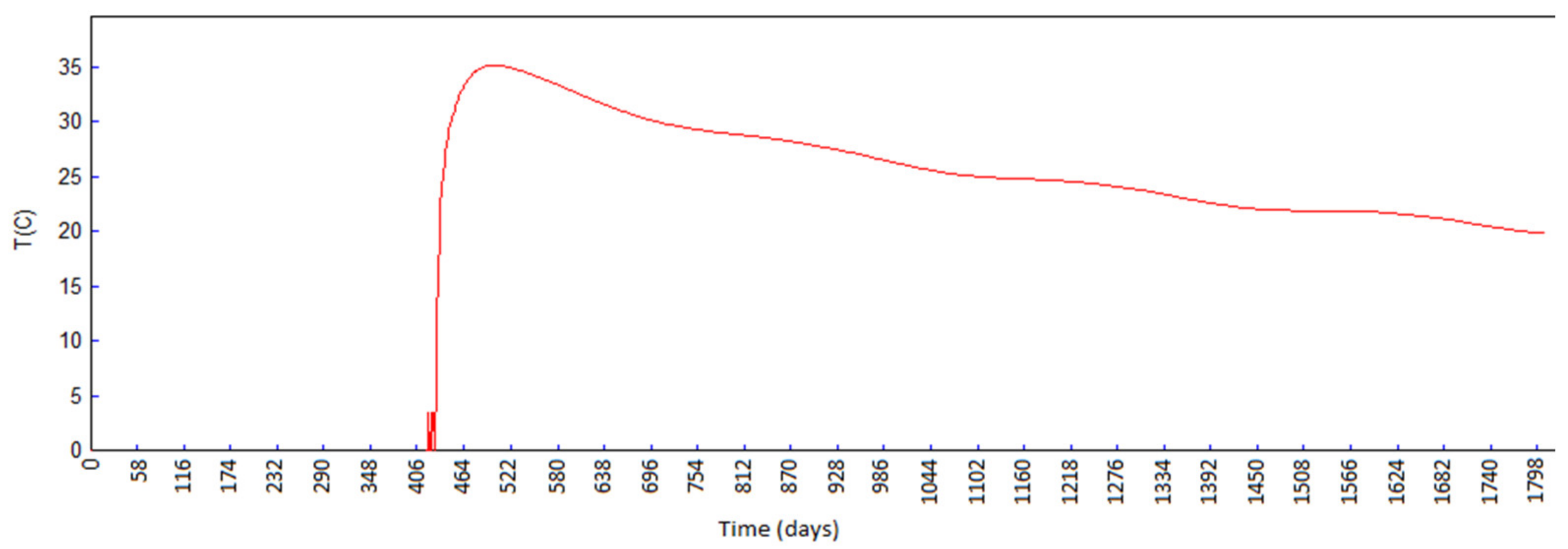
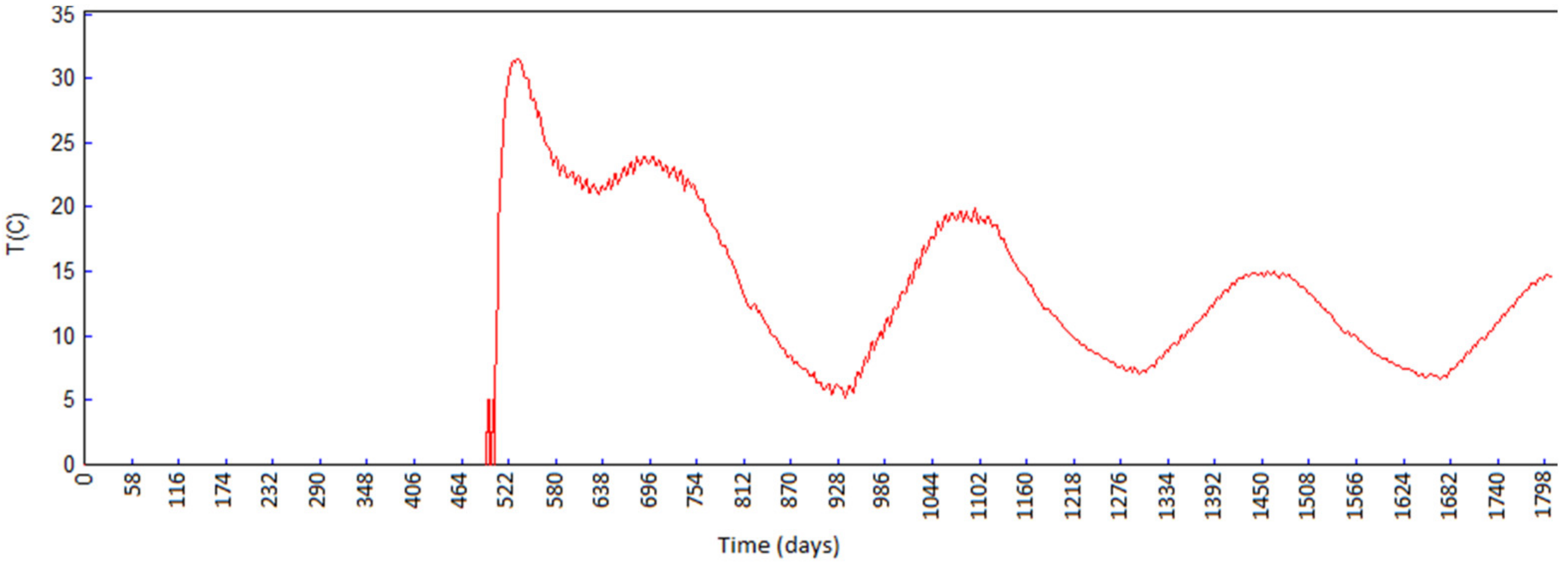
5.2. Results of Temperature Field Analysis
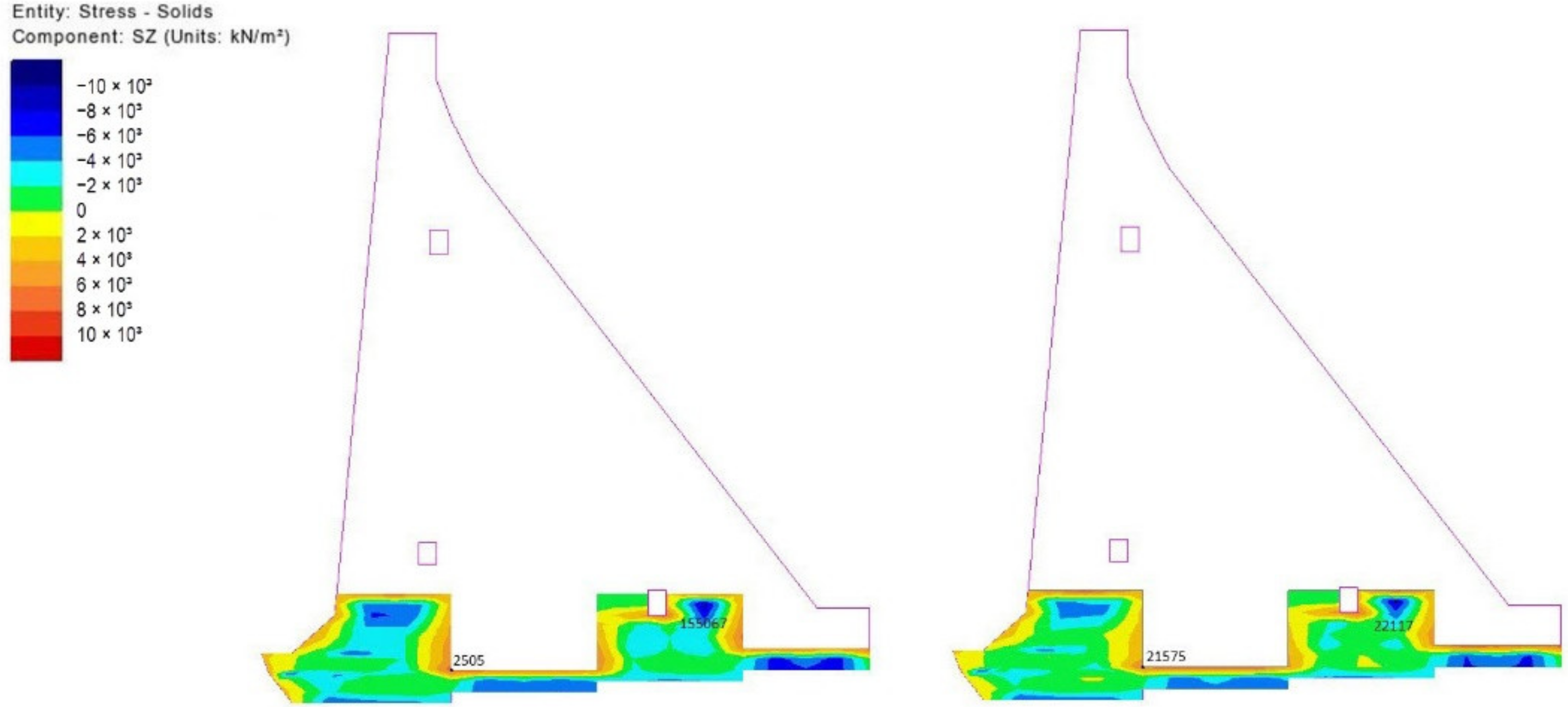
- The 84th day from the beginning of construction (10 January of the second year, 15 days from completing block 16, and at the moment of finishing the first break in the construction);
- The 283rd day from the beginning of construction (27 July of the second year, 40 days from completing block 52, and during the long (summer) break in the construction);
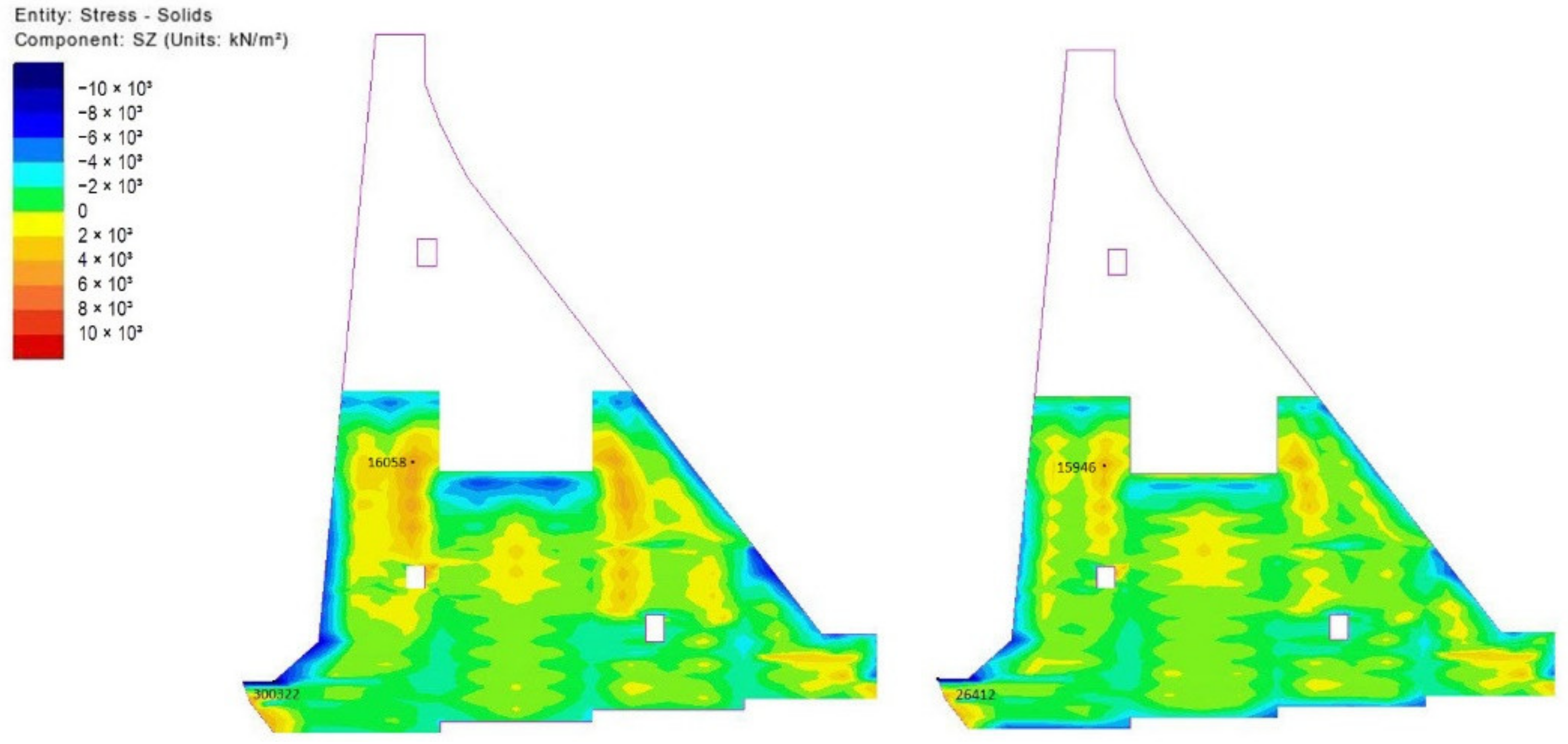
- The 512th day from the beginning of construction (13 March of the third year, after casting the last block 78);
- The 1080th day from the beginning of construction (02 October of the fourth year, during the filling of the reservoir);
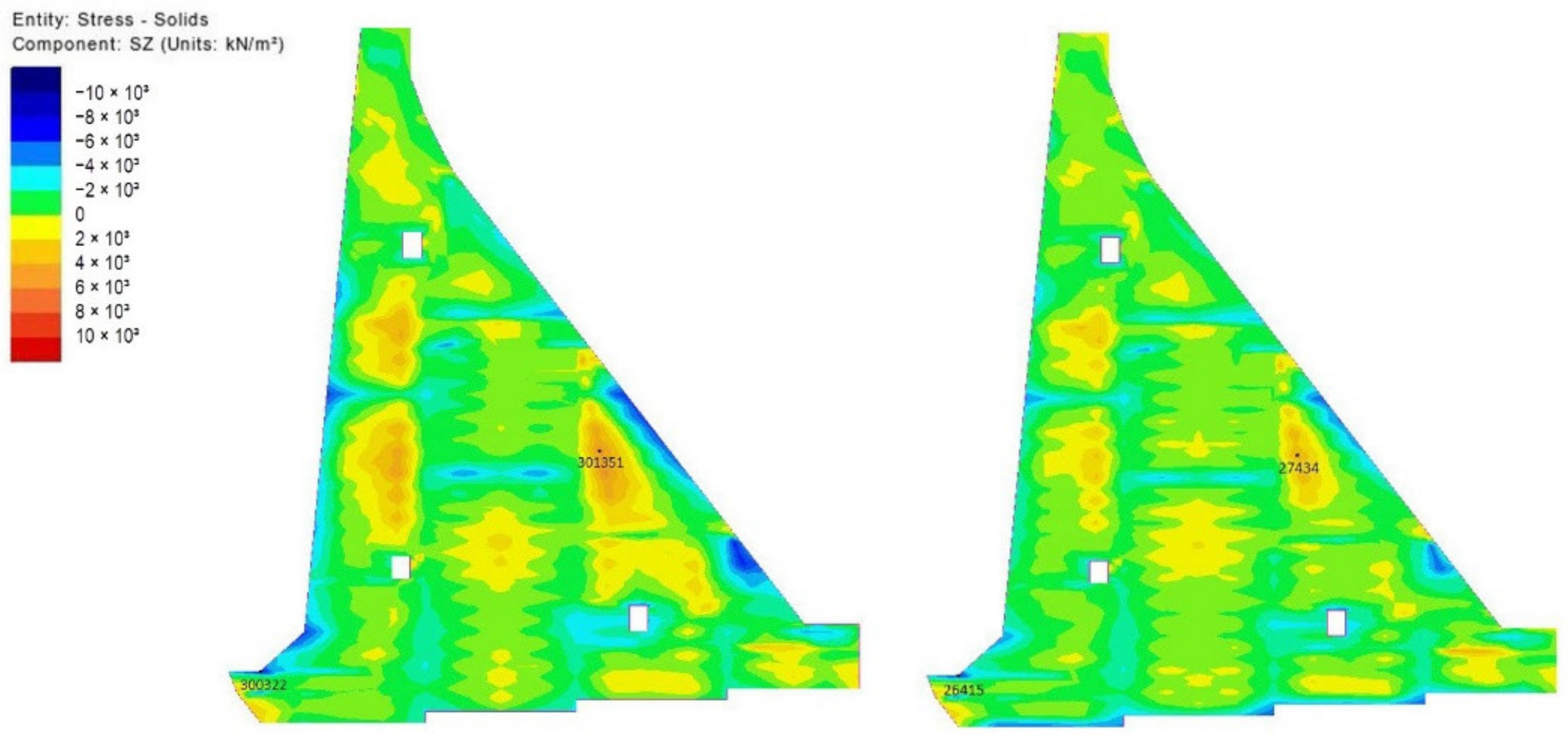
- The 1804th day from the beginning of construction (25 September of the sixth year, during the service life of the structure).
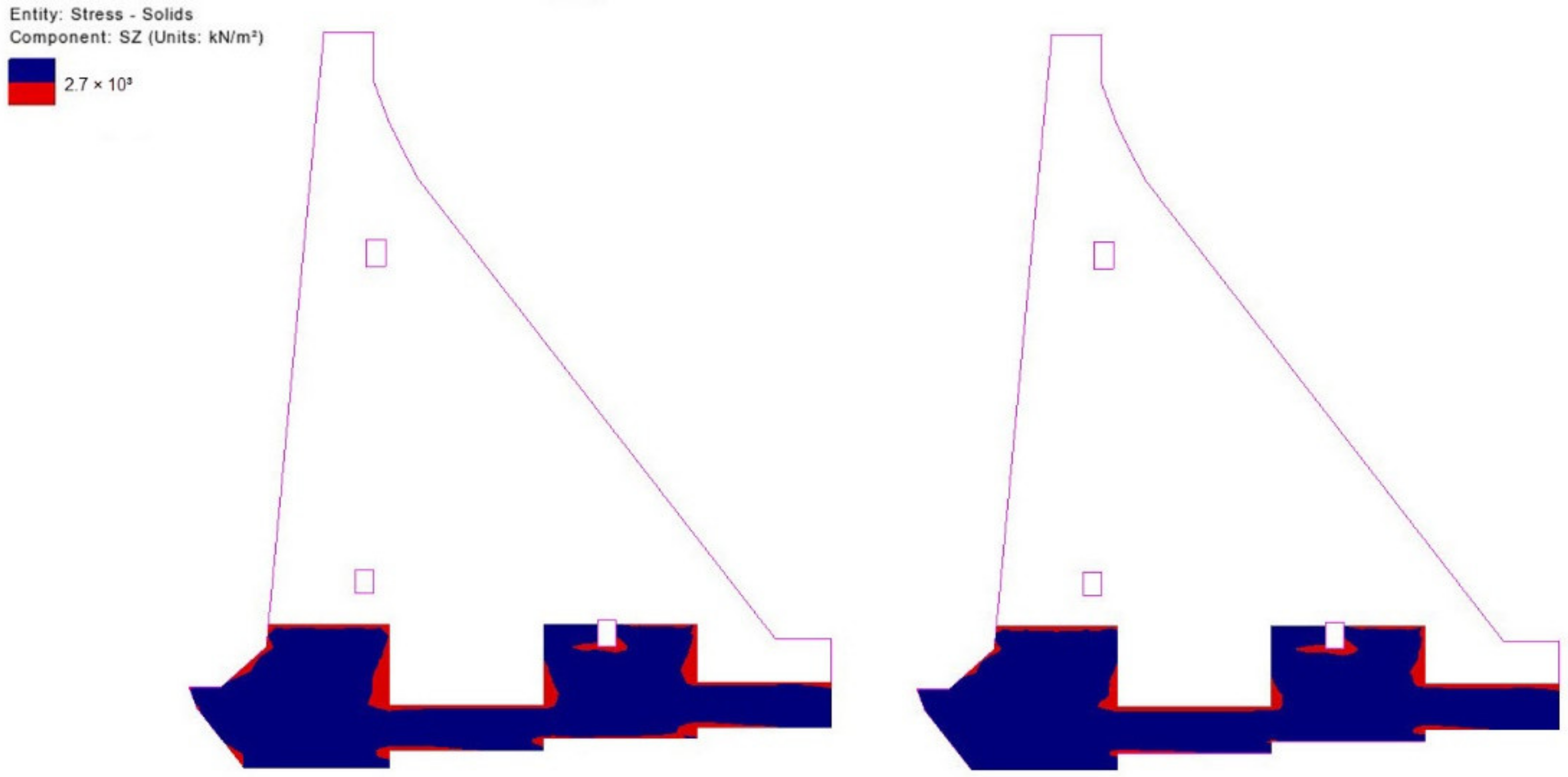
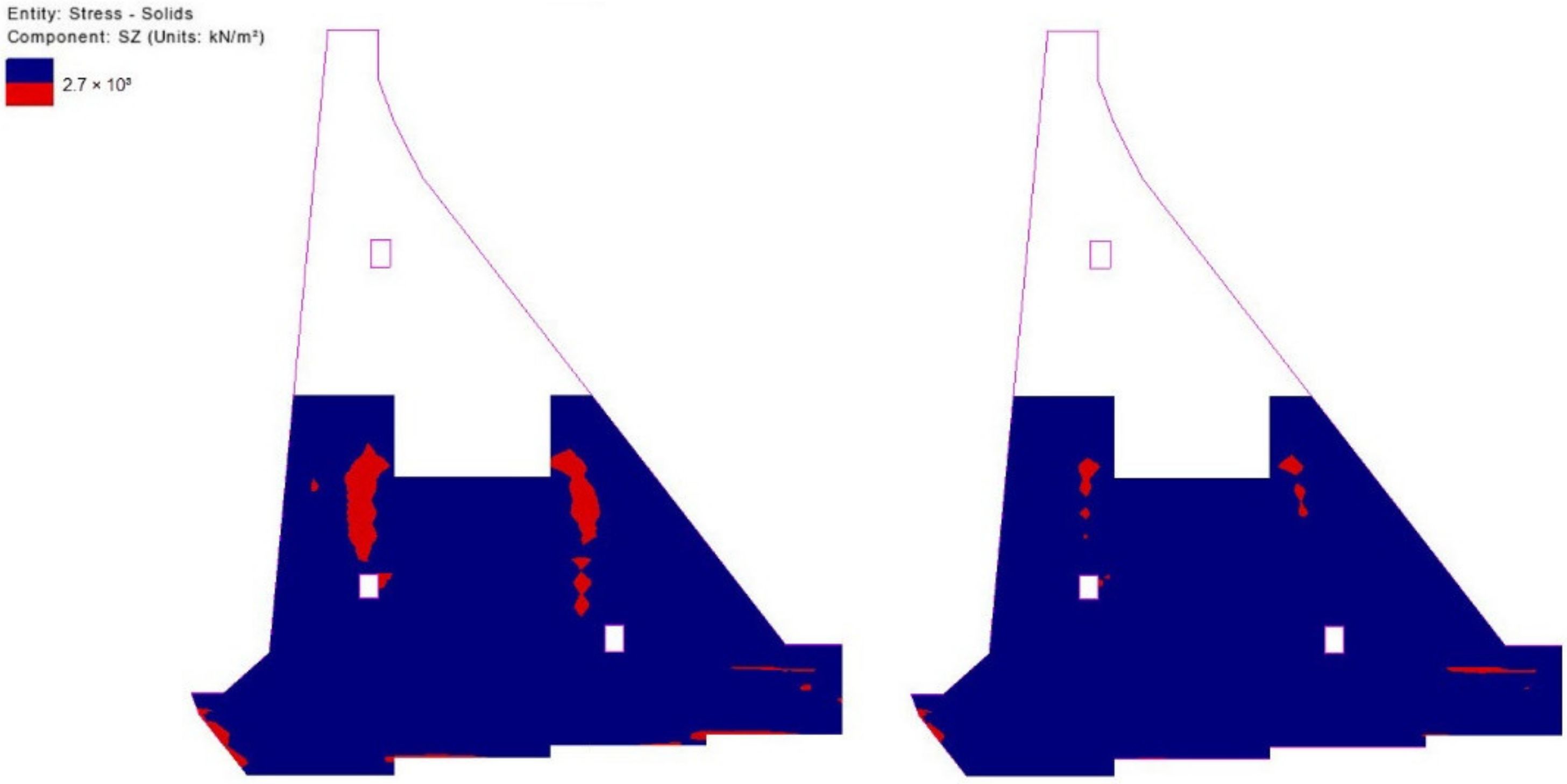
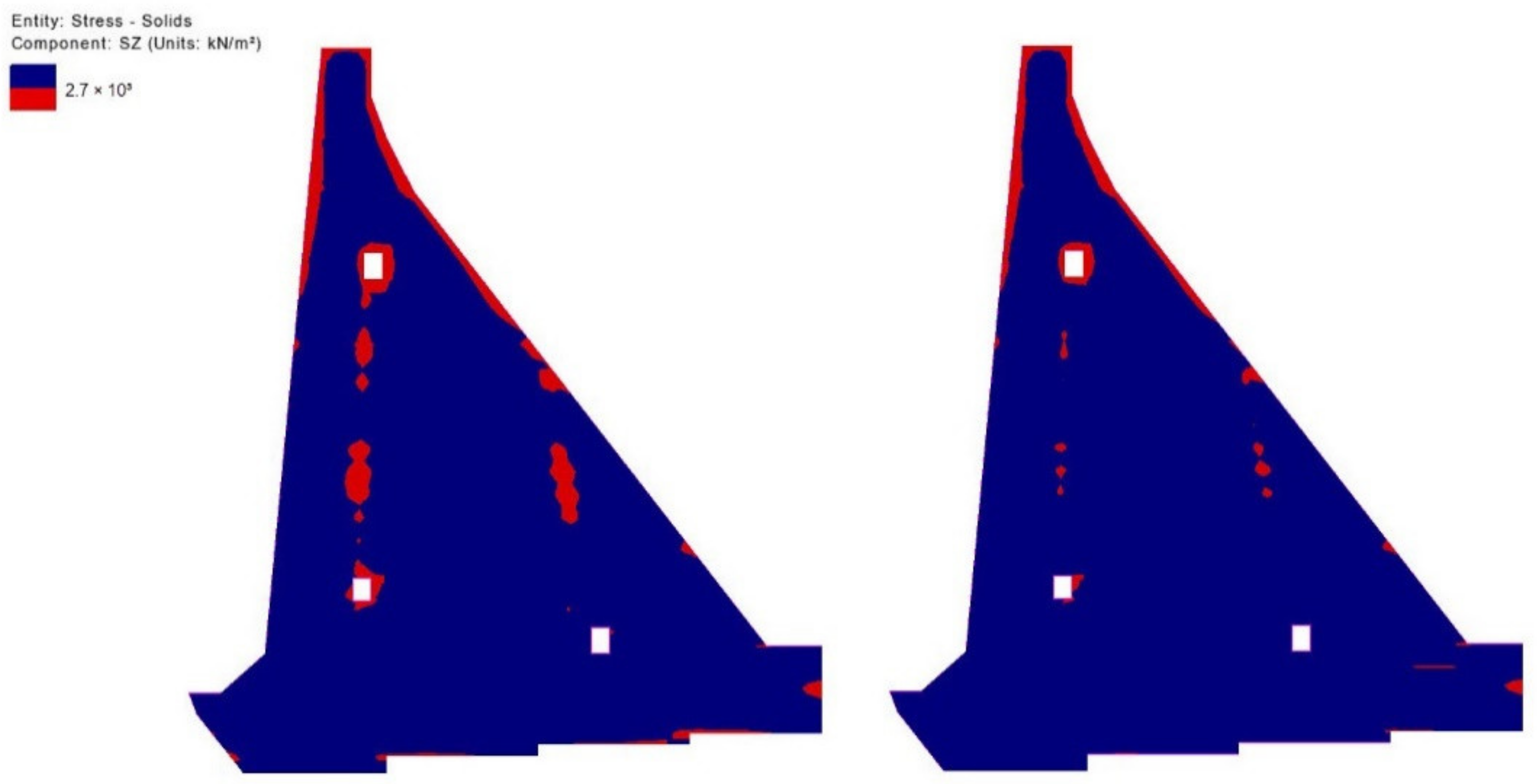
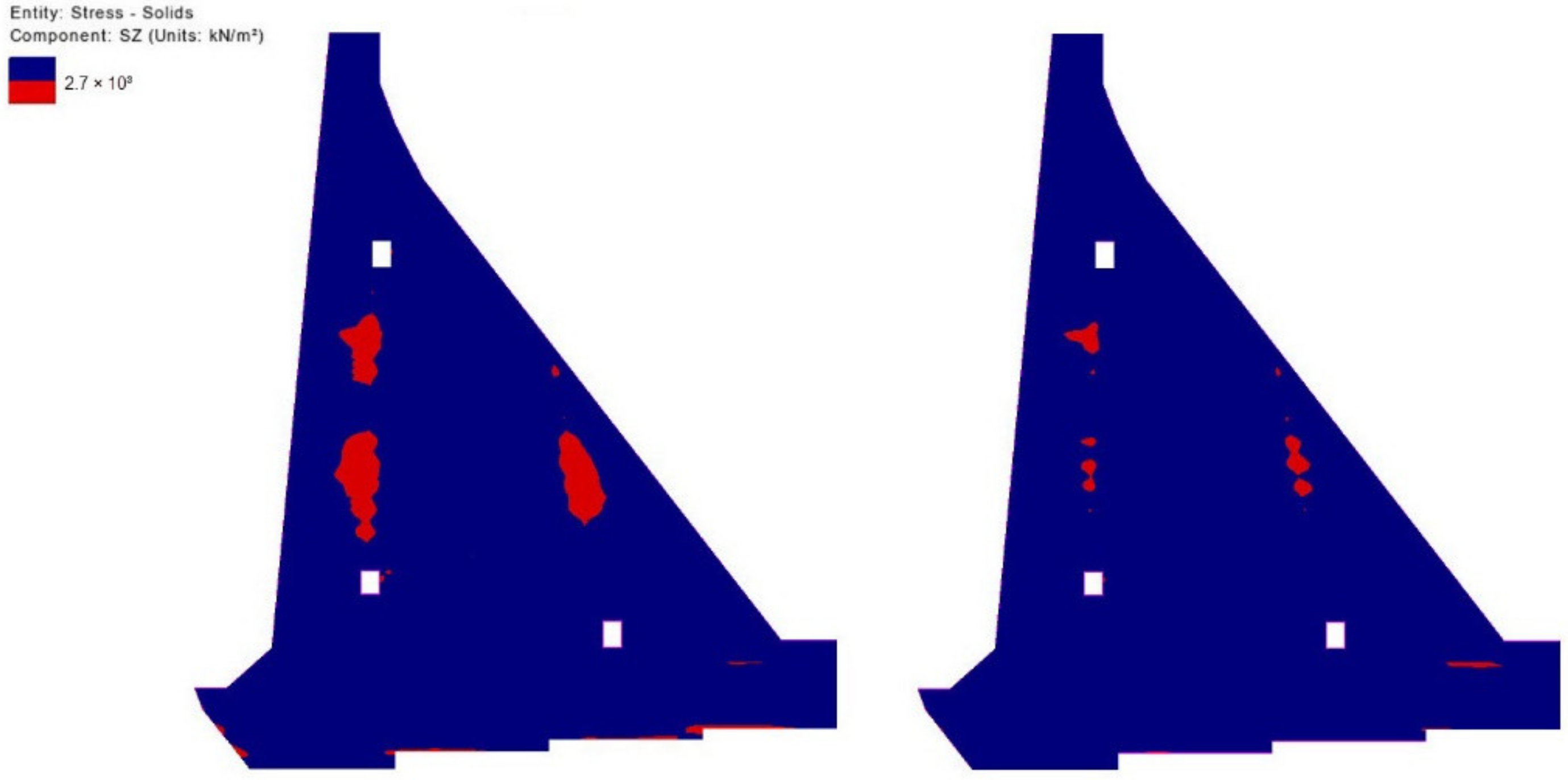
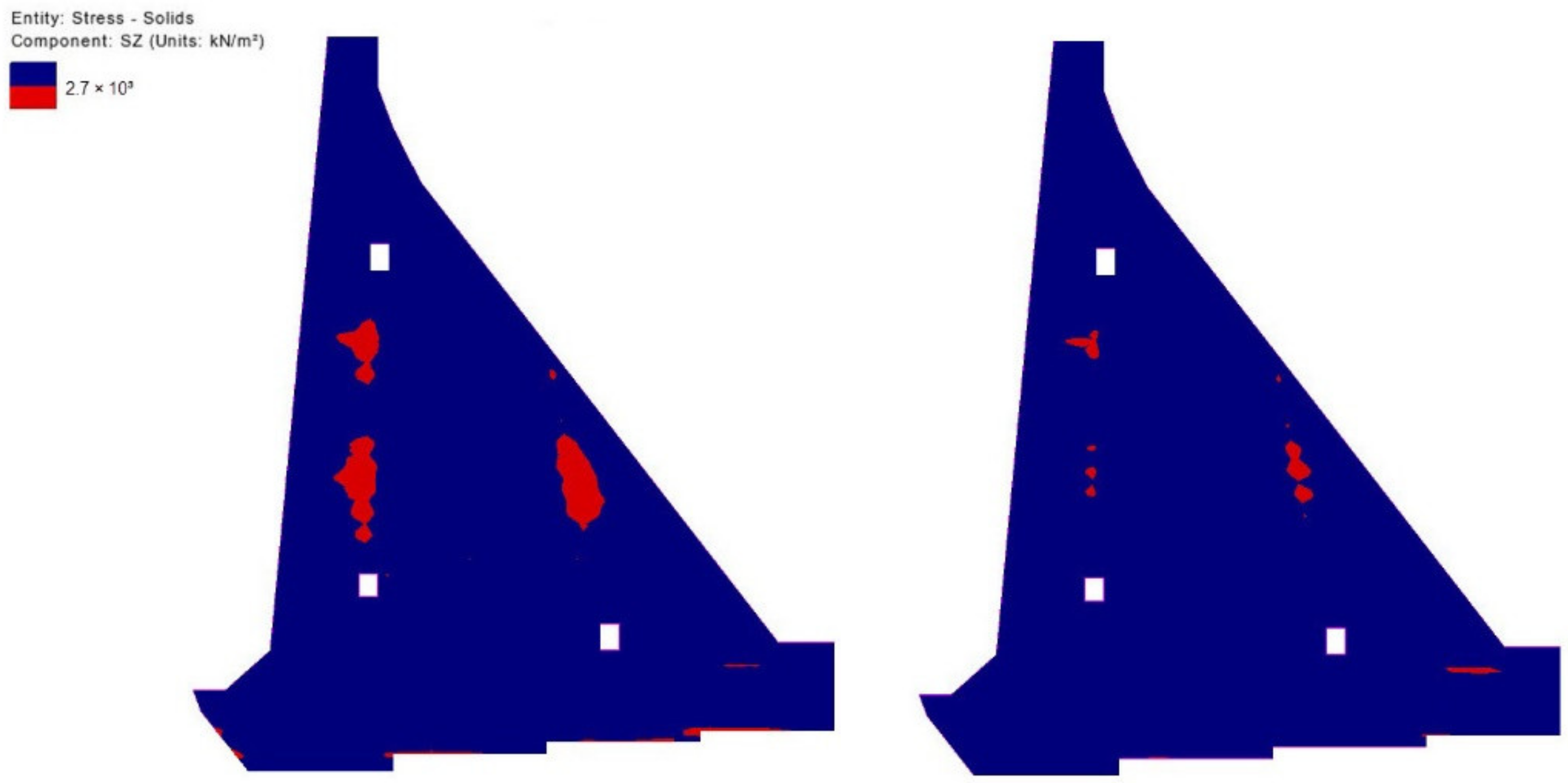
5.3. Results of Stress Field Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuzmanović, V. Thermal-Stress Analysis of Roller Compacted Concrete Dams. Ph.D. Thesis, Faculty of Civil Engineering, University of Belgrade, Belgrade, Serbia, 2007. [Google Scholar]
- Blomdahl, J.; Malm, R.; Nordström, E.; Hassanzadeh, M. Minimiarmering i Vattenkraftens Betongkonstruktioner; Energiforsk: Stockholm, Sweden, 2016; pp. 48–50. [Google Scholar]
- Malm, R. Guideline for FE Analyses of Concrete Dams; Energiforsk: Stockholm, Sweden, 2016; pp. 100–102. [Google Scholar]
- Tanchev, L. Dams and Appurtenant Hydraulic Structures, 2nd ed.; Taylor & Francis Group: London, UK, 2014; pp. 551–563. [Google Scholar]
- Eurocode 2: EN 1992-1-1:2015; Design of Concrete Structures—General Rules and Rules for Buildings. British Standards Institution: London, UK, 2015.
- Eurocode 2: EN 1992-1-2:2004; Design of Concrete Structures—General Rules—Structural Fire Design. British Standards Institution: London, UK, 2004.
- Savić, L. Uvod u Hidrotehničke Građevine, 2nd ed.; Građevinski Fakultet: Belgrade, Serbia, 2009; pp. 100–103. [Google Scholar]
- Cotoi, T. Dam Engineering. Available online: http://www.scribd.com/doc/280436707/Dam-Engineering-GRV-BUTT (accessed on 5 May 2019).
- Léger, P.; Venturelli, J.; Bhattacharjee, S.S. Seasonal temperature and stress distributions in concrete gravity dams. Part 1: Modeling. Can. J. Civ. Eng. 1993, 20, 999–1017. [Google Scholar] [CrossRef]
- Léger, P.; Venturelli, J.; Bhattacharjee, S.S. Seasonal temperature and stress distributions in concrete gravity dams. Part 2: Behavior. Can. J. Civ. Eng. 1993, 20, 1018–1029. [Google Scholar] [CrossRef]
- Saetta, A.; Scotta, R.; Vitaliani, R. Stress analysis of concrete structures subjected to variable thermal loads. J. Struct. Eng. 1995, 121, 446–457. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Simulation of construction of RCC dams-I: Temperature and aging. J. Struct. Eng. 2000, 126, 1053–1061. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Simulation of construction of RCC dams-II: Stress and damage. J. Struct. Eng. 2000, 126, 1062–1069. [Google Scholar] [CrossRef]
- Ponce-Farfán, C.; Santillán, D.; Toledo, M.Á. Thermal simulation of rolled concrete dams: Influence of the hydration model and the environmental actions on the thermal field. Water 2020, 12, 858. [Google Scholar] [CrossRef]
- Habib, A.; Houri, A.A.; Habib, M.; Elzokra, A.; Yildirim, U. Structural Performance and Finite Element Modeling of Roller Compacted Concrete Dams: A Review. Lat. Am. J. Solids Struct. 2021, 18, 1–18. [Google Scholar] [CrossRef]
- James, R.J.; Dollar, D.A. Thermal Engineering for the Construction of Large Concrete Arch Dams. In Proceedings of the 6th ASME-JSME Thermal Engineering Joint Conference, Kohala Coast, HI, USA, 16–20 March 2003. [Google Scholar]
- Malkawi, A.; Mutasher, S.; Qiu, T. Thermal-structural modeling and temperature control of roller compacted concrete gravity dam. Perform. Constr. Facil. 2003, 17, 177–187. [Google Scholar] [CrossRef]
- Sheibany, F.; Ghaemian, M. Effects of environmental action on thermal stress analysis of Karaj concrete arch dam. J. Eng. Mech. 2006, 132, 532–544. [Google Scholar] [CrossRef]
- Castilho, E.; Schclar, N.; Tiago, C.; Farinha, M.L.B. FEA model for the simulation of the hydration process and temperature evolution during the concreting of an arch dam. Eng. Struct. 2018, 174, 165–177. [Google Scholar] [CrossRef]
- Salazar, F.; Vicente, D.J.; Irazábal, J.; De-Pouplana, I.; San Mauro, J. A Review on Thermo-mechanical Modelling of Arch Dams During Construction and Operation: Effect of the Reference Temperature on the Stress Field. Arch. Comput. Methods Eng. 2020, 27, 1681–1707. [Google Scholar] [CrossRef]
- Kuzmanović, V.; Savić, L.; Mladenović, N. Computation of Thermal-Stresses and Contraction Joint Distance of RCC Dams. J. Therm. Stresses 2013, 36, 112–134. [Google Scholar] [CrossRef]
- Kuzmanović, V.; Savić, L.; Mladenović, N. Thermal-stress behaviour of RCC gravity dams. FME Trans. 2015, 43, 30–34. [Google Scholar] [CrossRef]
- Sayed, A.; Ezzeldin, Y.; Amr, A.A.; Rana, A.E. Concrete dams: Thermal-stress and construction stage analysis. Dams Reserv. 2018, 28, 12–30. [Google Scholar] [CrossRef]
- Ayotte, E.; Massicotte, B.; Houde, J.; Gocevski, V. Modeling the thermal stresses at early ages in a concrete monolith. ACI Mater. J. 1997, 94, 577–587. [Google Scholar]
- Khorasani, M.; Ghasemi, A.; Leary, M.; Sharabian, E.; Cordova, L.; Gibson, I.; Downing, D.; Bateman, S.; Brandt, M.; Rolfe, B. The effect of absorption ratio on meltpool features in laser-based powder bed fusion of IN718. Opt. Laser Technol. 2022, 153, 108263. [Google Scholar] [CrossRef]
- Khan, H.M.; Waqar, S.; Koç, E. Evolution of temperature and residual stress behavior in selective laser melting of 316L stainless steel across a cooling channel. Rapid Prototyp. J. 2022, 28, 1272–1283. [Google Scholar] [CrossRef]
- Sezer, H.; Tang, J.; Ahsan, A.N.; Kaul, S. Modeling residual thermal stresses in layer-by-layer formation of direct metal laser sintering process for different scanning patterns for 316L stainless steel. Rapid Prototyp. J. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Shaikh, M.Q.; Berfield, T.A.; Atre, S.V. Residual stresses in additively manufactured parts: Predictive simulation and experimental verification. Rapid Prototyp. J. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Jansen, R.B. Dams and Public Safety; US Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 1983; pp. 89–98. [Google Scholar]
- ICOLD (International Commission on Large Dams). Dam Safety Guidelines; ICOLD Bulletin 59; ICOLD: Paris, France, 1987. [Google Scholar]
- ICOLD (International Commission on Large Dams). Basic Elements in a Dam Safety Process; ICOLD Bulletin 138; ICOLD: Paris, France, 2009. [Google Scholar]
- Kim, S.G.; Wang, K. Effect of heat generation from cement hydration on mass concrete placement. Masters Abstr. Int. 2010, 49, 3. [Google Scholar]
- Bofang, Z. On pipe cooling of concrete dams. J. Hydraul. Eng. 2010, 5, 505–513. [Google Scholar]
- Bofang, Z. Compound Methods for Computing the Effect of Pipe Cooling in Concrete Dams. Water Resour. Hydropower Eng. 2013, 34, 47–50. [Google Scholar]
- ICOLD (International Commission on Large Dams). Dam Monitoring—General Considerations; ICOLD Bulletin 60; ICOLD: Paris, France, 1998. [Google Scholar]
- Swiss Committee on Dams. Methods of analysis for the prediction and the verification of dam behaviour. In Proceedings of the 21st Congress of the International Commission on Large Dams, Montreal, Switzerland, 16–20 June 2003. [Google Scholar]
- Bofang, Z. Introduction. In Thermal Stresses and Temperature Control of Mass Concrete; Butterworth-Heinemann: Oxford, UK, 2014; pp. 1–10. [Google Scholar] [CrossRef]
- Bofang, Z. Precooling and Surface Cooling of Mass Concrete. In Thermal Stresses and Temperature Control of Mass Concrete; Butterworth-Heinemann: Oxford, UK, 2014; pp. 401–408. [Google Scholar] [CrossRef]
- USACE. Gravity Dam Design; US Army Corps of Engineers: Washington, DC, USA, 1995; p. 2-1. [Google Scholar]
- Petrović, P. Hidrotehničke Konstrukcije, drugi deo; Građevinski Fakultet: Belgrade, Srbija, 2002. [Google Scholar]
- Schindler, A.K.; Folliard, K.J. Influence of supplementary cementing materials on the heat of hydration of concrete. In Proceedings of the Advances in Cement and Concrete IX Conference, Copper Mountain Conference Resort in Colorado, Copper Mountain, CO, USA, 10–14 August 2003. [Google Scholar]
- Malcolm Dunstan & Associates. Available online: https://rccdams.co.uk/dams/platanovryssi (accessed on 1 March 2022).
- LUSAS. Available online: https://www.lusas.com (accessed on 1 March 2022).
- Platanovryssi Hydroelectric Project. Measurement Results; Public Power Corporation: Athens, Greece, 2004. [Google Scholar]
- Bofang, Z. Prediction of Water Temperature in Deep Reservoirs. Dam Eng. 1997, 8, 13–25. [Google Scholar]




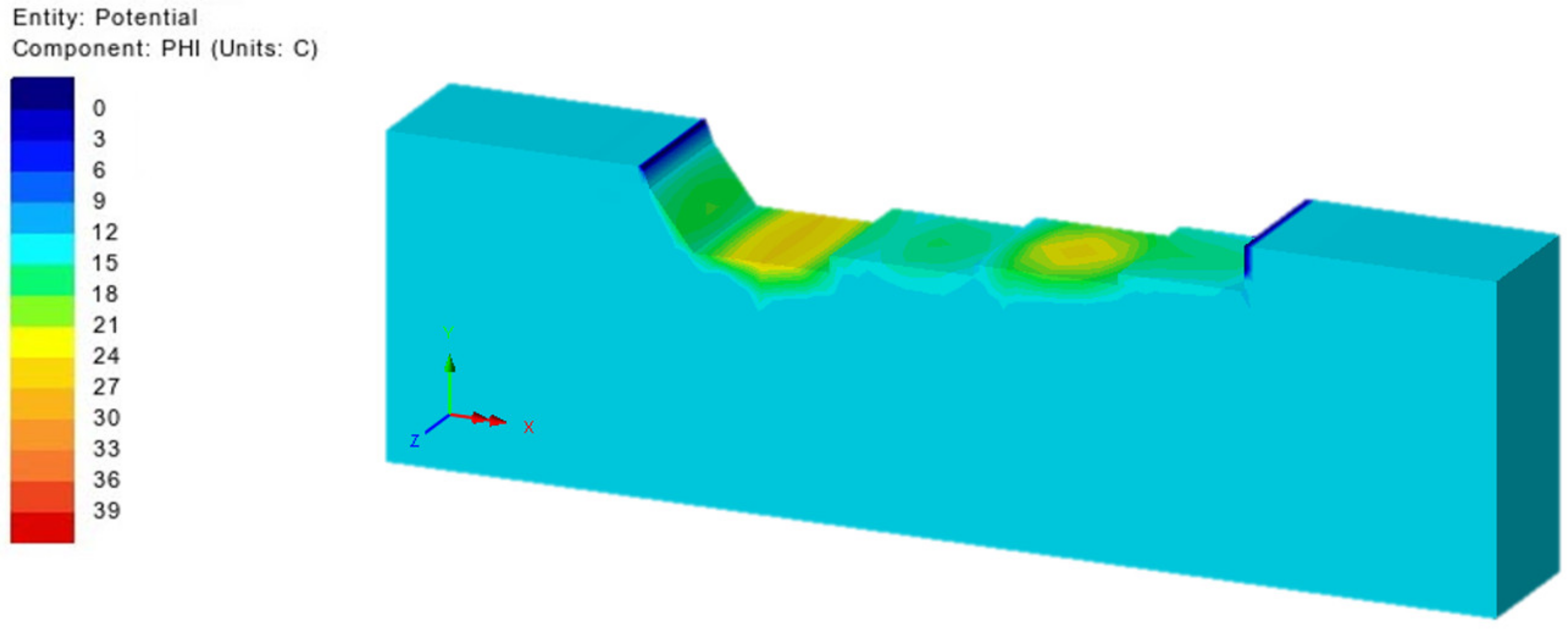
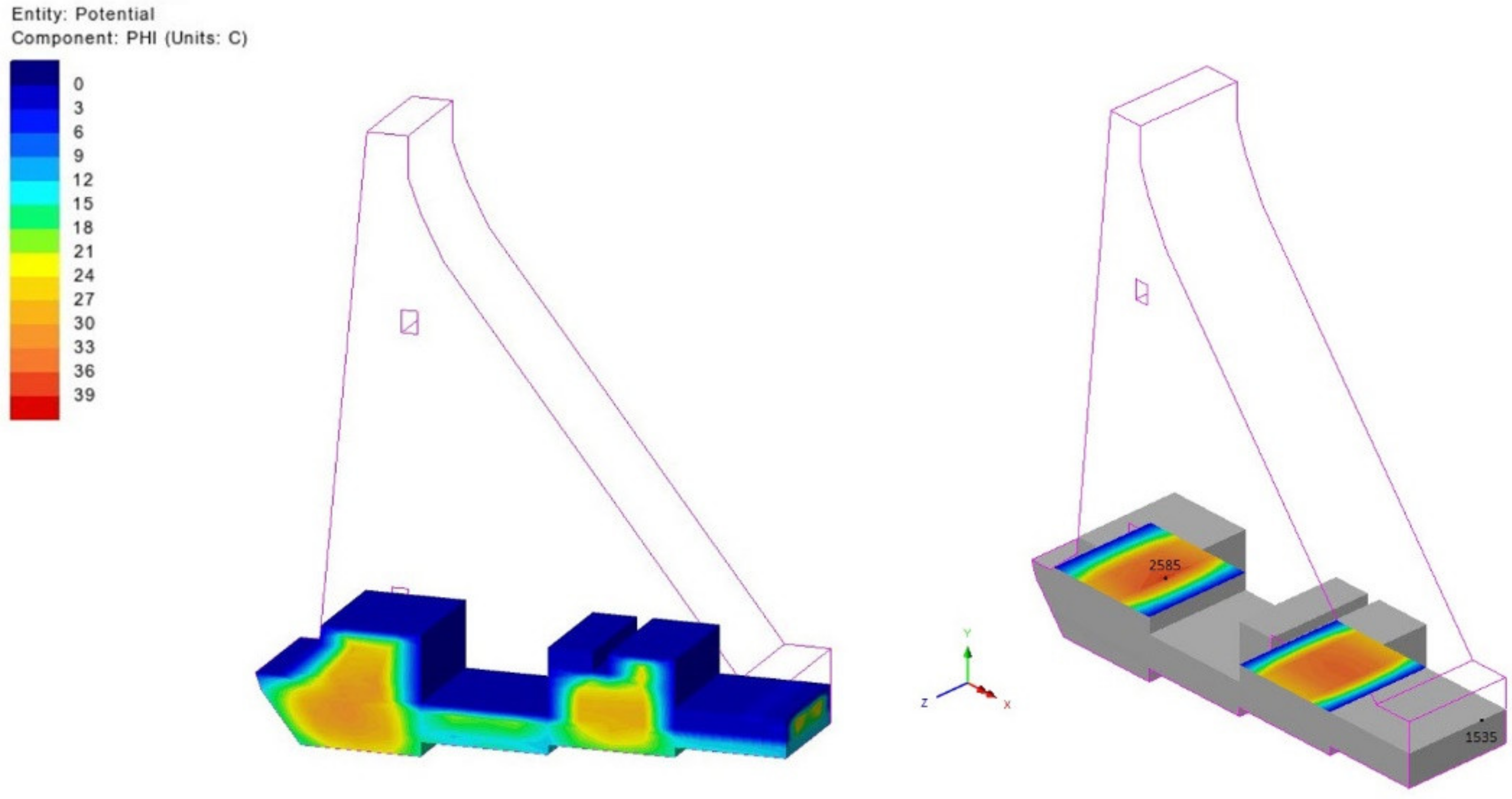

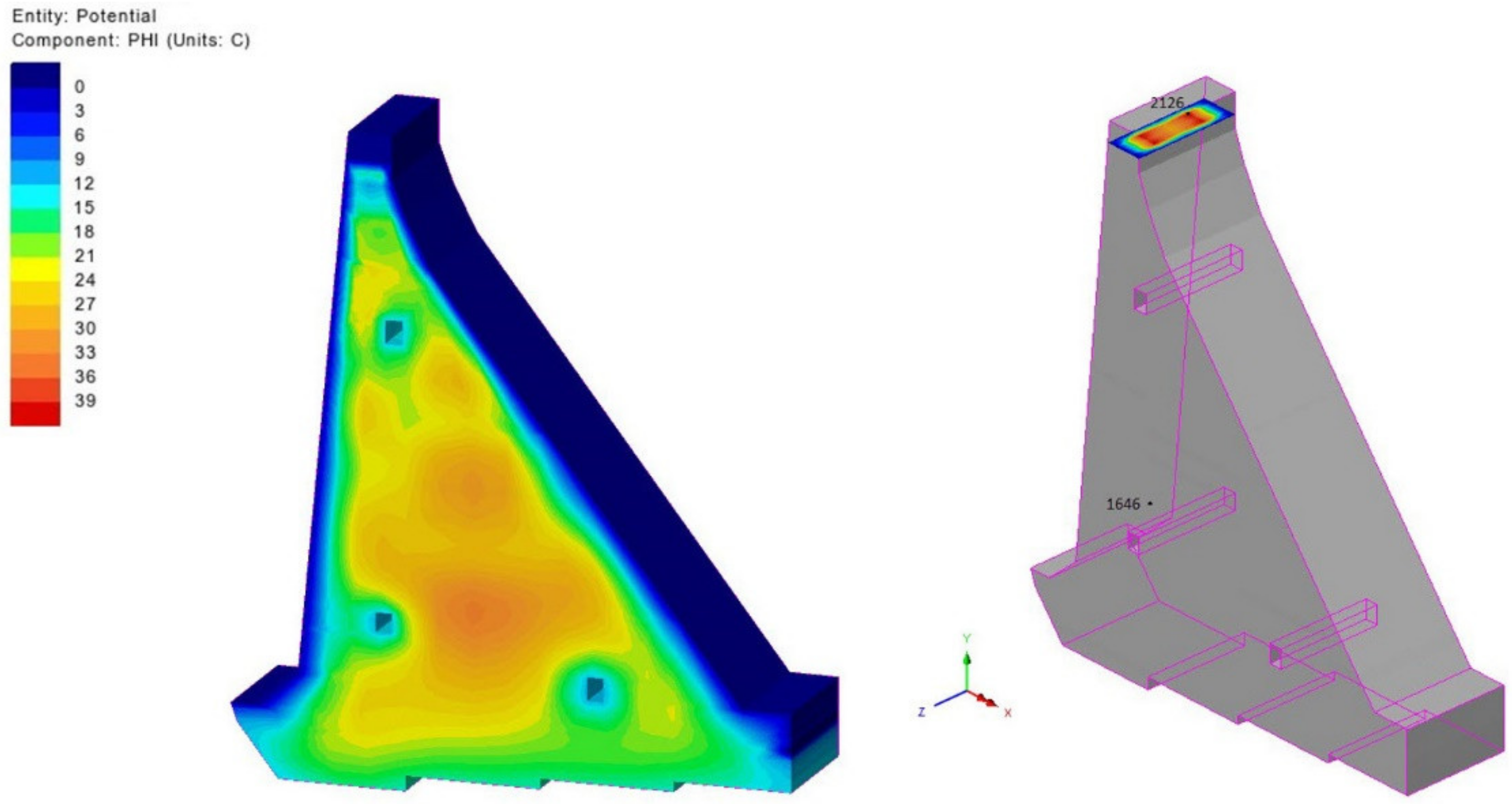
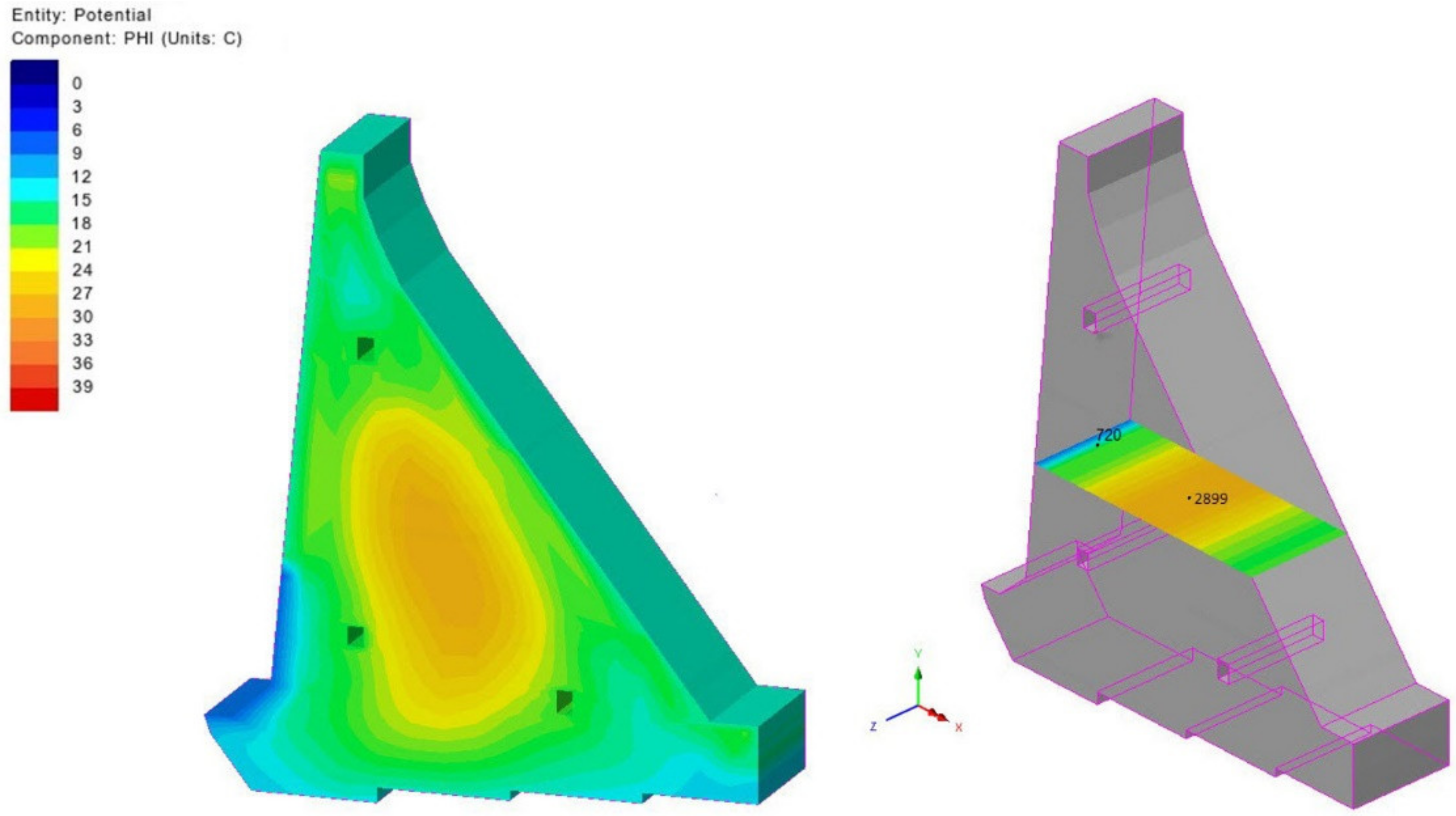





| Date/Time | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X 8-23 | 10.2 | 11.5 | 12.7 | 13.9 | 15.5 | 18.0 | 20.5 | 19.0 | 15.4 | 12.4 | 10.7 | 9.0 |
| X-XI 23-8 | 4.2 | 5.4 | 6.7 | 7.9 | 9.1 | 9.5 | 10.0 | 9.4 | 7.5 | 5.4 | 4.2 | 3.0 |
| XI 8-23 | 4.6 | 5.2 | 5.8 | 6.5 | 7.4 | 9.0 | 10.6 | 9.6 | 7.9 | 6.4 | 5.2 | 4.0 |
| XI-XII 23-8 | 2.2 | 2.4 | 2.6 | 2.8 | 3.3 | 4.5 | 5.8 | 5.4 | 4.5 | 3.7 | 2.8 | 2.0 |
| XII 8-23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.4 | 2.5 | 4.5 | 3.6 | 2.5 | 1.8 | 1.0 | 0.0 |
| XII-I 23-8 | 6.2 | 6.4 | 6.6 | 6.8 | 7.1 | 7.5 | 7.9 | 7.3 | 7.0 | 6.8 | 6.4 | 6.0 |
| I 8-23 | −1.8 | −1.6 | −1.4 | −1.2 | −0.5 | 1.5 | 3.6 | 3.3 | 2.7 | −0.4 | −1.2 | −2.0 |
| I-II 23-8 | 1.2 | 1.4 | 1.6 | 1.8 | 2.2 | 3.0 | 3.8 | 3.3 | 2.5 | 1.8 | 1.5 | 1.0 |
| II 8-23 | 2.0 | 2.0 | 2.0 | 2.0 | 2.4 | 4.0 | 5.6 | 5.4 | 4.5 | 3.6 | 2.9 | 2.0 |
| II-III 23-8 | 0.2 | 0.4 | 0.6 | 0.8 | 1.4 | 3.4 | 5.6 | 5.4 | 4.5 | 3.3 | 1.6 | 0.0 |
| III 8-18 | 1.2 | 1.4 | 1.6 | 1.8 | 2.3 | 3.5 | 4.8 | 3.7 | 2.5 | 2.0 | 1.6 | 1.0 |
| III 18-31 | 1.0 | 1.0 | 1.0 | 1.0 | 1.2 | 2.5 | 3.7 | 4.0 | 4.0 | 3.5 | 2.2 | 1.0 |
| IV 1-14 | 4.6 | 4.7 | 4.8 | 4.9 | 5.4 | 7.5 | 9.6 | 10.0 | 9.0 | 7.4 | 6.0 | 4.5 |
| IV 15-28 | 4.6 | 4.2 | 3.7 | 3.3 | 3.9 | 8.5 | 13.1 | 14.0 | 13.5 | 11.7 | 8.3 | 5.0 |
| IV-V 29-11 | 15.2 | 16.0 | 16.7 | 17.4 | 18.4 | 20.5 | 22.6 | 23.0 | 21.5 | 19.1 | 16.8 | 14.5 |
| V 12-26 | 13.0 | 14.1 | 15.1 | 16.2 | 17.7 | 21.0 | 24.3 | 24.3 | 23.0 | 20.3 | 16.2 | 12.0 |
| V-VI 27-9 | 15.2 | 14.9 | 14.6 | 14.2 | 14.9 | 19.5 | 24.1 | 25.0 | 24.0 | 21.7 | 18.6 | 15.5 |
| VI 10-24 | 17.0 | 17.0 | 17.0 | 17.0 | 17.9 | 22.5 | 27.1 | 28.0 | 26.5 | 23.7 | 20.3 | 17.0 |
| VI-VII 25-7 | 21.2 | 20.9 | 20.6 | 20.2 | 21.0 | 26.0 | 31.0 | 31.3 | 29.5 | 26.9 | 24.2 | 21.5 |
| VII 8-22 | 24.0 | 22.9 | 21.9 | 20.8 | 20.9 | 25.5 | 30.1 | 30.1 | 28.5 | 26.7 | 25.8 | 25.0 |
| VII-VIII 23-5 | 20.7 | 19.5 | 20.0 | 21.7 | 23.8 | 28.0 | 32.2 | 33.0 | 32.0 | 29.5 | 25.7 | 22.0 |
| VIII 6-19 | 20.3 | 18.7 | 19.0 | 20.7 | 22.7 | 26.0 | 29.3 | 30.7 | 29.5 | 27.0 | 24.5 | 22.0 |
| VIII-IX 20-2 | 16.2 | 15.3 | 16.0 | 17.7 | 19.6 | 22.5 | 25.4 | 24.7 | 23.5 | 22.0 | 19.5 | 17.0 |
| IX 3-9 | 15.2 | 14.3 | 14.7 | 16.0 | 17.5 | 20.0 | 22.5 | 23.0 | 22.0 | 20.2 | 18.1 | 16.0 |
| Month | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | 10 | 10 | 12 | 14 | 16 | 20 | 22 | 22 | 20 | 16 | 12 | 10 |
| Month | X | XI | XII | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|---|---|---|
| T (°C) | 10.0 | 9.7 | 9.5 | 9.5 | 9.7 | 9.7 | 12.3 | 13.1 | 12.9 |
| Parameter | Meaning | Value | Unit |
|---|---|---|---|
| k | Thermal conductivity coefficient | 1.80 | W/(m K) |
| c | Specific heat capacity | 950.0 | J/(kg K) |
| α | Coefficient of thermal expansion | 11.5·10−6 | 1/°C |
| h | Combined convective heat transfer coefficient | 20.10 | W/(m2 K) |
| Tref | Reference temperature | 13.0 | °C |
| Meaning | Value | Unit |
|---|---|---|
| Cement ratio (type I) in the concrete mass M (for Portland cement) | 50 | kg/m3 |
| 12.5·10−3 | 1/h | |
| Water-cement ratio Fly ash ratio in the concrete mass | 0.47 | - |
| 225.0 | kg/m3 | |
| CaO ratio in the fly ash | 17.0 | % |
| Parameter | Meaning | Value | Unit |
|---|---|---|---|
| k | Thermal conductivity coefficient | 2.40 | W/(m K) |
| c | Specific heat capacity | 880.0 | J/(kg K) |
| α | Coefficient of thermal expansion | 9.0·10−6 | 1/°C |
| Parameter | Meaning | Value | Unit |
|---|---|---|---|
| Volume density | 2360.0 | kg/m3 | |
| E | Elastic modulus | 30.0 | GPa |
| ν | Poisson’s ratio | 0.20 | - |
| Parameter | Meaning | Value | Unit |
|---|---|---|---|
| Volume density | 2430.0 | kg/m3 | |
| E | Elastic modulus | 20.0 | GPa |
| ν | Poisson’s ratio | 0.20 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirković, U.; Kuzmanović, V.; Todorović, G. Long-Term Thermal Stress Analysis and Optimization of Contraction Joint Distance of Concrete Gravity Dams. Appl. Sci. 2022, 12, 8163. https://doi.org/10.3390/app12168163
Mirković U, Kuzmanović V, Todorović G. Long-Term Thermal Stress Analysis and Optimization of Contraction Joint Distance of Concrete Gravity Dams. Applied Sciences. 2022; 12(16):8163. https://doi.org/10.3390/app12168163
Chicago/Turabian StyleMirković, Uroš, Vladan Kuzmanović, and Goran Todorović. 2022. "Long-Term Thermal Stress Analysis and Optimization of Contraction Joint Distance of Concrete Gravity Dams" Applied Sciences 12, no. 16: 8163. https://doi.org/10.3390/app12168163
APA StyleMirković, U., Kuzmanović, V., & Todorović, G. (2022). Long-Term Thermal Stress Analysis and Optimization of Contraction Joint Distance of Concrete Gravity Dams. Applied Sciences, 12(16), 8163. https://doi.org/10.3390/app12168163







