Model-Assisted Reduced-Order ESO Based Command Filtered Tracking Control of Flexible-Joint Manipulators with Matched and Mismatched Disturbances
Abstract
:1. Introduction
- (1)
- The FJMs in practical applications inevitably encounter various uncertainties including matched and mismatched disturbances. Unfortunately, the current researches focus on the matched disturbances, while the mismatched ones are not considered. Although the conventional ESO can transform a mismatched disturbance into a matched one, it requires a series of complex coordinate transformations, which make the control algorithms computationally complicated;
- (2)
- The backstepping technique employed for the control design of FJMs suffers from the drawback of “explosion of complexity”. Although the DSC or SCFCB can deal with the computation problem, the potential errors caused by the introduction of filters are not considered, which may greatly reduce the tracking accuracy.
- (1)
- The RESOs constructed with partial known model information are capable of estimating and compensating the matched and mismatched disturbances simultaneously. This is much different from the existing ESO-based methods where complex coordinate transformations are required to convert a mismatched disturbance into a matched one. The developed control algorithm is thus robust and efficient;
- (2)
- The inherent complexity problem of backstepping is addressed by employing the SCFB control, where the derivatives of the virtual control laws are obtained through integrations instead of differentiations. The transient control performance of the controller is thus improved;
- (3)
- The potential filtering errors caused by the command filters are taken into account, and they are reduced by the error compensation dynamic system, which improves the steady-state tracking control accuracy.
2. Problem Formulation
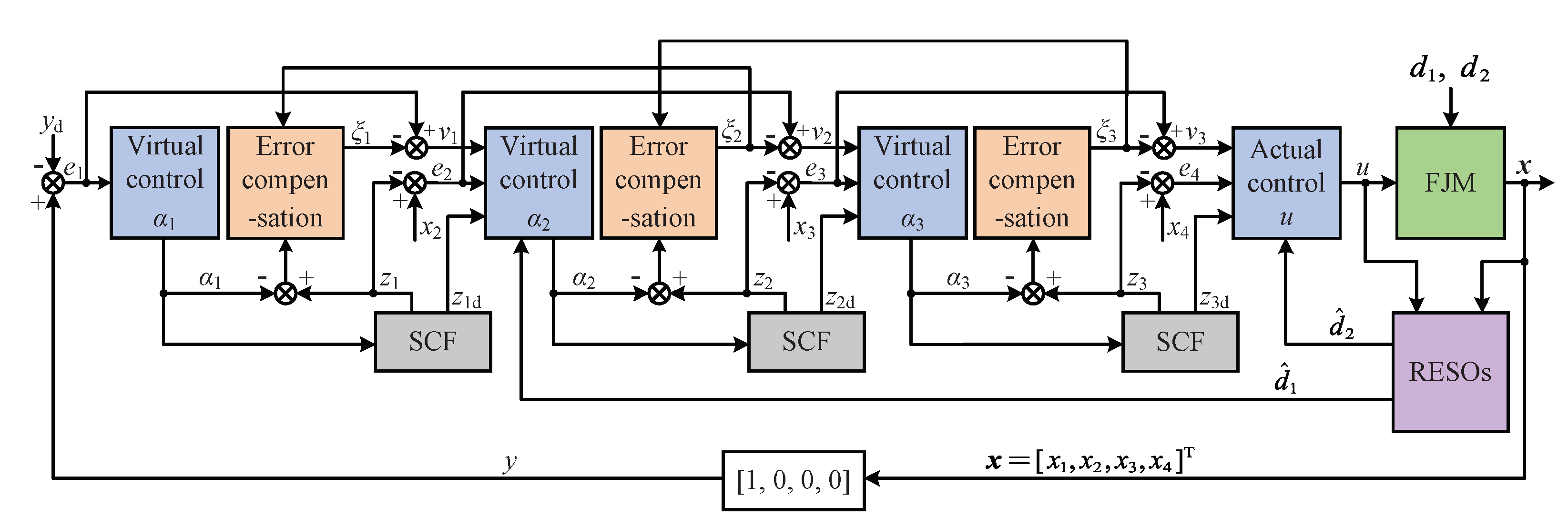
3. RESO-Based Backstepping Control Design
3.1. Reduced-Order ESO (RESO)
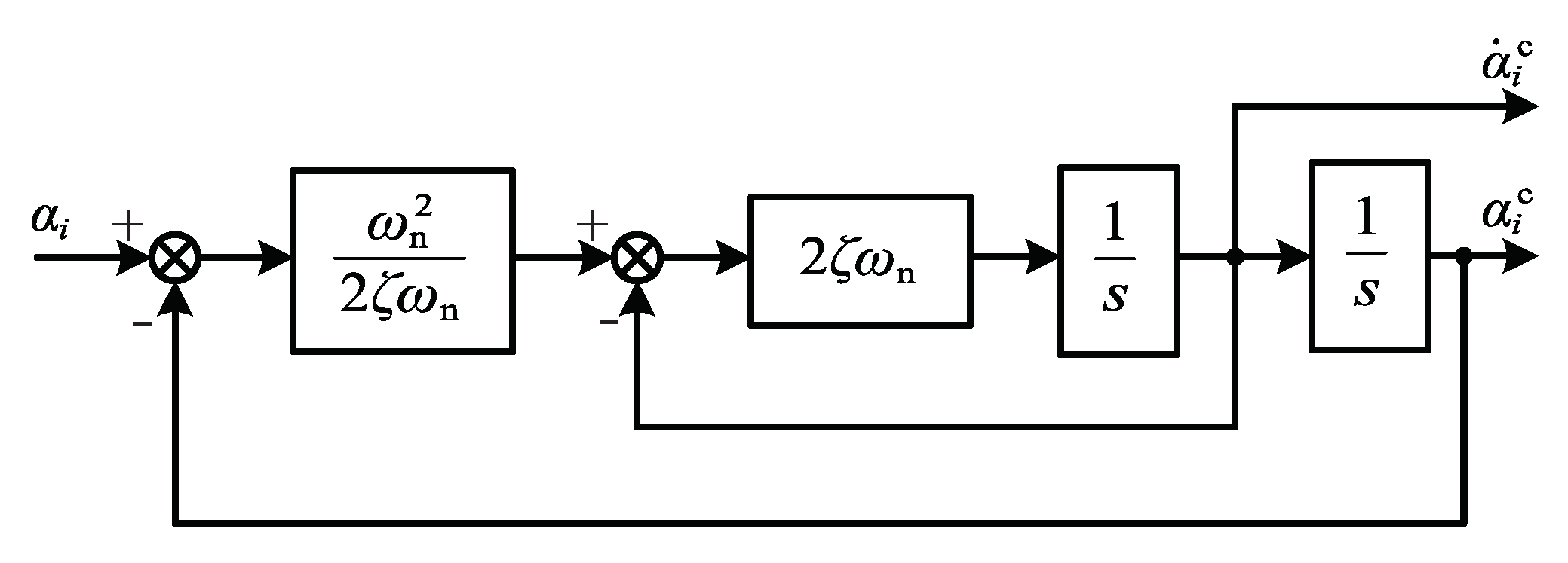
3.2. Second-Order Command Filtered Backstepping (SCFB) Controller
4. Stability Analysis
5. Numerical Simulations
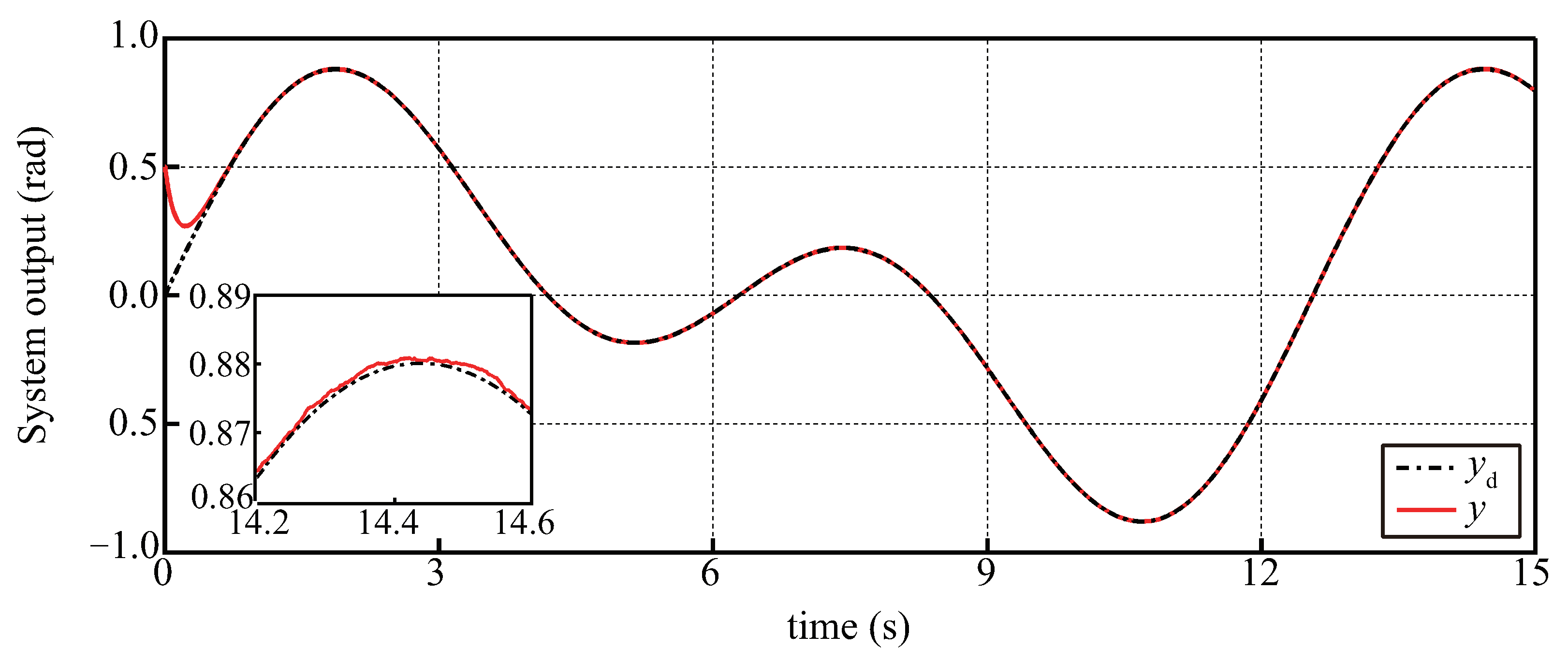
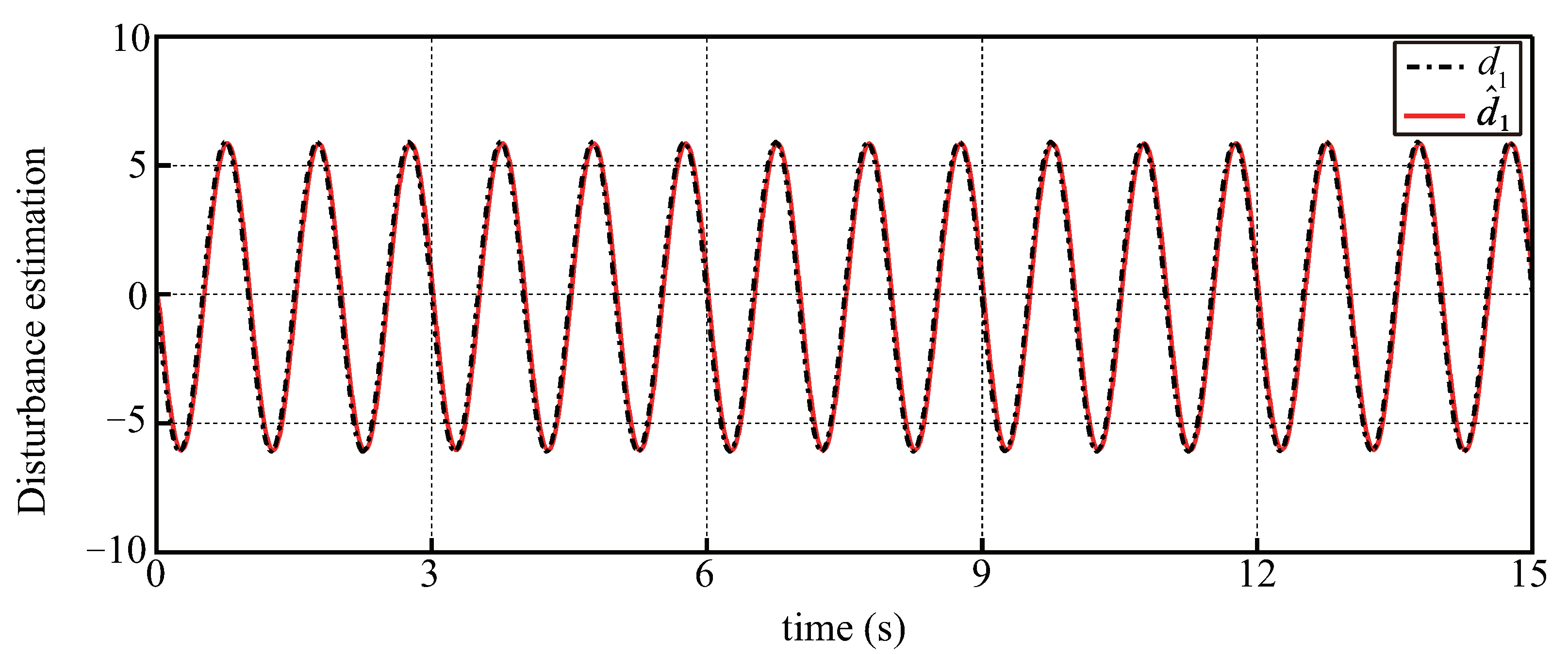
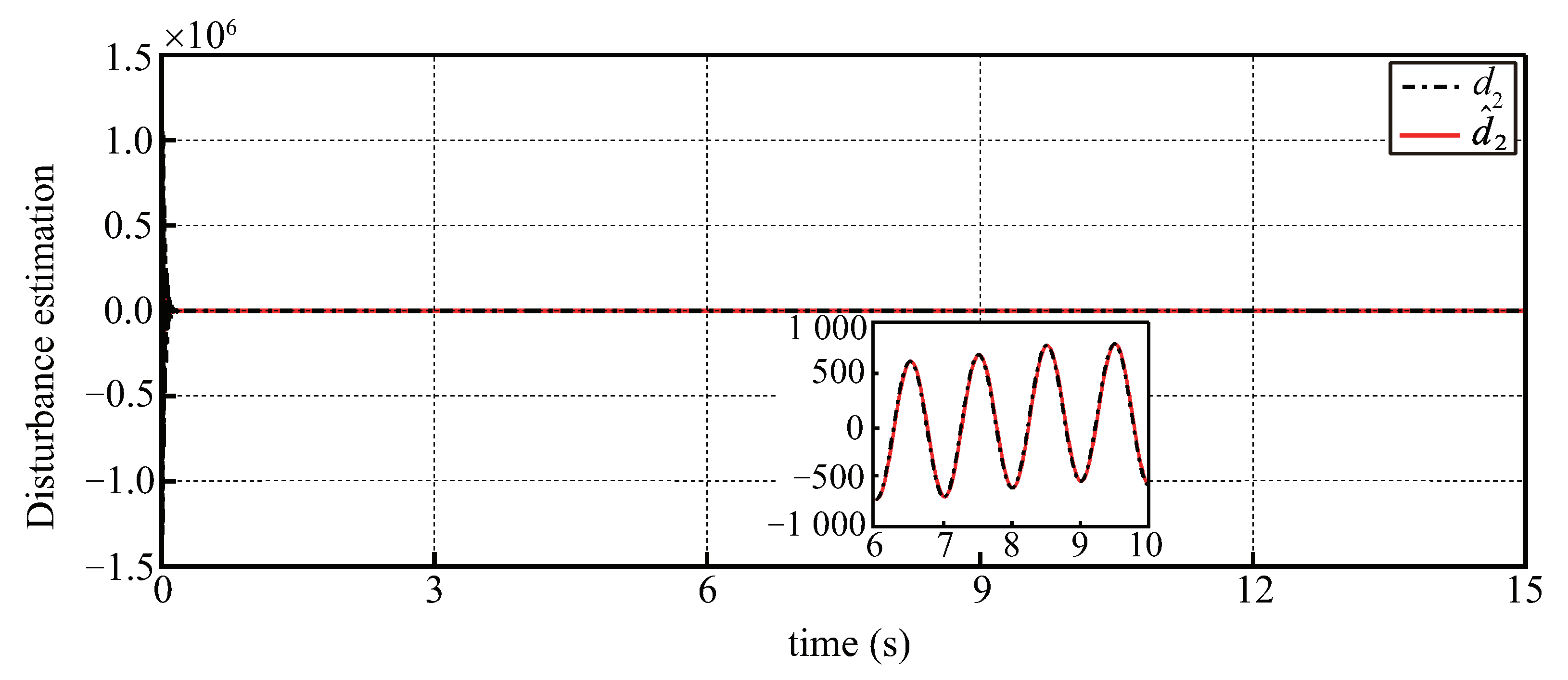
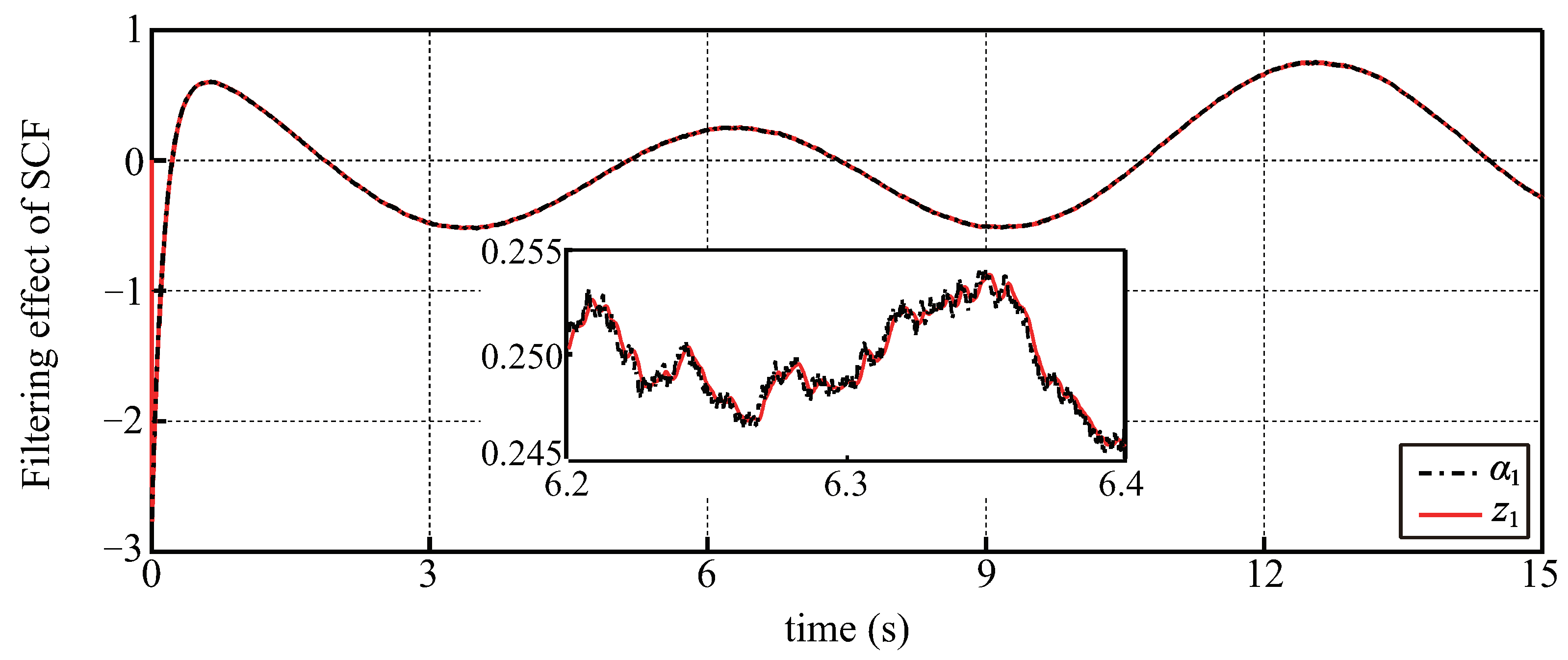
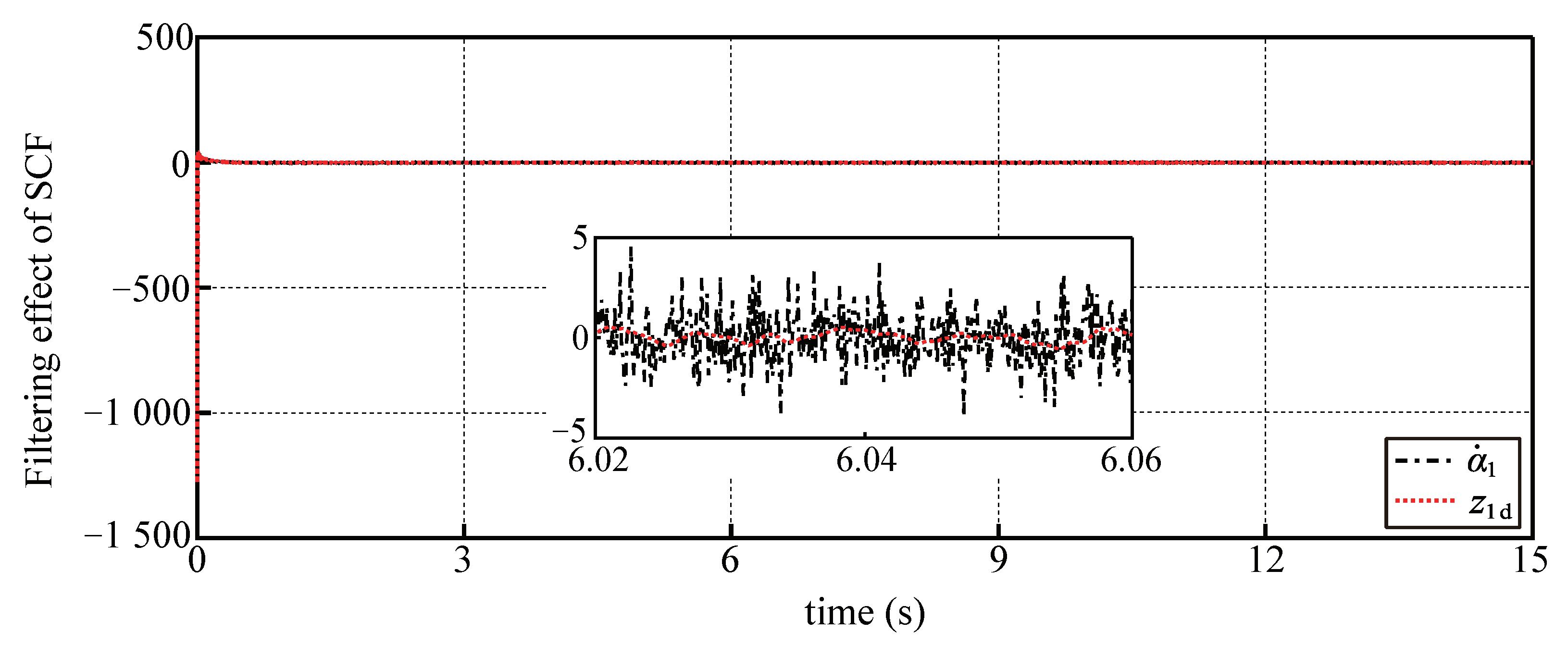
5.1. Simulation Results with Disturbances and Noises
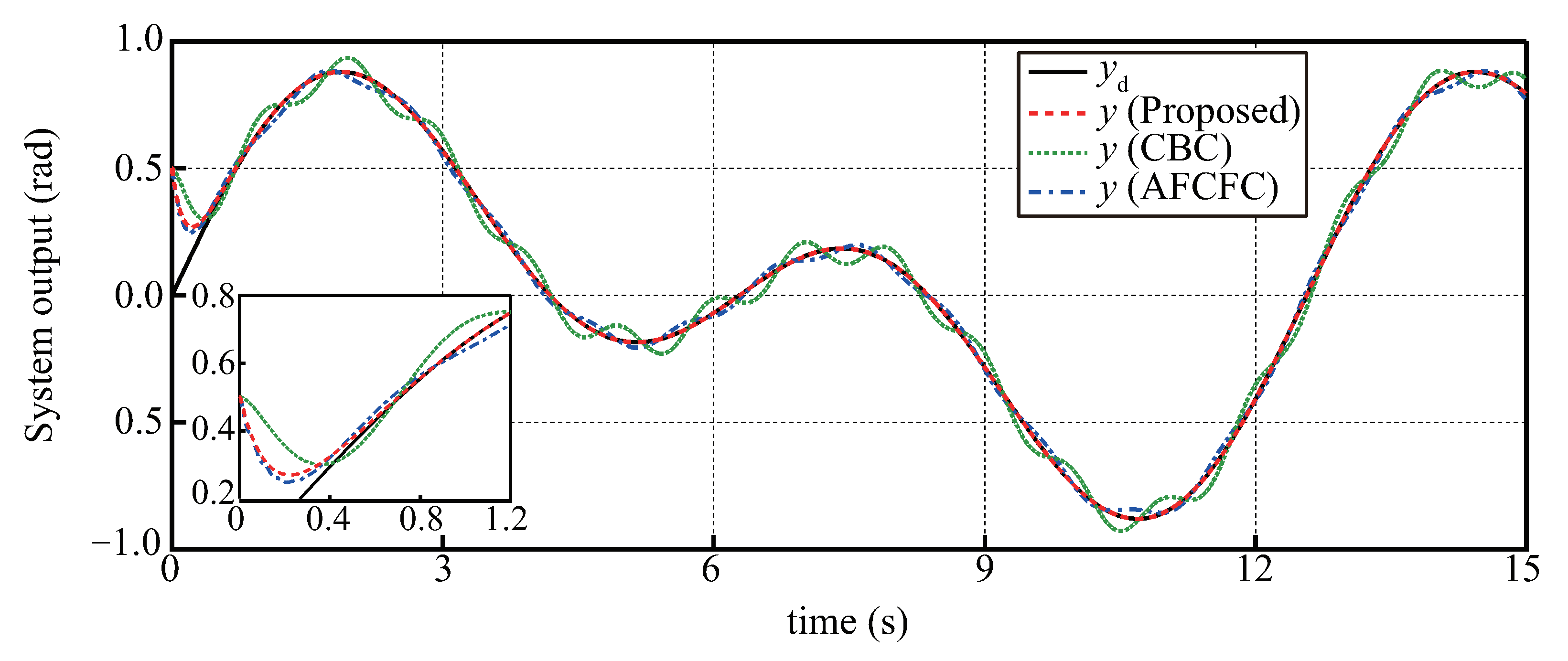
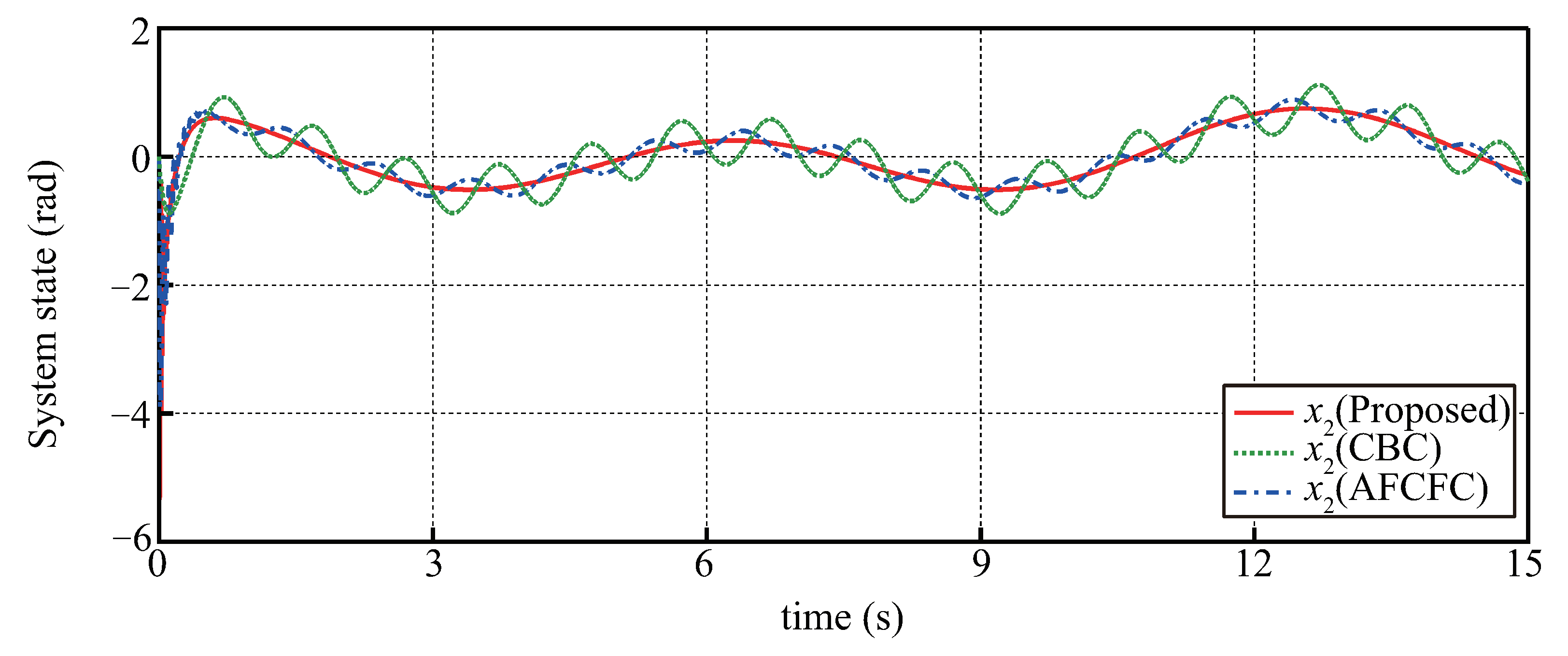
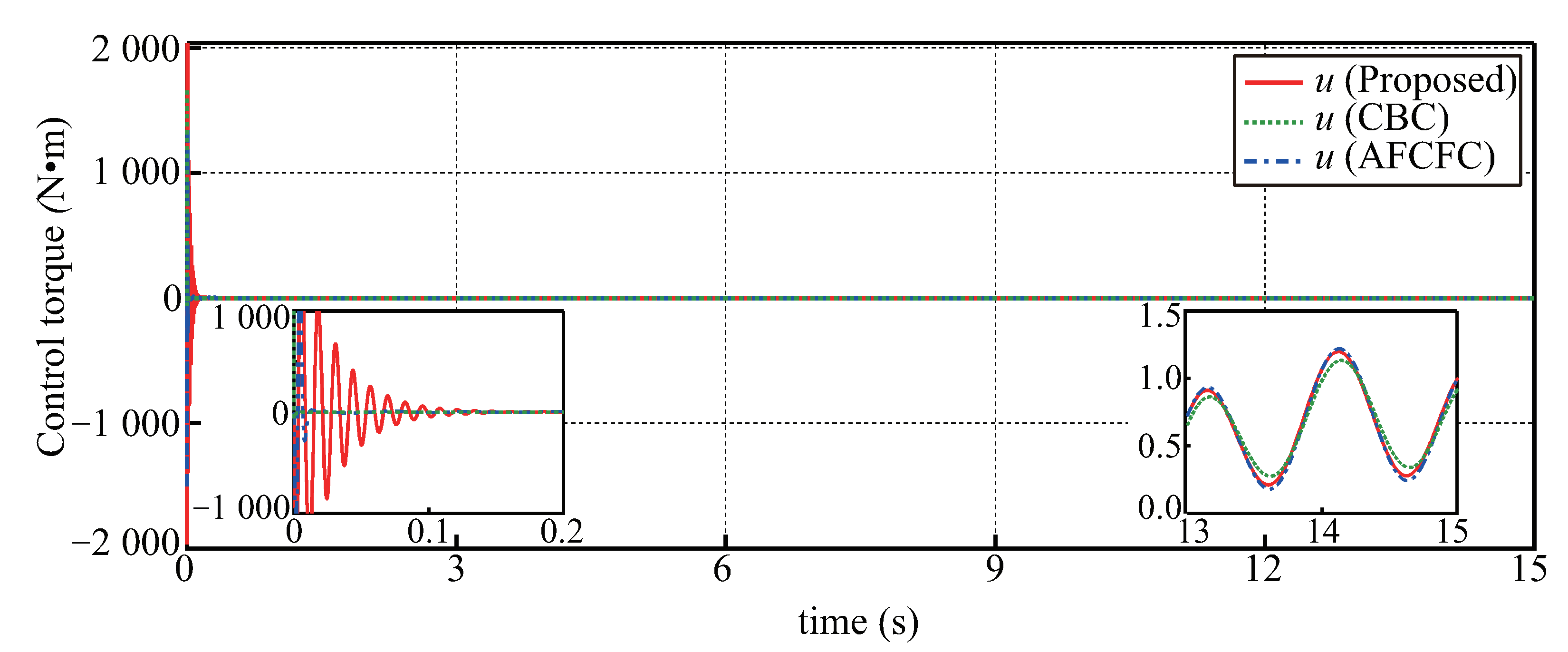
5.2. Comparison Results with CBC and AFCFC Methods
- (1)
- Conventional backstepping controller (CBC) proposed in [16]. The structure of the controller is given as:
- (2)
- Adaptive fuzzy command filtered controller (AFCFC) proposed in [30]. The structure of the controller is given as:where are the outputs of SCFs, are positive design parameters, is the estimation of the adaptive parameter , is the vector of fuzzy basis functions. More details about these control parameters are referred to in Ref. [30].
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barjuei, E.S.; Gasparetto, A. Predictive control of spatial flexible mechanisms. Int. J. Mech. Control 2015, 16, 85–96. [Google Scholar]
- Palomba, I.; Richiedei, D.; Trevisani, A. Reduced-order observers for nonlinear state estimation in flexible multibody systems. Shock Vib. 2018, 2018, 6538737. [Google Scholar] [CrossRef]
- Zhang, A.; Lin, Z.; Wang, B.; Han, Z. Nonlinear model predictive control of single-link flexible-joint robot using recurrent neural network and differential evolution optimization. Electronics 2021, 10, 2426. [Google Scholar] [CrossRef]
- Spyrakos-Papastavridis, E.; Da, J.S. Minimally model-based trajectory tracking and variable impedance control of flexible-joint robots. IEEE Trans. Ind. Electron. 2020, 68, 6031–6041. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C.; Su, C.Y.; Deng, A.; Fuchun, S.; Sun, F.; Zhang, W. Decentralized fuzzy control of multiple cooperating robotic manipulators with impedance interaction. IEEE Trans. Fuzzy Syst. 2014, 23, 1044–1056. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J. Distributed control of multiple flexible manipulators with unknown disturbances and dead-zone input. IEEE Trans. Ind. Electron. 2019, 67, 9937–9947. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; He, W.; Na, J.; Li, Z.; Xu, B. Adaptive parameter estimation and control design for robot manipulators with finite-time convergence. IEEE Trans. Ind. Electron. 2018, 65, 8112–8123. [Google Scholar] [CrossRef]
- Ibrahim, K.; Sharkawy, A.B. A hybrid PID control scheme for flexible joint manipulators and a comparison with sliding mode control. Ain Shams Eng. J. 2018, 9, 3451–3457. [Google Scholar] [CrossRef]
- Kelekci, E.; Kizir, S. Trajectory and vibration control of a flexible joint manipulator using interval type-2 fuzzy logic. ISA Trans. 2019, 94, 218–233. [Google Scholar] [CrossRef]
- Ak, A. Sliding mode controller design using fuzzy sliding surface for flexible joint manipulator. IETE J. Res. 2021, 68, 760–767. [Google Scholar] [CrossRef]
- Sun, T.; Liang, D.; Song, Y. Singular-perturbation-based nonlinear hybrid control of redundant parallel robot. IEEE Trans. Ind. Electron. 2017, 65, 3326–3336. [Google Scholar] [CrossRef]
- Chen, H.; Dong, X.; Yang, Y.; Liu, J. Backstepping sliding mode control of uncertainty flexible joint manipulator with actuator saturation. In Proceedings of the 2020 International Symposium on Automation, Information and Computing, Beijing, China, 2–4 December 2020; Volume 1828. [Google Scholar]
- Hooshmand, H.; Fateh, M.M. Voltage control of flexible-joint robot manipulators using singular perturbation technique for model order reduction. J. Electr. Comput. Eng. Innov. 2022, 10, 123–142. [Google Scholar]
- Korayem, M.H.; Nekoo, S.R.; Kazemi, S. Finite-time feedback linearization (FTFL) controller considering optimal gains on mobile mechanical manipulators. J. Intell. Robot. Syst. 2019, 94, 727–744. [Google Scholar] [CrossRef]
- Abdul-Adheem, W.R.; Ibraheem, I.K.; Humaidi, A.J.; Azar, A.T. Model-free active input–output feedback linearization of a single-link flexible joint manipulator: An improved active disturbance rejection control approach. Meas. Control 2021, 54, 856–871. [Google Scholar] [CrossRef]
- Oh, J.H.; Lee, J.S. Control of flexible joint robot system by backstepping design approach. Intell. Autom. Soft Comput. 1999, 5, 267–278. [Google Scholar] [CrossRef]
- Huang, A.C.; Chen, Y.C. Adaptive sliding control for single-link flexible-joint robot with mismatched uncertainties. IEEE Trans. Control Syst. Technol. 2004, 12, 770–775. [Google Scholar] [CrossRef]
- Dian, S.; Hu, Y.; Zhao, T.; Han, J. Adaptive backstepping control for flexible-joint manipulator using interval type-2 fuzzy neural network approximator. Nonlinear Dyn. 2019, 97, 1567–1580. [Google Scholar] [CrossRef]
- Wang, L.; Shi, Q.; Liu, J.; Zhang, D. Backstepping control of flexible joint manipulator based on hyperbolic tangent function with control input and rate constraints. Asian J. Control 2020, 22, 1268–1279. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Aautomatic Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Ling, S.; Wang, H.; Liu, P.X. Adaptive fuzzy dynamic surface control of flexible-joint robot systems with input saturation. IEEE/CAA J. Autom. Sin. 2019, 6, 97–107. [Google Scholar] [CrossRef]
- Yoo, S.J.; Park, J.B.; Choi, Y.H. Adaptive output feedback control of flexible-joint robots using neural networks: Dynamic surface design approach. IEEE Trans. Neural Netw. 2008, 19, 1712–1726. [Google Scholar] [PubMed]
- Li, Y.; Tong, S.; Li, T. Fuzzy adaptive dynamic surface control for a single-link flexible-joint robot. Nonlinear Dyn. 2012, 70, 2035–2048. [Google Scholar] [CrossRef]
- Xiong, G.; Xie, Z.; Huang, J.; Liu, H.; Jiang, Z.; Sun, K. Dynamic surface control-backstepping based impedance control for 5-DOF flexible joint robots. J. Cent. South Univ. Technol. 2010, 17, 807–815. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A.; Polycarpou, M.M.; Djapic, V.; Sharma, M. Command filtered adaptive backstepping. IEEE Trans. Control Syst. Technol. 2012, 20, 566–580. [Google Scholar] [CrossRef]
- Wang, L.; Yang, C. Neural network adaptive command filtered control of robotic manipulators with input saturation. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419894779. [Google Scholar] [CrossRef]
- Deng, Y. Adaptive finite-time fuzzy command filtered controller design for uncertain robotic manipulators. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419828148. [Google Scholar] [CrossRef]
- Lin, M.; Lei, Z.; Zhang, Y.; Li, P.; Wang, X. Command filter backstepping control with error compensation for flexible-joint manipulator. In Proceedings of the 2020 Chinese Control And Decision Conference, Hefei, China, 22–24 August 2020; pp. 3696–3701. [Google Scholar]
- Ling, S.; Wang, H.; Liu, P.X. Adaptive fuzzy tracking control of flexible-joint robots based on command filtering. IEEE Trans. Ind. Electron. 2019, 67, 4046–4055. [Google Scholar] [CrossRef]
- Liu, X.; Yang, C.; Chen, Z.; Wang, M.; Su, C. Neuro-adaptive observer based control of flexible joint robot. Neurocomputing 2018, 275, 73–82. [Google Scholar] [CrossRef]
- Sun, W.; Su, S.F.; Xia, J.; Nguyen, V. Adaptive fuzzy tracking control of flexible-joint robots with full-state constraints. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2201–2209. [Google Scholar] [CrossRef]
- Soltanpour, M.R.; Moattari, M. Voltage based sliding mode control of flexible joint robot manipulators in presence of uncertainties. Robot. Auton. Syst. 2019, 118, 204–219. [Google Scholar]
- Cheng, X.; Liu, H.; Lu, W. Chattering-suppressed sliding mode control for flexible-joint robot manipulators. Actuators Multidiscip. Digit. Publ. Inst. 2021, 10, 288. [Google Scholar] [CrossRef]
- Alam, W.; Ahmad, S.; Mehmood, A.; Iqbal, J. Robust sliding mode control for flexible joint robotic manipulator via disturbance observer. Interdiscip. Descr. Complex Syst. INDECS 2019, 17, 85–97. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R. Continuous fuzzy nonsingular terminal sliding mode control of flexible joints robot manipulators based on nonlinear finite time observer in the presence of matched and mismatched uncertainties. J. Frankl. Inst. 2020, 357, 6539–6570. [Google Scholar] [CrossRef]
- Ullah, H.; Malik, F.M.; Raza, A.; Mazhar, N.; Khan, R.; Saeed, A.; Ahmad, I. Robust output feedback control of single-link flexible-joint robot manipulator with matched disturbances using high gain observer. Sensors 2021, 21, 3252. [Google Scholar] [CrossRef]
- Hu, Y.; Dian, S.; Guo, R.; Li, S.; Zhao, T. Observer-based dynamic surface control for flexible-joint manipulator system with input saturation and unknown disturbance using type-2 fuzzy neural network. Neurocomputing 2021, 436, 162–173. [Google Scholar] [CrossRef]
- Han, J.Q. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Talole, S.E.; Kolhe, J.P.; Phadke, S.B. Extended-state-observer-based control of flexible-joint system with experimental validation. IEEE Trans. Ind. Electron. 2009, 57, 1411–1419. [Google Scholar] [CrossRef]
- Rsetam, K.; Cao, Z.; Man, Z. Cascaded-extended-state-observer-based sliding-mode control for underactuated flexible joint robot. IEEE Trans. Ind. Electron. 2019, 67, 10822–10832. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef]
- Shao, X.; Wang, H. Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO. ISA Trans. 2015, 57, 10–22. [Google Scholar]
- Zhou, Y.; Chang, S. A model-assisted reduced-order ESO based cascade controller for sensorless control of independent gear-shifting actuators. Appl. Sci. 2017, 7, 1283. [Google Scholar] [CrossRef]
- Xie, T.; Li, Y.; Jiang, Y.; An, L.; Wu, H. Backstepping active disturbance rejection control for trajectory tracking of underactuated autonomous underwater vehicles with position error constraint. Int. J. Adv. Robot. Syst. 2020, 17, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Rong, J.; Yu, L. Reduced-order extended state observer based event-triggered sliding mode control for DC-DC buck converter system with parameter perturbation. Asian J. Control 2021, 23, 1591–1601. [Google Scholar] [CrossRef]
- Zhai, J.; Li, S.; Xu, Z.; Zhang, L.; Li, J. Reduced-order extended state observer-based sliding mode control for all-clamped plate using an inertial actuator. Energies 2022, 15, 1780. [Google Scholar] [CrossRef]
- Chien, M.C.; Huang, A.C. Adaptive control for flexible-joint electrically driven robot with time-varying uncertainties. IEEE Trans. Ind. Electron. 2007, 54, 1032–1038. [Google Scholar] [CrossRef]
- Narendra, K.S.; Annaswamy, A.M. Robust Adaptive Control. Adaptive and Learning Systems; Springer: Boston, MA, USA, 1986; pp. 3–31. [Google Scholar]
- Yu, J.; Shi, P.; Dong, W.; Yu, H. Observer and command-filter-based adaptive fuzzy output feedback control of uncertain nonlinear systems. IEEE Trans. Ind. Electron. 2015, 62, 5962–5970. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Fei, X.; Xiao, J.; Xiong, P.; Li, Z.; Huang, H. Model-Assisted Reduced-Order ESO Based Command Filtered Tracking Control of Flexible-Joint Manipulators with Matched and Mismatched Disturbances. Appl. Sci. 2022, 12, 8511. https://doi.org/10.3390/app12178511
Pan C, Fei X, Xiao J, Xiong P, Li Z, Huang H. Model-Assisted Reduced-Order ESO Based Command Filtered Tracking Control of Flexible-Joint Manipulators with Matched and Mismatched Disturbances. Applied Sciences. 2022; 12(17):8511. https://doi.org/10.3390/app12178511
Chicago/Turabian StylePan, Changzhong, Xiangyin Fei, Jinsen Xiao, Peiyin Xiong, Zhijing Li, and Hao Huang. 2022. "Model-Assisted Reduced-Order ESO Based Command Filtered Tracking Control of Flexible-Joint Manipulators with Matched and Mismatched Disturbances" Applied Sciences 12, no. 17: 8511. https://doi.org/10.3390/app12178511
APA StylePan, C., Fei, X., Xiao, J., Xiong, P., Li, Z., & Huang, H. (2022). Model-Assisted Reduced-Order ESO Based Command Filtered Tracking Control of Flexible-Joint Manipulators with Matched and Mismatched Disturbances. Applied Sciences, 12(17), 8511. https://doi.org/10.3390/app12178511






