Numerical Analysis of Fluid Stream Division to Supply Multiple Hydraulic Receivers
Abstract
:1. Introduction
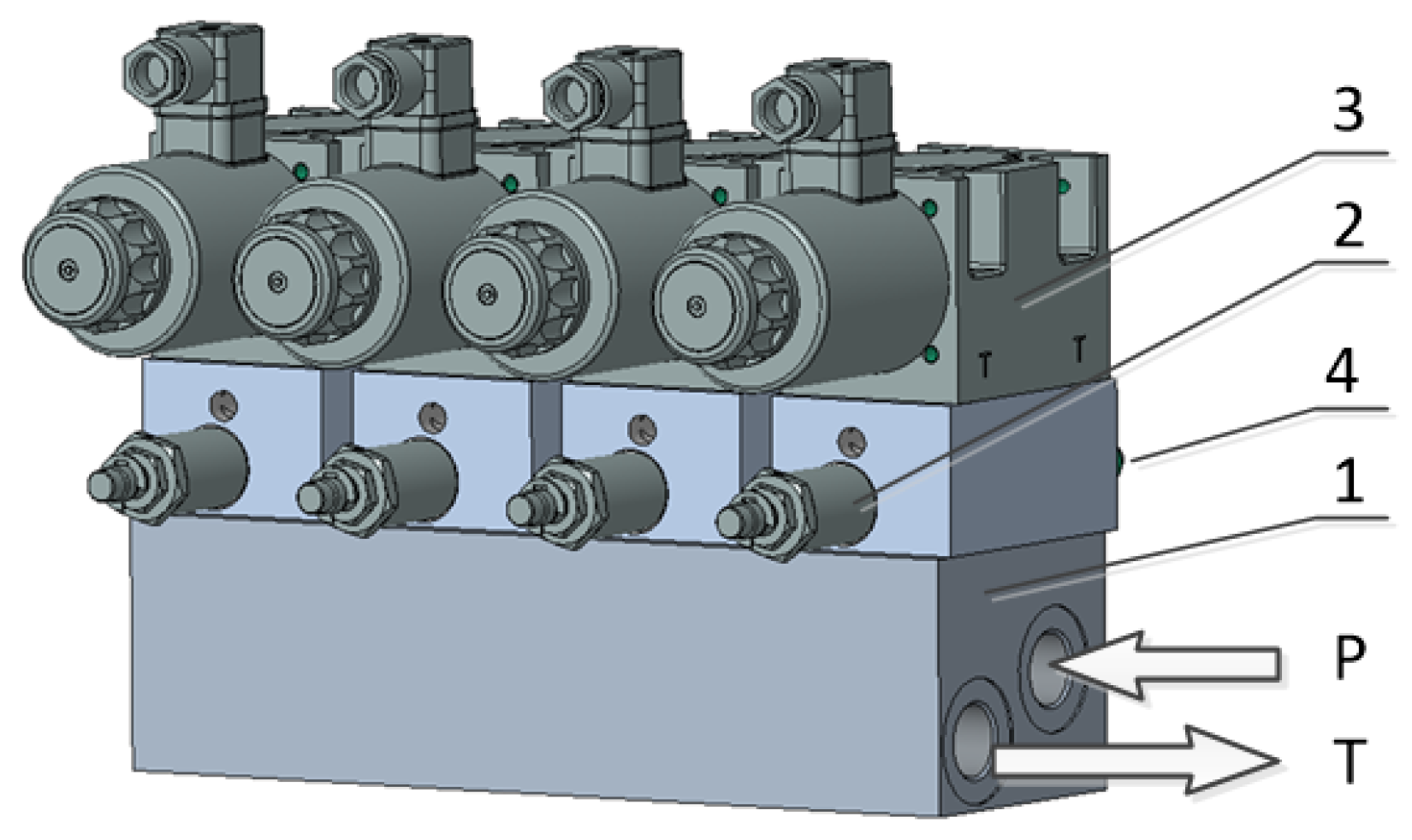
2. Working Principle of a Valve Block
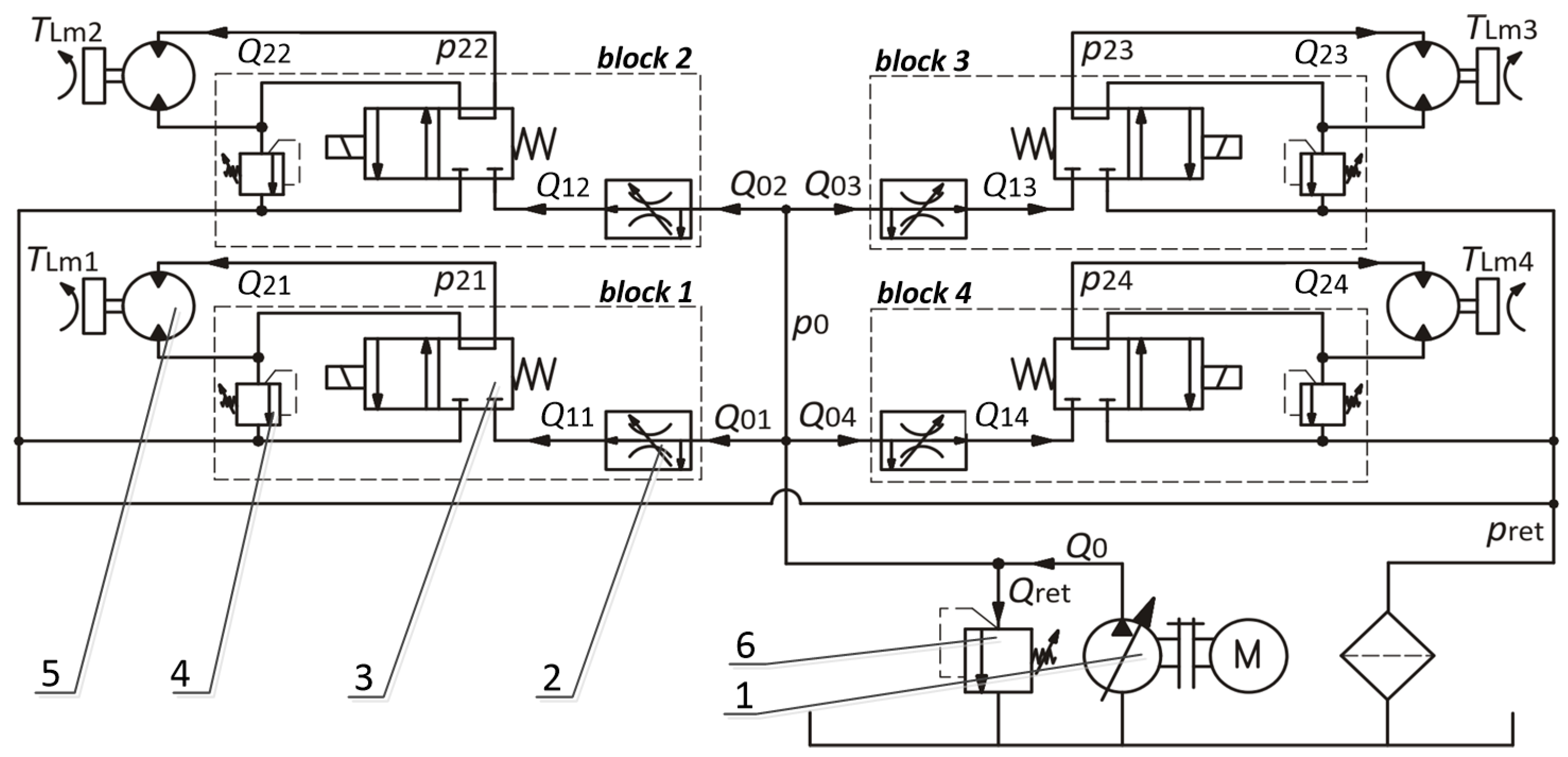
3. Mathematical Model of the System
4. Discrete Model and CFD Analysis
4.1. Determination of Boundary Conditions and Turbulence Model
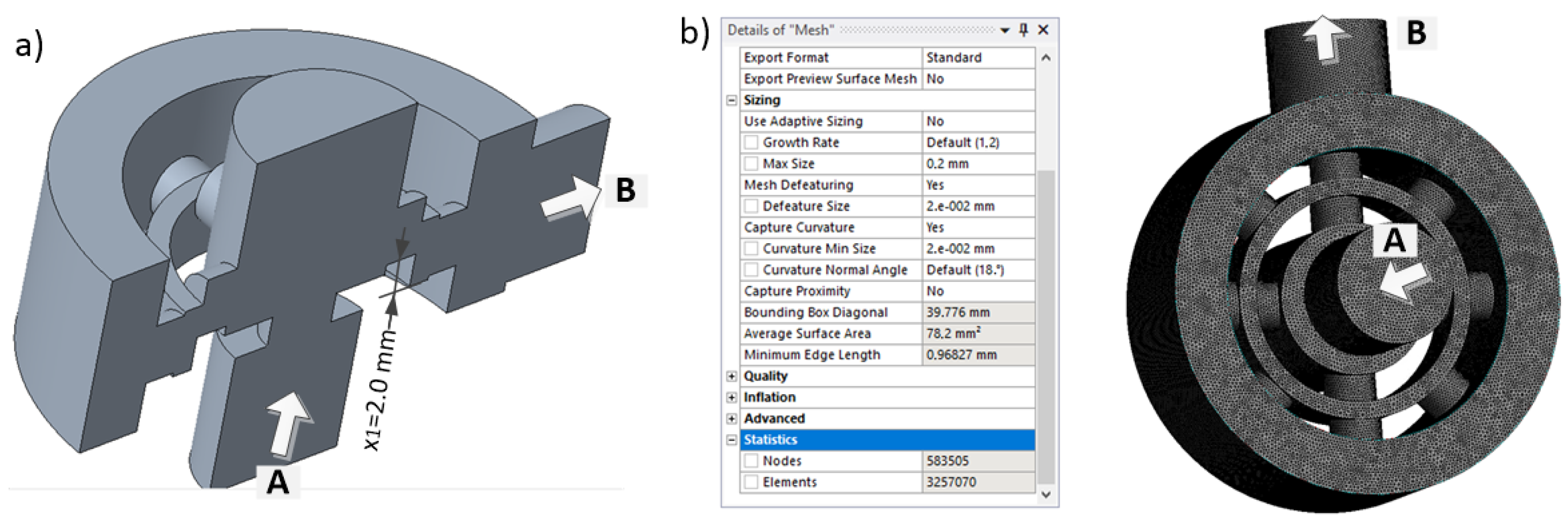
4.2. Meshing and Mesh Quality Assessment
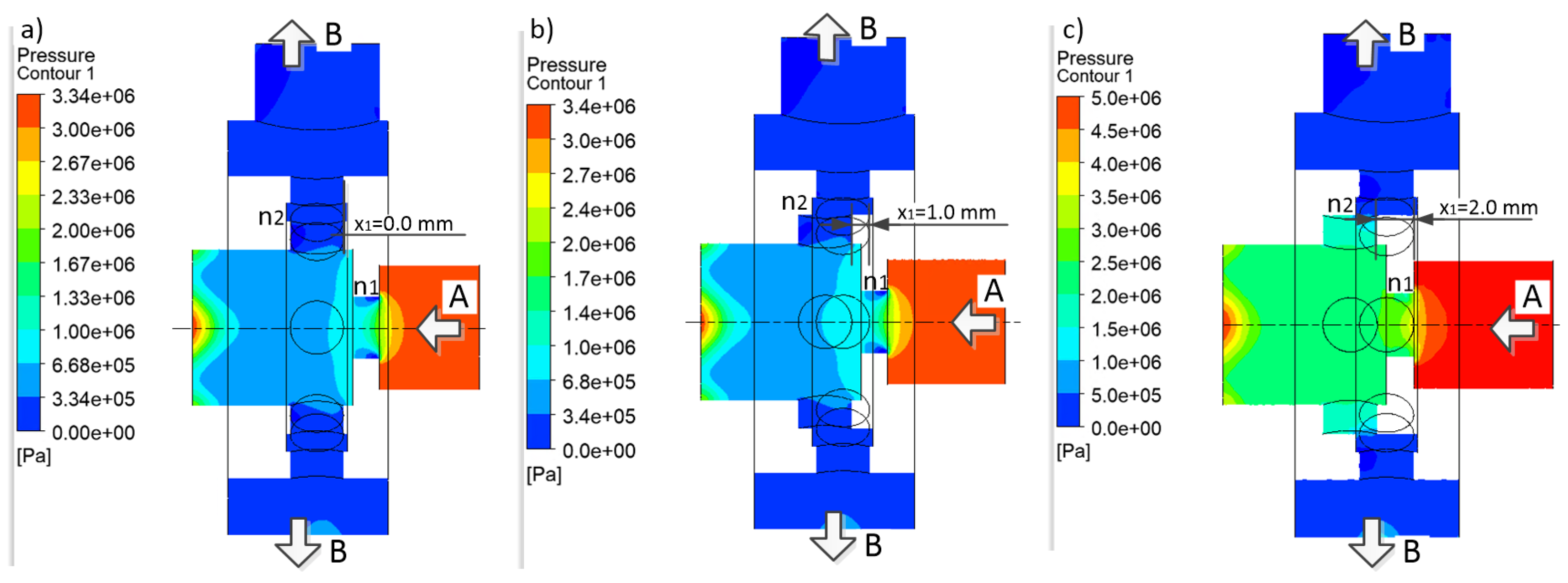
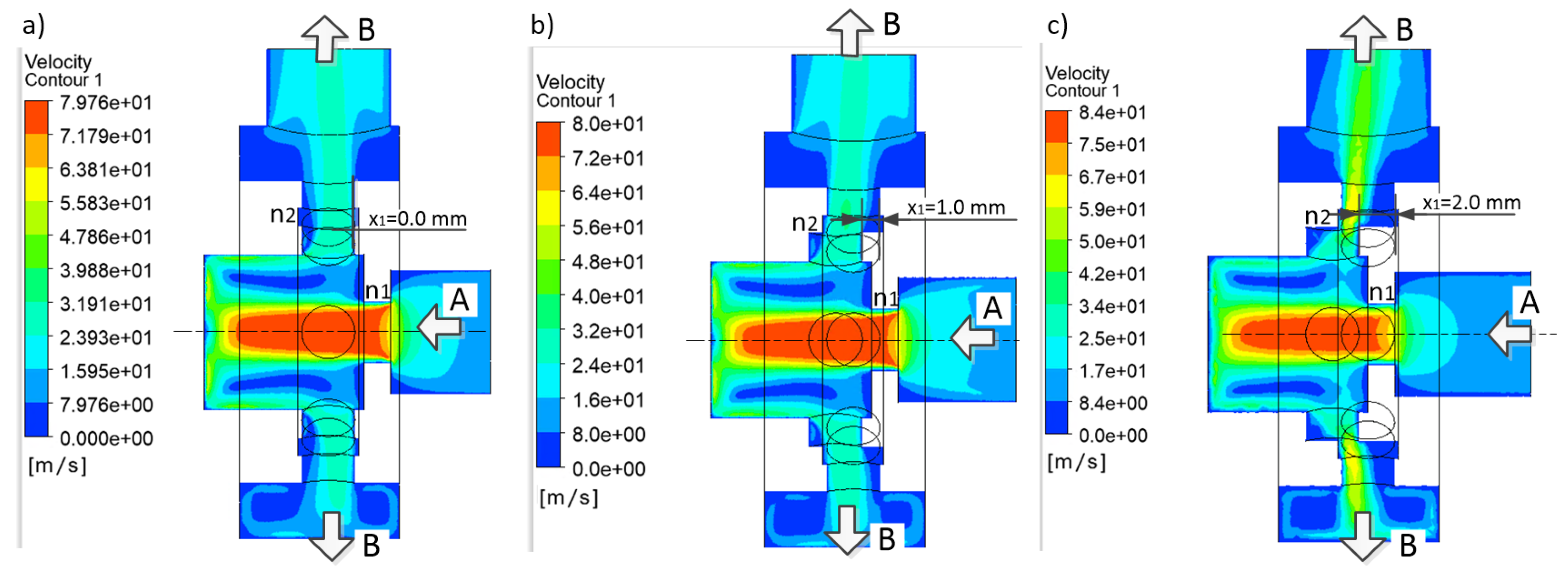
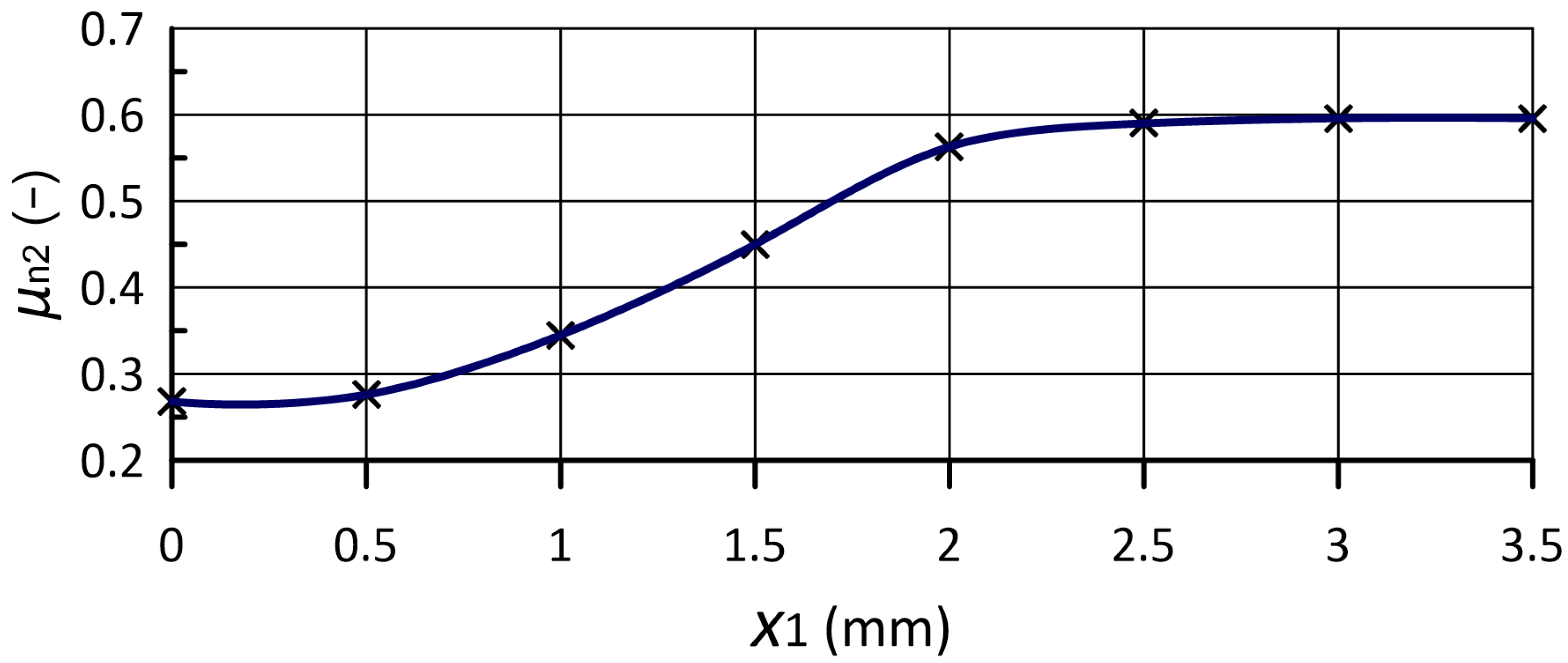
4.3. CFD Simulation Results
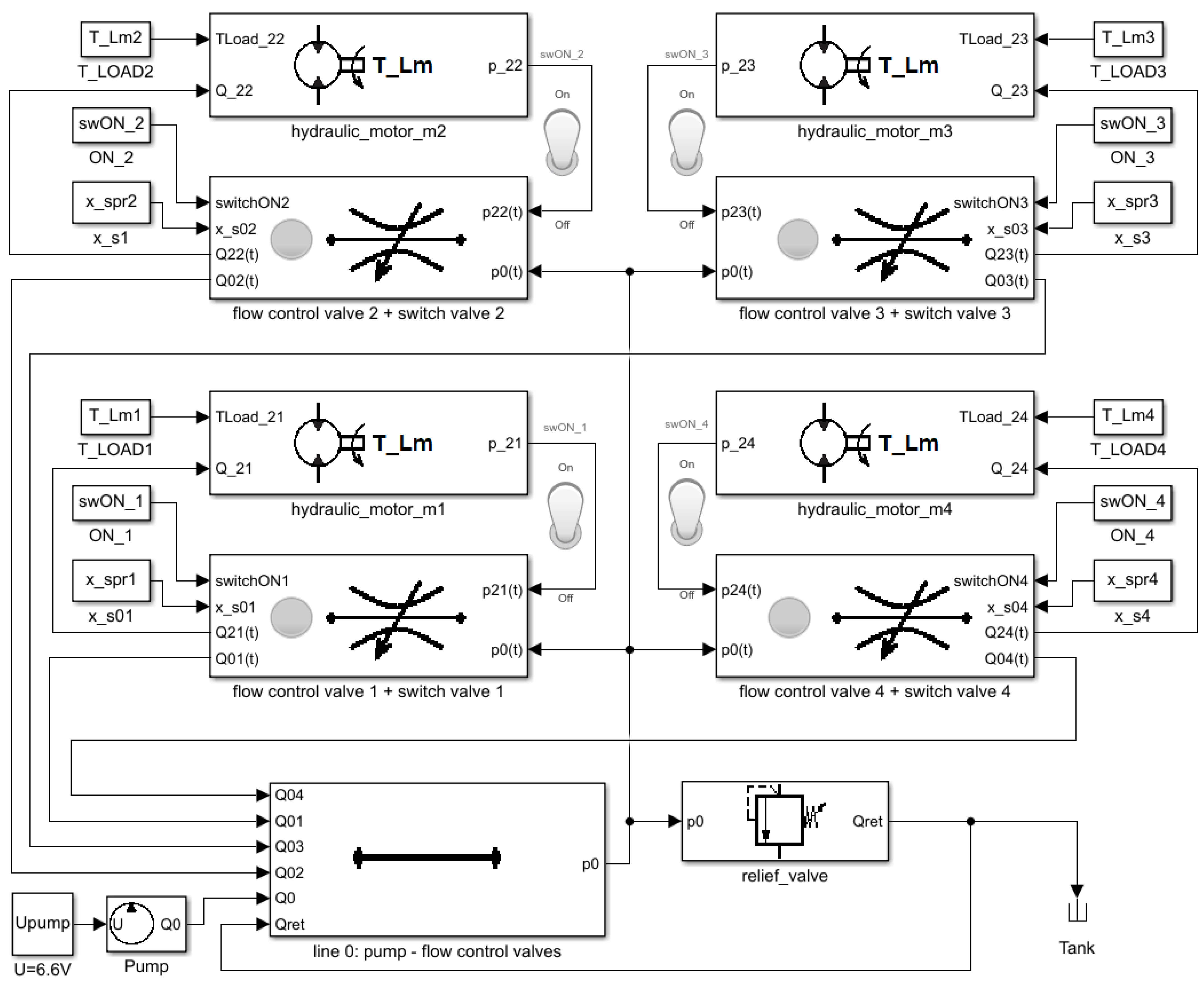
5. Modeling and Simulations in Matlab/Simulink
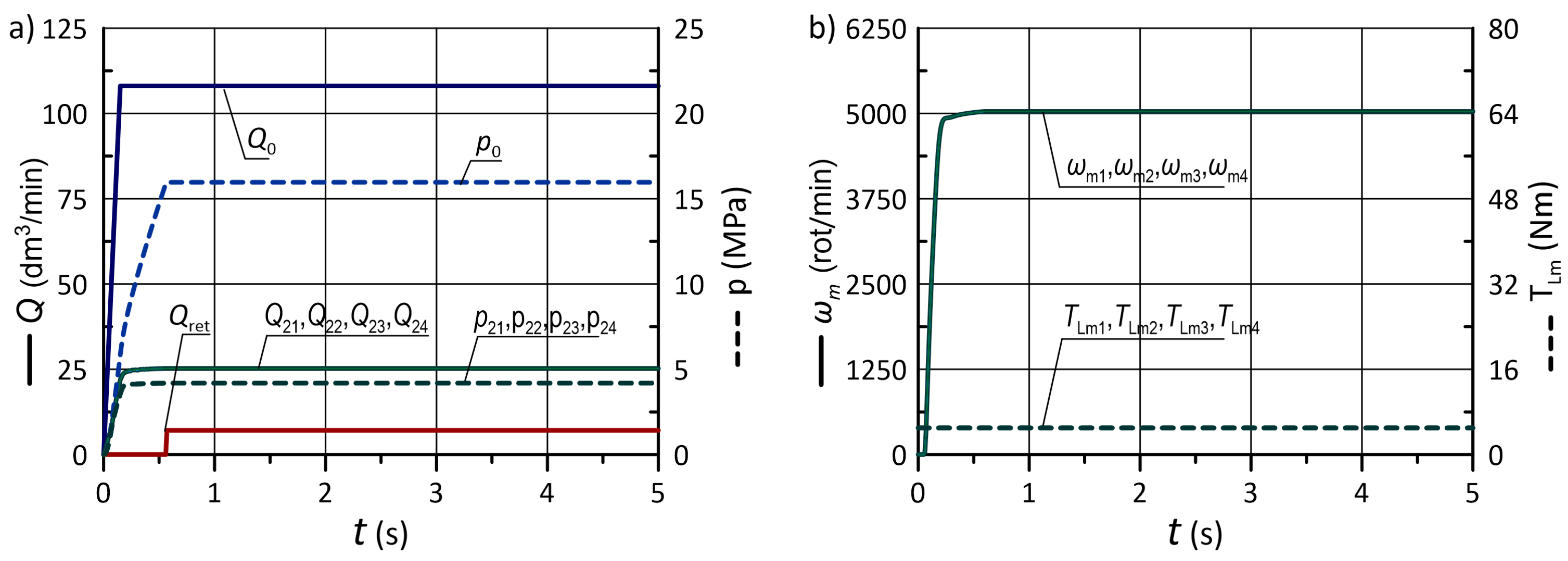
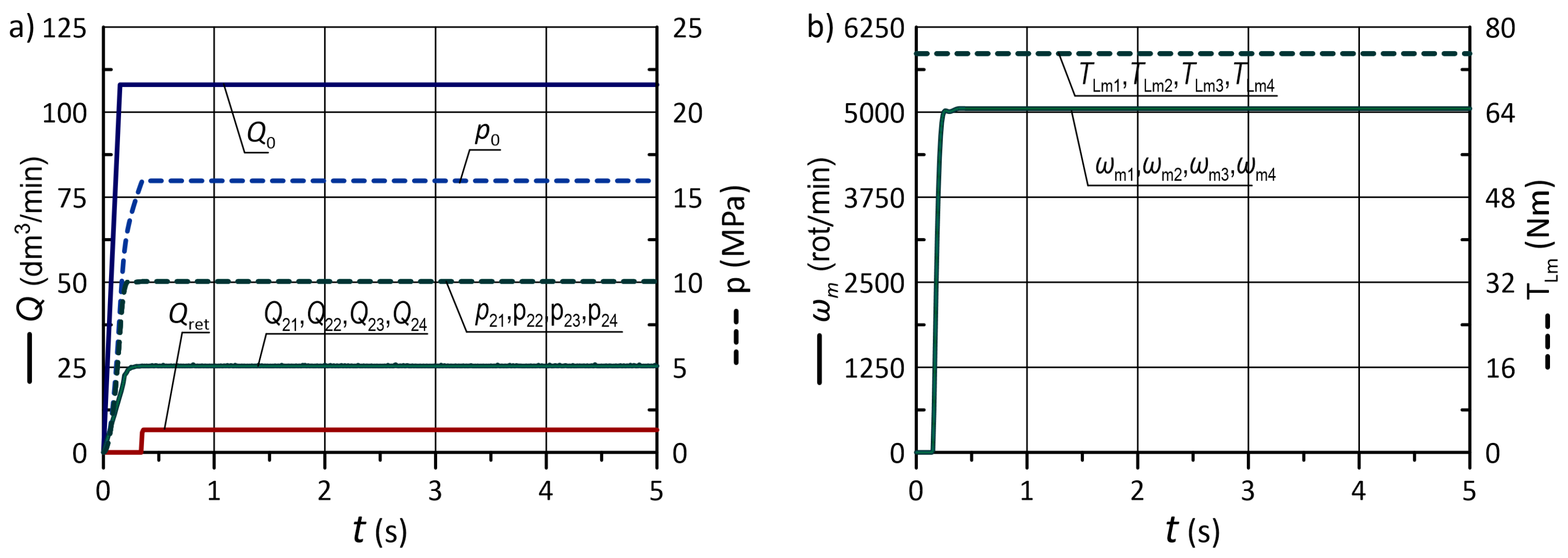
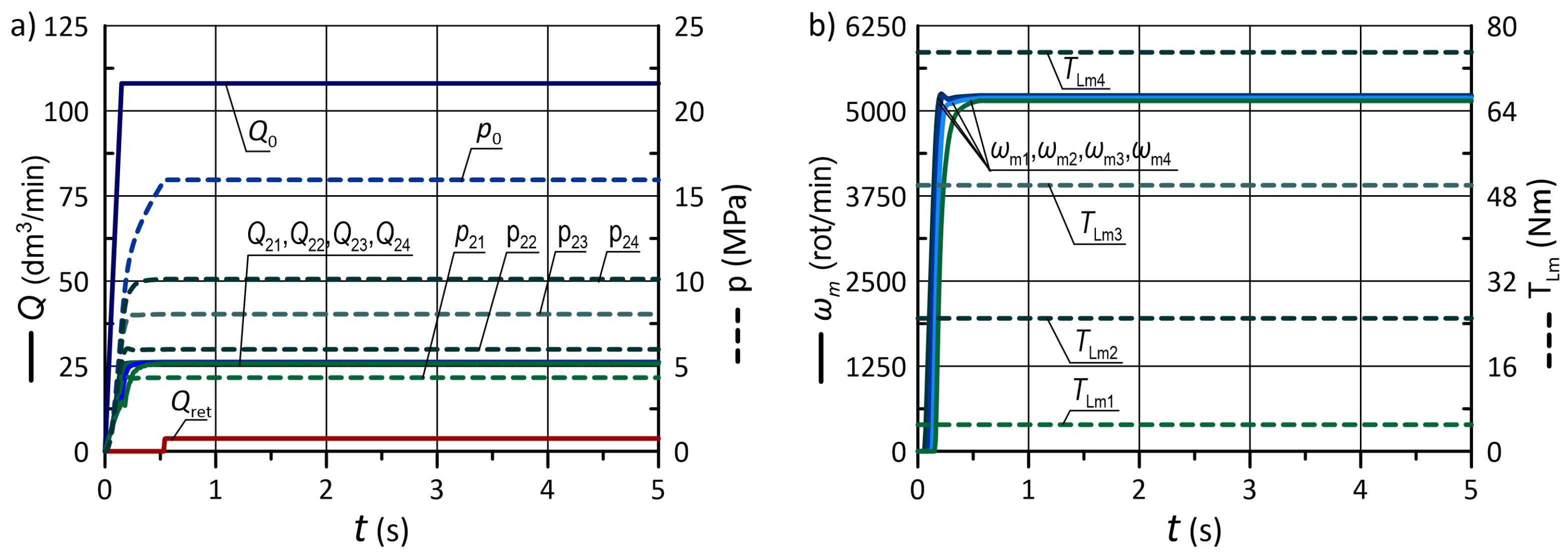
5.1. Simulations with Constant Load Torque
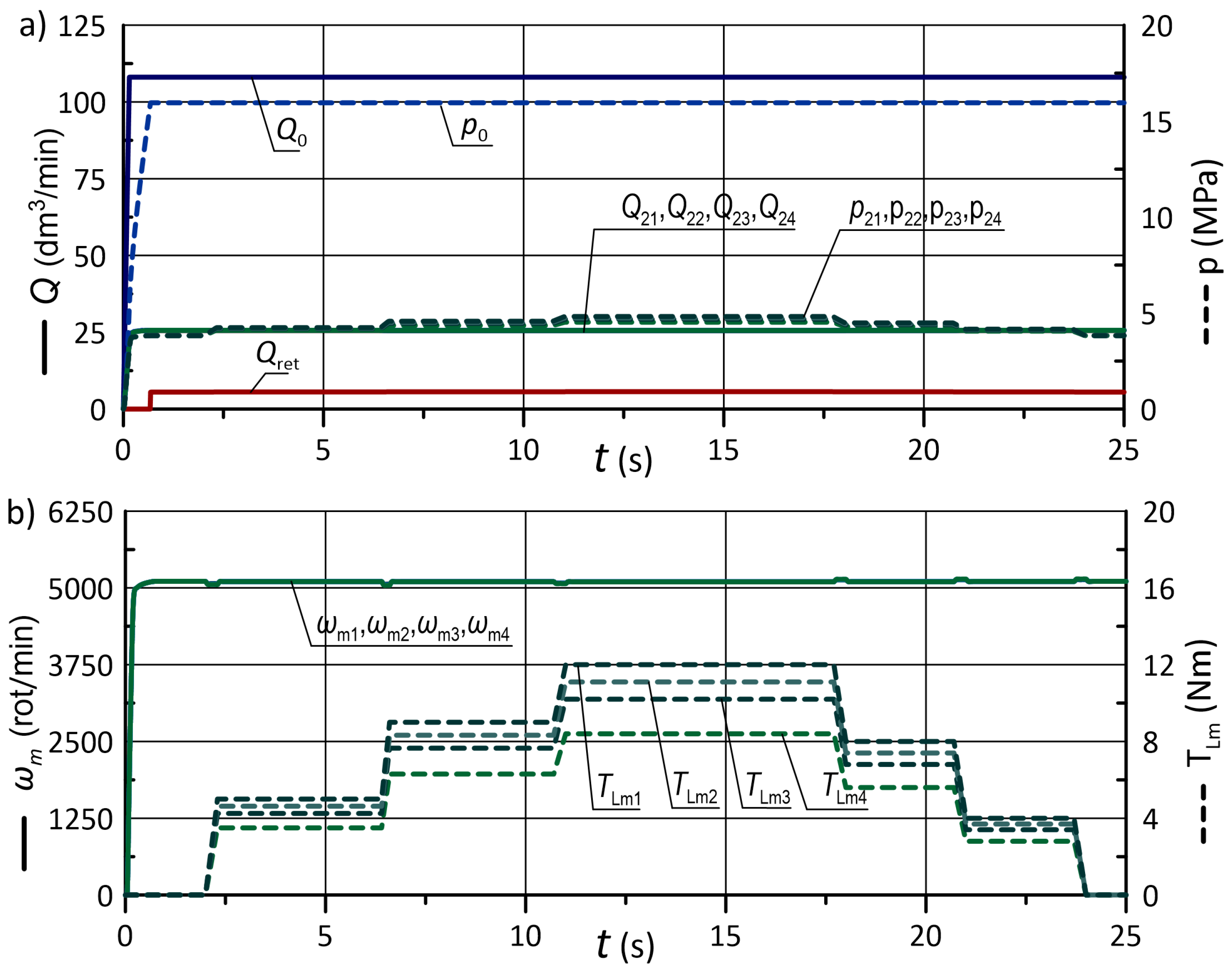
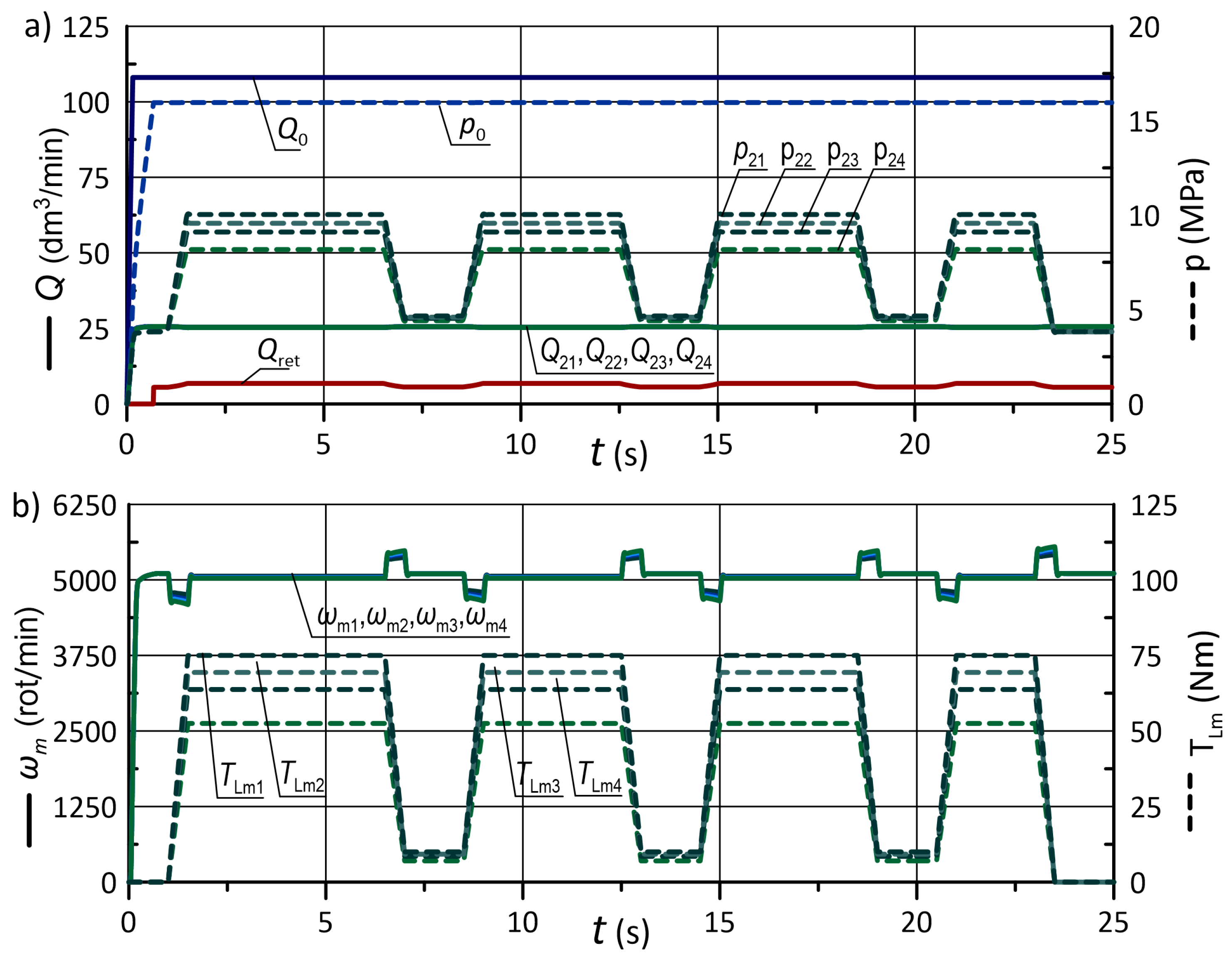
5.2. Simulations of Typical Operating Cycles
5.3. Discussion of the Results
6. Summary and Conclusions
- The proposed solution can be used in practice in systems with the requirement to keep the controlled parameter above the threshold value. This work concerned, in particular, the maintenance of the minimum flow rate, and thus required rotational speed of hydraulic motors regardless of the load;
- The applied hydraulic components do not require an electric power supply, which is especially important under the track grinder working conditions: continuous movement, high temperatures in the grinding area and the influence of weather conditions;
- The flow rate settings can be adjusted to a small extent by modifying the initial tension of the valve spring . The settings can be changed in a broader range by using a valve spring with a different stiffness . Finally, valves of larger or smaller nominal sizes can also be used;
- It is essential to pre-define a load torque range and adapt the relief valve settings to minimize energy loss during the implementation of operating cycles. The highest energy efficiency achieved when working under a load close to the maximum was approximately 80%. However, with a low load of about 10% of the allowable value, the energy efficiency drops to 30%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices | |
| 0 | supply line |
| i, where | flow control valve and hydraulic motor index |
| m | hydraulic motor |
| return line | |
| v | flow control valve |
| Parameters | |
| , | flow control valve , nozzle area, spool area (m2) |
| fluid bulk modulus (Pa) | |
| turbulence model constants (-) | |
| design parameters of a hydraulic motor (-) | |
| force acting on spool: hydrostatic 1, 2, spring, viscous friction (N) | |
| turbulence model factors: intensity, length scale (-, m) | |
| hydraulic motor shaft + grinding wheel moment of inertia (kg m2) | |
| , | supply power, useful power on the i-th motor (kW) |
| , | flow rate: pump, return line (dm3 min−1) |
| , | flow rate: inlet and outlet of flow control valve (dm3 min−1) |
| flow rate at inlet to hydraulic motor (dm3 min−1) | |
| , , | motor friction torque, Coulomb torque, static torque (N m) |
| torque load of the motor (N m) | |
| pump control signal (V) | |
| volume: supply line, inside flow control valves, motor lines (m3) | |
| valve spring stiffness (N m−1) | |
| valve spool mass (kg) | |
| pressure: supply line, return line (MPa) | |
| pressure: inside flow control valve, hydraulic motor line (MPa) | |
| , | pump piston stroke rate/max. stroke rate per revolution (m3 rev−1) |
| turbulence model constants (-) | |
| time, start-up time (s) | |
| valve spool position (m) | |
| initial tension of valve spring (m) | |
| z | number of pump pistons (-) |
| pressure drop at valve nozzle (MPa) | |
| effective power share (%) | |
| fluid dynamic viscosity (Pa s) | |
| fluid kinematic viscosity (m2 s−1) | |
| , | discharge coefficient of flow control valve nozzles (-) |
| turbulent viscosity (m2 s−1) | |
| fluid density (kg m−3) | |
| flow control valve spool damping coefficient (N s m−1) | |
| hydraulic motor damping factor (m) | |
| pump rotational speed, pump nominal speed (rev s−1) | |
| , | motor rotational speed, motor Stribeck velocity (rev s−1) |
References
- Bekele, T.; Åman, R.; Handroos, H. The Control of Multiple Actuators using Single IEHEC Pump/Motor. In Proceedings of the 10th International Fluid Power Conference Dresden (10. IFK), Dresden, Germany, 8–10 March 2016; pp. 73–88. [Google Scholar]
- Yao, J.; Wang, P.; Yin, Y.; Li, M.; Li, Y. Power management of multi-source network hydraulic system with multiple actuators. Energy Convers. Manag. 2020, 223, 113247. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G. Analysis of a proportional control valve flow coefficient with the usage of a CFD method. Flow Meas. Instrum. 2017, 53, 269–278. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, Z.; Shi, Y.; Yan, Y.; Guo, F. Synchronous control of multiple electrohydraulic actuators under distributed switching topologies with lumped uncertainty. J. Frankl. Inst. 2022, 359, 4288–4306. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, Z.; Shi, Y.; Li, X.; Yan, Y.; Guo, F.; Li, S. Synchronous control for multiple electrohydraulic actuators with feedback linearization. Mech. Syst. Signal Process. 2022, 178, 109280. [Google Scholar] [CrossRef]
- Lei, T.; Wang, J.; Yao, Z. Modelling and Stability Analysis of Articulated Vehicles. Appl. Sci. 2021, 11, 3663. [Google Scholar] [CrossRef]
- Han, J.; Wang, F.; Wang, Y. A Control Method for the Differential Steering of Tracked Vehicles Driven Independently by a Dual Hydraulic Motor. Appl. Sci. 2022, 12, 6355. [Google Scholar] [CrossRef]
- Huang, J.; Wang, X.; Wang, H.; Hao, H. Development of a flow control valve with digital flow compensator. Flow Meas. Instrum. 2019, 66, 157–169. [Google Scholar] [CrossRef]
- Okhotnikov, I.; Noroozi, S.; Sewell, P.; Godfrey, P. Evaluation of steady flow torques and pressure losses in a rotary flow control valve by means of computational fluid dynamics. Int. J. Heat Fluid Flow 2017, 64, 89–102. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G. CFD analysis of the characteristics of a proportional flow control valve with an innovative opening shape. Energy Convers. Manag. 2016, 123, 15–28. [Google Scholar] [CrossRef]
- Kumar, S.; Tewari, V.K.; Bharti, C.K.; Ranjan, A. Modeling, simulation and experimental validation of flow rate of electro-hydraulic hitch control valve of agricultural tractor. Flow Meas. Instrum. 2021, 82, 102070. [Google Scholar] [CrossRef]
- Adeoye, A.; Aderoba, A.; Oladapo, B. Simulated Design of a Flow Control Valve for Stroke Speed Adjustment of Hydraulic Power of Robotic Lifting Device. Procedia Eng. 2017, 173, 1499–1506. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Zhang, J.; Lei, F.; Zhao, D.; Hong, H. Multi-Objective Optimization Design of Key Parameters of a Stepless Flow Control System with Multi-System Coupling Characteristics. Appl. Sci. 2022, 12, 1301. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Chen, J.; Chen, W.; Li, C.; Huo, D. Design and control performance optimization of dual-mode hydraulic steering system for wheel loader. Autom. Constr. 2022, 143, 104539. [Google Scholar] [CrossRef]
- Leephakpreeda, T. Flow-sensorless control valve: Neural computing approach. Flow Meas. Instrum. 2003, 14, 261–266. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, D.; Xu, B.; Su, Q.; Lu, Z.; Wang, W. Flow control of a proportional directional valve without the flow meter. Flow Meas. Instrum. 2019, 67, 131–141. [Google Scholar] [CrossRef]
- Feng, H.; Song, Q.; Ma, S.; Ma, W.; Yin, C.; Cao, D.; Yu, H. A new adaptive sliding mode controller based on the RBF neural network for an electro-hydraulic servo system. ISA Trans. 2022, 129, 472–484. [Google Scholar] [CrossRef]
- Wachholz, L.; Valdiero, A.; Rasia, L. Mathematical modeling of a hydraulic motor operated and controlled by proportional valve. In Proceedings of the 25th ABCM International Congress of Mechanical Engineering, Uberlandia, Brazil, 20–25 October 2019. [Google Scholar] [CrossRef]
- Anh, P.N.; Bae, J.S.; Hwang, J.H. Computational Fluid Dynamic Analysis of Flow Rate Performance of a Small Piezoelectric-Hydraulic Pump. Appl. Sci. 2021, 11, 4888. [Google Scholar] [CrossRef]
- Jin-yuan, Q.; Lin, W.; Zhi-jiang, J.; Jian-kai, W.; Han, Z.; An-le, L. CFD analysis on the dynamic flow characteristics of the pilot-control globe valve. Energy Convers. Manag. 2014, 87, 220–226. [Google Scholar] [CrossRef]
- Domagała, M.; Momeni, H.; Fabiś-Domagała, J.; Saeed, B.; Filo, G.; Amzin, S. Fluid-Structure Interaction Simulation of Flow Control Valve. Mater. Res. Proc. 2020, 17, 036042. [Google Scholar] [CrossRef]
- Wen, Q.; Liu, Y.; Chen, Z.; Wang, W. Numerical simulation and experimental validation of flow characteristics for a butterfly check valve in small modular reactor. Nucl. Eng. Des. 2022, 391, 111732. [Google Scholar] [CrossRef]
- Domagała, M.; Momeni, H.; Fabiś-Domagała, J. The Influence of Oil Contamination on Flow Control Valve Operation. Mater. Res. Proc. 2022, 24, 001008. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G.; Rajda, J. Pressure compensation using flow forces in a multi-section proportional directional control valve. Energy Convers. Manag. 2015, 103, 1052–1064. [Google Scholar] [CrossRef]
- Chen, F.; Qian, J.; Chen, M.; Zhang, M.; Chen, L.; Jin, Z. Turbulent compressible flow analysis on multi-stage high pressure reducing valve. Flow Meas. Instrum. 2018, 61, 26–37. [Google Scholar] [CrossRef]
- Scuro, N.; Angelo, E.; Angelo, G.; Andrade, D. A CFD analysis of the flow dynamics of a directly-operated safety relief valve. Nucl. Eng. Des. 2018, 328, 321–332. [Google Scholar] [CrossRef]
- Filo, G.; Lisowski, E.; Rajda, J. Design and Flow Analysis of an Adjustable Check Valve by Means of CFD Method. Energies 2021, 14, 2237. [Google Scholar] [CrossRef]
- ANSYS Fluent in ANSYS Workbench User’s Guide, 1st ed.; ANSYS Inc.: Canonsburg, PA, USA, 2020; Available online: http://www.ansys.com (accessed on 19 September 2022).




| Kinematic Viscosity | Density | Temperature | Flow Rate | Outlet Pressure | Reynolds Number |
|---|---|---|---|---|---|
| T | |||||
| m2 · s−1 | kg m−3 | °C | dm3 min−1 | MPa | - |
| 870 | 50.0 | 25 | 0.1 |
| Kinetic Energy Constant | Kinetic Energy Dissipation Constants | Turbulent Viscosity Constant | Turbulence Intensity | Length Scale | ||
|---|---|---|---|---|---|---|
| (-) | (-) | (-) | (-) | (-) | I (%) | ℓ (mm) |
| 1.0 | 1.3 | 1.44 | 1.92 | 0.09 | 4.5–6.1 | 0.14–0.49 |
| Case | No. Nodes | No. Elements | Comput. Time | Pressure Drop |
|---|---|---|---|---|
| 1. Initial | 11 min | MPa | ||
| 2. | 105 min | MPa | ||
| 3. | ||||
| 4. | 1760 min | MPa |
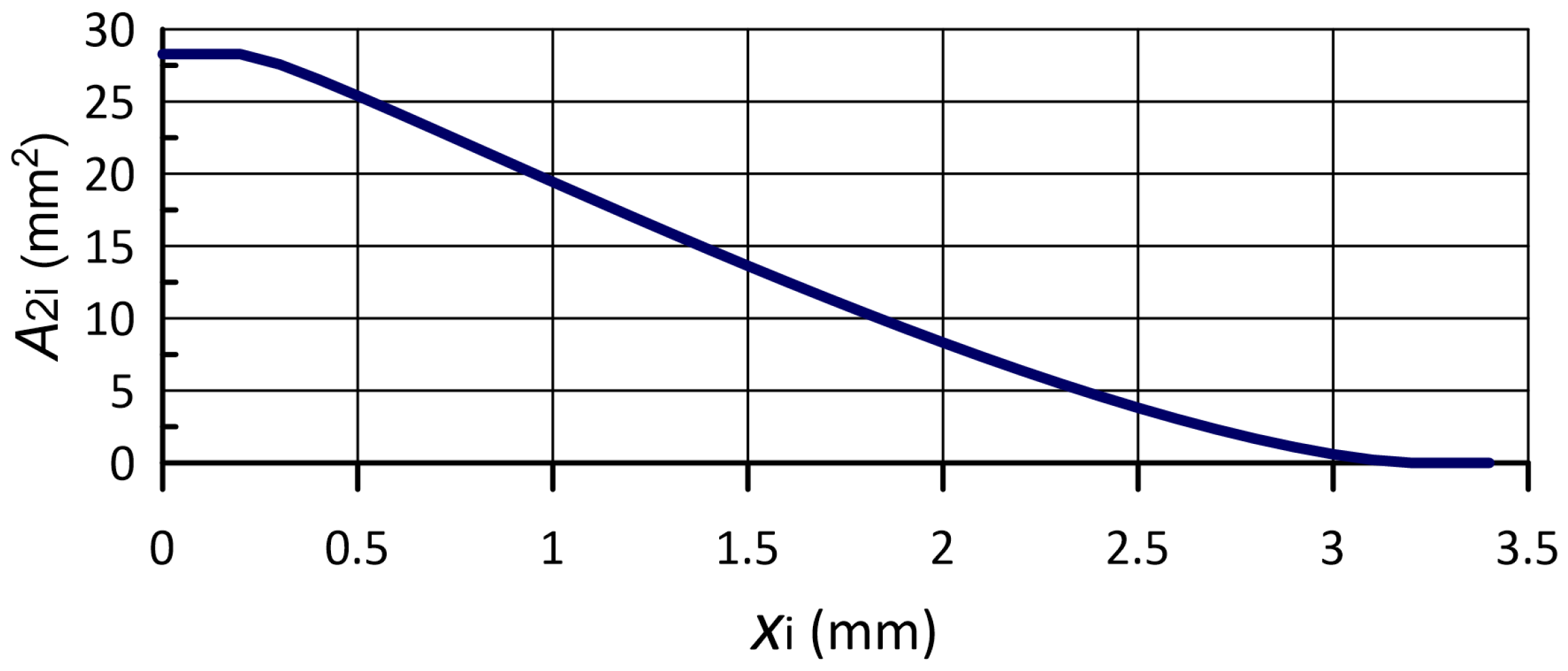
dm3 min−1 | mm | mm2 | MPa | MPa | MPa | (-) |
|---|---|---|---|---|---|---|
| 25 | 0.0 | 28.3 | 3.02 | 1.70 | 1.32 | 0.268 |
| 25 | 1.0 | 19.4 | 3.29 | 1.71 | 1.58 | 0.356 |
| 25 | 2.0 | 8.3 | 5.14 | 1.73 | 3.41 | 0.565 |
| Start-Up | Flow Control Valve | Hydraulic Motor | ||||
|---|---|---|---|---|---|---|
| Time | Spool Diam. | Diam. | Diam. | Spring Rate | Vol. Disp. | Mom. Inertia |
| s | mm | mm | mm | N mm−1 | cm3 rot−1 | kg m2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filo, G.; Lisowski, E. Numerical Analysis of Fluid Stream Division to Supply Multiple Hydraulic Receivers. Appl. Sci. 2022, 12, 10327. https://doi.org/10.3390/app122010327
Filo G, Lisowski E. Numerical Analysis of Fluid Stream Division to Supply Multiple Hydraulic Receivers. Applied Sciences. 2022; 12(20):10327. https://doi.org/10.3390/app122010327
Chicago/Turabian StyleFilo, Grzegorz, and Edward Lisowski. 2022. "Numerical Analysis of Fluid Stream Division to Supply Multiple Hydraulic Receivers" Applied Sciences 12, no. 20: 10327. https://doi.org/10.3390/app122010327






