Wavelet Analysis for Evaluating the Length of Precast Spliced Piles Using Low Strain Integrity Testing
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Driven Precast Piles
2.2. Low Strain Integrity Testing
2.3. Numerical Simulation of Low Strain Testing of Driven Precast Piles with Input Pulses of Different Durations
2.4. Complex Continuous Wavelet Transform
3. Results
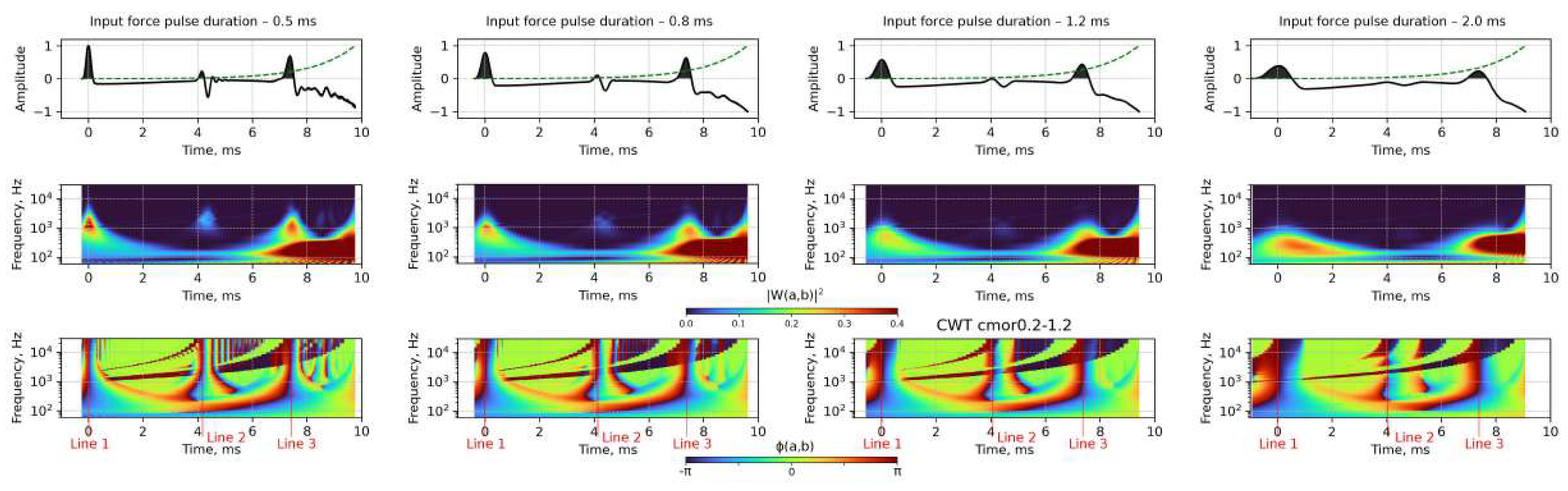
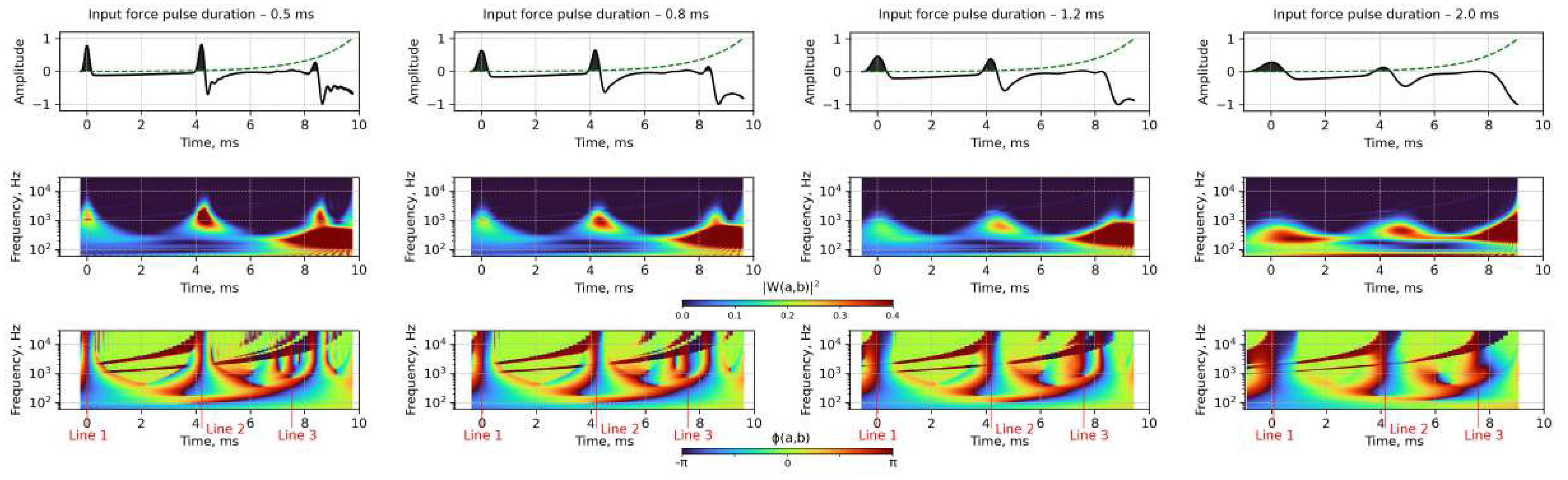
3.1. Application of Complex Continuous Wavelet Transform for the Numerical Simulation Results
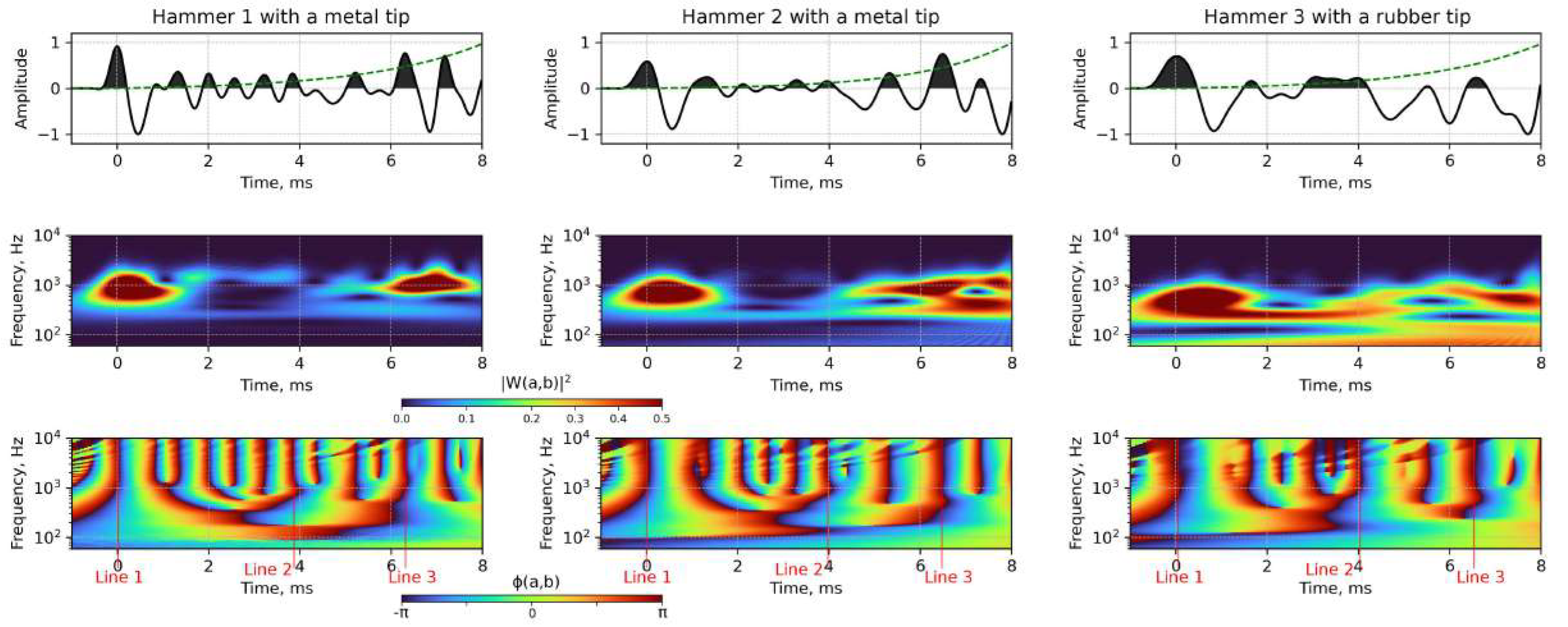
3.2. Application of Complex Continuous Wavelet Transform for the Field Low Strain Integrity Testing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Shabalov, M.Y.; Zhukovskiy, Y.L.; Buldysko, A.D.; Gil, B.; Starshaia, V.V. The influence of technological changes in energy efficiency on the infrastructure deterioration in the energy sector. Energy Rep. 2021, 7, 2664–2680. [Google Scholar] [CrossRef]
- Litvinenko, V.S. Digital Economy as a Factor in the Technological Development of the Mineral Sector. Nat. Resour. Res. 2020, 29, 1521–1541. [Google Scholar] [CrossRef]
- Filatova, I.; Nikolaichuk, L.; Zakaev, D.; Ilin, I. Public-Private Partnership as a Tool of Sustainable Development in the Oil-Refining Sector: Russian Case. Sustainability 2021, 13, 5153. [Google Scholar] [CrossRef]
- Mardashov, D.; Duryagin, V.; Islamov, S. Technology for improving the efficiency of fractured reservoir development using gel-forming compositions. Energies 2021, 14, 8254. [Google Scholar] [CrossRef]
- Kadochnikov, V.G.; Dvoynikov, M.V. Development of Technology for Hydromechanical Breakdown of Mud Plugs and Improvement of Well Cleaning by Controlled Buckling of the Drill String. Appl. Sci. 2022, 12, 6460. [Google Scholar] [CrossRef]
- Dvoynikov, M.; Sidorov, D.; Kambulov, E.; Rose, F.; Ahiyarov, R. Salt Deposits and Brine Blowout: Development of a Cross-Linking Composition for Blocking Formations and Methodology for Its Testing. Energies 2022, 15, 7415. [Google Scholar] [CrossRef]
- Dvoynikov, M.; Buslaev, G.; Kunshin, A.; Sidorov, D.; Kraslawski, A.; Budovskaya, M. New Concepts of Hydrogen Production and Storage in Arctic Region. Resources 2021, 10, 3. [Google Scholar] [CrossRef]
- Fleming, K.; Weltman, A.; Randolph, M.; Elson, K. Piling Engineering, 3rd ed.; Taylor & Francis: London, UK, 2008; pp. 253–283. [Google Scholar] [CrossRef]
- Mangushev, R.A.; Ershov, A.V.; Osokin, A.I. Modern Pile Technologies; ASV: Saint Petersburg, Russia, 2007; pp. 1–160. [Google Scholar]
- Verstov, V.V.; Gaido, A.N. Pile Foundation Technology; SPbGASU: Saint Petersburg, Russia, 2010; pp. 1–180. [Google Scholar]
- Churkin, A.A.; Ulybin, A.V.; Kapustin, V.V. Application of low strain impact testing to spliced driven piles quality control. Constr. Unique Build. Struct. 2021, 96, 1–14. [Google Scholar] [CrossRef]
- Amir, J.M. Pile integrity testing: History, present situation, and future agenda. In Proceeding of 3rd Bolivian International Conference on Deep Foundations, Santa Cruz de la Sierra, Bolivia, 29 April 2017. [Google Scholar]
- Churkin, A.A.; Kapustin, V.V.; Lozovsky, I.N.; Zhostkov, R.A. Research of the influence of the parameters of the ‘‘pile-soil’’ system on the dynamic attributes of the acoustic signal using numerical simulation. Bull. Tomsk. Polytech. Univ. Geo. Assets Eng. 2020, 332, 129–140. [Google Scholar] [CrossRef]
- Likins, G.; Rausche, F. Recent advances and proper use of PDI low strain pile integrity testing. In Proceedings of the 6th International Conference on the Application of Stress-Wave Theory to Piles, Sao Paulo, Brazil, 13 September 2000. [Google Scholar]
- Zheng, C.; Kouretzis, G.P.; Ding, X.; Liu, H.; Poulos, H.G. Threedimensional effects in low-strain integrity testing of piles: Analytical solution. Can. Geotech. J. 2015, 53, 225–235. [Google Scholar] [CrossRef]
- Potapov, A.I.; Kondratev, A.V. Non-destructive testing of multilayer medium by the method of velocity of elastic waves hodograph. J. Min. Inst. 2020, 243, 348. [Google Scholar] [CrossRef]
- Syas’ko, V.; Shikhov, A. Assessing the State of Structural Foundations in Permafrost Regions by Means of Acoustic Testing. Appl. Sci. 2022, 12, 2364. [Google Scholar] [CrossRef]
- ASTM D5882–16; Standard Test Method for Low Strain Impact Integrity Testing of Deep Foundations. ASTM International: West Conshohocken, PA, USA, 2016. [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Lee, G.R.; Gommers, R.; Wasilewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Byrnes, J.S.; Byrnes, J.L.; Hargreaves, K.A.; Berry, K. Wavelets and Their Applications; Jones and Barlett: Boston, MA, USA, 1992; pp. 1–434. [Google Scholar]
- Rhif, M.; Ben Abbes, A.; Farah, I.; Martínez, B.; Sang, Y. Wavelet Transform Application for/in Non-Stationary Time-Series Analysis: A Review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef]
- Nagornov, O.V.; Nikitaev, V.G.; Prostokishin, V.M. Wavelet Analysis in Examples; NRNU MEPhI: Moscow, Russia, 2010; pp. 1–120. [Google Scholar]
- Koronovsky, A.A.; Khramov, A.E. Continuous Wavelet Analysis and Its Applications; FIZMATLIT: Moscow, Russia, 2003; pp. 1–176. [Google Scholar]
- Yarmolenko, A.S.; Skobenko, O.V. Application of the theory of wavelets for compression and filtration of geoinformation. J. Min. Inst. 2018, 234, 612. [Google Scholar] [CrossRef]
- Addison, P.S.; Watson, J.N. Wavelet analysis for low strain integrity testing of foundation piles. In Proceedings of the 5th International Conference on Inspection, Appraisal, Repairs, Maintenance of Buildings and Structures, Singapore, 15−16 May 1997; pp. 15–16. [Google Scholar]
- Watson, J.N.; Addison, P.S.; Sibbald, A. The de-noising of sonic echo test data through wavelet transform reconstruction. Shock. Vib. 1999, 6, 175750. [Google Scholar] [CrossRef]
- Ni, S.H.; Isenhower, W.M.; Huang, Y.H. Continuous wavelet transform technique for low-strain integrity testing of deep drilled shafts. J. GeoEngineering 2012, 7, 97–105. [Google Scholar] [CrossRef]
- Ni, S.H.; Yang, Y.Z.; Tsai, P.H.; Chou, W.H. Evaluation of pile defects using complex continuous wavelet transform analysis. NDT E Int. 2017, 87, 50–59. [Google Scholar] [CrossRef]
- Ni, S.H.; Yang, Y.Z.; Lyu, C.R. Application of wavelet analysis for the impulse response of pile. Smart Struct. Syst. 2017, 19, 513–521. [Google Scholar] [CrossRef]
- Ni, S.H.; Li, J.L.; Yang, Y.Z.; Lai, Y.Y. Applicability of complex wavelet transform to evaluate the integrity of commonly used pile types. J. GeoEngineering 2019, 14, 21–30. [Google Scholar] [CrossRef]
- Zheng, W.; Zheng, W.; Wang, S.; Lin, C.; Yu, X.; Liu, J. Damage localization of piles based on complex continuous wavelet transform: Numerical example and experimental verification. Shock. Vib. 2020, 2020, 058640. [Google Scholar] [CrossRef]
- Liu, J.L.; Lin, C.X.; Ye, X.J.; Zheng, W.T.; Luo, Y.P. An improved algorithm for pile damage localization based on complex continuous wavelet transform. Smart Struct. Syst. 2021, 27, 493–506. [Google Scholar] [CrossRef]
- Lozovsky, I.N.; Loseva, E.S.; Syasko, V.A. Wavelet denoising for low strain pile integrity testing. Test. Diagn. 2022, 25, 36–45. [Google Scholar]
- Churkin, A.A.; Loseva, E.S.; Lozovsky, I.N.; Syasko, V.A. Increasing the reliability of the low strain integrity testing of piles under existing structures. Test. Diagn. 2022, 25, 24–32. [Google Scholar]
- GOST 19804-2012; Prefabricated Reinforced Concrete Piles. Specifications. Interstate Scientific and Technical Commission for Standardization, Technical Regulation and Conformity Assessment in Construction: Moscow, Russia, 2012.
- Series 1.011.1-10; Reinforced Concrete Driven Piles. Issue 8. Fundamentproekt Institute: Moscow, Russia, 2021.
- GOST 8510-86; Hot-Rolled Steel Unequal-Leg Angels. Dimensions. Interstate Council for Standardization, Metrology and Certification: Moscow, Russia, 2012.
- GOST 14098-2014; Welded Joints of Reinforcement and Inserts for Reinforced Concrete Structures. Types, Constructions and Dimensions. Interstate Council for Standardization, Metrology and Certification: Moscow, Russia, 2015.
- Cui, D.M.; Yan, W.; Wang, X.Q.; Lu, L.M. Towards intelligent interpretation of low strain pile integrity testing results using machine learning techniques. Sensors 2017, 7, 2443. [Google Scholar] [CrossRef]
- Kim, H.J.; Mission, J.L.; Dinoy, P.R.; Kim, H.S.; Park, T.W. Guidelines for impact echo test signal interpretation based on wavelet packet transform for the detection of pile defects. Appl. Sci. 2020, 10, 2633. [Google Scholar] [CrossRef]
- Zhostkov, R.A. A Software for Simulation of Low Integrity Testing for Cast-in-Place Piles. Patent RF. 2019.665449.
- Clough, R.W.; Penzien, J.; Griffin, D.S. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Stojić, D.; Nestorović, T.; Marković, N.; Marjanović, M. Experimental and numerical research on damage localization in plate-like concrete structures using hybrid approach. Struct. Control. Health Monit. 2018, 25, e2214. [Google Scholar] [CrossRef]
- Lozovsky, I.N.; Zhostkov, R.A.; Churkin, A.A. Numerical simulation of ultrasonic pile integrity testing. Russ. J. Nondestruct. Test. 2020, 56, 1–11. [Google Scholar] [CrossRef]
- Vasilyeva, N.V.; Boikov, A.V.; Erokhina, O.O.; Trifonov, A.Y. Automated digitization of radial charts. J. Min. Inst. 2021, 247, 82–87. [Google Scholar] [CrossRef]
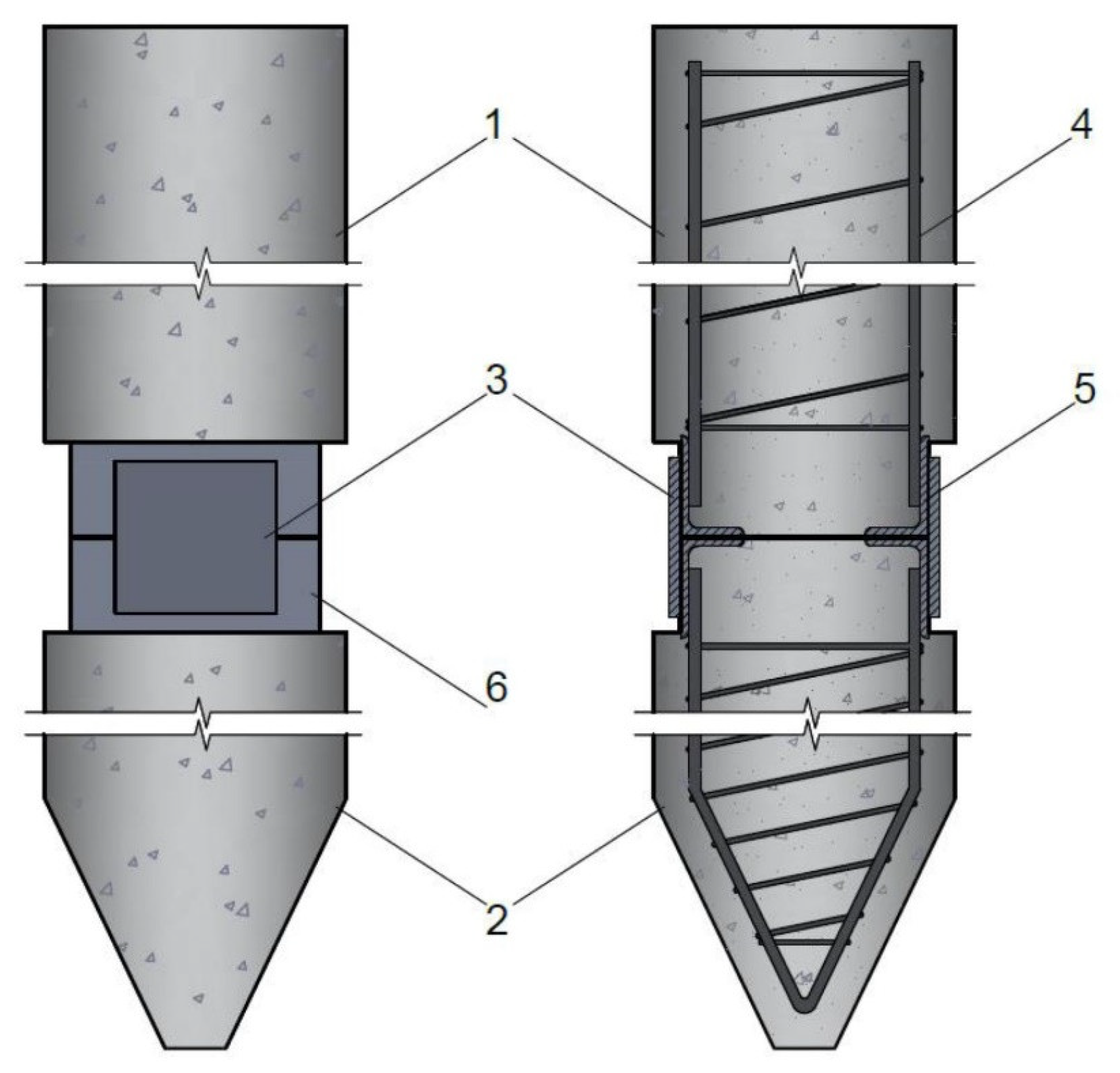
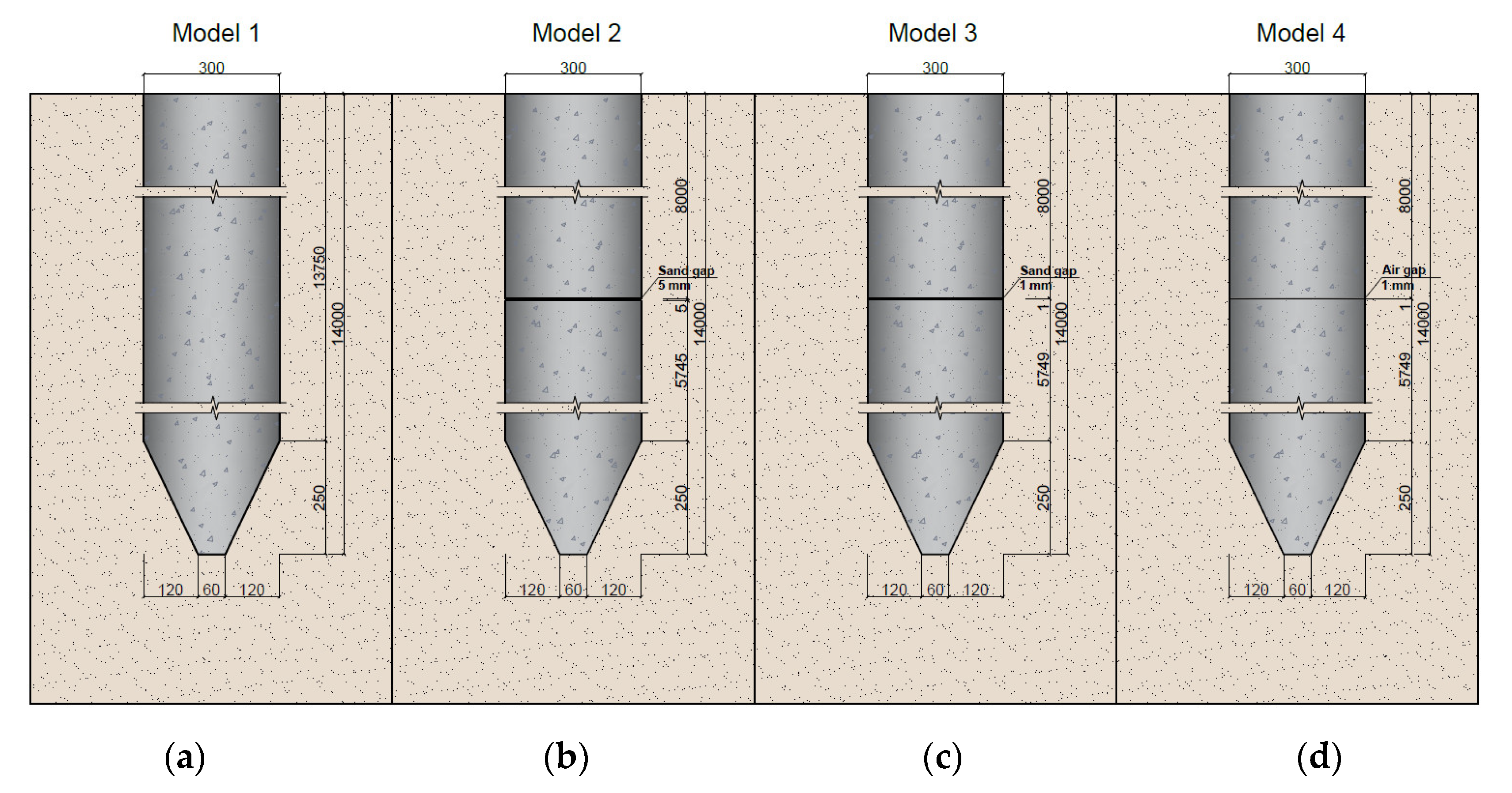
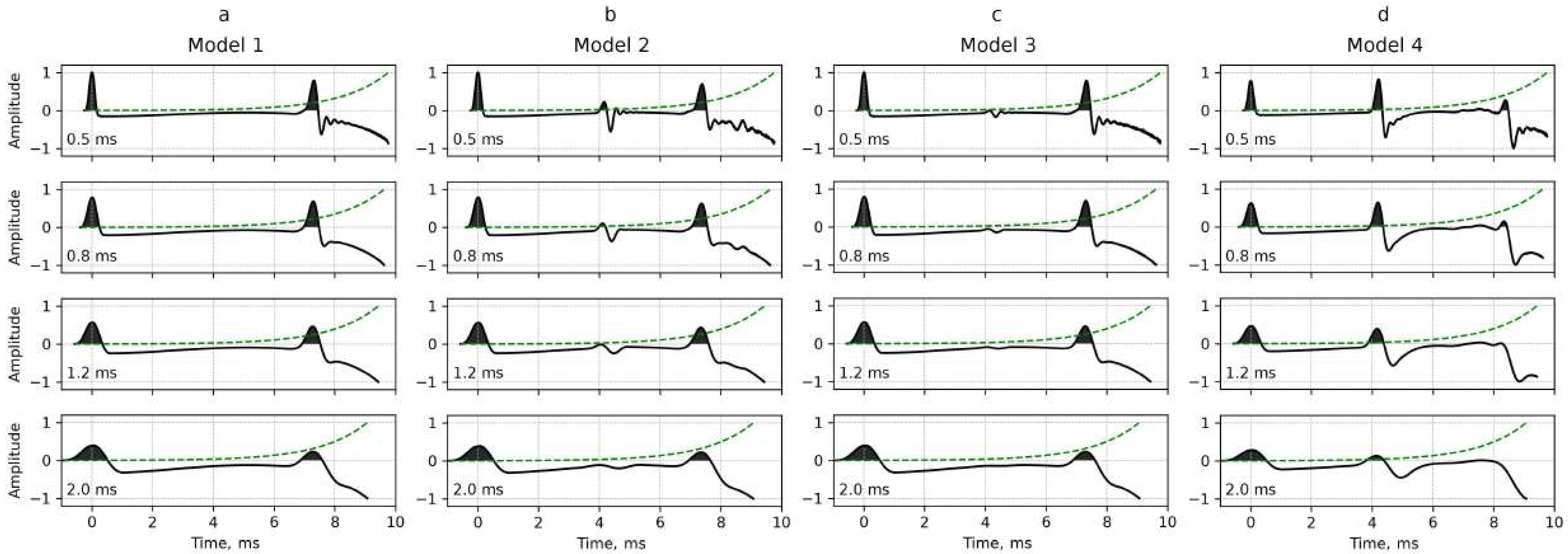
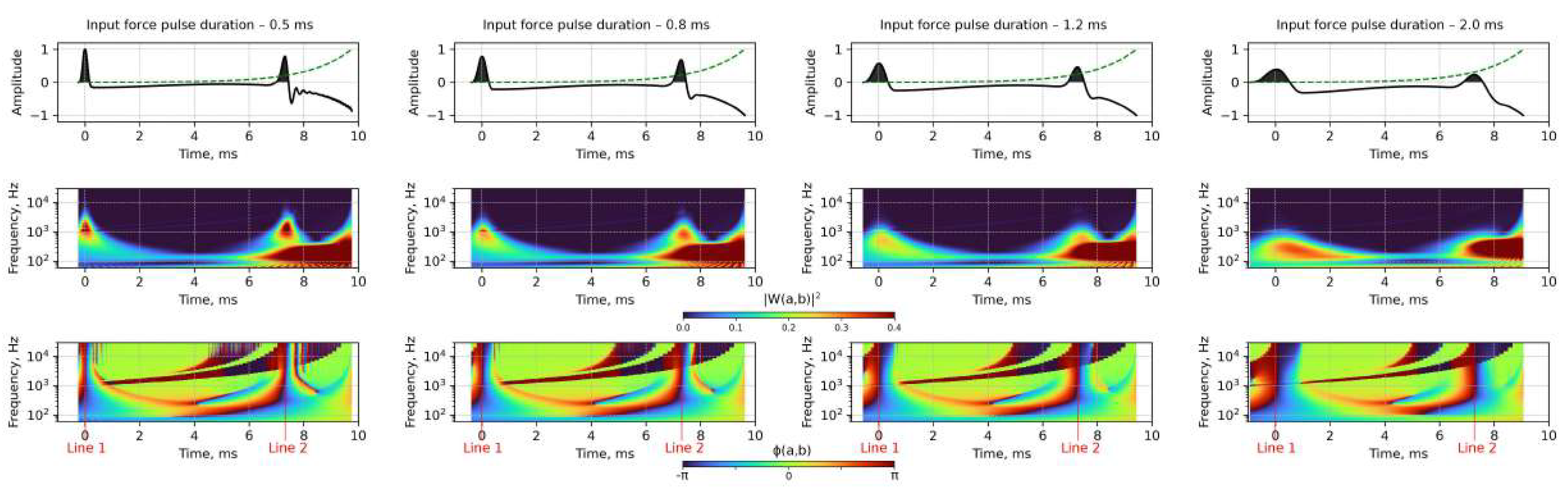

| Parameters | Density, kg/m3 | Pressure Wave Velocity, m/s | Shear Wave Velocity, m/s | Rayleigh Coefficients: α, s−1; β, s |
|---|---|---|---|---|
| Concrete | 2400 | 4000 | 2450 | 20; 10−8 |
| Sand | 1500 | 600 | 200 | 200; 10−7 |
| Air | 1275 | 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loseva, E.; Lozovsky, I.; Zhostkov, R.; Syasko, V. Wavelet Analysis for Evaluating the Length of Precast Spliced Piles Using Low Strain Integrity Testing. Appl. Sci. 2022, 12, 10901. https://doi.org/10.3390/app122110901
Loseva E, Lozovsky I, Zhostkov R, Syasko V. Wavelet Analysis for Evaluating the Length of Precast Spliced Piles Using Low Strain Integrity Testing. Applied Sciences. 2022; 12(21):10901. https://doi.org/10.3390/app122110901
Chicago/Turabian StyleLoseva, Elizaveta, Ilya Lozovsky, Ruslan Zhostkov, and Vladimir Syasko. 2022. "Wavelet Analysis for Evaluating the Length of Precast Spliced Piles Using Low Strain Integrity Testing" Applied Sciences 12, no. 21: 10901. https://doi.org/10.3390/app122110901
APA StyleLoseva, E., Lozovsky, I., Zhostkov, R., & Syasko, V. (2022). Wavelet Analysis for Evaluating the Length of Precast Spliced Piles Using Low Strain Integrity Testing. Applied Sciences, 12(21), 10901. https://doi.org/10.3390/app122110901






