Research on Fracture Mechanism and Stability of Slope with Tensile Cracks
Abstract
1. Introduction
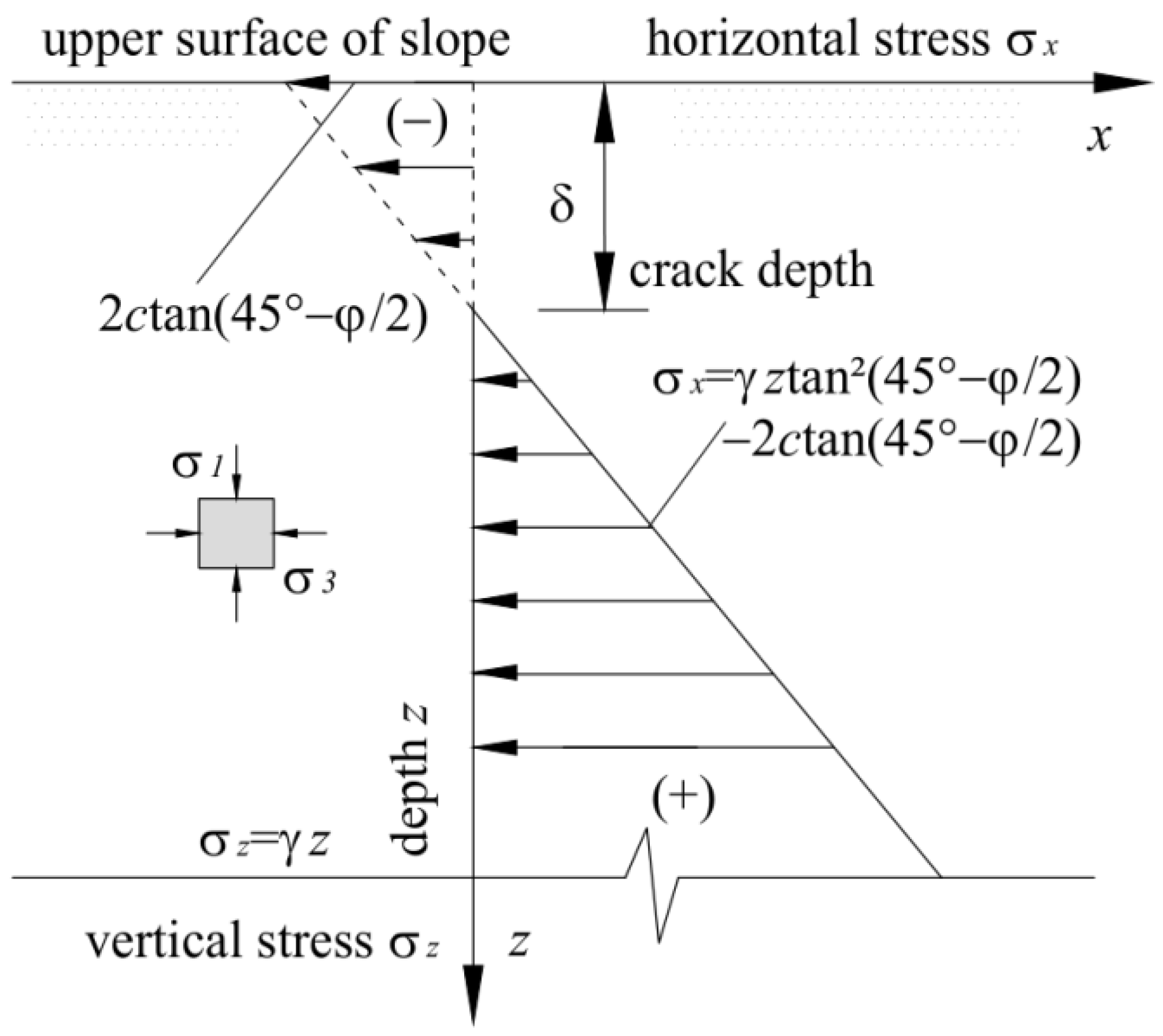
2. Formation Mechanism and Value of Vertical Crack
2.1. Cracking Mechanism
2.2. Maximum Value of Tensile Crack
2.3. Failure Mode of Slope with Crack
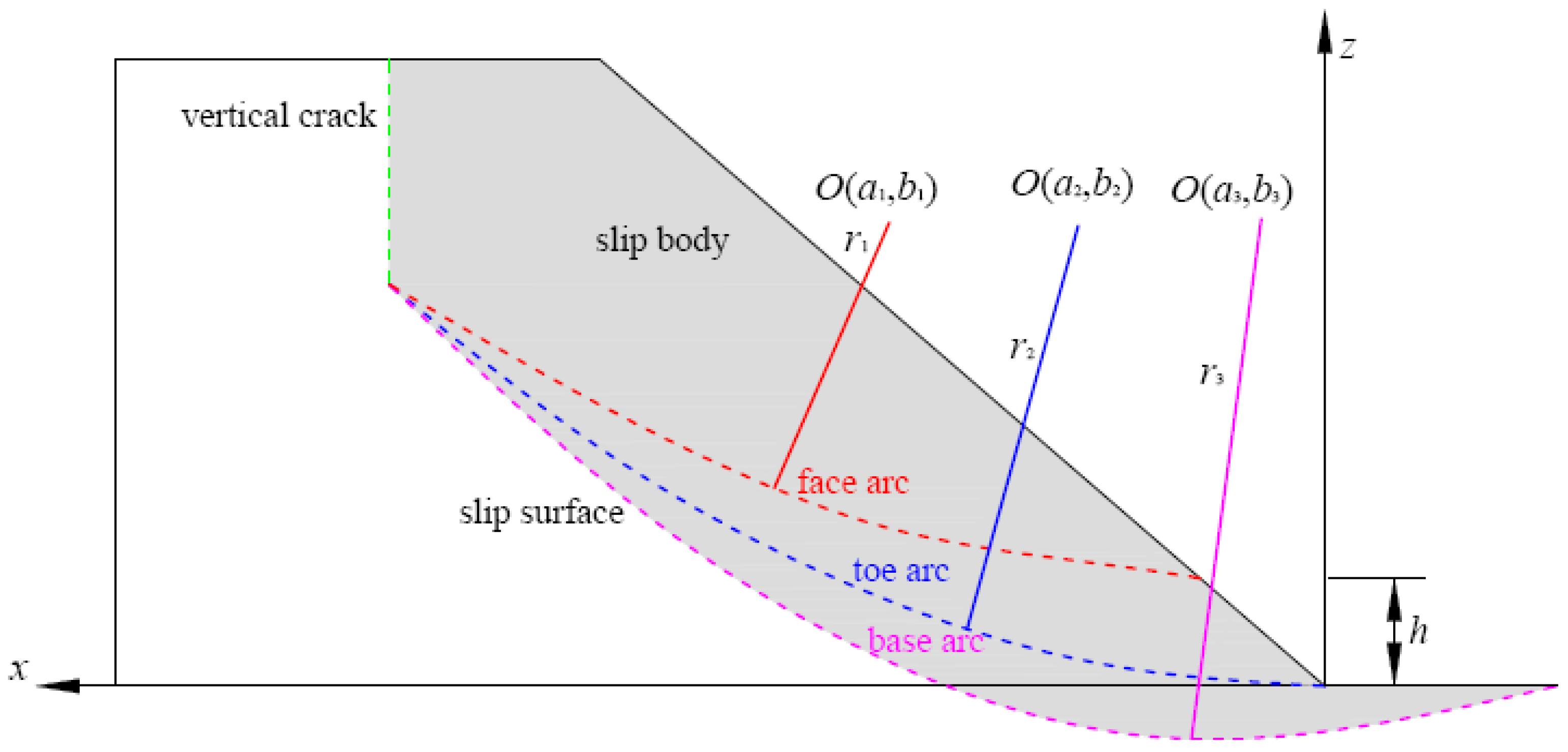
3. Analytical Method for Safety Factor of Slope with Crack
3.1. Analytical Method for Safety Factor of Toe Circle Slope
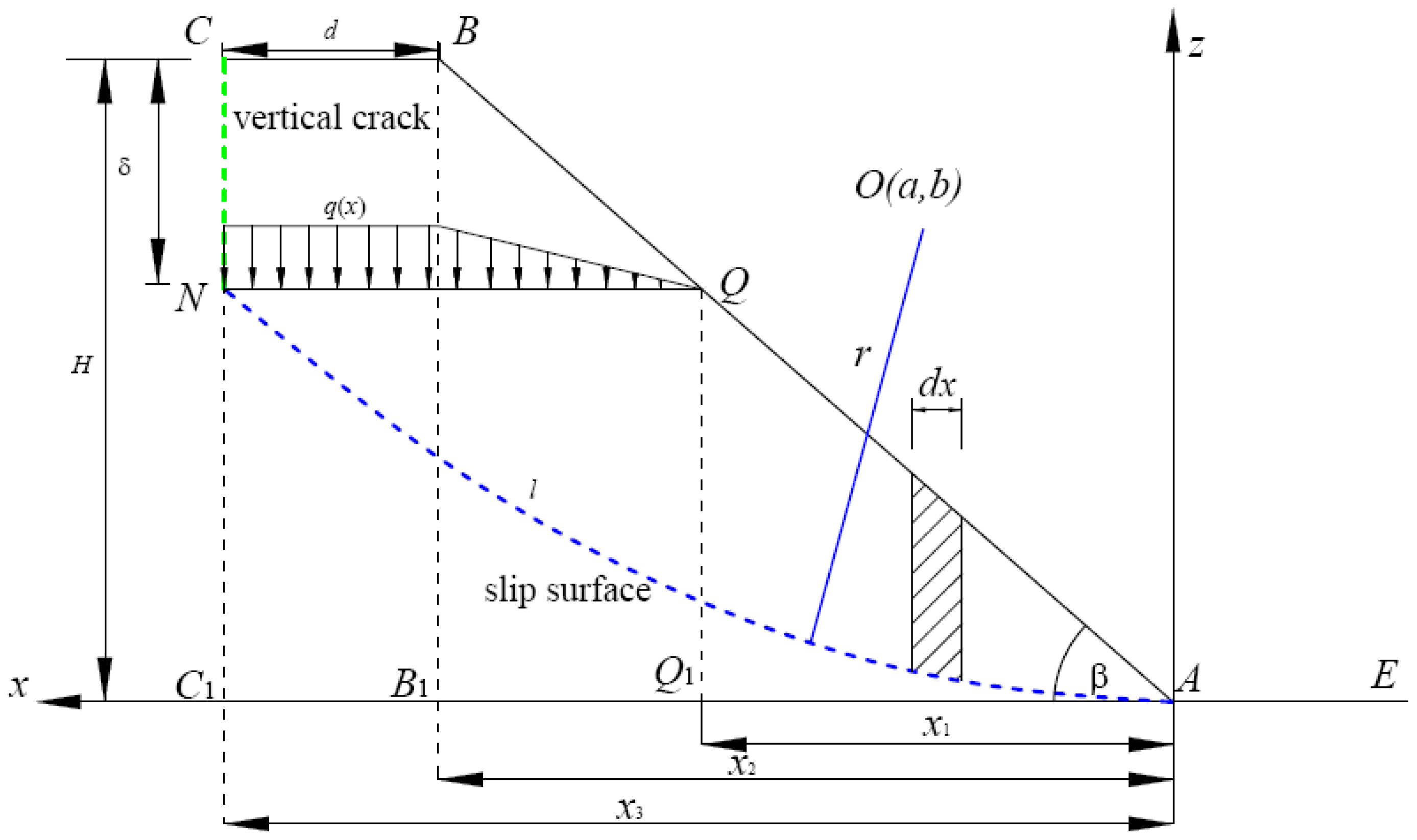
3.1.1. Calculated Model of Toe Circle Slope
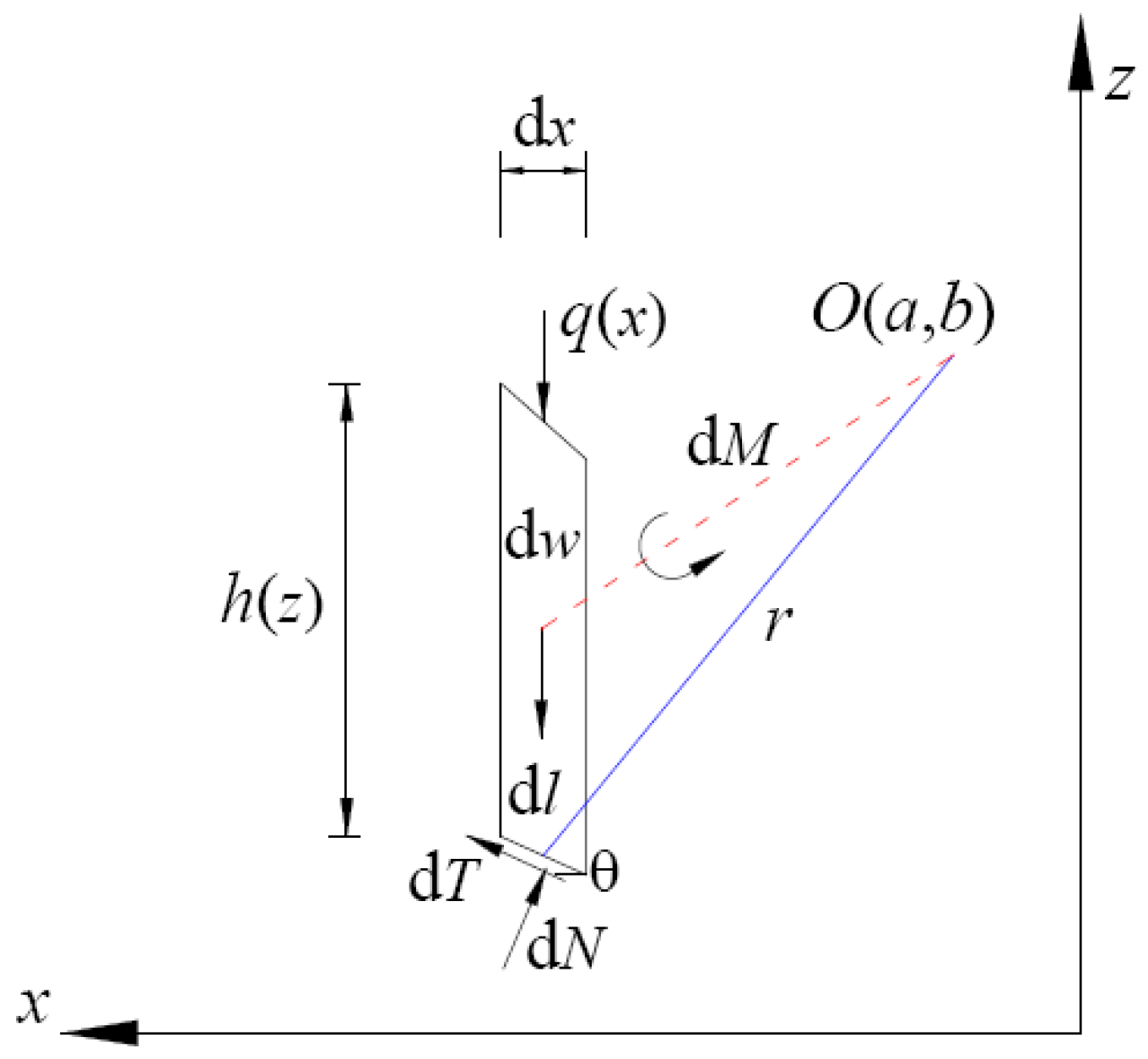
3.1.2. Determination of the Safety Factor
3.2. Analytical Method for Safety Factor of Base Circle Slope
3.2.1. Calculated Model of Base Circle Slope
3.2.2. Determination of the Safety Factor
3.3. Analytical Method for Safety Factor of Face Circle Slope
3.4. Analytical Calculate Process
4. Results Analysis
4.1. Verification of the Present Formulation
4.2. The Effects of Parameters on the Stability of Slope
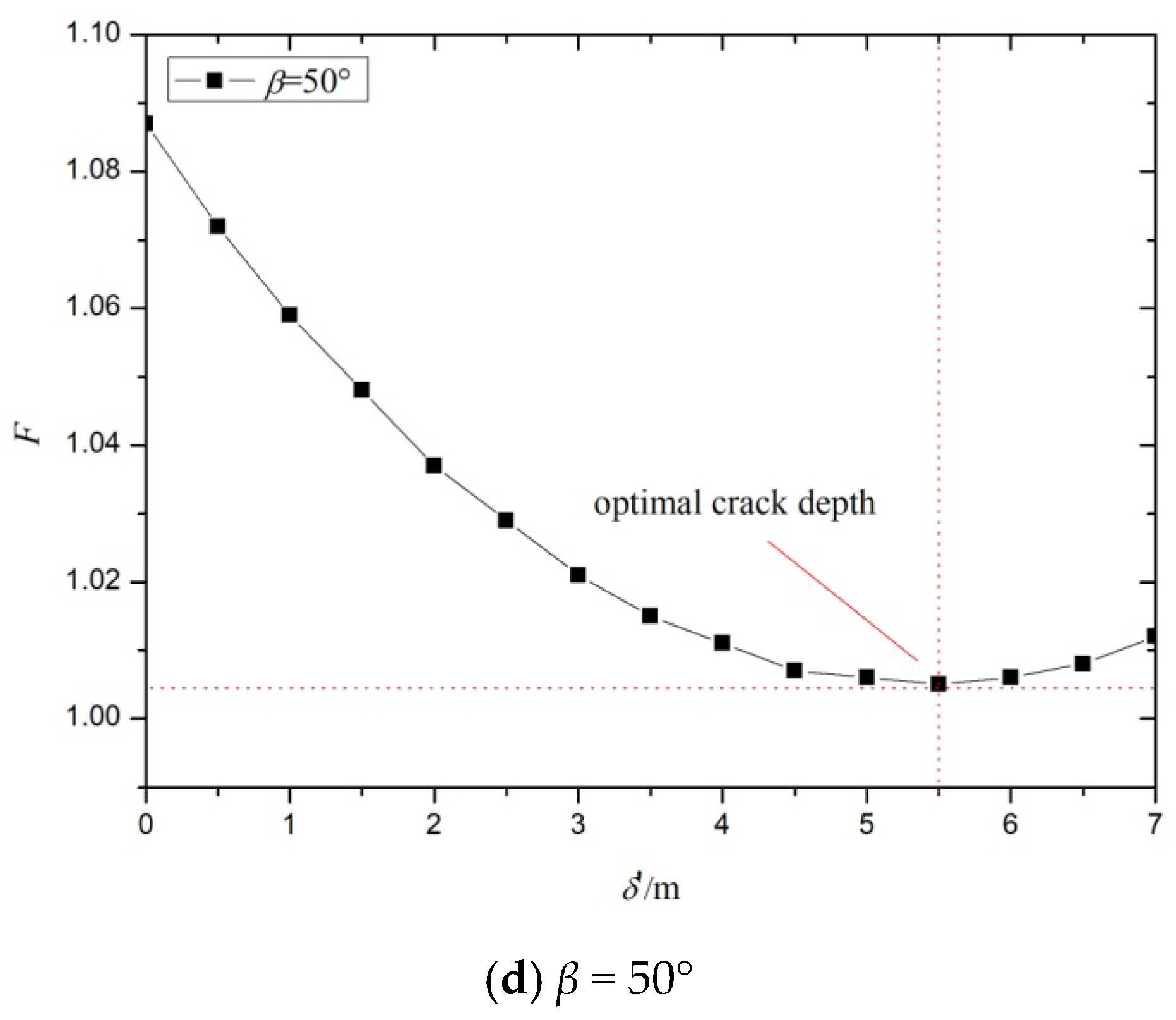
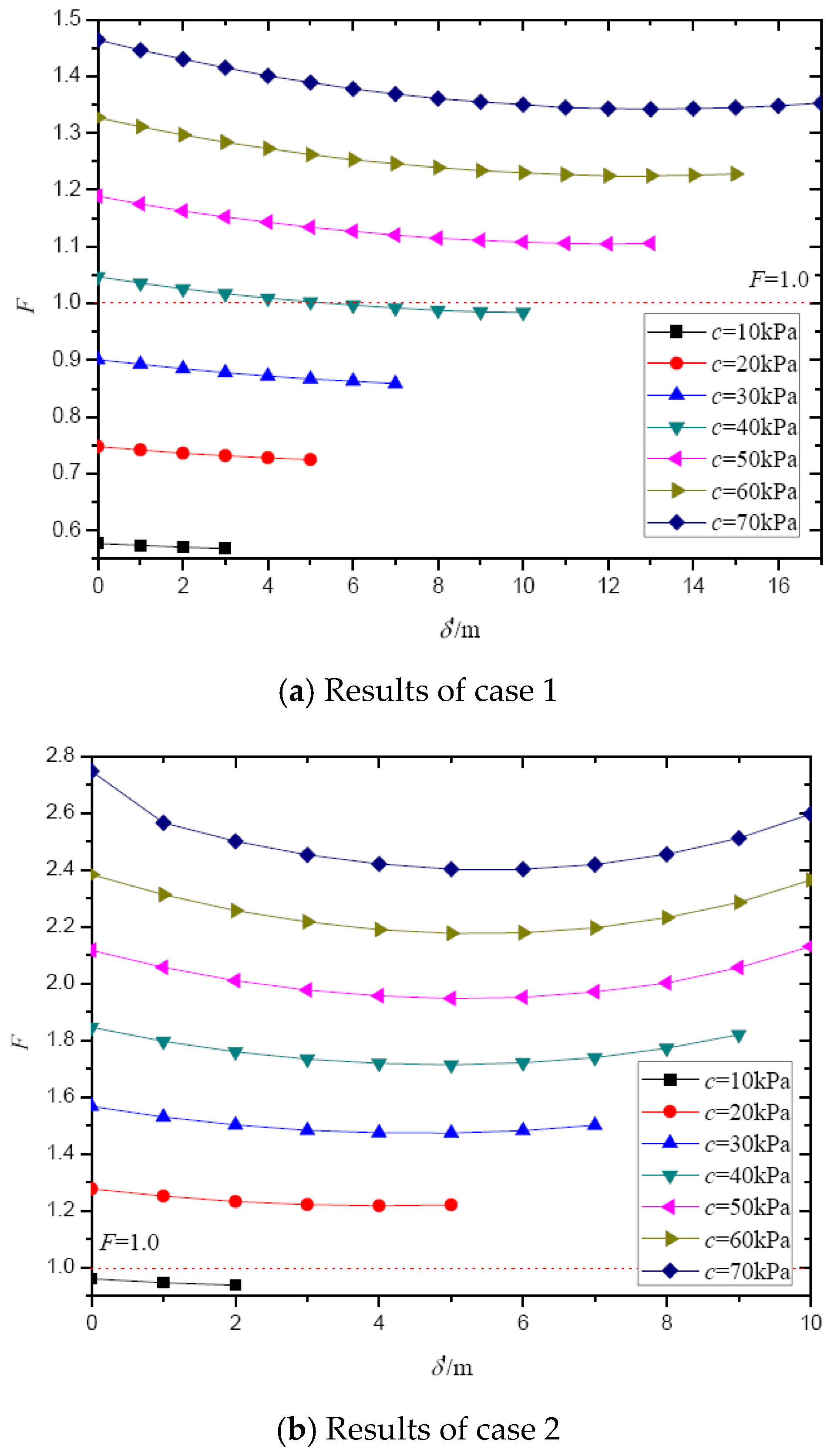
4.2.1. The Effects of Crack Depth and Slope Angle on the Safety Factor
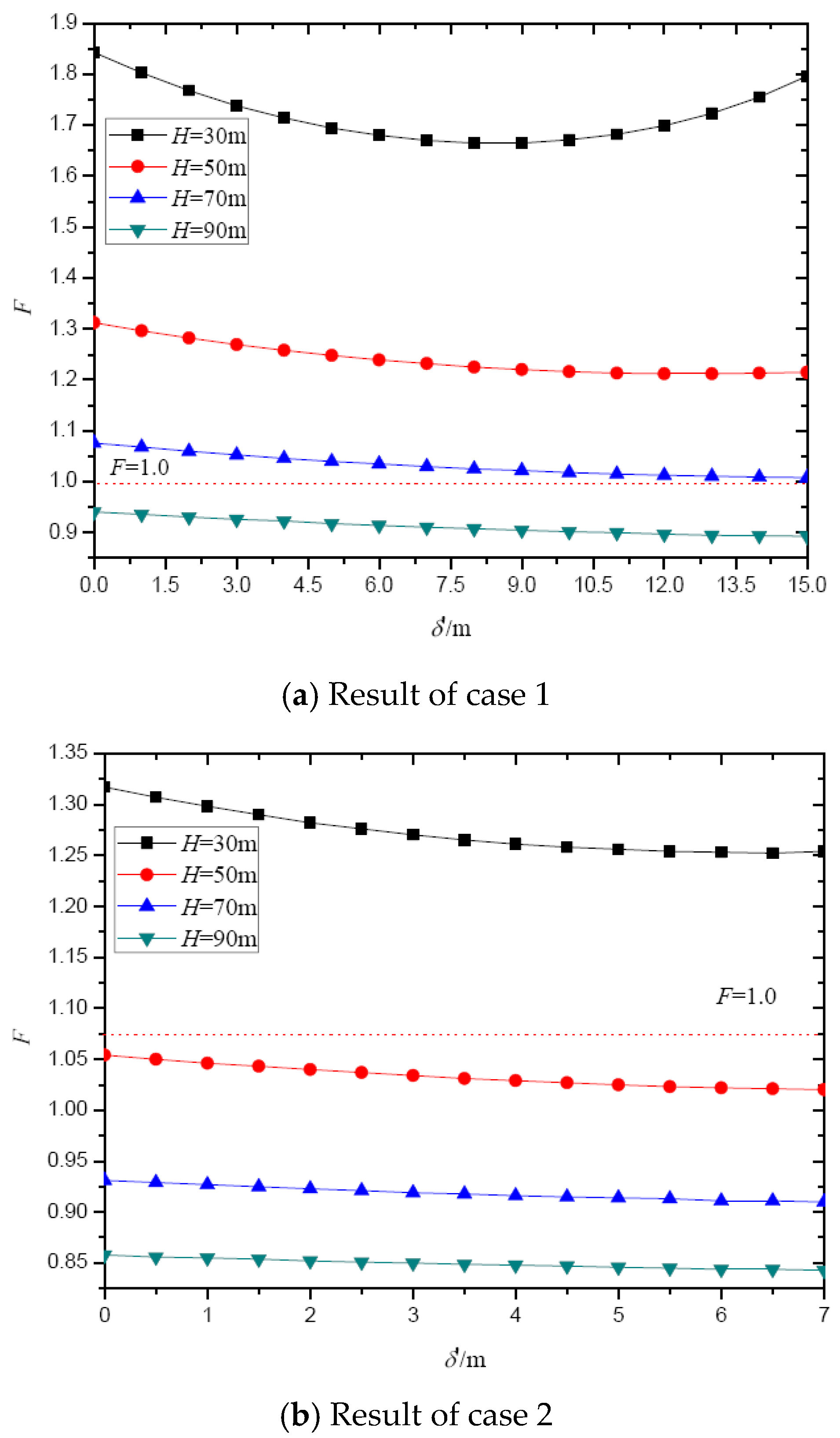
4.2.2. The Effects of Crack Depth and Slope Height on the Safety Factor
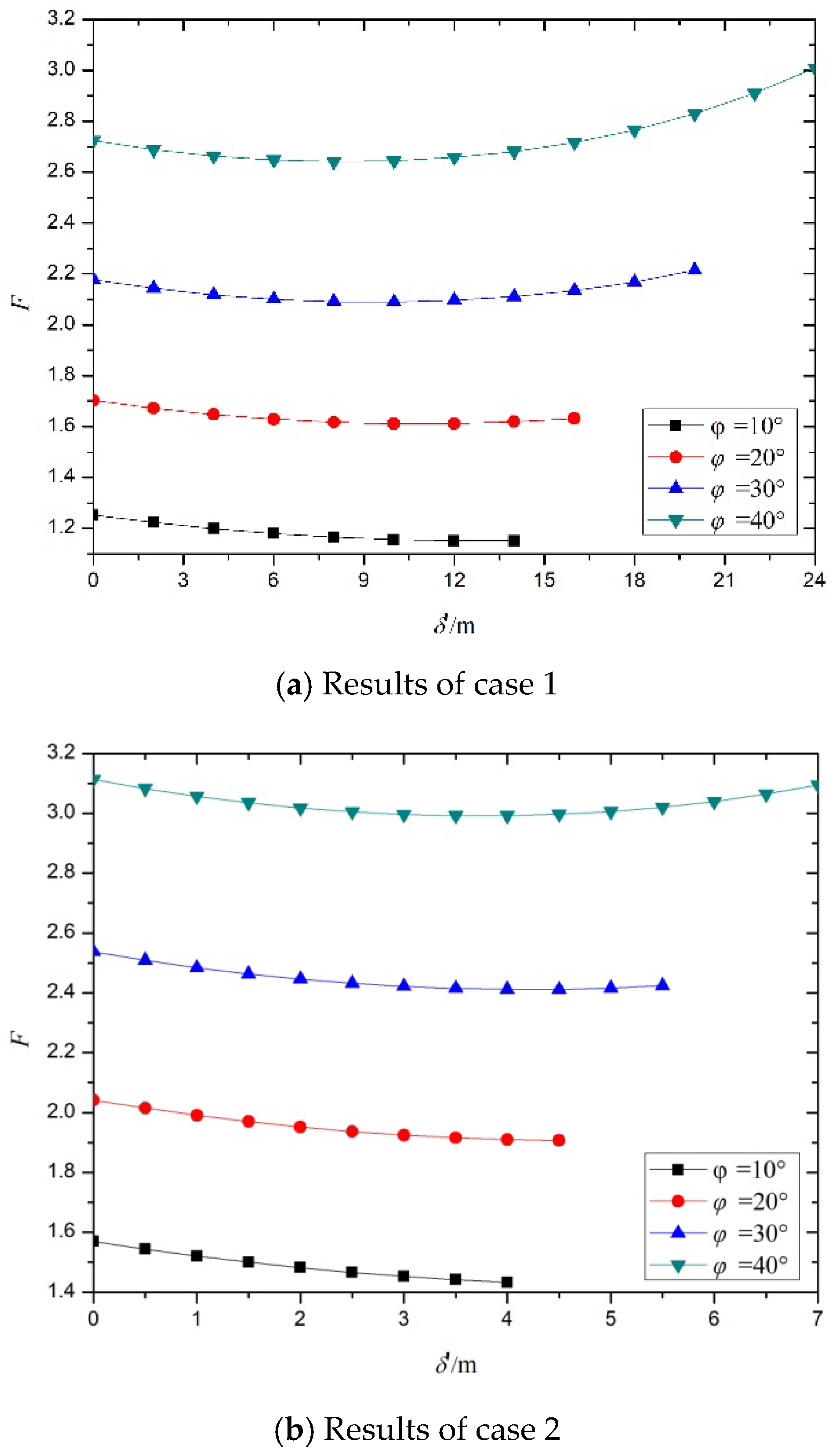
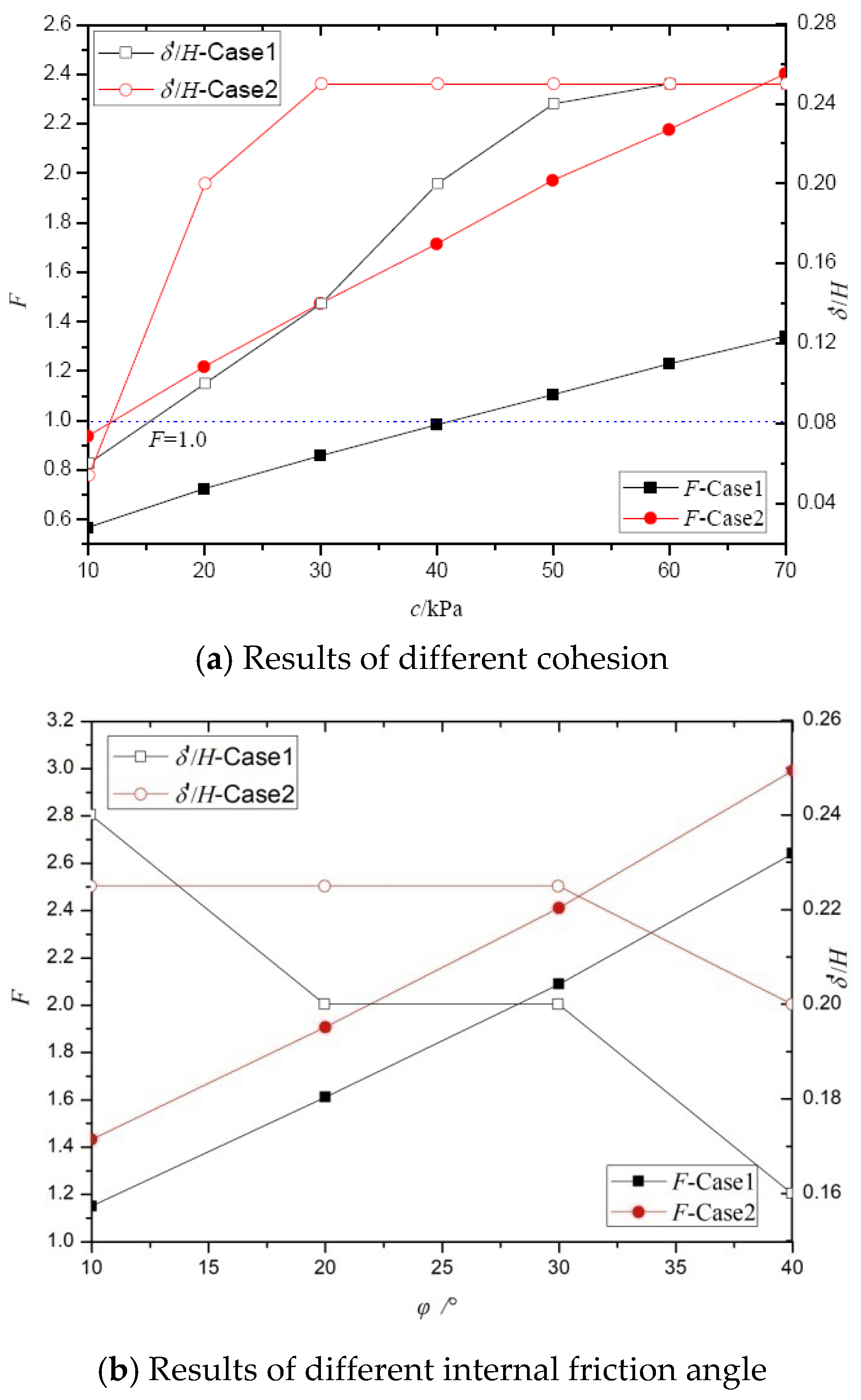
4.2.3. The Effects of Crack Depth and Internal Friction Angle on the Safety Factor
4.2.4. The Effects of Crack Depth and Cohesion on the Safety Factor
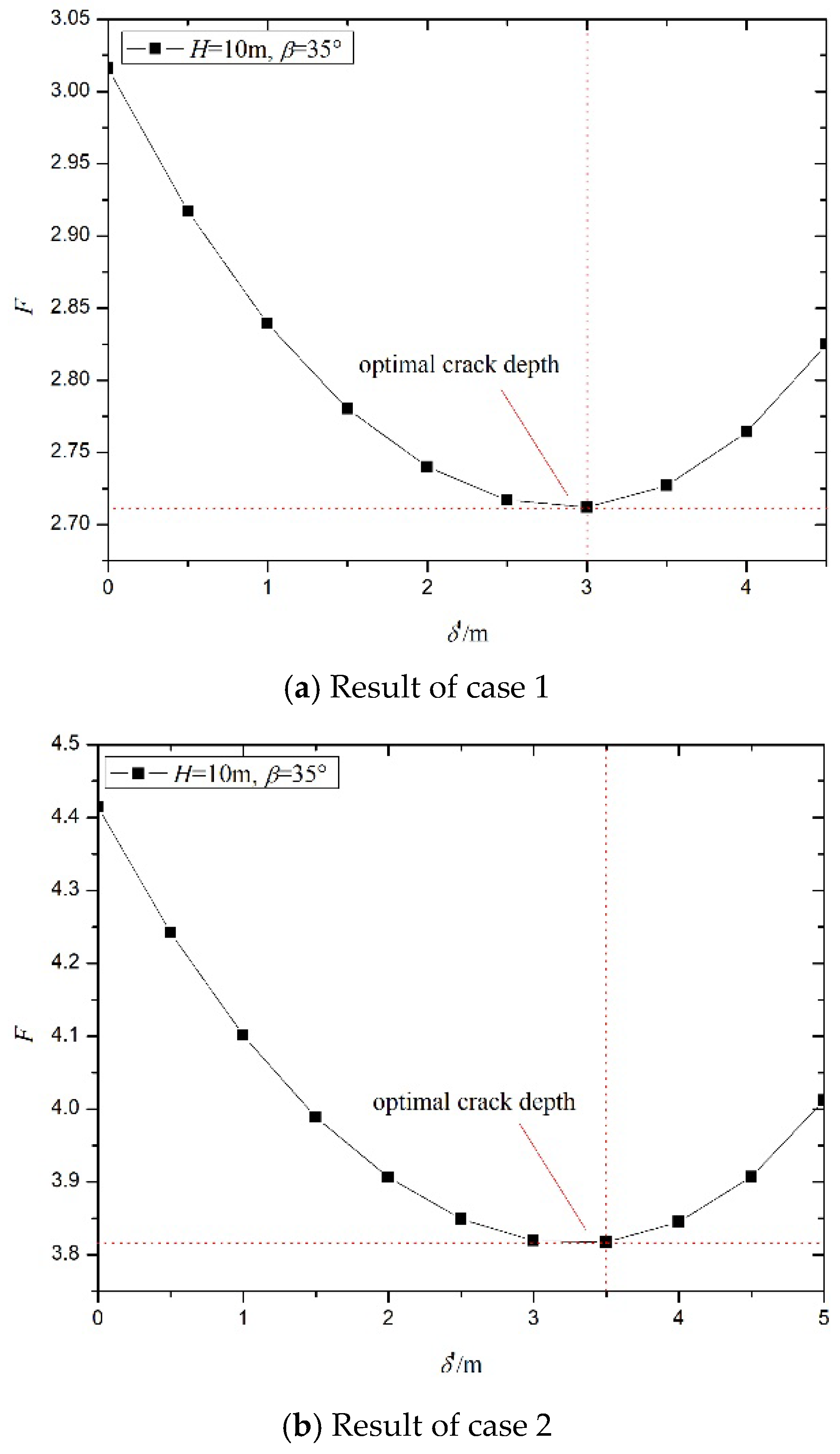
4.2.5. The Effect of Optimal Crack Depth on the Safety Factor
4.2.6. The Effects of Optimal Crack Parameters and Slip Body Morphology on the Safety Factor
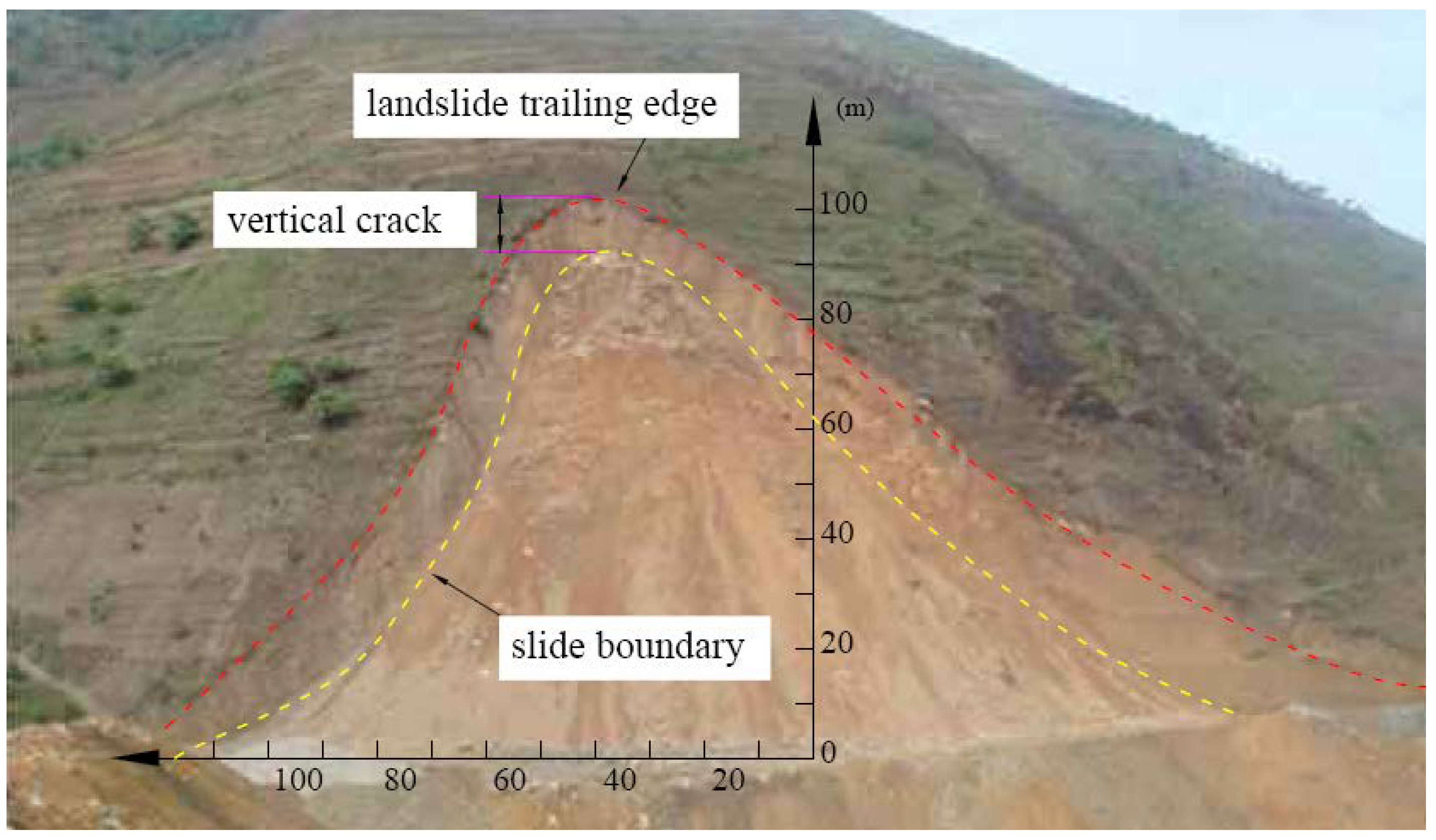
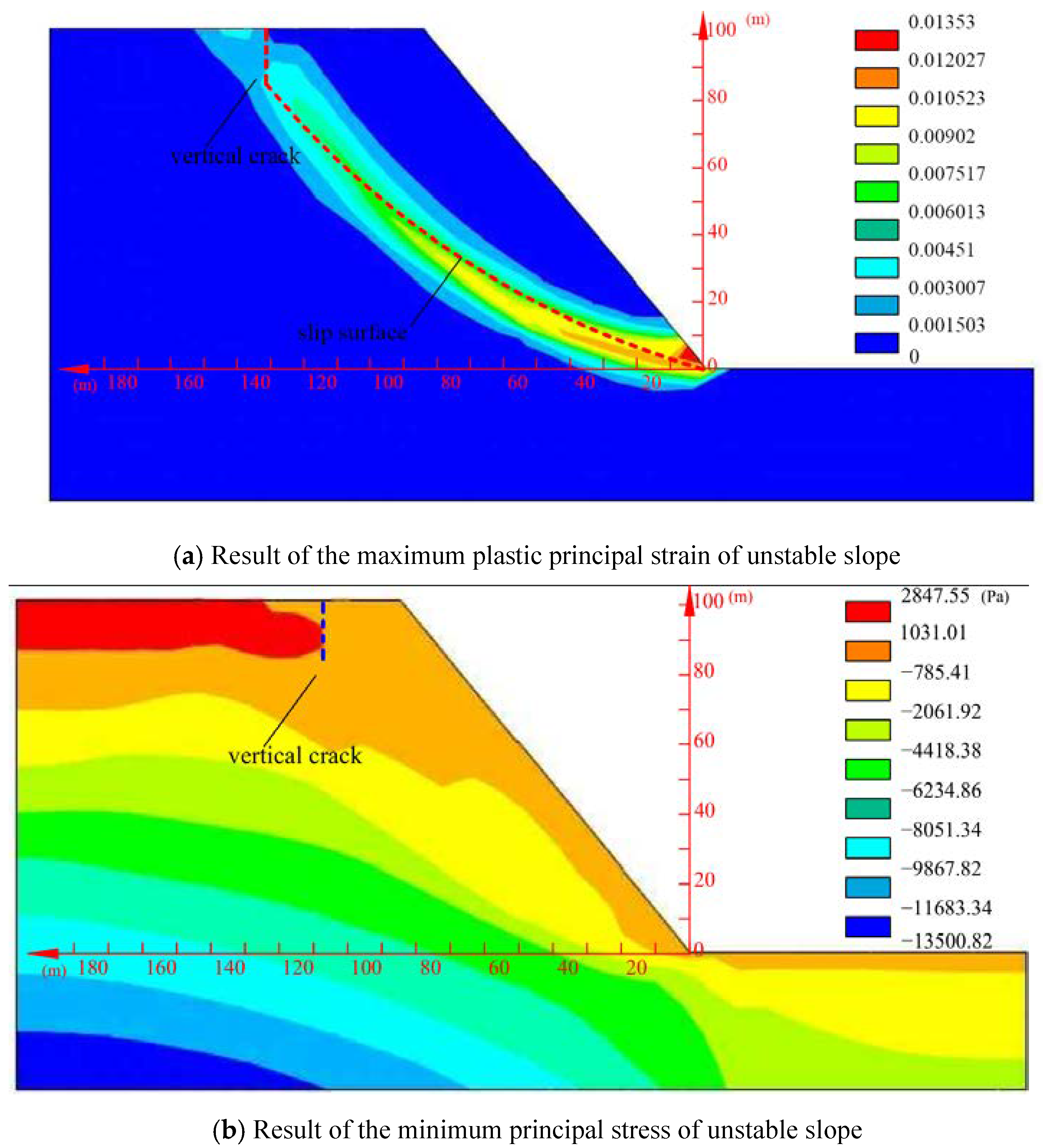
5. An Engineering Example Application: Determination of the Crack Depth and Safety Factor for a Highway Landslide
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, L.S.; Zhao, Z.L.; Luo, Z.G.; Sun, Y.L. What is the role of tensile cracks in cohesive slopes? J. Rock Mech. Geotech. Eng. 2019, 11, 314–324. [Google Scholar] [CrossRef]
- Mukhlisin, M.; Khiyon, K.N. The effects of cracking on slope stability. J. Geol. Soc. India 2018, 91, 704–710. [Google Scholar] [CrossRef]
- Dai, Z.H.; Lu, C.J. Mechanical explanations on mechanism of slope stability. Chin. J. Geotech. Eng. 2006, 28, 1191–1197. [Google Scholar]
- Wang, W.; Chen, G.Q.; Zhu, J.; Huang, R.Q. Slope stability calculated with strength reduction method considering tensile and shear progress failure. Chin. J. Rock Mech. Eng. 2018, 37, 2064–2074. [Google Scholar]
- Kong, X.A.; Cai, G.Q.; Zhao, C.G. Study on tenso-shear coupling strength of clays. Rock Soil Mech. 2016, 37, 2285–2292. [Google Scholar]
- Wu, X.Y.; Niu, F.J.; Liang, Q.G.; Li, G.Y. Study on tensile strength and tensile-shear coupling mechanism of loess around Lanzhou and Yanan city in China by unconfined penetration test. KSCE J. Civ. Eng. 2019, 23, 2471–2482. [Google Scholar] [CrossRef]
- Hou, H.J.; Zhu, Z.W.; Wang, B.; Zhou, W.B. A practical model study on the mechanism of clay landslide under static loads: From the perspective of major crack–stress–displacement. Appl. Sci. 2022, 12, 3224. [Google Scholar] [CrossRef]
- Khan, M.I.; Wang, S.H. Slope stability analysis to correlate shear strength with slope angle and shear stress by considering saturated and unsaturated seismic conditions. Appl. Sci. 2021, 11, 4568. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley and Sons: New York, NY, USA, 1943. [Google Scholar]
- Cousine, B.F. Stability charts for simple earth slopes allowing for tension cracks. In Proceedings of the Third Australia-New Zealand Conference on Soft Soils, Wellington, New Zealand, 12–16 May 1980. [Google Scholar]
- Spencer, E. Effect of tension on stability of embankments. J. Soil Mech. Found. Div. 1968, 94, 1159–1176. [Google Scholar] [CrossRef]
- Zhang, N.X.; Li, X. The new formula of the limit equilibrium horizontal top vertical slope. J. Eng. Geol. 2008, 16 (Suppl. 1), 251–256. [Google Scholar]
- Chowdhury, R.N.; Zhang, S. Tension cracks and slope failure. In Slope Stability Engineering Developments and Applications: Proceedings of the International Conference on Slope Stability Organized by the Institution of Civil Engineers and Held on the Isle of Wight on 15–18 April 1991; Thomas Telford: London, UK, 1991; Volume 5, pp. 27–32. [Google Scholar]
- Baker, R. Sufficient conditions for existence of physically significant solutions in limiting equilibrium slope stability analysis. Int. J. Solids Struct. 2003, 40, 3717–3735. [Google Scholar] [CrossRef]
- Utili, S. Investigation by limit analysis on the stability of slopes with cracks. Géotechnique 2013, 63, 140–154. [Google Scholar] [CrossRef]
- Michalowski, R.L. Stability assessment of slopes with cracks using limit analysis. Can. Geotech. J. 2013, 50, 1011–1021. [Google Scholar] [CrossRef]
- Gao, Y.F.; Song, W.Z.; Zhang, F.; Qin, H.Y. Limit analysis of slopes with cracks: Comparisons of results. Eng. Geol. 2015, 188, 97–100. [Google Scholar] [CrossRef]
- Ducan, J.M.; Wright, S.G.; Brandon, T.L. Soil Strength and Slope Stability; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Moawwez, M.A.; Wang, J.P.; Hussain, M.A. Development of empirical correlations for limit equilibrium methods of slope stability analysis. Arab. J. Geosci. 2021, 14, 2020. [Google Scholar] [CrossRef]
- Azmoon, B.; Biniyaz, A.; Liu, Z. Evaluation of deep learning against conventional limit equilibrium methods for slope stability analysis. Appl. Sci. 2021, 11, 6060. [Google Scholar] [CrossRef]
- Baker, R. Tensile strength, tension cracks, and stability of slopes. Soils Found. 1981, 21, 1–17. [Google Scholar]
- Kaniraj, S.R.; Abdullah, H. Effect of berms and tension crack on the stability of embankments on soft soils. Soils Found. 1993, 33, 99107. [Google Scholar] [CrossRef]
- Baker, R.; Leshchinsky, D. Spatial distribution of safety factors: Cohesive vertical cut. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 1057–1078. [Google Scholar] [CrossRef]
- Norly, B.; Roberto, Ú.; Alfredo, C.; Ferri, H. Safety factor on rock slopes with tensile cracks using numerical and limit equilibrium models. Geotech. Geol. Eng. 2021, 39, 2287–2300. [Google Scholar]
- Li, Y.X.; Yang, X.L. Stability analysis of crack slope considering nonlinearity and water pressure. KSCE J. Civ. Eng. 2016, 20, 2289–2296. [Google Scholar] [CrossRef]
- Zhou, Y.D.; Zhang, F.; Wang, J.Q.; Gao, Y.F.; Dai, G.Y. Seismic stability of earth slopes with tension crack. Front. Struct. Civ. Eng. 2019, 13, 950–964. [Google Scholar] [CrossRef]
- Hou, C.Q.; Zhang, T.T.; Sun, Z.B.; Dias, D.; Shang, M.T. Seismic analysis of nonhomogeneous slopes with cracks using a discretization kinematic approach. Int. J. Géoméch. 2019, 19, 04019104. [Google Scholar] [CrossRef]
- Li, Z.W.; Xiang, X.L.; Li, T.Z. Static and seismic stability assessment of 3D slopes with cracks. Eng. Geol. 2020, 265, 105450. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Liu, Y.; Yuan, R.; He, Y. Comparison of seismic stability for slopes with tensile strength cut-off and cracks. J. Mt. Sci. 2021, 18, 3336–3347. [Google Scholar] [CrossRef]
- He, Y.; Yu, J.Y.; Yuan, R.; Wang, W.F.; Nikitas, N. Stability and failure mechanisms in three-dimensional cracked slope: Static and dynamic analysis. Comput. Geotech. 2022, 144, 104626. [Google Scholar] [CrossRef]
- Chen, X.R.; Lu, Y.L.; Bo, J.S.; Lin, W.; Wang, L. Discussion of the depth of slope posterior crack with tension shear failure review. Water Power. 2018, 44, 45–49. [Google Scholar]
- He, Y.; Liu, Y.; Zhang, Y.B.; Yuan, R. Stability assessment of three-dimensional slopes with cracks. Eng. Geol. 2019, 252, 136–144. [Google Scholar] [CrossRef]
- Kong, X.A.; Cheng, Y.F.; Zhao, B.B.; Liu, Y.; Han, J.S. The tension-shear and compression-shear joint strength model for unsaturated clay and its application to slopes. Front. Earth Sci. 2022, 10, 916805. [Google Scholar] [CrossRef]
- He, K.; Song, C.; Fell, R. Numerical modelling of transverse cracking in embankment dams. Comput. Geotech. 2021, 132, 104028. [Google Scholar] [CrossRef]
- Stockton, E.; Leshchinsky, B.A.; Olsen, M.J.; Evans, T.M. Influence of both anisotropic friction and cohesion on the formation of tension cracks and stability of slopes. Eng. Geol. 2018, 249, 31–44. [Google Scholar] [CrossRef]
- Zhu, L.X.; Zhou, Z.J.; Chen, L.; Xu, T.Y.; Zhang, Z.P.; Chen, C.R.; Xu, F. Limit equilibrium theory-based investigation on the critical tension crack depth in loess slope. Env. Ear. Sci. 2021, 80, 349. [Google Scholar] [CrossRef]
- Lu, Y.L.; Bo, J.S.; Chen, X.R.; Wang, L.; Lu, T. Analytical formation of slope stability based on Sweden arc integral model. Chin. J. Appl. Mech. 2017, 34, 257–262. [Google Scholar]
- Lu, Y.L.; Chen, X.R.; Wang, L. Analytical computation of sandy slope stability under the groundwater seepage and earthquake conditions. Adv. Civ. Eng. 2022, 2022, 5286878. [Google Scholar] [CrossRef]
- Zhang, T.B. Stability Analysis of Soil Slope and Slope Design of Geotechnical Structures; Chengdu University of Science and Technology Press: Chengdu, China, 1987. [Google Scholar]
- Chen, Z.Y.; Zhou, J.X.; Wang, H.J. Soil Mechanics; Tsinghua University Press: Beijing, China, 1994. [Google Scholar]
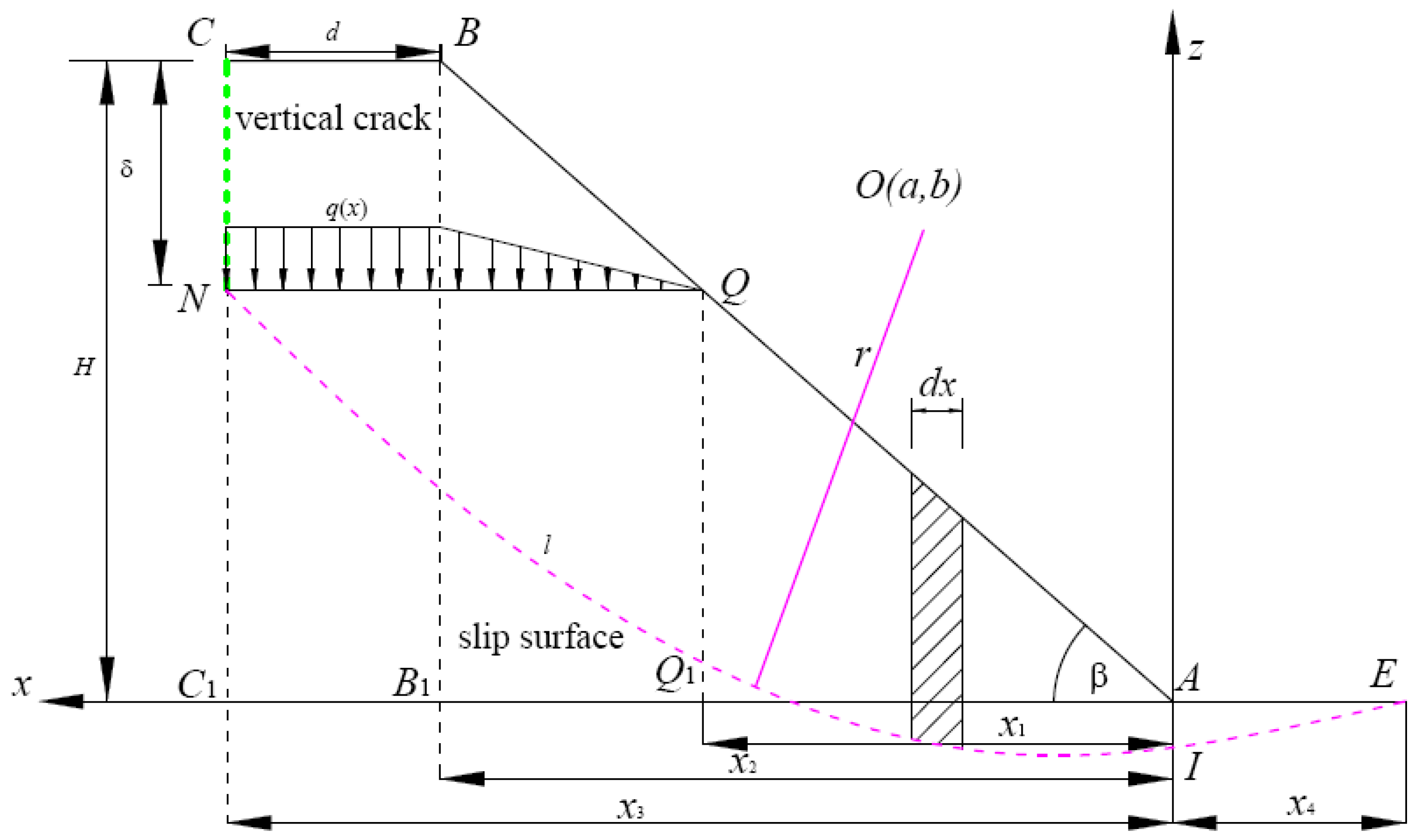
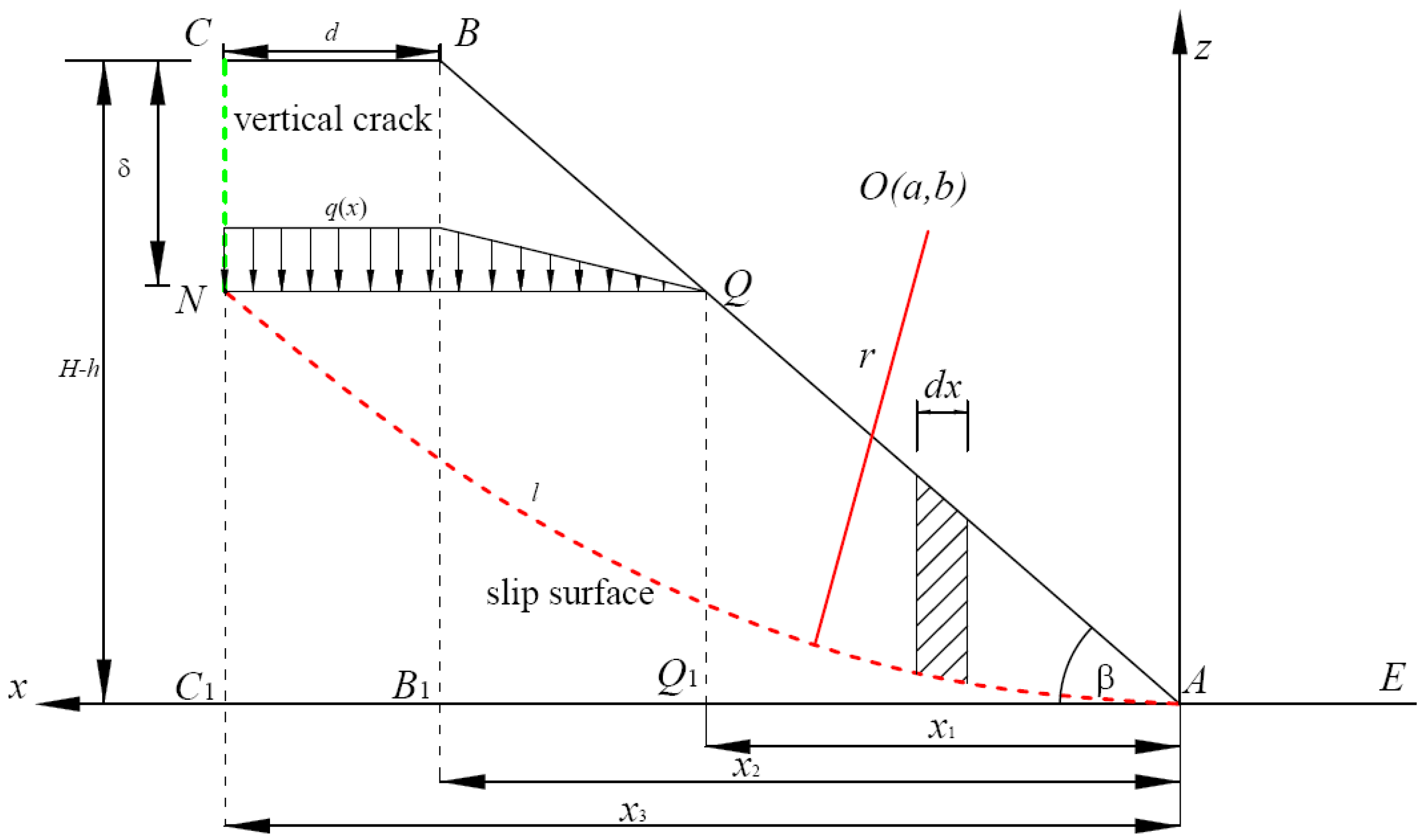
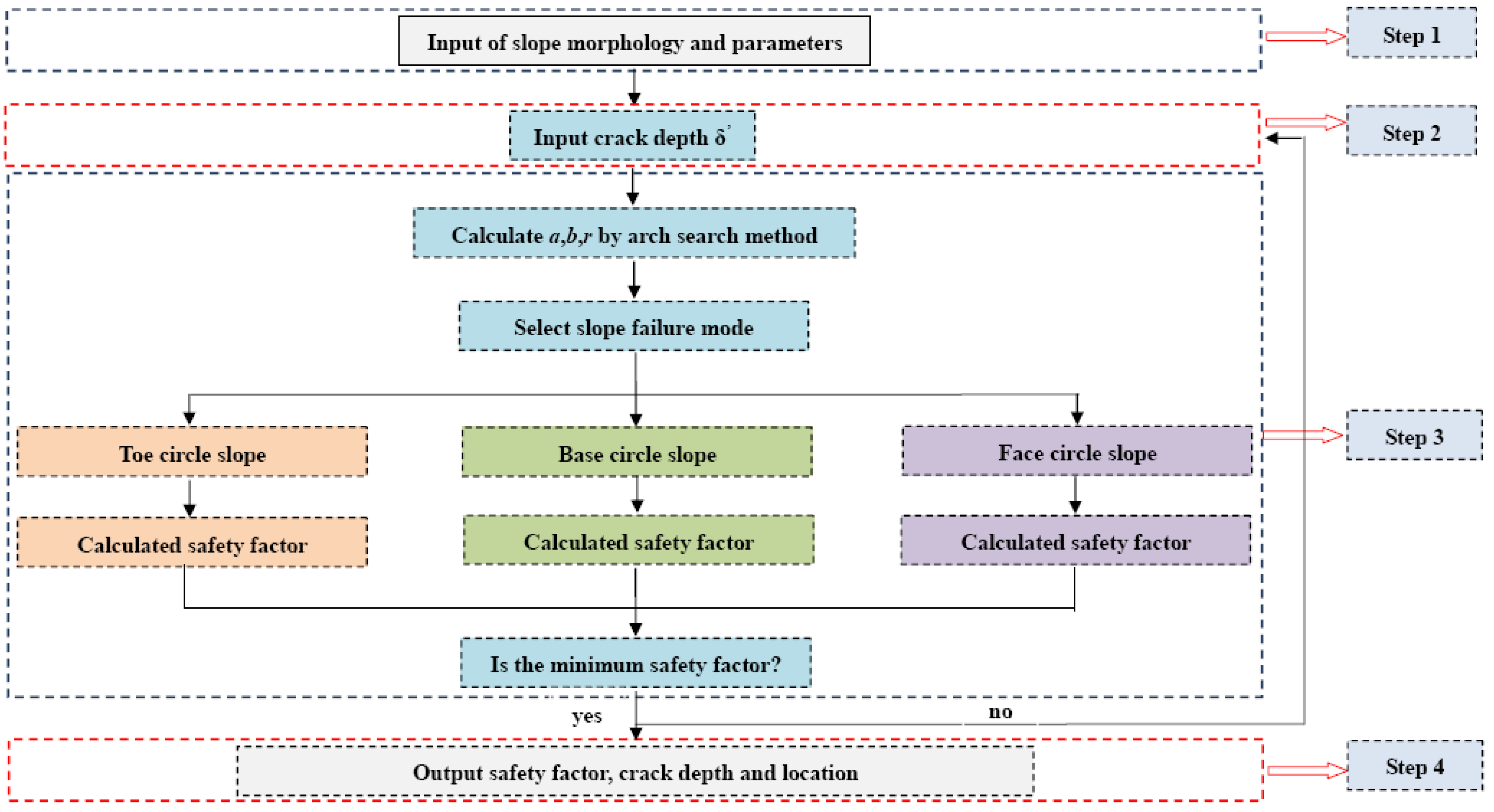
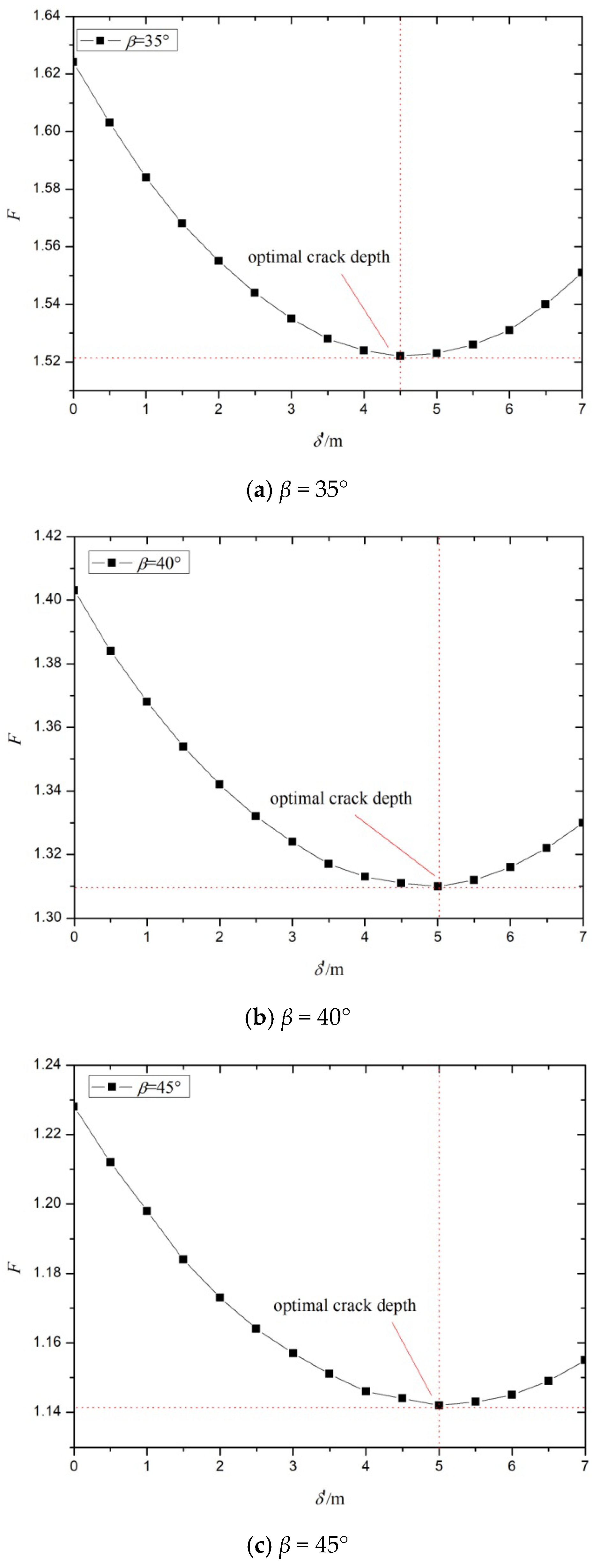


| Slope Angle β/° | a/m | b/m | Radius r/m | F | F | F |
|---|---|---|---|---|---|---|
| Sweden Method | Bishop Method | Present Study | ||||
| 24 | 34.77 | 110.51 | 117.75 | 1.044 | 1.102 | 1.113 |
| 21.8 | 40.38 | 115.76 | 125.81 | 1.102 | 1.169 | 1.224 |
| 20.0 | 47.74 | 119.38 | 134.84 | 1.158 | 1.254 | 1.304 |
| 18.4 | 53.09 | 128.99 | 143.96 | 1.220 | 1.300 | 1.389 |
| 17.1 | 59.20 | 134.72 | 152.13 | 1.277 | 1.365 | 1.465 |
| slope Angle β/° | a/m | b/m | Radius r/m | F | F | F | F |
|---|---|---|---|---|---|---|---|
| FEM Method | Spencer Method | Bishop Method | Present Study | ||||
| 35 | −4.720 | 72.185 | 72.293 | 1.34 | 1.318 | 1.259 | 1.387 |
| 40 | −3.901 | 66.488 | 66.614 | 1.22 | 1.212 | 1.153 | 1.197 |
| 45 | −9.041 | 75.044 | 75.611 | 1.12 | 1.115 | 1.062 | 1.057 |
| 50 | −3.47 | 66.621 | 66.711 | 1.06 | 1.038 | 0.992 | 0.925 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Chen, X.; Wang, L. Research on Fracture Mechanism and Stability of Slope with Tensile Cracks. Appl. Sci. 2022, 12, 12687. https://doi.org/10.3390/app122412687
Lu Y, Chen X, Wang L. Research on Fracture Mechanism and Stability of Slope with Tensile Cracks. Applied Sciences. 2022; 12(24):12687. https://doi.org/10.3390/app122412687
Chicago/Turabian StyleLu, Yulin, Xiaoran Chen, and Li Wang. 2022. "Research on Fracture Mechanism and Stability of Slope with Tensile Cracks" Applied Sciences 12, no. 24: 12687. https://doi.org/10.3390/app122412687
APA StyleLu, Y., Chen, X., & Wang, L. (2022). Research on Fracture Mechanism and Stability of Slope with Tensile Cracks. Applied Sciences, 12(24), 12687. https://doi.org/10.3390/app122412687







