Static Bending and Vibration Analysis of a Rectangular Functionally Gradient Piezoelectric Plate on an Elastic Foundation
Abstract
:1. Introduction
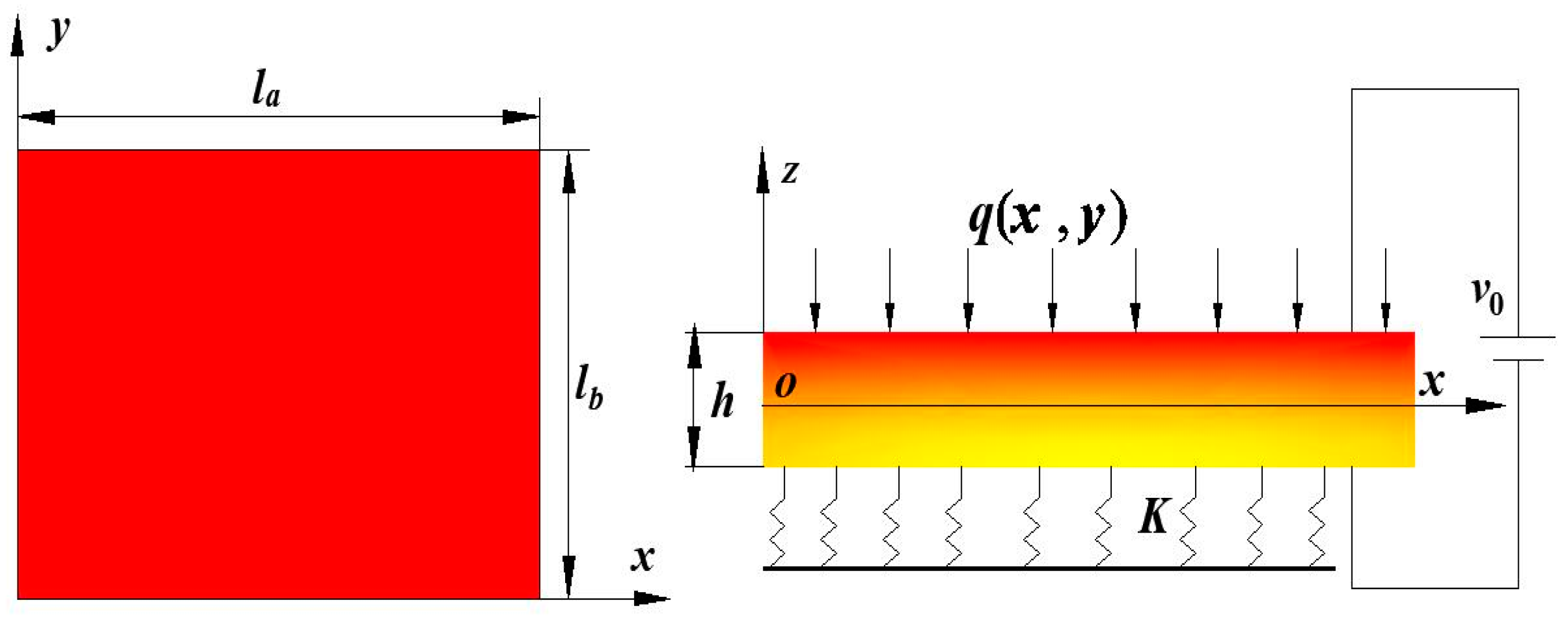
2. Governing Equations
3. Calculation Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rabin, B.H.; Shiota, I. Functionally gradient materials. J. MRS Bull. 1995, 20, 14–18. [Google Scholar] [CrossRef]
- Wu, C.C.M.; Kahn, M.; Moy, W. Piezoelectric ceramics with functional gradients: A new Application in Material design. J. Am. Ceram. Soc. 1996, 79, 809–812. [Google Scholar] [CrossRef]
- Zhu, X.H.; Meng, Z.Y. Operational principle, fabrication and displacement characteristics of a functionally gradient piezoelectric ceramic actuator. J. Sens. Actuators A 1995, 48, 169–173. [Google Scholar] [CrossRef]
- Fan, G.F.; Tang, Y.Q.; Lu, W.Z. Reduce synthesis temperature and improve dispersion of YAG nanopowders based on the co-crystallization method. J. Alloy. Comped. 2015, 618, 1–6. [Google Scholar] [CrossRef]
- Su, X.; Zhou, J.; Bai, G. Low temperature synthesis and characterization of YAG nanopowders by polyacrylamide gel method. Ceram. Int. 2016, 42, 17497–17502. [Google Scholar] [CrossRef]
- Wu, D.; Cheng, Y.; Feng, S.; Yao, Z.; Zhang, M. Crystallization Behavior of Polylactide/Graphene Composites. Ind. Eng. Chem. Res. 2013, 52, 6731–6739. [Google Scholar] [CrossRef]
- Lim, J.W.; Lee, D.G. Carbon fiber/polyethylene bipolar plate-carbon felt electrode assembly for vanadium redox flow batteries (VRFB). J. Compos. Struct. 2015, 134, 483–492. [Google Scholar] [CrossRef]
- Daugherty, M.C.; Siyong, G.; Aaron, D.S. Graphene quantum dot-decorated carbon electrodes for energy storage in vanadium redox flow batteries. J. Nanoscale 2020, 12, 7834–7842. [Google Scholar] [CrossRef]
- Zhou, W.B. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2 + Ni) functionally graded bolted joint. J. Compos. Part B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Bian, Z.G.; Ying, J.; Chen, W.Q.; Ding, H.J. Bending and free vibration analysis of a smart functionally gradedplate. J. Struct. Eng. Mech. 2006, 23, 97–113. [Google Scholar] [CrossRef]
- Fakhari, V.; Ohadi, A.; Yousefian, P. Nonlinear free and forced vibration behavior of functionally graded plate with piezoelectric layers in thermal environment. J. Compos. Struct. 2011, 93, 2310–2321. [Google Scholar] [CrossRef]
- Fakhari, V.; Ohadi, A. Nonlinear vibration control of functionally graded plate with piezoelectric layers in thermal environment. J. Vib. Control 2011, 17, 449–469. [Google Scholar] [CrossRef]
- Jandaghian, A.A.; Rahmani, O. Size-dependent free vibration analysis of functionally graded piezoelectric plate subjected to thermoelectro-mechanical loading. J. Intell. Mater. Syst. Struct. 2017, 28, 3039–3053. [Google Scholar] [CrossRef]
- Li, J.Q.; Xue, Y.; Li, F.M.; Narita, Y. Active vibration control of functionally graded piezoelectric material plate. J. Compos. Struct. 2019, 207, 509–518. [Google Scholar] [CrossRef]
- Farzam, A.; Hassani, B. Size-dependent analysis of FG microplates with temperature-dependent material properties using modified strain gradient theory and isogeometric approach. J. Compos. Struct. 2019, 161, 150–168. [Google Scholar] [CrossRef]
- Karamanli, A.; Aydogdu, M.; Vo, T.P. A comprehensive study on the size-dependent analysis of strain gradient multi-directional functionally graded microplates via finite element model. J. Aerosp. Sci. Technol. 2021, 111, 106550. [Google Scholar] [CrossRef]
- Mao, K. Free Vibration Analysis of Functionally Gradient Sandwich Composite Plate Embedded SMA Wires in Surface Layer. Appl. Sci. 2020, 10, 3921. [Google Scholar]
- Cho, J.R. Hierarchic models for the free vibration analysis of functionally gradient plates. Int. J. Mech. Mater. Des. 2021, 17, 489–501. [Google Scholar] [CrossRef]
- Mehrabadi, S.J.; Kargarnovin, M.H.; Najafizadeh, M.M. Free vibration analysis of functionally Graded coupled circular plate with piezoelectric layer. J. Mech. Sci. Technol. 2009, 23, 2008–2021. [Google Scholar] [CrossRef]
- Yao, L. Analysis of the Vibration Behaviors of Rotating Composite Nano-Annular Plates Based on Nonlocal Theory and Different Plate Theories. J. Appl. Sci. 2021, 12, 230. [Google Scholar]
- Mlab, C.; Cgs, C.; Rya, B. A novel shear deformation theory for static analysis of functionally graded plates—ScienceDirect. J. Compos. Struct. 2020, 250, 12559. [Google Scholar]
- Zenkour, A.M.; Hafed, Z.S. Bending analysis of functionally graded piezoelectric plates via quasi-3D trigonometric theory. J. Mech. Adv. Mater. Struc. 2019, 18, 1–12. [Google Scholar] [CrossRef]
- Amini, M.H.; Soleimani, M.; Rastgoo, A. Three-dimensional free vibration analysis of functionally graded material plates resting on an elastic foundation. J. Smart Mater. Struct. 2009, 18, 085015. [Google Scholar] [CrossRef]
- Musa, A.; Alshugaa, M.A.; Algahtani, H.J. EnergyBased Solution for Bending Analysis of Thin Plates on Nonhomogeneous Elastic Foundation. Arab. J. Sci Eng. 2020, 45, 3817–3827. [Google Scholar] [CrossRef]
- Pham, P. Free vibration of cracked FGM plates with variable thickness resting on elastic foundations. Thin-Walled Struct. 2021, 161, 107425. [Google Scholar]
- Merazka, B.; Bouhadra, A.; Menasria, A. Hygro-thermo-mechanical bending response of FG plates resting on elastic foundations. Steel Compos. Struct. 2021, 39, 631–643. [Google Scholar]
- Tounsi, A.; Al-Dulaijan, S.U.; Al-Osta, M. A four variable trigonometric integral plate theory for hygro-thermo-mechanical bending analysis of AFG ceramic-metal plates resting on a two-parameter elastic foundation. Steel Compos. Struct. 2020, 34, 511–524. [Google Scholar]
- Ebrahimi, F.; Barati, M.R.A. Nonlocal Higher Order Shear Deformation Beam Theory for Vibration Analysis of Size-Dependent Functionally Graded Nanobeams. Arab. J. Sci. Eng. 2016, 41, 1679–1690. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer: London, UK, 2000. [Google Scholar]
- Ming, S.; Zhi, Y. Thermoelectromechanical Properties of Piezoelectric Nanoplates with Flexoelectricity. J. Mech. Phys. Solids 2020, 41, 444–454. [Google Scholar]
| This paper | 0.3123 | 0.6565 | 0.8203 | |
| literature [30] | 0.3123 | 0.6565 | 0.8203 | |
| This paper | 0.8571 | 1.6502 | 8.2253 | |
| literature [30] | 0.8571 | 1.6502 | 8.2253 |
| Properties | |||
|---|---|---|---|
| Elastic constant ) | 81.3 | 60.6 | |
| 25.6 | 23.0 | ||
| 30.5 | 35.5 | ||
| Piezoelectric constant ) | −4.1 | −17.05 | |
| Dielectric constant ) | 10.27 × 10−9 | 25.54 × 10−9 | |
| Thermoelastic modulus (N/m−2K−1) | 4.738 × 105 | 4.738 × 105 | |
| Pyroelectric constant (C/m−2K−1) | 2.5 × 10−5 | 2.5 × 10−5 | |
| density ) | 7500 | 7500 |
| 0 | 0.0478 | 0.1915 |
| 10 | 0.0365 | 0.2185 |
| 30 | 0.0246 | 0.2645 |
| 50 | 0.0184 | 0.3035 |
| 100 | 0.0112 | 0.3841 |
| PZT-4 | 1 | 2 | 3 | PZT-5 | |
|---|---|---|---|---|---|
| 1 | 0.0184 | 0.0189 | 0.0195 | 0.0164 | 0.0193 |
| 2 | 0.0059 | 0.0063 | 0.0068 | 0.0047 | 0.0066 |
| 3 | 0.0017 | 0.0018 | 0.0020 | 0.0013 | 0.0019 |
| 4 | 5.771 × 10−4 | 6.162 × 10−4 | 6.782 × 10−4 | 4.326 × 10−4 | 6.523 × 10−4 |
| (v) | 0 | 100 | 300 | 500 |
|---|---|---|---|---|
| −0.4 | 0 | 8.221 | 14.28 | 18.44 |
| 0 | 0.2996 | 8.259 | 14.30 | 18.46 |
| 0.2 | 0.6367 | 8.278 | 14.31 | 18.47 |
| 0.4 | 0.8492 | 8.297 | 14.32 | 18.48 |
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 10 | 1.324 × 10−5 | 5.117 × 10−6 | 2.448 × 10−6 | 1.396 × 10−6 |
| 20 | 2.353 × 10−5 | 9.091 × 10−6 | 4.348 × 10−6 | 2.478 × 10−6 |
| 30 | 5.287 × 10−5 | 2.043 × 10−5 | 9.760 × 10−6 | 5.553 × 10−6 |
| 40 | 2.098 × 10−4 | 8.103 × 10−5 | 3.852 × 10−5 | 2.172 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Li, H.; Yao, L. Static Bending and Vibration Analysis of a Rectangular Functionally Gradient Piezoelectric Plate on an Elastic Foundation. Appl. Sci. 2022, 12, 1517. https://doi.org/10.3390/app12031517
Wang W, Li H, Yao L. Static Bending and Vibration Analysis of a Rectangular Functionally Gradient Piezoelectric Plate on an Elastic Foundation. Applied Sciences. 2022; 12(3):1517. https://doi.org/10.3390/app12031517
Chicago/Turabian StyleWang, Wei, Haonan Li, and Linquan Yao. 2022. "Static Bending and Vibration Analysis of a Rectangular Functionally Gradient Piezoelectric Plate on an Elastic Foundation" Applied Sciences 12, no. 3: 1517. https://doi.org/10.3390/app12031517





