Analytical Study on the Frictional Behavior of Sliding Surfaces Depending on Ceramic Friction Materials
Abstract
1. Introduction
2. Preliminary Friction Test for the Ceramic Friction Material
2.1. Test Setup and Material Properties
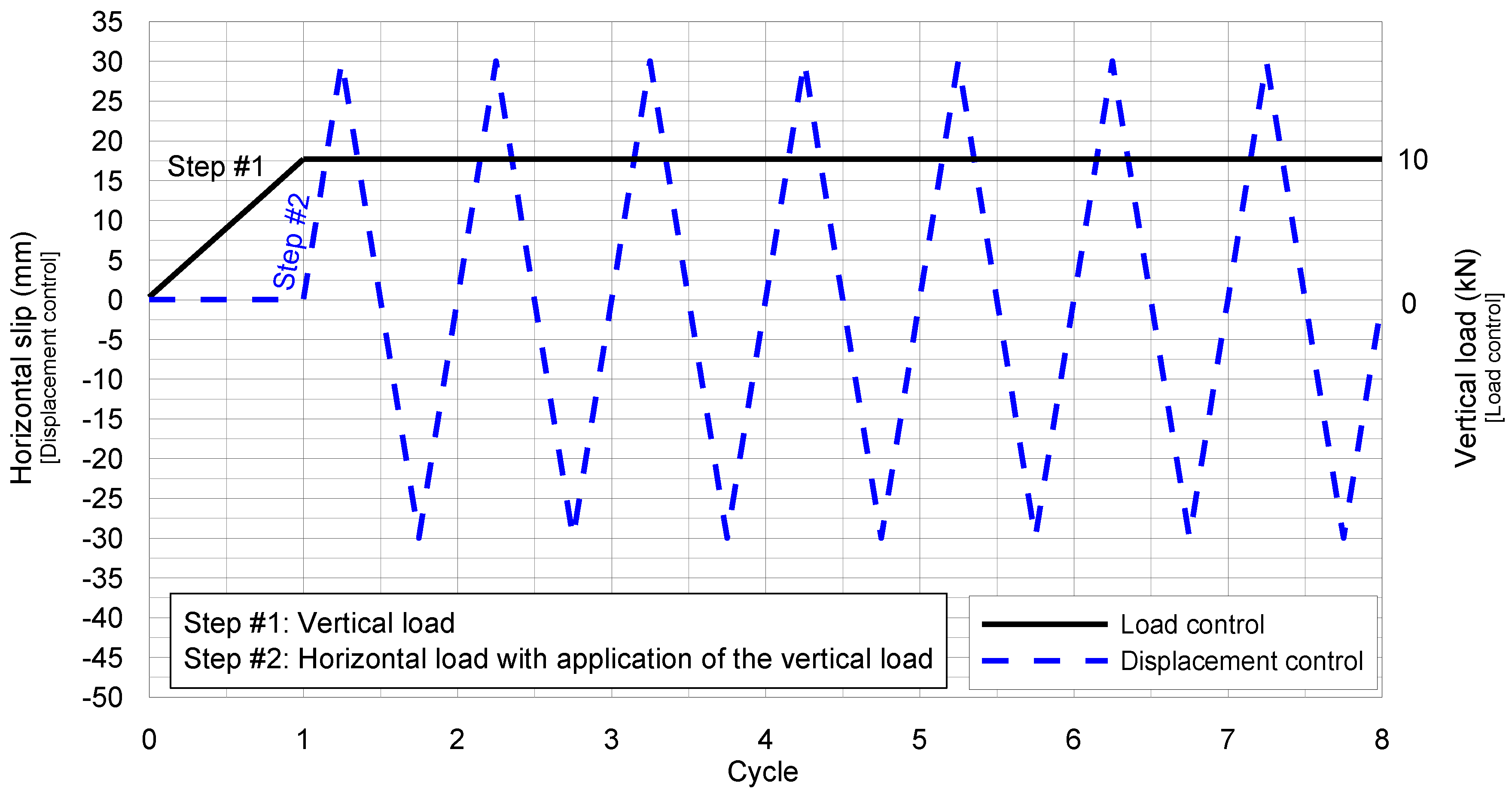
2.2. Test Procedure
2.3. Test Results
3. Finite Element Model
3.1. Test Specimens
3.2. Analysis Method
3.3. Geometry and Meshing of Finite Element Model
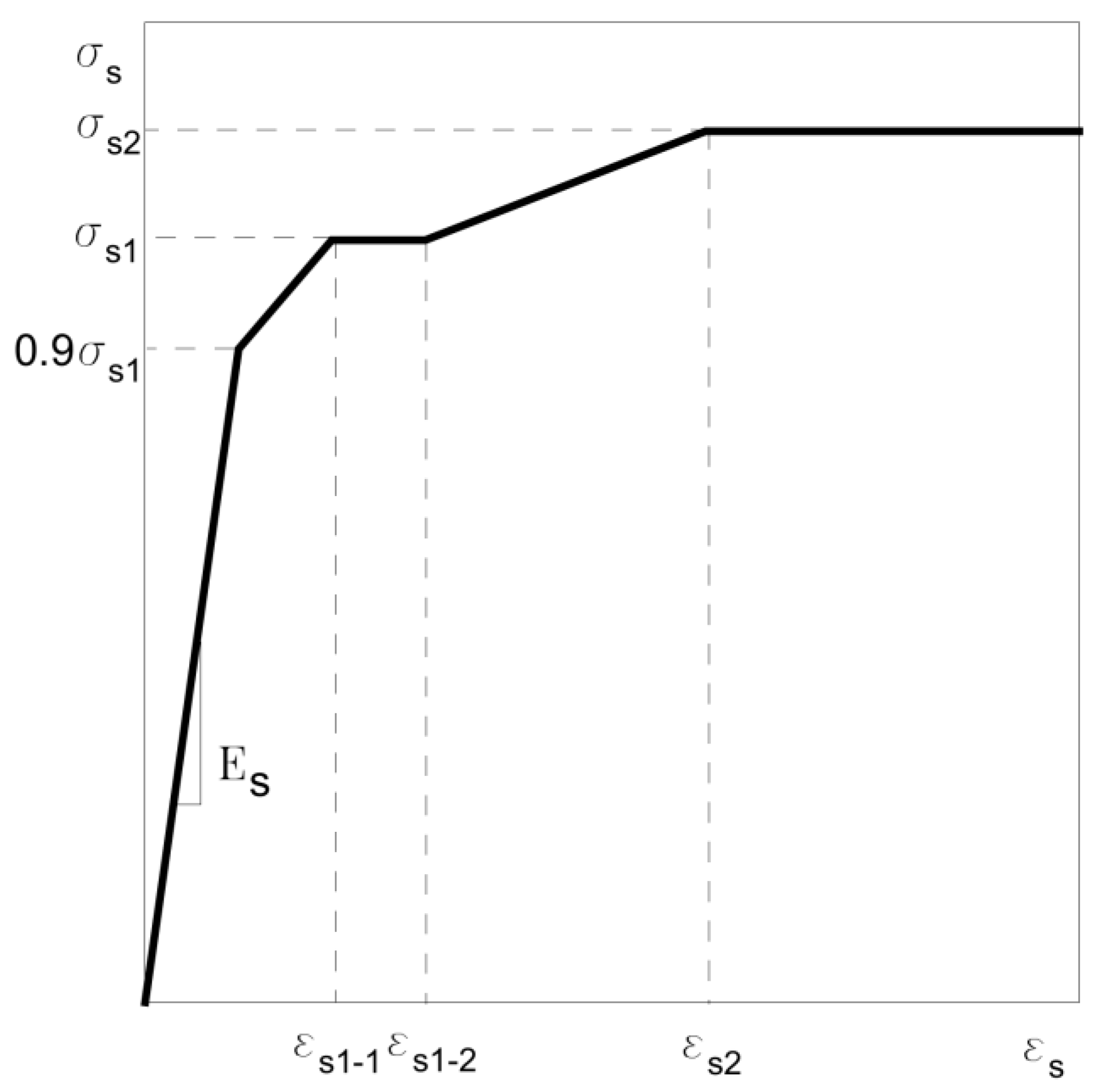
3.4. Material Properties
3.5. Interactions and Load Conditions
4. Numerical Results
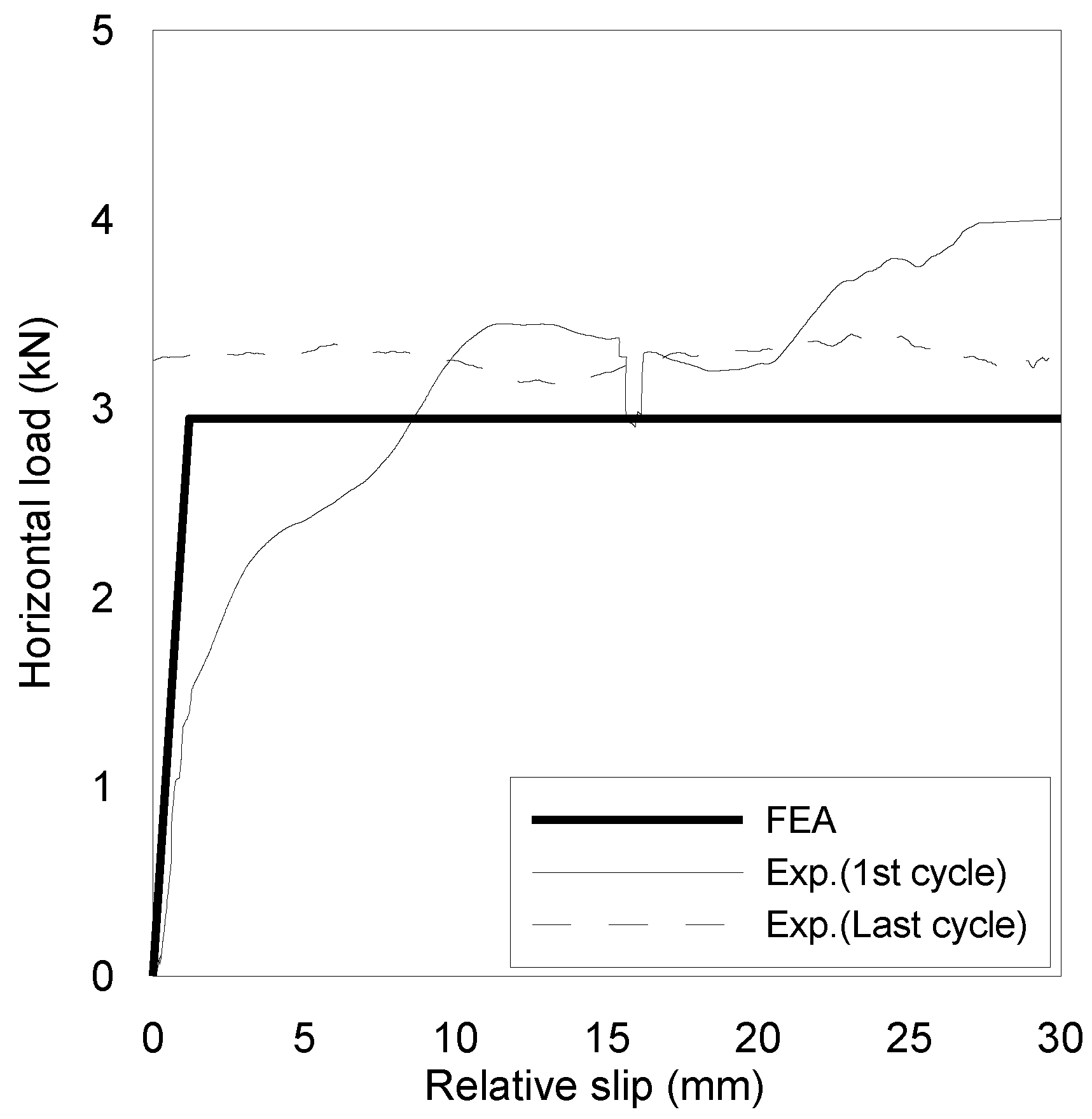
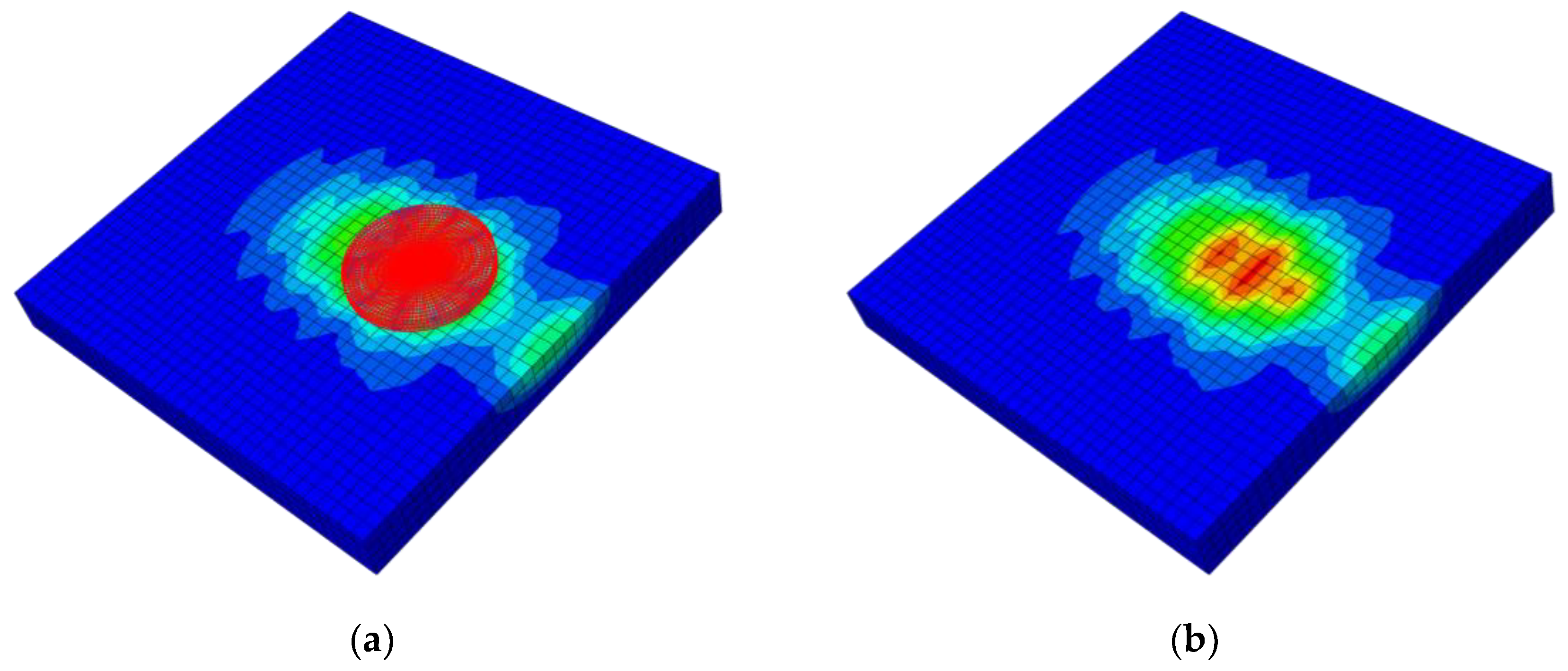
4.1. Verification of Finite Element Model
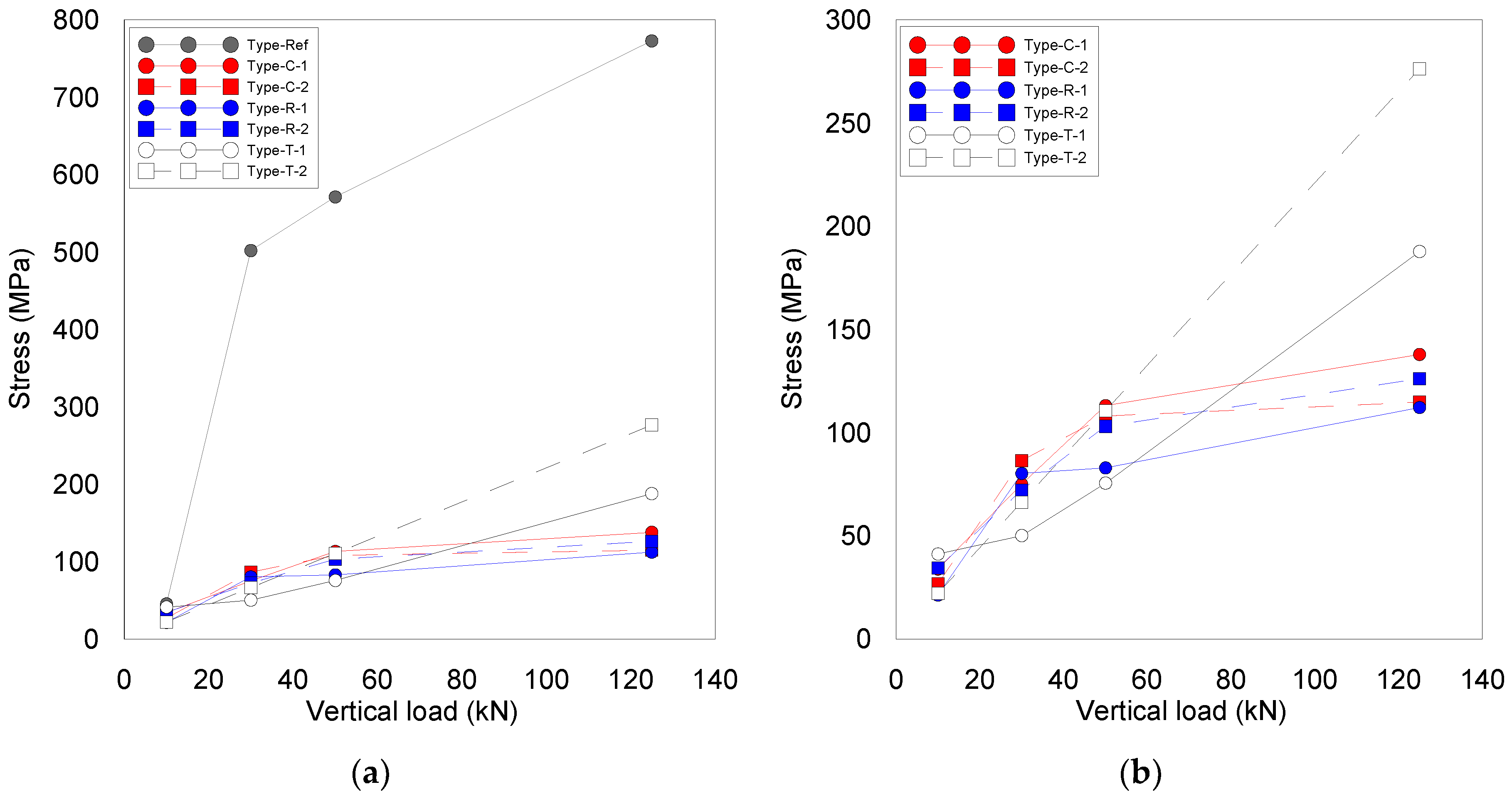
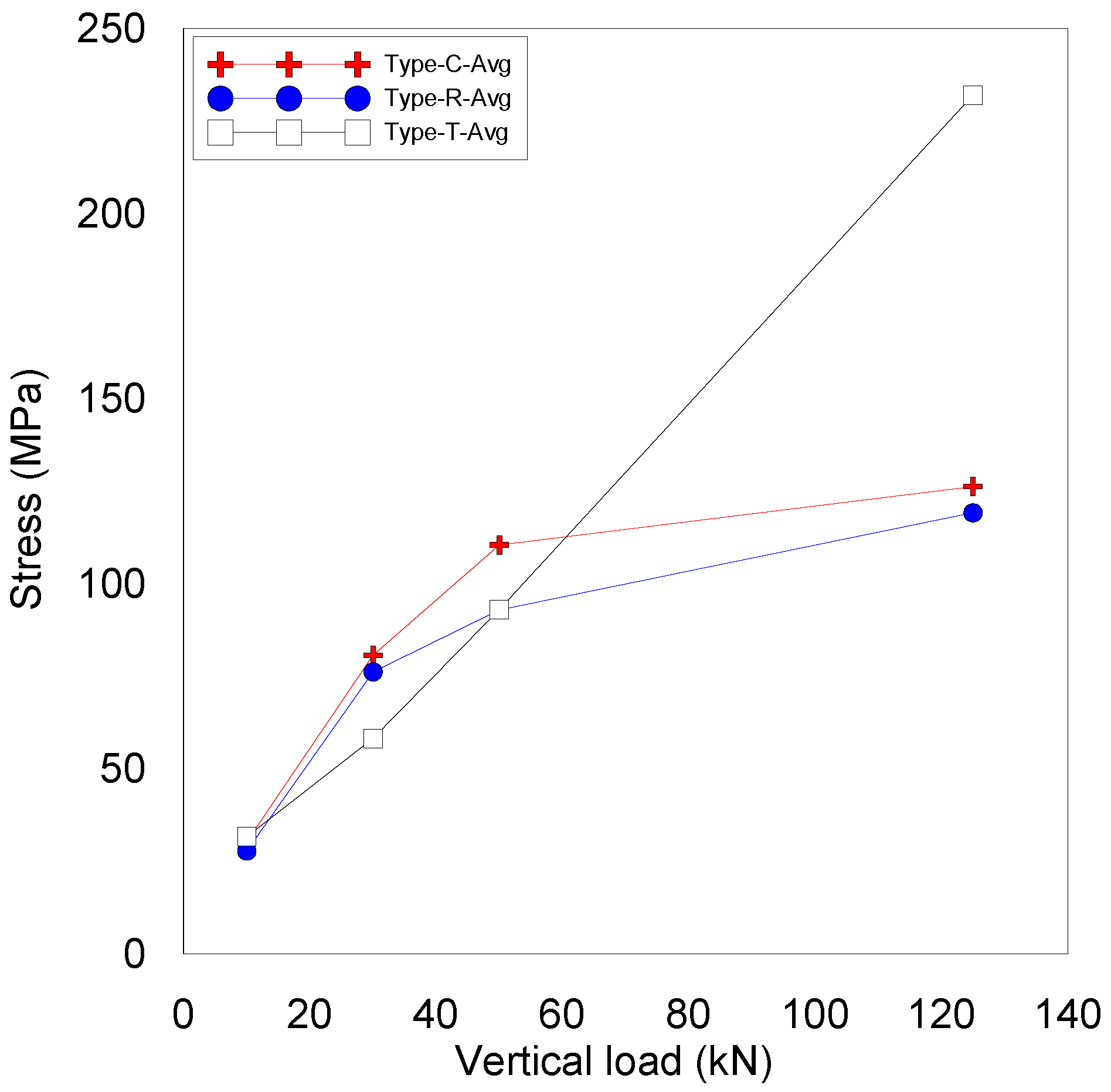
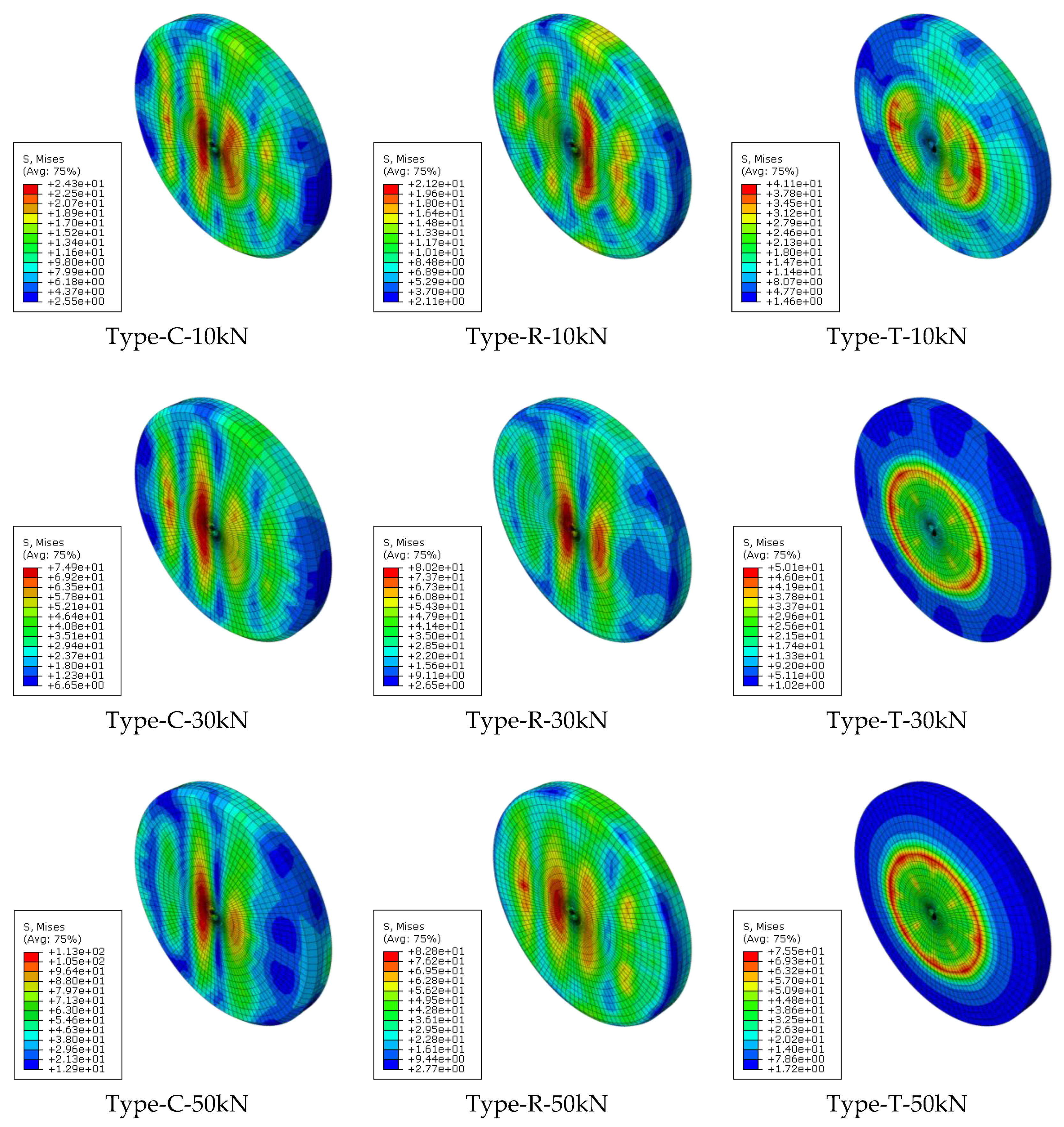
4.2. Frictional Behavior of Improved Sliding Surfaces
5. Conclusions
- (1)
- The horizontal motion of the ceramic friction material allowed it to penetrate the underlying stainless-steel sliding plate because of the higher hardness of the ceramic compared to that of the stainless-steel. Compared to the actual test, the finite element model under-evaluated the horizontal load by less than 4.3% and overestimated the relative slip at the maximum horizontal load. Such slight discrepancy could be attributed to the fact that the finite element model was constructed in idle conditions and adopted elastic conditions for the ceramic. On the other hand, the manufacturing tolerance of the actual specimen caused a large slip to occur when the horizontal load was applied. Nevertheless, the developed model provided sufficient accuracy for the evaluation of the frictional behavior.
- (2)
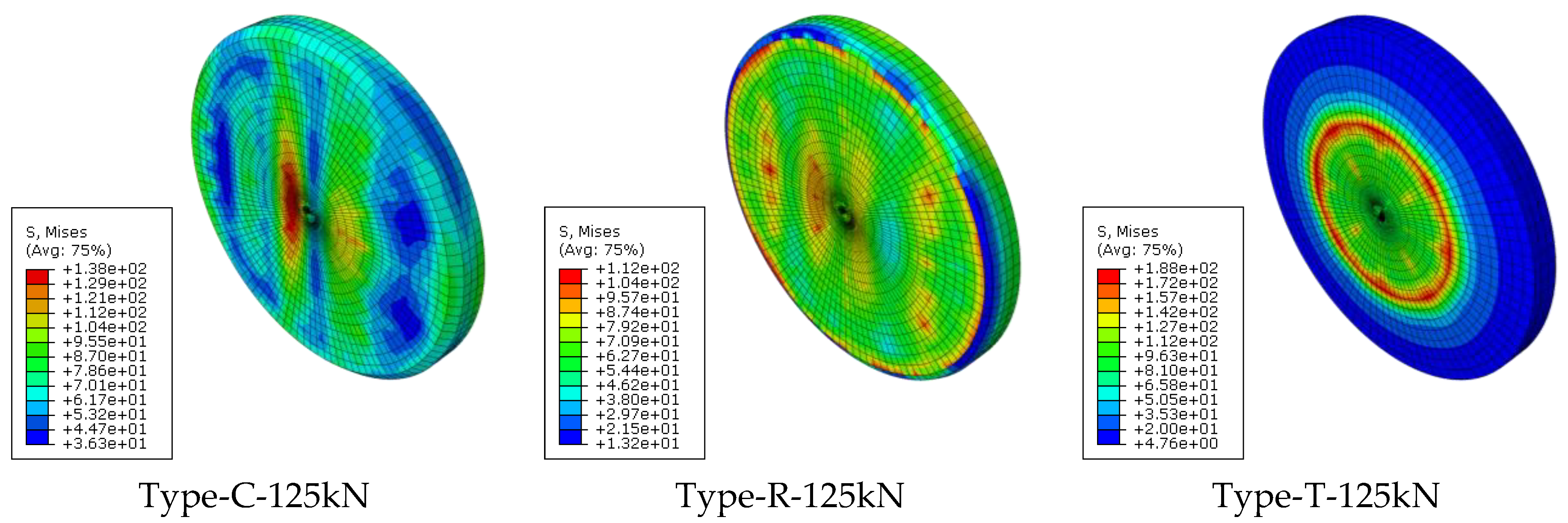
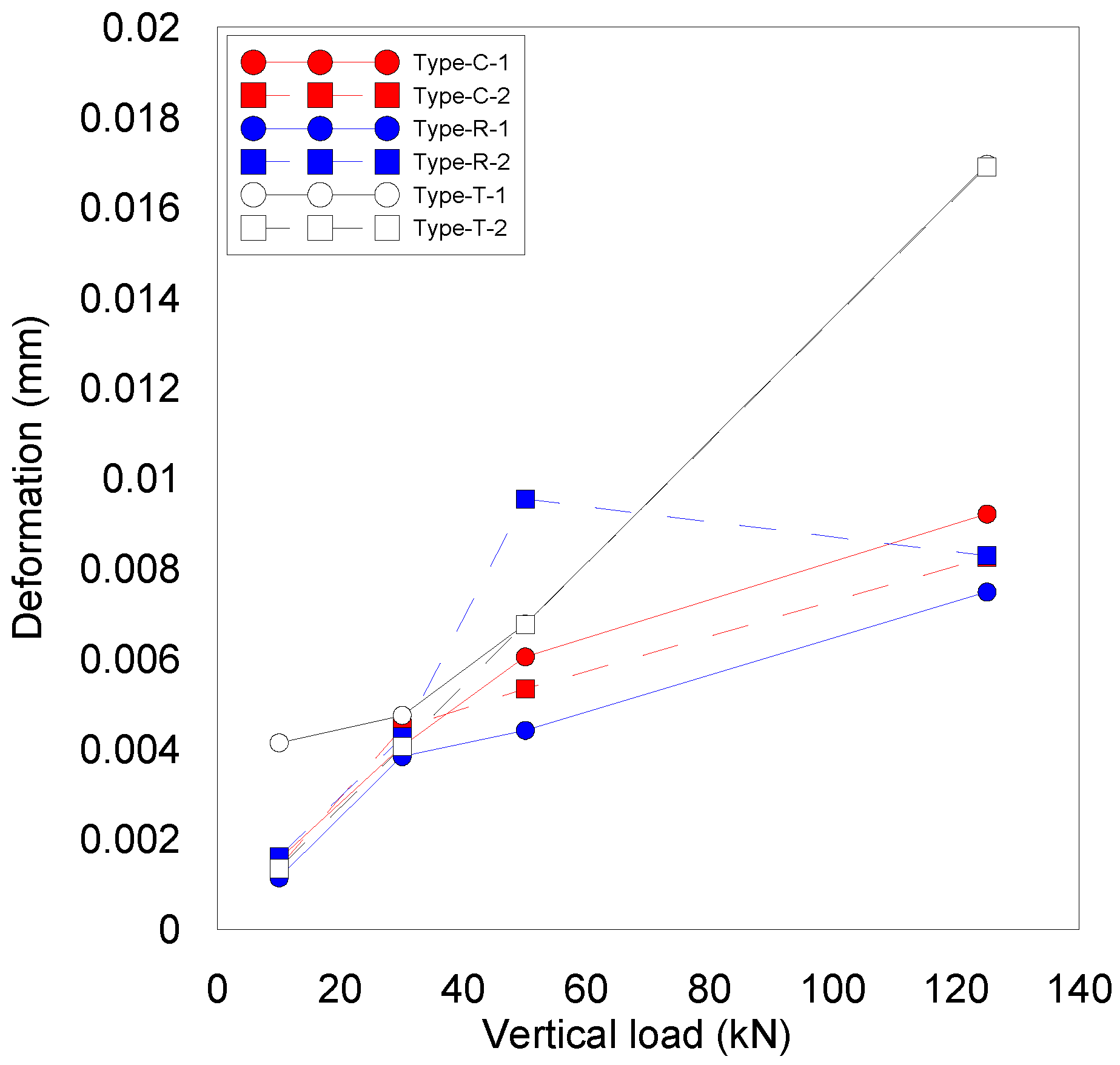
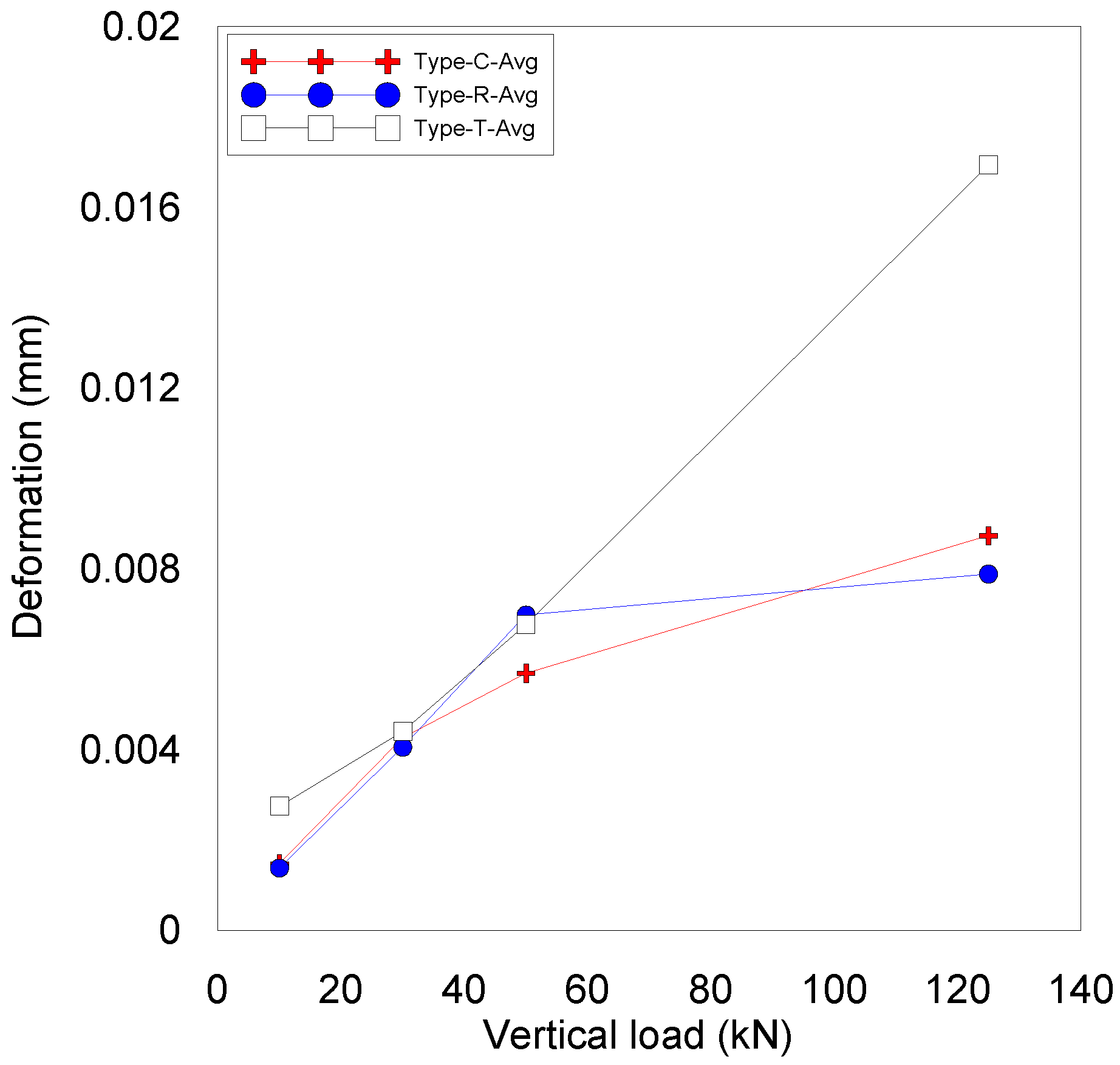
- The stress and deformation of the ceramic friction material increased with larger vertical loads, but the increments varied depending on the improved edges of the ceramic friction material. The improved shapes adopting chamber and round edges achieved a low increment in stress and deformation, whereas the tapered edge provided stress and deformation increments proportional to the increase in the vertical load. The size effect for the camber and round edges was relatively low with a difference in stress and deformation below 10%.
- (3)
- All C, R, and T types have the effect of improving friction behavior, but in the case of type T, there is a risk of damage if a load larger than the design load occurs. The C and R types show similar behaviors, but it can be seen that it is advantageous to use type C, which is easy to process, as a friction material in terms of productivity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Zhang, Y.; Ju, J. Study on the mechanical properties of a type of spherical bearing. J. Theor. Appl. Mech. 2021, 59, 539–550. [Google Scholar] [CrossRef] [PubMed]
- Peng, T.; Yan, B.; Li, F. The hysteresis model of the friction pendulum bearing based on the moment balance theory. Ain Shams Eng. J. 2022, 13, 101707. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P. Influence Analysis of the Antifriction Layer Materials and Thickness on the Contact Interaction of Spherical Bearings Elements. Lubricants 2022, 10, 30. [Google Scholar] [CrossRef]
- Askari, E.; Flores, P. Coupling multi-body dynamics and fluid dynamics to model lubricated spherical joints. Arch. Appl. Mech. 2020, 90, 2091–2111. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, S.; Tan, P.; Zhu, H. Mechanical performance and shear constitutive model study of a new high-capacity polyurethane elastomeric bearing. Constr. Build. Mater. 2020, 232, 117227. [Google Scholar] [CrossRef]
- Wei, W.; Yuan, Y.; Igarashi, A.; Zhu, H.; Luo, K. Generalized hyper-viscoelastic modeling and experimental characterization of unfilled and carbon black filled natural rubber for civil structural applications. Constr. Build. Mater. 2020, 253, 119211. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskih, A.A.; Pankova, A.P. Numerical analysis of the spherical bearing geometric configuration with antifriction layer made of different materials. PNRPU Mech. Bull. 2020, 4, 15–26. [Google Scholar] [CrossRef]
- Joh, C.; Yoon, H.; Kim, Y.J. Accumulated Sliding Distance of the Sliding Element in the Bridge Bearing; Korean Society of Civil Engineers: Seoul, Republic of Korea, 2006; pp. 1320–1323. [Google Scholar]
- Oh, S.T.; Lee, D.J.; Yeon, J.S.; Lee, H.J.; Jeong, S.H. Dynamic Behaviors of Bearings of the Two-Span Continuous PSC Box Bridge with 40 m Span for KTX Vehicle. In Proceedings of the 25th Annual Conference, KSR2013A032; The Korean Society for Railway: Daegu, Republic of Korea, 2013; pp. 130–132. [Google Scholar]
- EN 1337-2:2004; Structural Bearings—Part 2: Sliding Elements. European Committee for Standardization: Brussels, Belgium, 2004.
- Choi, E.S.; Choi, Y.B.; Lee, J.I.; Lee, S.J. Assessment of friction of EP frictional materials used for spherical bearings of railway bridges. J. Korean Soc. Steel Const. 2019, 31, 293–299. [Google Scholar] [CrossRef]
- Dong, S.; Jung, G.H.; Lee, G.S. Effect of surface roughness of counterface on tribological characteristics of PTFE and UHMWPE. J. Korean Soc. Tribol. Lubr. 2011, 27, 293–301. [Google Scholar] [CrossRef][Green Version]
- Kamenskih, A.; Trufanov, N. Numerical analysis of the stress state of a spherical contact system with an interlayer of antifriction material. Comput. Contin. Mech. 2013, 6, 54–61. [Google Scholar] [CrossRef]
- Pavlenko, V.I.; Bondarenko, G.G.; Tarasov, D.G.; Edamenko, O.D. Gamma modification of radiation-resistant fluoroplastic composite. Inorg. Mater. Appl. Res. 2013, 4, 389–393. [Google Scholar] [CrossRef]
- Oh, S.T.; Lee, D.J.; Jun, S.M.; Jeong, S.H. A long-term friction test of bridge bearings considering running speed of next generation train. J. Korea Inst. Struct. Maint. Insp. 2016, 20, 34–39. [Google Scholar]
- Wang, H.; Sun, A.; Qi, X.; Dong, Y.; Fan, B. Experimental and analytical investigations on tribological properties of PTFE/AP composites. Polymers 2021, 13, 4295. [Google Scholar] [CrossRef]
- Mnif, R.; Ben Jemaa, M.C.; Kacem, N.H.; Elleuch, R. Impact of viscoelasticity on the tribological behavior of PTFE composites for valve Seals application. Tribol. Trans. 2013, 56, 879–886. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Zhang, Q.; Zhou, Y. Experimental and theoretical research on the stress-relaxation behaviors of PTFE coated fabrics under different temperatures. Adv. Mater. Sci. Eng. 2015, 2015, 319473. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, D.; Chen, K. In situ microscopic observations of dynamic viscoelastic contact and deformation at a friction interface. Mater. Express 2019, 9, 235–244. [Google Scholar] [CrossRef]
- Oh, J.; Jang, C.; Kim, J.H. A study on the characteristics of bridge bearings behavior by finite element analysis and model test. J. Vibroeng. 2015, 17, 2559–2571. [Google Scholar]
- Lee, K.H.; Park, D.B.; Jang, K.S.; Sim, K.C.; Choi, J.S. Evaluate the Friction Coefficient of Friction Pendulum Bearing applied New Friction Material; Korean Society of Civil Engineers: Seoul, Republic of Korea, 2017; pp. 1353–1354. [Google Scholar]
- Kim, M. Study on tensile properties of polyamide 12 produced by laser-based additive manufacturing process. J. Korea Acad. Ind. Coop. Soc. 2019, 20, 217–223. [Google Scholar]
- Jae, H. The trend of the recent analysis of engineering plastics. Conf. Polym. Soc. Korea 2020, 45, 47–48. [Google Scholar]
- Lee, S.H. A Study on Engineering Plastic Bearing Cage Injection Process; The Korean Society of Manufacturing Process Engineers: Seoul, Republic of Korea, 2020; p. 244. [Google Scholar]
- Kang, D.H.; Hyun, J.H. Evaluation of the durability of spherical bridge bearing using polyamide engineering plastic middle plate. J. Korean Soc. Urban Railw. 2021, 9, 1021–1031. [Google Scholar] [CrossRef]
- Korea Highway Bridge Specifications; Korean Ministry of Construction and Transportation: Sejong, Republic of Korea, 2016.
- Roughness EN ISO 4288; 1997 Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Rules and Procedures for the Assessment of Surface Texture (ISO 4288:1996). ISO: Geneva, Switzerland, 1996.
- Frantsen, J.E.; Mathiesen, T. Specifying Stainless Steel Surfaces for the Brewery, Dairy and Pharmaceutical Sectors; Nace Corrosion: Houston, TX, USA, 2009; p. 9573. [Google Scholar]
- EN 1337-7:2004; Structural Bearings—Part 7: Spherical and Cylindrical PTFE Bearings. European Committee for Standardization: Brussels, Belgium, 2004.
- Abaqus Documentation, Version 6.12; Dassault System: Waltham, MA, USA, 2012.
- Kim, K.S.; Han, O.; Gombosuren, M.; Kim, S.H. Numerical simulation of Y-type perfobond rib shear connectors using finite element analysis. Steel Compos. Struct. 2019, 31, 53–67. [Google Scholar]
- Tahmasebinia, F.; Ranzi, G.; Zona, A. Probabilistic three-dimensional finite element study on composite beams with steel trapezoidal decking. J. Constr. Steel Res. 2013, 80, 394–411. [Google Scholar] [CrossRef]
- Qureshi, J.; Lam, D.; Ye, J. The influence of profiled sheeting thickness and shear connector’s position on strength and ductility of headed shear connector. Eng. Struct. 2011, 33, 1643–1656. [Google Scholar] [CrossRef]
- Qureshi, J.; Lam, D.; Ye, J. Effect of shear connector spacing and layout on the shear connector capacity in composite beams. J. Constr. Steel Res. 2011, 67, 706–719. [Google Scholar] [CrossRef]
- Veritas, D.N. DNV-RP-C208: Determination of Structural Capacity by Non-Linear FE Analysis Methods; Det Norske Veritas: Bærum, Norway, 2013. [Google Scholar]






| Technical Specification | Value |
|---|---|
| Maximum vertical load | 100 kN |
| Maximum vertical loading rate | 100 mm/s |
| Maximum vertical stroke | ±100 mm |
| Maximum horizontal load | 50 kN |
| Maximum horizontal loading rate | 100 mm/s |
| Maximum horizontal stroke | ±100 mm |
| Specification | Ceramic | Stainless-Steel |
|---|---|---|
| Young’s modulus (GPa) | 220 | 210 |
| Compressive/Tensile strength (MPa) | 3,997 | 656 |
| Poisson’s ratio | 0.297 | 0.3 |
| Hardness (Vickers hardness) | 1,100 | 152 |
| Roughness | 0.8 | 0.8 |
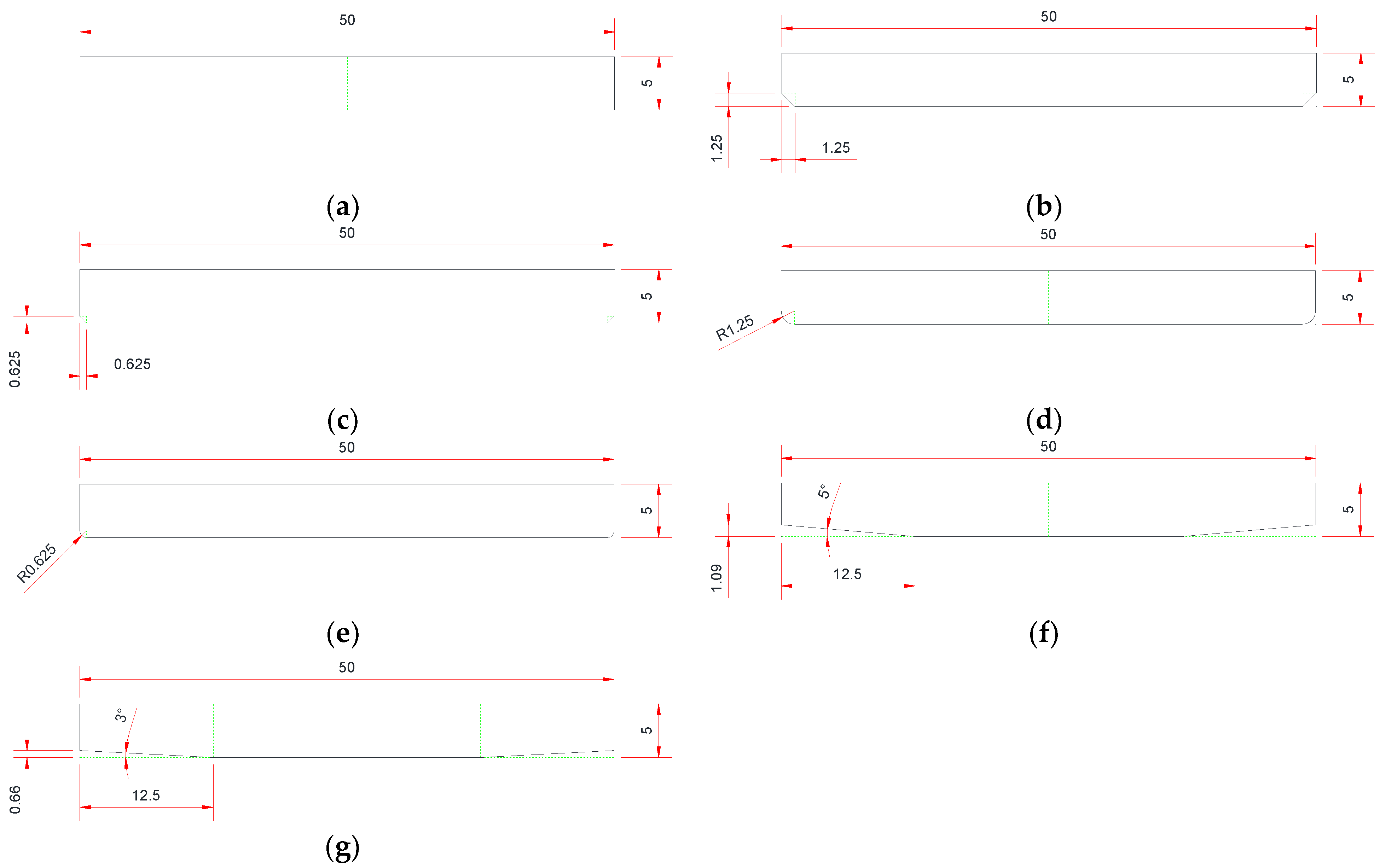
| Specimen Designation | Edge Type | Edge Size/Angle |
|---|---|---|
| Type-Ref | Not modified | – |
| Type-C-1 | Camber | 1.25 |
| Type-C-2 | Camber | 0.625 |
| Type-R-1 | Round | 1.25 |
| Type-R-2 | Round | 0.625 |
| Type-T-1 | Taper | 5° |
| Type-T-2 | Taper | 3° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, O.; Kwark, J.-W.; Lee, J.-W.; Han, W.-J. Analytical Study on the Frictional Behavior of Sliding Surfaces Depending on Ceramic Friction Materials. Appl. Sci. 2023, 13, 234. https://doi.org/10.3390/app13010234
Han O, Kwark J-W, Lee J-W, Han W-J. Analytical Study on the Frictional Behavior of Sliding Surfaces Depending on Ceramic Friction Materials. Applied Sciences. 2023; 13(1):234. https://doi.org/10.3390/app13010234
Chicago/Turabian StyleHan, Oneil, Jong-Won Kwark, Jung-Woo Lee, and Woo-Jin Han. 2023. "Analytical Study on the Frictional Behavior of Sliding Surfaces Depending on Ceramic Friction Materials" Applied Sciences 13, no. 1: 234. https://doi.org/10.3390/app13010234
APA StyleHan, O., Kwark, J.-W., Lee, J.-W., & Han, W.-J. (2023). Analytical Study on the Frictional Behavior of Sliding Surfaces Depending on Ceramic Friction Materials. Applied Sciences, 13(1), 234. https://doi.org/10.3390/app13010234





