Textile Physical Barriers: An Assessment of the Prison Effect as a Design Criterion to Increase the Porosity without Loss of Efficacy
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
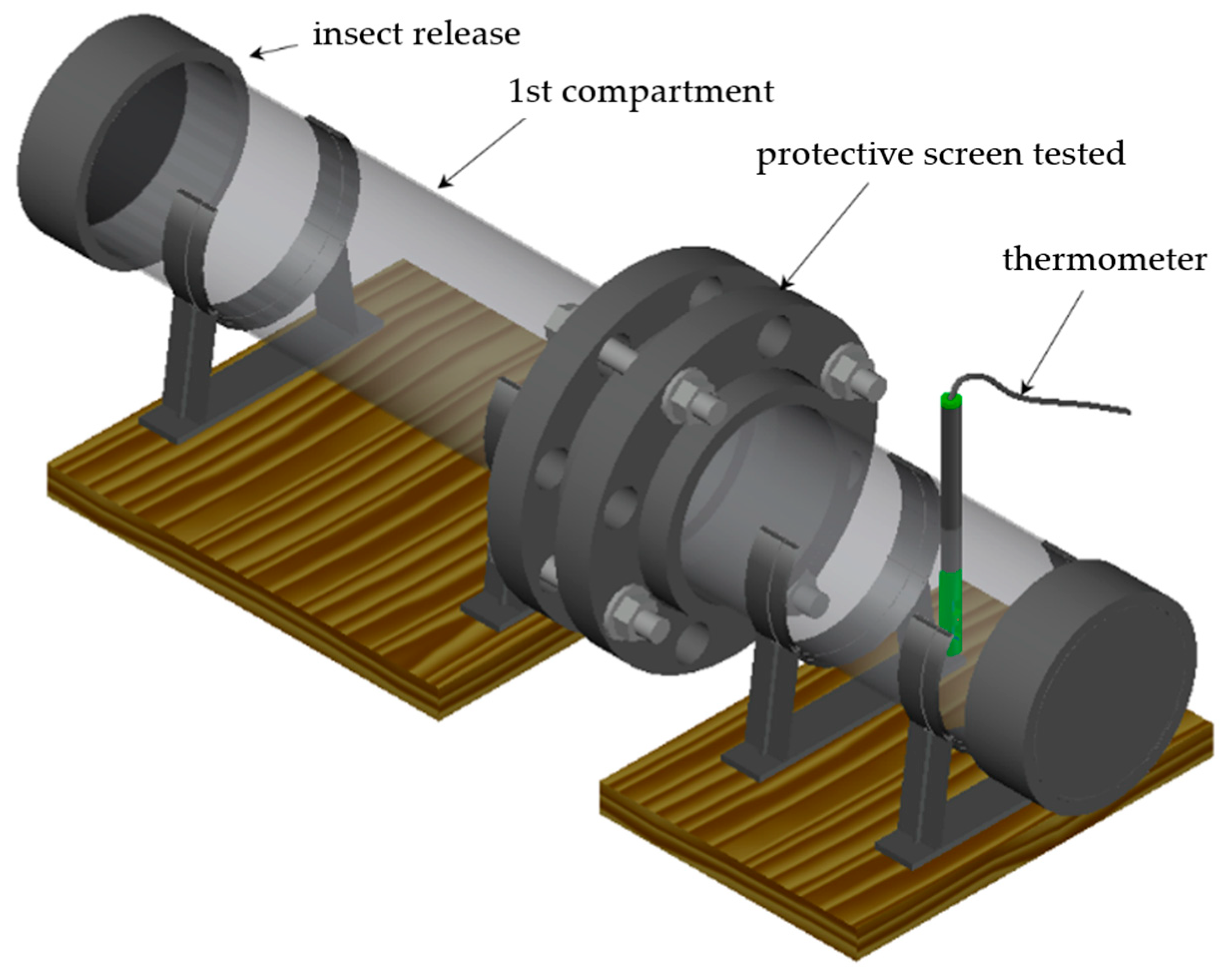
2.1. Device to Measure the Efficacy of Textiles against Insects
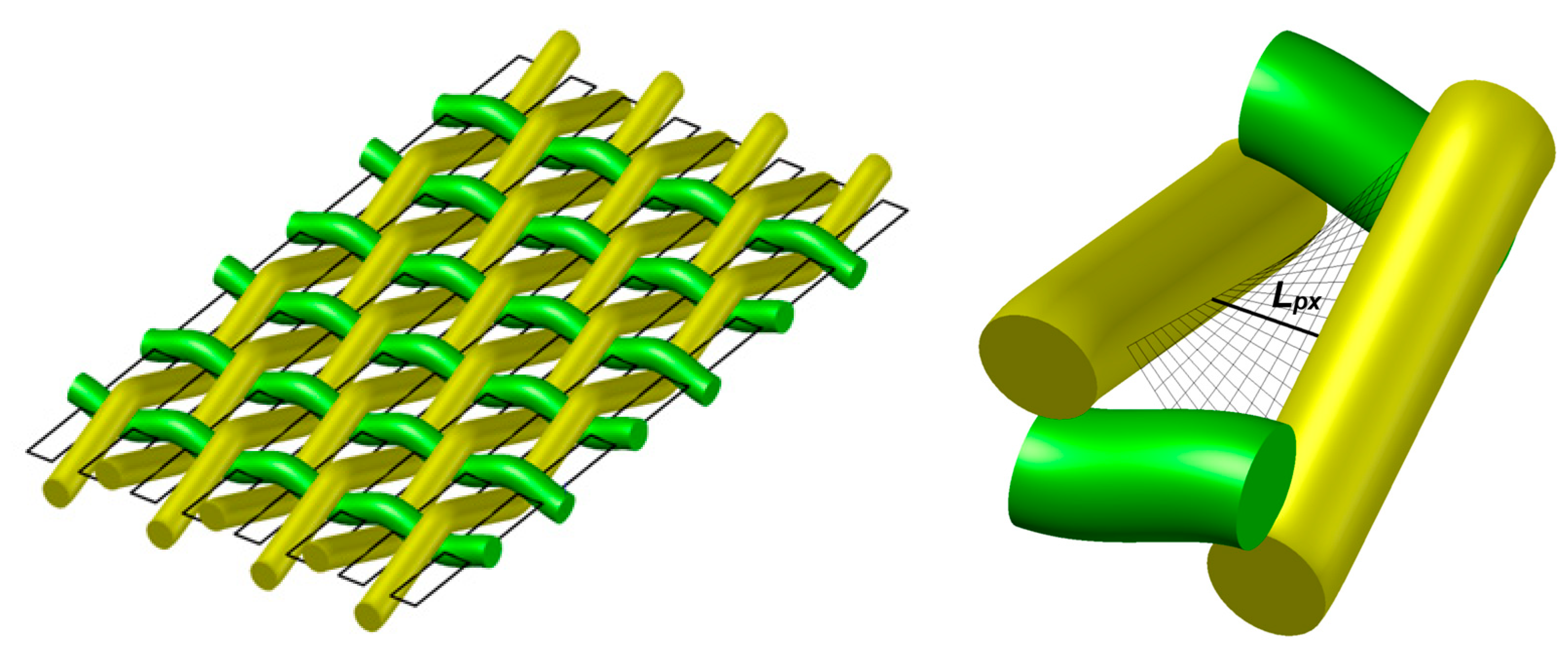
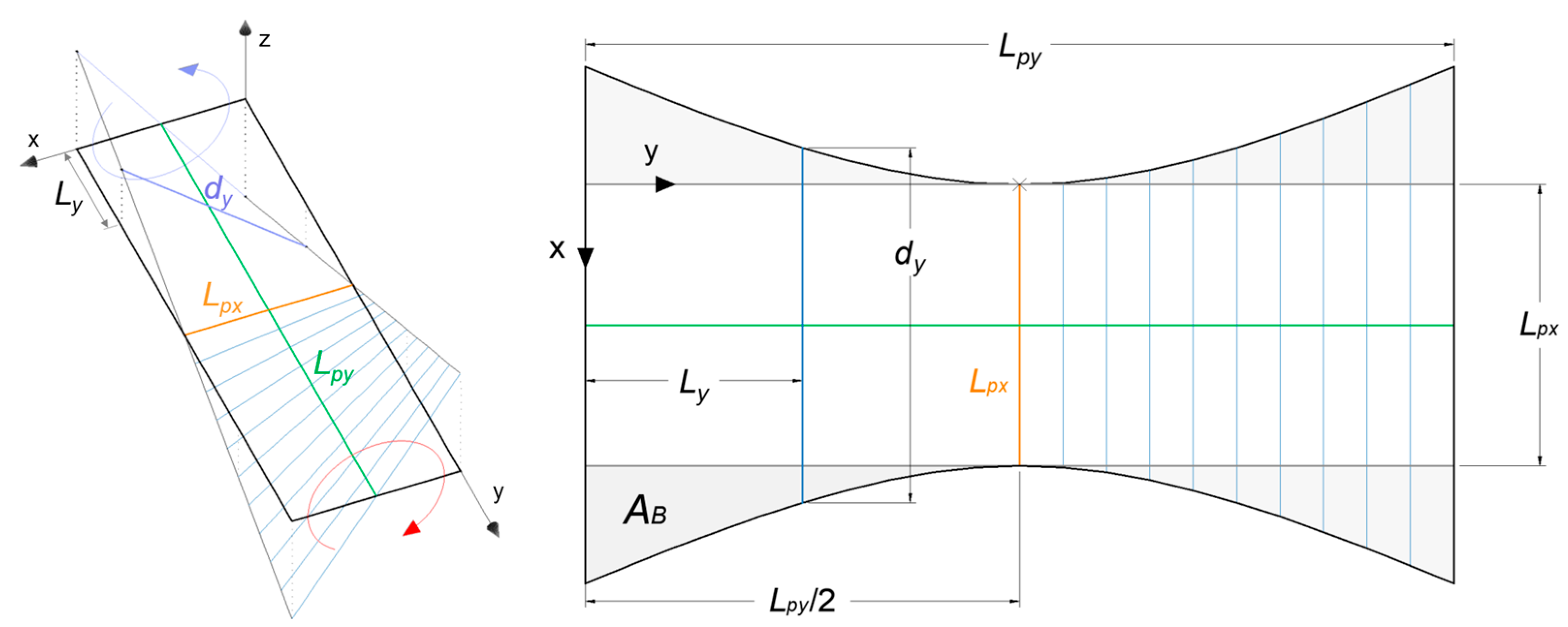
2.2. Selection and Geometric Characterization of the Protective Screens
2.3. Three-Dimensional Characterization of Protective Screens
2.4. Determination of the Sample Size
3. Results
3.1. Morphometric Analysis of B. tabaci
3.2. Geometric Characterization of the Selected Textiles
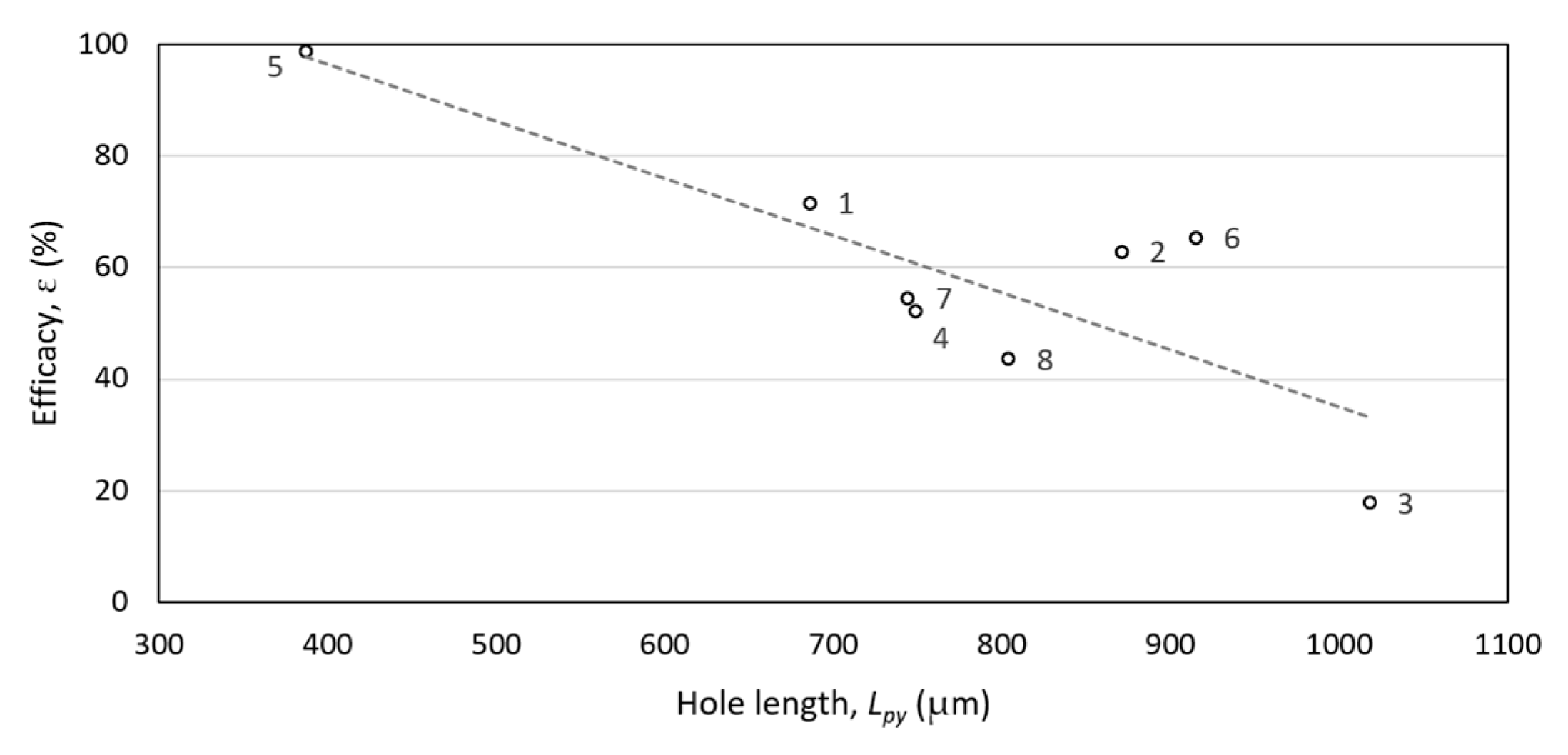
3.3. Efficacy of Textile Physical Barriers
4. Discussion
4.1. Hole Dimensions vs. Insect Size
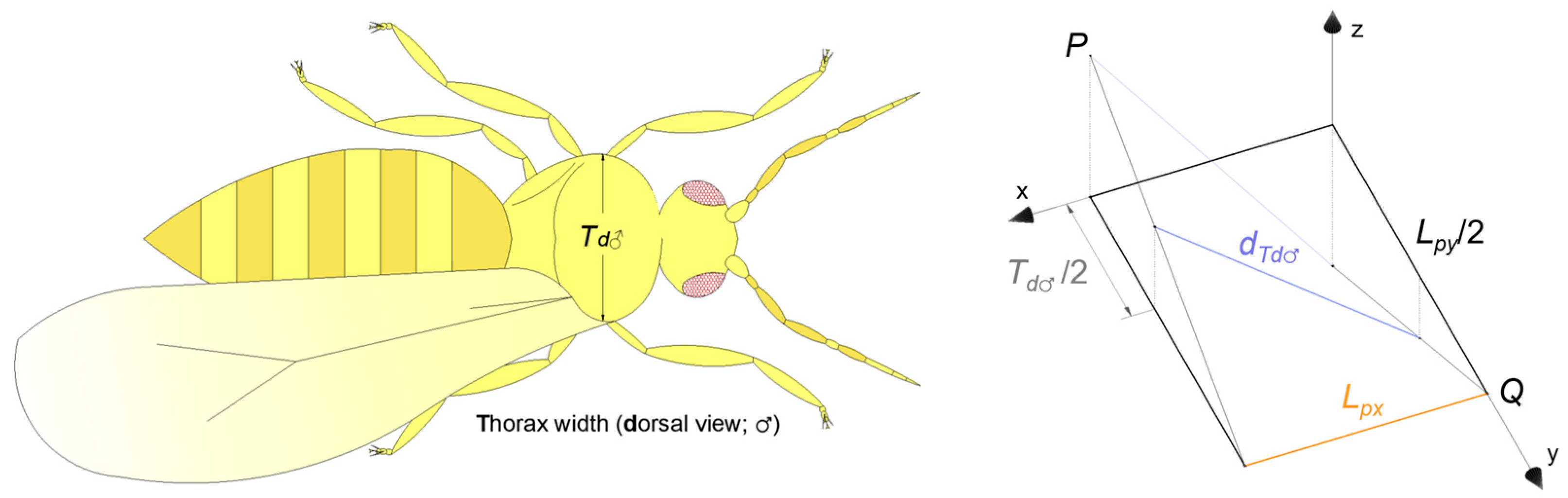
4.2. Prison Effect Assessment
- If the hole is long enough, one of the halves will offer a porous surface large enough for the insect to pass through. Additionally, that is what happens in holes as their length increases: the spatial separation of the warp threads increases from the segment defining the axis of the hole, and the insects find a larger free surface to pass through the textile.
- However, if the hole, although rectangular, is not long enough, the insect will not be able to pass through any of the halves defined by the central axis, and in these cases, the spacing between the weft threads according to the design criterion will improve the porosity without loss of efficacy, considering that the hole width is well defined according to the target pest species.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bailey, B. Screens stop insects but slow airflow. Fruit Veg. Technol. 2003, 3, 6–8. [Google Scholar]
- Berlinger, M.J.; Gol’berg, A.M.; Dahan, R.; Cohen, S. The use of plastic covering to prevent the spread of tomato yellow leaf curl virus in greenhouses. Hassadeh 1983, 63, 1862–1865. [Google Scholar]
- Berlinger, M.J.; Dahan, R.; Mordechai, S. Integrated pest management of organically grown tomatoes in Israel. Appl. Agric. Res. 1988, 3, 233–238. [Google Scholar]
- Berlinger, M.J.; Lebiush-Mordechi, S.; Leeper, A. Application of screens to prevent whitefly penetration into greenhouses in the Mediterranean basin. Bull. OILB SROP 1991, 14, 105–110. [Google Scholar]
- Berlinger, M.J.; Leblush-Mordechl, S.; Fridja, D.; Mor, N. The effect of types of greenhouse screens on the presence of western flower thrips: A preliminary study. OILB-SROP Bull. 1992, 16, 13–19. [Google Scholar]
- Robb, K.L.; Parrella, M.P. Chemical and no-chemical control of western flower thrips. In Proceedings of the Fourth Conference of Insect and Disease Management on Ornamentals, Kansas City, MO, USA, 1–3 March 1988; pp. 94–103. [Google Scholar]
- Baker, J.R.; Jones, R.K. Screening as part of insect and disease management in the greenhouse. N.C. Flower Grow. Bull. 1989, 34, 1–9. [Google Scholar]
- Roberts, W.J.; Vasvary, L.; Kania, S. Screening for insect control in mechanically ventilated greenhouses. ASAE 1995, 95-4541, 12. [Google Scholar]
- Baker, J.R.; Shearin, E.A. An update on screening for the exclusion of insect pest. N.C. Flower Grow. Bull. 1994, 39, 6–11. [Google Scholar]
- Ross, D.S.; Gill, S.A. Insect screening for greenhouses. In Agricultural Engineering Information Facts; University of Maryland: College Park, MD, USA, 1994; Volume 186, pp. 1–21. [Google Scholar]
- Teitel, M. The effect of insect-proof screens in roof openings on greenhouse microclimate. Agric. For. Meteorol. 2001, 110, 13–25. [Google Scholar] [CrossRef]
- Soni, P.; Salokhe, V.M.; Tantau, H.J. Effect of screen mesh size on vertical temperature distribution in naturally ventilated tropical greenhouses. Biosyst. Eng. 2005, 92, 469–482. [Google Scholar] [CrossRef]
- Bethke, J.A. Screening Greenhouses for Insect Size. Grow. Talks 1990, 102. [Google Scholar]
- Bethke, J.A.; Paine, T.D. Screen hole size and barriers for exclusion on insect pest of glasshouse crops. J. Entomol. Sci. 1991, 26, 169–177. [Google Scholar] [CrossRef]
- Bethke, J.A. Considering installing screening? This is what you need to know. Greenh. Manag. 1994, 13, 34–37. [Google Scholar]
- Kanakala, S.; Ghanim, M. Global genetic diversity and geographical distribution of Bemisia tabaci and its bacterial endosymbionts. PLoS ONE 2019, 14, e0213946. [Google Scholar] [CrossRef] [PubMed]
- Burban, C.; Fishpool, L.D.C.; Fauquet, C.; Fargette, D.; Thovenel, J.C. Host-associated biotypes within west African populations of the whitefly Bemisia tabaci (Gennadius), (Hom., Aleyrodidae). J. Appl. Entomol. 1992, 113, 416–423. [Google Scholar] [CrossRef]
- Jones, D.R. Plant viruses transmitted by whiteflies. Eur. J. Plant. Pathol. 2003, 109, 195–219. [Google Scholar] [CrossRef]
- Navas-Castillo, J.; Fiallo-Olivé, E.; Sánchez-Campos, S. Emerging virus diseases transmitted by whiteflies. Ann. Rev. Phytopathol. 2011, 49, 219–248. [Google Scholar] [CrossRef]
- Álvarez, A.J.; Oliva, R.M. First laboratory experiences and field observations on the validity of the prison effect. 2021; unpublished work. [Google Scholar]
- Álvarez, A.J.; Oliva, R.M.; Valera, D.L. Software for the geometric characterisation of insect-proof screens. Comput. Electron. Agric. 2012, 82, 134–144. [Google Scholar] [CrossRef]
- ISO 5084:1996; Textiles—Determination of Thickness of Textiles and Textile Products. International Organization for Standardization: Geneva, Switzerland, 1996; 5p.
- Álvarez, A.J.; Oliva, R.M.; Jiménez-Vargas, A.; Villegas-Vallecillos, M. A three-dimensional approach to the porous surface of screens. J. Text. Inst. 2019, 110, 639–646. [Google Scholar] [CrossRef]
- Álvarez, A.J. Estudio de las características geométricas y del comportamiento aerodinámico de las mallas antiinsectos utilizadas en los invernaderos como medida de protección vegetal. Editor. Univ. Almer. 2010, 273, 446. [Google Scholar]
- Triola, M.F. Elementary Statistics, 9th ed.; Pearson Education, Inc.: London, UK, 2004; pp. 296–347. [Google Scholar]
- Atkinson, D. Temperature and organism size: A biological law for ectotherms? Adv. Ecol. Res. 1994, 25, 1–58. [Google Scholar]
- Oliva, R.M.; Álvarez, A.J. Factors influencing the efficacy of insect-proof screens. Acta Hortic. 2017, 1170, 1027–1034. [Google Scholar] [CrossRef]
- Álvarez, A.J.; Oliva, R.M. Insect exclusion screens: The size of the holes from a three-dimensional perspective. Acta Hortic. 2017, 1170, 1035–1042. [Google Scholar] [CrossRef]

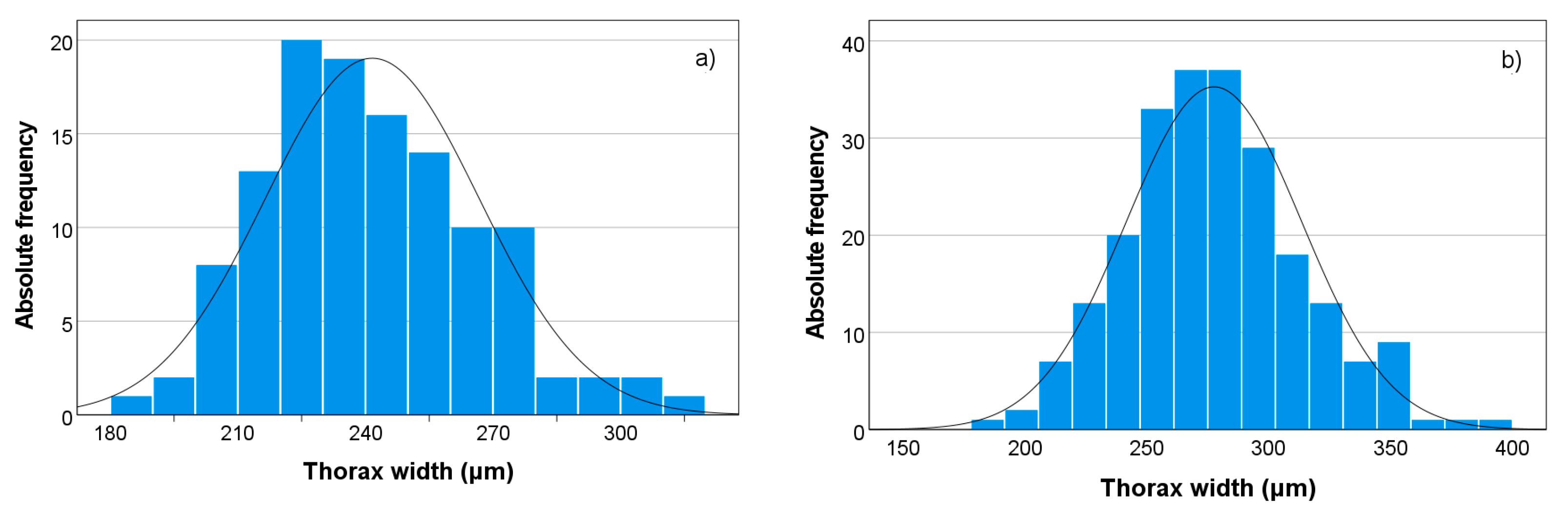
| Tagma | Minimum (µm) | Mean ± SD (µm) | Maximum (µm) | n | ||||
|---|---|---|---|---|---|---|---|---|
| ♂ | ♀ | ♂ | ♀ | ♂ | ♀ | ♂ | ♀ | |
| Thorax (Td) | 190 | 181 | 242 ± 25 | 278 ± 36 | 314 | 387 | 120 | 229 |
| Abdomen | 119 | 163 | 162 ± 29 | 292 ± 39 | 286 | 399 | ||
| Length | 587 | 629 | 804 ± 75 | 968 ± 88 | 1009 | 1246 | ||
| Textile | Thread Color | ρx × ρy (Threads cm−2) | Lpx ± SD (μm) | Lpy ± SD (μm) | Dhx ± σ (μm) | Dhy ± σ (μm) | φ (%) |
|---|---|---|---|---|---|---|---|
| 5 | crystal | 15.9 × 16.1 | 363 ± 21 | 387 a ± 26 | 240 ± 13 | 258 ± 10 | 35.7 |
| 1 | black | 10.5 × 16.3 | 355 ± 25 | 686 b ± 57 | 263 ± 7 | 258 ± 9 | 42.0 |
| 7 | crystal | 9.7 × 16.7 | 355 ± 31 | 744 b ± 22 | 288 ± 10 | 244 ± 11 | 42.9 |
| 4 | crystal | 10.0 × 16.3 | 358 ± 25 | 749 b ± 22 | 251 ± 9 | 256 ± 10 | 43.8 |
| 8 | crystal | 9.5 × 15.9 | 367 ± 34 | 804 b ± 27 | 249 ± 7 | 263 ± 21 | 44.5 |
| 2 | crystal | 8.9 × 16.8 | 348 ± 30 | 871 b ± 26 | 247 ± 8 | 247 ± 8 | 45.7 |
| 6 | white | 8.7 × 16.8 | 361 ± 17 | 915 c ± 28 | 230 ± 10 | 233 ± 10 | 48.8 |
| 3 | crystal | 7.9 × 16.5 | 349 ± 38 | 1018 c ± 22 | 252 ± 6 | 257 ± 10 | 46.3 |
| Textile | tt ± SD (μm) | (Dhx + Dhy)/tt (μm μm−1) | Lpx/Lpy (μm μm−1) | dTd♂ (μm) | DPQ (μm) | Lpy/2 (μm) | A2D ± SD (mm2) | A≅3D (mm2) | (%) | ε (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 454 ± 5 | 0.91 | 0.938 | 370 | 423 | 194 | 0.140 ± 0.013 | 0.153 | 8.3 | 98.8 |
| 1 | 474 ± 5 | 0.91 | 0.517 | 382 | 505 | 343 | 0.244 ± 0.027 | 0.262 | 6.7 | 71.6 |
| 7 | 486 ± 5 | 0.91 | 0.477 | 391 | 528 | 372 | 0.264 ± 0.024 | 0.288 | 8.2 | 54.5 |
| 4 | 404 ± 5 | 0.80 | 0.478 | 372 | 523 | 375 | 0.267 ± 0.022 | 0.277 | 3.7 | 52.2 |
| 8 | 472 ± 4 | 0.92 | 0.456 | 395 | 554 | 402 | 0.295 ± 0.029 | 0.313 | 5.9 | 43.6 |
| 2 | 444 ± 5 | 0.90 | 0.400 | 376 | 566 | 436 | 0.303 ± 0.027 | 0.321 | 5.6 | 62.8 |
| 6 | 464 ± 5 | 1.00 | 0.395 | 399 | 594 | 458 | 0.330 ± 0.018 | 0.355 | 7.0 | 65.3 |
| 3 | 418 ± 4 | 0.82 | 0.343 | 370 | 622 | 509 | 0.355 ± 0.040 | 0.369 | 3.8 | 17.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez, A.J.; Oliva, R.M. Textile Physical Barriers: An Assessment of the Prison Effect as a Design Criterion to Increase the Porosity without Loss of Efficacy. Appl. Sci. 2023, 13, 6254. https://doi.org/10.3390/app13106254
Álvarez AJ, Oliva RM. Textile Physical Barriers: An Assessment of the Prison Effect as a Design Criterion to Increase the Porosity without Loss of Efficacy. Applied Sciences. 2023; 13(10):6254. https://doi.org/10.3390/app13106254
Chicago/Turabian StyleÁlvarez, Antonio J., and Rocío M. Oliva. 2023. "Textile Physical Barriers: An Assessment of the Prison Effect as a Design Criterion to Increase the Porosity without Loss of Efficacy" Applied Sciences 13, no. 10: 6254. https://doi.org/10.3390/app13106254
APA StyleÁlvarez, A. J., & Oliva, R. M. (2023). Textile Physical Barriers: An Assessment of the Prison Effect as a Design Criterion to Increase the Porosity without Loss of Efficacy. Applied Sciences, 13(10), 6254. https://doi.org/10.3390/app13106254







