Unconventional Arrays for 3D Electrical Resistivity and Induced Polarization Tomography to Detect Leachate Concentration in a Waste Landfill
Abstract
:1. Introduction
2. Materials and Methods
2.1. Electrode Areal Arrangements in Square Surfaces
2.2. Choice of the Electrode Array Configurations
2.3. Apparent Resistivity Data Calculation
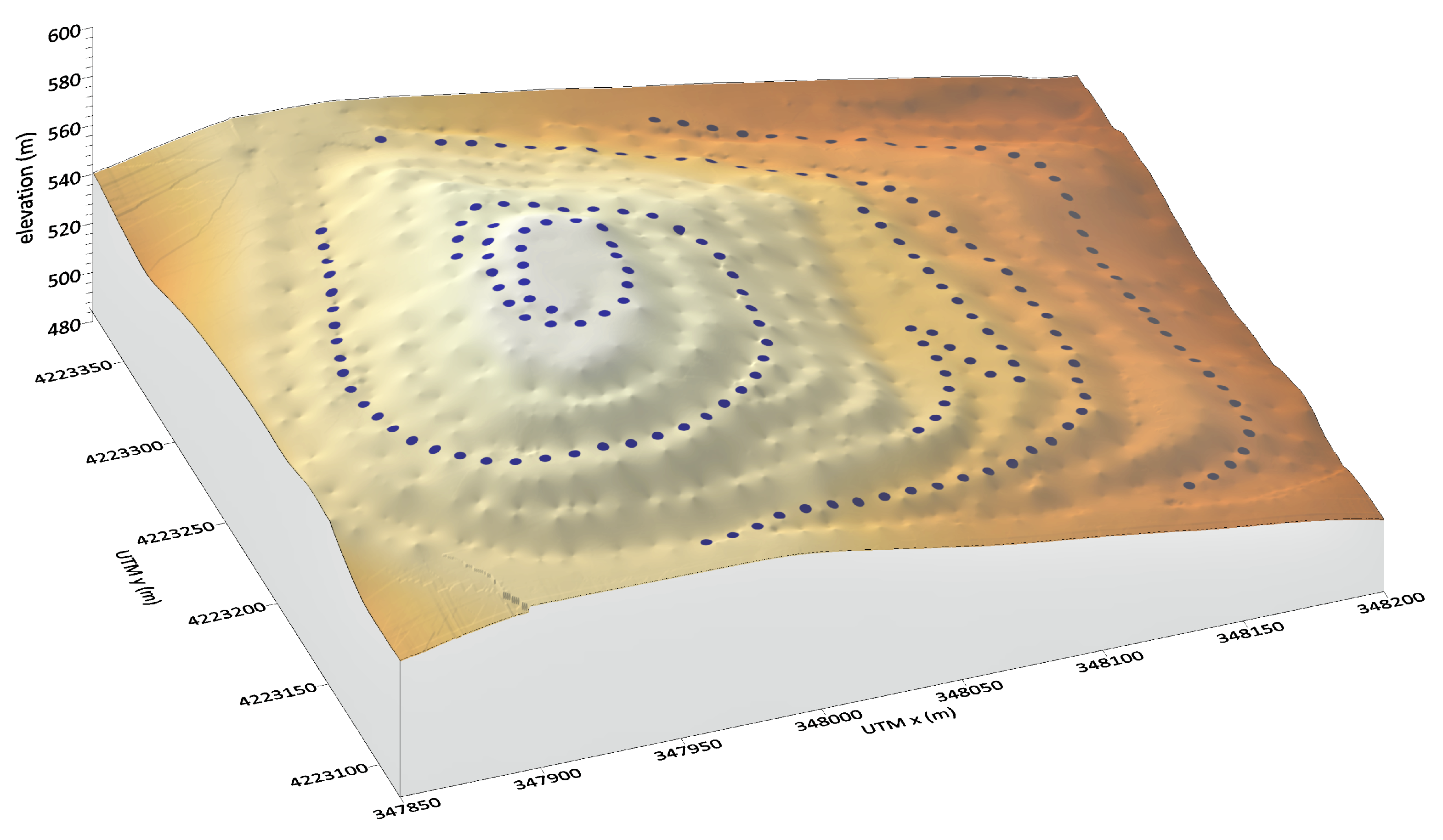
2.4. The Test Site
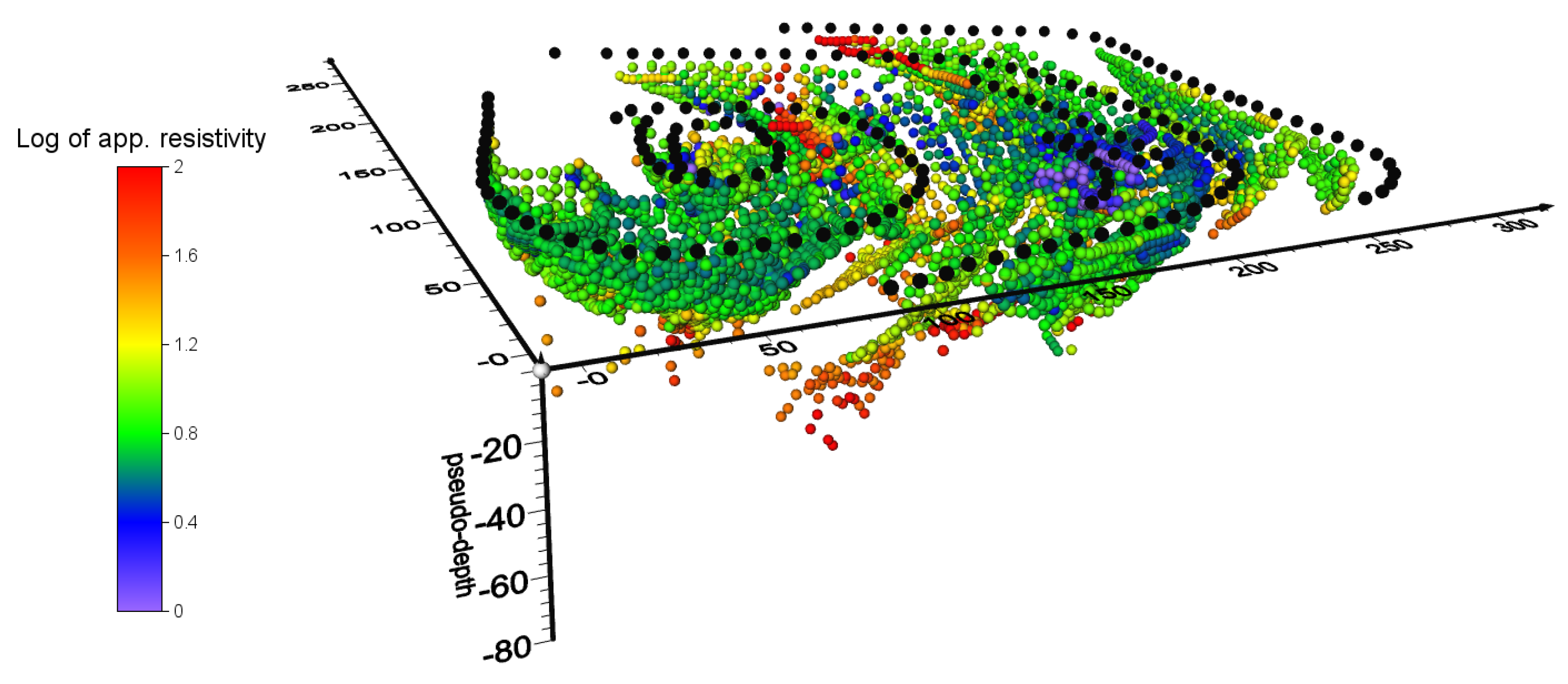
2.5. Data Processing and Inversion
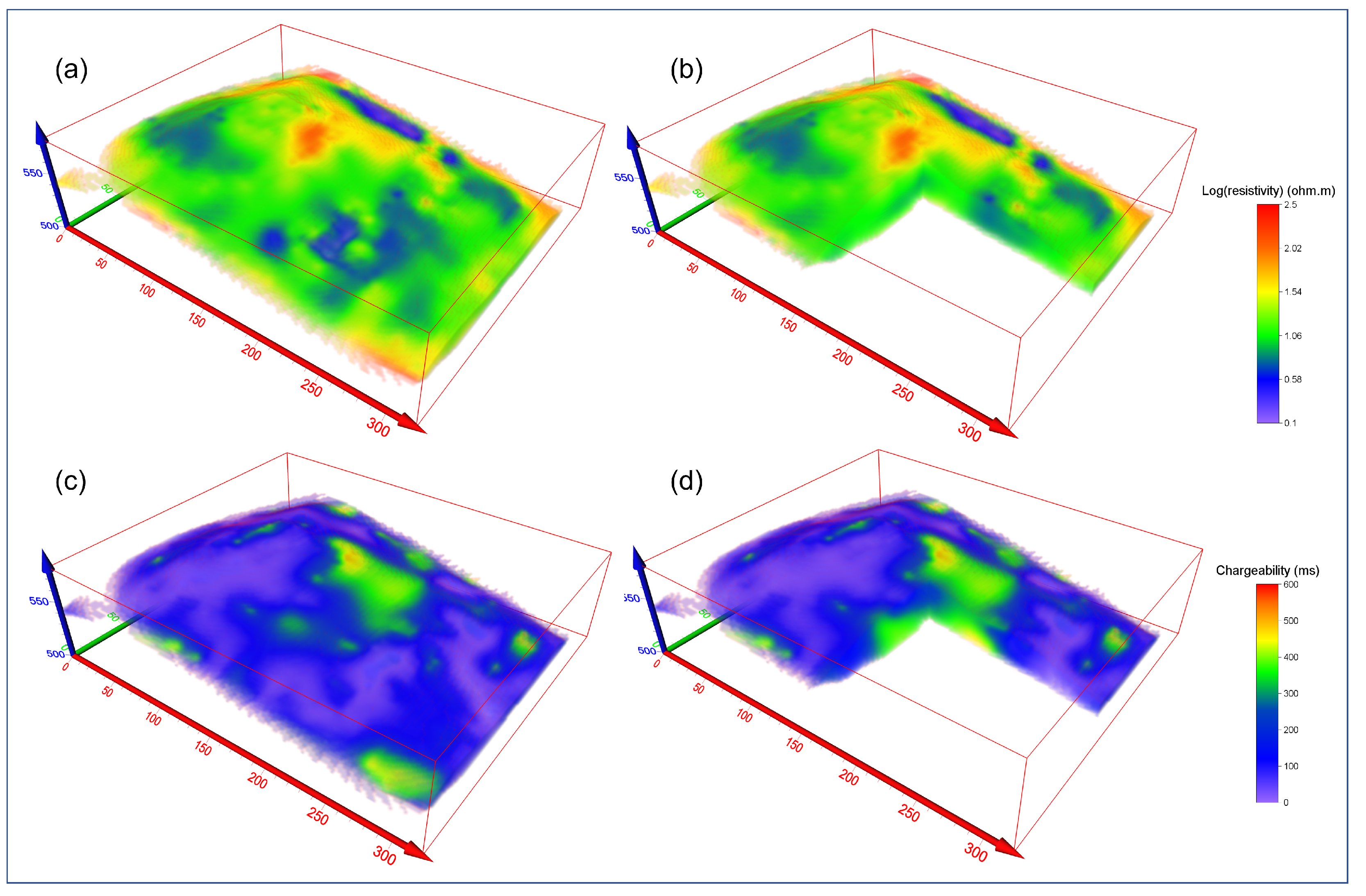
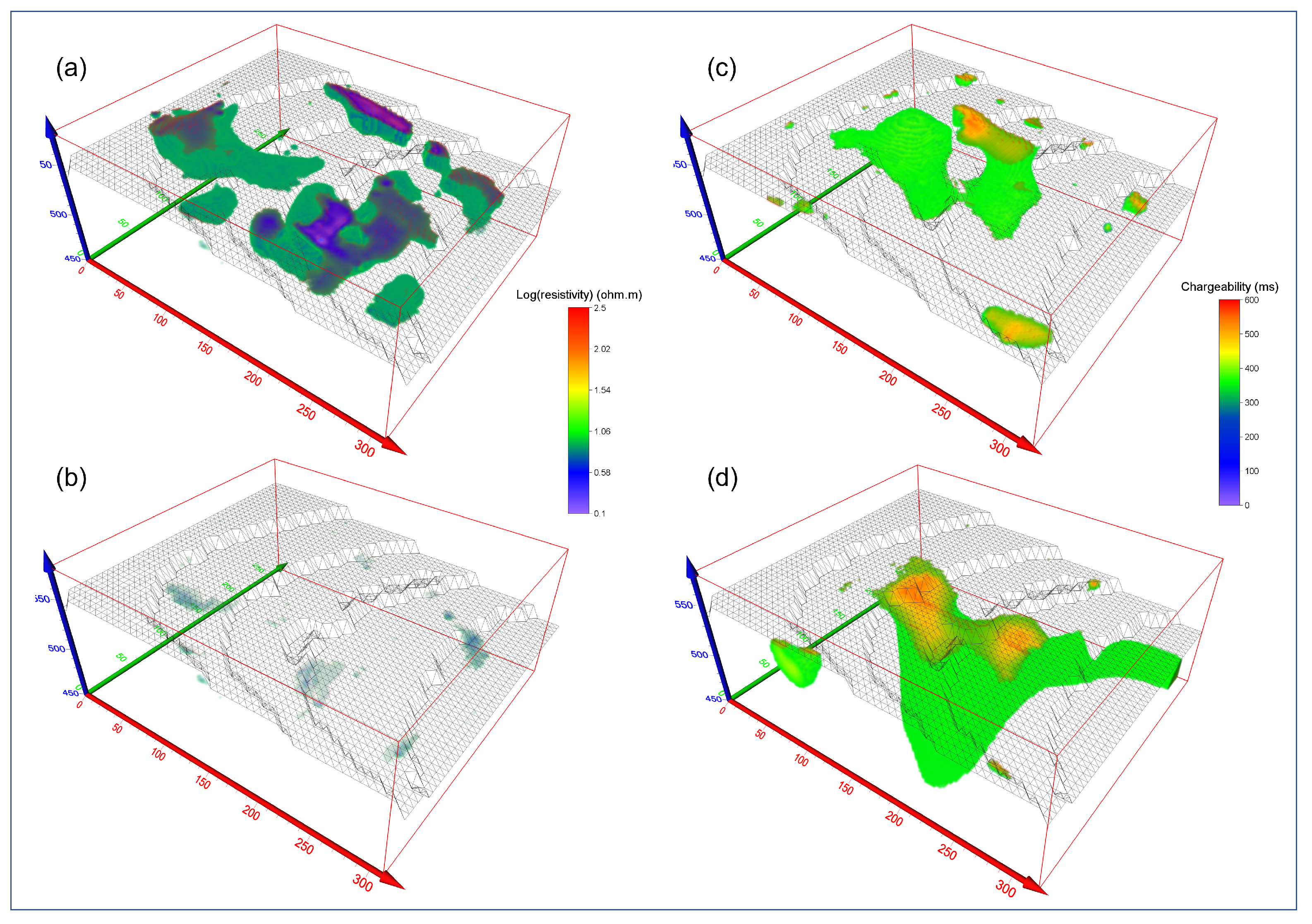
3. Results
3.1. Inverse Models from the Simulated Data
3.2. Results of 3D ERT and IP on the Waste Landfill
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koefoed, O. Resistivity Sounding measurements. Geosound. Princ. 1979, 1, 19–27. [Google Scholar]
- Dey, A.; Morrison, H. Resistivity modelling for arbitrarily shaped two-dimensional structures. Geophys. Prospect. 1979, 27, 106–136. [Google Scholar] [CrossRef]
- Coggon, J. Electromagnetic and electrical modeling by the finite element method. Geophysics 1971, 36, 132–155. [Google Scholar] [CrossRef]
- Inman, J.R. Resistivity inversion with ridge regression. Geophysics 1975, 40, 798–817. [Google Scholar] [CrossRef]
- Lapenna, V.; Lorenzo, P.; Perrone, A.; Piscitelli, S.; Sdao, F.; Rizzo, E. High-resolution geoelectrical tomographies in the study of Giarrossa landslide (southern Italy). Bull. Eng. Geol. Environ. 2003, 62, 259–268. [Google Scholar] [CrossRef]
- Lehmann, P.; Gambazzi, F.; Suski, B.; Baron, L.; Askarinejad, A.; Springman, S.M.; Holliger, K.; Or, D. Evolution of soil wetting patterns preceding a hydrologically induced landslide inferred from electrical resistivity survey and point measurements of volumetric water content and pore water pressure. Water Resour. Res. 2013, 49, 7992–8004. [Google Scholar] [CrossRef]
- Revil, A.; Glover, P. Nature of surface electrical conductivity in natural sands, sandstones, and clays. Geophys. Res. Lett. 1998, 25, 691–694. [Google Scholar] [CrossRef]
- Chirindja, F.; Dahlin, T.; Juizo, D.; Steinbruch, F. Reconstructing the formation of a costal aquifer in Nampula province, Mozambique, from ERT and IP methods for water prospection. Environ. Earth Sci. 2017, 76, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Gonzales Amaya, A.; Dahlin, T.; Barmen, G.; Rosberg, J.E. Electrical resistivity tomography and induced polarization for mapping the subsurface of alluvial fans: A case study in Punata (Bolivia). Geosciences 2016, 6, 51. [Google Scholar] [CrossRef] [Green Version]
- Kemna, A.; Binley, A.; Cassiani, G.; Niederleithinger, E.; Revil, A.; Slater, L.; Williams, K.H.; Orozco, A.F.; Haegel, F.H.; Hördt, A.; et al. An overview of the spectral induced polarization method for near-surface applications. Near Surf. Geophys. 2012, 10, 453–468. [Google Scholar] [CrossRef] [Green Version]
- Merritt, A.; Chambers, J.; Murphy, W.; Wilkinson, P.; West, L.; Gunn, D.; Meldrum, P.; Kirkham, M.; Dixon, N. 3D ground model development for an active landslide in Lias mudrocks using geophysical, remote sensing and geotechnical methods. Landslides 2014, 11, 537–550. [Google Scholar] [CrossRef] [Green Version]
- Okay, G.; Leroy, P.; Ghorbani, A.; Cosenza, P.; Camerlynck, C.; Cabrera, J.; Florsch, N.; Revil, A. Spectral induced polarization of clay-sand mixtures: Experiments and modelingPolarization of clay-sand mixtures. Geophysics 2014, 79, E353–E375. [Google Scholar] [CrossRef] [Green Version]
- Loke, M.; Chambers, J.; Rucker, D.; Kuras, O.; Wilkinson, P. Recent developments in the direct-current geoelectrical imaging method. J. Appl. Geophys. 2013, 95, 135–156. [Google Scholar] [CrossRef]
- Griffiths, D.; Turnbull, J. A multi-electrode array for resistivity surveying. First Break 1985, 3, 7. [Google Scholar] [CrossRef]
- Loke, M.; Barker, R. Practical techniques for 3D resistivity surveys and data inversion1. Geophys. Prospect. 1996, 44, 499–523. [Google Scholar] [CrossRef]
- Dahlin, T.; Bernstone, C. A roll-along technique for 3D resistivity data acquisition with multi-electrode arrays. In Proceedings of the 10th EEGS Symposium on the Application of Geophysics to Engineering and Environmental Problems. European Association of Geoscientists & Engineers, Nashville, TN, USA, 25–29 March 1997; p. 204. [Google Scholar]
- Martorana, R.; Capizzi, P.; D’Alessandro, A.; Luzio, D. Comparison of different sets of array configurations for multichannel 2D ERT acquisition. J. Appl. Geophys. 2017, 137, 34–48. [Google Scholar] [CrossRef]
- Fiandaca, G.; Martorana, R.; Messina, P.; Cosentino, P. The MYG methodology to carry out 3D electrical resistivity tomography on media covered by vulnerable surfaces of artistic value. Nuovo Cim. B 2010, 125, 711–718. [Google Scholar]
- Gharibi, M.; Bentley, L.R. Resolution of 3-D electrical resistivity images from inversions of 2-D orthogonal lines. J. Environ. Eng. Geophys. 2005, 10, 339–349. [Google Scholar] [CrossRef] [Green Version]
- Chambers, J.; Wilkinson, P.; Penn, S.; Meldrum, P.; Kuras, O.; Loke, M.; Gunn, D. River terrace sand and gravel deposit reserve estimation using three-dimensional electrical resistivity tomography for bedrock surface detection. J. Appl. Geophys. 2013, 93, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Capizzi, P.; Martorana, R. Integration of constrained electrical and seismic tomographies to study the landslide affecting the cathedral of Agrigento. J. Geophys. Eng. 2014, 11, 045009. [Google Scholar] [CrossRef]
- Chávez, G.; Tejero, A.; Alcantara, M.; Chavez, R. The ‘L-Array’, a tool to characterize a fracture pattern in an urban zone: Extended Abstracts of the 2011 Near Surface Geophysics meeting. In Proceedings of the European Section Meeting, Hull, UK, 17–22 July 2011. [Google Scholar]
- Tejero-Andrade, A.; Cifuentes, G.; Chávez, R.E.; López-González, A.E.; Delgado-Solórzano, C. L-and CORNER-arrays for 3D electric resistivity tomography: An alternative for geophysical surveys in urban zones. Near Surf. Geophys. 2015, 13, 355–368. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Bouzidi, Y.; Ullah, S.; Asim, M. A full-range gradient survey for 2D electrical resistivity tomography. Near Surf. Geophys. 2020, 18, 609–626. [Google Scholar] [CrossRef]
- Dahlin, T.; Zhou, B. Multiple-gradient array measurements for multichannel 2D resistivity imaging. Near Surf. Geophys. 2006, 4, 113–123. [Google Scholar] [CrossRef] [Green Version]
- Martorana, R.; Fiandaca, G.; Casas Ponsati, A.; Cosentino, P. Comparative tests on different multi-electrode arrays using models in near-surface geophysics. J. Geophys. Eng. 2009, 6, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Loke, M. 3-D Resistivity and Ip forward Modeling Using the Finite-Difference and Finite-Element Methods. Instruction Manual for RES3DMOD Ver. 2.14 and RES3DMODx64 Ver. 3.04; Geotomosoft Solutions: Kuala Lumpur, Malaysia, 2017. [Google Scholar]
- Abdullah, F.M.; Loke, M.H.; Nawawi, M.; Abdullah, K. Improving the resolution of 3-D resistivity surveys along the perimeter of a confined area using optimized arrays. Pure Appl. Geophys. 2019, 176, 1701–1715. [Google Scholar] [CrossRef]
- Edwards, L. A modified pseudosection for resistivity and IP. Geophysics 1977, 42, 1020–1036. [Google Scholar] [CrossRef]
- Catalano, R.; Basilone, L.; Di Maggio, C.; Gasparo Morticelli, M.; Agate, M.; Avellone, G. Note Illustrative della Carta Geologica d’Italia alla Scala 1: 50.000 del Foglio 594–585 “Partinico-Mondello”; ISPRA—Servizio Geologico d’Italia: Rome, Italy, 2013.
- Contino, A.; Cusimano, G.; Frias Forcada, A. Modello idrogeologico dei Monti di Palermo. In Proceedings of the Atti del 79 Congresso Nazionale della Società Geologica Italiana, Palermo, Italy, 21–23 September 1998; pp. 21–23. [Google Scholar]
- Costanzo, A.; Pisciotta, A.; Pannaccione Apa, M.I.; Bongiovanni, S.; Capizzi, P.; D’Alessandro, A.; Falcone, S.; La Piana, C.; Martorana, R. Integrated use of unmanned aerial vehicle photogrammetry and terrestrial laser scanning to support archaeological analysis: The Acropolis of Selinunte case (Sicily, Italy). Archaeol. Prospect. 2021, 28, 153–165. [Google Scholar] [CrossRef]
- Rani, P.; Cassiani, G. Tracking contaminant transport using time-lapse geophysics: A review on applications of electrical methods. Water Secur. 2022, 17, 100127. [Google Scholar] [CrossRef]
- Bernstone, C.; Dahlin, T. DC resistivity mapping of old landfills: Two case studies. Eur. J. Environ. Eng. Geophys. 1997, 2, 121–136. [Google Scholar]
- Aristodemou, E.; Thomas-Betts, A. DC resistivity and induced polarisation investigations at a waste disposal site and its environments. J. Appl. Geophys. 2000, 44, 275–302. [Google Scholar] [CrossRef]
- Bernstone, C.; Dahlin, T.; Ohlsson, T.; Hogland, H. DC-resistivity mapping of internal landfill structures: Two pre-excavation surveys. Environ. Geol. 2000, 39, 360–371. [Google Scholar] [CrossRef] [Green Version]
- Guérin, R.; Munoz, M.L.; Aran, C.; Laperrelle, C.; Hidra, M.; Drouart, E.; Grellier, S. Leachate recirculation: Moisture content assessment by means of a geophysical technique. Waste Manag. 2004, 24, 785–794. [Google Scholar] [CrossRef] [PubMed]
- Chambers, J.E.; Kuras, O.; Meldrum, P.I.; Ogilvy, R.D.; Hollands, J. Electrical resistivity tomography applied to geologic, hydrogeologic, and engineering investigations at a former waste-disposal site. Geophysics 2006, 71, B231–B239. [Google Scholar] [CrossRef] [Green Version]
- De Carlo, L.; Perri, M.T.; Caputo, M.C.; Deiana, R.; Vurro, M.; Cassiani, G. Characterization of a dismissed landfill via electrical resistivity tomography and mise-à-la-masse method. J. Appl. Geophys. 2013, 98, 1–10. [Google Scholar] [CrossRef]
- Guinea, A.; Bicknell, J.; Cox, N.; Swan, H.; Simmons, N. Characterization of legacy landfills with electrical resistivity tomography; a comparative study. J. Appl. Geophys. 2022, 203, 104716. [Google Scholar] [CrossRef]
- Chambers, J.; Meldrum, P.; Ogilvy, R.; Wilkinson, P. Characterisation of a NAPL-contaminated former quarry site using electrical impedance tomography. Near Surf. Geophys. 2005, 3, 81–92. [Google Scholar] [CrossRef]
- Dahlin, T.; Bernstone, C.; Loke, M.H. A 3-D resistivity investigation of a contaminated site at Lernacken, Sweden. Geophysics 2002, 67, 1692–1700. [Google Scholar] [CrossRef] [Green Version]
- Clément, R.; Descloitres, M.; Günther, T.; Oxarango, L.; Morra, C.; Laurent, J.P.; Gourc, J.P. Improvement of electrical resistivity tomography for leachate injection monitoring. Waste Manag. 2010, 30, 452–464. [Google Scholar] [CrossRef]
- Maurya, P.; Rønde, V.; Fiandaca, G.; Balbarini, N.; Auken, E.; Bjerg, P.L.; Christiansen, A. Detailed landfill leachate plume mapping using 2D and 3D electrical resistivity tomography-with correlation to ionic strength measured in screens. J. Appl. Geophys. 2017, 138, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Martorana, R.; Capizzi, P.; D’Alessandro, A.; Luzio, D. Electrical resistivity and induced polarization tomographies to test the efficiency and safety of the new landfill of Bellolampo (Palermo, Italy). Boll. Geofis. Teor. Appl. 2016, 57, 313–327. [Google Scholar]
- Loke, M. Rapid 3-D Resistivity and IP Inversion Using the Least-Squares Method. Instruction Manual for RES3DINVx64 Ver. 3.13; Geotomosoft Solutions: Kuala Lumpur, Malaysia, 2017. [Google Scholar]

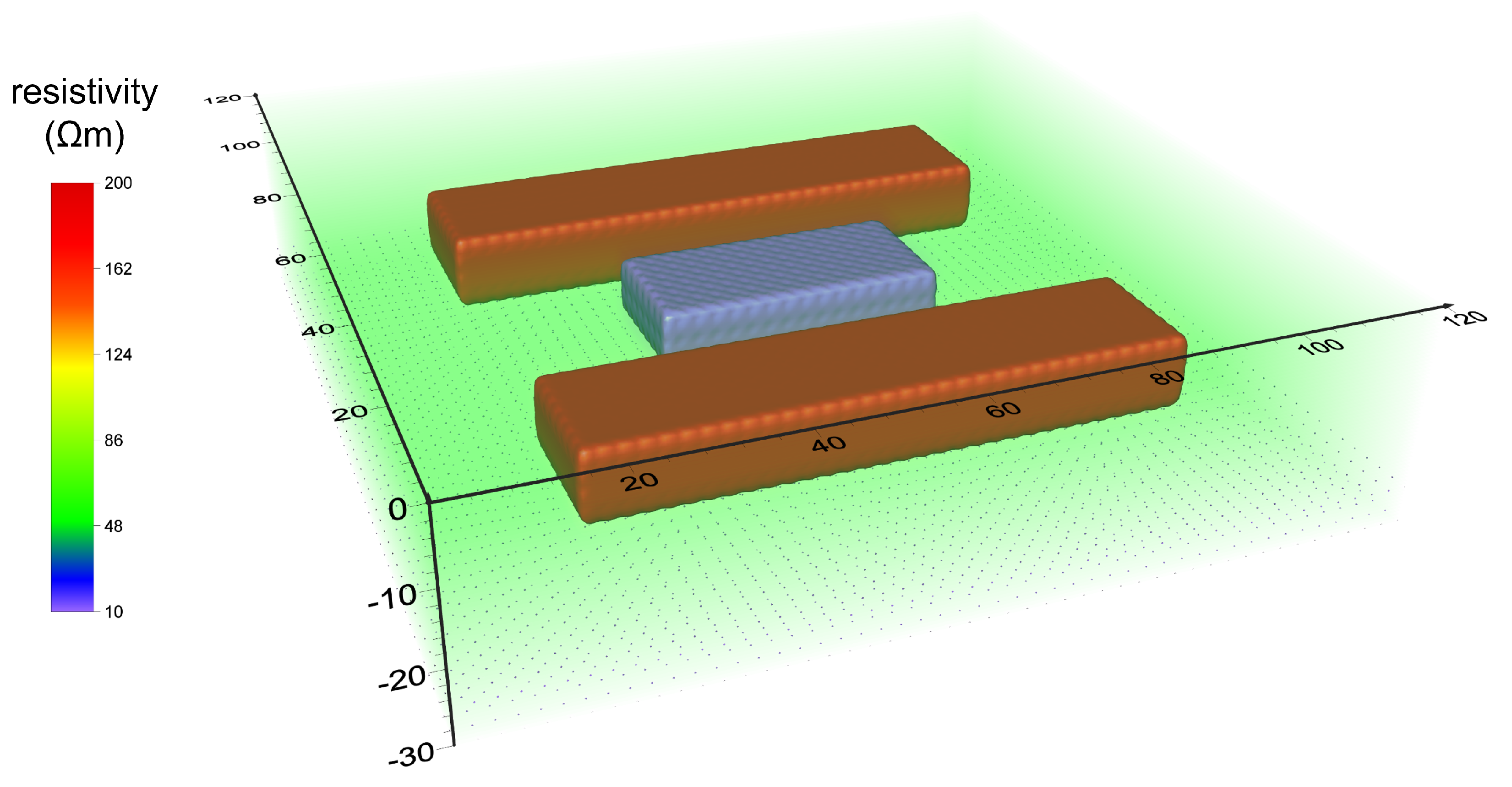


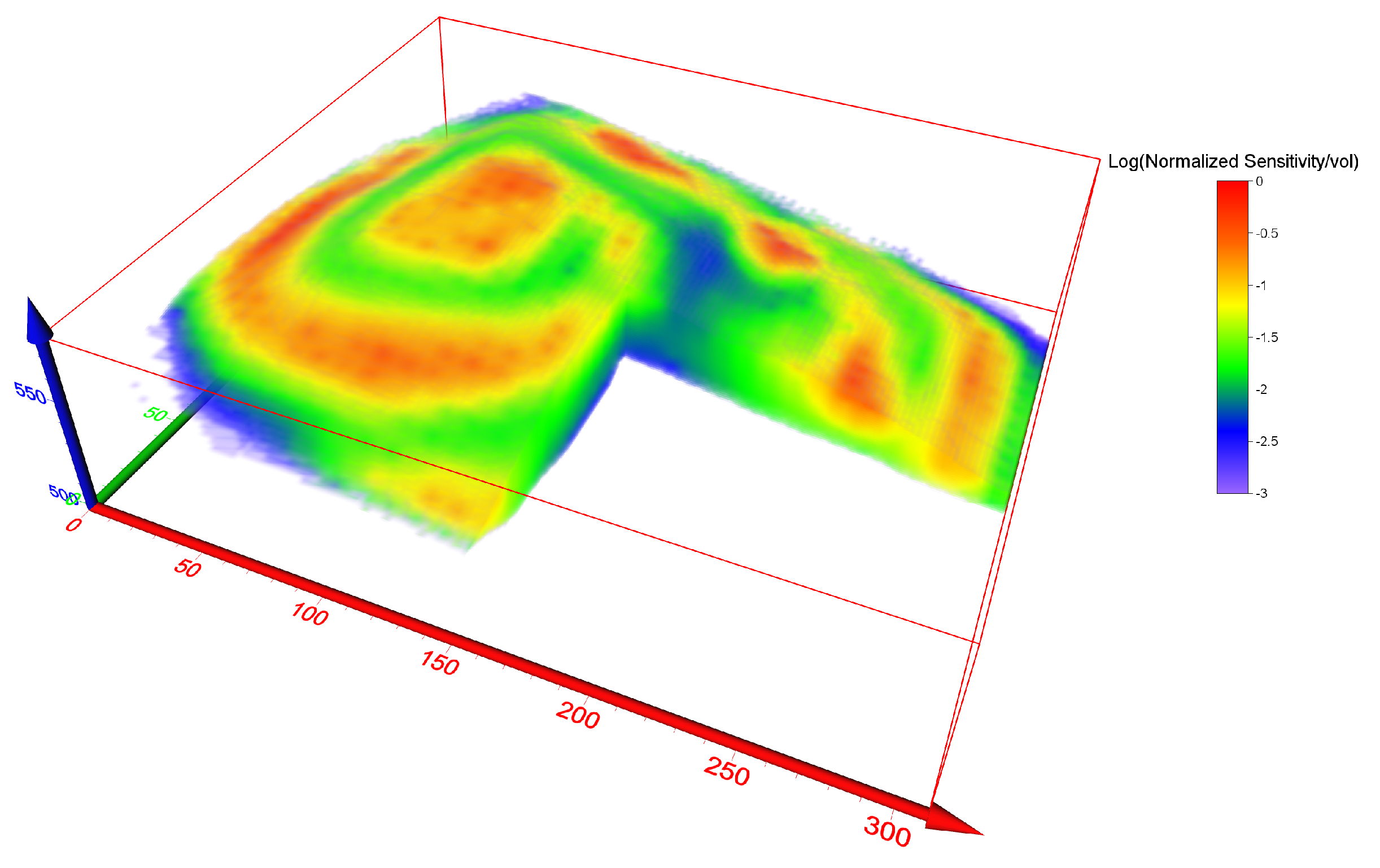

| Electrode Areal Arrangement | Electrode Array Configuration | Amount of Data | Number of Current Dipoles | Average Number of Potential Measures per Current Dipole |
|---|---|---|---|---|
| A | 7255 | 793 | 9 | |
| 8584 | 524 | 16 | ||
| 7326 | 160 | 46 | ||
| B | 21,240 | 980 | 21 | |
| 8766 | 480 | 18 | ||
| 13,114 | 390 | 69 | ||
| C | 21,618 | 982 | 22 | |
| 12,730 | 590 | 21 | ||
| 8303 | 293 | 28 |
| Electrode Areal Arrangement | Electrode Array Configuration | Volume of Resistive Anomalies (m) | % of Volume of the Resistive Prisms | Volume of Conductive Anomalies (m) | % of Volume of the Conductive Prisms |
|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | ||
| B | 11,940 | 37 | 4041 | 51 | |
| 76,581 | 239 | 9536 | 119 | ||
| 57,684 | 180 | 10,933 | 137 | ||
| C | 20,920 | 65 | 6161 | 77 | |
| 26,809 | 84 | 8916 | 111 | ||
| 43,492 | 136 | 10,125 | 127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martorana, R.; Capizzi, P.; Pirrera, C. Unconventional Arrays for 3D Electrical Resistivity and Induced Polarization Tomography to Detect Leachate Concentration in a Waste Landfill. Appl. Sci. 2023, 13, 7203. https://doi.org/10.3390/app13127203
Martorana R, Capizzi P, Pirrera C. Unconventional Arrays for 3D Electrical Resistivity and Induced Polarization Tomography to Detect Leachate Concentration in a Waste Landfill. Applied Sciences. 2023; 13(12):7203. https://doi.org/10.3390/app13127203
Chicago/Turabian StyleMartorana, Raffaele, Patrizia Capizzi, and Calogero Pirrera. 2023. "Unconventional Arrays for 3D Electrical Resistivity and Induced Polarization Tomography to Detect Leachate Concentration in a Waste Landfill" Applied Sciences 13, no. 12: 7203. https://doi.org/10.3390/app13127203
APA StyleMartorana, R., Capizzi, P., & Pirrera, C. (2023). Unconventional Arrays for 3D Electrical Resistivity and Induced Polarization Tomography to Detect Leachate Concentration in a Waste Landfill. Applied Sciences, 13(12), 7203. https://doi.org/10.3390/app13127203








