Force Analysis and Strength Determination of the Cemented Paste Backfill Roof in Underhand Drift Cut-and-Fill Stopping
Abstract
:1. Introduction
2. Field Measurements
2.1. Introduction to the Case Study
2.2. Measurement Equipment and Solutions
2.2.1. Measurement Equipment
2.2.2. Measurement Solutions
3. Results and Analysis
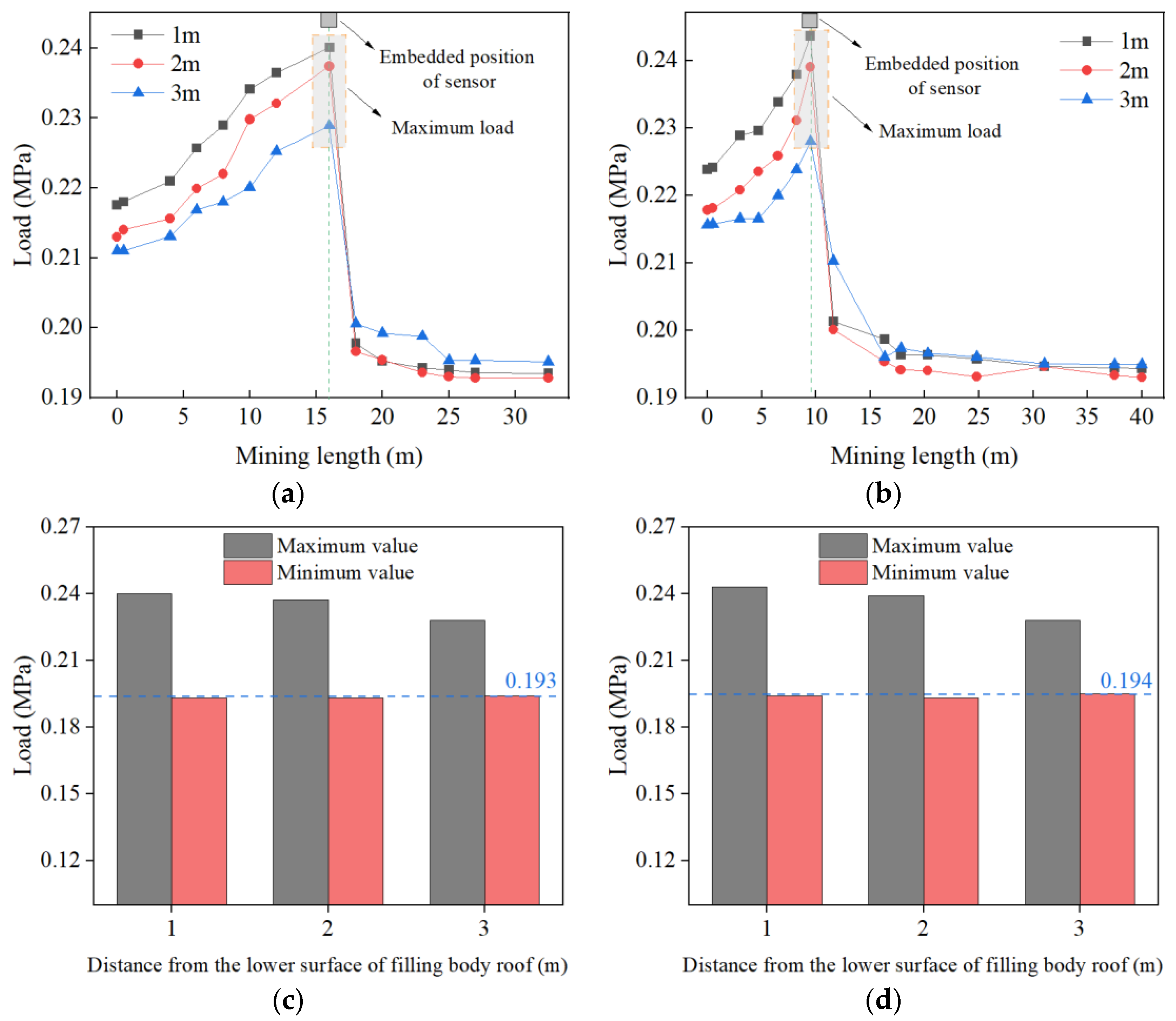
3.1. Distribution Pattern of the Load on the CPB Roof during the Mining Process
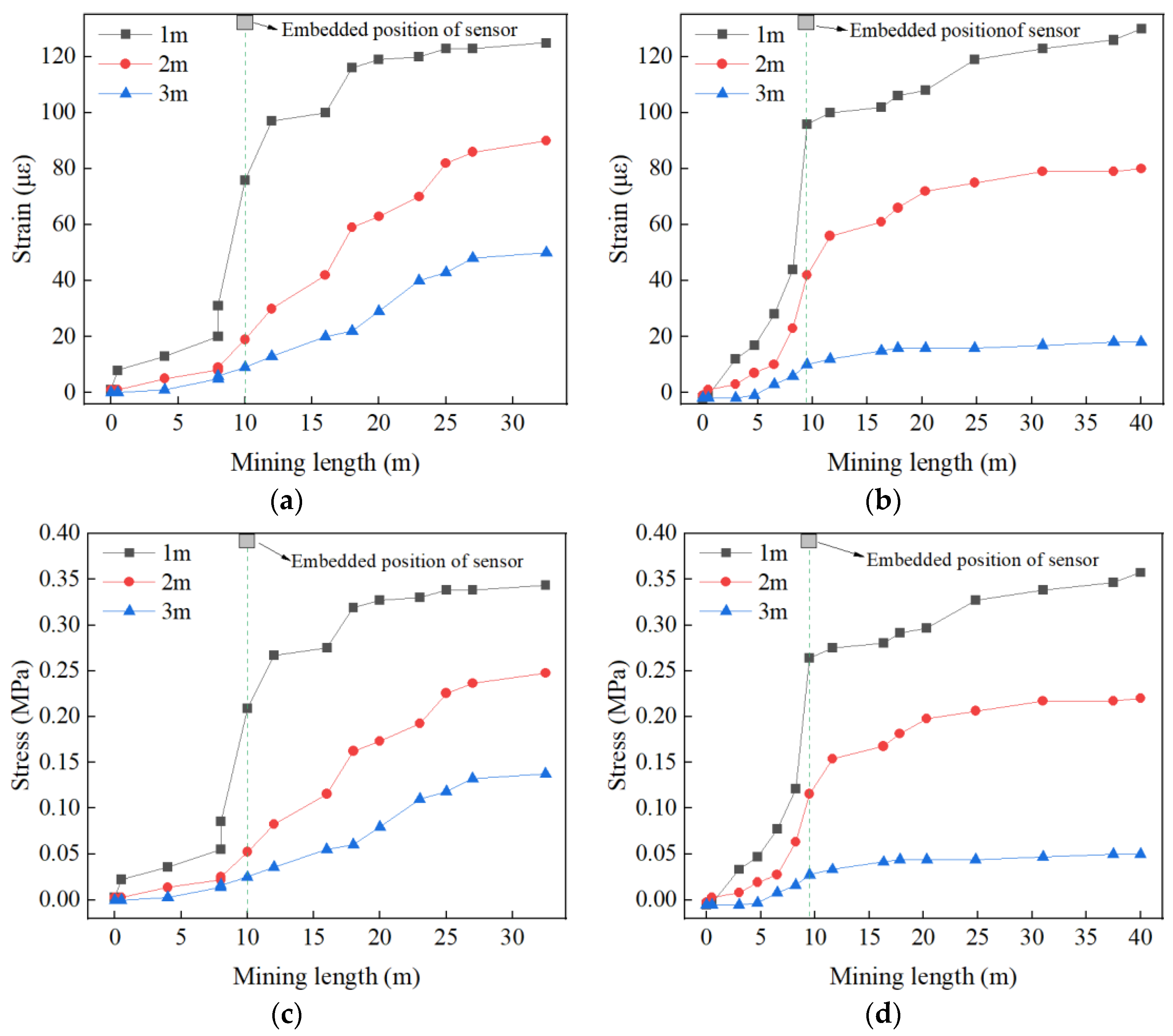
3.2. Stress–Strain Evolution Pattern of CPB Roof during Mining
3.3. Theoretical Analysis
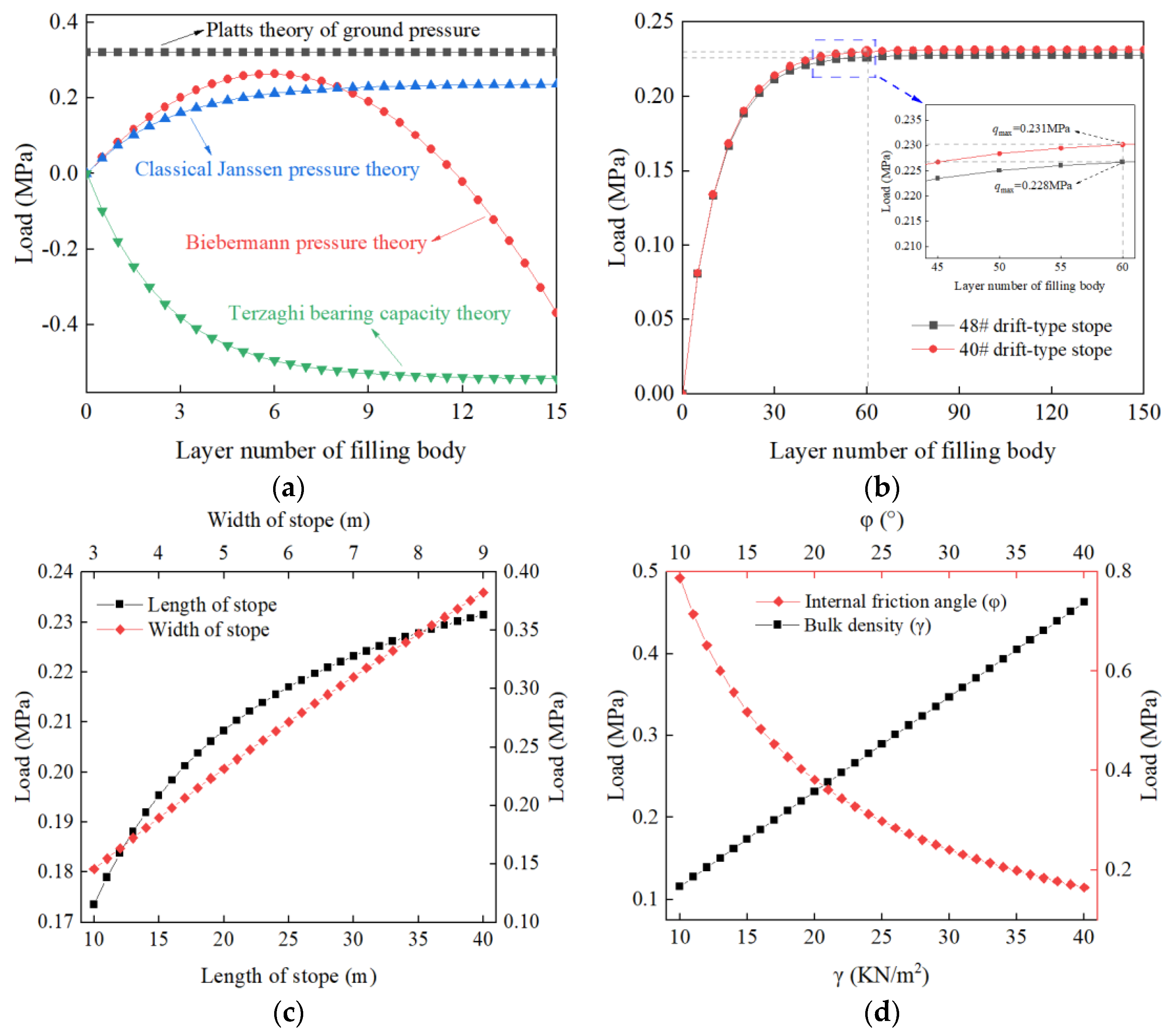
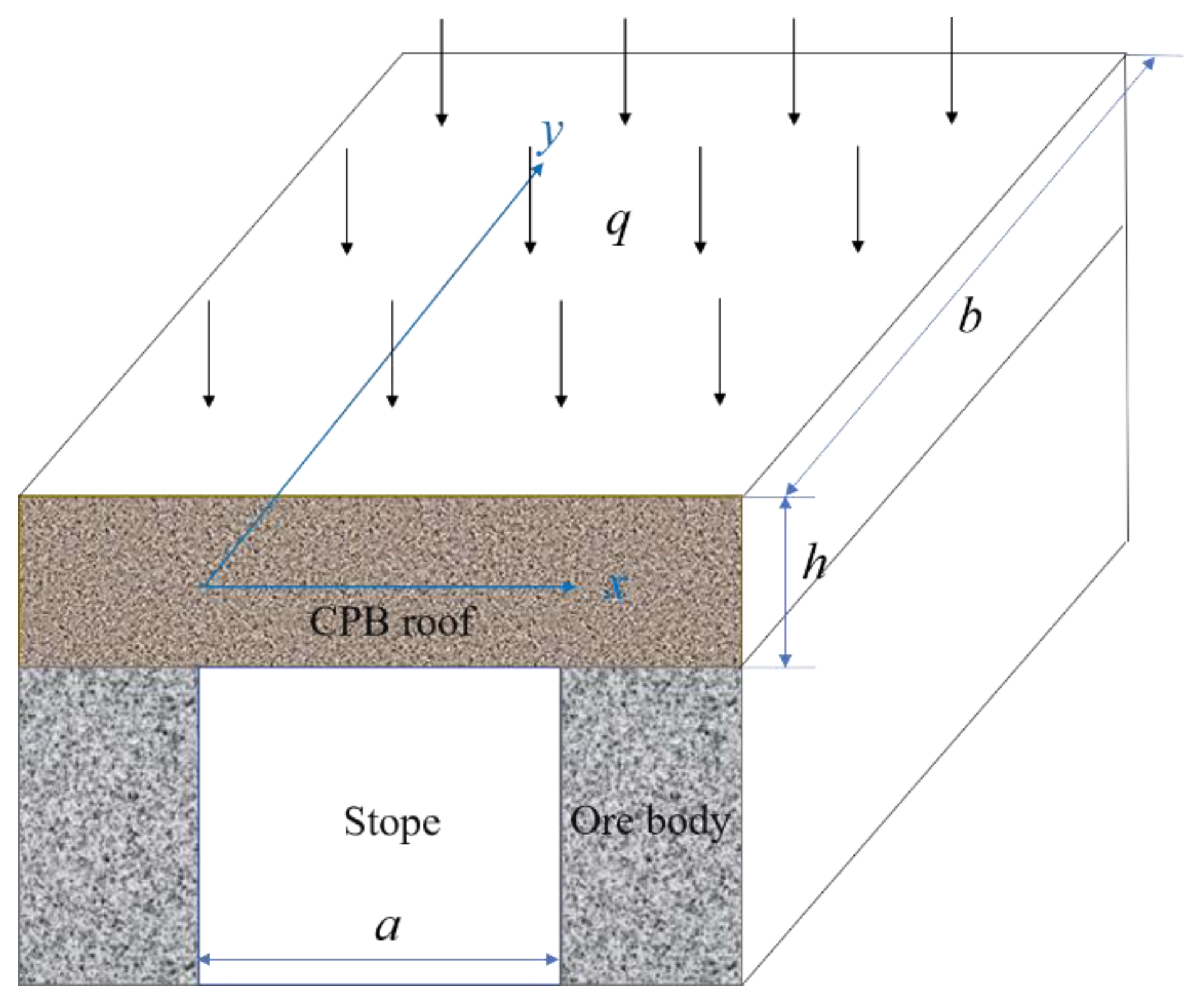
3.3.1. Calculation of Overlying Load of CPB Roof
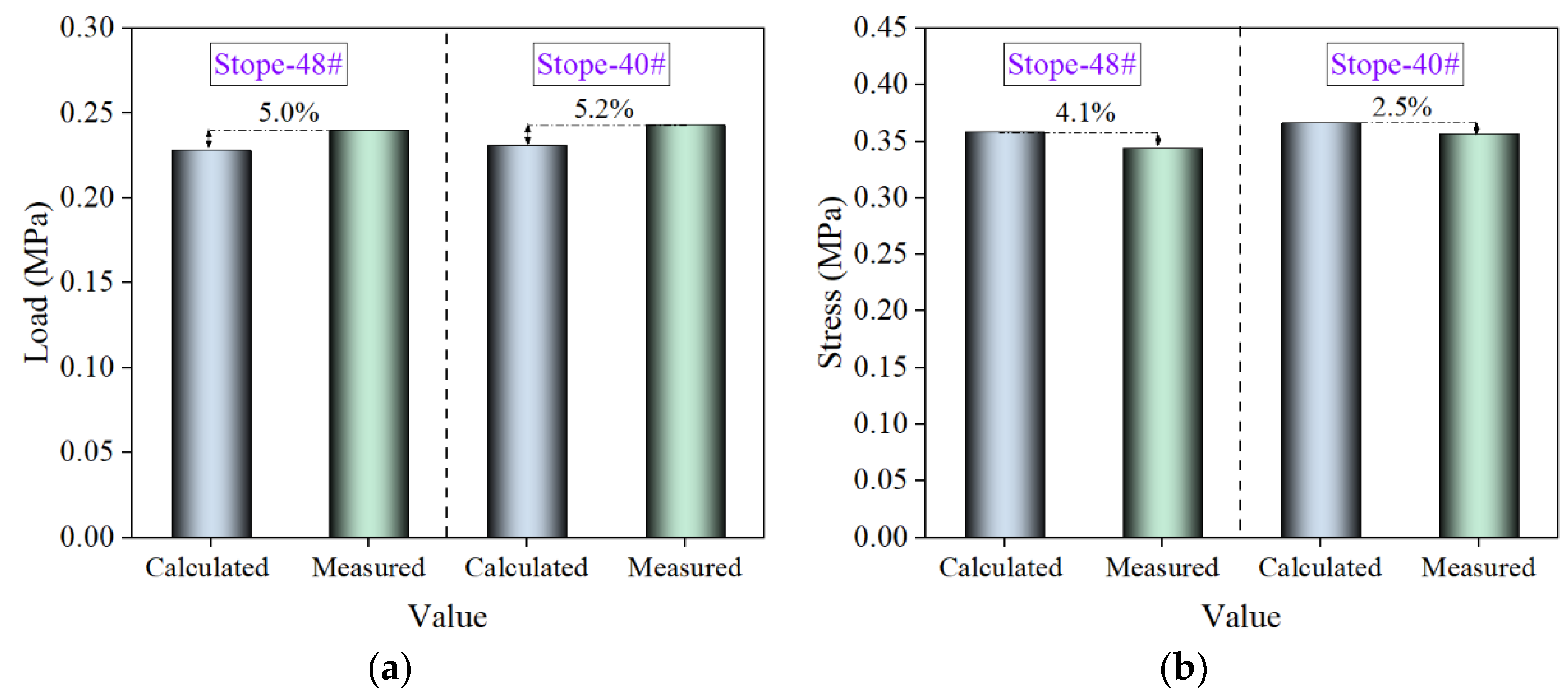
3.3.2. Evaluation of the Applicability of the Model
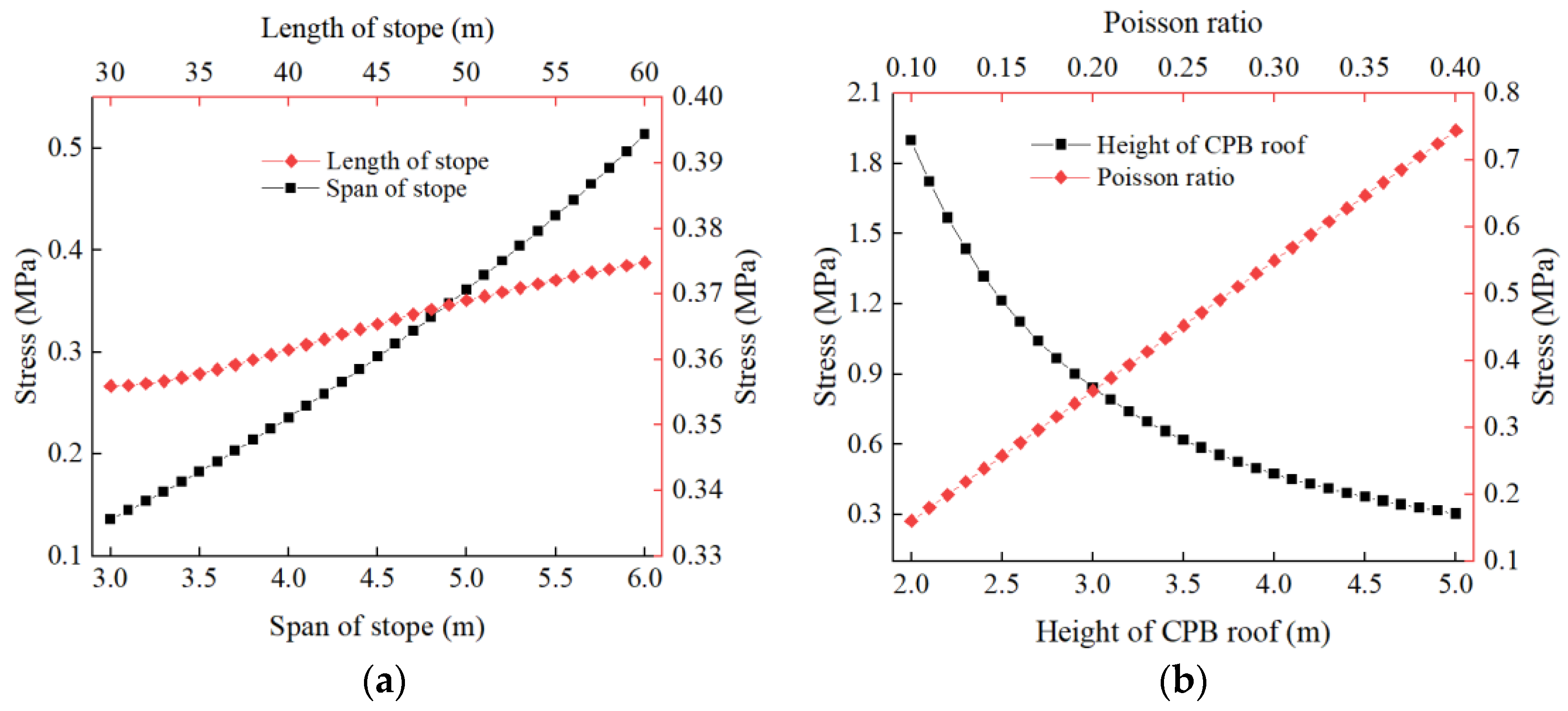
3.3.3. Analysis of Stresses on CPB Roof
3.3.4. Evaluation of the Applicability of the Model
3.3.5. Examination of the Mechanical Model of the Filling Body
4. Discussion
4.1. Engineering Application
4.2. Stability Monitoring
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Zhang, Y.; Yang, L.; Du, F.; Sai, L.; Zhang, B. Decoupling analysis of China’s mining industrial development and water usage: Based on production-based and consumption-based perspectives. J. Clean. Prod. 2022, 385, 135668. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Osanloo, M.; Azimi, Y. Evaluation of positive and negative impacts of mining on sustainable development by a semi-quantitative method. J. Clean. Prod. 2022, 366, 132955. [Google Scholar] [CrossRef]
- Nguyen, H.; Vo, D.; Bui, H.; Le, T.; Vo, B. An efficient approach for mining weighted uncertain interesting patterns. Inform. Sci. 2022, 615, 1–23. [Google Scholar] [CrossRef]
- Wang, L.; Lu, Z.; Chen, D.; Liu, Q.; Chu, P.; Shu, L.; Ullah, B.; Wen, Z. Safe strategy for coal and gas outburst prevention in deep-and-thick coal seams using a soft rock protective layer mining. Saf. Sci. 2020, 129, 104800. [Google Scholar] [CrossRef]
- Dong, L.; Sun, D.; Shu, W.; Li, X. Exploration: Safe and clean mining on Earth and asteroids. J. Clean. Prod. 2020, 257, 120899. [Google Scholar] [CrossRef]
- Jian-Ming, Z.; Zhong-Wen, M.; Jin-Hai, X.; Ji-Nan, W. Research on the Technology of Filling and Repeated Mining in Thick Coal Seam Affected by Small Mine Gob Area. Procedia Eng. 2011, 26, 1150–1156. [Google Scholar] [CrossRef] [Green Version]
- Shiqing, N.; Qian, G.; Zenghui, L. Numerical Simulation of Fluid-Solid Coupling in Surrounding Rock and Parameter Optimization for Filling Mining. Procedia Eng. 2011, 26, 1639–1647. [Google Scholar] [CrossRef] [Green Version]
- Sirait, B.; Wattimena, R.K.; Widodo, N.P. Rockburst Prediction of a Cut and Fill Mine by using Energy Balance and Induced Stress. Procedia Earth Planet. Sci. 2013, 6, 426–434. [Google Scholar] [CrossRef] [Green Version]
- Ran, J.J. Safe mining practices under wide spans in underground non-caving mines—Case studies. Int. J. Min. Sci. Technol. 2019, 29, 535–540. [Google Scholar] [CrossRef]
- Pagé, P.; Li, L.; Yang, P.; Simon, R. Numerical investigation of the stability of a base-exposed sill mat made of cemented backfill. Int. J. Rock Mech. Min. 2019, 114, 195–207. [Google Scholar] [CrossRef]
- Yang, Z. Key Technology Research on the Efficient Exploitation and Comprehensive Utilization of Resources in the Deep Jinchuan Nickel Deposit. Engineering 2017, 3, 559–566. [Google Scholar] [CrossRef]
- Porter, T.M.M. Regional tectonics, geology, magma chamber processes and mineralisation of the Jinchuan nickel-copper-PGE deposit, Gansu Province, China: A review. Geosci. Front. 2016, 7, 431–451. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Zhong, S.; Pan, P.; Shi, Y.; Guo, H.; Kou, Y. Observe the temporal evolution of deep tunnel’s 3D deformation by 3D laser scanning in the Jinchuan No. 2 Mine. Tunn. Undergr. Sp. Tech. 2020, 97, 103237. [Google Scholar] [CrossRef]
- Yan, R.; Yin, S.; Zhang, H.; Wang, L.; Chen, D. Effect of superplasticizer on the setting behaviors and mechanical properties of tailings-waste rock cemented paste backfills. Case Stud. Constr. Mater. 2023, 18, e1714. [Google Scholar] [CrossRef]
- Hughes, P.B.; Pakalnis, R.; Hitch, M.; Corey, G. Composite paste barricade performance at Goldcorp Inc. Red Lake Mine, Ontario, Canada. Int. J. Min. Reclam. Environ. 2010, 24, 138–150. [Google Scholar] [CrossRef]
- Ma, S.; Hu, J.; Qin, Y.; Ren, Q.; Yang, D. Bearing mechanism and thickness optimization of ore roof in bauxite stope. T. Nonferr. Metal. Soc. 2022, 32, 285–295. [Google Scholar] [CrossRef]
- Zhao, X.; Zeng, N.; Deng, L.; Zhu, Q.; Zhao, Y.; Yang, S. Optimization Drift Support Design Based on Engineering Geological and Geotechnical Analysis in Deep Hard-Rock Mine: A Case Study. Appl. Sci. 2022, 12, 10224. [Google Scholar] [CrossRef]
- Zhang, H.; Xue, Y.; Li, Y.; Yin, J. Study on Initial Fracture Characteristics of the Main Roof in Fully Mechanized Caving Mining of Inclined Coalbed. Sustain. -Basel 2022, 14, 13782. [Google Scholar] [CrossRef]
- Talibe Keita, A.M.; Jahanbakhshzadeh, A.; Li, L. Numerical analysis of the stability of arched sill mats made of cemented backfill. Int. J. Rock Mech. Min. 2021, 140, 104667. [Google Scholar] [CrossRef]
- Mitchell, R.J. Sill mat evaluation using centrifuge models. Min. Sci. Technol. 1991, 13, 301–313. [Google Scholar] [CrossRef]
- Sobhi, M.A.; Li, L.; Aubertin, M. Numerical investigation of earth pressure coefficient along central line of backfilled stopes. Can. Geotech. J. 2017, 54, 138–145. [Google Scholar] [CrossRef] [Green Version]
- Jahanbakhshzadeh, A.; Aubertin, M.; Li, L. A New Analytical Solution for the Stress State in Inclined Backfilled Mine Stopes. Geotech. Geol. Eng. 2017, 35, 1151–1167. [Google Scholar] [CrossRef]
- Falaknaz, N.; Aubertin, M.; Li, L. Numerical analyses of the stress state in two neighboring stopes excavated and backfilled in sequence. Int. J. Geomech. 2015, 15, 04015005. [Google Scholar] [CrossRef]
- Deng, H.; Liu, Y.; Zhang, W.; Yu, S.; Tian, G. Study on the Strength Evolution Characteristics of Cemented Tailings Backfill from the Perspective of Porosity. Minerals 2021, 11, 82. [Google Scholar] [CrossRef]
- Lv, W.; Wu, Y.; Ming, L.; Yin, J. Migration Law of the Roof of a Composited Backfilling Longwall Face in a Steeply Dipping Coal Seam. Minerals 2019, 9, 188. [Google Scholar] [CrossRef] [Green Version]
- Chang, Q.; Sun, Y.; Leng, Q.; Liu, Z.; Zhou, H.; Sun, Y. Stability Analysis of Paste Filling Roof by Cut and Fill Mining. Sustain. -Basel 2021, 13, 10899. [Google Scholar] [CrossRef]
- Sun, J. Mechanics criterion and factors affecting overburden stability in solid dense filling mining. Int. J. Min. Sci. Technol. 2017, 27, 407–413. [Google Scholar] [CrossRef]
- Zhu, H.; Han, L.; Meng, Q.; Tian, M.; Meng, L.; Zhao, Z. Determining the minimum thickness of a crown pillar and optimizing the cross-sectional size of point pillars for the safe exploitation of a subsea gold mine. Arab. J. Geosci. 2021, 14, 1275. [Google Scholar] [CrossRef]
- Xu, S.; Liang, R.; Suorineni, F.T.; Li, Y. Evaluation of the use of sublevel open stoping in the mining of moderately dipping medium-thick orebodies. Int. J. Min. Sci. Technol. 2021, 31, 333–346. [Google Scholar] [CrossRef]
- Chang, Q.; Tang, W.; Xu, Y.; Zhou, H. Research on the width of filling body in gob-side entry retaining with high-water materials. Int. J. Min. Sci. Technol. 2018, 28, 519–524. [Google Scholar] [CrossRef]
- Shi, X.; Gou, Y.; Chen, X.; Luo, J. Determination and application of the backfill thickness in the residual ore recovery of crown and sill pillar. Caikuang Yu Anquan Gongcheng Xuebao/J. Min. Saf. Eng. 2016, 33, 1080–1088. [Google Scholar]
- Wu, A.; Zhang, A.; Wang, H.; Li, G.; Rong, K. The mechanical model for the paste false roof and finite element analysis. Caikuang Yu Anquan Gongcheng Xuebao/J. Min. Saf. Eng. 2017, 34, 587–593. [Google Scholar]
- Sun, Q.; Zhang, J.; Zhou, N. Study and discussion of short- strip coal pillar recovery with cemented paste backfill. Int. J. Rock Mech. Min. 2018, 104, 147–155. [Google Scholar] [CrossRef]
- Raffaldi, M.J.; Seymour, J.B.; Richardson, J.; Zahl, E.; Board, M. Cemented Paste Backfill Geomechanics at a Narrow-Vein Underhand Cut-and-Fill Mine. Rock Mech. Rock Eng. 2019, 52, 4925–4940. [Google Scholar] [CrossRef]
- Basarir, H.; Sun, Y.; Li, G. Gateway stability analysis by global-local modeling approach. Int. J. Rock Mech. Min. 2019, 113, 31–40. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Basarir, H.; Karrech, A.; Azadi, M.R. Laboratory evaluation of shear strength properties for cement-based grouted coal mass. Arab. J. Geosci. 2019, 12, 690. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Qian, D. Stability Control for the Rheological Roadway by a Novel High-Efficiency Jet Grouting Technique in Deep Underground Coal Mines. Sustain. -Basel 2019, 11, 6494. [Google Scholar] [CrossRef] [Green Version]
- Chang, Q.; Sun, X.; Dong, X.; Shao, S. Stability analysis of cemented paste backfill false roof in highwall mining: A case study. Desalin. Water Treat. 2021, 219, 96–102. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, N.; Chang, Q.; Xu, J.; Zhang, J. Development of ensemble learning models to evaluate the strength of coal-grout materials. Int. J. Min. Sci. Technol. 2021, 31, 153–162. [Google Scholar] [CrossRef]
- Ma, F.; Liu, F.; Guo, J.; Lu, R.; Guo, H.; Kou, Y. Backfill stability analysis of steep dip mine using filling method. J. Eng. Geol. 2018, 26, 1351–1359. [Google Scholar]
- Sears, M.M.; Slaker, B.; Rashed, G.; Winfield, J. Numerical model validation and analysis of a dipping limestone pillar using FLAC3D. In 53rd U.S. Rock Mechanics/Geomechanics Symposium, Brooklyn, NY, United States, 2019; American Rock Mechanics Association (ARMA): Brooklyn, NY, USA, 2019. [Google Scholar]
- Sun, Y.; Bi, R.; Chang, Q.; Taherdangkoo, R.; Zhang, J.; Sun, J.; Huang, J.; Li, G. Stability Analysis of Roadway Groups under Multi-Mining Disturbances. Appl. Sci. 2021, 11, 7953. [Google Scholar] [CrossRef]
- Wu, K.; Shao, Z.; Qin, S.; Wei, W.; Chu, Z. A critical review on the performance of yielding supports in squeezing tunnels. Tunn. Undergr. Sp. Tech. 2021, 115, 103815. [Google Scholar] [CrossRef]
- Wu, K.; Shao, Z.; Sharifzadeh, M.; Hong, S.; Qin, S. Analytical computation of support characteristic curve for circumferential yielding lining in tunnel design. J. Rock Mech. Geotech. Eng. 2022, 14, 144–152. [Google Scholar] [CrossRef]
- He, M.; Wang, Q. Excavation compensation method and key technology for surrounding rock control. Eng. Geol. 2022, 307, 106784. [Google Scholar] [CrossRef]
- Shahinpoor, M. Exact bounds on average granular pressures in a general bin model. Appl. Math. Model. 1981, 5, 185–188. [Google Scholar] [CrossRef] [Green Version]
- Peng, M.; Peng, H. The ultimate bearing capacity of shallow strip footings using slip-line method. Soils Found. 2019, 59, 601–616. [Google Scholar] [CrossRef]
- Yang, L.; Hou, C.; Zhu, W.; Liu, X.; Yan, B.; Li, L. Monitoring the failure process of cemented paste backfill at different curing times by using a digital image correlation technique. Constr. Build. Mater. 2022, 346, 128487. [Google Scholar] [CrossRef]
- Namdar, A. The crack zone simulation of clay backfill under seismic load. Procedia Struct. Integr. 2022, 39, 57–64. [Google Scholar] [CrossRef]
- Xu, W.; Tian, M.; Li, Q. Time-dependent rheological properties and mechanical performance of fresh cemented tailings backfill containing flocculants. Miner. Eng. 2020, 145, 106064. [Google Scholar] [CrossRef]
- Yin, S.; Hou, Y.; Chen, X.; Zhang, M. Mechanical, flowing and microstructural properties of cemented sulfur tailings backfill: Effects of fiber lengths and dosage. Constr. Build. Mater. 2021, 309, 125058. [Google Scholar] [CrossRef]
- Bertocchi, E.; Mantovani, S.; Ciavarella, M. A simple method of analysis of partial slip in shrink-fitted shafts under torsion. Int. J. Mech. Sci. 2018, 142–143, 541–546. [Google Scholar] [CrossRef]
- Höller, R.; Aminbaghai, M.; Eberhardsteiner, L.; Eberhardsteiner, J.; Blab, R.; Pichler, B.; Hellmich, C. Rigorous amendment of Vlasov’s theory for thin elastic plates on elastic Winkler foundations, based on the Principle of Virtual Power. Eur. J. Mech. A/Solids 2019, 73, 449–482. [Google Scholar] [CrossRef]
- Senjanović, I.; Vladimir, N.; Tomić, M. On new first-order shear deformation plate theories. Mech. Res. Commun. 2016, 73, 31–38. [Google Scholar] [CrossRef]



| Type | Appearance | Model Number | Measurement Range | Resolution | Precision/%FS |
|---|---|---|---|---|---|
| Strain gauge |  | YHZ-0130 | ±1500 με | 1 με | ±0.5 |
| Pressure sensor |  | YHZ-0701 | 1 MPa | 0.1 KPa | ±0.5 |
| Stope | Size/m (Length × Width × Height) | Measurement Solutions | |||
|---|---|---|---|---|---|
| Type | Buried Depth/m | Type | Buried Depth/m | ||
| 48# | 35 × 5.0 × 4.5 | Load | 1.0/2.0/3.0 | Stress/Strain | 0.5/1.0/2.0 |
| 40# | 40 × 5.0 × 4.5 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Han, B.; Zhang, B.; Li, K. Force Analysis and Strength Determination of the Cemented Paste Backfill Roof in Underhand Drift Cut-and-Fill Stopping. Appl. Sci. 2023, 13, 855. https://doi.org/10.3390/app13020855
Hu Y, Han B, Zhang B, Li K. Force Analysis and Strength Determination of the Cemented Paste Backfill Roof in Underhand Drift Cut-and-Fill Stopping. Applied Sciences. 2023; 13(2):855. https://doi.org/10.3390/app13020855
Chicago/Turabian StyleHu, Yafei, Bin Han, Bo Zhang, and Keqing Li. 2023. "Force Analysis and Strength Determination of the Cemented Paste Backfill Roof in Underhand Drift Cut-and-Fill Stopping" Applied Sciences 13, no. 2: 855. https://doi.org/10.3390/app13020855
APA StyleHu, Y., Han, B., Zhang, B., & Li, K. (2023). Force Analysis and Strength Determination of the Cemented Paste Backfill Roof in Underhand Drift Cut-and-Fill Stopping. Applied Sciences, 13(2), 855. https://doi.org/10.3390/app13020855





