Research on the Dynamic Characteristics Analysis and Power Control Method of Heat Pipe Reactors

Abstract

A heat pipe reactor (HPR) is a kind of modular small reactor with broad application prospects, and its dynamic characteristics and nuclear power control are essential to the safe and stable operation of nuclear power plants. Taking the MegaPower HPR as an example, the dynamic characteristics of the HPR are analyzed, and its power control method is designed in this paper. Based on the lumped parameter idea, the equivalent processing of the structure of the HPR core is carried out, and the main parameters of the heat pipe heat exchanger are designed at first. A lightweight dynamic model of the HPR is established using a thermal resistance network, and the accuracy of the model is verified using the solution of the model under the steady-state full power condition. Then, the dynamic characteristics of the HPR without a controller are analyzed respectively with the disturbance reactivity and mass flow rate, indicating strong self-stability and self-regulation of the HPR. Finally, a reinforcement learning (RL) controller based on the twin delayed deep deterministic policy gradient (TD3) algorithm is designed for the HPR power control, and it is adjusted through appropriately setting states, network structures, reward functions, etc. To verify the performance of the controller, a step response simulation ranging from 100%FP to 90%FP, a compound conditions simulation, and a large load change simulation are carried out, respectively. The results show that the RL controller can find the optimal control strategy through training. Meanwhile, it significantly improves the dynamic and steady-state performance of nuclear power compared with uncontrolled case and PID controller case, and it has the ability of power control under all operating conditions.

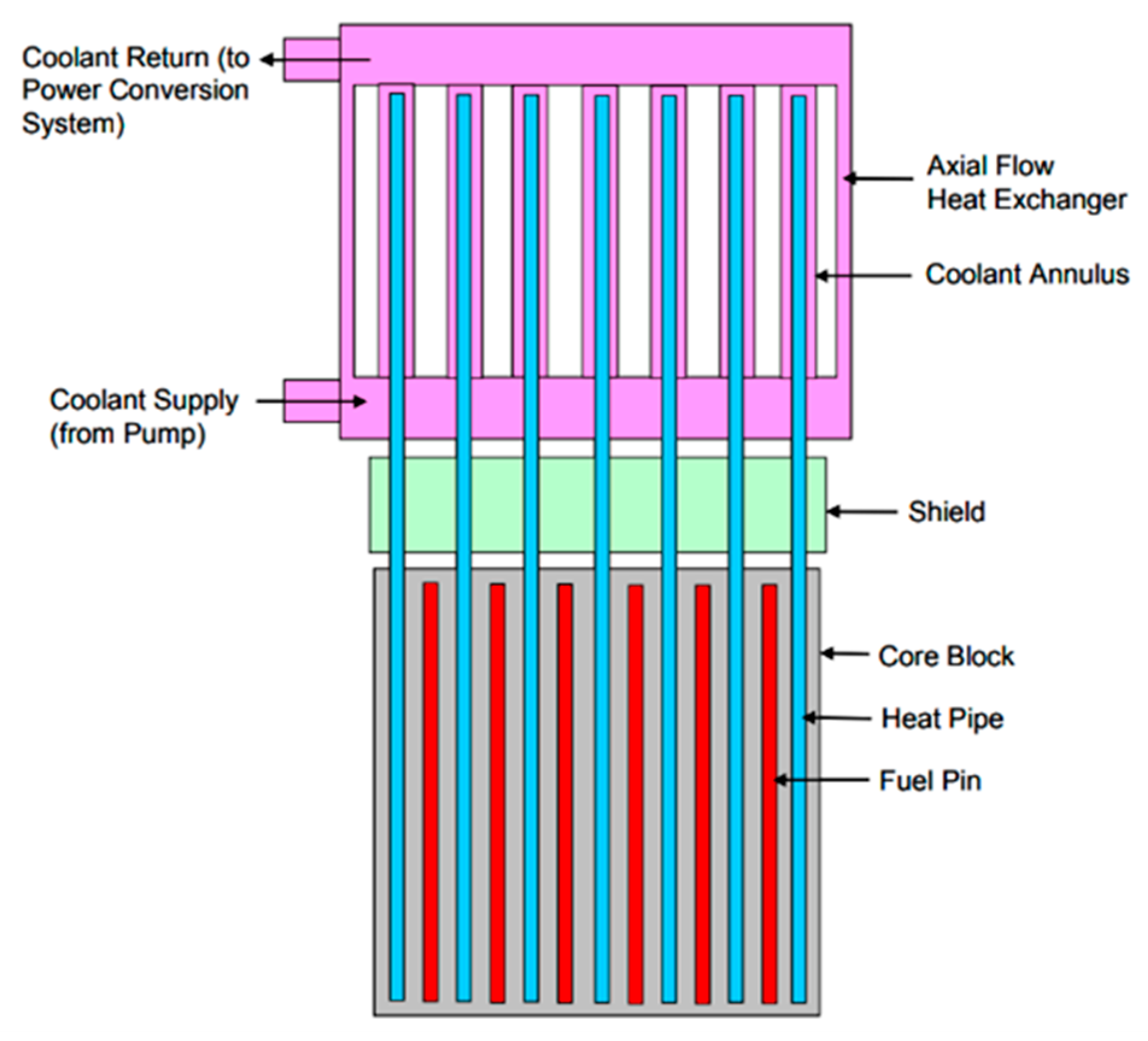
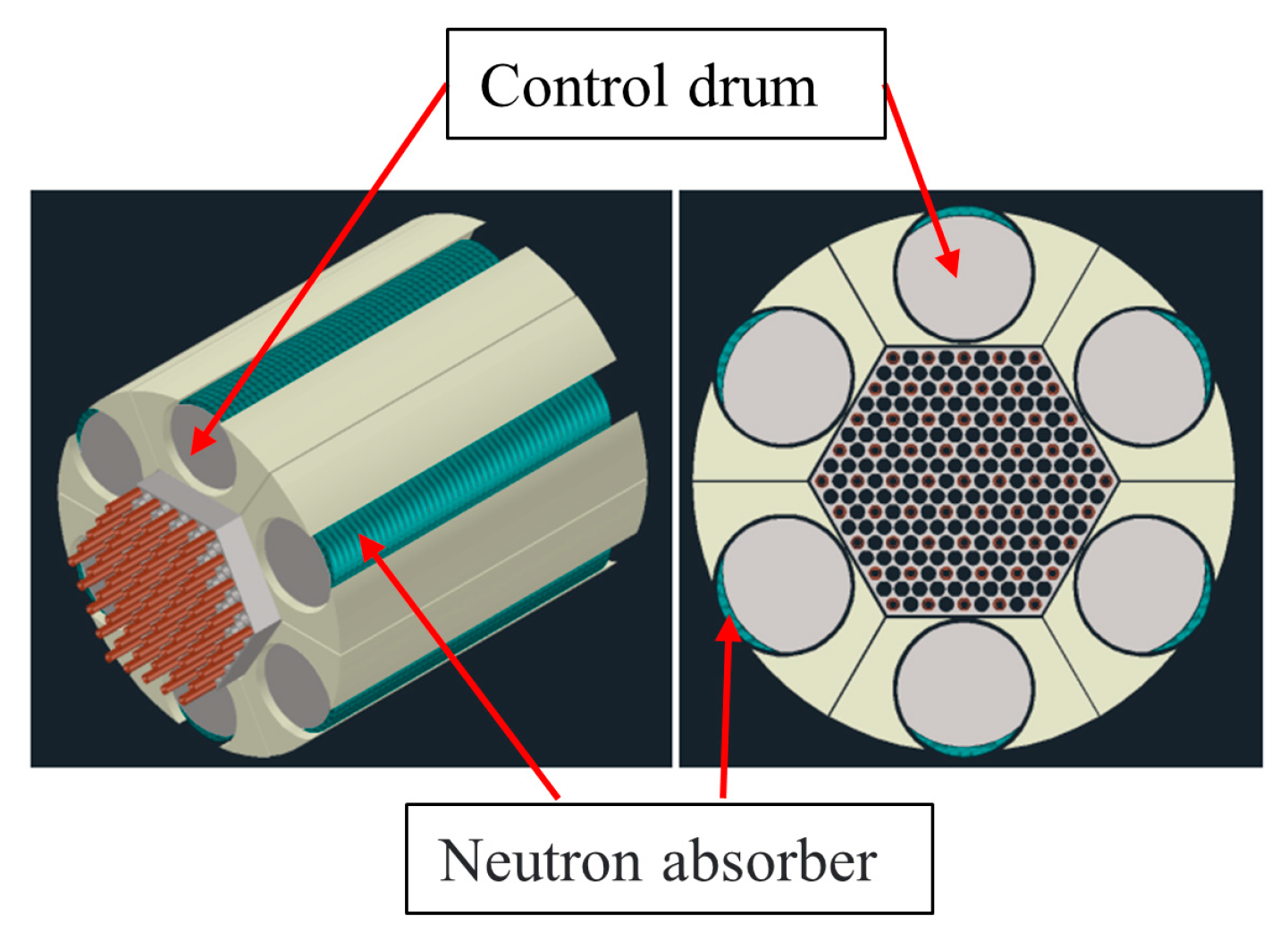
1. Introduction

According to the International Atomic Energy Agency (IAEA), micro nuclear reactors are classified as a type of small modular reactor (SMR) that possess an electrical power output of less than 10 MW [1]. One of the modern reactors in SMR systems is the HPR, which has a solid core and utilizes heat pipes to transfer heat from the core. Thanks to the solid-state property of the reactor and the use of heat pipes, the HPR possesses several advantageous features, including inherent safety, compactness, simple system architecture, and strong transportability. Furthermore, HPRs exhibit broad application prospects in low-power, unmanned applications, such as remote islands and underwater vehicles [2].

Since the 1960s, space exploration has made significant contributions to the advancement of space reactors, including HPRs, liquid metal reactors, and gas-cooled reactors. In 1968, a space power system was conceptualized by C. A. Heath and colleagues, which utilized a heat pipe to establish a connection between the core and the thermionic diodes [3]. The proposed design concept effectively mitigated the adverse effects of high neutron flux and core expansion on the performance of thermionic diodes through utilizing heat pipes to transfer heat and isolate them from the harsh reactor environment. Anderson et al. conducted a study in the same year on a space reactor power system that utilized heat pipes for heat transfer, out-of-pile thermionic diodes for electricity generation, and dual central absorber rods for reactor power control. This resulted in a reduction in the size and weight of the reactor system compared to the conventional space reactor that employs thermionic diodes within the reactor at the same power capacity [4]. A study conducted by the Los Alamos National Laboratory (LANL) in the United States involved the comparison of three distinct designs of heat pipe cooled reactors. The electrical power output of these reactors ranged from 1 to 500 kW, with core temperatures up to 1200–1700 K [5]. According to the calculation results and analysis, it was determined that none of the three HPRs surpassed the safety thresholds for any of the operation parameters. The authors of the study noted that augmenting the power of the HPR would necessitate an increase in the quantity of heat pipes, which would result in the amplification of system weight, size, and intricacy.

Since the 21st century, the development of materials, high-temperature heat pipes, and other key technologies have once again promoted the development of HPRs. In 2000, based on LANL’s heat-pipe power system (HPS) project, Poston et al. proposed a heat-pipe cooled nuclear reactor power system [6] for a Mars exploration mission and gradually developed it into the heat-pipe-operated mars exploration reactor (HOMER) [7] in subsequent studies. After that, many institutions put forward different HPR designs for the different application scenarios and requirements: for example, SAIRS [8] and HP-STMCs [9] proposed by NMU, MSR-A [10] proposed by MIT, Kilopower [11] proposed by LANL, eVinci [12] proposed by Westinghouse, etc. In 2012, LANL and NASA’s Glenn Research Center (GRC) conducted the first nuclear test in the history of the HPR, in which the heat pipe exported heat from the core and served as a heat source for a Stirling engine to generate kilowatts of electrical power [11]. LANL and the GRC then continued to refine the Kilopower project, culminating in the development of the KRUSTY (kilowatt reactor using Stirling technology) [13,14,15]. After almost six decades of development, the HPR has established a comprehensive design plan and technical route and has achieved significant advancements in numerous pivotal technologies. The HPR also faces several obstacles, including the manufacturing process of heat pipes that can withstand high temperatures, the use of monolith and cladding materials that are resistant to high temperatures, effective thermoelectric conversion technology, and independent and reliable control methods.

One of the challenges encountered in the modeling of the HPR is related to heat transfer models for high-temperature heat pipes. The modeling methods are divided into the thermal resistance network model method and the two-phase flow model method. And the thermal resistance network modeling method is a fast and approximate method for calculating transient and steady-state heat transfer in heat pipes with low computational complexity [16]. Zuo and Faghri proposed the first practical thermal resistance network for analyzing the transient processes in heat pipes in 1998. They abstracted the sections of the heat pipe into thermal resistances, while assuming that the heat transfer in the evaporation and condensation sections only occurs in the radial direction and that heat transfer in the adiabatic section only occurs in the axial direction [17]. This method adopts the idea of lumped parameters, which greatly simplifies the heat pipe model and reduces the heat transfer equation of the heat pipe to a set of non-homogeneous linear equations. Guo et al. established the super thermal conductivity model (STCM) based on the thermal resistance network model, which can not only calculate the heat transfer process of the heat pipe but also calculate the flow rates of liquid and gas working fluids [18]. Through introducing the calculation of heat transfer limits, the STCM can analyze the safety margin of the heat pipe. Jibin et al. equate the solid region and the liquid region as different thermal resistive, thermal capacitive, or thermal inductive elements, thus establishing a lumped parameter network model of the wick-type heat pipe. The simulation results show that the total thermal resistance of the heat pipe decreases with increasing input heat flux, but there is a lower limit for the total thermal resistance. And the total thermal resistance of the heat pipe is closely related to the thickness and porosity of the wick and the type of working fluid of the heat pipe [19].

During the process of heating up from a cold to a hot state in solid-state reactors such as HPRs, the density of the material in the reactor core increases as its temperature increases, and the distance between the molecules or atoms of the material increases, which results in an increase in the leakage rate of the neutrons. So, the thermal expansion effect of the material causes changes in the HPR’s reactivity. Traditional nuclear–thermal analysis is no longer sufficient to meet the requirements of HPR simulation analysis; therefore, some high-fidelity simulation methods are adopted to study the transient phenomena of HPRs nowadays. For example, Wei Xiao et al. built a high-fidelity 3D neutronics–thermal elasticity multi-physics coupling model of the HPR KRUSTY using the open-source software OpenMC, Nektar++, and SfePy based on the Monte Carlo and finite element methods [20]. Their calculation results showed that the reactivity change due to thermal expansion accounted for 89.4% of the total reactivity feedback, and even if a limited number of heat pipe failure accidents occurred, the remaining heat pipes could still provide sufficient thermal conductivity to ensure the safety of the core. GUO et al. proposed a coupled calculation method called “thermalMechanicsFoam” for solving transient multi-physics fields in HPRs which uses Reactor Monte Carlo (RMC) to calculate the power distribution within the core and cooperates with OpenFOAM to calculate core temperature and expansion [21]. Tao Li et al. established a transient analysis method combining three-dimensional core heat transfer with two-dimensional heat pipe heat transfer [22]. In the study of the steady-state operating conditions of the HPR, it showed that the isothermal properties of the heat pipe improved the axial and radial heat transfer in the reactor. The research on the start-up condition found that the isothermal characteristics of the heat pipe caused the reverse heat transfer between the heat pipe and the core structure, which could flatten the temperature distribution in the reactor core.

For the structure, design, and safety analysis of HPRs, the high-fidelity simulation method of the neutronics–thermal elasticity multi-physics coupling model mentioned above is necessary. However, its cost is the complexity of the calculation process and a high computational workload. When studying control methods for the HPR, the model not only needs to accurately reflect changes in parameters during the dynamic process but also requires a small amount of calculation to adapt to the rapid simulation verification of the control method.

In the aspect of reactor control, ensuring energy balance is one of the most important control objectives of nuclear reactor installation. The proportion–integration-–differentiation (PID) algorithm has become the most widely used controller due to its simple principle and easy implementation. However, before the PID controller is put into use, it must go through a tedious parameter-setting process, and once the operating state of the control object changes significantly, a PID controller with the same parameters may not achieve the same control effect as before. Therefore, optimization algorithms such as the genetic algorithm and particle swarm optimization algorithm [23,24] and intelligent algorithms such as fuzzy theory [25] are often used to improve the traditional PID control algorithm to achieve better control effects.

In addition, control methods based on deep reinforcement learning (DRL) are also applied to reactor control. Chen et al. used the deep deterministic policy gradient (DDPG) strategy to train the RL controller for the power control of a boiling water reactor [26]. In the simulation of continuously introducing disturbances, the reactor power has obvious oscillation under the control of the method, but after using the RL method, the reactor system can overcome various disturbances and ensure that the power regulation process is rapid and stable. In fact, the control methods based on reinforcement learning regard the reactor system as a “black box”, and the agent is trained in the virtual environment and learns how to obtain higher rewards driven by specific learning strategies such as deep Q-network (DQN), DDPG, and TD3 [27].

In this work, in response to the requirements of speed and accuracy of the simulation model for research on HPR power control methods, a lightweight dynamic model of the HPR from core to heat pipe exchanger is established. Taking the MegaPower HPR as example, the arrangement of the components in the core is summarized, and the lumped parameter method is used to make the single heat-generating component of the core equivalent to a cylindrical shape. Meanwhile, the simplified thermal resistance network method is used to analyze the heat transfer process of the heat pipe, and the core parameters of the heat pipe heat exchanger are designed. Secondly, the dynamic characteristics of HPRs with reactivity disturbance and flow disturbance are analyzed separately. Finally, the TD3 algorithm, with excellent performance in continuous control, is selected as the core algorithm of HPR power control, and the application of the reinforcement learning control method in HPR power regulation is explored.

2. Dynamic Modelling of HPR

To facilitate the study of power control methods for HPRs, a lightweight dynamic model of an HPR is first required. In this paper, the “MegaPower” HPR designed by Los Alamos National Laboratory (LANL) is taken as an example. The “MegaPower” HPR is a kind of fast reactor, and its fuel enrichment is as high as 20%. More than a thousand heat pipes settled in the core are used to effectively export the heat, and the supercritical carbon dioxide (SCO₂) Brayton cycle is used to realize thermoelectric conversion. Its structure diagram is shown in Figure 1.

2.1. Neutron Dynamics Model

To design the reactor power control method, it is necessary to focus on the total power of the reactor only. Therefore, the point reactor neutron dynamics model is used to describe the relationship between nuclear power and reactivity. The equation of a point reactor with six groups of delayed neutrons is shown in Equation (1):

$$\left\{\begin{array}{l}\frac{d{n}_r}{dt}=\frac{\rho -\beta }{l}{n}_r+{\displaystyle \sum _{i=1}^6{\lambda }_i{c}_{i,r}}\\ \frac{d{c}_{i,r}}{dt}=\frac{\beta }{l}{n}_r-{\lambda }_i{c}_{i,r}\end{array}\right.$$

(1)

where $n_0$ is the initial neutron density at steady state; $n_r=n/n_0$ is the ratio of neutron density to the initial neutron density, which can represent the relative nuclear power; $c_{i,r}=$ is the ratio of ith group precursor density to $n_0$; ${\beta }_i$ is the fraction of ith group delayed fission neutrons; ${\lambda }_i$ is the effective ith group precursor radioactive decay constant; $\beta$ is the total fraction of delayed fission neutrons; and $l$ is the effective prompt neutron lifetime.

Reactivity feedback in the HPR is mainly caused by the Doppler and expansion effects of the fuel and monolith. ${\alpha }_f$ and ${\alpha }_m$ are the total feedback coefficients for the fuel and monolith, respectively, which both incorporate the Doppler and expansion effects, and are derived from the literature [28]. The reactivity feedback equation is shown in Equation (2).

$$\left\{\begin{array}{l}\rho ={\rho }_r+{\rho }_f+{\rho }_m\\ {\rho }_f={\alpha }_f\cdot \Delta T_f\\ {\rho }_m={\alpha }_m\cdot \Delta T_m\end{array}\right.$$

(2)

where ${\rho }_r$ is the reactivity of the external input, ${\rho }_f$ is the reactivity caused by fuel temperature change, and ${\rho }_m$ is the reactivity caused by monolith temperature change. ${∆T}_f$ and ${∆T}_m$ are the deviation in the fuel temperature and the monolith temperature relative to the initial temperature, respectively.

2.2. Equivalent Thermal Conductivity Model of Core

The arrangement of heat pipes, the monolith, and fuel rods in the MegaPower core is shown in Figure 2. Excluding the edge of the core, each heat pipe is surrounded by six fuel elements, and each fuel element is surrounded by three fuel rods and three heat pipes. In Figure 3, each heat pipe and six fuel elements are regarded as a hexagonal assembly. Each fuel element in the hexagonal assembly gives 1/3 of its own heat to the central heat pipe, so the central heat pipe corresponds to two fuel elements in view of heat transfer ($1/3\times 6=2$). To simplify the heat transfer analysis, a single hexagonal component can be equivalent to a cylinder component [29], as shown in Figure 3.

In the cylindrical thermal conduction model, the equivalent fuel element on the periphery is equated from two actual fuel elements to keep the thermal power constant. The monolith is equivalent to cylindroid from an irregular shape, but its own volume and heat transfer area with heat pipe remain unchanged. The thickness of the helium gap needs to be changed before and after equivalence as both contact areas of the monolith and the fuel to the helium gap are changed after equivalence. Since the contact area between the air gap and other materials changes after equivalence, the principle of helium gap equivalence is to keep the thermal conductivity resistance unchanged, so the thickness of the helium gap needs to be changed. The heat pipe is in the center of the assembly and does not change after equivalence, but it is worth noting that the monolith also acts as the wall of the evaporation section of the heat pipe in the “MegaPower” reactor design.

2.3. Control Drums Model

The control drums are arranged around the core as in Figure 2. A layer of neutron-absorbing material is arranged at an angle within the control drum, and the core reactivity is controlled through rotating the drums to different angles to vary the neutron absorption rate. If ${\rho }_D$ is the integral value of the control drum, and $\theta$ is the angle of rotation of the control drums ($0\le \theta \le {180}^{\circ }$), then the relationship between them can be expressed by Equation (3) [28].

$${\rho }_D=0.03581-\frac{0.09647}{1+\exp (\frac{\theta -94.8083}{27.09451})}$$

(3)

2.4. Design of Heat Exchanger

A heat pipe heat exchanger (HE) is similar to a shell and tube heat exchanger, and the cooling fluid flows through the condensing section of the heat pipe in the circular flow channel, as shown in Figure 4. The MegaPower does not give specific design parameters for the heat pipe heat exchanger, so this paper requires a combination of existing design parameters and reasonable assumptions to determine the core parameters of the heat exchanger. For this heat exchanger, the most important parameters are the SCO₂ flow rate and the flow channel width, which are subject to certain constraints.

First, the unit used to express the flow rate of the cooling mass $\dot{m}$ is $\mathrm{k}\mathrm{g}/\mathrm{s}$. The HE should be able to export the heat from the core, and the heat generated by the core under steady-state initial conditions $P_{full}$ should be equal to the heat removed by the cooling mass:

$$P_{full}=\dot{m}(h_{out}-h_{in})$$

(4)

where $h_{out}$ and $h_{in}$ are the specific enthalpy of SCO₂ at the outlet and inlet, respectively.

Although the MegaPower project has described the inlet and outlet temperatures, inlet pressure, and overall pressure drop of the heat exchanger SCO₂, there is no specific analysis of the feasibility [2]. In contrast, the SCO₂ Brayton cycle conversion system of Sandia National Laboratories (SNL) [30] has passed experimental verification after years of development, so the inlet and outlet parameters of the SNL heat exchanger are used in this paper as the boundary conditions for the heat exchanger model at a steady state under full power. The inlet temperature $T_{in}=698 \mathrm{K}$, the outlet temperature $T_{out}=810 \mathrm{K}$, the inlet pressure $P_{in}=13612 \mathrm{k}\mathrm{P}\mathrm{a}$, and the heat exchanger pressure drop $DP=113 \mathrm{k}\mathrm{P}\mathrm{a}$.

Secondly, determine the width of the flow channel. It is mainly restricted by two aspects: one is the constraint of the size of the heat pipes in the core, and the other is the constraint of the wall temperature of the condenser section of the heat pipes. The center distance between two adjacent flow channels is consistent with the center distance between adjacent heat pipes in the reactor core. There is the following relationship among the center distance between two adjacent flow channels $\delta$, the radius of heat pipes $r_{hp}$, and the width of flow channel $d$:

$$2d<\delta -2r_{hp}$$

(5)

When analyzing the thermal safety characteristics of MegaPower HPR in references [31,32], the cooling fluid is air. The use of different cooling fluids will change the convective heat transfer conditions on the surface of the condensation section of the heat pipe, but it will not directly affect the heat transfer in the core. In order to keep the full power steady state temperatures of the fuel, monolith, and heat pipe consistent with the references, it is necessary to keep the wall temperature of the condensation section of the heat pipes unchanged before and after switching to cooling medium, that is, Equation (6):

$$P_{full}=\frac{T_{c,w}-T_a}{R_{ref}}$$

(6)

where $T_{c,w}$ is the wall temperature of the condensing section of the heat pipe. $T_a$ is the average temperature of the cooling fluid, which is the arithmetic average of the inlet and outlet temperatures. The reference thermal resistance $R_{ref}$ is the convective heat transfer resistance that satisfies the condition of keeping the wall temperature of the condensing section of the heat pipe constant, calculated from the literature [32].

According to the above two constraints, an iterative calculation method can be designed to determine the parameters of heat exchanger, as shown in Figure 5.

During the circulation, the Reynolds number $Re$ is determined by the mass flow rate $\dot{m}$, hydraulic diameter $D_h$, flow path cross-sectional area $A$, and the dynamic viscosity $\mu$.

$$Re=\frac{\dot{m}{D}_h}{A\mu }$$

(7)

The hydraulic diameter $D_h$ is four times the ratio of the cross-sectional area of the flow channel to the wetted perimeter, and the hydraulic diameter is equal to twice the width of the flow channel in a circular annular channel: $D_h=2d$.

The Nusselt number and friction factor are calculated using the Gnielinski equation and Filonenko equation, respectively, and their application ranges are $2300<Re<5\times {10}^6,0.2<Pr<2000$.

$$\left\{\begin{array}{l}Nu=\frac{{(f/8)}^{0.5}(Re-1000)Pr}{1+12.7(P{r}^{2/3}-1)}\\ f={(1.82{\log }_{10}Re-1.64)}^{-2}\end{array}\right.$$

(8)

The convective heat transfer coefficient between the cooling fluid and the surface of the heat pipe wall $h_{\mathrm{c}}$ and the convective heat transfer thermal resistance $R_c$ are calculated as follows:

$$\left\{\begin{array}{l}{h}_c=\frac{Nu\cdot \lambda }{D_h}\\ R_c=\frac{1}{h_c{A}_c}\end{array}\right.$$

(9)

where $\lambda$ is the thermal conductivity of the cooling fluid, and $A_c$ is the heat transfer area between the cooling fluid and the condensing section of the heat pipe.

2.5. Thermal Resistance Network for HPR

The thermal resistance network for the heat transfer process in the core of the HPR is shown in Figure 6. The evaporation section of the heat pipe in the core does not have a heat pipe wall, and the monolith is used as the nominal heat pipe wall for the evaporation section. The helium gap between the fuel and the monolith is very thin, so its heat capacity is neglected and only the thermal conductivity is calculated.

In Figure 6, $P_f$ is the heat generated by equivalent fuel in W, $R_g$ is the thermal resistance of the air gap, $R_m$ is the thermal resistance of the matrix, $R_1$ is the radial thermal resistance of the suction core in the evaporation section, $R_2$ is the radial thermal resistance of the suction core in the condensation section, $R_3$ is the radial thermal resistance of the heat tube wall in the condensation section, $R_c$ is the thermal resistance of the convective heat transfer between the coolant and the heat tube wall in the condensation section, and the unit of the thermal resistance is $\mathrm{K}/\mathrm{W}$. $T_a$ is the average temperature of SCO₂ in the cooling medium in K.

The general form of heat transfer equations of fuel and each thermal resistance is shown in Equation (10).

$$\begin{array}{l}{(mc)}_f\frac{d{T}_f}{\hspace{0.33em}dt}=P_f-P_g\\ {(mc)}_m\frac{d{T}_m}{\hspace{0.33em}dt}=P_{m,in}-P_{m,out}\\ {(mc)}_i\frac{d{T}_i}{\hspace{0.33em}dt}=P_{i,in}-P_{i,out},i=1,2,3\\ {(mc)}_c\frac{d{T}_a}{\hspace{0.33em}dt}=P_{c,in}-P_{c,out}\end{array}$$

(10)

where ${\left(mc\right)}_f$ is the heat capacity of the equivalent fuel, ${\left(mc\right)}_m$ is the heat capacity of the equivalent monolith, ${\left(mc\right)}_i$ is the heat capacity of each part of the heat pipe, and ${\left(mc\right)}_c$ is the heat capacity of SCO₂ in a single channel, both in units of $J/K$. The thermal calculations for the fuel, monolith, heat pipe, and cooling fluid are based on the collective parameter method. The fuel temperature is $T_f$, the monolith temperature is $T_m$, the temperature of each part of the heat pipe is $T_i$, and their units are all $K$. $P_f$ is the heat generated by equivalent fuel, ${ P}_g$ is the heat input to the air gap. $P_{m,in}$ and $P_{m,out}$ are the heat input to and output from the monolith, respectively. $P_{i,in}$ and $P_{i,out}$ are the heat input to and output from various parts of the heat pipe, respectively. $P_{c,in}$ and $P_{c,out}$ are the heat input to SCO₂ and the heat carried away by SCO_2, respectively, and the unit of the heat is $W$.

Based on the theorems related to heat transfer, the input and output thermal power is calculated as in Equation (11).

$$\begin{array}{c}{P}_f=P_{full}\cdot n_r\\ P_g=\frac{T_f-T_{m,1}}{\hspace{0.33em}{R}_g}=P_{m,1}=\frac{T_{m,1}-T_m}{\hspace{0.33em}{R}_m/2}=\frac{T_f-T_m}{\hspace{0.33em}{R}_g+R_m/2}\\ P_{m,2}=\frac{T_m-T_{m,2}}{\hspace{0.33em}{R}_m/2}\\ P_{i,1}=\frac{T_{i,1}-T_i}{\hspace{0.33em}{R}_i/2},P_{i,2}=\frac{T_i-T_{i,2}}{\hspace{0.33em}{R}_i/2},i=1,2,3\\ P_{c,in}=\frac{T_3-T_a}{\hspace{0.33em}{R}_3/2+R_{c{o}_2}},P_{c,out}=\dot{m}{c}_p(T_{out}-T_{in})\end{array}$$

(11)

where $P_0$ is the nuclear power at the initial steady state, and $c_p$ is the specific heat capacity of the coolant at a constant pressure. In the thermal resistance network, in order to calculate the input and output heat for the monolith and each part of heat pipe, the front-end temperatures of the monolith and heat pipe thermal resistance in Figure 5 are defined as $T_{m,1}$ and $T_{i,1}$ and the back-end temperatures are defined as $T_{m,2}$ and $T_{i,2}$, respectively; $i$ refers to thermal resistances 1 to 3 in Figure 5.

The heat transfer equation for the HPR thermal resistance network model is obtained through substituting Equation (11) into Equation (10) and is shown in Equation (12).

$$\begin{array}{ll}\frac{d{T}_f}{\hspace{0.33em}dt}& =\frac{1}{{(mc)}_f}\left[P_{full}\cdot n_r-\frac{2}{\hspace{0.33em}2R_g+R_m}{T}_f+\frac{2}{\hspace{0.33em}2R_g+R_m}{T}_m\right]\\ \frac{d{T}_m}{\hspace{0.33em}dt}& =\frac{1}{{(mc)}_m}\left[\begin{array}{l}\frac{2}{\hspace{0.33em}2R_g+R_m}{T}_f+\\ \frac{4R_g({\xi }_{m1}-1)+2R_m({\xi }_{m1}-2)}{\hspace{0.33em}(2R_g+R_m)R_m}{T}_m+\frac{2{\xi }_{1m}}{\hspace{0.33em}{R}_m}{T}_1\end{array}\right]\\ \frac{d{T}_1}{\hspace{0.33em}dt}& =\frac{2}{{(mc)}_1{R}_1}\left[{\xi }_{m1}{T}_m+({\xi }_{1m}+{\xi }_{12}-2)T_1+{\xi }_{21}{T}_2\right]\\ \frac{d{T}_2}{\hspace{0.33em}dt}& =\frac{2}{{(mc)}_2{R}_2}\left[{\xi }_{12}{T}_1+({\xi }_{21}+{\xi }_{23}-2)T_2+{\xi }_{32}{T}_3\right]\\ \frac{d{T}_3}{\hspace{0.33em}dt}& =\frac{2}{{(mc)}_3{R}_3}\left[{\xi }_{23}{T}_2+({\xi }_{32}+{\xi }_{3a}-2)T_3+{\xi }_{a3}{T}_a\right]\\ \frac{d{T}_a}{\hspace{0.33em}dt}& =\frac{1}{{(mc)}_c}[\frac{2}{R_3+2R_c}{T}_3-(\frac{2}{R_3+2R_c}+2\dot{m}{c}_p)T_a+2\dot{m}{c}_p{T}_{in}]\end{array}$$

(12)

where the constants are calculated as follows:

$$\left\{\begin{array}{l}{\xi }_{m1}=\frac{1/R_m}{1/R_m+1/R_1},{\xi }_{1m}=\frac{1/R_1}{1/R_1+1/R_m}\\ {\xi }_{ij}=\frac{1/R_i}{1/R_i+1/R_j},{\xi }_{ji}=\frac{1/R_j}{1/R_i+1/R_j}\\ {\xi }_{3c}=\frac{2/R_3}{2/R_3+1/R_c},{\xi }_{c3}=\frac{1/R_c}{2/R_3+1/R_c}\end{array}\right.$$

(13)

2.6. Model Validation

According to the heat transfer Equation (12), the solution program is established in MATLAB. The initial condition of the program is the steady-state full power condition. And the comparison between the model solution values and the reference values is shown in

Table 1. Comparison between model solution values and reference values (unit: K).

Temperature	Model Solution Values	Reference Temperature [31]
$T_f$	993	1026
$T_m$	984	969
Average temperature of the heat pipe	977	950

. As can be seen from Table 1, although the temperature of each part solved in the model has deviation from the reference value, the error is small and can be acceptable as a lumped parameter model. This result also verifies the effectiveness of the model.

3. Analysis of Dynamic Characteristics of HPR

The Simulink model for the HPR model in this paper is shown in Figure 7. Under the steady-state full power initial condition and the uncontrolled condition, reactivity disturbance and SCO₂ mass flow disturbance were introduced to observe and analyze the response characteristics of the relative power, fuel temperature, monolith temperature, and SCO₂ heat exchanger outlet temperature.

3.1. The Disturbance of Reactivity

At $t=100$ s, a reactivity step disturbance of −10 PCM is introduced to obtain the relative power and temperature response of the reactor. The response curves of the HPR under the reactivity disturbance are shown in Figure 8.

As can be seen from Figure 8, within about 100 s after the introduction of negative reactivity, the reactor power decreases rapidly and the heat generated by the fuel elements decreases simultaneously, causing the fuel and monolith temperatures to decrease fast as well. The decrease in fuel and monolith temperature introduces positive reactivity, which makes the decreasing trend in reactor power slow down gradually. At the same time, the energy output to SCO₂ decreases, making its outlet temperature lower and taking away less heat. After the fuel and monolith temperatures drop to 986 K and 977 K, respectively, the reactivity fed back to the core from the fuel and monolith is sufficient to compensate for the introduced reactivity disturbance, and then the reactor power gradually picks up. After a small oscillation, the reactor power, fuel temperature, monolith temperature, and SCO₂ heat exchanger outlet temperature all re-stabilize at a new level, and the system gradually enters a new steady state after about 1000 s. The new steady state values of nuclear power and each temperature have decreased compared to the initial state.

3.2. The Disturbance of SCO₂ Mass Flow Rate

At $t=100s$, the SCO₂ mass flow rate in the heat exchanger is reduced by a step of 5%. The response curves of the HPR under this disturbance are shown in Figure 9.

As indicated by Equation (4), reducing the SCO₂ mass flow rate leads to a decreased capacity for heat transfer from the reactor, resulting in the heat transferred by the heat pipe to SCO₂ being higher than the heat taken away by SCO₂. Consequently, the heat exchanger outlet temperature of SCO₂ is initially elevated. During the first 100 s, the fuel and monolith are gradually increased because the heat production by the core is higher than the heat that SCO₂ can take away, and the negative reactivity resulting from its negative feedback effect causes the core power to gradually decrease. Subsequently, the decrease in reactor power causes the fuel and monolith to transfer more heat outward than they receive, leading to their temperatures decreasing. But the fuel and monolith temperatures are still higher than their initial temperatures during 200–330 s, which means that they still introduce negative reactivity into the core due to the negative feedback effect, resulting in a continuous decrease in reactor power. As the temperatures of the fuel and monolith fall below their initial values, the temperature feedback effect causes a positive reactivity to be introduced into the core, leading to a subsequent increase in reactor power. Then, the system gradually enters a new steady state, and all parameters are changed from the initial state.

In summary, the HPR can overcome the impact of the above two typical disturbances on its own and finally reach the new steady state, indicating that it has good self-stability and self-regulation. Although the HPR can reach the new stable state only relying on the reactivity feedback of fuel and monolith under the uncontrolled condition, the regulation time is too long, and the parameter dynamics change greatly under various disturbances. After stabilization, all parameters vary from the initial state, which makes it difficult to meet the requirements for HPR operation. For example, under reactivity disturbance, the nuclear power of the HPR varies greatly, and the power deviates from the power set point. Therefore, an automatic controller needs to be designed to suppress changes in parameters and shorten the regulation time during the dynamic process.

4. Research on Power Control Method of HPR

The current control method for practical application of reactor power control is mainly PID control. However, tuning the parameters of the PID controller is a tedious procedure and depends on the experience of the designer. Furthermore, the parameter adjustment of the PID controller is generally performed for full power conditions, which can meet the requirements for the power control of large-size nuclear power plants that mainly operate stably at full power conditions. However, for the HPR, which requires the ability to track load changes, it is difficult to obtain the same control performance under different power levels using a set of fixed parameters for the PID controller. Therefore, it is necessary to study an intelligent optimal control algorithm applicable to the HPR.

RL control is a form of direct adaptive optimization control [33], and the training is a process of searching for optimal control strategies under the control rule constraints and the guidance of optimization objectives, which does not require priori knowledge. RL based control can adapt to the impact of variations in the characteristics of the control object and the associated uncertainties, thereby facilitating the attainment of the optimization objective of the control system. The TD3 algorithm is a kind of reinforcement learning algorithm with good convergence and can be used for the continuous control problem, and it can be applied to the power optimization control of HPRs.

4.1. TD3 Algorithm

The TD3 algorithm is a model-free, off-line, policy-based reinforcement learning method [34]. The TD3 algorithm is an improvement on the DDPG algorithm. And the DDPG algorithm originates from the DQN algorithm, combining the actor–critic network with the DQN algorithm. It not only solves the problems that the actor–critic network can only view one-sidedly and finds difficult to converge but also can handle the continuous control problem. However, the DQN algorithm is prone to overestimate the Q value, which also appears in the DDPG algorithm. To solve this problem, the DDQN algorithm eliminates overestimation through separating action selection and target Q value prediction. The TD3 algorithm uses three key techniques: the double network, target policy smoothing regularization, and the delayed policy update to further optimize the DDPG algorithm and avoid the overestimation problem.

A double network refers to the use of two sets of critic networks, thus expanding the four neural networks of the DDPG algorithm into six neural networks of the TD3 algorithm. The network architecture of TD3 is shown in Figure 10. Through setting a dual critic network, the TD3 algorithm takes the minimum of output values $Q_{tar\_1}$ and $Q_{tar\_2}$ of two target networks as the prediction income, so as to calculate the temporal difference error, which makes the TD3 algorithm able to effectively deal with the overestimation problem.

Target policy smoothing regularization is a regularization strategy based on the SARSA algorithm, which aims to solve the overestimated problem of value networks. The TD3 algorithm accomplishes the operation of target policy smoothing regularization through adding random noise to the output of the actor target network.

The delayed policy update means that the update of the actor network lags behind the critic network. The actor network is updated through maximizing the cumulative expected reward, and it needs to use the critic network to evaluate the value of the action. If the critic network is unstable, the actor network will naturally oscillate as well. Therefore, the Critic network needs to be updated more frequently than the actor network, i.e., it should wait for the critic network to stabilize before updating the actor network. The update strategy adopted in the TD3 algorithm is to update the critic network once at each step, while the actor network is updated every d steps.

The pseudo-code of the TD3 algorithm [35] is as follows. The algorithm first needs to create the actor and critic neural networks and randomly initialize the network parameters. At the beginning of the training, the algorithm undergoes a process of accumulating initial experiences, during which the algorithm will not be trained. The current critic networks are gradually updated in the direction of smaller TD error, while the current actor network of is updated in the direction of actions with higher reward. Compared with completely updating the target network in DQN, the method of updating TD3 algorithm is soft, that is, it merges two sets of network parameters using a small constant τ (0 < τ ≪ 1). The soft update method of the TD3 algorithm results in a small change in the parameters of the target network and a relatively flat change in the calculated target value. This allows the algorithm to maintain some stability even if the target network is updated frequently.

Algorithm: TD3
Create Actor network $\pi \left(s\right|\theta )$ and Critic network $Q_1(s,a|{\omega }_1)$& $Q_2(s,a|{\omega }_2)$   with randomly initializing the parameters $\theta$, ${\omega }_1$ and ${\omega }_2$ respectively.
Create target network ${\pi }^{\prime }\left(s\right|\theta )$, $Q_1^{\prime }(s,a|{\omega }_1^{\prime })$ and $Q_2^{\prime }(s,a|{\omega }_2^{\prime })$, which set the   parameters: ${\theta }^{\prime }\leftarrow \theta ,{\omega }_i^{\prime }\leftarrow {\omega }_i$, $i=\mathrm{1,2}$.
Create an empty experience replay buffer $R$.
Initialize sampling time $T_s$, maximum simulation time $T_{max}$, number of episodes $Ep$, and   calculate the maximum steps $St=T_{max}/T_s$.

4.2. Settings of TD3 Algorithm

When using the TD3 algorithm to create the HPR controller, it is necessary to focus on the states $\mathit{s}$, the structure of the actor–critic network, the reward functions, the decay strategy of the learning rate, and other hyperparameters.

During the training and use of an RL agent, it needs to continuously acquire the states of the environment to determine the next action. There is a limited number of states acquired by the intelligent body. On the one hand, too many states will lead to useful information being overwhelmed; on the other hand, the more states, the larger the size of the neural network which has more parameters need to be trained, thus leading to an increase in training time. Therefore, in this paper, based on practical needs and experience, 5 states are selected as a set of states $\mathit{s}=[{\mathit{s}}_{\mathbf{0}},{\mathit{s}}_{\mathbf{1}},{\mathit{s}}_{\mathbf{2}},{\mathit{s}}_{\mathbf{3}},{\mathit{s}}_{\mathbf{4}}]$. The meaning of each state is shown in

Table 2. Meaning of the 5 states.

Status	Formula	Description
${\mathit{s}}_{\mathbf{0}}$	$n_t$	Nuclear power at time $t$
${\mathit{s}}_{\mathbf{1}}$	$n_{ref}$	Load power
${\mathit{s}}_{\mathbf{2}}$	$N_{t-1}$	The speed of control drums at time $t-1$
${\mathit{s}}_{\mathbf{3}}$	$n_{ref}-n_t$	The deviation between the actual nuclear power and the set value at time $t$
${\mathit{s}}_{\mathbf{4}}$	$\frac{n_t-n_{t-1}}{h}$	Rate of change in nuclear power

. ${\mathit{s}}_{\mathbf{0}},{\mathit{s}}_{\mathbf{1}}$ are the basic states of the controlled parameters, which represent the actual and set values of nuclear power, respectively. ${\mathit{s}}_{\mathbf{2}}$ is the speed of control drums at the previous moment. The speed of control drums is both the output and the input of the agent, which is beneficial for the agent to learn the advantages and disadvantages of the control action to produce a better control strategy. ${\mathit{s}}_{\mathbf{3}}$ is the difference between the actual nuclear power and the load power, indicating the deviation in the nuclear power. And ${\mathit{s}}_{\mathbf{4}}$ indicates the rate of change in nuclear power and represents how fast the power changes.

Both the actor network and the critic network adopt the double network structure form of the DQN algorithm; that is, each network exists in both the current network and target network, and the current network has the same network structure as the target network, but the network parameters are different. Therefore, the TD3 algorithm contains two types of neural networks and a total of six neural networks. The structures of the actor network and the critic network are shown in Figure 11. The actor network uses a three-layer fully connected neural network, and the activation function uses the ReLU function and the tanh function, where the tanh function is used to restrict the output of the actor network between −1 and 1. The critic network has two branches, one for receiving the observed states and the other for receiving the control drums’ speed. The two branches are combined by ADD layers and processed by a three-layer fully connected network to obtain the evaluation values of states and actions.

As for the learning rates of actor networks and critic networks, they cannot be set too large to prevent the network from hovering around the optimal value and not converging. At the same time, too small a learning rate will lead to slow convergence of the network and even fall into a local optimum. In order to set the learning rate of the network reasonably, this paper adopts the exponential decay of learning rate strategy shown in Equation (14) to adjust the learning rate dynamically. The learning rate will decay at certain episodic intervals. However, the learning rate cannot be decayed infinitely, and the lower limit of learning rate decay should be set appropriately.

$$Lr=Lr\cdot \mu , \mathrm{if} ep \mathrm{mod} I=0$$

(14)

where Lr is the learning rate, ep is the size of the current training curtain, and I is the episode interval between two adjacent learning rate decays.

Reward is an extremely important part of reinforcement learning that allows the algorithm to evaluate what actions to take to get better results. In this paper, through designing a reasonable reward function, the reinforcement learning algorithm is provided with appropriate rewards and punishments, so that the algorithm learns a better control strategy and converges quickly. See Equation (15); the reward function consists of three parts, which are the load tracking part $R_{t+1}^{TR}$, a control drums part $R_{t+1}^{CD}$, and the nuclear power overrun part $R_{t+1}^{OR}$.

$$R_{t+1}=R_{t+1}^{TR}+R_{t+1}^{CD}+R_{t+1}^{OR}$$

(15)

Load tracking means that the controller controls the nuclear power to stabilize at the set power. The amount of the reward for load tracking is proportional to the absolute value of the deviation between the nuclear power and the load power, as in Equation (16). Where $n_{t+1}$ is the actual nuclear power at the time $t+1$,${\phi }_{TR}$ is a positive number that represents the adjustable scaling factor of the load tracking reward. Since the algorithm is updated in the direction of increasing reward value, a negative sign is used in Equation (16) to ensure that the smaller the power deviation, the larger the reward $R_{t+1}^{TR}$.

$$R_{t+1}^{TR}=-{\phi }_{TR}\cdot \left|n_{t+1}-n_{ref}\right|$$

(16)

The control drum is a kind of electric mechanical device with service life. If its speed changes frequently, it will accelerate the aging of the control drum and increase the possibility of its malfunction or even failure. Therefore, this paper introduces $R_{t+1}^{CD}$ to optimize the rotation strategy of the control drums, as in Equation (17), where $N_t^{CD}$ and $N_{t-1}^{CD}$ are, respectively, the control drum’s rotation speed at the time $t$ and $t-1$, and ${\phi }_{CD}$ is the positive scale factor of the control drum reward term.

$$R_{t+1}^{CD}=-{\phi }_{CD}\cdot \left|N_t^{CD}-N_{t-1}^{CD}\right|$$

(17)

In the process of regulating nuclear power, if the power of the nuclear power deviates too much from the set power, then this control is bound to fail. In order for the agent to learn the strategy to deal with the above situation in time, the nuclear power overrun part $R_{t+1}^{OR}$ in Equation (18) is used, where $L$ is the penalty value given in case of nuclear power overrunning, $n_0$ is the initial nuclear power, and “$20\%FP$” refers to 20% of the full power.

$$\left\{\begin{array}{l}{R}_{t+1}^{OR}=-L, \mathrm{if} \left|n_{t+1}-n_{ref}\right|>\left|n_0-n_{ref}\right|+20\%FP \\ R_{t+1}^{OR}=0, \mathrm{otherwise}\end{array}\right.$$

(18)

In summary, in order to make the TD3 algorithm applicable to HPR power control, the hyperparameters of the algorithm are set in this paper, and most of them are listed in

Table 3. Hyper-parameters of TD3 algorithm.

Hyper-Parameters	Values	Hyper-Parameters	Values
$\mathrm{Sample} \mathrm{time} T_s$	0.1 s	Gradient threshold	1
$\mathrm{Step} \mathrm{size} \mathrm{of} \mathrm{RK}4 h$	0.001 s	Optimization algorithm	Adam
$\mathrm{Time} \mathrm{simulated} \mathrm{per} \mathrm{episode} T_{\mathit{max}}$	180 s	Frequency of soft update	10 steps
$\mathrm{Number} \mathrm{of} \mathrm{episodes} \mathit{Ep}$	600	$\mathrm{Soft} \mathrm{update} \mathrm{ratio} \tau$	$5\times {10}^{-3}$
Size of experience buffer R	${10}^6$	Action space	(−1, 1)
Size of mini batch N	1024	The initial noise variance	0.1
$\mathrm{Discount} \mathrm{rate} \gamma$	0.99	Decay rate of noise variance	${10}^{-4}$
$\mathrm{Initial} \mathrm{learning} \mathrm{rate} \mathrm{of} \mathrm{Actor} \mathrm{network} {\alpha }_1$	${10}^{-3}$	The minimum noise variance	0.001
Interval of learning rate decay I	2 episodes	${\phi }_{TR}$	10
$\mathrm{Initial} \mathrm{learning} \mathrm{rate} \mathrm{of} \mathrm{Critic} \mathrm{network} {\alpha }_2$	${10}^{-4}$	${\phi }_{CD}$	0.1
Learning rate decay rate μ	0.98	$L$	100
Minimum learning rate	${10}^{-5}$

.

5. Results and Discussion

The training condition in this paper is limited to between 100%FP and 10%FP. First, it decreases from 100%FP with 10%FP as a power step down to 10%FP, and then with the same power step up to 100%FP. Each episode running time is 180 s. During training, the fourth-order Runge–Kutta method (RK4) is used as the solution algorithm of the HPR dynamic model, and the calculation step is 0.001 s. The sampling time of the RL controller is 0.1 s; that is, the controller controls every 0.1 s. In order to verify the effectiveness of the RL controller, three simulations are designed to analyze its control performance.

5.1. The Optimization Results of the RL Controller

During a training session, the curves of episode reward, average reward, and Q value of each episode changes along with the training and are shown in Figure 12. It can be seen that the nuclear power limit is often exceeded during the early training of the agent, which leads to the training in one episode being terminated in advance, so that the reward obtained by the RL agent is tiny. After a period of training, the agent gains enough operational experience to gradually learn the control strategy of nuclear power. At the end of training, the upward trend of episode reward, average reward, and Q value gradually stops; that is, the training of the RL agent has converged.

5.2. Control Performance Analysis

Taking load power from 100%FP to 90%FP as an example, the comparison of an uncontrolled case and an RL-controlled case is shown in Figure 13. The rise time, overshoot, settle time, and steady-state error of nuclear power are listed in

Table 4. Comparison of performance between uncontrolled and PID controller.

Characteristics	Uncontrolled	RL Controller
Rise time, $RT$	27.32 s	0.67 s
Overshoot, $OS$	22.54%	0.96%
Settle time, $ST$	1003.25 s	0.92 s
Steady-state error, $SSE$	21.14%	0.06%

. Nuclear power reaches the new steady state after 1003.25 s without control, and the steady state error is as high as 21.14%. However, under RL controlling, the control drums respond promptly and quickly, so that nuclear power only spends 0.92 s to match the load power, and the steady-state error is reduced to 0.06%. It can be seen that the RL controller based on TD3 algorithm training in this paper can effectively adjust the HPR power.

The interference of the HPR system in operation is often varied and complicated, and the nuclear power changes frequently. To verify the control performance of the controller, a complex condition with multiple disturbances and variable load power is designed. The following disturbance or variable power instructions are introduced to the reactor system:

(1)

Linear introduction of −10 PCM reactivity into the reactor between 40 s and 50 s.

(2)

The load power decreases linearly by 10%FP from 100 s to 130 s.

(3)

The load power is reduced to 70%FP at 200 s.

(4)

The load power is restored to 100%FP at 300 s.

Among them, the traditional PID control method is used as the control method in this paper, and the comparison between PID’s control effect and RL’s control effect is shown in Figure 14. The parameters of the PID controller were obtained automatically using a PID tuner in Simulink under the 100FP-90%FP condition, and the PID parameters were $K_P=1.02$, $K_I=0.01$, and $K_D=3.21$.

Table 5. A comparison of control performance between RL control and PID control at compound condition.

Characteristics	PID Controller	RL Controller
Max rise time	10.25 s	2.16 s
Max overshoot	17.27%	6.07%
Max settle time	73.96 s	5.57 s
Max steady-state error	0.04%	0.57%

states the control performance of the two control methods. It is worth noting that the dynamic characteristics in Table 5 refer to the maximum value of characteristics in the whole simulation process. In the simulation, RL control has a faster response speed and can track load changes more quickly than the PID control. For example, under reactivity disturbance, the RL controller makes the nuclear power peak less than 0.3%, while the nuclear power peak reaches 2% with the PID controller. During the linear change in load power, the actual nuclear power is basically consistent with the load power under the regulation of the RL controller. In the subsequent power reduction and power upturn, the overshoot from PID controlling is higher than 17% and the settle time is greater than 70 s, while the overshoot from the RL controlling is less than 7% and the settle time is less than 6 s, which indicates that the RL controller can effectively improve the dynamic performance of nuclear power. At the same time, the highest steady-state error of nuclear power under RL control is only 0.57%, which shows good steady-state performance.

To verify the control stability of the RL controller in the full power range, the control effect of the RL controller and the PID controller is compared under significant load power fluctuations. In the simulation, the load changes are 100%FP–70%FP–40%FP–20%FP–40%FP–70%FP–100%FP, and the PID parameters are the same as above. The response of nuclear power is shown in Figure 15. Meanwhile, the response characteristics of nuclear power at each step are calculated, as shown in

Table 6. The control performance of RL control and PID control under significant load power fluctuations.

Load Power Step	Characteristics	PID	RL
100%FP–70%FP	OS	14.56%	2.74%
	ST	77.27 s	14.99 s
	SSE	0.01%	0.67%
70%FP–40%FP	OS	17.55%	3.73%
	ST	86.26 s	31.05 s
	SSE	0.55%	1.19%
40%FP–20%FP	OS	23.31%	4.51%
	ST	192.69 s	51.70 s
	SSE	0.52%	2.37%
20%FP–40%FP	OS	33.84%	7.38%
	ST	80.95 s	18.33 s
	SSE	0.07%	1.20%
40%FP–70%FP	OS	23.04%	3.71%
	ST	76.93 s	11.08 s
	SSE	0.08%	0.69%
70%FP–100%FP	OS	17.263	2.98%
	ST	65.12 s	6.25 s
	SSE	0.09%	0.48%

. Under different power conditions of the HPR, the operation characteristics of the HPR change. Therefore, the control performance of a PID controller tuned under the high-power condition gradually deteriorates during the power reduction process. During the power decrease, the overshoot and settle time of the nuclear power gradually become larger, and even a slight oscillation occurs at the step from 40%FP to 20%FP. These show that PID control has a small application range in the power control of HPRs, and only one setting of PID parameters cannot successfully complete the power control task within the full power range. For the RL controller, the dynamic performance is better in the whole power adjustment task, the overshoot is less than 7.38%, and the settle time is less than 51.70 s. Although the control performance of the RL controller is slightly reduced under the condition of low power, the control performance of the RL controller is obviously better than that of the PID control.

6. Conclusions

In this paper, a lightweight dynamic model of the “MegaPower” HPR is established through equating the core of the HPR, designing the heat pipe heat exchanger, and building the thermal resistance network based on the lumped parameter idea. After the simulation, the absolute value of the steady-state error between the model solution and the reference value in the steady-state full power case does not exceed 3.2%, and the model can be used for the analysis of the dynamic characteristics and the study of the power control method of the HPR. Through introducing a reactivity step disturbance of −10 PCM and a 5% step disturbance of mass flow rate to the HPR, the dynamic characteristics of the HPR are analyzed. It shows that the HPR can reach the new steady state using its own temperature negative feedback characteristics and has good self-stability and self-regulation. But its adjustment time is long, and the parameters of each part are accompanied by oscillation changes. In order to improve the anti-disturbance and load tracking capability of the HPR, this paper designs an RL controller for reactor power control based on the TD3 algorithm, with reasonable settings of the states $\mathit{s}$, the structure of the neural network, the reward functions, and other hyperparameters of the TD3 algorithm. To verify the RL controller, the control performance of the RL control was compared with that of the uncontrolled case in a step simulation from 100%FP to 90%FP, and the control performance of the RL controller and the PID controller under the compound condition and the condition of significant load power fluctuations was also compared. The results show that the RL controller can quickly regulate the reactor power and suppress the impact of disturbances, and the settle time of nuclear power is less than 51.70 s and the steady-state error is less than 2.37% in both simulations, which means that the RL controller can improve the dynamic and steady-state performance of the HPR and has the ability to control nuclear power in all operating conditions.

The influence of the SCO₂ Brayton cycle on reactor power control is not considered in this paper. On the basis of this paper, some propositional research can be carried out from the following aspects in the future: On the one hand, appropriate collaborative control strategies and methods can be proposed based on the safe operation requirements of the HPR and SCO₂ Brayton cycle. On the other hand, in view of the possibility that the HPR nuclear power plant will operate in the unmanned condition in the future, autonomous control strategies and other key technologies, such as situational awareness technology and autonomous fault-tolerant control technology, can be studied.