Riverbank Following Planner (RBFP) for USVs Based on Point Cloud Data
Abstract
:1. Introduction
1.1. Background
1.2. Contributions
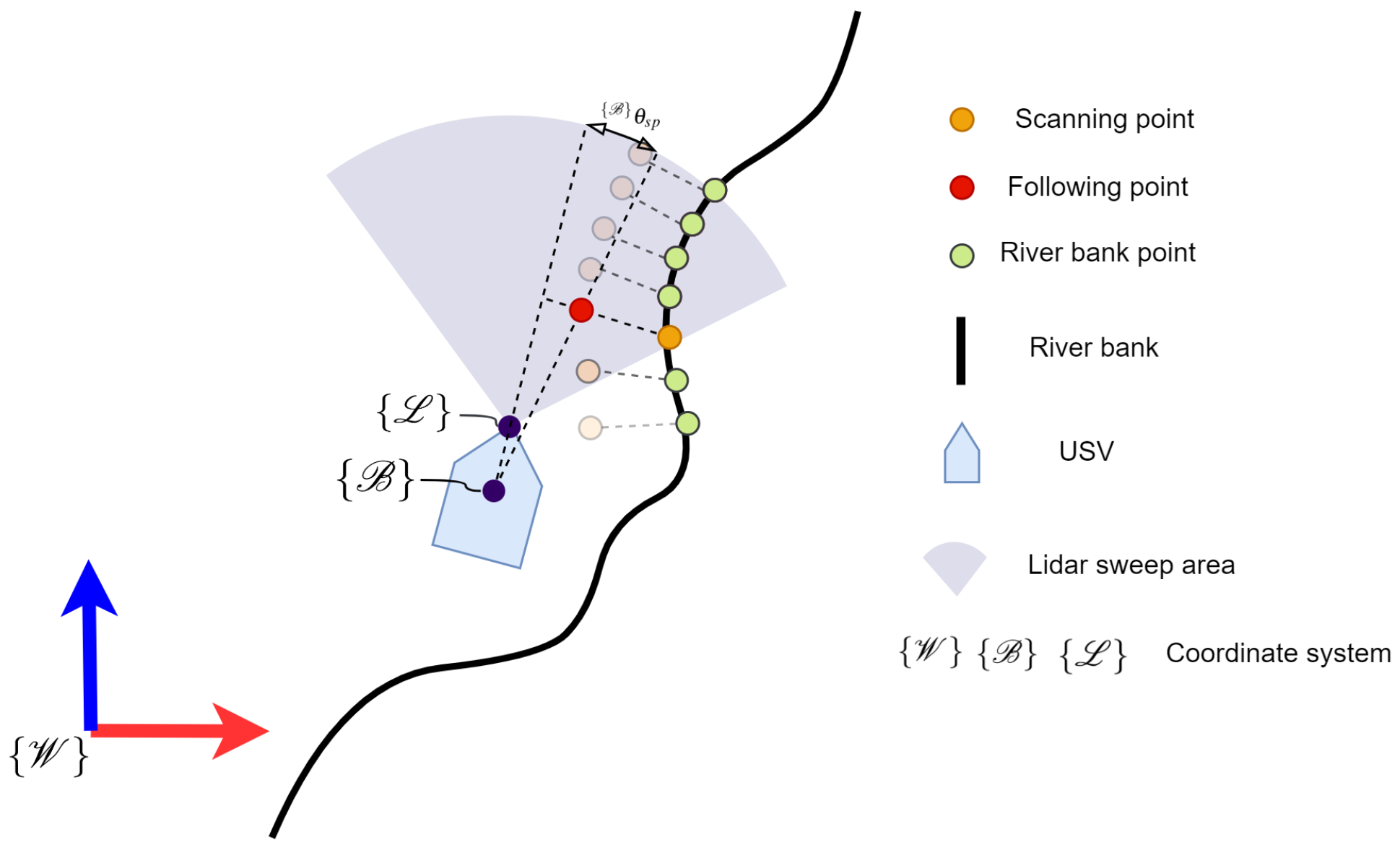
- The following points of the path for the USV are automatically calculated by the RBFP planer using massive point cloud data collected by the LiDAR on the USV.
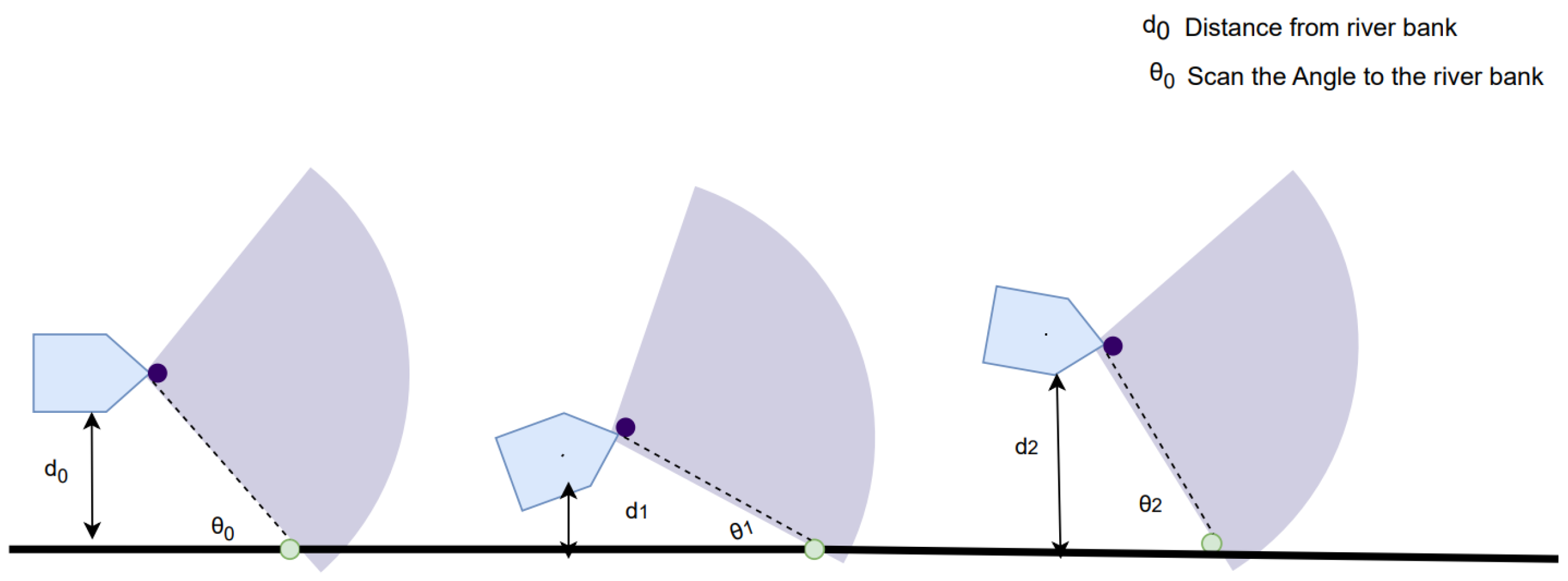
- The distance between the USV and the riverbank can be flexibly defined by users before the autonomous navigation, ensuring the USV’s adaptability to a diverse range of applications.
- Unlike other path planning algorithms that need to set target points before navigation, our algorithm can automatically navigate following to the shape of the riverbank without any predefined target points and can maintain a constant distance from the riverbank.
2. Related Work
2.1. Path Planning
2.2. Proportional-Integral-Derivative Control
2.3. River Shoreline and Water-Shore-Line Inspection Review
3. Methodology of RBFP
3.1. System Overview
3.2. Point Cloud Processing
3.3. RBFP Formulation
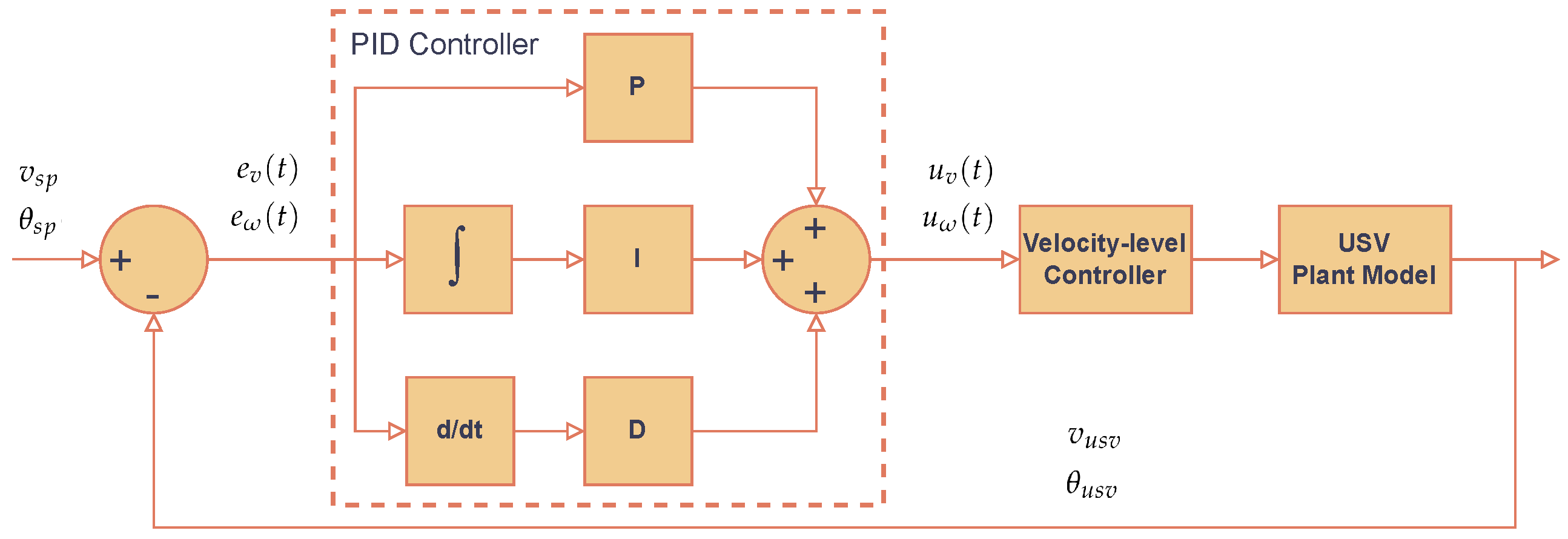
3.4. Controller Design
4. Experiments
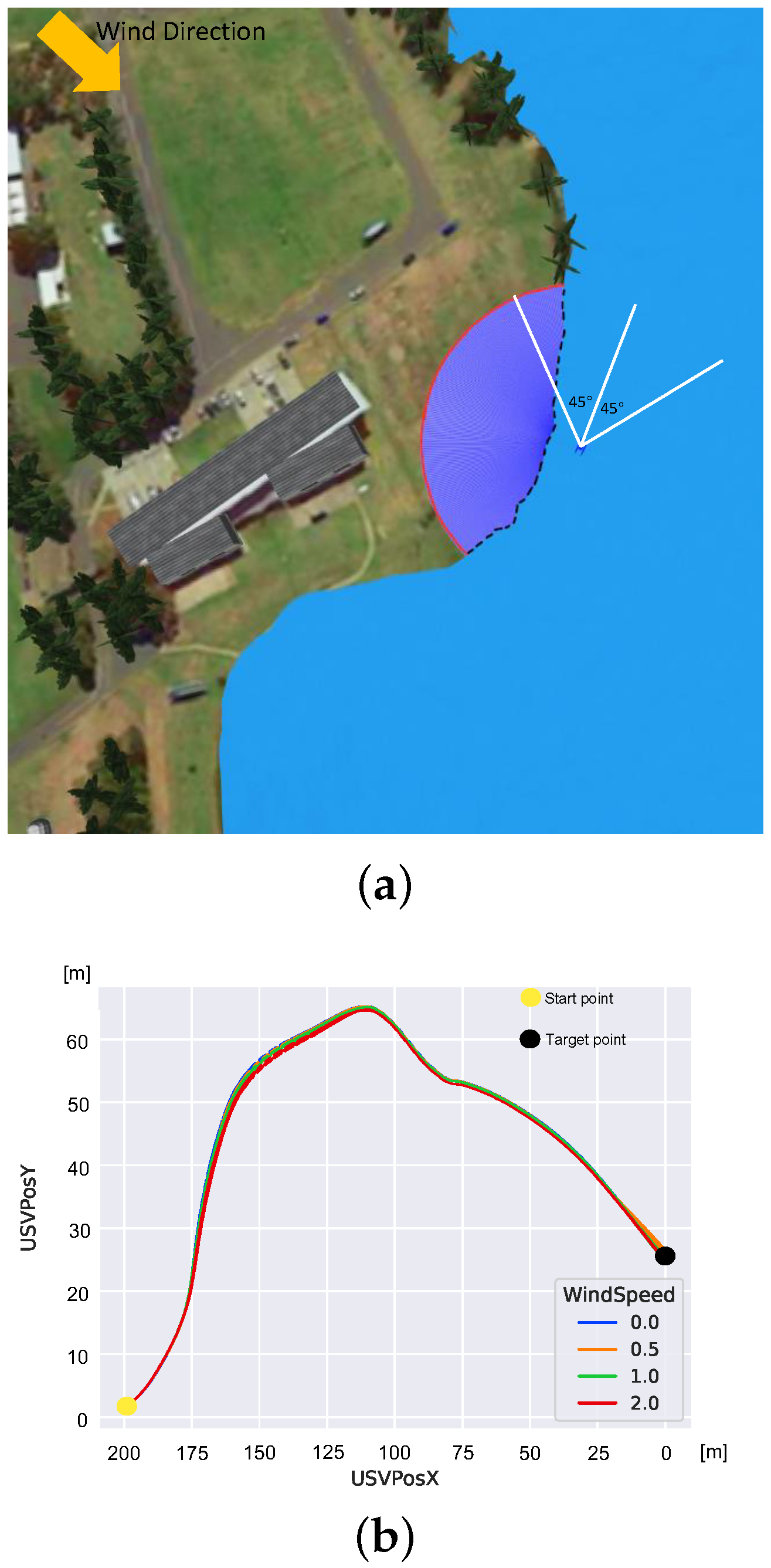
4.1. High-Fidelity ROS Simulation
4.1.1. Virtual RobotX
- Random or fixed wind speed represents the effect on the motion of USVs.
- LiDAR simulation, including interaction with the riverbank.
- Six degree-of-freedom models for USVs with configurable actuators.
4.1.2. Simulation Parameters and Implementation Details
4.2. Simulation Results
4.2.1. Results for Straight Riverbank
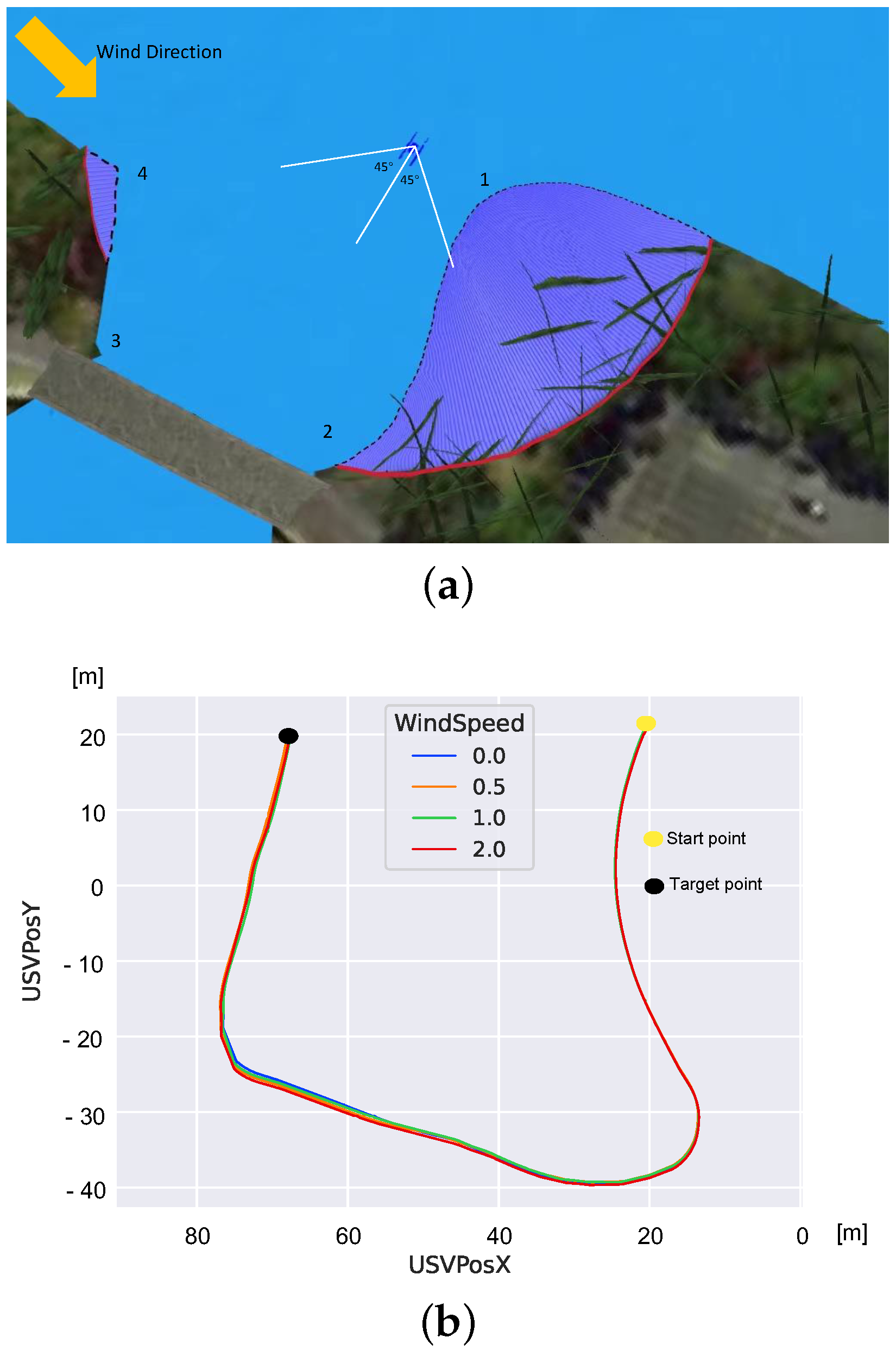
4.2.2. Results for Convex Riverbank
4.2.3. Results for Concave Riverbank
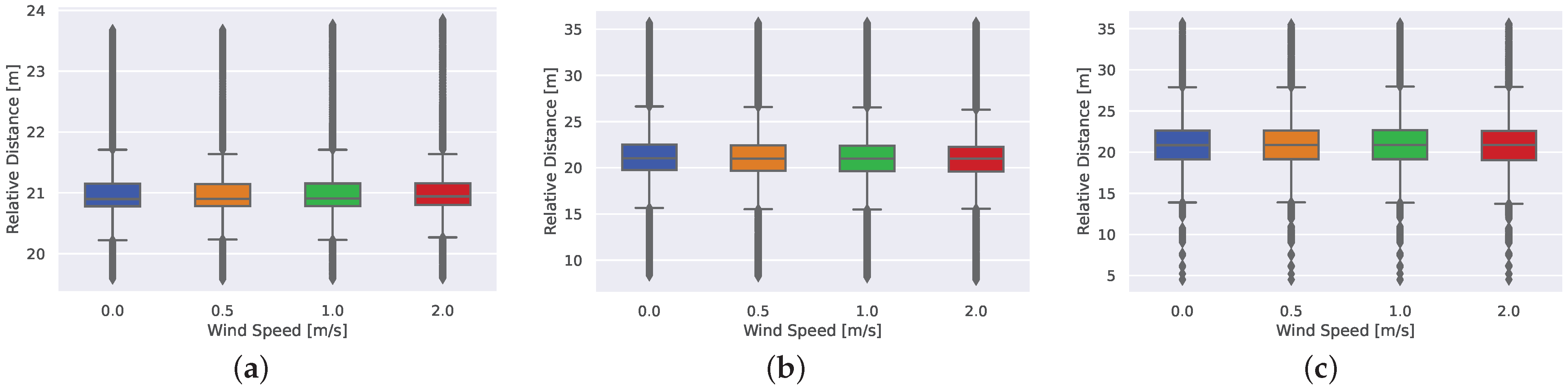
4.3. Statistics
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| USVs | Unmanned surface vehicles |
| RBFP | Riverbank Following Planner |
| VO | Visual odometry |
| PCD | Point Cloud Data |
| FOV | Field-Of-View |
| IQR | Interquartile range |
| APF | Artificial potential field |
| VRX | Virtual RobotX |
| ROS | Robot operating system |
| MATLAB | Matrix Laboratory |
| PID | Proportion–Integration–Differentiation |
| Max | Maximum |
| Min | Minimum |
| IMU | Inertial Measurement Unit |
| GPS | Global Positioning System |
References
- Manley, J.E. Unmanned surface vehicles, 15 years of development. In Proceedings of the OCEANS, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–4. [Google Scholar]
- Jorge, V.A.; Granada, R.; Maidana, R.G.; Jurak, D.A.; Heck, G.; Negreiros, A.P.; Dos Santos, D.H.; Gonçalves, L.M.; Amory, A.M. A survey on unmanned surface vehicles for disaster robotics: Main challenges and directions. Sensors 2019, 19, 702. [Google Scholar] [CrossRef] [PubMed]
- Specht, M.; Specht, C.; Szafran, M.; Makar, A.; Dąbrowski, P.; Lasota, H.; Cywiński, P. The use of USV to develop navigational and bathymetric charts of yacht ports on the example of national sailing centre in Gdańsk. Remote Sens. 2020, 12, 2585. [Google Scholar] [CrossRef]
- Veers, J.; Bertram, V. Development of the USV multi-mission surface vehicle III. In Proceedings of the 5th International Conference on Computer Applications and Information Technology in the Maritime Industries, Drübeck, Germany, 23–25 May 2006. [Google Scholar]
- Chen, H.; Zhu, C.; Chen, J.; Peng, Y.; Yao, J. Design of Unmanned Surface Vehicle for Submarine Pipeline Detection. In Proceedings of the 2018 IEEE 4th Information Technology and Mechatronics Engineering Conference (ITOEC), London, UK, 14–16 December 2018; pp. 198–202. [Google Scholar] [CrossRef]
- Kurowski, M.; Thal, J.; Damerius, R.; Korte, H.; Jeinsch, T. Automated survey in very shallow water using an unmanned surface vehicle. IFAC-PapersOnLine 2019, 52, 146–151. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, Y.; Wen, Y. A Global Path Planning Algorithm of Unmanned Vessel in Inland Waterway. In ICTIS 2013: Improving Multimodal Transportation Systems-Information, Safety, and Integration; ASCE: Reston, VA, USA, 2013; pp. 2106–2113. [Google Scholar]
- Yang, P.; Song, C.; Chen, L.; Cui, W. Image Based River Navigation System of Catamaran USV with Image Semantic Segmentation. In Proceedings of the 2022 WRC Symposium on Advanced Robotics and Automation (WRC SARA), Beijing, China, 20 August 2022; pp. 147–151. [Google Scholar] [CrossRef]
- Scherer, S.; Rehder, J.; Achar, S.; Cover, H.; Chambers, A.; Nuske, S.; Singh, S. River mapping from a flying robot: State estimation, river detection, and obstacle mapping. Auton. Robot. 2012, 33, 189–214. [Google Scholar] [CrossRef]
- Son, N.S.; Yoon, H.K. Study on a waypoint tracking algorithm for unmanned surface vehicle (USV). J. Navig. Port Res. 2009, 33, 35–41. [Google Scholar] [CrossRef]
- Stateczny, A.; Wlodarczyk-Sielicka, M.; Gronska, D.; Motyl, W. Multibeam Echosounder and LiDAR in process of 360-degree numerical map production for restricted waters with HydroDron. In Proceedings of the 2018 Baltic Geodetic Congress (BGC Geomatics), Olsztyn, Poland, 21–23 June 2018; pp. 288–292. [Google Scholar]
- Zhuang, Y.; Sun, Y.; Wang, W. Mobile robot hybrid path planning in an obstacle-cluttered environment based on steering control and improved distance propagating. Int. J. Innov. Comput. Inf. Control 2012, 8, 4095–4109. [Google Scholar]
- Zhou, C.; Gu, S.; Wen, Y.; Du, Z.; Xiao, C.; Huang, L.; Zhu, M. The review unmanned surface vehicle path planning: Based on multi-modality constraint. Ocean Eng. 2020, 200, 107043. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, Y.; Gong, C.; Zhou, Y.; Zeng, C.; Zhu, S. Improved dynamic window approach for Unmanned Surface Vehicles’ local path planning considering the impact of environmental factors. Sensors 2022, 22, 5181. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Autonomous Robot Vehicles; Springer: Berlin/Heidelberg, Germany, 1986; pp. 396–404. [Google Scholar]
- Chu, Y.; Wu, Z.; Yue, Y.; Zhu, X.; Lim, E.G.; Paoletti, P. PK-APF: Path-Keeping Algorithm for USVs Based on Artificial Potential Field. Appl. Sci. 2022, 12, 8201. [Google Scholar] [CrossRef]
- Zhang, L.; Mou, J.; Chen, P.; Li, M. Path planning for autonomous ships: A hybrid approach based on improved apf and modified vo methods. J. Mar. Sci. Eng. 2021, 9, 761. [Google Scholar] [CrossRef]
- Lin, P.; Choi, W.Y.; Chung, C.C. Local path planning using artificial potential field for waypoint tracking with collision avoidance. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–7. [Google Scholar]
- Ngah, W.; Buniyamin, N.; Mohamad, Z. Point to point sensor based path planning algorithm for autonomous mobile robots. In Proceedings of the 9th WSEAS International Conference on System Science and Simulation in Engineering, Tenerife, Spain, 16–18 December 2010; pp. 186–191. [Google Scholar]
- Lumelsky, V.; Stepanov, A. Dynamic path planning for a mobile automaton with limited information on the environment. IEEE Trans. Autom. Control 1986, 31, 1058–1063. [Google Scholar] [CrossRef]
- Ng, J.; Bräunl, T. Performance comparison of bug navigation algorithms. J. Intell. Robot. Syst. 2007, 50, 73–84. [Google Scholar] [CrossRef]
- Yufka, A.; Parlaktuna, O. Performance comparison of bug algorithms for mobile robots. In Proceedings of the 5th International Advanced Technologies Symposium, Karabuk, Turkey, 4–7 September 2009; pp. 13–15. [Google Scholar]
- Feng, P.; Wu, J.; Yang, X.; Zhang, W.; Guo, H. Design and Realization of LQR Course Keeping Control for Small Unmanned Surface Vehicle. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 6640–6645. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Y. Autonomous Trajectory Tracking Integrated Control of Unmanned Surface Vessel. J. Mar. Sci. Eng. 2023, 11, 568. [Google Scholar] [CrossRef]
- Bingul, Z.; Gul, K. Intelligent-PID with PD Feedforward Trajectory Tracking Control of an Autonomous Underwater Vehicle. Machines 2023, 11, 300. [Google Scholar] [CrossRef]
- Fan, Y.; Sun, X.; Wabg, G.; Guo, C. On fuzzy self-adaptive PID control for USV course. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 8472–8478. [Google Scholar]
- Fefilatyev, S.; Goldgof, D.; Shreve, M.; Lembke, C. Detection and tracking of ships in open sea with rapidly moving buoy-mounted camera system. Ocean Eng. 2012, 54, 1–12. [Google Scholar] [CrossRef]
- Mou, X.; Wang, H. Image-based maritime obstacle detection using global sparsity potentials. J. Inf. Commun. Converg. Eng. 2016, 14, 129–135. [Google Scholar] [CrossRef]
- Prasad, D.K.; Rajan, D.; Prasath, C.K.; Rachmawati, L.; Rajabally, E.; Quek, C. MSCM-LiFe: Multi-scale cross modal linear feature for horizon detection in maritime images. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 1366–1370. [Google Scholar]
- Liu, H.; Javed, O.; Taylor, G.; Cao, X.; Haering, N. Omni-directional surveillance for unmanned water vehicles. In Proceedings of the Eighth International Workshop on Visual Surveillance-VS2008, Santorini, Greece, 6–8 June 2008. [Google Scholar]
- Kristan, M.; Kenk, V.S.; Kovačič, S.; Perš, J. Fast image-based obstacle detection from unmanned surface vehicles. IEEE Trans. Cybern. 2015, 46, 641–654. [Google Scholar] [CrossRef]
- Alpert, S.; Galun, M.; Brandt, A.; Basri, R. Image segmentation by probabilistic bottom-up aggregation and cue integration. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 315–327. [Google Scholar] [CrossRef]
- Xu, S.; Ye, N.; Xu, S. A new method for shoreline extraction from airborne LiDAR point clouds. Remote Sens. Lett. 2019, 10, 496–505. [Google Scholar] [CrossRef]
- Lee, I.C.; Cheng, L.; Li, R. Optimal parameter determination for mean-shift segmentation-based shoreline extraction using lidar data, aerial orthophotos, and satellite imagery. In Proceedings of the ASPRS Conference, Orlando, FL, USA, 15–18 November 2010. [Google Scholar]
- Liu, H.; Wang, L.; Sherman, D.J.; Wu, Q.; Su, H. Algorithmic foundation and software tools for extracting shoreline features from remote sensing imagery and LiDAR data. J. Geogr. Inf. Syst. 2011, 3, 99. [Google Scholar] [CrossRef]
- Lee, I.C.; Wu, B.; Li, R. Shoreline extraction from the integration of lidar point cloud data and aerial orthophotos using mean-shift segmentation. In Proceedings of the ASPRS Annual Conference, Baltimore, MA, USA, 3–6 June 2009; Volume 2, pp. 3033–3040. [Google Scholar]
- Li, W.; Liu, H.; Qin, C. A method for the extraction of shorelines from airborne lidar data in muddy areas and areas with shoals. Remote Sens. Lett. 2022, 13, 480–491. [Google Scholar] [CrossRef]
- tf—ROS Wiki. Available online: http://wiki.ros.org/tf (accessed on 23 July 2023).
- Stateczny, A.; Burdziakowski, P. Universal autonomous control and management system for multipurpose unmanned surface vessel. Pol. Marit. Res. 2019, 26, 30–39. [Google Scholar] [CrossRef]
- Klinger, W.B.; Bertaska, I.R.; von Ellenrieder, K.D.; Dhanak, M.R. Control of an Unmanned Surface Vehicle with Uncertain Displacement and Drag. IEEE J. Ocean. Eng. 2017, 42, 458–476. [Google Scholar] [CrossRef]
- Holland, D.; Landaeta, E.; Montagnoli, C.; Ayars, T.; Barnes, J.; Barthelemy, K.; Brown, R.; Delp, G.; Garnier, T.; Halleran, J.; et al. Design of the Minion Research Platform for the 2022 Maritime RobotX Challenge. Available online: https://robotx.org/programs/robotx-challenge-2022/ (accessed on 10 October 2023).
- Bingham, B.; Aguero, C.; McCarrin, M.; Klamo, J.; Malia, J.; Allen, K.; Lum, T.; Rawson, M.; Waqar, R. Toward Maritime Robotic Simulation in Gazebo. In Proceedings of the MTS/IEEE OCEANS Conference, Seattle, WA, USA, 4–7 October 2019. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 8–12 July 2009; Volume 3, p. 5. [Google Scholar]
- Quigley, M.; Gerkey, B.; Smart, W.D. Programming Robots with ROS: A Practical Introduction to the Robot Operating System; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2015. [Google Scholar]



| Variable [Unit] | Value | Description |
|---|---|---|
| wave_gain [1] | 0.1 | Gain of wavefield model envelope |
| wave_period [s] | 5.0 | Peak period of wavefield model envelop |
| wave_angle [deg] | 0.4 | Horizontal angles of the constituent waves |
| wave_dx [m] | 1.0 | Wave direction in x-axis |
| wave_dy [m] | 0.0 | Wave direction in y-axis |
| LiDAR FOV [deg] | [−45, 45] | Field of view of 2D LiDAR sensor |
| wind_mean_vel [m/s] | 0, 0.5, 1, 2 | Constant mean wind speed |
| wind_direction [deg] | 135 | Constant wind direction |
| wind_std [m/s] | 1.5 | Standard deviation of the wind speed |
| distance_to_bank [m] | 20 | Distance between the USV and riverbank |
| [m/s] | 1.0 | Maximum linear velocity of the USV |
| [rad/s] | 1.0 | Maximum angular velocity of the USV |
| Scenario | Wind | Max [m] | Min [m] | Mean [m] | Variance [m] | ±15% Error Ratio |
|---|---|---|---|---|---|---|
| Straight | 0.0 | 23.67 | 19.58 | 20.99 | 0.43 | 96.97% |
| 0.5 | 23.68 | 19.57 | 20.98 | 0.42 | 96.99% | |
| 1.0 | 23.76 | 19.58 | 20.99 | 0.43 | 96.89% | |
| 2.0 | 23.85 | 19.59 | 21.02 | 0.44 | 96.82% | |
| Convex | 0.0 | 35.68 | 8.34 | 21.42 | 24.95 | 66.97% |
| 0.5 | 35.69 | 8.25 | 21.36 | 24.65 | 67.27% | |
| 1.0 | 35.69 | 8.14 | 21.31 | 24.58 | 67.45% | |
| 2.0 | 35.69 | 7.86 | 21.23 | 25.12 | 67.51% | |
| Concave | 0.0 | 35.69 | 4.48 | 20.94 | 14.31 | 61.23% |
| 0.5 | 35.59 | 4.49 | 20.92 | 14.51 | 61.23% | |
| 1.0 | 35.63 | 4.47 | 20.95 | 14.76 | 60.90% | |
| 2.0 | 35.61 | 4.50 | 20.90 | 14.83 | 61.23% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Y.; Wu, Z.; Zhu, X.; Yue, Y.; Lim, E.G.; Paoletti, P.; Ma, J. Riverbank Following Planner (RBFP) for USVs Based on Point Cloud Data. Appl. Sci. 2023, 13, 11319. https://doi.org/10.3390/app132011319
Chu Y, Wu Z, Zhu X, Yue Y, Lim EG, Paoletti P, Ma J. Riverbank Following Planner (RBFP) for USVs Based on Point Cloud Data. Applied Sciences. 2023; 13(20):11319. https://doi.org/10.3390/app132011319
Chicago/Turabian StyleChu, Yijie, Ziniu Wu, Xiaohui Zhu, Yong Yue, Eng Gee Lim, Paolo Paoletti, and Jieming Ma. 2023. "Riverbank Following Planner (RBFP) for USVs Based on Point Cloud Data" Applied Sciences 13, no. 20: 11319. https://doi.org/10.3390/app132011319
APA StyleChu, Y., Wu, Z., Zhu, X., Yue, Y., Lim, E. G., Paoletti, P., & Ma, J. (2023). Riverbank Following Planner (RBFP) for USVs Based on Point Cloud Data. Applied Sciences, 13(20), 11319. https://doi.org/10.3390/app132011319










