Delamination Detection Framework for the Imbalanced Dataset in Laminated Composite Using Wasserstein Generative Adversarial Network-Based Data Augmentation
Abstract
:1. Introduction
2. Proposed Methodology
2.1. Overview
2.2. Previous Works
2.2.1. Adaptive Synthetic Sampling
2.2.2. System Identification
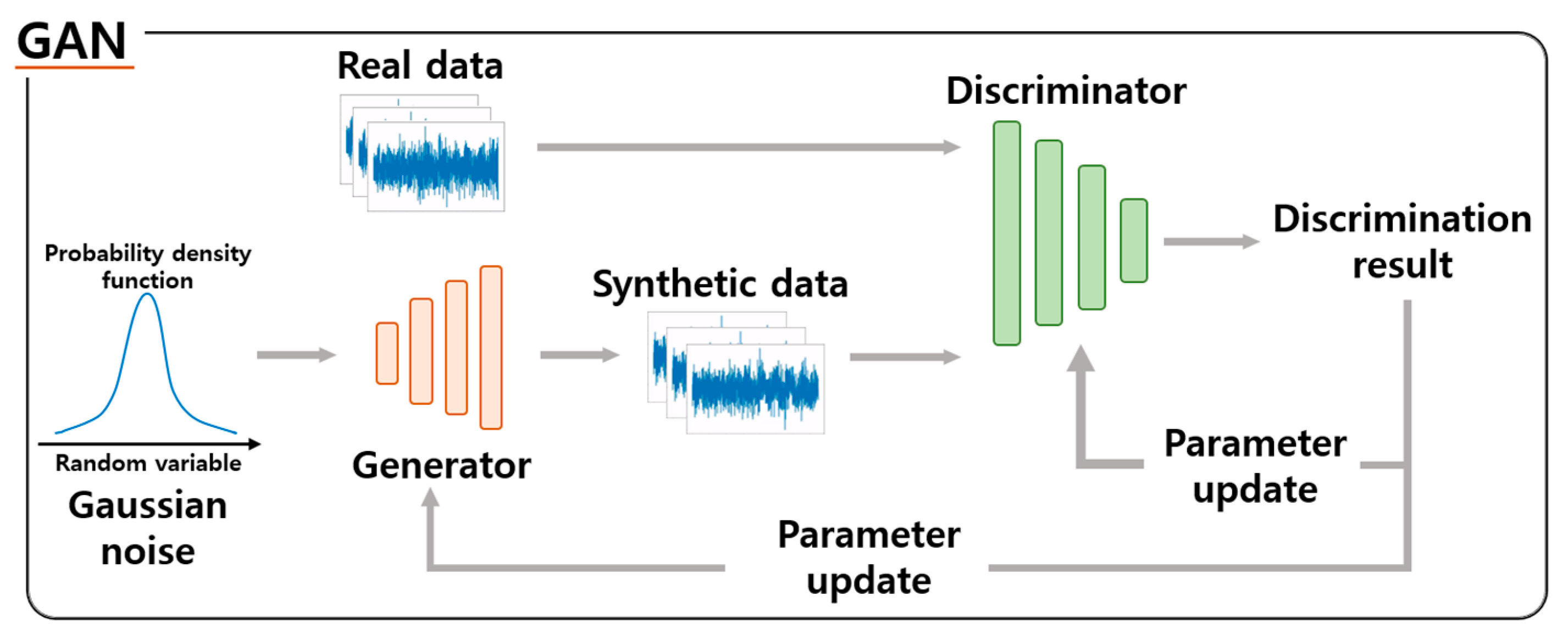
2.2.3. Generative Adversarial Network
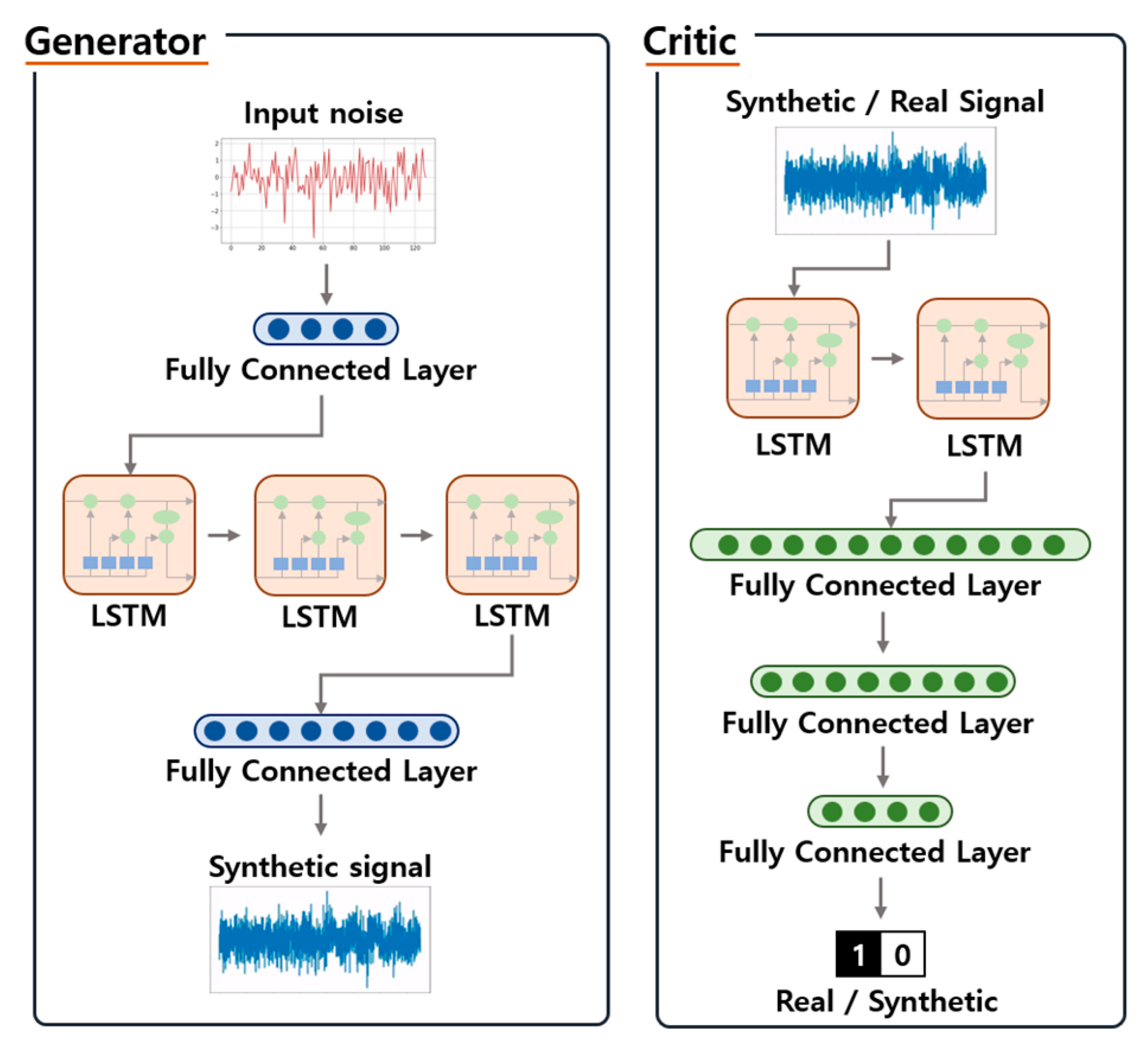
2.3. Wasserstein Generative Adversarial Network
2.4. One-Dimensional Convolutional Neural Network
3. Experimental Validation
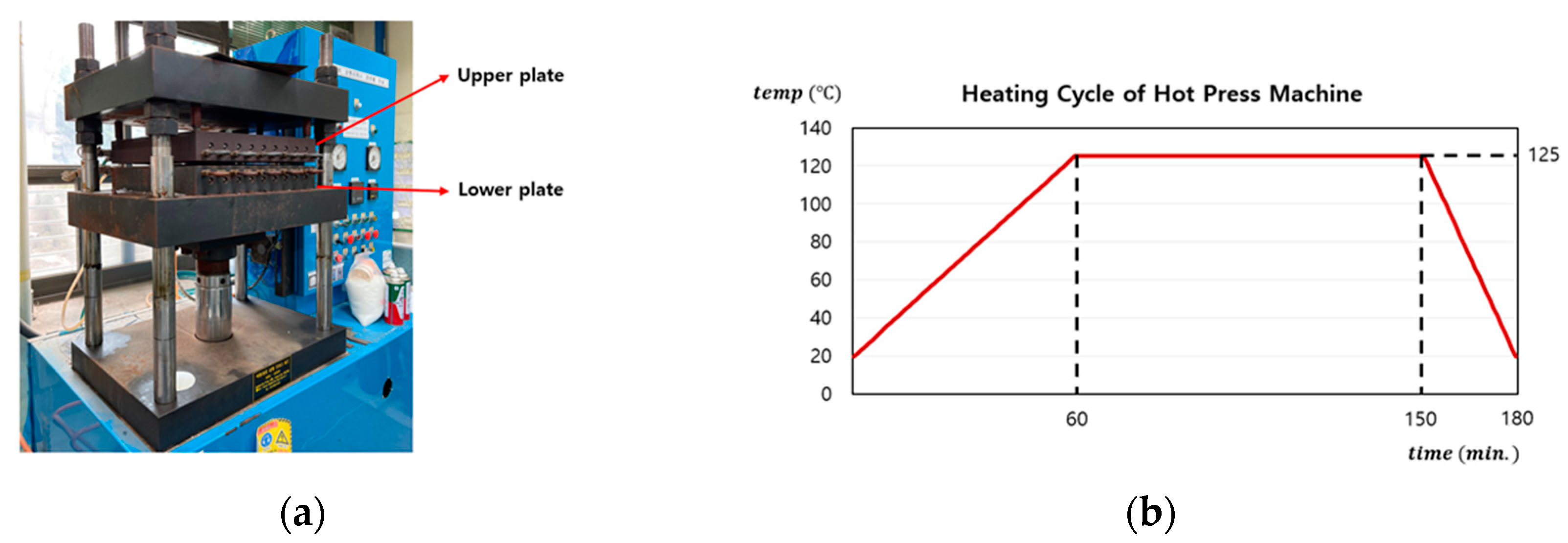
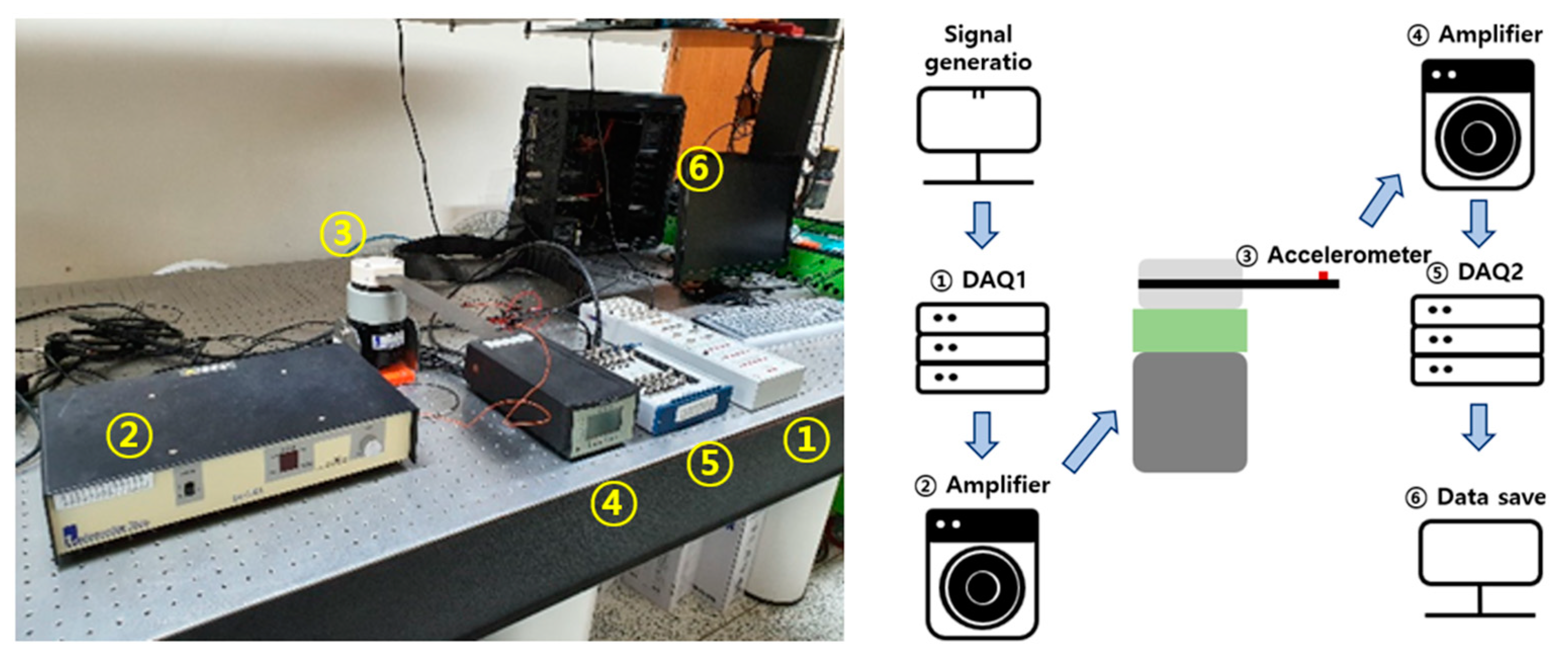
3.1. Experimental Setup and Data Acquisition
3.2. Data Augmentation Using WGAN Model
4. Fault Diagnosis Results
4.1. Evaluation Metrics
4.2. Fault Diagnosis Results
4.3. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, Present and Future Prospective of Global Carbon Fibre Composite Developments and Applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
- Azad, M.M.; Ejaz, M.; Shah, A.R.; Kamran Afaq, S.; Song, J. Static Mechanical Properties of Bio-Fiber-Based Polymer Composites. In Advances in Bio-Based Fiber; Elsevier: Amsterdam, The Netherlands, 2022; pp. 97–139. [Google Scholar]
- Bui, T.Q.; Hu, X. A Review of Phase-Field Models, Fundamentals and Their Applications to Composite Laminates. Eng. Fract. Mech. 2021, 248, 107705. [Google Scholar] [CrossRef]
- Khalid, S.; Kim, H.S. Recent Studies on Stress Function-Based Approaches for the Free Edge Stress Analysis of Smart Composite Laminates: A Brief Review. Multiscale Sci. Eng. 2022, 4, 73–78. [Google Scholar] [CrossRef]
- Banks-Sills, L. Interface Fracture and Delaminations in Composite Materials; SpringerBriefs. In Applied Sciences and Technology; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-60326-1. [Google Scholar]
- Mortell, D.J.; Tanner, D.A.; McCarthy, C.T. In-Situ SEM Study of Transverse Cracking and Delamination in Laminated Composite Materials. Compos. Sci. Technol. 2014, 105, 118–126. [Google Scholar] [CrossRef]
- Azad, M.M.; Kim, S.; Cheon, Y.B.; Kim, H.S. Intelligent Structural Health Monitoring of Composite Structures Using Machine Learning, Deep Learning, and Transfer Learning: A Review. Adv. Compos. Mater. 2023, 1–27. [Google Scholar] [CrossRef]
- Liu, G.; Li, L.; Zhang, L.; Li, Q.; Law, S.S. Sensor Faults Classification for SHM Systems Using Deep Learning-Based Method with Tsfresh Features. Smart Mater. Struct. 2020, 29, 075005. [Google Scholar] [CrossRef]
- Deng, F.; Tao, X.; Wei, P.; Wei, S. A Robust Deep Learning-Based Damage Identification Approach for SHM Considering Missing Data. Appl. Sci. 2023, 13, 5421. [Google Scholar] [CrossRef]
- Finotti, R.P.; Cury, A.A.; Barbosa, F.D.S. An SHM Approach Using Machine Learning and Statistical Indicators Extracted from Raw Dynamic Measurements. Lat. Am. J. Solids Struct. 2019, 16, e165. [Google Scholar] [CrossRef]
- Song, G.; Wang, C.; Wang, B. Structural Health Monitoring (SHM) of Civil Structures. Appl. Sci. 2017, 7, 789. [Google Scholar] [CrossRef]
- Galan-Uribe, E.; Morales-Velazquez, L.; Osornio-Rios, R.A. FPGA-Based Methodology for Detecting Positional Accuracy Degradation in Industrial Robots. Appl. Sci. 2023, 13, 8493. [Google Scholar] [CrossRef]
- Zhang, C.; Mousavi, A.A.; Masri, S.F.; Gholipour, G.; Yan, K.; Li, X. Vibration Feature Extraction Using Signal Processing Techniques for Structural Health Monitoring: A Review. Mech. Syst. Signal Process. 2022, 177, 109175. [Google Scholar] [CrossRef]
- Sohn, H.; Farrar, C.R. Damage Diagnosis Using Time Series Analysis of Vibration Signals. Smart Mater. Struct. 2001, 10, 446–451. [Google Scholar] [CrossRef]
- Tcherniak, D.; Mølgaard, L.L. Vibration-Based SHM System: Application to Wind Turbine Blades. J. Phys. Conf. Ser. 2015, 628, 012072. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal Processing Techniques for Vibration-Based Health Monitoring of Smart Structures. Arch. Comput. Methods Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of Machine Learning to Machine Fault Diagnosis: A Review and Roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Hoang, D.-T.; Kang, H.-J. A Survey on Deep Learning Based Bearing Fault Diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Jiang, L.; Yin, H.; Li, X.; Tang, S. Fault Diagnosis of Rotating Machinery Based on Multisensor Information Fusion Using SVM and Time-Domain Features. Shock Vib. 2014, 2014, 418178. [Google Scholar] [CrossRef]
- Samanta, B.; Al-Balushi, K.R. Artificial Neural Network Based Fault Diagnostics of Rolling Element Bearings Using Time-Domain Features. Mech. Syst. Signal Process. 2003, 17, 317–328. [Google Scholar] [CrossRef]
- Ye, L.; Ma, X.; Wen, C. Rotating Machinery Fault Diagnosis Method by Combining Time-Frequency Domain Features and CNN Knowledge Transfer. Sensors 2021, 21, 8168. [Google Scholar] [CrossRef]
- Li, C.; Sanchez, V.; Zurita, G.; Cerrada Lozada, M.; Cabrera, D. Rolling Element Bearing Defect Detection Using the Generalized Synchrosqueezing Transform Guided by Time–Frequency Ridge Enhancement. ISA Trans. 2016, 60, 274–284. [Google Scholar] [CrossRef]
- Hemmati, F.; Orfali, W.; Gadala, M.S. Roller Bearing Acoustic Signature Extraction by Wavelet Packet Transform, Applications in Fault Detection and Size Estimation. Appl. Acoust. 2016, 104, 101–118. [Google Scholar] [CrossRef]
- He, D.; Li, R.; Zhu, J. Plastic Bearing Fault Diagnosis Based on a Two-Step Data Mining Approach. IEEE Trans. Ind. Electron. 2012, 60, 3429–3440. [Google Scholar] [CrossRef]
- Saravanan, N.; Kumar Siddabattuni, V.N.S.; Ramachandran, K.I. A Comparative Study on Classification of Features by SVM and PSVM Extracted Using Morlet Wavelet for Fault Diagnosis of Spur Bevel Gear Box. Expert Syst. Appl. 2008, 35, 1351–1366. [Google Scholar] [CrossRef]
- Amarnath, M.; Sugumaran, V.; Kumar, H. Exploiting Sound Signals for Fault Diagnosis of Bearings Using Decision Tree. Measurement 2013, 46, 1250–1256. [Google Scholar] [CrossRef]
- Zhong, S.; Fu, S.; Lin, L. A Novel Gas Turbine Fault Diagnosis Method Based on Transfer Learning with CNN. Measurement 2019, 137, 435–453. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van De Walle, R.; Van Hoecke, S. Convolutional Neural Network Based Fault Detection for Rotating Machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Hsueh, Y.-M.; Ittangihal, V.R.; Wu, W.-B.; Chang, H.-C.; Kuo, C.-C. Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry 2019, 11, 1212. [Google Scholar] [CrossRef]
- Khan, A.; Ko, D.-K.; Lim, S.C.; Kim, H.S. Structural Vibration-Based Classification and Prediction of Delamination in Smart Composite Laminates Using Deep Learning Neural Network. Compos. Part B Eng. 2019, 161, 586–594. [Google Scholar] [CrossRef]
- Tang, X.; Xu, Z.; Wang, Z. A Novel Fault Diagnosis Method of Rolling Bearing Based on Integrated Vision Transformer Model. Sensors 2022, 22, 3878. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L. A Transfer Convolutional Neural Network for Fault Diagnosis Based on ResNet-50. Neural. Comput. Appl. 2020, 32, 6111–6124. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, S.; Jin, B. Sequential Fault Diagnosis Based on LSTM Neural Network. IEEE Access 2018, 6, 12929–12939. [Google Scholar] [CrossRef]
- Yuan, M.; Wu, Y.; Lin, L. Fault Diagnosis and Remaining Useful Life Estimation of Aero Engine Using LSTM Neural Network. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 8–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 135–140. [Google Scholar]
- Sabir, R.; Rosato, D.; Hartmann, S.; Guehmann, C. LSTM Based Bearing Fault Diagnosis of Electrical Machines Using Motor Current Signal. In Proceedings of the 2019 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 613–618. [Google Scholar]
- Zhang, T.; Fei, Q.; Li, N.; Ma, D. Fault Diagnosis Based on Modified BiLSTM Neural Network. In Proceedings of the 2020 5th International Conference on Intelligent Information Technology, Hanoi, Vietnam, 19–22 February 2020; ACM Association for Computing Machinery: New York, NY, USA, 2020; pp. 21–26. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Jia, X.-D.; Ma, H.; Luo, Z.; Li, X. Machinery Fault Diagnosis with Imbalanced Data Using Deep Generative Adversarial Networks. Measurement 2020, 152, 107377. [Google Scholar] [CrossRef]
- Khan, A.; Azad, M.M.; Sohail, M.; Kim, H.S. A Review of Physics-Based Models in Prognostics and Health Management of Laminated Composite Structures. Int. J. Precis. Eng. Manuf. Green Technol. 2023, 1–21. [Google Scholar] [CrossRef]
- Jung, K.-C.; Chang, S.-H. Advanced Deep Learning Model-Based Impact Characterization Method for Composite Laminates. Compos. Sci. Technol. 2021, 207, 108713. [Google Scholar] [CrossRef]
- Sikdar, S.; Liu, D.; Kundu, A. Acoustic Emission Data Based Deep Learning Approach for Classification and Detection of Damage-Sources in a Composite Panel. Compos. Part B Eng. 2022, 228, 109450. [Google Scholar] [CrossRef]
- Liao, Y.; Qing, X.; Wang, Y.; Zhang, F. Damage Localization for Composite Structure Using Guided Wave Signals with Gramian Angular Field Image Coding and Convolutional Neural Networks. Compos. Struct. 2023, 312, 116871. [Google Scholar] [CrossRef]
- Feng, B.; Cheng, S.; Deng, K.; Kang, Y. Localization of Low-Velocity Impact in CFRP Plate Using Time–Frequency Features of Guided Wave and Convolutional Neural Network. Wave Motion 2023, 119, 103127. [Google Scholar] [CrossRef]
- Cheng, L.; Tong, Z.; Xie, S.; Kersemans, M. IRT-GAN: A Generative Adversarial Network with a Multi-Headed Fusion Strategy for Automated Defect Detection in Composites Using Infrared Thermography. Compos. Struct. 2022, 290, 115543. [Google Scholar] [CrossRef]
- Meister, S.; Möller, N.; Stüve, J.; Groves, R.M. Synthetic Image Data Augmentation for Fibre Layup Inspection Processes: Techniques to Enhance the Data Set. J. Intell. Manuf. 2021, 32, 1767–1789. [Google Scholar] [CrossRef]
- Cheng, L.; Kersemans, M. Dual-IRT-GAN: A Defect-Aware Deep Adversarial Network to Perform Super-Resolution Tasks in Infrared Thermographic Inspection. Compos. Part B Eng. 2022, 247, 110309. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1322–1328. [Google Scholar]
- Marra, A.L.; Juliani, R.; Garcia, C. Data Augmentation for Vibration Signals Using System Identification Techniques. In Proceedings of the 2021 5th International Conference on System Reliability and Safety (ICSRS), Palermo, Italy, 24–26 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 281–285. [Google Scholar]
- Khan, A.; Raouf, I.; Noh, Y.R.; Lee, D.; Sohn, J.W.; Kim, H.S. Autonomous Assessment of Delamination in Laminated Composites Using Deep Learning and Data Augmentation. Compos. Struct. 2022, 290, 115502. [Google Scholar] [CrossRef]
- Phan, M.; Solbeck, J.; Ray, L. A Direct Method for State-Space Model and Observer/Kalman Filter Gain Identification. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, American Institute of Aeronautics and Astronautics, Providence, RI, USA, 16–19 August 2004. [Google Scholar]
- Yang, Z.; Li, Y.; Zhou, G. TS-GAN: Time-Series GAN for Sensor-Based Health Data Augmentation. ACM Trans. Comput. Healthc. 2023, 4, 1–21. [Google Scholar] [CrossRef]
- Lu, H.; Du, M.; Qian, K.; He, X.; Wang, K. GAN-Based Data Augmentation Strategy for Sensor Anomaly Detection in Industrial Robots. IEEE Sens. J. 2022, 22, 17464–17474. [Google Scholar] [CrossRef]
- Smith, K.E.; Smith, A.O. Conditional GAN for Timeseries Generation. arXiv 2020, arXiv:2006.16477v1. [Google Scholar]
- Boicea, V.A.; Ulmeanu, A.P.; Vulpe-Grigoraşi, A. A Novel Approach for Power Load Forecast Based on GAN Data Augmentation. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1254, 012030. [Google Scholar] [CrossRef]
- Arjovsky, M.; Bottou, L. Towards Principled Methods for Training Generative Adversarial Networks. arXiv 2017, arXiv:1701.04862v1. [Google Scholar]
- Goodfellow, I. NIPS 2016 Tutorial: Generative Adversarial Networks. arXiv 2017, arXiv:1701.00160v4. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875v3. [Google Scholar]
- Tang, S.; Yuan, S.; Zhu, Y. Data Preprocessing Techniques in Convolutional Neural Network Based on Fault Diagnosis towards Rotating Machinery. IEEE Access 2020, 8, 149487–149496. [Google Scholar] [CrossRef]
- Neupane, D.; Kim, Y.; Seok, J.; Hong, J. CNN-Based Fault Detection for Smart Manufacturing. Appl. Sci. 2021, 11, 11732. [Google Scholar] [CrossRef]
- Chen, C.-C.; Liu, Z.; Yang, G.; Wu, C.-C.; Ye, Q. An Improved Fault Diagnosis Using 1D-Convolutional Neural Network Model. Electronics 2020, 10, 59. [Google Scholar] [CrossRef]
- Fu, Q.; Wang, H. A Novel Deep Learning System with Data Augmentation for Machine Fault Diagnosis from Vibration Signals. Appl. Sci. 2020, 10, 5765. [Google Scholar] [CrossRef]
- Thanh-Tung, H.; Tran, T.; Venkatesh, S. Improving Generalization and Stability of Generative Adversarial Networks. arXiv 2019, arXiv:1902.03984v1. [Google Scholar]





| Tensile Modulus | Tensile Strength | Elongation | Thermal Conductivity | Density | Filament Diameter |
|---|---|---|---|---|---|
| 230 GPa | 4900 MPa | 2.1% | 9.4 W/m∙K | 1.8 g/cm3 | 7 μm |
| Healthy | Delamination 1 | Delamination 2 | |
|---|---|---|---|
| Number of sensors | P01–P10 | P01 | P01 |
| Number of data | 1000 | 60 | 60 |
| Signal length | 1875 | 1875 | 1875 |
| Healthy | Delamination 1 | Delamination 2 | |
|---|---|---|---|
| Beta 1 | 0.5 | 0.5 | 0.5 |
| Beta 2 | 0.9 | 0.9 | 0.9 |
| Training critic/Training generator | 3 | 5 | 5 |
| Learning rate | 3 × 10−4 | 3 × 10−4 | 3 × 10−4 |
| Epoch | 2000 | 2000 | 2000 |
| Batch size | 8 | 8 | 8 |
| Network Layer | Output Data Size | Parameters |
|---|---|---|
| Input Layer | 1875 × 1 | 1875 length signal input |
| Conv1D | 1875 × 32 | 32 @ 3 × 1, stride = 1, activation = ReLU |
| Conv1D | 1875 × 32 | 32 @ 3 × 1, stride = 1, activation = ReLU |
| Max pooling 1D | 937 × 32 | 2 × 1, stride = 2, activation = ReLU |
| Conv1D | 937 × 64 | 64 @ 3 × 1, stride = 1, activation = ReLU |
| Conv1D | 937 × 64 | 64 @ 3 × 1, stride = 1, activation = ReLU |
| Max pooling 1D | 468 × 64 | 2 × 1, stride = 2, activation = ReLU |
| Conv1D | 468 × 128 | 128 @ 2 × 1, stride = 1, activation = ReLU |
| Max pooling 1D | 234 × 128 | 2 × 1, stride = 2, activation = ReLU |
| Conv1D | 234 × 128 | 128 @ 2 × 1, stride = 1, activation = ReLU |
| Max pooling 1D | 117 × 128 | 2 × 1, stride = 2, activation = ReLU |
| Conv1D | 117 × 256 | 256 @ 2 × 1, stride = 1, activation = ReLU |
| Max pooling 1D | 58 × 256 | 2 × 1, stride = 2, activation = ReLU |
| Conv1D | 58 × 256 | 256 @ 2 × 1, stride = 1, activation = ReLU |
| Max pooling 1D | 29 × 256 | 2 × 1, stride = 2, activation = ReLU |
| Flatten Layer | 1 × 7424 | 7424 neurons |
| Input Layer | 1 × 7424 | 7424 neurons |
| Dense | 1 × 1024 | 1024 neurons |
| Dropout | 1 × 1024 | Dropout rate: 0.4 |
| Dense | 1 × 512 | 512 neurons |
| Dropout | 1 × 512 | Dropout rate: 0.4 |
| Dense | 1 × 128 | 128 neurons |
| Dropout | 1 × 128 | Dropout rate: 0.4 |
| Dense | 1 × 3 | 128 neurons |
| SoftMax | 1 × 3 | Classification Layer |
| Healthy | Delamination 1 | Delamination 2 | |
|---|---|---|---|
| Beta 1 | 0.5 | 0.5 | 0.5 |
| Beta 2 | 0.999 | 0.999 | 0.999 |
| Learning rate | 1 × 10−3 | 1 × 10−3 | 1 × 10−3 |
| Epoch | 1200 | 1200 | 1200 |
| Batch size | 8 | 8 | 8 |
| Healthy | Delamination 1 | Delamination 2 | |
|---|---|---|---|
| Experimental data only | 800 | 48 | 48 |
| ADASYN | 800 | 793 | 798 |
| SI | 3000 | 3000 | 3000 |
| GAN | 3000 | 3000 | 3000 |
| WGAN | 3000 | 3000 | 3000 |
| Accuracy (%) | Precision (%) | Sensitivity (%) | F1 Score | |
|---|---|---|---|---|
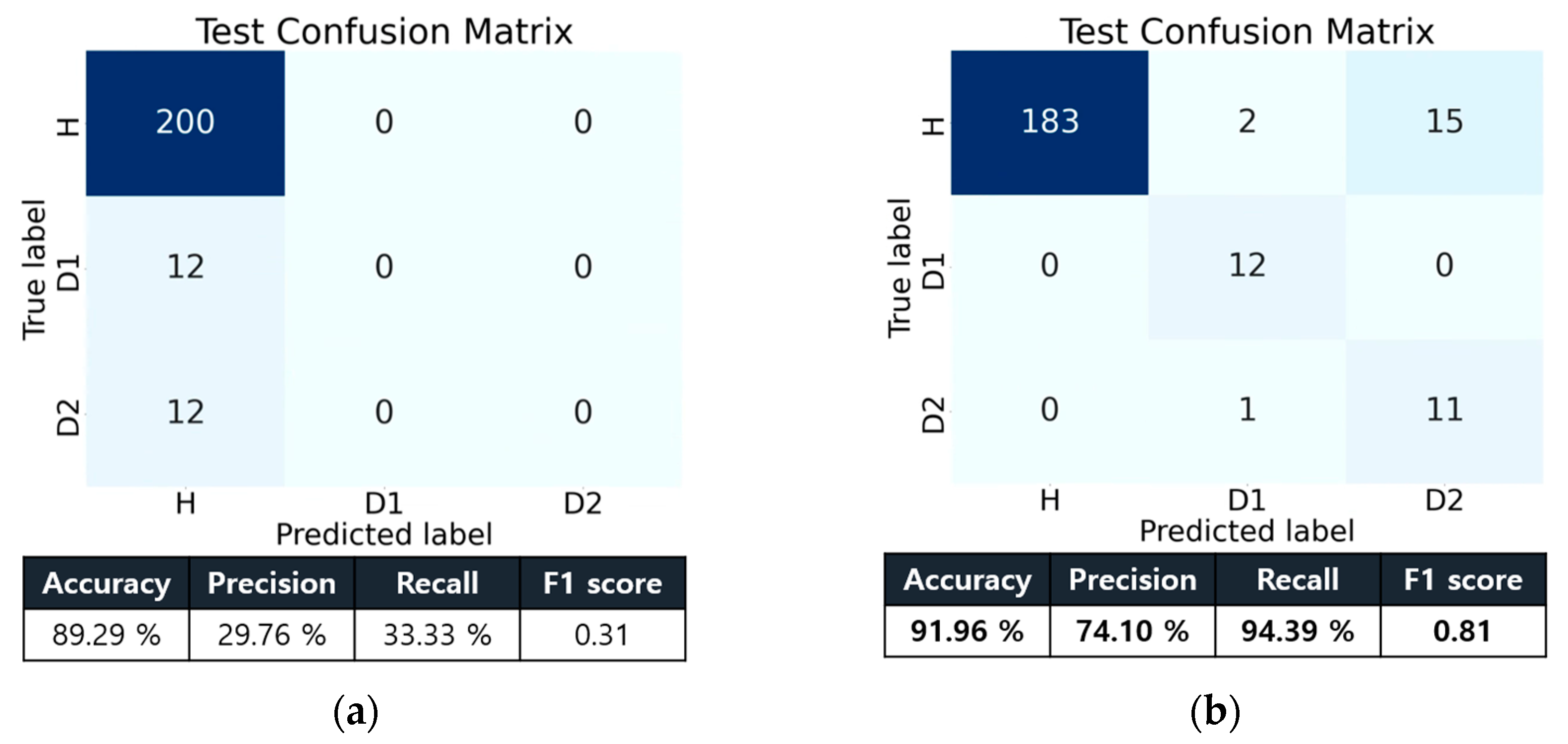
| Experimental data only | 89.29 | 29.76 | 33.33 | 0.31 |
| ADASYN | 90.63 | 77.80 | 91.28 | 0.81 |
| SI | 5.80 | 35.13 | 35.00 | 0.04 |
| GAN | 86.61 | 53.83 | 55.83 | 0.55 |
| WGAN | 91.96 | 74.10 | 94.39 | 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Azad, M.M.; Song, J.; Kim, H. Delamination Detection Framework for the Imbalanced Dataset in Laminated Composite Using Wasserstein Generative Adversarial Network-Based Data Augmentation. Appl. Sci. 2023, 13, 11837. https://doi.org/10.3390/app132111837
Kim S, Azad MM, Song J, Kim H. Delamination Detection Framework for the Imbalanced Dataset in Laminated Composite Using Wasserstein Generative Adversarial Network-Based Data Augmentation. Applied Sciences. 2023; 13(21):11837. https://doi.org/10.3390/app132111837
Chicago/Turabian StyleKim, Sungjun, Muhammad Muzammil Azad, Jinwoo Song, and Heungsoo Kim. 2023. "Delamination Detection Framework for the Imbalanced Dataset in Laminated Composite Using Wasserstein Generative Adversarial Network-Based Data Augmentation" Applied Sciences 13, no. 21: 11837. https://doi.org/10.3390/app132111837
APA StyleKim, S., Azad, M. M., Song, J., & Kim, H. (2023). Delamination Detection Framework for the Imbalanced Dataset in Laminated Composite Using Wasserstein Generative Adversarial Network-Based Data Augmentation. Applied Sciences, 13(21), 11837. https://doi.org/10.3390/app132111837








