Local Thickness Optimization of Functionally Graded Lattice Structures in Compression
Abstract
:1. Introduction
1.1. Functionally Graded Lattice Structures
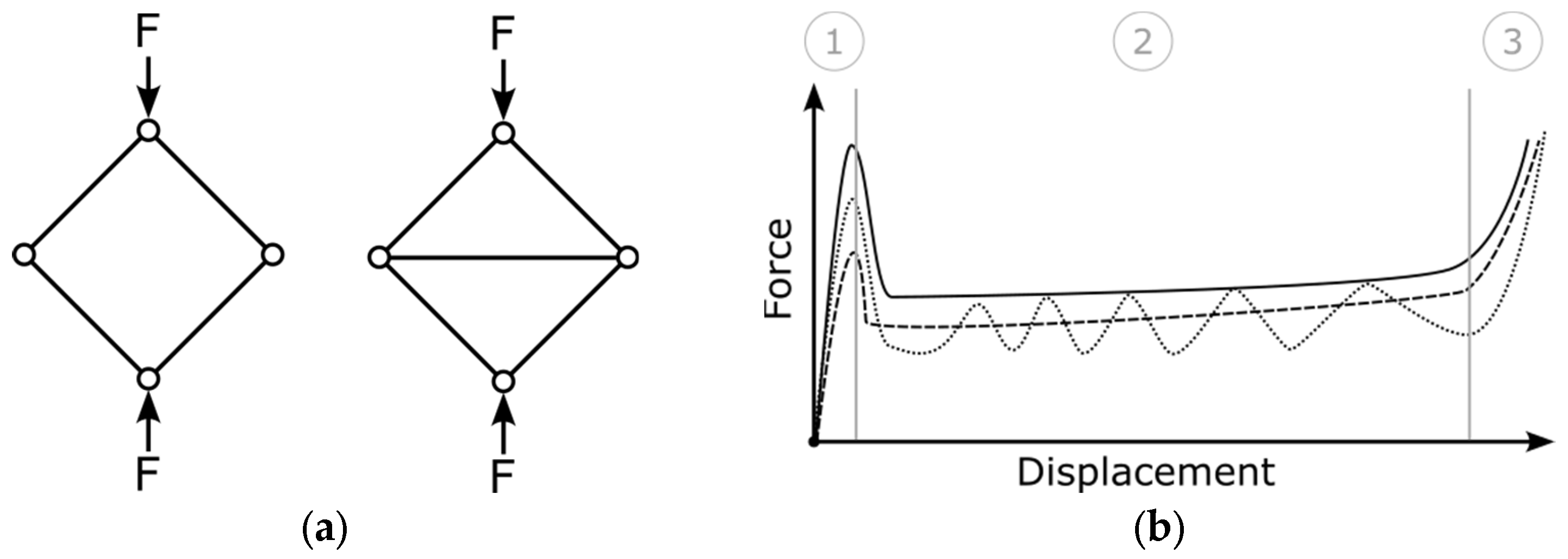
1.2. Functionally Graded Lattice Structures Incorporating a Thickness Gradient under Compressive Loads
1.3. Motivation, Aim, and Scope
2. Materials and Methods
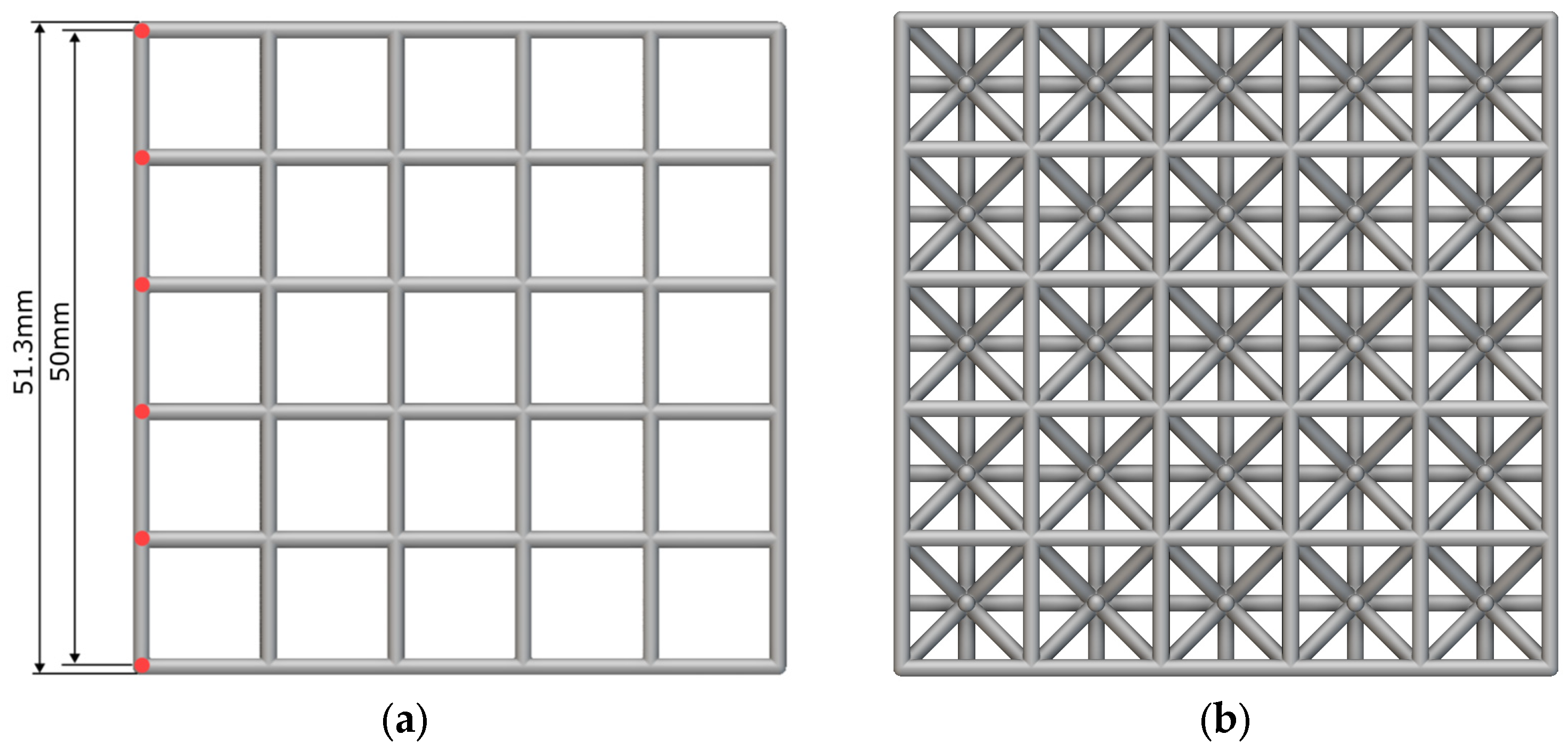
2.1. Geometry
2.2. Material Parameters and Sample Manufacturing
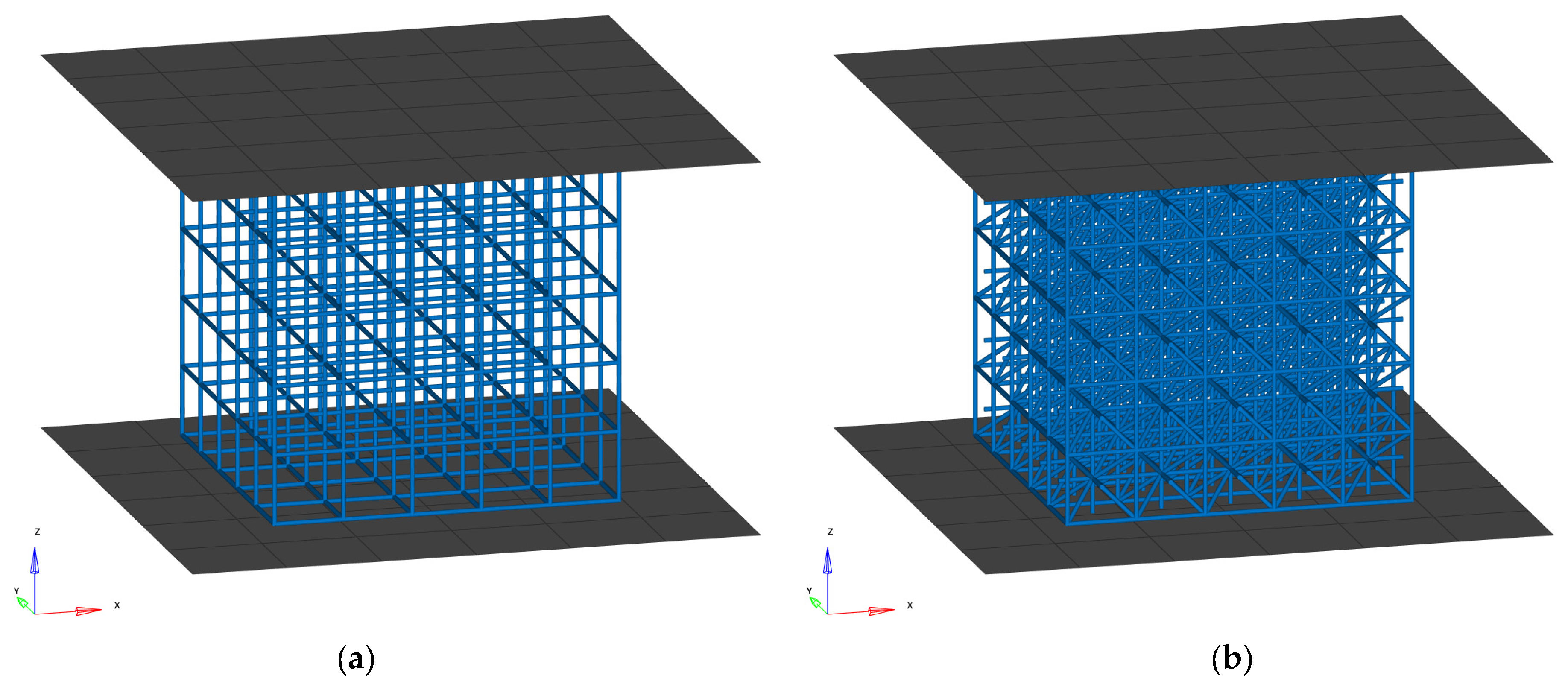
2.3. Finite Element Model and Optimization Setup
2.3.1. The Finite Element Model Setup
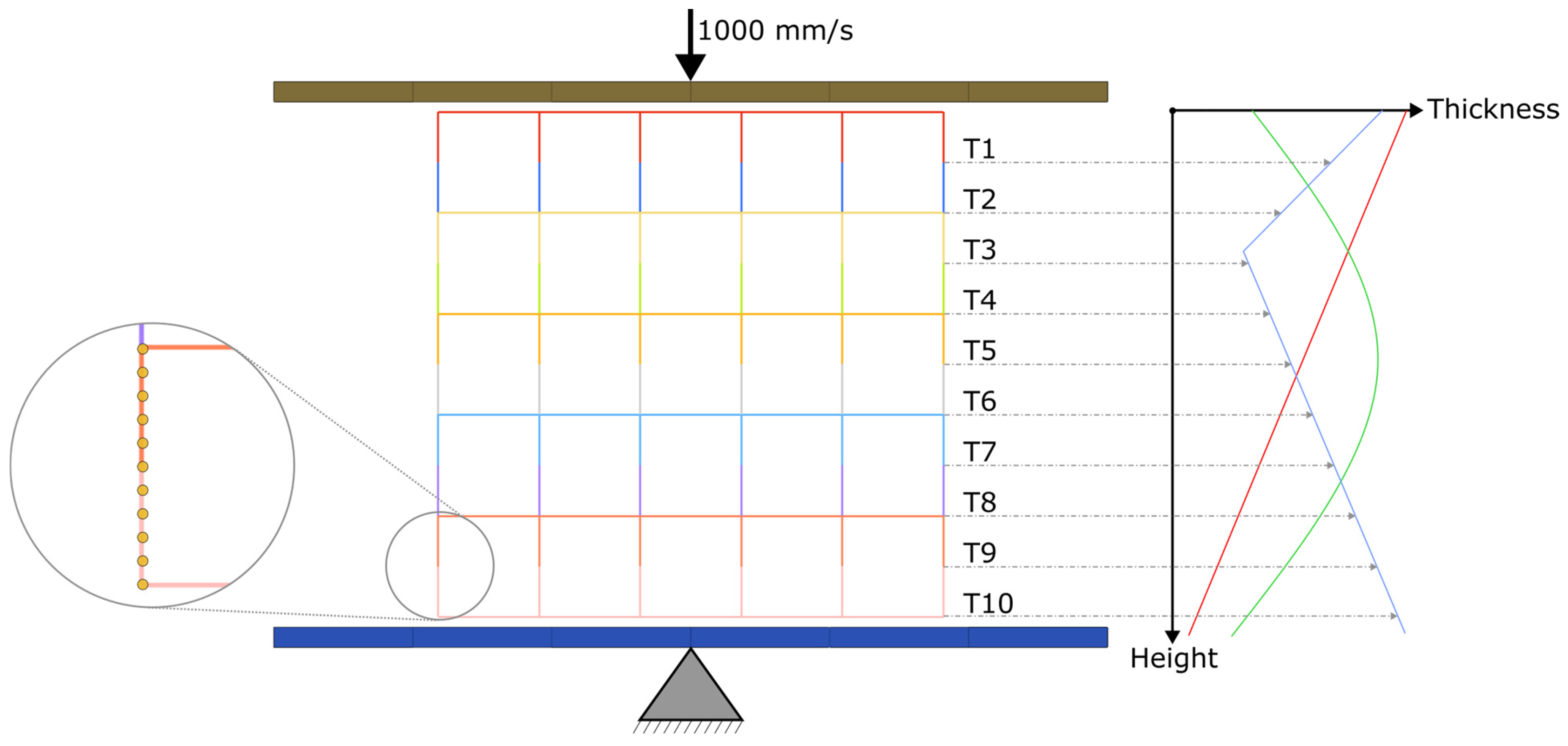
2.3.2. Splitting and Linking of the Lattice
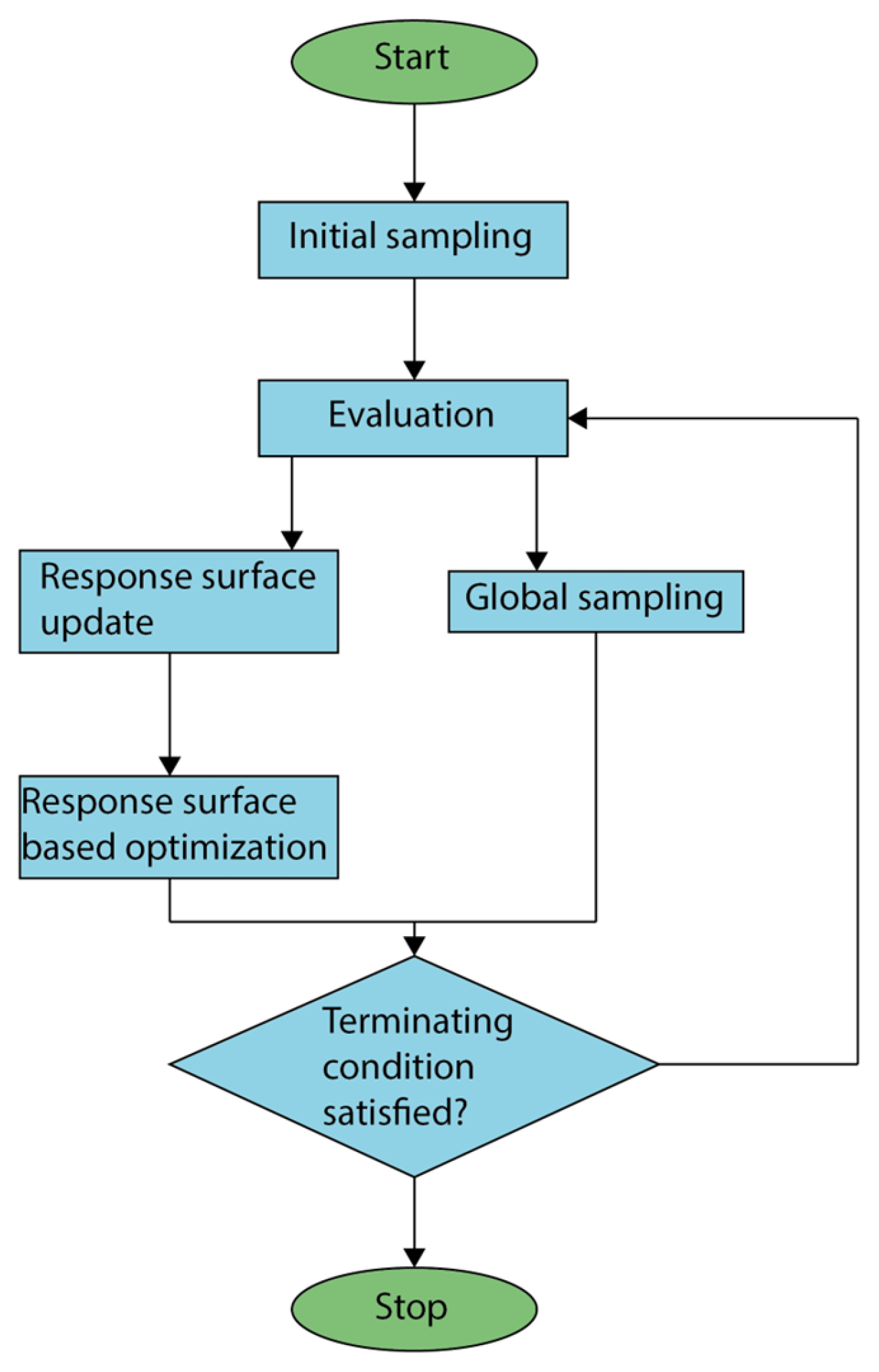
2.3.3. Thickness Optimization Procedure
2.4. Physical Testing
3. Results
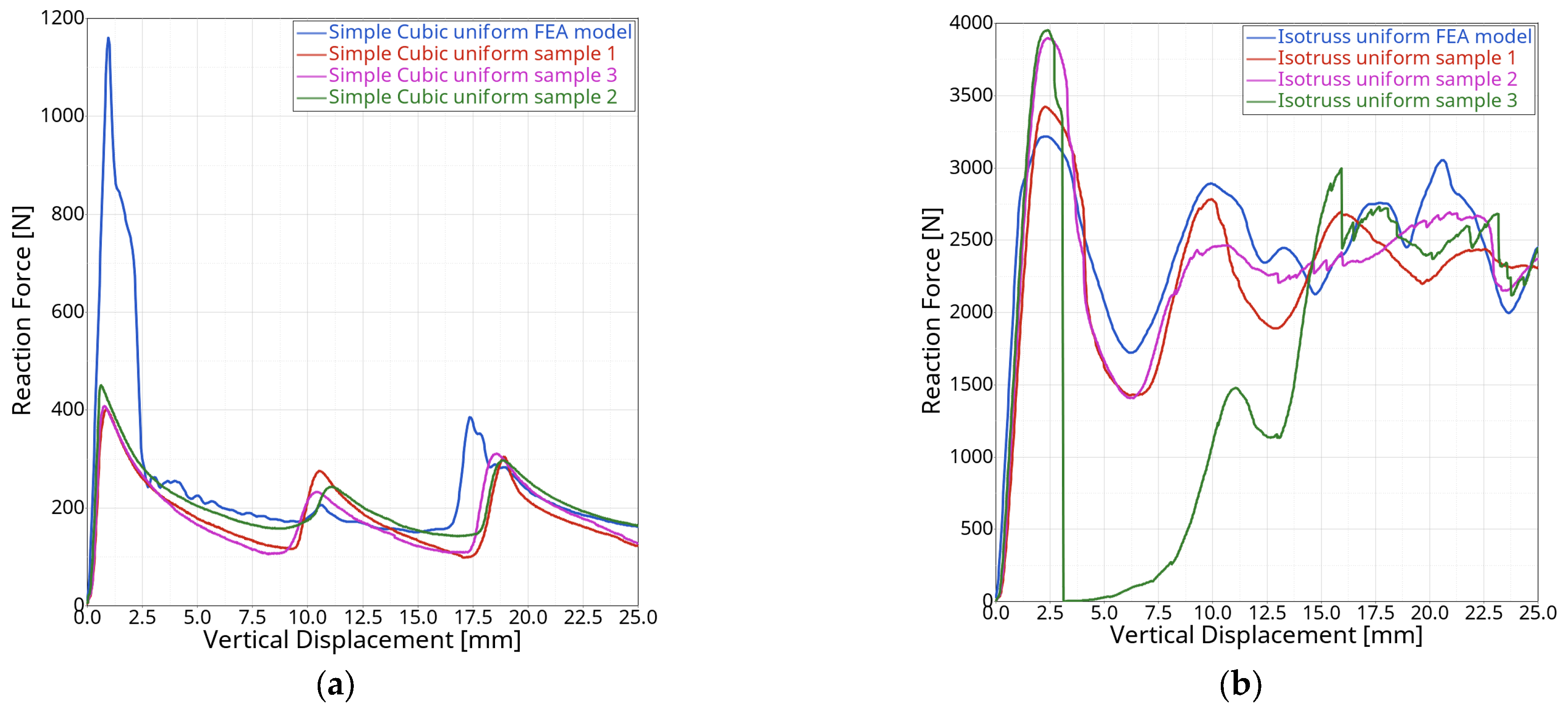
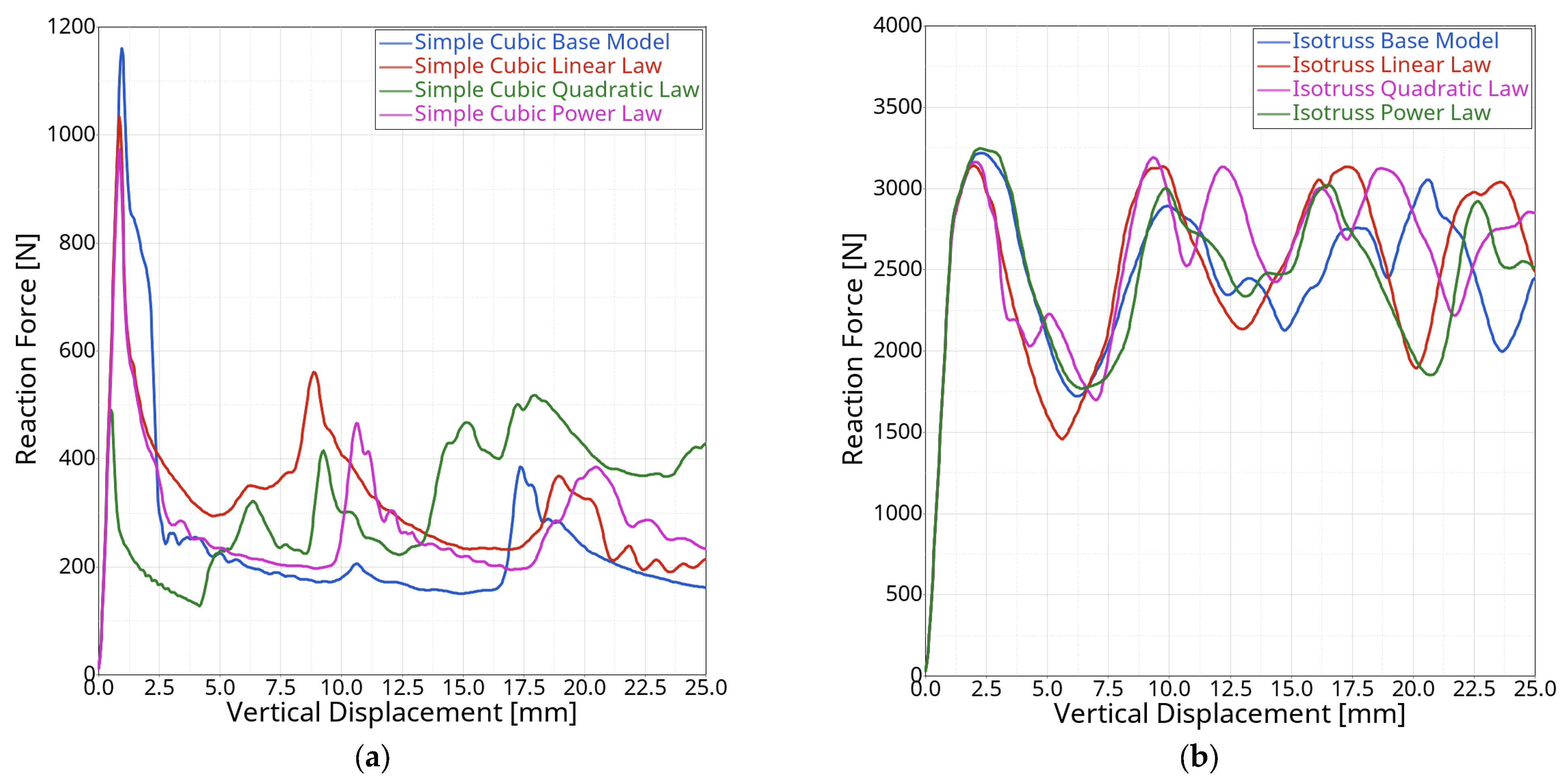
3.1. Physical Test of Uniform Lattice Structures
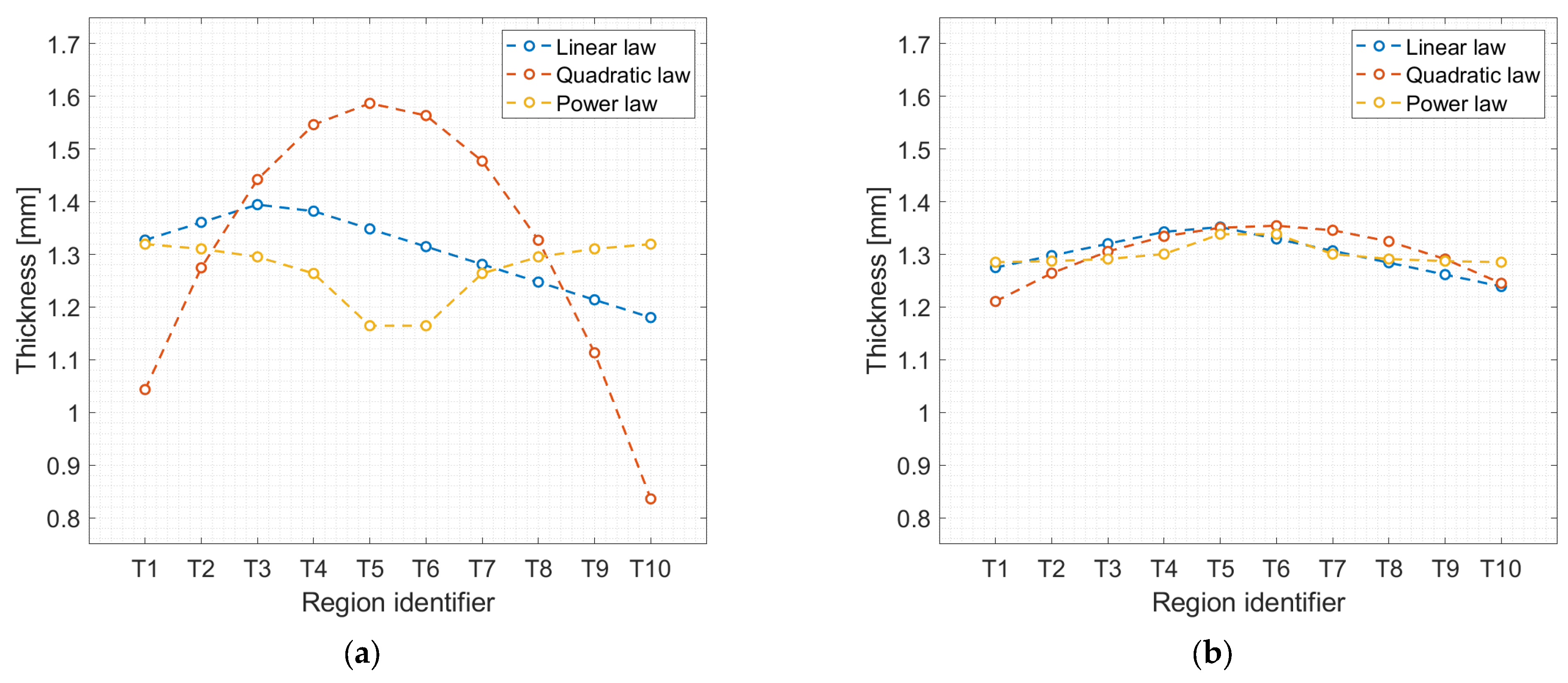
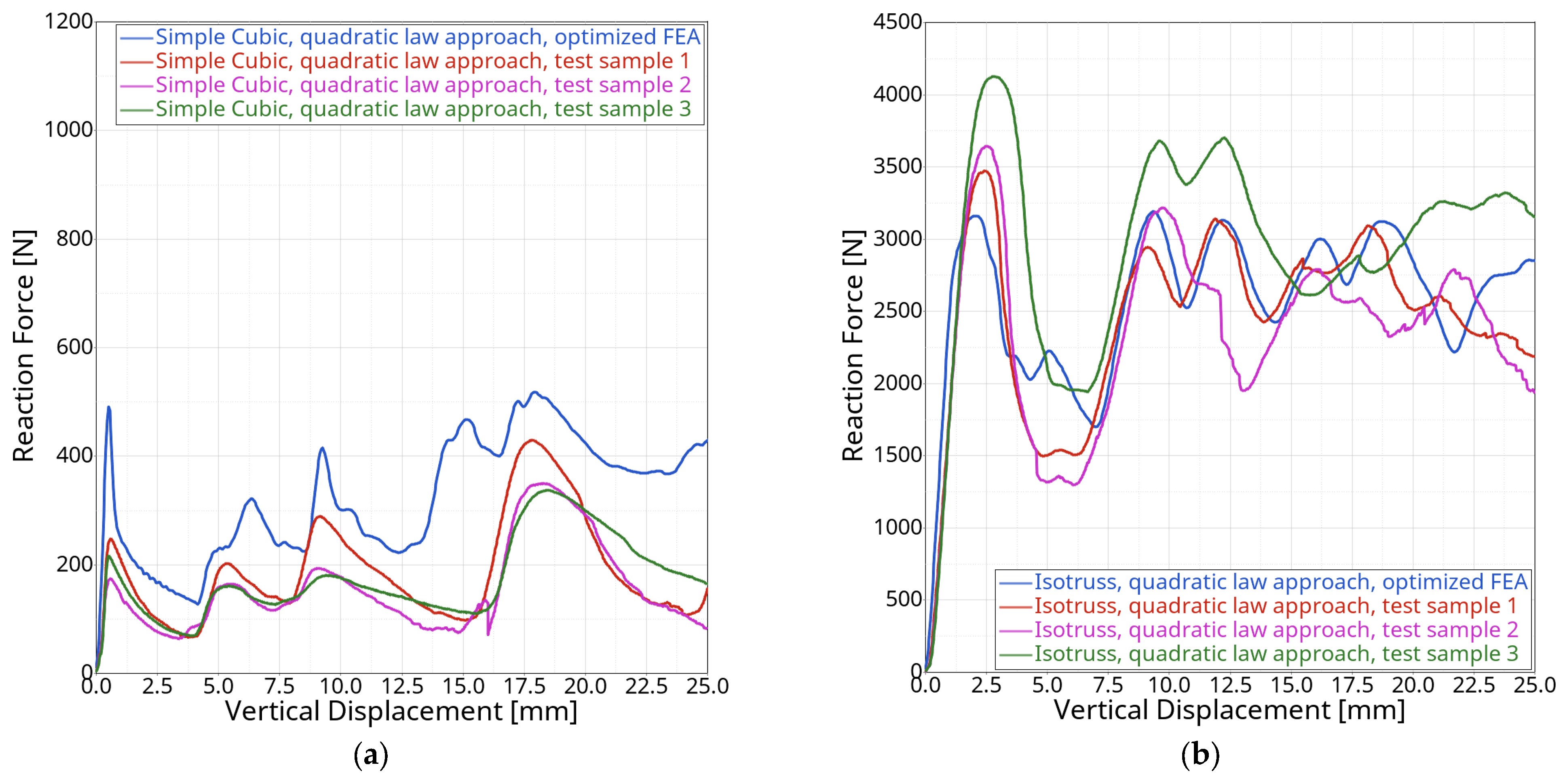
3.2. FEA Optimization Results
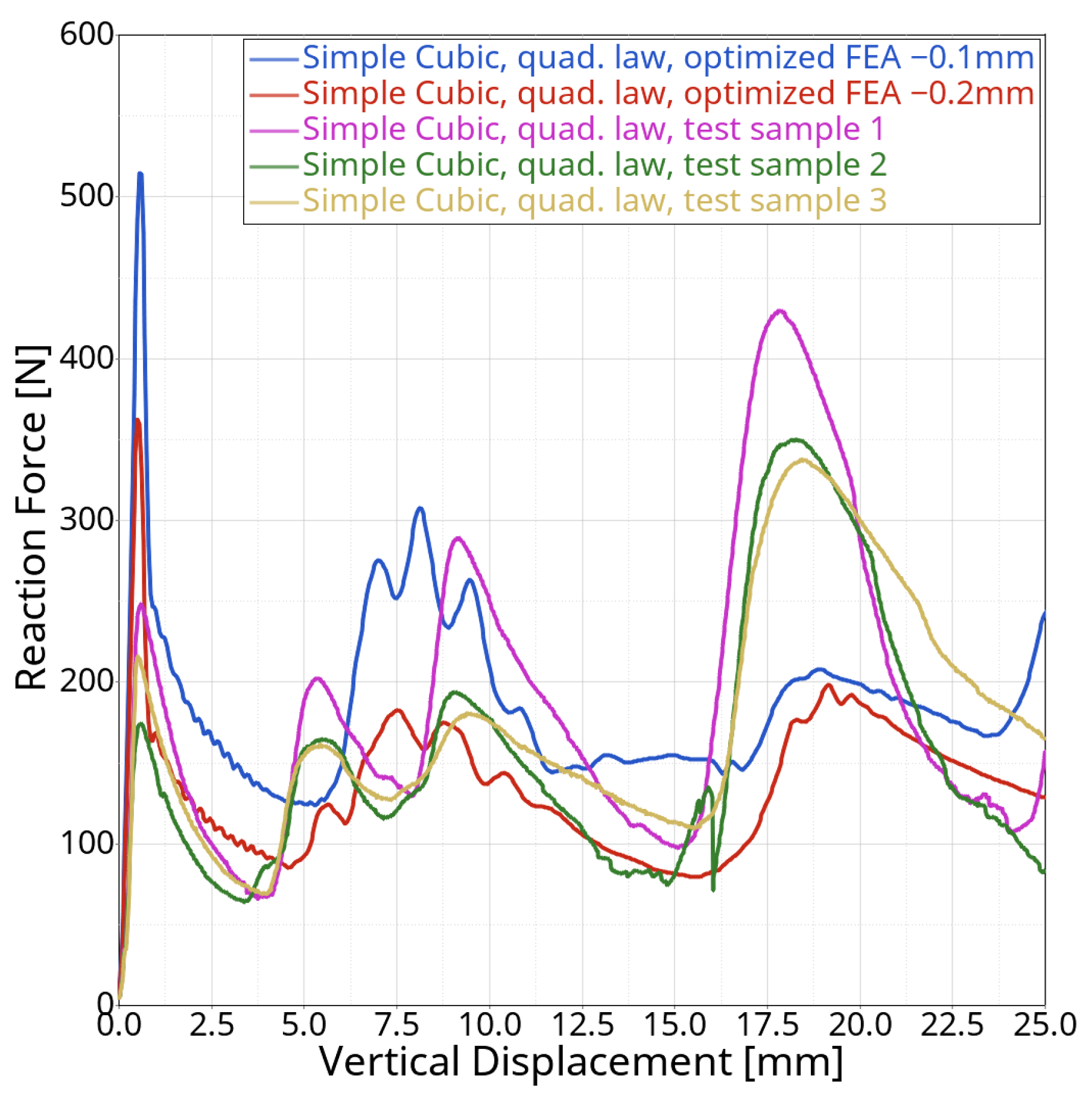
3.3. Physical Test Results of Optimized Lattices
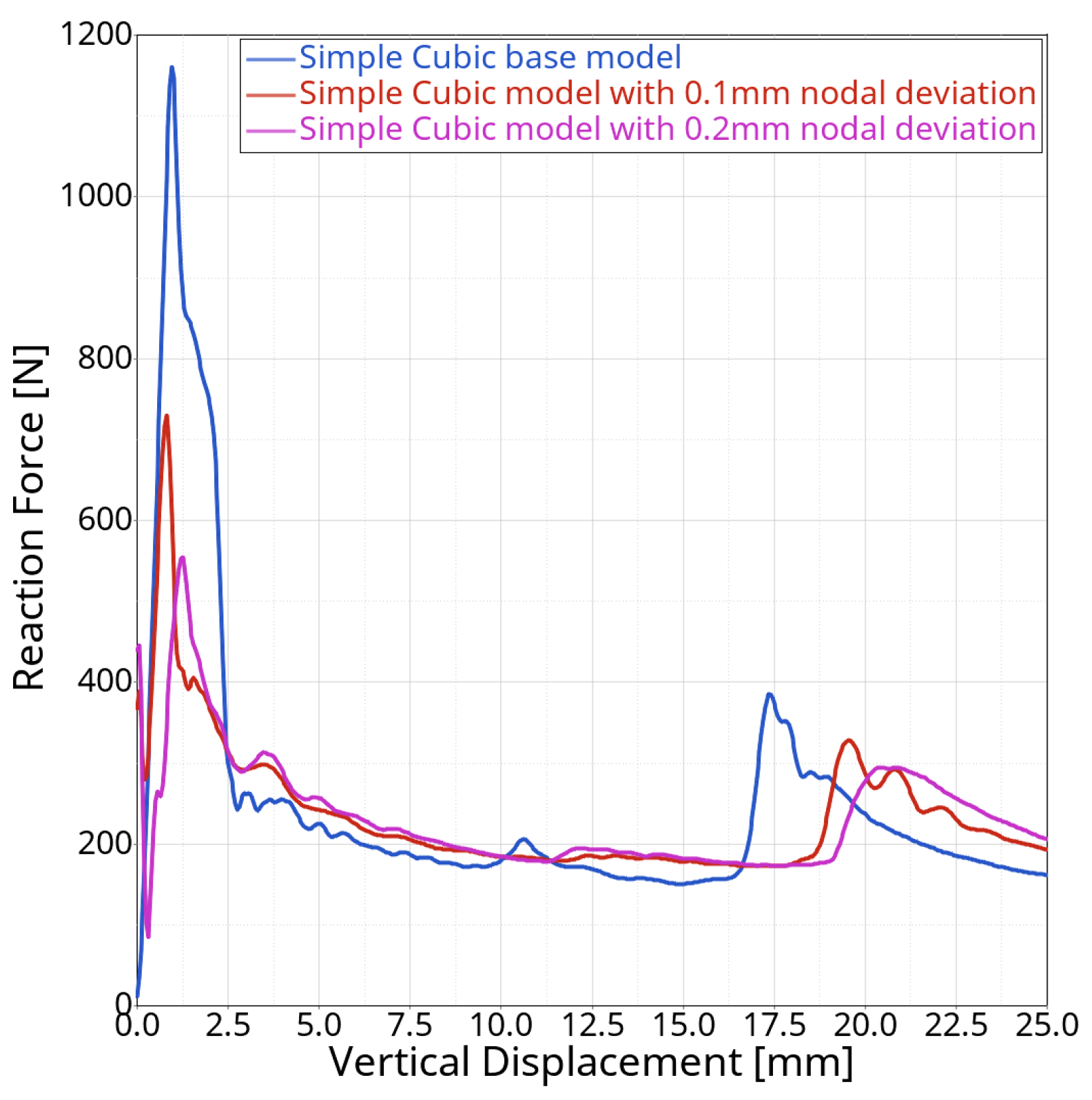
3.4. Discussion of the Results
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anné, G.; Vleugels, J.; Van Der Biest, O. Functionally graded ceramics. In Ceramic-Matrix Composites: Microstructure, Properties and Applications; Elsevier: Amsterdam, The Netherlands, 2006; pp. 575–596. [Google Scholar] [CrossRef]
- Shabana, Y.M.; Noda, N.; Tohgo, K. Elasto-plastic thermal stresses in functionally graded materials considering microstructure effects. In Proceedings of the Seventh Cairo University International MDP Conference, Cairo, Egypt, 15–17 February 2000. [Google Scholar]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2 + Ni) functionally graded bolted joint. Compos. Part B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Noronha, J.; Dash, J.; Leary, M.; Watson, M.; Qian, M.; Kyriakou, E.; Brandt, M. Additively Manufactured Functionally Graded Lattices: Design, Mechanical Response, Deformation Behavior, Applications, and Insights. JOM 2023, 75, 5729–5754. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure & Properties; Cambridge University Press: Oxford, UK, 1988. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, X.; Liu, S. Finite-element-mesh based method for modeling and optimization of lattice structures for additive manufacturing. Materials 2018, 11, 2073. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Chen, X.; Sun, Y.; Zhang, J.; Feng, C.; Wang, Y.; Wang, K.; Bai, L. Compressive properties of bidirectionally graded lattice structures. Mater. Des. 2022, 218, 110683. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Zhou, W.; Fan, R.; Yu, B.; Lu, Y.; Li, L. Topology optimization-guided lattice composites and their mechanical characterizations. Compos. Part B Eng. 2018, 160, 402–411. [Google Scholar] [CrossRef]
- Rahman, H.; Yarali, E.; Zolfagharian, A.; Serjouei, A.; Bodaghi, M. Energy absorption and mechanical performance of functionally graded soft–hard lattice structures. Materials 2021, 14, 1366. [Google Scholar] [CrossRef] [PubMed]
- Pham, M.-S.; Liu, C.; Todd, I.; Lertthanasarn, J. Damage-tolerant architected materials inspired by crystal microstructure. Nature 2019, 565, 305–311. [Google Scholar] [CrossRef] [PubMed]
- Daynes, S.; Feih, S.; Lu, W.F.; Wei, J. Optimisation of functionally graded lattice structures using isostatic lines. Mater. Des. 2017, 127, 215–223. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.M.; Wu, X.; Wang, Z.; Li, Q.; Zhou, S. On hybrid cellular materials based on triply periodic minimal surfaces with extreme mechanical properties. Mater. Des. 2019, 183, 108109. [Google Scholar] [CrossRef]
- Wu, J.; Aage, N.; Westermann, R.; Sigmund, O. Infill Optimization for Additive Manufacturing—Approaching Bone-Like Porous Structures. IEEE Trans. Vis. Comput. Graph. 2017, 24, 1127–1140. [Google Scholar] [CrossRef] [PubMed]
- Niknam, H.; Akbarzadeh, A. Graded lattice structures: Simultaneous enhancement in stiffness and energy absorption. Mater. Des. 2020, 196, 109129. [Google Scholar] [CrossRef]
- Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Dynamic crushing and energy absorption of regular, irregular and functionally graded cellular structures. Int. J. Solids Struct. 2011, 48, 506–516. [Google Scholar] [CrossRef]
- Maskery, I.; Hussey, A.; Panesar, A.; Aremu, A.; Tuck, C.; Ashcroft, I.; Hague, R. An investigation into reinforced and functionally graded lattice structures. J. Cell. Plast. 2016, 53, 151–165. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J.M. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Choy, S.Y.; Sun, C.-N.; Leong, K.F.; Wei, J. Compressive properties of functionally graded lattice structures manufactured by selective laser melting. Mater. Des. 2017, 131, 112–120. [Google Scholar] [CrossRef]
- Tao, W.; Liu, Y.; Sutton, A.; Kolan, K.; Leu, M.C. EasyChair Preprint Design of Lattice Structures with Graded Density Fabricated by Additive Manufacturing “Design of lattice structures with graded density fabricated by additive manufacturing”. In Proceedings of the 2018 International Symposium on Flexible Automation, ISFA 2018, Kanazawa, Japan, 15–19 July 2018. [Google Scholar]
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical properties and energy absorption capabilities of functionally graded lattice structures: Experiments and simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- nTop. Available online: https://www.ntop.com (accessed on 31 October 2023).
- HP MJF. Available online: https://www.hp.com/us-en/printers/3d-printers/learning-center/3d-printing-process.html#section=hp-multi-jet-fusion (accessed on 31 October 2023).
- Decker, T.; Kedziora, S.; Museyibov, E. Comparison of Strength Properties of Common Powder Bed Fusion and Stereolithography Materials. In Proceedings of the 11th International Conference on Nano and Materials Science, Singapore, 13–15 January 2023. [Google Scholar]
- Faes, M.; Wang, Y.; Lava, P.; Moens, D. Variability in the mechanical properties of laser sintered PA-12 components. In Proceedings of the 26th Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 10–12 August 2015; SFF: Singapore, 2015; pp. 847–856. [Google Scholar]
- Aldahash, S.A. Friction and wear properties of oriented Polaymide 12 objects manufactured by SLS Technology. J. Engin. Appl. Sci. 2019, 15, 9–25. [Google Scholar]
- Roppenecker, D.B.; Grazek, R.; Coy, J.A.; Irlinger, F.; Lueth, T.C. Friction coefficients and surface properties for laser sintered parts. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Proceedings (IMECE), San Diego, CA, USA, 15–21 November 2013; Volume 2, pp. 1–10. [Google Scholar]
- Altair. Available online: https://altair.com (accessed on 31 October 2023).
- Altair HyperMesh. Available online: https://altair.com/hypermesh/ (accessed on 31 October 2023).
- Altair HyperStudy. Available online: https://altair.com/hyperstudy/ (accessed on 31 October 2023).
- Fischer, S.F.; Thielen, M.; Loprang, R.R.; Seidel, R.; Fleck, C.; Speck, T.; Bührig-Polaczek, A. Pummelos as concept generators for biomimetically inspired low weight structures with excellent damping properties. Adv. Eng. Mater. 2010, 12, B658–B663. [Google Scholar] [CrossRef]
- Modifiable Extensible Lattice Sequence (MELS). Available online: https://2021.help.altair.com/2021.2/hwdesktop/hst/topics/design_exploration/method_modified_extensible_lattice_sequence_doe_r.htm (accessed on 31 October 2023).
- Global Response Search Method (GRSM). Available online: https://2021.help.altair.com/2021.2/hwdesktop/hst/topics/design_exploration/method_global_response_surface_method_r.htm (accessed on 31 October 2023).
- Liu, X.; Wada, T.; Suzuki, A.; Takata, N.; Kobashi, M.; Kato, M. Understanding and suppressing shear band formation in strut-based lattice structures manufactured by laser powder bed fusion. Mater. Des. 2021, 199, 109416. [Google Scholar] [CrossRef]







| Physical Properties of HP PA12 | |
|---|---|
| Secant modulus at 0.1% strain | 1480 MPa |
| Poisson’s ratio | 0.4 (from [24]) |
| Density | 0.94 g/cm³ |
| Ultimate tensile strength | 50.6 MPa |
| Offset yield strength, | 29.6 MPa |
| Engineering strain at break | 5.1% |
| a | b | c | |
|---|---|---|---|
| Linear law | ±0.02 | ±4 | ±200 |
| Quadratic law | ±0.001 | ±1 | ±50 |
| Power law | ±2 | ±2 | ±2 |
| Simple Cubic Lattice | Isotruss Lattice | |
|---|---|---|
| FEA model weight (g) | 6.74 | 22.22 |
| nTop model weight (g) | 6.2 | 19.0 |
| Actual weights (g) | 5.9/6.0/5.7 | 20.0/18.7/20.3 |
| Average of actual weights (g) | 5.86 | 19.67 |
| Simple Cubic Lattice | Isotruss Lattice | |||||
|---|---|---|---|---|---|---|
| Absorbed Energy (J) | Weight (g) | SEA (J/kg) | Absorbed Energy (J) | Weight (g) | SEA (J/kg) | |
| Sample 1 | 4.6 | 5.9 | 777 | 56.2 | 20.0 | 2809 |
| Sample 2 | 5.2 | 6.0 | 866 | 58.2 | 18.7 | 3114 |
| Sample 3 | 4.6 | 5.7 | 810 | 42.3 * | 20.3 | 2084 |
| Avg. samples | 4.8 | 5.9 | 818 | 52.2 | 19.7 | 2669 |
| Simulated | 6.3 | 6.74 | 940 | 61.8 | 22.22 | 2780 |
| Grading Approach | Simple Cubic Lattice | Isotruss Lattice | ||||
|---|---|---|---|---|---|---|
| Absorbed Energy (J) | Weight (g) | SEA (J/kg) | Absorbed Energy (J) | Weight (g) | SEA (J/kg) | |
| Baseline value | 6.3 | 6.74 g | 940 | 61.8 | 22.22 g | 2780 |
| Linear law | 8.1 | 6.71 g | 1213 (+29.0%) | 62.6 | 22.20 g | 2819 (+1.4%) |
| Quadratic law | 8.2 | 6.74 g | 1210 (+28.7%) | 65.1 | 22.27 g | 2921 (+5.1%) |
| Power law | 7.2 | 6.51 g | 1105 (+17.5%) | 61.7 | 22.23 g | 2775 (−0.2%) |
| Simple Cubic Lattice | Isotruss Lattice | |||||
|---|---|---|---|---|---|---|
| Absorbed Energy (J) | Weight (g) | SEA (J/kg) | Absorbed Energy (J) | Weight (g) | SEA (J/kg) | |
| Sample 1 | 4.7 | 6.0 | 784 | 61.5 | 18.8 | 3269 |
| Sample 2 | 3.9 | 5.4 | 719 | 58.8 | 18.9 | 3109 |
| Sample 3 | 4.4 | 5.8 | 752 | 73.9 | 20.3 | 3939 |
| Avg. samples | 4.1 | 5.7 | 752 | 64.7 | 19.3 | 3439 |
| Simulated | 8.2 | 6.74 | 1210 | 65.1 | 22.27 | 2921 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Decker, T.; Kedziora, S. Local Thickness Optimization of Functionally Graded Lattice Structures in Compression. Appl. Sci. 2023, 13, 12969. https://doi.org/10.3390/app132312969
Decker T, Kedziora S. Local Thickness Optimization of Functionally Graded Lattice Structures in Compression. Applied Sciences. 2023; 13(23):12969. https://doi.org/10.3390/app132312969
Chicago/Turabian StyleDecker, Thierry, and Slawomir Kedziora. 2023. "Local Thickness Optimization of Functionally Graded Lattice Structures in Compression" Applied Sciences 13, no. 23: 12969. https://doi.org/10.3390/app132312969
APA StyleDecker, T., & Kedziora, S. (2023). Local Thickness Optimization of Functionally Graded Lattice Structures in Compression. Applied Sciences, 13(23), 12969. https://doi.org/10.3390/app132312969






