Closed-Loop Current Stimulation Feedback Control of a Neural Mass Model Using Reservoir Computing
Abstract
1. Introduction
2. Methods
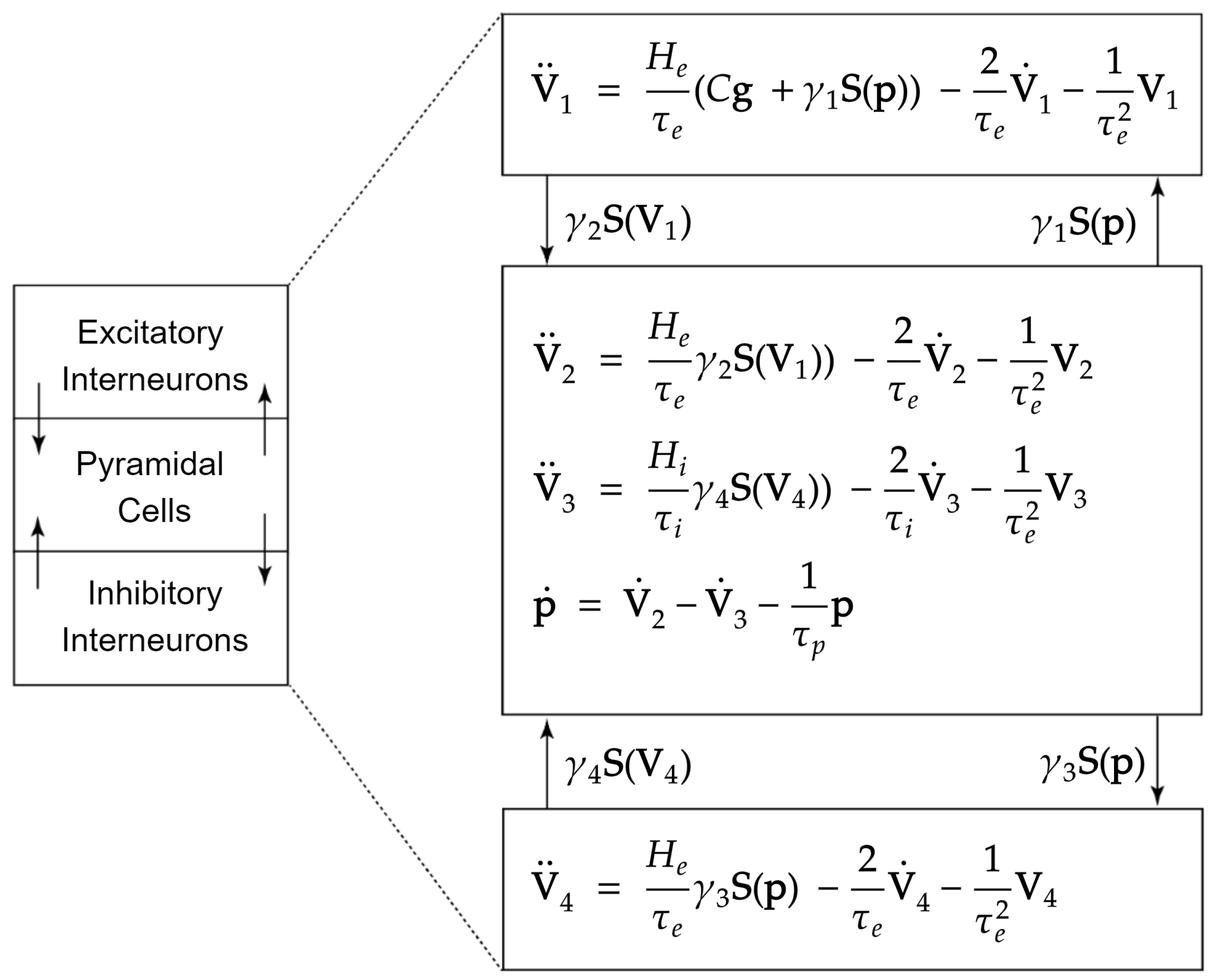
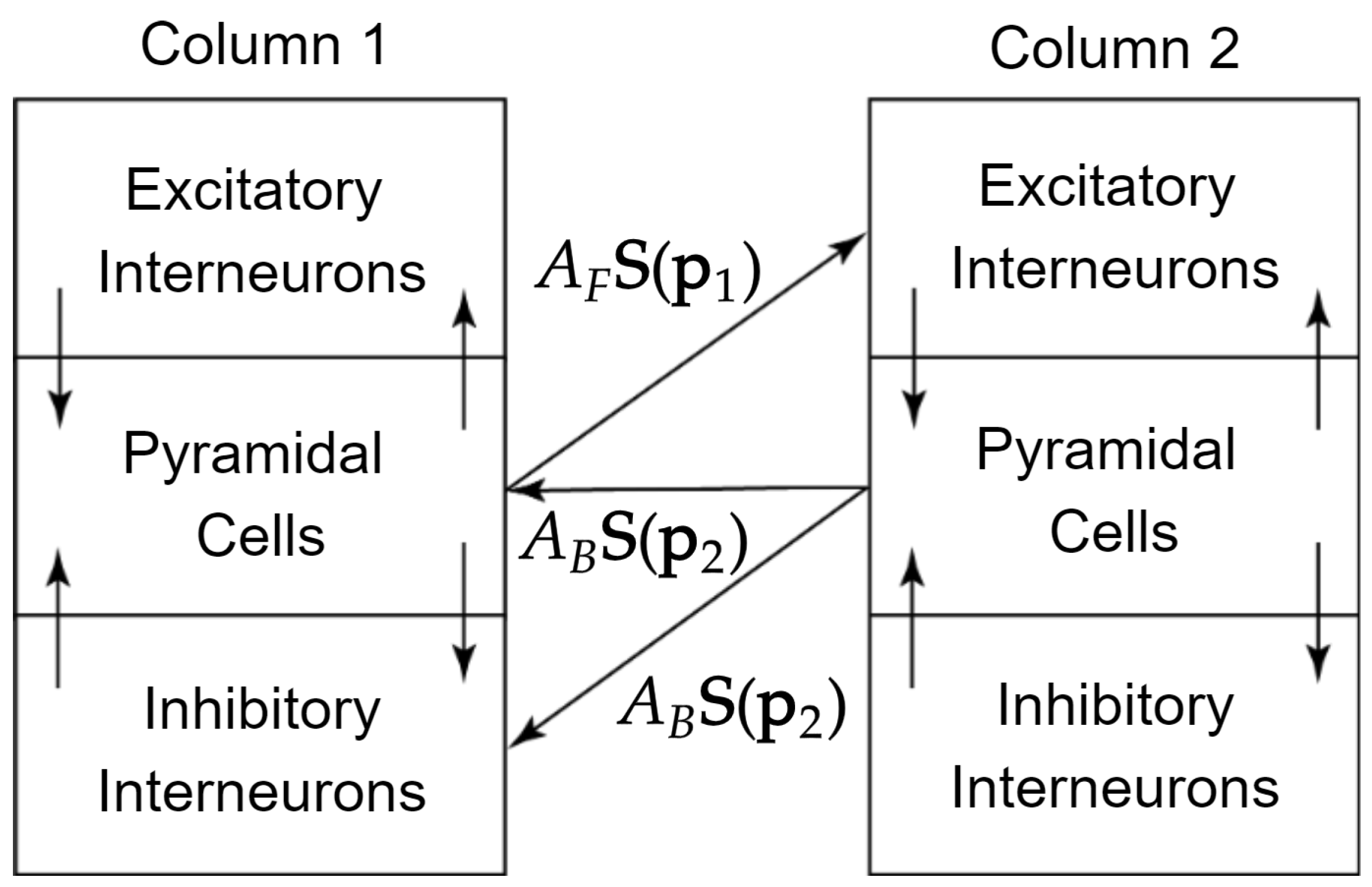
2.1. Jansen and Rit Neural Mass Model
2.2. Echo State Networks for Nonlinear Control
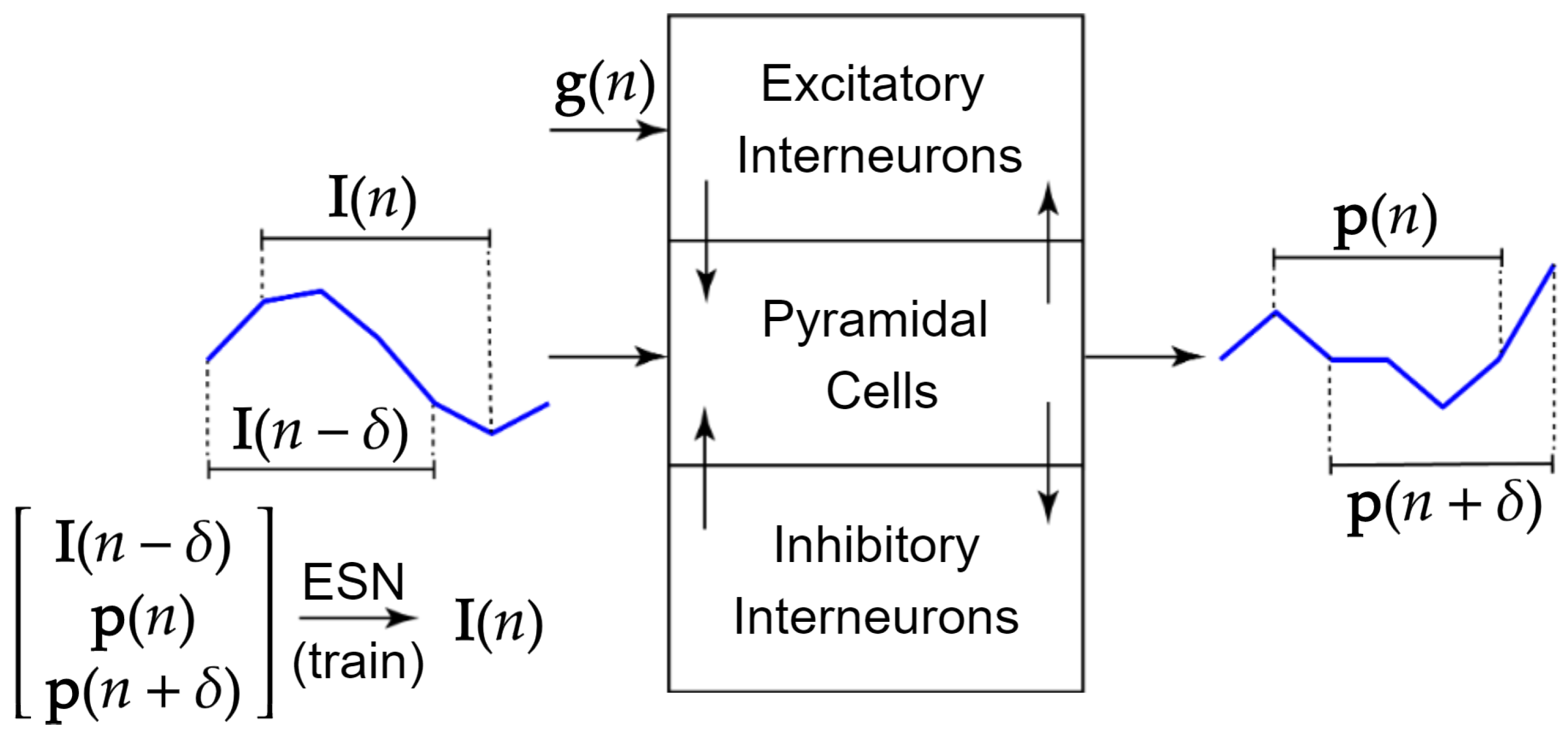
2.3. Current Stimulation Input Prediction
2.4. Training Set Generation
2.5. Training Parameters
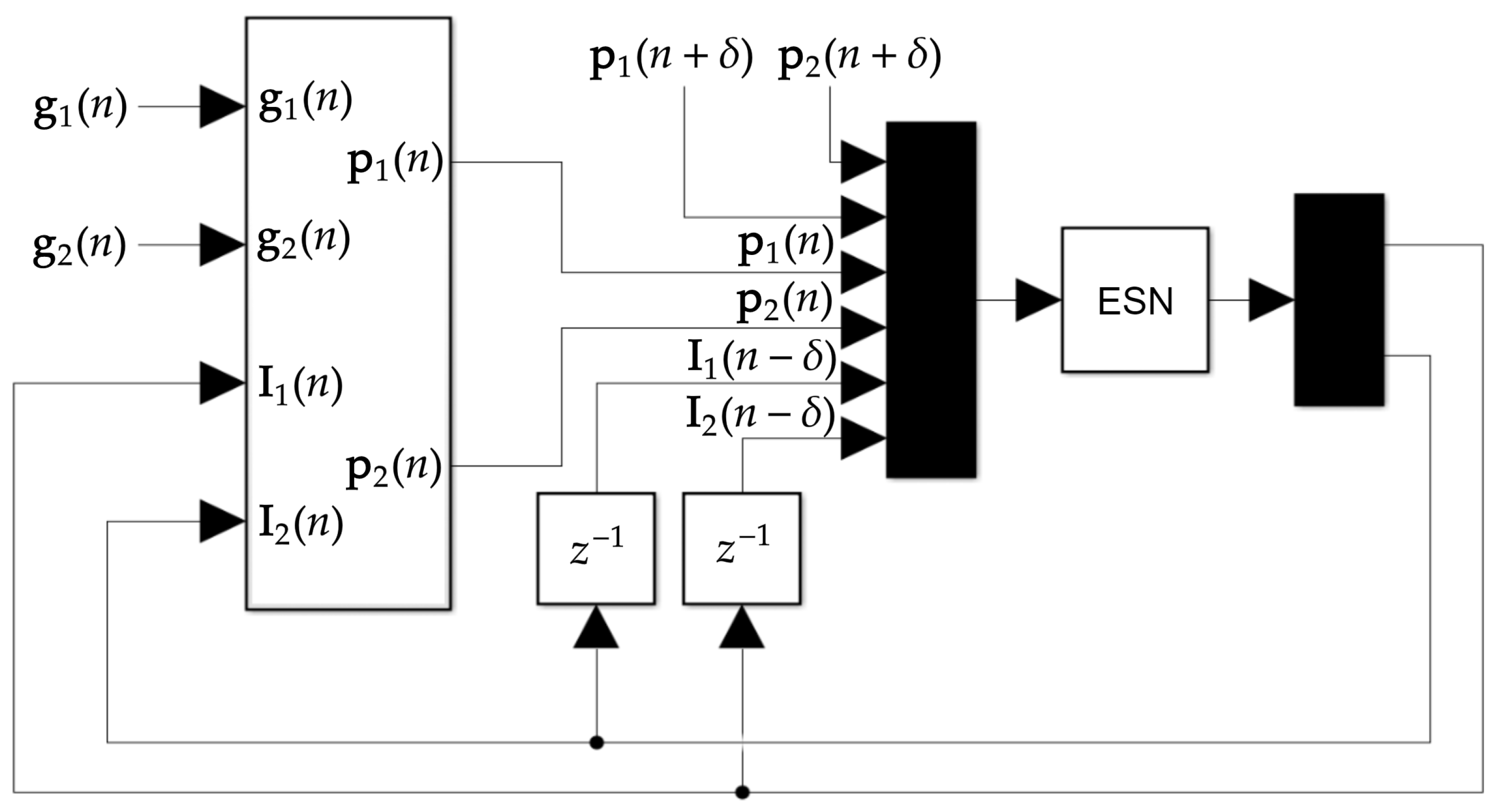
2.6. Closed-Loop Feedback Loop Using the ESN
2.7. ESN Performance Metrics
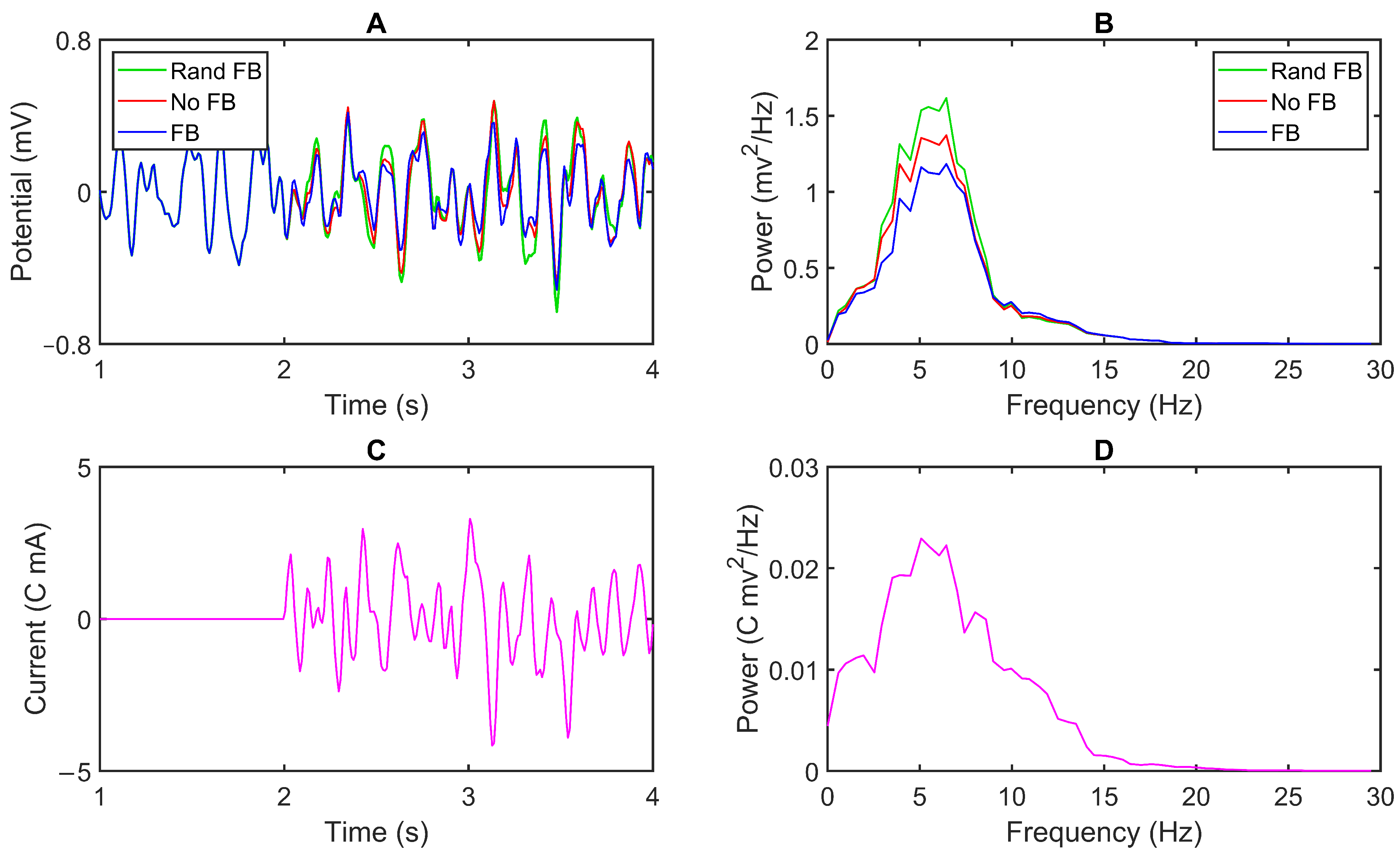
3. Results
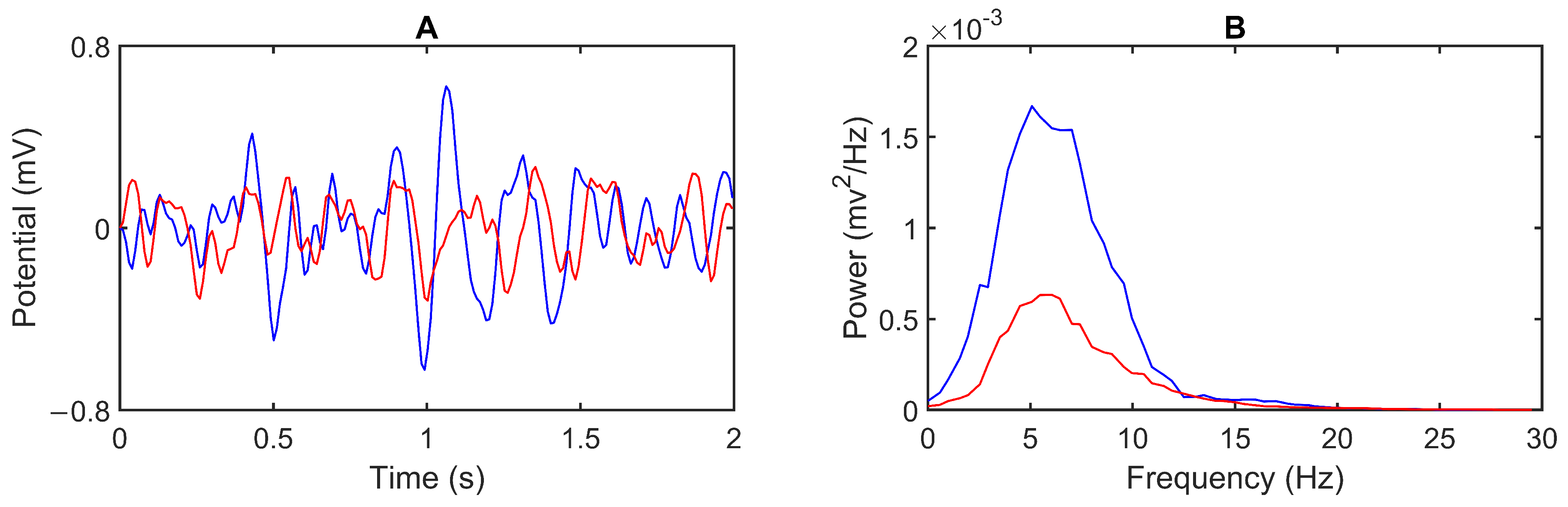
3.1. Model Output
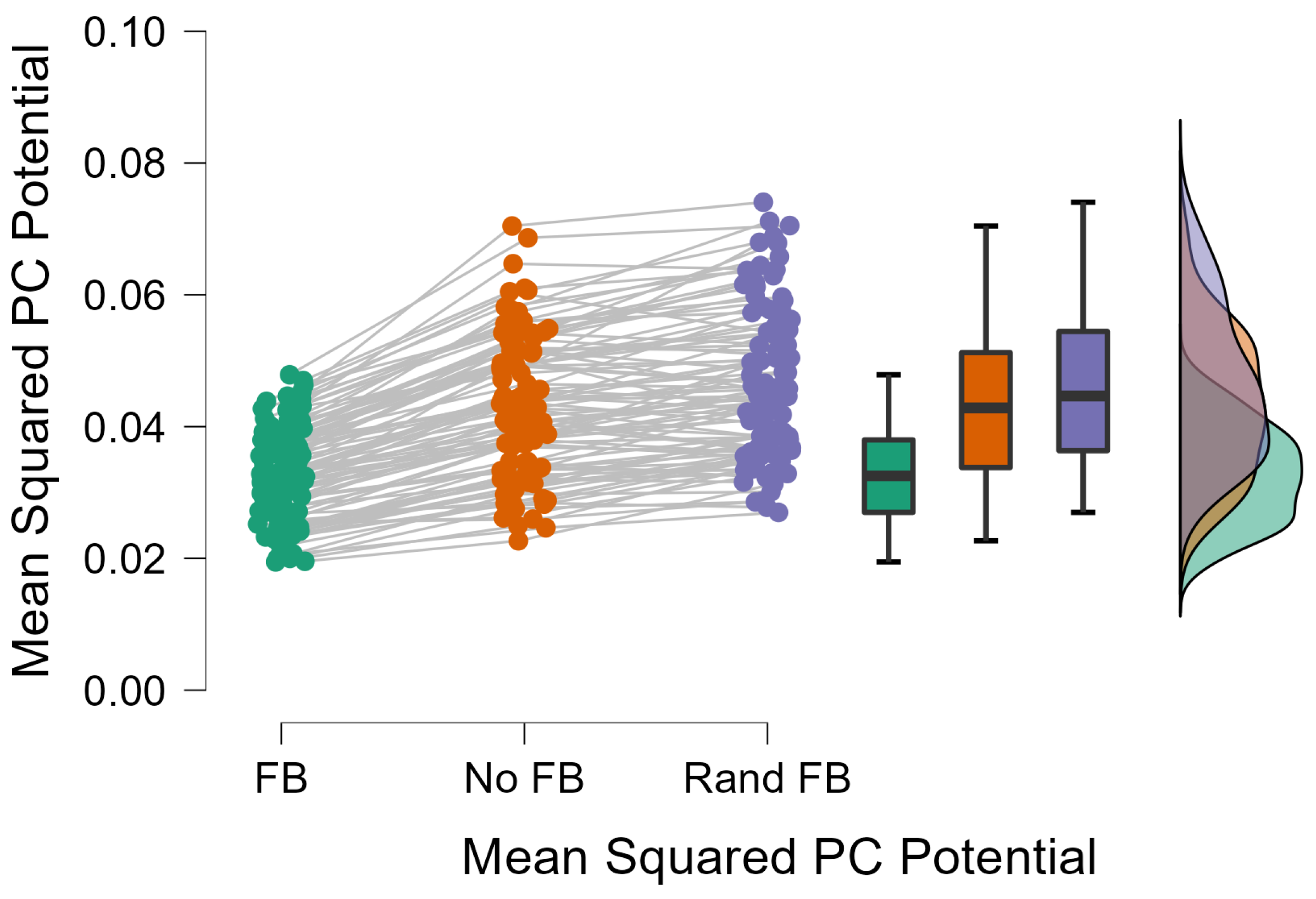
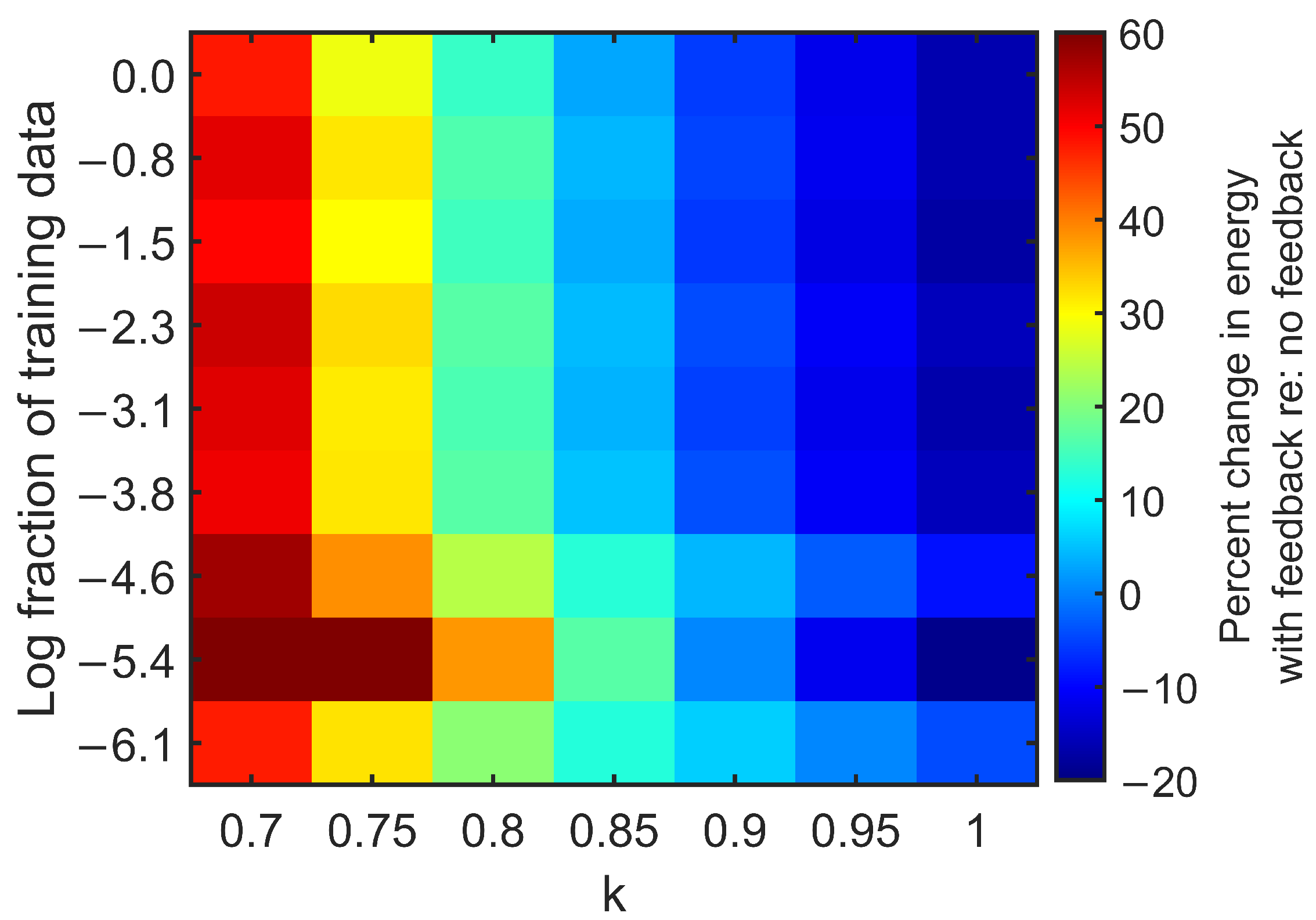
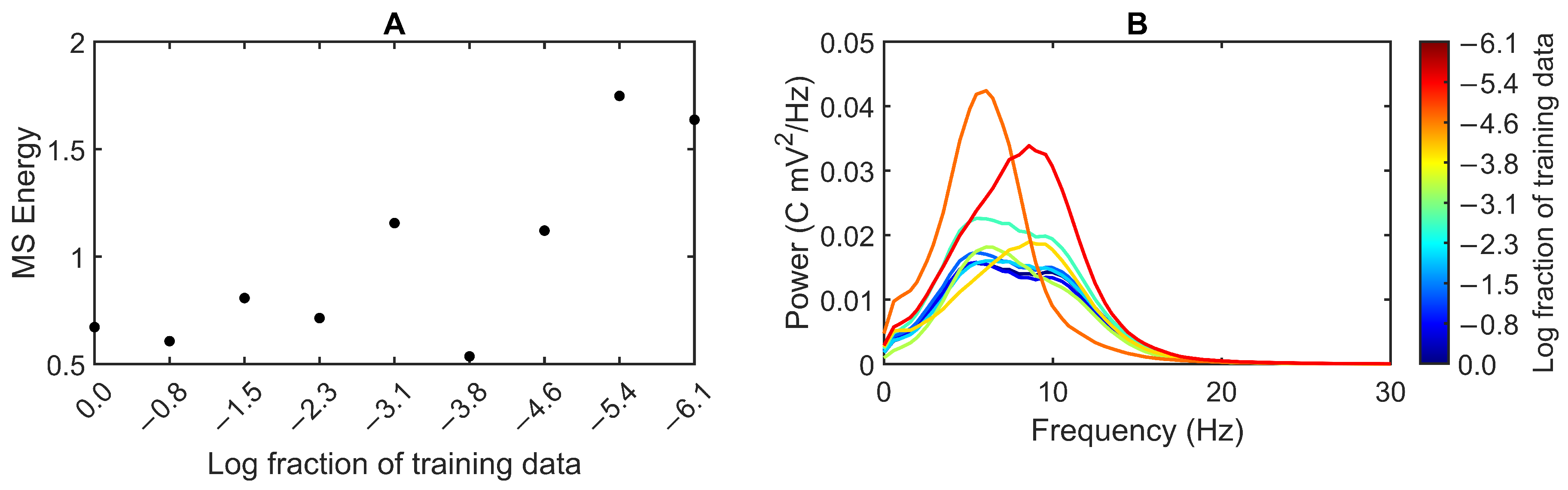
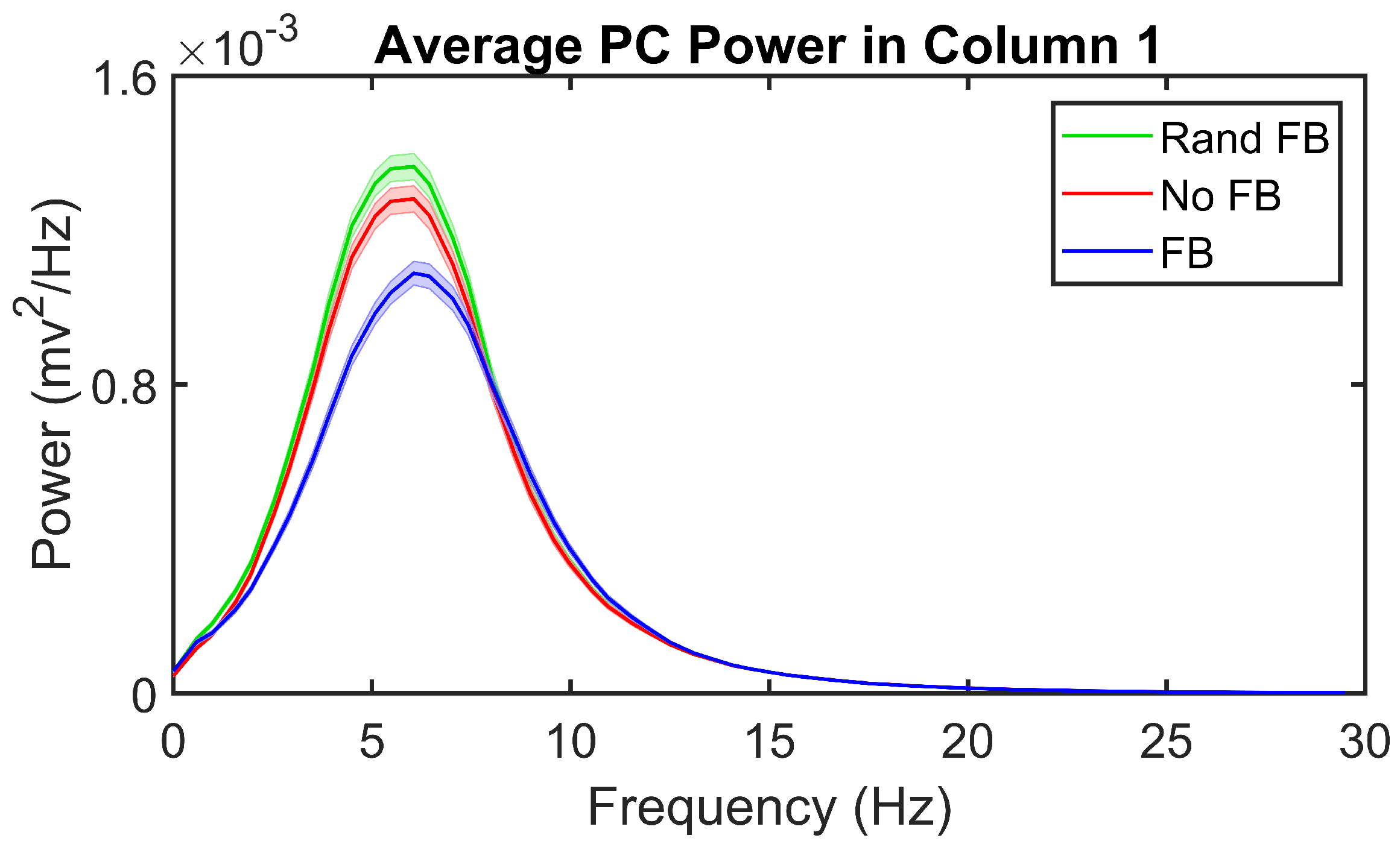
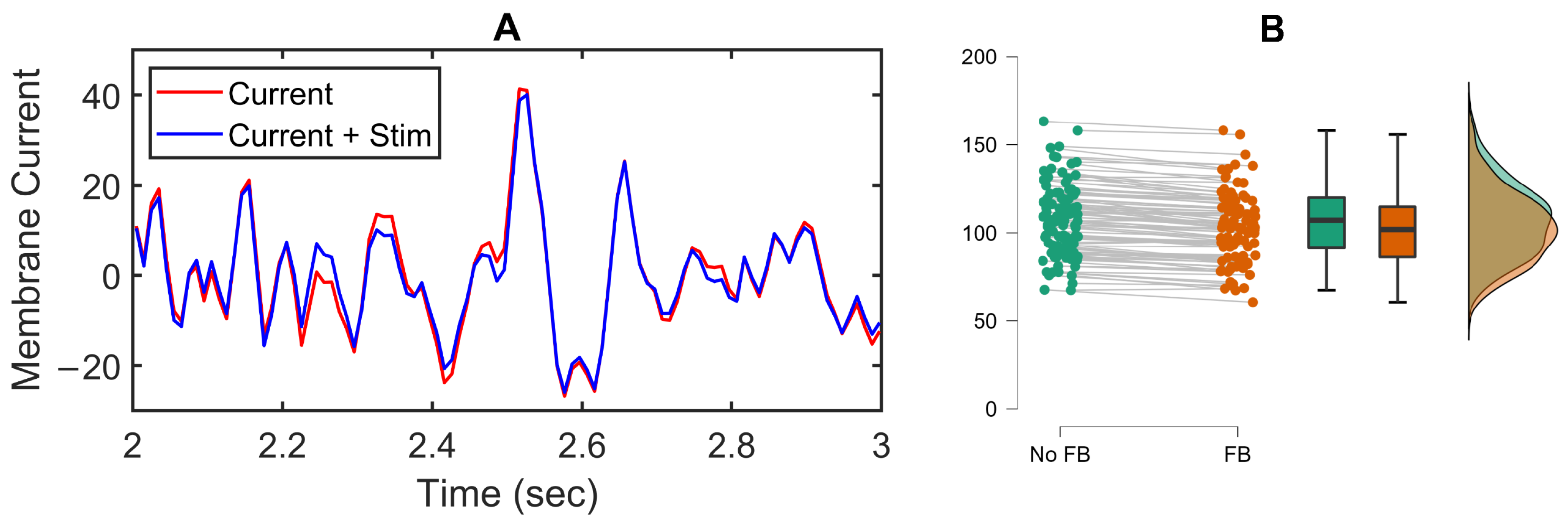
3.2. Feedback Results
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. State Equations for the Two-Column Neural Mass Model
Appendix B. Exploring ESN Parameters
References
- Teplan, M. Fundamentals of EEG Measurement. Meas. Sci. Rev. 2002, 2, 1–11. [Google Scholar]
- Thut, G.; Miniussi, C.; Gross, J. The Functional Importance of Rhythmic Activity in the Brain. Curr. Biol. 2012, 22, R658–R663. [Google Scholar] [CrossRef]
- Herrmann, C.S.; Rach, S.; Neuling, T.; Strüber, D. Transcranial alternating current stimulation: A review of the underlying mechanisms and modulation of cognitive processes. Front. Hum. Neurosci. 2013, 7, 279. [Google Scholar] [CrossRef] [PubMed]
- Kasten, F.H.; Wendeln, T.; Stecher, H.I.; Herrmann, C.S. Hemisphere-specific, differential effects of lateralized, occipital-parietal α-versus γ-tACS on endogenous but not exogenous visual-spatial attention. Sci. Rep. 2020, 10, 12270. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Reinhart, R.M.; Choi, I.; Shinn-Cunningham, B. Causal links between parietal alpha activity and spatial auditory attention. eLife 2019, 8, e51184. [Google Scholar] [CrossRef] [PubMed]
- Dallmer-Zerbe, I.; Popp, F.; Lam, A.P.; Philipsen, A.; Herrmann, C.S. Transcranial Alternating Current Stimulation (tACS) as a Tool to Modulate P300 Amplitude in Attention Deficit Hyperactivity Disorder (ADHD): Preliminary Findings. Brain Topogr. 2020, 33, 191–207. [Google Scholar] [CrossRef]
- Reinhart, R.M.; Nguyen, J.A. Working memory revived in older adults by synchronizing rhythmic brain circuits. Nat. Neurosci. 2019, 22, 820–827. [Google Scholar] [CrossRef]
- Hoy, K.E.; Bailey, N.; Arnold, S.; Windsor, K.; John, J.; Daskalakis, Z.J.; Fitzgerald, P.B. The effect of γ-tACS on working memory performance in healthy controls. Brain Cogn. 2015, 101, 51–56. [Google Scholar] [CrossRef]
- Geisler, C.D.; Goldberg, J.M. A Stochastic Model of the Repetitive Activity of Neurons. Biophys. J. 1966, 6, 53–69. [Google Scholar] [CrossRef]
- Liu, A.; Vöröslakos, M.; Kronberg, G.; Henin, S.; Krause, M.R.; Huang, Y.; Opitz, A.; Mehta, A.; Pack, C.C.; Krekelberg, B.; et al. Immediate neurophysiological effects of transcranial electrical stimulation. Nat. Commun. 2018, 9, 5092. [Google Scholar] [CrossRef]
- Pei, A.; Shinn-Cunningham, B.G. Alternating current stimulation entrains and connects cortical regions in a neural mass model. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Glasgow, UK, 11–15 July 2022; pp. 760–763. [Google Scholar] [CrossRef]
- Huang, W.A.; Stitt, I.M.; Negahbani, E.; Passey, D.J.; Ahn, S.; Davey, M.; Dannhauer, M.; Doan, T.T.; Hoover, A.C.; Peterchev, A.V.; et al. Transcranial alternating current stimulation entrains alpha oscillations by preferential phase synchronization of fast-spiking cortical neurons to stimulation waveform. Nat. Commun. 2021, 12, 3151. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.M.; Sellers, K.K.; Fröhlich, F. Transcranial alternating current stimulation modulates large-scale cortical network activity by network resonance. J. Neurosci. 2013, 33, 11262–11275. [Google Scholar] [CrossRef]
- Veniero, D.; Benwell, C.S.; Ahrens, M.M.; Thut, G. Inconsistent effects of parietal α-tACS on Pseudoneglect across two experiments: A failed internal replication. Front. Psychol. 2017, 8, 952. [Google Scholar] [CrossRef]
- Mioni, G.; Shelp, A.; Stanfield-Wiswell, C.T.; Gladhill, K.A.; Bader, F.; Wiener, M. Modulation of Individual Alpha Frequency with tACS shifts Time Perception. Cereb. Cortex Commun. 2020, 1, 1–9. [Google Scholar] [CrossRef]
- Gulbinaite, R.; Van Viegen, T.; Wieling, M.; Cohen, M.X.; Vanrullen, R. Individual Alpha Peak Frequency Predicts 10 Hz Flicker Effects on Selective Attention. J. Neurosci. 2017, 37, 10173. [Google Scholar] [CrossRef]
- Kasten, F.H.; Duecker, K.; Maack, M.C.; Meiser, A.; Herrmann, C.S. Integrating electric field modeling and neuroimaging to explain inter-individual variability of tACS effects. Nat. Commun. 2019, 10, 5427. [Google Scholar] [CrossRef] [PubMed]
- Thut, G.; Bergmann, T.O.; Fröhlich, F.; Soekadar, S.R.; Brittain, J.S.; Valero-Cabré, A.; Sack, A.T.; Miniussi, C.; Antal, A.; Siebner, H.R.; et al. Guiding transcranial brain stimulation by EEG/MEG to interact with ongoing brain activity and associated functions: A position paper. Clin. Neurophysiol. 2017, 128, 843–857. [Google Scholar] [CrossRef] [PubMed]
- Dmochowski, J.P.; Datta, A.; Bikson, M.; Su, Y.; Parra, L.C. Optimized multi-electrode stimulation increases focality and intensity at target. J. Neural Eng. 2011, 8, 046011. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Liu, T.; Wang, J. Improving the Effect of Transcranial Alternating Current Stimulation (tACS): A Systematic Review. Front. Hum. Neurosci. 2021, 15, 255. [Google Scholar] [CrossRef]
- Neuling, T.; Ruhnau, P.; Weisz, N.; Herrmann, C.S.; Demarchi, G. Faith and oscillations recovered: On analyzing EEG/MEG signals during tACS. NeuroImage 2017, 147, 960–963. [Google Scholar] [CrossRef]
- Kohli, S.; Casson, A.J. Removal of Transcranial a.c. Current Stimulation artifact from simultaneous EEG recordings by superposition of moving averages. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; pp. 3436–3439. [Google Scholar] [CrossRef]
- Zarubin, G.; Gundlach, C.; Nikulin, V.; Villringer, A.; Bogdan, M. Transient Amplitude Modulation of Alpha-Band Oscillations by Short-Time Intermittent Closed-Loop tACS. Front. Hum. Neurosci. 2020, 14, 366. [Google Scholar] [CrossRef] [PubMed]
- Robinson, C.S.; Bryant, N.B.; Maxwell, J.W.; Jones, A.P.; Robert, B.; Lamphere, M.; Combs, A.; Al Azzawi, H.M.; Gibson, B.C.; Sanguinetti, J.L.; et al. The Benefits of Closed-Loop Transcranial Alternating Current Stimulation on Subjective Sleep Quality. Brain Sci. 2018, 8, 204. [Google Scholar] [CrossRef] [PubMed]
- Jansen, B.H.; Rit, V.G. Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biol. Cybern. 1995, 73, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Calvet, J.P.; Arkun, Y. Feedforward and Feedback Linearization of Nonlinear Systems and Its Implementation Using Internal Model Control (IMC). Ind. Eng. Chem. Res. 1988, 27, 1822–1831. [Google Scholar] [CrossRef]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks-with an Erratum Note 1; German National Research Center for Information Technology GMD Technical Report: Bonn, Germany, 2001; Volume 148, p. 13. [Google Scholar]
- Canaday, D.; Pomerance, A.; Gauthier, D.J. Model-free control of dynamical systems with deep reservoir computing. J. Phys. Complex. 2021, 2, 035025. [Google Scholar] [CrossRef]
- Cakan, C.; Obermayer, K. Biophysically grounded mean-field models of neural populations under electrical stimulation. PLoS Comput. Biol. 2020, 16, e1007822. [Google Scholar] [CrossRef]
- Dutta, A.; Nitsche, M.A. State-space analysis of Hodgkin-Huxley axonal neural mass model during subthreshold high frequency alternating current stimulation. In Proceedings of the International IEEE/EMBS Conference on Neural Engineering, NER, San Diego, CA, USA, 6–8 November 2013; pp. 1100–1103. [Google Scholar] [CrossRef]
- David, O.; Harrison, L.; Friston, K.J. Modelling event-related responses in the brain. NeuroImage 2005, 25, 756–770. [Google Scholar] [CrossRef]
- Pei, A.; Shinn-Cunningham, B.G. Effects of Broadband, Bandstop and Amplitude-Modulated Alternating Current Stimulation on a Neural Mass Model. In Proceedings of the 2022 IEEE Biomedical Circuits and Systems Conference (BioCAS), Taiwan, China, 13–15 October 2022; pp. 284–287. [Google Scholar] [CrossRef]
- Oostenveld, R.; Fries, P.; Maris, E.; Schoffelen, J.M. FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 2011, 156869. [Google Scholar] [CrossRef]
- Haluszczynski, A.; Räth, C. Controlling nonlinear dynamical systems into arbitrary states using machine learning. Sci. Rep. 2021, 11, 12991. [Google Scholar] [CrossRef]
- Neuling, T.; Rach, S.; Wagner, S.; Wolters, C.H.; Herrmann, C.S. Good vibrations: Oscillatory phase shapes perception. NeuroImage 2012, 63, 771–778. [Google Scholar] [CrossRef]
- Grimbert, F.; Faugeras, O. Bifurcation analysis of Jansen’s neural mass model. Neural Comput. 2006, 18, 3052–3068. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, T.; Komaki, F. Time series decomposition into oscillation components and phase estimation. Neural Comput. 2017, 29, 332–367. [Google Scholar] [CrossRef] [PubMed]
- Wodeyar, A.; Schatza, M.; Widge, A.S.; Eden, U.T.; Kramer, M.A. A state space modeling approach to real-time phase estimation. Elife 2021, 10, e68803. [Google Scholar] [CrossRef]
- Michel, C.M.; Brunet, D. EEG source imaging: A practical review of the analysis steps. Front. Neurol. 2019, 10, 325. [Google Scholar] [CrossRef] [PubMed]
- Kayser, J.; Tenke, C.E. On the benefits of using surface Laplacian (Current Source Density) methodology in electrophysiology. Int. J. Psychophysiol. Off. J. Int. Organ. Psychophysiol. 2015, 97, 171. [Google Scholar] [CrossRef]
- Castellano, M.; Ibañez-Soria, D.; Kroupi, E.; Acedo, J.; Campolo, M.; Soria-Frisch, A.; Valls-Sole, J.; Verma, A.; Ruffini, G. Intermittent tACS during a visual task impacts neural oscillations and LZW complexity. Exp. Brain Res. 2020, 238, 1411–1422. [Google Scholar] [CrossRef]


| Parameter | Description | Value |
|---|---|---|
| Max amplitude of post-synaptic potential | 3.25, 29.3 (mV) | |
| Lumped time constants of dendritic delays | 10, 15, 20 () | |
| Max firing rate of neural population | 2.5 () | |
| Steepness of the sigmoid function | 0.56 () | |
| Number of synapses in neural population | 50, 40, 12, 12 | |
| C | Connectivity scalar for extrinsic inputs | 1000 |
| Parameter | Value |
|---|---|
| Spectral radius | 0.5 |
| N input units | 6 |
| N internal units | 10 |
| Input scaling | |
| Input shift | |
| Teacher scaling | |
| Teacher shift | |
| Feedback scaling |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, A.; Shinn-Cunningham, B.G. Closed-Loop Current Stimulation Feedback Control of a Neural Mass Model Using Reservoir Computing. Appl. Sci. 2023, 13, 1279. https://doi.org/10.3390/app13031279
Pei A, Shinn-Cunningham BG. Closed-Loop Current Stimulation Feedback Control of a Neural Mass Model Using Reservoir Computing. Applied Sciences. 2023; 13(3):1279. https://doi.org/10.3390/app13031279
Chicago/Turabian StylePei, Alexander, and Barbara G. Shinn-Cunningham. 2023. "Closed-Loop Current Stimulation Feedback Control of a Neural Mass Model Using Reservoir Computing" Applied Sciences 13, no. 3: 1279. https://doi.org/10.3390/app13031279
APA StylePei, A., & Shinn-Cunningham, B. G. (2023). Closed-Loop Current Stimulation Feedback Control of a Neural Mass Model Using Reservoir Computing. Applied Sciences, 13(3), 1279. https://doi.org/10.3390/app13031279







