Passively Tuning the Resonant Frequency of Kinetic Energy Harvesters Using Distributed Loaded Proof Mass
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Concept
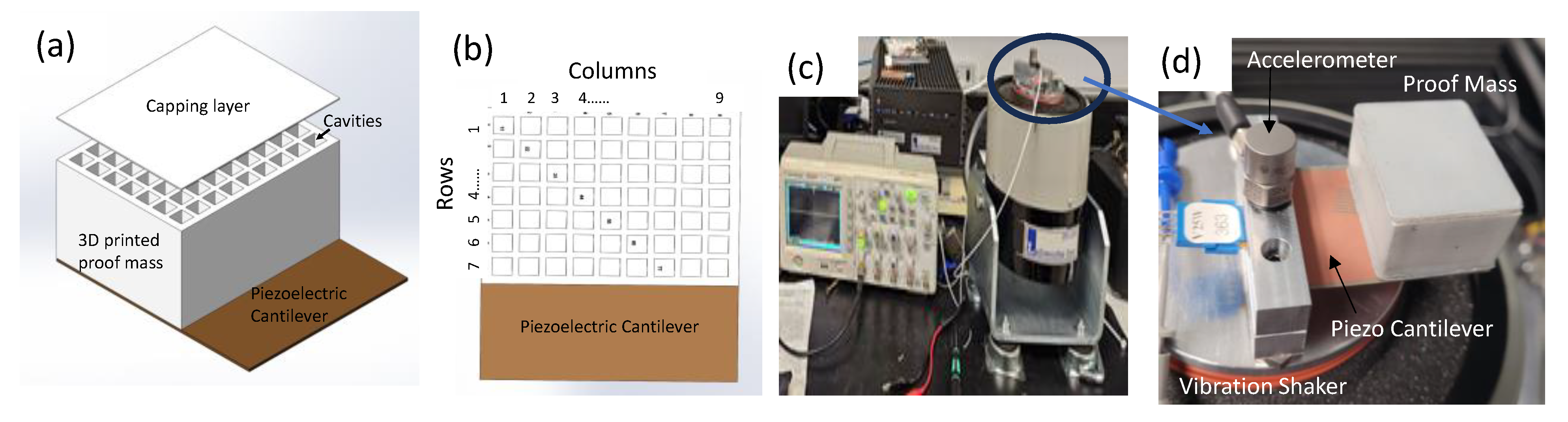
2.2. Energy-Harvesting Device
2.3. Cavity Filling
2.4. Experimental Testing
2.5. Computational Modelling
3. Results and Discussion
3.1. Density of Fillers
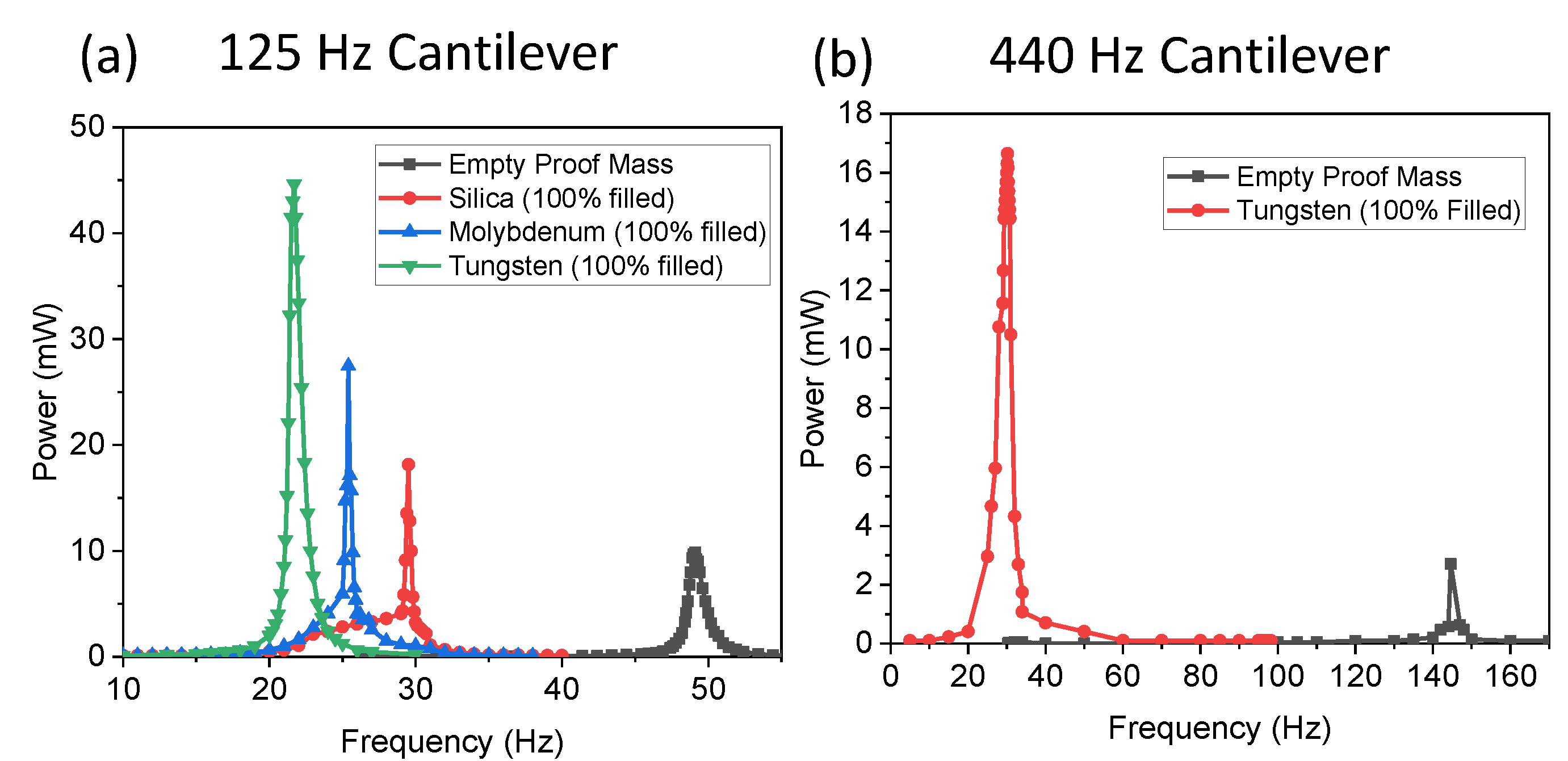
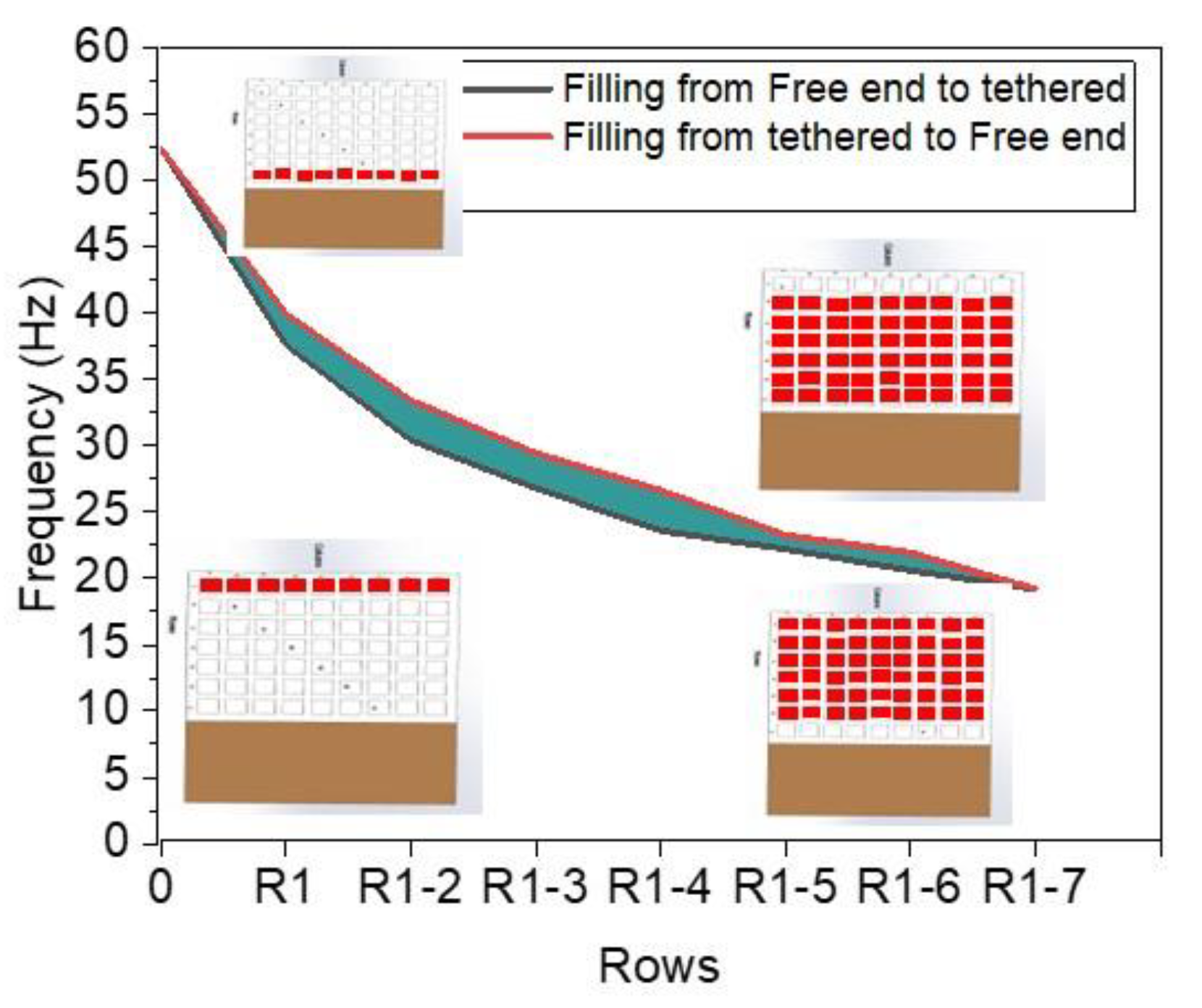
3.2. Tuning Range
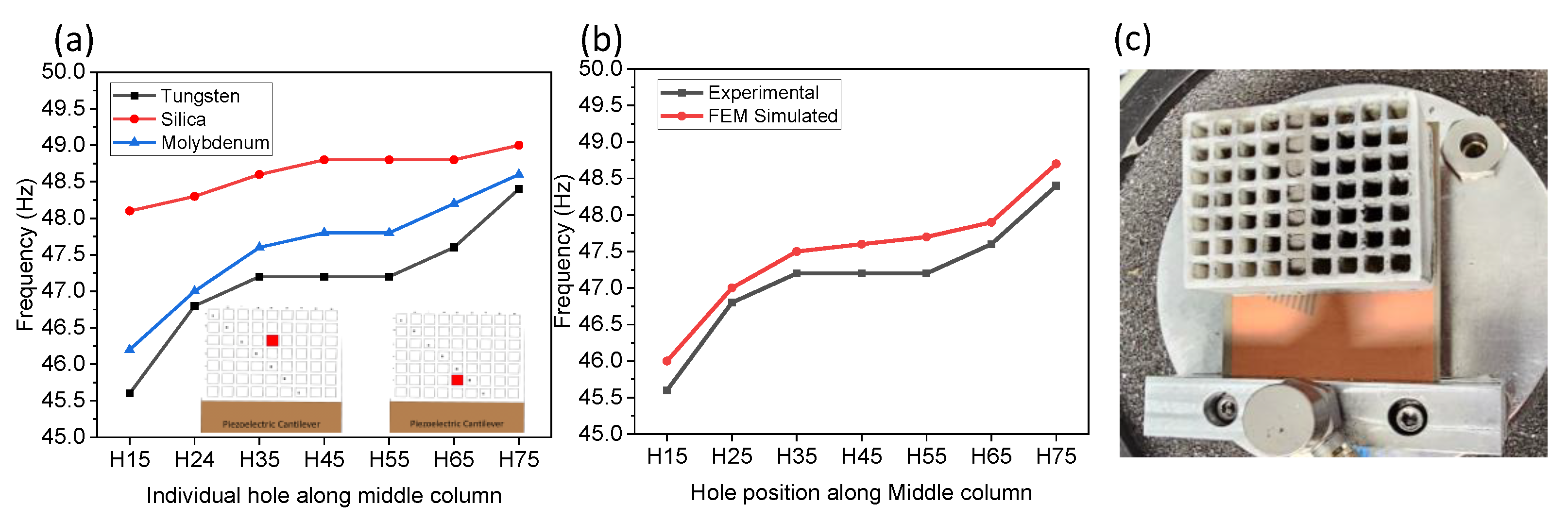
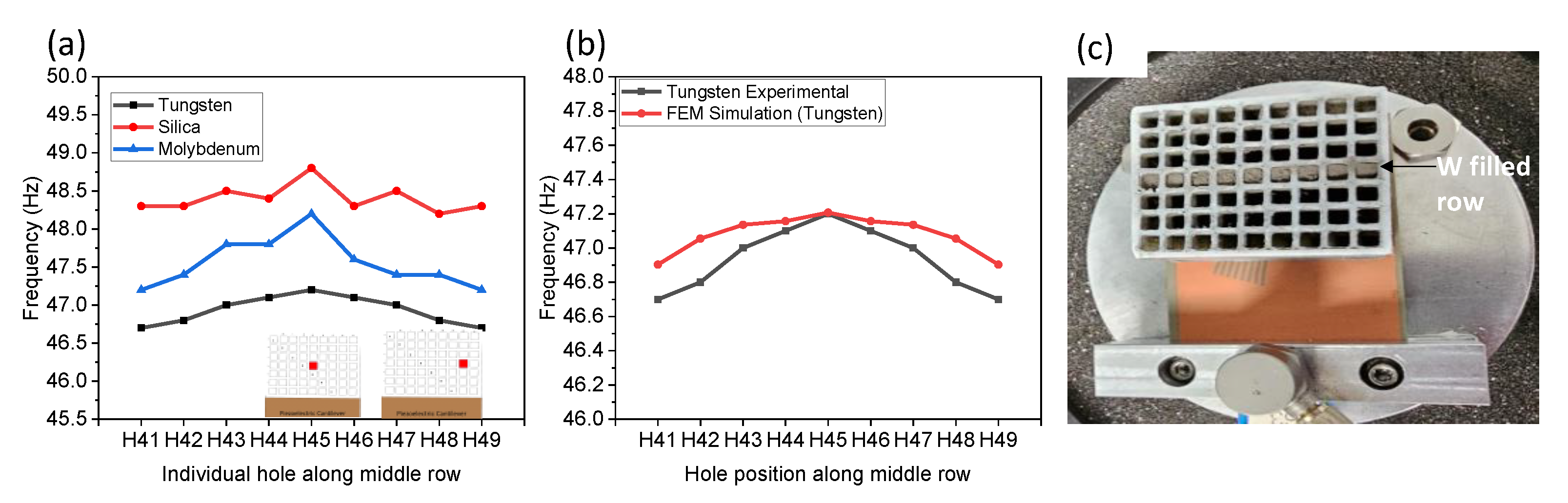
3.3. Tuning Resolution
3.4. MEMS Tuning Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hidalgo-Leon, R.; Urquizo, J.; Silva, C.E.; Silva-Leon, J.; Wu, J.; Singh, P.; Soriano, G. Powering nodes of wireless sensor networks with energy harvesters for intelligent buildings: A review. Energy Rep. 2022, 8, 3809–3826. [Google Scholar] [CrossRef]
- Shaikh, F.K.; Zeadally, S. Energy harvesting in wireless sensor networks: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Adu-Manu, K.S.; Adam, N.; Tapparello, C.; Ayatollahi, H.; Heinzelman, W. Energy-Harvesting Wireless Sensor Networks (EH-WSNs) A Review; ACM Transactions on Sensor Networks (TOSN): New York, NY, USA, 2018; Volume 14, pp. 1–50. [Google Scholar]
- Iqbal, M.; Nauman, M.M.; Khan, F.U.; Abas, P.E.; Cheok, Q.; Iqbal, A.; Aissa, B. Vibration-based piezoelectric, electromagnetic, and hybrid energy harvesters for microsystems applications: A contributed review. Int. J. Energy Res. 2020, 45, 65–102. [Google Scholar] [CrossRef]
- Andosca, R.; McDonald, T.G.; Genova, V.; Rosenberg, S.; Keating, J.; Benedixen, C.; Wu, J. Experimental and theoretical studies on MEMS piezoelectric vibrational energy harvesters with mass loading. Sens. Actuators A Phys. 2012, 178, 76–87. [Google Scholar] [CrossRef]
- Jackson, N.; O’keeffe, R.; Waldron, F.; O’neill, M.; Mathewson, A. Evaluation of low-acceleration MEMS piezoelectric energy harvesting devices. Microsyst. Technol. 2013, 20, 671–680. [Google Scholar] [CrossRef]
- Lee, M.-S.; Kim, C.-I.; Park, W.-I.; Cho, J.-H.; Paik, J.-H.; Jeong, Y.H. Energy harvesting performance of unimorph piezoelectric cantilever generator using interdigitated electrode lead zirconate titanate laminate. Energy 2019, 179, 373–382. [Google Scholar] [CrossRef]
- Pertin, O.; Shrivas, P.; Guha, K.; Rao, K.S.; Iannacci, J. New and efficient design of multimode piezoelectric vibration energy harvester for MEMS application. Microsyst. Technol. 2021, 27, 3523–3531. [Google Scholar] [CrossRef]
- Ren, Z.; Wu, L.; Zhang, J.; Wang, Y.; Wang, Y.; Li, Q.; Wang, F.; Liang, X.; Yang, R. Trapezoidal Cantilever-Structure Triboelectric Nanogenerator Integrated with a Power Management Module for Low-Frequency Vibration Energy Harvesting. ACS Appl. Mater. Interfaces 2022, 14, 5497–5505. [Google Scholar] [CrossRef]
- Song, H.-C.; Kumar, P.; Maurya, D.; Kang, M.-G.; Reynolds, W.T.; Jeong, D.-Y.; Kang, C.-Y.; Priya, S. Ultra-Low Resonant Piezoelectric MEMS Energy Harvester with High Power Density. J. Microelectromech. Syst. 2017, 26, 1226–1234. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, L.; Luo, G.; Zhao, Y.; Yang, P.; Jiang, Z.; Maeda, R. System level design of wireless sensor node powered by piezoelectric vibration energy harvesting. Sens. Actuators A Phys. 2020, 310, 112039. [Google Scholar] [CrossRef]
- Hajati, A.; Kim, S.-G. Ultra-wide bandwidth piezoelectric energy harvesting. Appl. Phys. Lett. 2011, 99, 083105. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. Nonlinear Multi-Mode Wideband Piezoelectric MEMS Vibration Energy Harvester. IEEE Sens. J. 2019, 19, 4837–4848. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Halvorsen, E. Nonlinear Springs for Bandwidth-Tolerant Vibration Energy Harvesting. J. Microelectromech. Syst. 2011, 20, 1225–1227. [Google Scholar] [CrossRef]
- Upadrashta, D.; Yang, Y. Nonlinear piezomagnetoelastic harvester array for broadband energy harvesting. J. Appl. Phys. 2016, 120, 054504. [Google Scholar] [CrossRef]
- Chandwani, J.; Somkuwar, R.; Deshmukh, R. Multi-band piezoelectric vibration energy harvester for low-frequency applications. Microsyst. Technol. 2019, 25, 3867–3877. [Google Scholar] [CrossRef]
- Doria, A.; Marconi, E.; Moro, F. Tuning of Vibration Energy Harvesters by Means of Liquid Masses. In Proceedings of the 2021 Sixteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 5–7 May 2021; pp. 1–7. [Google Scholar]
- Jackson, N.; Rodriguez, L.A.; Adhikari, R. Wide Bandwidth Vibration Energy Harvester with Embedded Transverse Movable Mass. Sensors 2021, 21, 5517. [Google Scholar] [CrossRef] [PubMed]
- Jackson, N.; Stam, F. Sloshing liquid-metal mass for widening the bandwidth of a vibration energy harvester. Sens. Actuators A Phys. 2018, 284, 17–21. [Google Scholar] [CrossRef]
- Jackson, N.; Stam, F.; Olszewski, O.Z.; Doyle, H.; Quinn, A.; Mathewson, A. Widening the bandwidth of vibration energy harvesters using a liquid-based non-uniform load distribution. Sens. Actuators A Phys. 2016, 246, 170–179. [Google Scholar] [CrossRef]
- Shi, G.; Yang, Y.; Chen, J.; Peng, Y.; Xia, H.; Xia, Y. A broadband piezoelectric energy harvester with movable mass for frequency active self-tuning. Smart Mater. Struct. 2020, 29, 055023. [Google Scholar] [CrossRef]
- Somkuwar, R.; Chandwani, J.; Deshmukh, R. Bandwidth widening of piezoelectric energy harvester by free moving cylinders in liquid medium. Microsyst. Technol. 2020, 27, 1959–1970. [Google Scholar] [CrossRef]
- Song, H.; Hwang, G.-T.; Ryu, J.; Choi, H. Stable output performance generated from a magneto-mechano-electric generator having self-resonance tunability with a movable proof mass. Nano Energy 2022, 101, 107607. [Google Scholar] [CrossRef]
- Anand, A.; Pal, S.; Kundu, S. Bandwidth and power enhancement in the MEMS-based piezoelectric energy harvester using magnetic tip mass. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70. [Google Scholar] [CrossRef]
- Jackson, N. PiezoMEMS Nonlinear Low Acceleration Energy Harvester with an Embedded Permanent Magnet. Micromachines 2020, 11, 500. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wu, S.; Luk, P.C.K.; Gu, M.; Jiao, Z. Enhanced Bandwidth Nonlinear Resonance Electromagnetic Human Motion Energy Harvester Using Magnetic Springs and Ferrofluid. IEEE/ASME Trans. Mechatron. 2019, 24, 710–717. [Google Scholar] [CrossRef]
- Tang, Q.C.; Yang, Y.L.; Li, X. Bi-stable frequency up-conversion piezoelectric energy harvester driven by non-contact magnetic repulsion. Smart Mater. Struct. 2011, 20, 125011. [Google Scholar] [CrossRef]
- Jackson, N.; Kumar, K.; Olszewski, O.; Schenning, A.P.H.J.; Debije, M.G. Tuning MEMS cantilever devices using photoresponsive polymers. Smart Mater. Struct. 2018, 28, 085024. [Google Scholar] [CrossRef]
- Lallart, M.; Anton, S.R.; Inman, D.J. Frequency Self-tuning Scheme for Broadband Vibration Energy Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 897–906. [Google Scholar] [CrossRef]
- Jackson, N. Tuning and widening the bandwidth of vibration energy harvesters using a ferrofluid embedded mass. Microsyst. Technol. 2020, 26, 2043–2051. [Google Scholar] [CrossRef]
- Jia, Y.; Seshia, A.A. Power Optimization by Mass Tuning for MEMS Piezoelectric Cantilever Vibration Energy Harvesting. J. Microelectromech. Syst. 2015, 25, 108–117. [Google Scholar] [CrossRef]
- Podder, P.; Constantinou, P.; Mallick, D.; Amann, A.; Roy, S. Magnetic Tuning of Nonlinear MEMS Electromagnetic Vibration Energy Harvester. J. Microelectromech. Syst. 2017, 26, 539–549. [Google Scholar] [CrossRef]
- Rivadeneyra, A.; Soto-Rueda, J.M.; O’keeffe, R.; Banqueri, J.; Jackson, N.; Mathewson, A.; López-Villanueva, J.A. Tunable MEMS piezoelectric energy harvesting device. Microsyst. Technol. 2015, 22, 823–830. [Google Scholar] [CrossRef]
- Kouritem, S.A.; Al-Moghazy, M.A.; Noori, M.; Altabey, W.A. Mass tuning technique for a broadband piezoelectric energy harvester array. Mech. Syst. Signal Process. 2022, 181, 109500. [Google Scholar] [CrossRef]
- Adhikari, R.; Jackson, N. Passive Frequency Tuning of Piezoelectric Energy Harvester using Embedded Masses. In Proceedings of the 2021 IEEE 20th International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS), Exeter, UK, 6–8 December 2021; pp. 176–179. [Google Scholar]
- Shen, D.; Park, J.-H.; Ajitsaria, J.; Choe, S.-Y.; Wikle, H.C.; Kim, D.-J. The design, fabrication and evaluation of a MEMS PZT cantilever with an integrated Si proof mass for vibration energy harvesting. J. Micromech. Microeng. 2008, 18, 055017. [Google Scholar] [CrossRef]
- Somkuwar, R.; Chandwani, J.; Deshmukh, R. Wideband auto-tunable vibration energy harvester using change in centre of gravity. Microsyst. Technol. 2018, 24, 3033–3044. [Google Scholar] [CrossRef]



| Filler Material (Avg. Size) | Average Density (g cm−3) | Average Fill Factor (%) |
|---|---|---|
| Tungsten (75 μm) | 4.33 ± 0.152 | 61.8% ± 2.8% |
| Molybdenum (40 μm) | 2.19 ± 0.085 | 73.2% ± 1.5% |
| Silica (45 μm) | 1.48 ± 0.088 | 69.4% ± 1.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adhikari, R.; Jackson, N. Passively Tuning the Resonant Frequency of Kinetic Energy Harvesters Using Distributed Loaded Proof Mass. Appl. Sci. 2024, 14, 156. https://doi.org/10.3390/app14010156
Adhikari R, Jackson N. Passively Tuning the Resonant Frequency of Kinetic Energy Harvesters Using Distributed Loaded Proof Mass. Applied Sciences. 2024; 14(1):156. https://doi.org/10.3390/app14010156
Chicago/Turabian StyleAdhikari, Rahul, and Nathan Jackson. 2024. "Passively Tuning the Resonant Frequency of Kinetic Energy Harvesters Using Distributed Loaded Proof Mass" Applied Sciences 14, no. 1: 156. https://doi.org/10.3390/app14010156
APA StyleAdhikari, R., & Jackson, N. (2024). Passively Tuning the Resonant Frequency of Kinetic Energy Harvesters Using Distributed Loaded Proof Mass. Applied Sciences, 14(1), 156. https://doi.org/10.3390/app14010156








