Laboratory Evaluation of Tensile Creep Behavior of Concrete at Early Ages
Abstract
:Featured Application
Abstract
1. Introduction
2. Theoretical Background
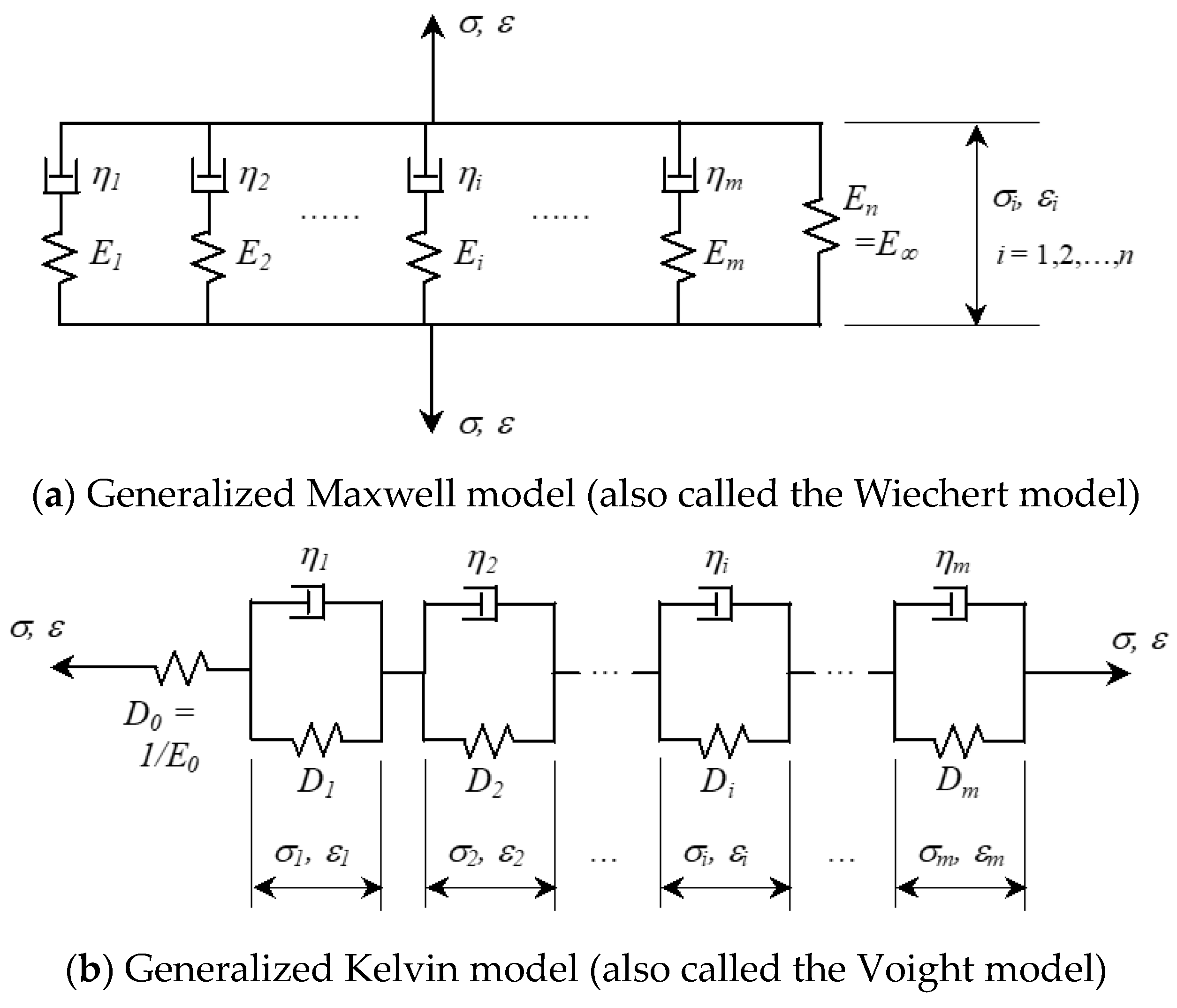
2.1. Constitutive Relations
2.2. Creep and Relaxation Characteristics
3. Tensile Creep Tests
3.1. Materials
3.2. Procedures
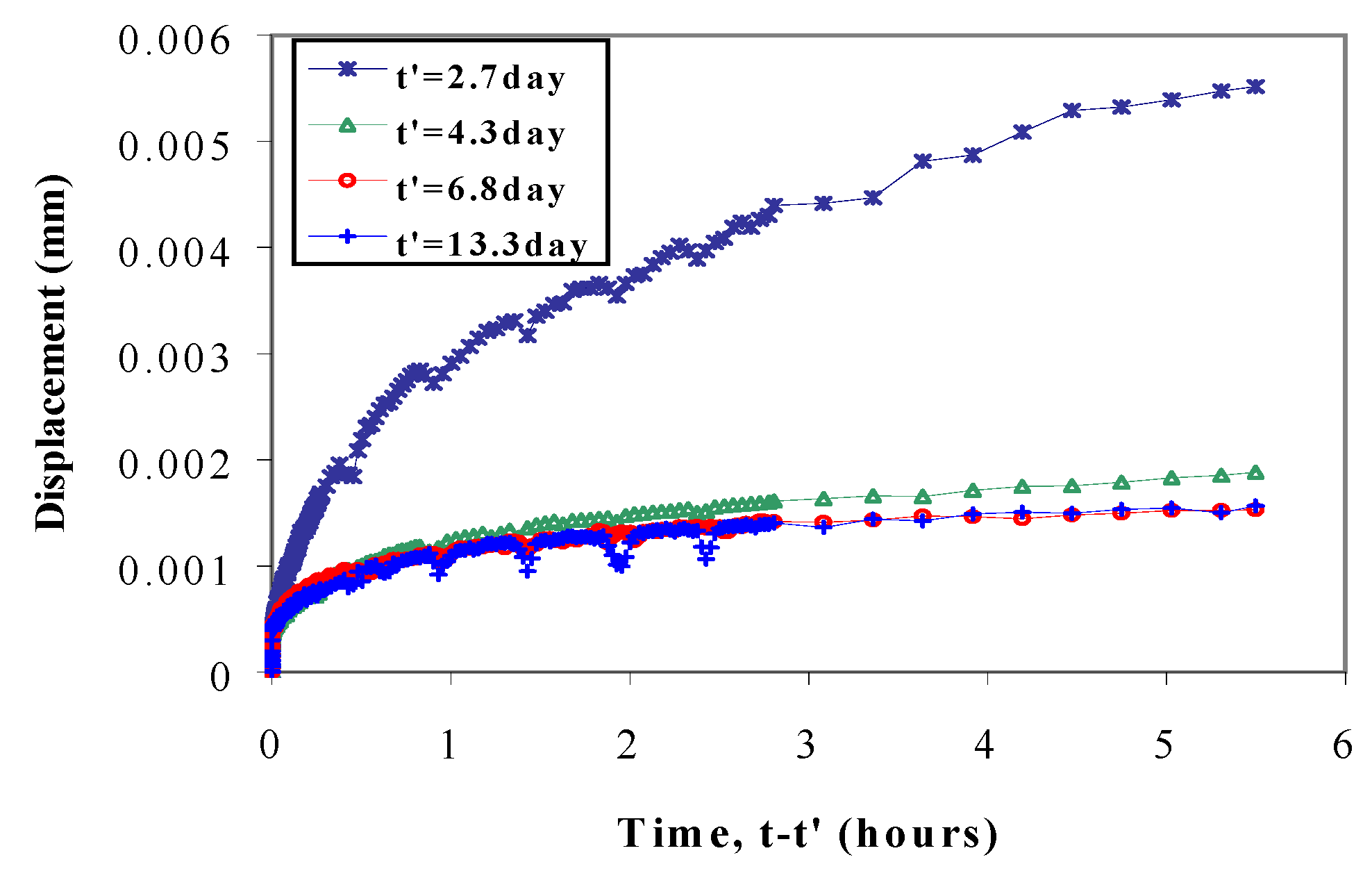
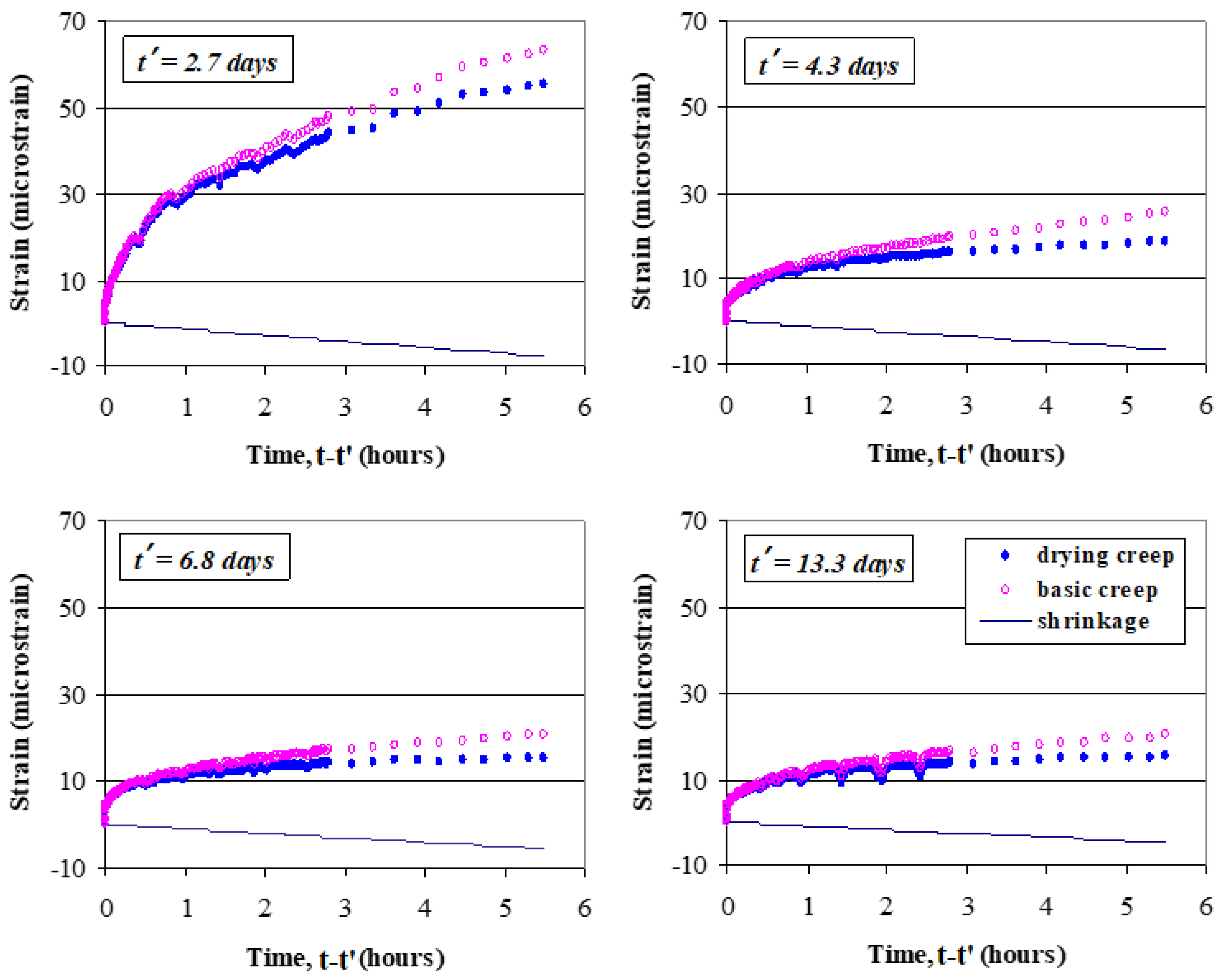
4. Test Results
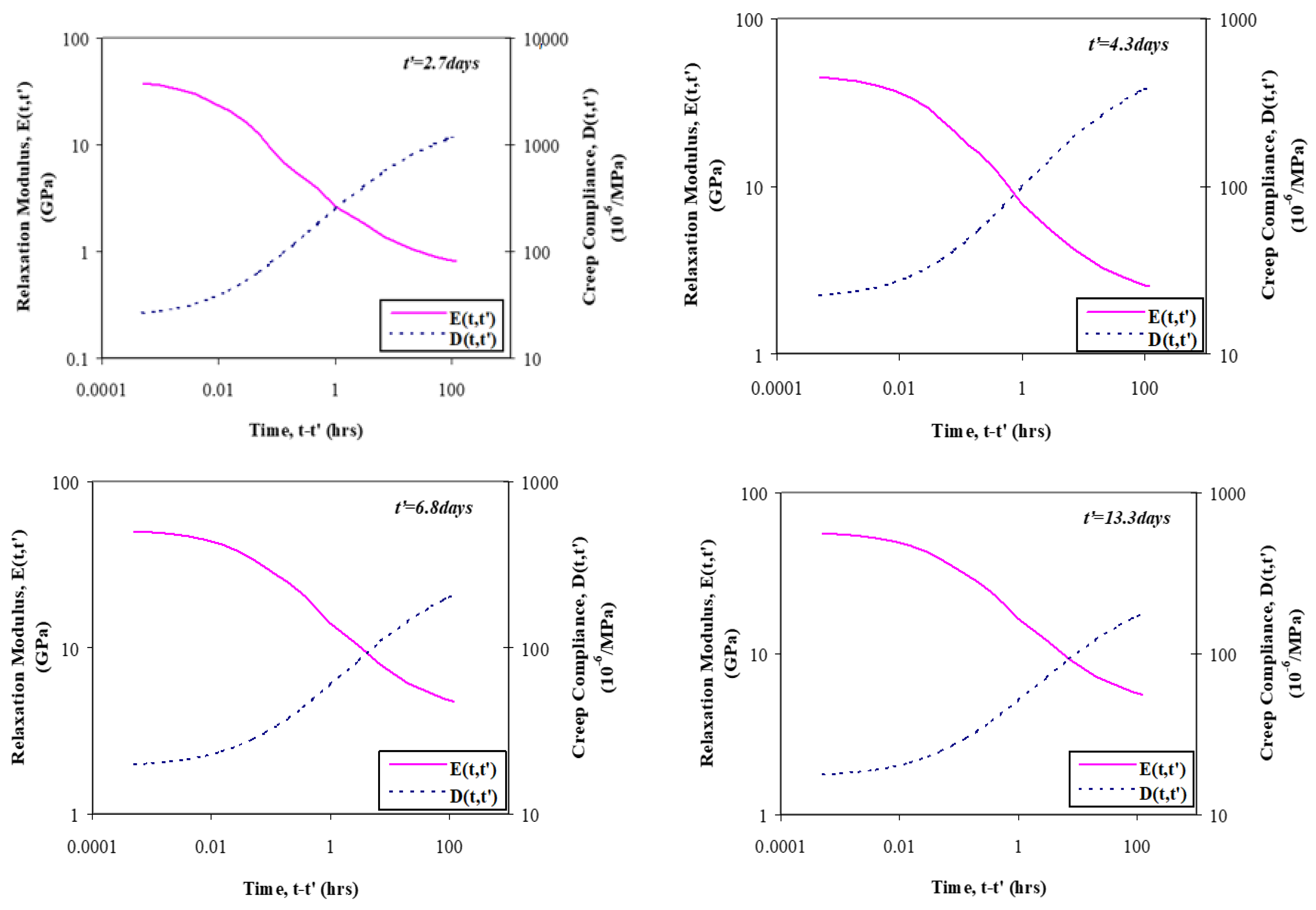
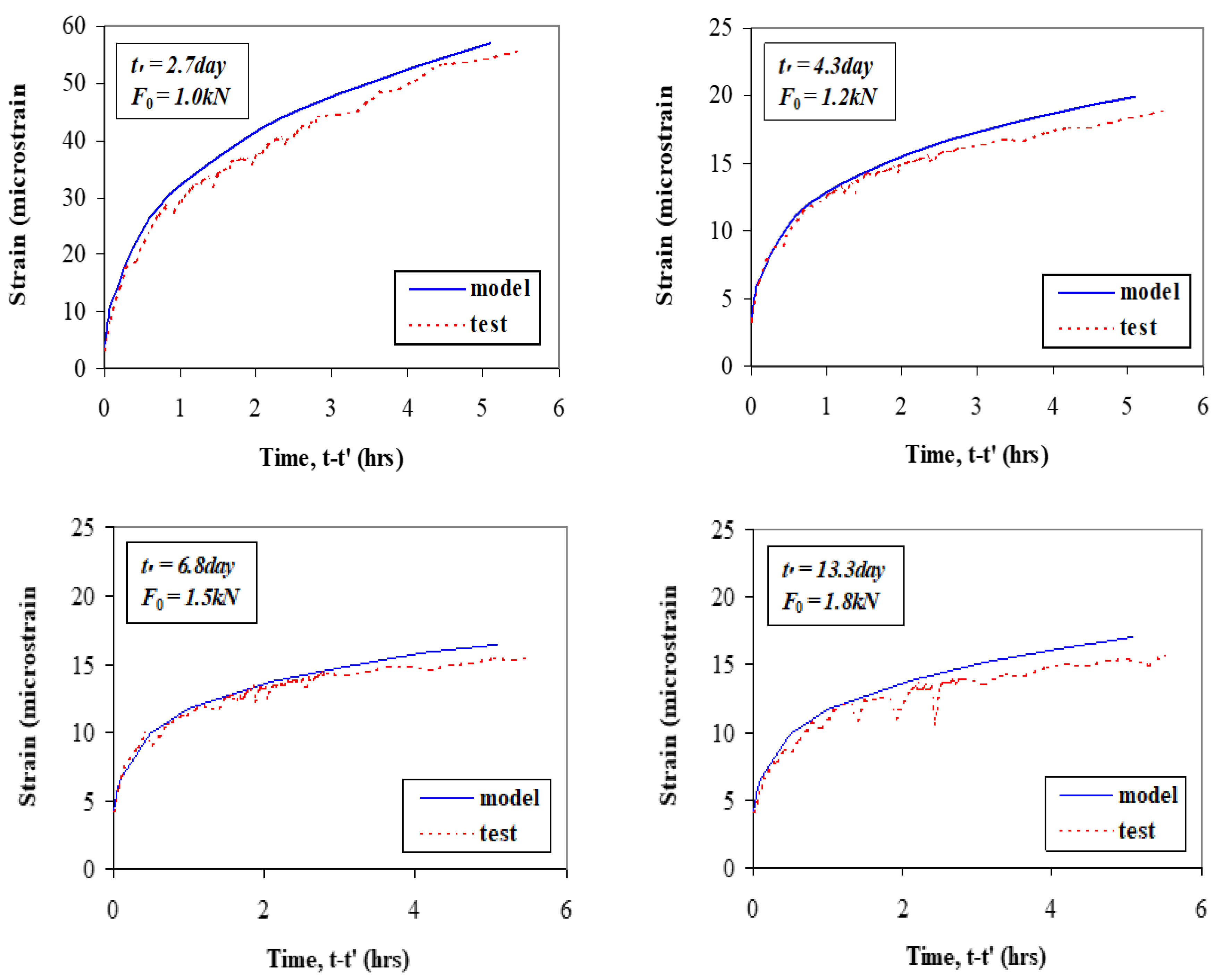
4.1. Creep Compliance
4.2. Dirichlet Series Creep Function
4.3. Relaxation Modulus
5. Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Powers, T. The thermodynamics of volume change and creep. Mater. Struct. 1968, 1, 487–507. [Google Scholar] [CrossRef]
- Neville, A. Creep of Concrete: Plain, Reinforced, and Prestressed; Elsevier: New York, NY, USA, 1970. [Google Scholar]
- Wittmann, F.; Roelfstra, P. Total deformation of loaded drying concrete. Cem. Concr. Res. 1980, 10, 601–610. [Google Scholar] [CrossRef]
- Yang, S.; Lee, H. Coefficient of thermal expansion of RCA concretre made by equivalent mortar volume. Appl. Sci. 2021, 11, 8214. [Google Scholar] [CrossRef]
- Lim, S. Viscoelastic Age-Dependent Analysis of Restrained Shrinkage Stress Development in Early-Age Concrete. Ph.D. Dissertation, Department of Civil Engineering, Texas A&M University, College Station, TX, USA, 2002. [Google Scholar]
- Wei, Y.; Liang, S.; Huang, J. Concrete creep modeling: Application to slabs on ground. J. Eng. Mech. 2019, 145, 04019078. [Google Scholar] [CrossRef]
- Krstulovich, J.; Dam, T.; Smith, K.; Gawedzinski, M. Evaluation of potential long-term durability of joints cut with early-entry saws on rigid pavements. Tranp. Res. Rec. 2011, 2235, 103–112. [Google Scholar] [CrossRef]
- Mehta, P.; Monteiro, P. Concrete Structure, Properties, and Materials; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Mindess, S.; Young, J.; Darwin, D. Concrete, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2003. [Google Scholar]
- Chen, J.; Zhou, L.; Zhu, Z.; Ma, L.; Wang, M.; Deng, Z. Crack propagation analysis and mechanical properties of basalt fibre reinforced cement composites with changing fibre surface characteristics. Constr. Build. Mater. 2023, 392, 131738. [Google Scholar] [CrossRef]
- Kanstard, G.; Bjøntegaard, Ø.; Sellevold, E. Tensile and compressive creep deformations of hardening concrete containing mineral additives. Mater. Struct. 2013, 46, 1167–1182. [Google Scholar]
- Wei, Y.; Liang, L.; Guo, W. Decoupling of autogenous shrinkage and tensile creep strain in high strength concrete at early ages. Exp. Mech. 2017, 57, 475–485. [Google Scholar] [CrossRef]
- Charpin, L.; Pape, Y.; Coustabeau, É.; Toppani, É.; Heinfling, G.; Bellego, C.; Masson, B.; Montalvo, L.; Courtois, A.; Sanahuja, J.; et al. A 12 year EDF study of concrete creep under uniaxial and biaxial loading. Cem. Concr. Res. 2018, 103, 140–159. [Google Scholar] [CrossRef]
- Huynh, T.; Hwang, C.; Limongan, A. The long-term creep and shrinkage behaviors of green concrete designed for bridge girder using a densified mixture design algorithm. Cem. Concr. Compos. 2018, 87, 79–88. [Google Scholar] [CrossRef]
- Roy, R.; Maou, F.; Torrenti, J. Long term basic creep behavior of high performance concrete: Data and modelling. Mater. Struct. 2017, 50, 85. [Google Scholar] [CrossRef]
- Hilaire, A.; Benboudjema, F.; Darquennes, A.; Berthaud, Y.; Nahas, G. Modeling basic creep in concrete at early-age under compressive and tensile loading. Nucl. Eng. Des. 2014, 269, 222–230. [Google Scholar] [CrossRef]
- Klausen, A.; Kanstad, T.; Bjøntegaard, Ø.; Sellevold, E. Comparison of tensile and compressive creep of fly ash concretes in the hardening phase. Cem. Concr. Res. 2017, 95, 188–194. [Google Scholar] [CrossRef]
- American Concrete Institute. ACI Manual of Concrete Practice 209R-92. Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 1997; pp. 1–47. [Google Scholar]
- Bazant, Z.; Chern, J. Triple power law for concrete creep. J. Eng. Mech. 1985, 111, 63–84. [Google Scholar] [CrossRef]
- Bazant, Z.; Prasannan, S. Solidification theory for concrete creep: I. Formulation. J. Eng. Mech. 1989, 115, 1691–1703. [Google Scholar] [CrossRef]
- Bazant, Z.; Prasannan, S. Solidification theory for concrete creep: II. Verification and application. J. Eng. Mech. 1989, 115, 1704–1725. [Google Scholar] [CrossRef]
- Bazant, Z.; Havlásek, P.; Jirásek, M. Microprestress-solidification theory: Modeling of size effect on drying creep. In Computational Modelling of Concrete Structures; Taylor & Francis Group: London, UK, 2014; pp. 749–758. [Google Scholar]
- Muller, H.; Hilsdorf, H. CEB 1990, “Evaluation of the Time Dependent Behavior of Concrete”, Bulletin d’Information No.199; Comite European du Be-ton/Federation Internationale de la Precontrainte: Lausanne, Switzerland, 1991. [Google Scholar]
- Westman, G. Basic creep and relaxation of young concrete. In Thermal Cracking in Concrete at Early Ages; E&FN Spon: London, UK, 1994; pp. 87–94. [Google Scholar]
- Ostergaard, L.; Lange, D.; Altoubat, S.; Stang, H. Tensile basic creep of early-age concrete under constant load. Cem. Concr. Res. 2001, 31, 1895–1899. [Google Scholar] [CrossRef]
- Yeon, J.; Choi, S.; Ha, S.; Won, M. Effects of creep and built-in curling on stress development of Portland cement concrete pavement under environmental loadings. J. Transp. Eng. 2012, 139, 147–155. [Google Scholar] [CrossRef]
- Lim, J.; Kim, S.; Jeong, J. Testing and analysis of viscoelastic characteristics of solidifying concrete pavement slabs. KSCE J. Civ. Eng. 2014, 18, 1063–1071. [Google Scholar] [CrossRef]
- Hu, C.; Sun, Z.; Wang, L. Early-age creep effects of cement concrete pavement. Eng. Mech. 2022, 39, 123–137. [Google Scholar]
- Bazant, Z. Mathematical models for creep and shrinkage of concrete. In Creep and Shrinkage in Concrete Structures; Bazant, Z., Wittmann, F., Eds.; John Wiley and Sons: New York, NY, USA, 1982; pp. 163–256. [Google Scholar]
- Christensen, R. Theory of Viscoelasticity: An Introduction, 2nd ed.; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Schapery, R. Approximate methods of transform inversion for viscoelastic stress analysis. In Proceedings of the 4th US National Congress on Applied Mechanics, Berkeley, CA, USA, 18–21 June 1962; ASME: New York, NY, USA, 1962; Volume 2, pp. 1075–1085. [Google Scholar]
- Bazant, Z.; Wu, S. Dirichlet series creep function for aging concrete. J. Eng. Mech. Div. 1973, 99, 367–387. [Google Scholar] [CrossRef]
- Bazant, Z.; Wu, S. Rate-type creep law of aging concrete based on Maxwell chain. Mater. Struct. 1974, 7, 45–60. [Google Scholar]
- Illston, J. The creep of concrete under uniaxial tension. Mag. Concr. Res. 1965, 17, 77–84. [Google Scholar] [CrossRef]
- Hauggaard, A.; Damkilde, L.; Hansen, P. Transitional thermal creep of early age concrete. J. Eng. Mech. 1999, 125, 458–465. [Google Scholar] [CrossRef]
- Bissonnette, M.; Boily, D.; Bastien, J.; Fafard, M. Tensile creep of concrete repair materials: Recent experimental findings towards optimization. In Proceedings of the Creep, Shrinkage and Durability Mechanics of Concrete and Other Quasi-Brittle Materials, Proceedings of the 6th International Conference, RILEM, Cambridge, MA, USA, 20–22 August 2001; pp. 599–604. [Google Scholar]
- Picket, G. Shrinkage stresses in concrete. J. Amer. Concr. Inst. Proc. 1946, 42, 165–204. [Google Scholar]
- Wittmann, F. Creep and Shrinkage Mechanisms. In Creep and Shrinkage in Concrete Structures; Bazant, Z.P., Wittmann, F.H., Eds.; John Wiley and Sons: New York, NY, USA, 1982; pp. 129–161. [Google Scholar]
- Bazant, Z.; Panula, L. Practical prediction of time-dependent deformations of concrete; Part I: Shrinkage, Part II: Basic creep. Mater. Struct. 1978, 11, 307–328. [Google Scholar]
- Bazant, Z.; Kim, J. Improved prediction model for time-dependent deformations of concrete: Part 2-Basic creep. Mater. Struct. 1991, 24, 409–421. [Google Scholar] [CrossRef]




| Unit Content (kg/m3) | w/c | ||||
|---|---|---|---|---|---|
| Cement | Fly Ash | Fine Aggregate | Coarse Aggregate | Water | |
| 200.5 | 66.4 | 800.3 | 1037.1 | 143.5 | 0.54 |
| Age at Test (Day) | fc(t) by ACI (MPa) | fc(t) by ACI (MPa) | Test Load | σt/ft(t) (%) | |
|---|---|---|---|---|---|
| Ft (kN) | σt (MPa) | ||||
| 2.7 | 6.65 | 0.83 | 1.0 | 0.127 | 15.3 |
| 4.3 | 8.71 | 1.09 | 1.3 | 0.166 | 15.2 |
| 6.8 | 10.78 | 1.35 | 1.6 | 0.204 | 15.1 |
| 13.3 | 13.48 | 1.68 | 1.9 | 0.242 | 14.4 |
| Parameter | Retardation Time (h) | Internal Compliance for the Kelvin Units (10−6/MPa) | |||
|---|---|---|---|---|---|
| t′ = 2.7-Day (64.8 h) | t′ = 4.3-Day (103.2 h) | t′ = 6.8-Day (163.2 h) | t′ = 13.3-Day (319.2 h) | ||
| D0 | Instant | 24.25 | 21.50 | 20.35 | 17.60 |
| D1 | 0.0005 | 0.91 | 0.42 | 0.28 | 0.22 |
| D2 | 0.005 | 4.35 | 1.85 | 1.15 | 0.98 |
| D3 | 0.05 | 27.54 | 11.08 | 7.68 | 5.72 |
| D4 | 0.5 | 122.27 | 38.75 | 23.93 | 18.47 |
| D5 | 5 | 348.61 | 115.45 | 64.54 | 50.08 |
| D6 | 50 | 779.63 | 221.38 | 110.61 | 88.67 |
| Parameter | Relaxation Time (h) | Internal Spring Modulus for the Maxwell Units (GPa) | |||
|---|---|---|---|---|---|
| t′ = 2.7-Day (64.8 h) | t′ = 4.3-Day (103.2 h) | t′ = 6.8-Day (163.2 h) | t′ = 13.3-Day (319.2 h) | ||
| E0 | 0.0004 | 0.285 | 0.931 | 0.838 | 0.862 |
| E1 | 0.004 | 12.666 | 4.841 | 3.230 | 3.619 |
| E2 | 0.04 | 19.491 | 19.531 | 15.727 | 16.809 |
| E3 | 0.4 | 5.038 | 13.216 | 17.323 | 19.265 |
| E4 | 4 | 1.355 | 3.872 | 7.247 | 8.588 |
| E5 | 40 | 0.426 | 1.295 | 2.377 | 2.816 |
| E6 | infinite | 0.788 | 2.467 | 4.637 | 5.447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, S.; Yang, S. Laboratory Evaluation of Tensile Creep Behavior of Concrete at Early Ages. Appl. Sci. 2024, 14, 1275. https://doi.org/10.3390/app14031275
Lim S, Yang S. Laboratory Evaluation of Tensile Creep Behavior of Concrete at Early Ages. Applied Sciences. 2024; 14(3):1275. https://doi.org/10.3390/app14031275
Chicago/Turabian StyleLim, Seungwook, and Sungchul Yang. 2024. "Laboratory Evaluation of Tensile Creep Behavior of Concrete at Early Ages" Applied Sciences 14, no. 3: 1275. https://doi.org/10.3390/app14031275
APA StyleLim, S., & Yang, S. (2024). Laboratory Evaluation of Tensile Creep Behavior of Concrete at Early Ages. Applied Sciences, 14(3), 1275. https://doi.org/10.3390/app14031275






