Impact of the New International Land–Sea Transport Corridor on Port Competition between Neighboring Countries Based on a Spatial Duopoly Model
Abstract
:1. Introduction
2. Problem Formulation
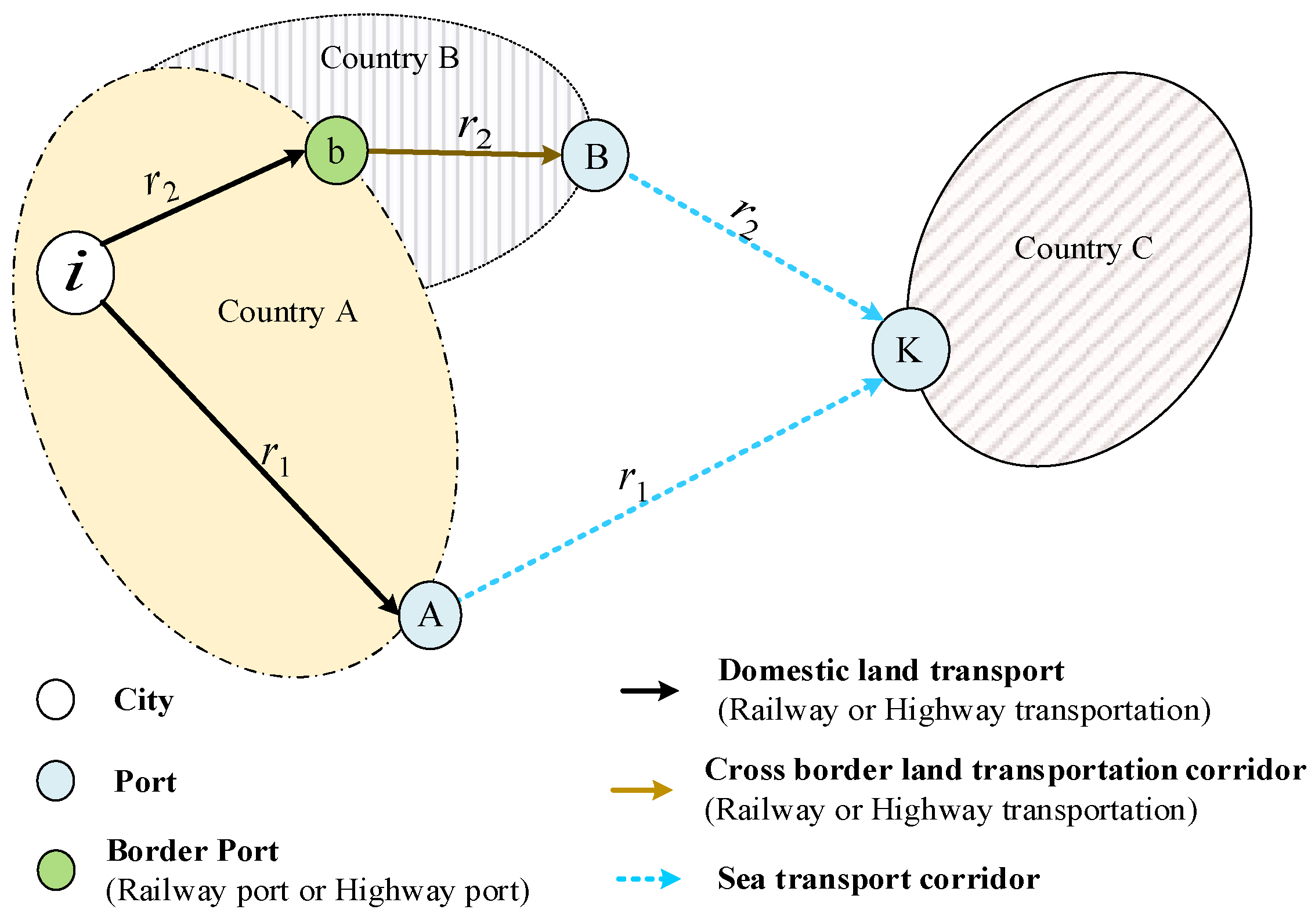
2.1. Problem Description and Assumptions
- (1)
- Port: port A and port B are on a line of length 1, at 0 and 1, respectively (see Figure 2). The hinterlands of the two ports overlap, and they are in a competitive state. Both ports can provide the same transshipment loading and unloading services, and their service prices (i.e., port charges to be paid by cargo owners or shippers) are and , respectively. It is assumed that the port costs (i.e., the costs of transshipment and handling services) provided by port A and port B are and , respectively. The maritime transportation costs (i.e., sea freight to be paid by the cargo owner or shipper) from port A and port B to the overseas destination port K are and , respectively.
- (2)
- Cargo owners or shippers: the cargo owner is at a certain point within the [0,1] range, and border port is located between the cargo owner and port B, that is, . Cargo owners and port operators act rationally, making decisions based on their interests and anticipated outcomes. Cargo owners prioritize the most efficient transportation route, while port operators set port service prices to maximize profit or cargo throughput. For simplicity, we assume that cargo demand in the port’s hinterland is inelastic, meaning the demand is constant.
- (3)
- Transportation model: The cargo owner in point x can select port A or port B to transfer the cargo to port K. The land transportation cost of goods from point x to port A is , and the land transportation cost of goods from point x to port B is , where is the domestic land transportation cost from point to border port , and is the cross-border land transportation cost from border port b to port B.
2.2. Land Transportation Cost in the Port Hinterland
2.3. Port Cargo Demand
3. Analysis of Port Competition Mode and Equilibrium Result
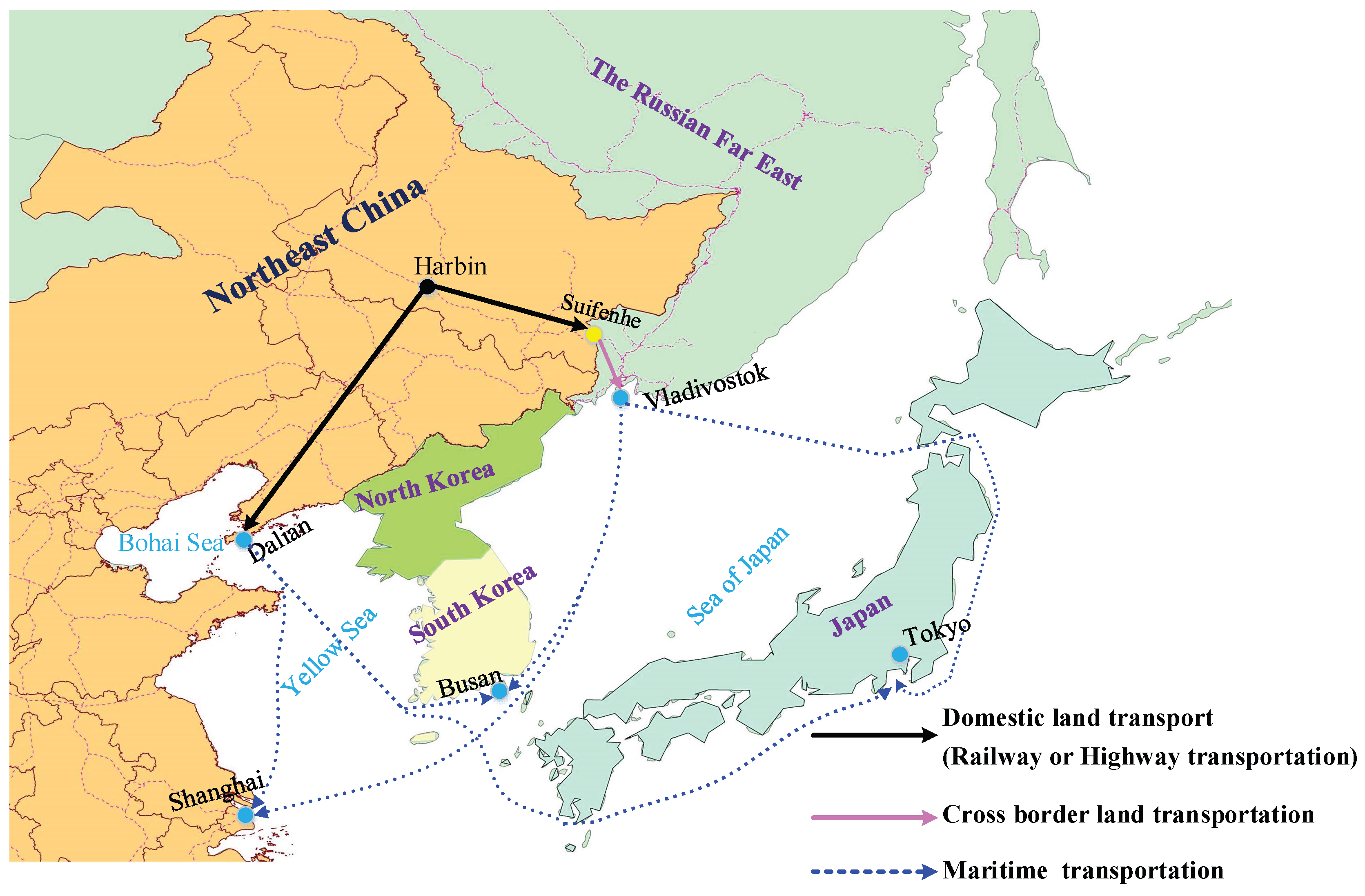
4. Numerical Analysis
4.1. Data and Parameters
4.2. Sensitivity Analysis
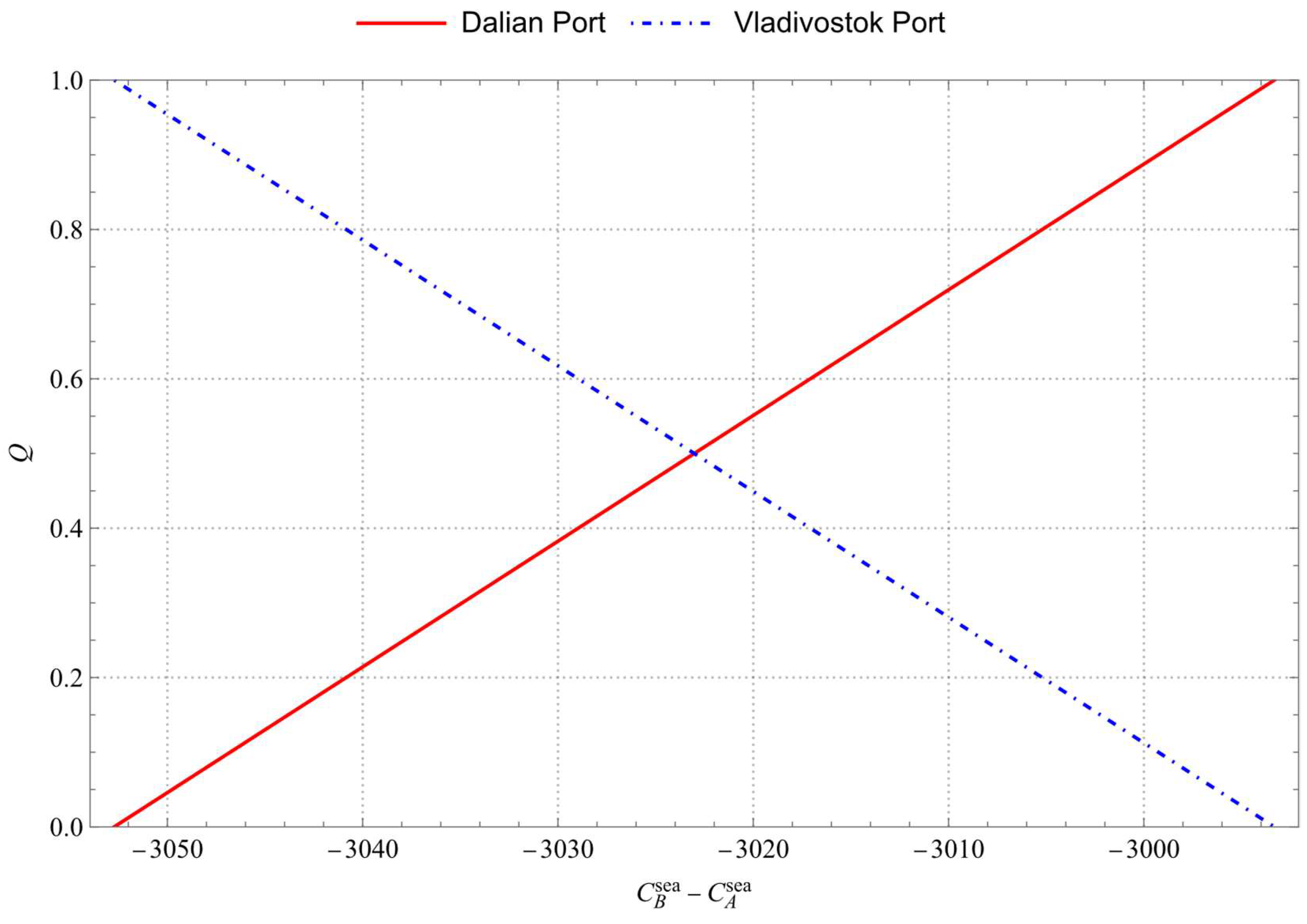
4.2.1. Sensitivity Analysis of Maritime Transportation Cost to Equilibrium Price and Port Cargo Demand
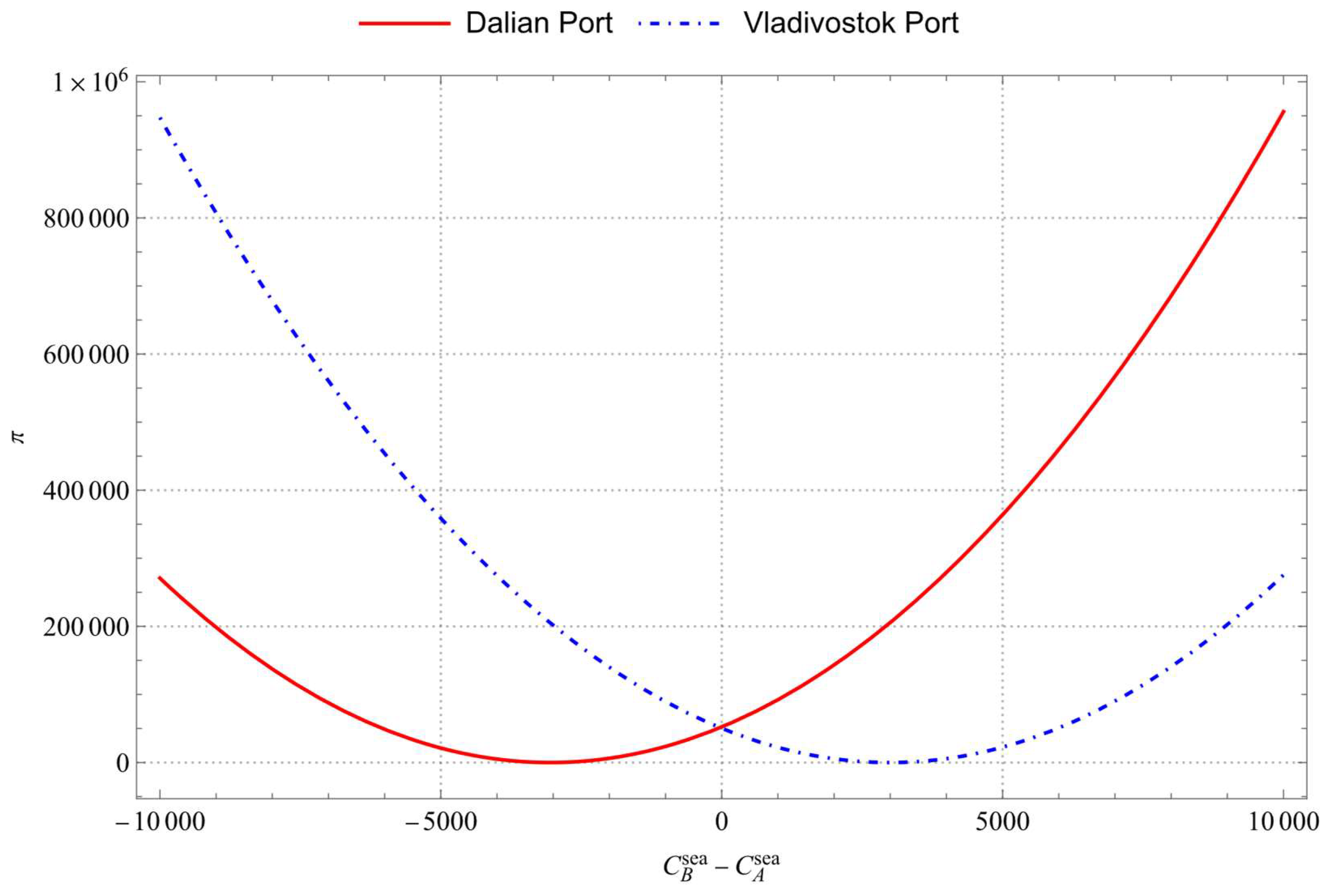
4.2.2. Sensitivity Analysis of Maritime Transportation Cost to Port Equilibrium Profit
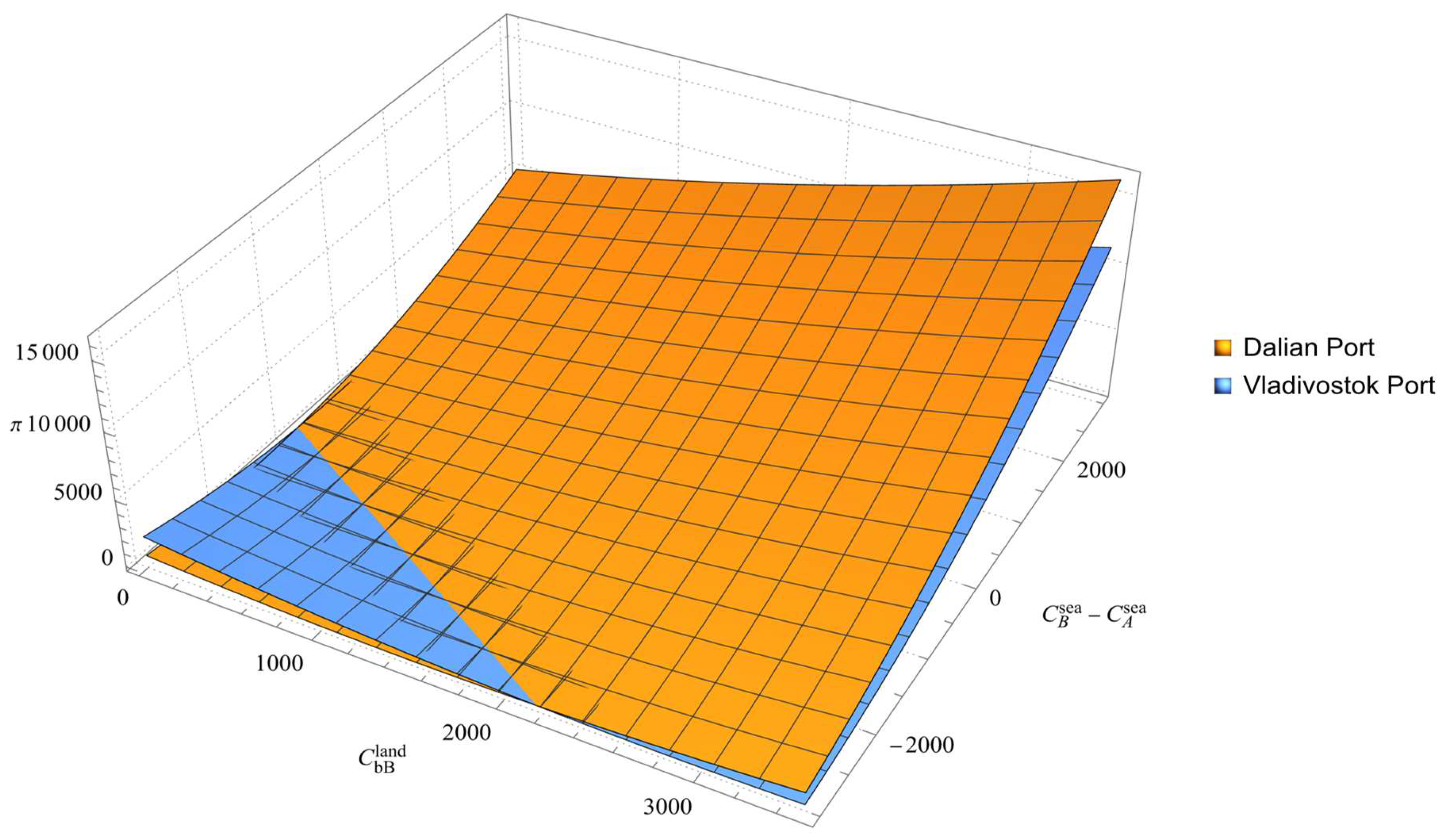
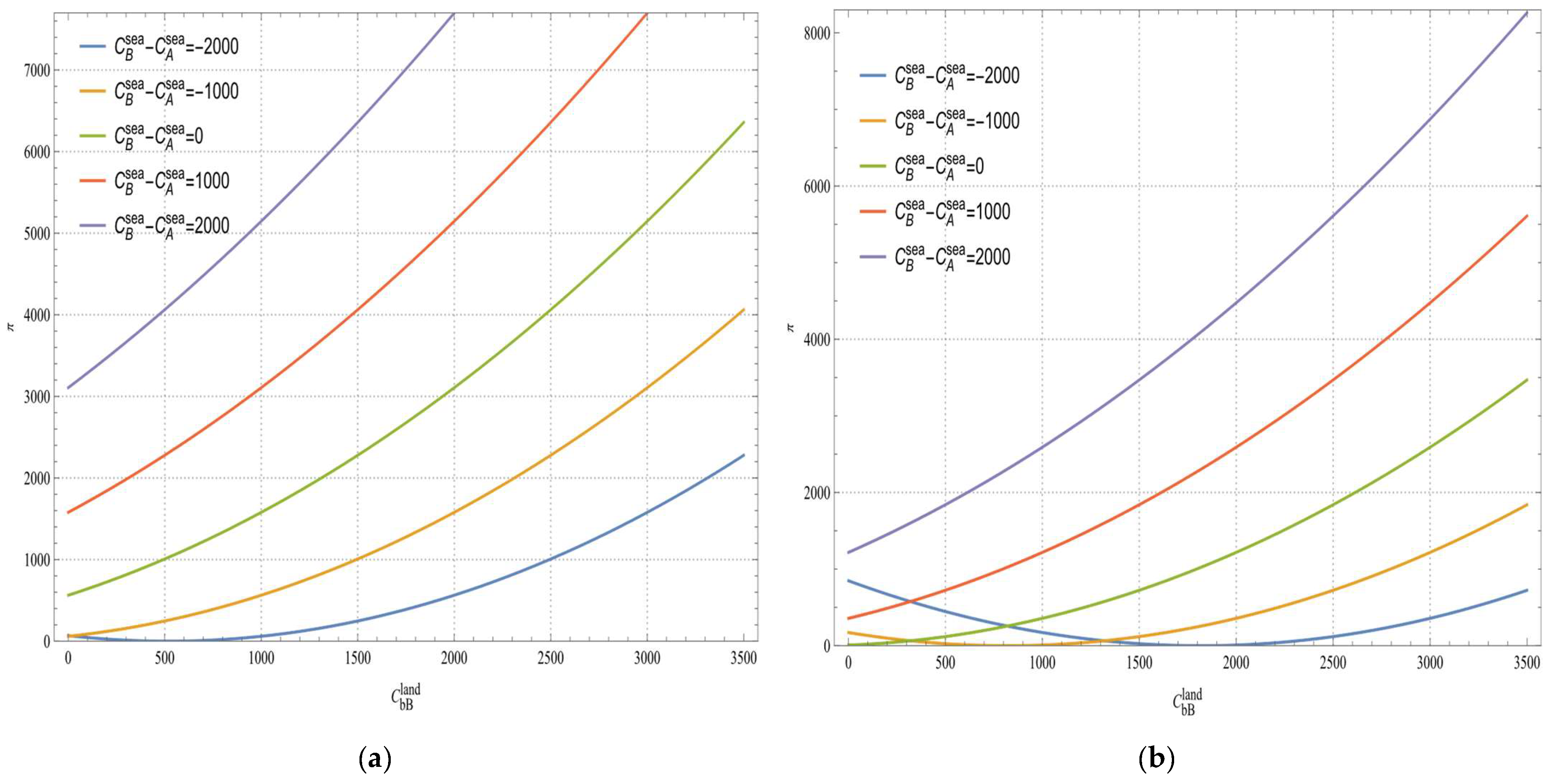
4.2.3. Sensitivity Analysis of Cross-Border Land transportation Cost and Maritime Transportation Cost to Port Equilibrium Profit
5. Conclusions
- (1)
- The higher the cross-border land transportation cost of goods transported to the overseas port and the maritime transportation cost of goods transported from the overseas port to the destination port, the lower the demand and price of goods of the overseas port in this region, putting it at a disadvantage compared to the port in this region. It is worth mentioning that the operational efficiency and capacity of the new international land–sea transport corridor would also be affected by international politics, geopolitics, market environment, and other factors, so the operational efficiency and cost of the international land–sea transport corridor is one of the important factors that restrict the expansion of overseas ports to the hinterland of the region.
- (2)
- In the case that overseas ports have a cost disadvantage compared with domestic ports when their maritime transportation cost is higher, the profit increase in domestic ports will be greater. Conversely, if overseas ports have a cost advantage over domestic ports, even if their maritime transportation cost is higher, the profit of domestic ports will decrease accordingly.
- (3)
- When the overseas port has an advantage in maritime transportation costs, an increase in cross-border transportation costs can enhance its competitiveness. Conversely, when there is no such advantage, cross-border transport costs need to be large enough to offset the disadvantage and thereby increase profits. Given the current conditions of the PITC, high cross-border transportation costs are not conducive to improving the competition of Vladivostok Port in the transportation market of Northeast China. Therefore, further reducing the cross-border transportation cost of the PITC is an important factor to expand the market scope of Vladivostok Port and maintain its profits.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffman, A.J. Optimized Border System for Land-Based Transport. IEEE Intell. Transp. Syst. Mag. 2023, 15, 6–21. [Google Scholar] [CrossRef]
- Liu, C.; Fan, H.; Zhang, X.; Fan, H.; Miao, H. Impact of the Primorsky International Transport Corridor on the Hinterland Competition between Ports in Northeast China and Russian Far East. Res. Transp. Bus. Manag. 2024, 52, 101084. [Google Scholar] [CrossRef]
- Jiang, Y.; Qiao, G.; Lu, J. Impacts of the New International Land–Sea Trade Corridor on the Freight Transport Structure in China, Central Asia, the ASEAN Countries and the EU. Res. Transp. Bus. Manag. 2020, 35, 100419. [Google Scholar] [CrossRef]
- Luo, M.; Chen, F.; Zhang, J. Relationships among Port Competition, Cooperation and Competitiveness: A Literature Review. Transp. Policy 2022, 118, 1–9. [Google Scholar] [CrossRef]
- Lagoudis, I.N.; Theotokas, I.; Broumas, D. A Literature Review of Port Competition Research. Int. J. Shipp. Transp. Logist. 2017, 9, 724–762. [Google Scholar] [CrossRef]
- Huybrechts, M.; Meersman, H.; Van de Voorde, E.; Van Hooydonk, E.; Verbeke, A.; Winkelmans, W. Port Competitiveness: An Economic and Legal Analysis of the Factors Determining the Competitiveness of Seaports; De Boeck: Antwerpen, Belgium, 2002. [Google Scholar]
- Huang, Z.; Yang, Y.; Zhang, F. Configuration Analysis of Factors Influencing Port Competitiveness of Hinterland Cities under TOE Framework: Evidence from China. J. Mar. Sci. Eng. 2022, 10, 1558. [Google Scholar] [CrossRef]
- Dong, G.; Huang, R. Inter-Port Price Competition in a Multi-Port Gateway Region. Res. Transp. Econ. 2022, 94, 101178. [Google Scholar] [CrossRef]
- Yu, S.; Gong, L.; Qi, M. Efficiency Analysis of the Coastal Port Group in the Yangtze River Delta. J. Mar. Sci. Eng. 2022, 10, 1575. [Google Scholar] [CrossRef]
- Chang, Y.T.; Talley, W.K. Port Competitiveness, Efficiency, and Supply Chains: A Literature Review. Transp. J. 2019, 58, 1–20. [Google Scholar] [CrossRef]
- Parola, F.; Risitano, M.; Ferretti, M.; Panetti, E. The Drivers of Port Competitiveness: A Critical Review. Transp. Rev. 2017, 37, 116–138. [Google Scholar] [CrossRef]
- Wang, J.; Mo, L.L.; Ma, Z. Evaluation of Port Competitiveness along China’s “Belt and Road” Based on the Entropy-TOPSIS Method. Sci. Rep. 2023, 13, 15717. [Google Scholar] [CrossRef]
- Zhong, H.L.; Ou, Y.H.; Chen, J.W.; Wan, Y.C. Empirical Study on Sustainable Competitiveness Evaluation of Guangzhou Port Based on Improved Matter-Element Model. In Proceedings of the 2017 International Conference on Service Systems and Service Management, Dalian, China, 16–18 June 2017. [Google Scholar]
- Wang, P.; Hu, Q.Y.; Xu, Y.J.; Mei, Q.; Wang, F. Evaluation Methods of Port Dominance: A Critical Review. Ocean Coast. Manag. 2021, 215, 105954. [Google Scholar] [CrossRef]
- Ren, J.Z.; Dong, L.; Sun, L. Competitiveness Prioritisation of Container Ports in Asia under the Background of China’s Belt and Road Initiative. Transp. Rev. 2018, 38, 436–456. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Zheng, R.; Na, S.; Liu, C. Evaluation Analysis of the Operational Efficiency and Total Factor Productivity of Container Terminals in China. Sustainability 2022, 14, 13007. [Google Scholar] [CrossRef]
- Lozano, S. Estimating Productivity Growth of Spanish Ports Using a Non-Radial, Non-Oriented Malmquist Index. Int. J. Shipp. Transp. Logist. 2009, 1, 227–248. [Google Scholar] [CrossRef]
- Ben Mabrouk, M.; Elmsalmi, M.; Aljuaid, A.M.; Hachicha, W.; Hammami, S. Joined Efficiency and Productivity Evaluation of Tunisian Commercial Seaports Using DEA-Based Approaches. J. Mar. Sci. Eng. 2022, 10, 626. [Google Scholar] [CrossRef]
- Yap, W.Y.; Lam, J.S.L. Competition Dynamics between Container Ports in East Asia. Transp. Res. Part A-Policy Pract. 2006, 40, 35–51. [Google Scholar] [CrossRef]
- Dias, J.C.Q.; Azevedo, S.G.; Ferreira, J.; Palma, S.F. A Comparative Benchmarking Analysis of Main Iberian Container Terminals: A DEA Approach. Int. J. Shipp. Transp. Logist. 2009, 1, 260–275. [Google Scholar] [CrossRef]
- Li, H.; Jiang, L.L.; Liu, J.N.; Su, D.D. Research on the Evaluation of Logistics Efficiency in Chinese Coastal Ports Based on the Four-Stage DEA Model. J. Mar. Sci. Eng. 2022, 10, 1147. [Google Scholar] [CrossRef]
- Yen, B.T.H.; Huang, M.-J.; Lai, H.-J.; Cho, H.-H.; Huang, Y.-L. How Smart Port Design Influences Port Efficiency—A DEA-Tobit Approach. Res. Transp. Bus. Manag. 2023, 46, 100862. [Google Scholar] [CrossRef]
- Svanberg, M.; Holm, H.; Cullinane, K. Assessing the Impact of Disruptive Events on Port Performance and Choice: The Case of Gothenburg. J. Mar. Sci. Eng. 2021, 9, 145. [Google Scholar] [CrossRef]
- De Langen, P.W.; Heij, C. Corporatisation and Performance: A Literature Review and an Analysis of the Performance Effects of the Corporatisation of Port of Rotterdam Authority. Transp. Rev. 2014, 34, 396–414. [Google Scholar] [CrossRef]
- Borges Vieira, G.B.; Kliemann Neto, F.J.; Amaral, F.G. Governance, Governance Models and Port Performance: A Systematic Review. Transp. Rev. 2014, 34, 645–662. [Google Scholar] [CrossRef]
- Garcia-Alonso, L.; Sanchez-Soriano, J. Port Selection from a Hinterland Perspective. Marit. Econ. Logist. 2009, 11, 260–269. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X. Port Selection Based on Customer Questionnaire: A Case Study of German Port Selection. Eur. Transp. Res. Rev. 2019, 11, 48. [Google Scholar] [CrossRef]
- Feng, H.; Lin, Q.; Zhang, X.; Lam, J.S.L.; Yap, W.Y. Port Selection by Container Ships: A Big AIS Data Analytics Approach. Res. Transp. Bus. Manag. 2024, 52, 101066. [Google Scholar] [CrossRef]
- Pujats, K.; Golias, M.; Konur, D. A Review of Game Theory Applications for Seaport Cooperation and Competition. J. Mar. Sci. Eng. 2020, 8, 100. [Google Scholar] [CrossRef]
- Verhoeff, J.M. Seaport Competition: Some Fundamental and Political Aspects. Marit. Policy Manag. 1981, 8, 49–60. [Google Scholar] [CrossRef]
- Yu, M.; Shan, J.; Ma, L. Regional Container Port Competition in a Dual Gateway-Port System. J. Syst. Sci. Syst. Eng. 2016, 25, 491–514. [Google Scholar] [CrossRef]
- van Reeven, P. The Effect of Competition on Economic Rents in Seaports. J. Transp. Econ. Policy 2010, 44, 79–92. [Google Scholar]
- Yip, T.L.; Liu, J.J.; Fu, X.; Feng, J. Modeling the Effects of Competition on Seaport Terminal Awarding. Transp. Policy 2014, 35, 341–349. [Google Scholar] [CrossRef]
- Cui, H.; Notteboom, T. Modelling Emission Control Taxes in Port Areas and Port Privatization Levels in Port Competition and Co-Operation Sub-Games. Transp. Res. Part D Transp. Environ. 2017, 56, 110–128. [Google Scholar] [CrossRef]
- Czerny, A.; Höffler, F.; Mun, S. Hub Port Competition and Welfare Effects of Strategic Privatization. Econ. Transp. 2014, 3, 211–220. [Google Scholar] [CrossRef]
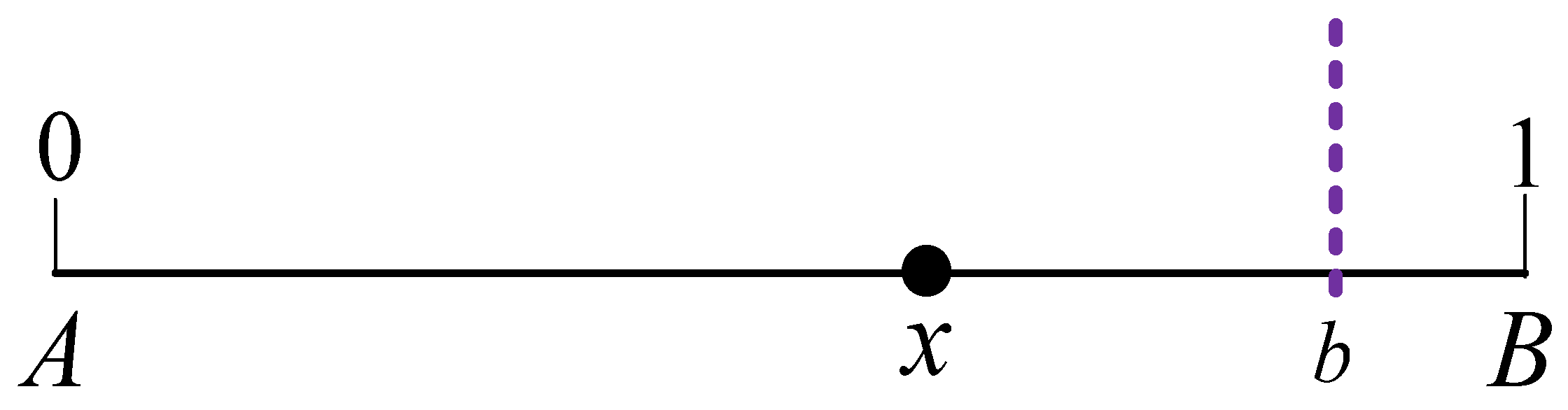


| Dalian Prot | Vladivostok Port | |
|---|---|---|
| Number of container terminals | 12 | 6 |
| Number of berths at container terminals | 18 | 10 |
| Number of bridge cranes | 35 | 14 |
| Container yard area (million square meters) | 2.93 | 1.2 |
| Container cargo throughput (million TEU) | 445.9 | 76.8 |
| Parameter | Value |
|---|---|
| Freight sharing rate | , |
| Transportation cost per unit distance (RMB/TEU·km) | , |
| Average operating speed (km/h) | , |
| Cross-border transportation cost (RMB) | 2102 |
| Port charge (RMB/TEU) | 667, 1590 |
| Time value (RMB/TEU) | = 40 |
| Marginal congestion cost of port (RMB/TEU) | |
| Container cargo handling capacity (TEU) | , |
| Shipping Route | Direction | Maritime Transportation Cost * (Ocean Freight) | Maritime Transportation Cost Difference () |
|---|---|---|---|
| Shipping routes to Japanese and Korean ports | Dalian–Buan | 2783.45 | −352.34 |
| Vladivostok–Buan | 2431.11 | ||
| Dalian–Tokoy | 2818.68 | 563.74 | |
| Vladivostok–Tokoy | 3382.42 | ||
| Shipping routes to Chinese coastal ports | Dalian–Shanghai | 1674.00 | 1109.45 |
| Vladivostok–Shanghai | 2783.45 | ||
| Dalian–Xiamen | 1464.00 | 2376.45 | |
| Vladivostok–Xiamen | 3840.45 | ||
| Dalian–Nansha | 1335.00 | 2505.45 | |
| Vladivostok–Nansha | 3840.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Fan, H.; Miao, H.; Fan, H.; Zhang, X. Impact of the New International Land–Sea Transport Corridor on Port Competition between Neighboring Countries Based on a Spatial Duopoly Model. Appl. Sci. 2024, 14, 1857. https://doi.org/10.3390/app14051857
Liu C, Fan H, Miao H, Fan H, Zhang X. Impact of the New International Land–Sea Transport Corridor on Port Competition between Neighboring Countries Based on a Spatial Duopoly Model. Applied Sciences. 2024; 14(5):1857. https://doi.org/10.3390/app14051857
Chicago/Turabian StyleLiu, Chuanying, Houming Fan, Hongzhi Miao, Hao Fan, and Xiang Zhang. 2024. "Impact of the New International Land–Sea Transport Corridor on Port Competition between Neighboring Countries Based on a Spatial Duopoly Model" Applied Sciences 14, no. 5: 1857. https://doi.org/10.3390/app14051857
APA StyleLiu, C., Fan, H., Miao, H., Fan, H., & Zhang, X. (2024). Impact of the New International Land–Sea Transport Corridor on Port Competition between Neighboring Countries Based on a Spatial Duopoly Model. Applied Sciences, 14(5), 1857. https://doi.org/10.3390/app14051857





