Innovative Approaches to Wear Reduction in Horizontal Powder Screw Conveyors: A Design of Experiments-Guided Numerical Study

Abstract

Numerical simulations play a vital role in the modern engineering industry, especially when faced with interconnected challenges such as particle interactions and the structural integrity of conveyor systems. This article focuses on the handling of materials and emphasizes the importance of using parametric numerical analysis to improve efficiency, reduce wear, and enhance the structural integrity of horizontal screw conveyors. Through the utilization of the Design of Experiments, we systematically investigated critical parameters such as screw pitch, clearance, wear, rotational velocity, and additional structural factors. This examination was carried out within a well-defined parametric framework, utilizing a combination of software tools provided by the Ansys suite and Minitab. The findings demonstrate the effectiveness of the Design of Experiments analysis in achieving improved performance and provide valuable insights for engineers and researchers involved in the design of conveyor systems. Furthermore, this comprehensive approach clarifies how conveyor systems respond to changes in parameters and highlights the complex interaction between transported particles and the conveyor system. We present a detailed analysis that clarifies the complex relationships and dependencies among different parameters, providing engineers and researchers with valuable insights. By understanding the interactions of these factors, the methodology provides not only results but also a strategic framework for advancing conveyor system design and engineering practices.

1. Introduction

In the era of Industry 4.0 and highly developed economies, ensuring the efficient and reliable transportation of bulk solids is crucial for the smooth operation of various industrial sectors. Transport systems play a central role in production infrastructure, serving as the driving force that facilitates the smooth supply of essential raw materials for manufacturing processes and other logistical operations [1]. The transportation of diverse materials constitutes a considerable aspect of industrial production. An underexplored realm within this domain refers to the processes associated with materials in solid aggregate states, specifically in the form of bulk solids, along with their transportation—a substantial component across diverse industrial sectors [2]. The composition and condition of bulk solids in the input or output stages, along with the associated costs during the manipulation and transportation of raw materials or final products, play a vital role in most of the listed industries [3]. Therefore, investigations into the behaviour of bulk solids are crucial to ensure precision and optimize production efficiency, particularly in the context of the bulk material handling industry.

Despite extensive theoretical research and conventional experiments conducted in the past to increase the performance of different conveyors, we still face limitations in providing detailed particle-level data. This information is vital for comprehending the fundamental mechanisms governing the material flow of granular materials and powders, which are key aspects in understanding the phenomena and overall performance of conveyors. In some cases, due to demanding boundary conditions and complex mathematical models, both analytical and empirical approaches may fall short of providing an accurate description of the system. As a result, modern methodologies for numerical simulation of material handling systems rely on sophisticated numerical techniques. Numerical modelling of particle systems is nowadays crucial for designing modern material handling systems and understanding interactions among discrete particles, ranging from fine powders to larger granular materials. Discrete Element Methods (DEM) have been in use for decades, with their origins found in B. Alder’s work on Molecular Dynamics (MD) over fifty years ago [4]. Nevertheless, the significant adoption of DEM began in 1979 when Cundall and Strack introduced an efficient tool for tackling diverse challenges in particle mechanics [5]. The development of DEM over the years has positioned DEM as a powerful tool for designing and understanding the challenges of material handling systems [6].

Among basic material handling systems, screw conveyors have become a fundamental material handling device in various industries, including ports, agriculture, and industrial processes [7]. The screw conveyor is a widely used material handling device for transporting granular material and powder in various industries such as food, pharmaceutical, chemical, and agricultural. It is favoured for its efficiency, cost-effectiveness, compact structure, and ability to provide accurate and uniform feeding [8]. Screw conveyors are primarily employed for mixing [9,10], short-distance transportation, and lifting of bulk materials and powders [11]. In the past, researchers in the design of screw conveyors relied on theoretical descriptions based on partially derived analytical solutions [12,13,14,15]. This approach is suitable for addressing idealized geometries and simplified systems. These analyses cannot provide insights into phenomena such as particle-particle interaction, particle-wall interaction, and inter-particle forces [16]. In practice, the design phase relies on standards [17,18], empirical estimates, experiential results, and results from partial experiments. Experiments with technical devices are usually cost-intensive and time-consuming. They cannot be avoided entirely, as they are often necessary for determining basic contact parameters and calibrating the numerical model [19]. More suitable and increasingly used are discrete numerical methods, which enable the description and even optimization of highly complex geometries and conveyors. Although their mechanical design appears simple, the behaviour of granular solids and powders during transport is highly complex [16]. Screw conveyors have previously been examined and analyzed in the existing literature, with DEM analysis presented in reference [20]. This analysis specifically investigated screw and shaftless screw conveyors for various free-flowing bulk solids, which are typically easy to handle. As demonstrated in reference [21], multiple existing studies have already addressed the impact of geometric design, operating parameters, and mixing characteristics on various types of screw conveyors and feeders. Owen et al. [22] investigated how varying inclination angles, rotational speeds, and filling rates impact conveyor performance including conveying velocity, mass flow rate and power consumption. Hu et al. [23] utilize the Discrete Element Method (DEM) to assess the efficiency of a screw conveyor. The analysis involves visualizing particle motion, determining angular and axial particle velocities, calculating overall torque and total force, and evaluating kinetic energy and total energy dissipation within the system. Wang et al. [24] simulated particle flow in a screw conveyor, observing increased mass flow rates with higher speeds and filling levels. Fernandez et al. [25] studied screw feeders with different blade designs. It reveals critical factors impacting flow uniformity, power consumption, and wear, emphasizing the importance of screw design in optimizing feeder performance. Provided studies are limited. They examined the screw conveying characteristics, omitted significant material properties, including particle shape and size, and neglected to properly calibrate material properties. Govender et al. [26] take a step further when they address the impact of particle shape, particularly faceted polyhedral particles, on the behaviour of materials in screw conveyors. It finds that while spheres hold similar bulk discharge rates to certain polyhedra at lower speeds, polyhedra generally exhibit a larger fraction of normal impacts between particles and increased abrasion, while spheres dissipate more energy as shear between particles. Sun et al. [27] also studied significance of particle shape on conveying performance and wear, with particles’ shape index affecting collision frequency and energy consumption, particularly in particle-wall collisions.

In summary, existing research on screw conveyors has provided insights into conveyor performance under varying operational conditions such as rotational velocities, filling rates, and screw designs, influencing mass flow rates. However, these studies often overlook particle properties like shape, size and calibration overall, limiting the accuracy of conveyor descriptions and study applicability across different operating regimes and states of conveying materials. Additionally, despite a partial understanding of how input parameters impact specific conveyor configurations, there remains a notable absence of studies where optimization is conducted to determine optimum parameters. This was also recently highlighted by Chen et al. [14], who first proposed a method based on the combination of DEM and NSGA-II algorithms to analyze and improve the conveying efficiency while reducing blade wear in vertical screw conveyors transporting cohesive particles. Moreover, there are multiple research papers focusing on the combined analysis of observing different outputs of the system. For example, conveying efficiency and blade wear or conveying efficiency and power consumption, highlighting a significant gap in the literature. Moreover, there’s an additional gap in addressing structural integrity concerns during conveyor design. To further bridge this gap during this study we adopted an approach integrating the Discrete Element Method (DEM) with Finite Element Analysis (FEA) and Design of Experiments (DOE) to thoroughly investigate the geometry properties and dynamics of screw conveyors. This approach considers both geometric and kinematic parameters for analysis, calibration, and optimization. A methodological approach is adopted using numerical simulations to optimize equipment design for transporting abrasive powder materials. By calibrating material models and integrating various simulation methods, we identify critical parameters and optimize system performance, focusing on mass flow and wear reduction of screw blades. The outcomes of our study contribute to understanding screw conveyor systems and provide valuable insights for enhancing efficiency and reducing wear in handling abrasive powders. Additionally, it highlights the importance and significance of specific variables across different response metrics. Based on the described main research questions where the following:

• Can the abrasive powder material model be effectively calibrated through a combination of literature review, angle of repose, and shear tests to ensure an accurate representation of material behaviour within DEM simulations?
• Can Design of Experiments (DOE) be applied to systematically analyze the impact of various factors, such as screw pitch, clearance, wear, and rotational velocity, on critical screw conveyor performance metrics including mass flow, power consumption, wear, stresses, deformations, and their dependencies?
• Can response surface optimization be applied to identify optimum parameters for maximizing mass flow while minimizing wear?
• Can insights from parametric numerical analysis and utilization of DOE and response surface optimization be translated into practical guidelines for engineers designing efficient conveyor systems?

2. Materials and Methods

Given that the modelling methodology relies on the DEM, it is appropriate to give a short overview in the subsequent sections. This includes a discussion of the associated models and contemporary approaches incorporated into the numerical model.

2.1. Discrete Element Method

The DEM is a Lagrangian numerical method where each particle is treated as a distinct entity possessing individual characteristics. Thus, $m_i$ is the mass of the specified particle, $I_i$ is the corresponding moment of inertia, which, for spherical objects, is not tensorial but is expressed as a simple scalar. $R_i$ is the associated radius, and ${\mathsf{\nu }}_i$ represents the Poisson’s ratio. The temporal evolution of these attributes follows the integration of Newton’s second law of motion.

In our study, we employ spherical elements, and for a spherical particle, this results in a system of three vector equations (nine equations in total in three dimensions) [28].

$$m_i {\mathit{a}}_i=m_i \frac{d}{dt}{\mathit{v}}_i=\sum _{\mathit{j}=1}^{ nc}{{\mathit{F}}_{ij}^c}_{ }+\sum _{k=1}^{ nw}{{\mathit{F}}_{ik}^w}_{ }+{\mathit{F}}_i^g+{\mathit{F}}_i^{ext}$$

(1)

$$I_i {\mathit{\vartheta }}_i=I_i \frac{d}{dt}{\mathit{\omega }}_i=\sum _{\mathit{j}=1}^{ nc}{{\mathit{T}}_{ij}^c}_{ }+{\mathit{T}}_{ij}^{rol}+\sum _{\mathit{j}=1}^{ nw}{{\mathit{T}}_{ik}^c}_{ }+{\mathit{T}}_{ik}^{rol}$$

(2)

where ${\mathit{F}}_{ij}^c$ is the force at the contact point between particles i and j. ${\mathit{F}}_{ik}^w$ analogously follows as the force at the contact point between particle i and a wall section $k$ within the bounding box. ${\mathit{F}}_i^g$ is a body force on the particles (e.g., gravity) while ${\mathit{F}}_i^{ext}$ represents non-contact forces such as electrostatic, van der Waals, cohesive forces or particle-fluid interaction forces. Finally, ${\mathit{T}}_{ij}^c$ and ${\mathit{T}}_{ij}^{rol}$ are the contact torque and rolling friction torque applied to particle i due to contact i-j, and ${\mathit{T}}_{ik}^c$ and ${\mathit{T}}_{ik}^{rol}$are the corresponding torque components for particle wall collisions.

Contact Model

Introducing the variables ${\delta }_{ }^n$and ${\delta }_{ }^t$ to signify normal and tangential overlap, respectively, the “soft sphere” modelling approach involves rigid particles that simulate deformation through superposition. The computation of normal and tangential contact forces involves determining fabricated overlaps between “non-deformable” particles in their respective directions. This is shown schematically in Figure 1a. There are many force models within DEM where the normal and tangential contact forces typically consist of elastic (spring) and dissipative (dashpot) forces, giving rise to the depicted generalized spring and dashpot model [28].

$${{\mathit{F}}_{ij}^c=}_{ }{\mathit{F}}_{ij}^n+{\mathit{F}}_{ij}^t=\left(-\left(k_n{\delta }_{ }^n\right){\mathit{n}}_{ij}-\left({\eta }^n {\mathit{v}}_{rel}^n\right)\right)+\left(-\left(k_t {\mathit{\delta }}_{ }^t\right)-\left({\eta }^t {\mathit{v}}_{rel}^t\right)\right)$$

(3)

In the Equation (3) we introduced spring stiffness coefficients $k_n$ and $k_t$ in the normal ${\mathit{n}}_{ij}$ and tangential directions ${\mathit{t}}_{ij}$, while similarly denoting the damping coefficient with the symbol η for both mentioned directions. To compute arbitrary contact models, it is necessary to calculate the velocities in the normal ${\mathit{v}}_{rel}^n$and tangential ${\mathit{v}}_{rel}^t$ directions.

In this study, we utilized the Hertzian model in the normal direction and the Mindlin-Deresiewicz model in the tangential direction, as illustrated in Figure 1b. The rolling friction model C was utilized which allows the rolling resistance torque to vary within the defined limits, addressing the discontinuity observed in Model A at zero angular velocity, which is present when using Rolling friction type A [29].

In particulate systems, the interactions between particles and boundaries induce shear forces, denoted by the tangential component of contact. Previous research [30,31] has explored the relationship between the energy resulting from shear-normal impacts and the wear rate in mechanical contacts. These studies emphasize the significant impact of shear component-related energy on surface material removal rates. The analysis of wear within this model delves into the concept of shear intensity, a fundamental measure representing the power transferred per unit area. The application of shear intensity in this model provided a method for qualitatively assessing wear phenomena. By quantifying the power transferred per unit area during collisions, the model can offer insights into the extent of wear on geometric surfaces. This energy metric finds application in abrasive wear models, particularly in assessing shear wear on geometric surfaces. The model can be directly correlated with wear phenomena, facilitating the determination of abrasive wear on geometric surfaces. All forms of intensity derived from boundary collision statistics are calculated per individual boundary triangle [32].

$$I_{b,T}^{Shear}=\frac{{\displaystyle {\sum }_{\kappa =1}^{N_{\kappa ,T}}}{\left(W_{\kappa }^{Shear}\right)}_b}{A_T∆t_{out}}$$

(4)

where $A_T$ is the boundary area, $∆t_{out}$ data collection time interval and $W_{\kappa }^{Shear}$ is the shear work of a particle-boundary collision. For additional information, please refer to [32]. Additionally, an extra wear model, namely the Archard model, was incorporated. This model, based on the research of John F. Archard, ref. [33] suggests that the amount of material removed from the surface correlates directly with the frictional work executed by particles in motion on the surface. Despite qualitative analysis, we have the ability to visually depict surface wear more elegantly and streamline the summation of surface wear, exclusively within the final idealized model. Refer to literature sources [32] for a detailed discussion on the exact computations of coefficients. Due to conciseness, a comprehensive explanation is omitted here.

The coupling between DEM and FEA enables the prediction of stress and strain responses in structures under bulk material loading conditions. An essential objective involves determining the node forces according to the applied load for every element. M. Dratt et al. [34] showed while this process is straightforward for basic meshes, it necessitates further consideration when accommodating modern high-order shell and volume elements. In this study, coupling DEM-FEA was conducted through a well-established workflow within the Ansys Workbench environment, specifically between Ansys Rocky and Ansys Transient. By running Boundary Collision Statistics, we can capture the average collision forces exerted on boundaries. These forces can be exported to external software for structural analysis. Typically, boundary conditions for such analyses require nodal forces, which are the forces acting on the vertices of the triangles forming the boundaries. Thus, to streamline the data transfer to finite element software, Rocky offers these nodal force values, derived from the collected forces per boundary triangle. The determination of these forces is achieved using the following expression [32].

$$F_{b,T}^{\mathsf{\gamma }}=\frac{{\displaystyle {\sum }_{\kappa =1}^{N_{\kappa ,T}}}{J_{\kappa }^{\mathsf{\gamma }}}_{ }}{∆t_{out}}$$

(5)

The impulse associated with the total force exerted over a boundary triangle during a collision is denoted as $J_{\kappa }^{\mathsf{\gamma }}$ where γ is a component for any of the Cartesian components. the summation in this equation encompasses all collisions recorded against boundary triangle T during the data collection interval $∆t_{out}$. To derive the nodal force values, it is assumed that collisions over a boundary triangle are uniformly distributed, allowing the resulting force on the boundary triangle to be evenly divided among its three vertices.

2.2. Used Particle Properties

Alumina also referred to as aluminium oxide (Al₂O₃), has exceptional qualities such as hardness, wear resistance, and chemical inertness, making it a premier choice for various industrial applications involving abrasion. In the field of grinding tools, alumina is a standout choice, serving as either an abrasive grain or a crucial component in abrasive formulations. Alongside alumina, a diverse range of abrasive materials, including silicon carbide, diamond, cubic boron nitride, and corundum, plays a significant role in this sector. The applications of aluminium oxide are extensive, spanning from wear protection coatings in machines and plants to corrosion protection in the chemical industry. Additionally, it finds use as insulation material in electronics and high-temperature applications. The suitability of aluminium oxide, corundum, and other materials depends on factors such as their content, grain size, and porosity, all of which are decisive for their specific areas of application in diverse industrial scenarios involving abrasion, wear protection, and corrosion resistance [35,36].

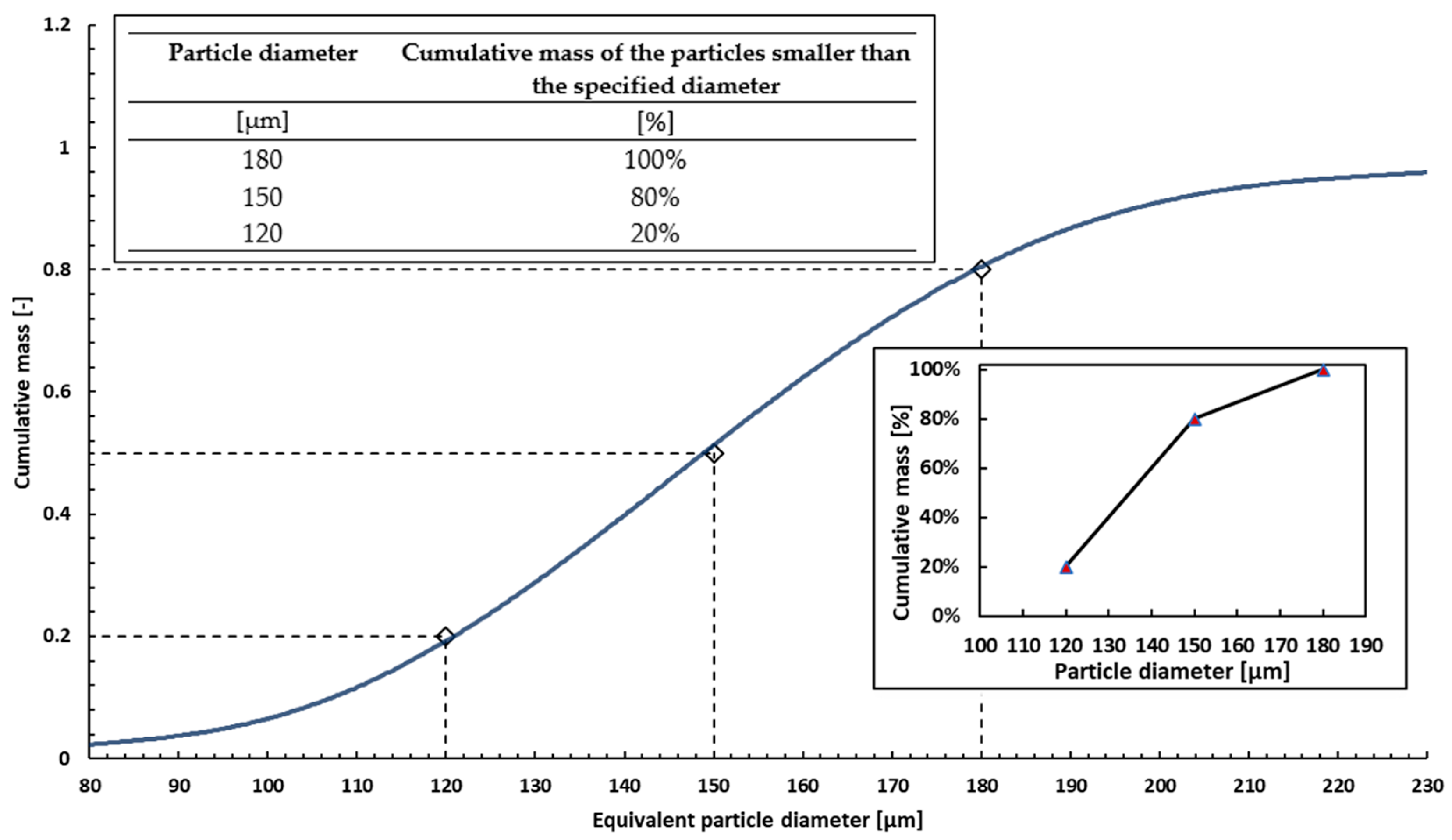
Particle Shape and Size Distribution

The potential for modelling at the particle level is a key advantage of the Discrete Element Method (DEM). However, real-world applications encounter a significant challenge due to the uncontrollable increase in number of particles. These systems, often comprising millions or even billions of individual particles, result in computationally expensive simulations that are frequently impractical. As computational capabilities have advanced, more complex non-spherical shapes have been incorporated using various techniques [32]. It’s essential to note that the particle shape and size significantly impact all other model parameters requiring calibration and should be the initial consideration when conducting numerical simulations. In the case of conducting numerical simulations of abrasive powders (Figure 2), physical particles exhibit non-spherical shapes. Accurately characterizing these shapes remains exceedingly difficult due to their irregular nature. Due to a lack of computing resources, we implemented

Coarse graining (CGM) is the process of simplifying a system by representing groups of fine-scale particles or degrees of freedom with fewer, coarser-scale entities, necessitating adjustments to the contact model while maintaining similarity to the original system [37]. The particle group has a unique scale factor $f_{CGM}$ that determines the parcel size and the number of original particles represented. The aim is to maintain the same energy density and the evolution of energy density as per the real base model with real particle size distribution. The CGM approach utilized by Rocky is founded on the research conducted by Bierwisch et al. [38]. The scale factor utilizes multiplication to increase the original particle size from Figure 3, defining the new parcel size and, consequently, determining the number of original particles the parcel represents. The gravitational potential energy density remains constant regardless of the particle diameter as long as the solid density and the volume fraction of the particles remain unchanged. In order to maintain the conservation of kinetic energy variation $∆E_{kin}$, the velocity variation of a scaled-up system for the relative velocities of the particles before ($v_a^{ })$ and after the contact ($v_b^{ })$ with a constant effective contact mass $m^{*}$ must remain equal to that of the original system during contact.

$$∆E_{kin}=\frac{m^{\ast }}{2}·\left(v_b^2-v_a^2\right)$$

(6)

Continuing, dimension analysis and adjustments to all contact parameters, including but not limited to contact stiffness and damping coefficients, are necessary to ensure compatibility with the coarse-grained model. These modifications are extensively discussed in the work by [38], and interested readers are advised to refer to it.

In Rocky [32] the resultant Particle Size Distribution (PSD) following the DEM simulation will maintain the original distribution shape, yet each particle within the simulation will be scaled by a factor of $f_{CGM}$ compared to its original size. In our case, the simulation model utilized coarse-grained particles with a scale factor of 18. A practical solution had to be implemented by approximating particles through spherical representations. This involved grouping spheres into three distinct size classes, as illustrated in Figure 3, where dashed lines delineate the proportional distribution and magnitudes of selected particle sizes. Supplementary visual aids include a smaller graph and a table illustrating the particle distribution function utilized in simulation before coarse-graining. The simulated particle sizes can be derived by multiplying the representative particle sizes from the table in Figure 3 by a scale factor $f_{CGM}$. The parcel is a representation of ${f_{CGM}}^3$ original particles due to the relationship between the scale-factor and volume. Due to all aproximations made calibration plays an essential role in ensuring the production of robust and dependable simulation results.

Due to simplicity, an assumption was made that calibrated spherical particles would sufficiently describe material flow. Following this, a thorough material calibration, detailed in subsequent sections, was conducted. This calibration process integrated the coarse-grain methodology and categorization based on particle size distribution. In the context of analyzing abrasive powders, precise material calibration becomes crucial, particularly when faced with computational limitations for handling extensive simulations.

The highly irregular and random shape of sand particles represents significant challenges, making it inconvenient to account for particle shape. Additionally, substantial computing power is required for accurate shape analysis. In our study, we utilized a technique described by C.M. Wensrich and A. Katterfeld [29] to adjust rolling friction, aiming to compensate for the effects of shape. Recognizing the computational challenges associated with accurately modelling shape in discrete element method (DEM) simulations, we turned to friction parameters to approximate its influence. This approach, although not the most precise method available, provided a pragmatic solution given our resource constraints, as accurately capturing the intricate geometries involved in granular materials can be computationally expensive. Despite employing coarse-graining and adopting an idealized particle shape, the accurate modelling of bulk density is achieved through the calibration of particle (solid) density simulation parameters. In our research, we took over a commonly used technique for experimentally measuring the material’s bulk density, angle of repose, and shear cell properties.

2.3. Numerical Calibration

Calibration, or parameter identification as mentioned in many sources, involves determining a suitable set of parameters that yields a simulated bulk material behaviour closely resembling that observed in real-world experiments. Industrially significant powders often comprise various components, each exhibiting a particle size distribution (PSD) ranging from microns to millimetres. Simulating these powder processing systems using the Discrete Element Method (DEM) and contemporary computing technology is obstructed by the small particle sizes. Establishing a direct and precise correspondence between a DEM particle and an actual particle is very rarely achievable within the scope of numerous industrial applications. In the framework of our research, we implemented a well-established material calibration process. It was observed that the particles did not exhibit significant cohesive behaviour. Hence, we implemented a calibration procedure specifically designed for free-flowing, non-cohesive materials. The procedural details are explained in the flowchart presented in Figure 4, as outlined in the work of Coetzee and Katterfeld [39]. This flowchart functions as a comprehensive guide, providing references to sections explaining the impact of specific parameters on bulk behaviour, along with suggested experiments for calibrating each parameter. Our study follows this established procedure, ensuring a comprehensive and informed approach to material calibration within the field of non-cohesive materials. Lommen et al. [40] explored the impact of stiffness reduction on bulk behaviour through an analysis of multiple case studies. Their findings indicated that maintaining the particle shear modulus above 1 × 10⁸ Pa, resulting in overlaps of 0.3% or less did not significantly change resistance. Conversely, lower stiffness values, leading to overlaps exceeding 0.3%, resulted in smoother interaction and resistance. Due to computational limitations, the modulus was reduced, a decision supported by findings in articles [41,42], where a similar analysis was conducted with erosive sand of comparable sizes. Calibration based on these considerations provided a satisfactory approximation for entry data. Moreover, throughout all simulations, contact overlap was consistently monitored during simulations. We investigated sliding friction between powder and steel by employing an inclined plate (Figure 4), where particles were adhered to the contact surface of a suitably large object. In our examination of rolling and sliding friction between powder particles and steel, we adopted a method involving a steel ball. By compacting the powder and observing the ball’s rolling behaviour, we addressed the complexities associated with fine powders. While this method didn’t yield superior results, it provided results fine-tuned enough for our numerical simulations. The material properties utilized in the simulation are presented in Table 1. Calibration also involved conducting a direct shear test using a 60 × 60 mm shear box. Previous findings indicated that differences in shear results are unclear when the shear velocity is below 0.1 m/s. This velocity significantly differs from the experimental test, where particle contacts might dissipate kinetic energy due to damping.

Consequently, the lower part of the shear box was moving at a constant speed of 0.001 m/s, while the upper part remained stationary. All other procedures were adhered to as outlined in [43,44,45].

Table 1. Basic obtained material properties and simulation parameters.

Property	Unit	Value	Note/Reference
Geometry:
Geometry density ${\rho }_g$	[$kg$/$m^3$]	$7800$	Structural steel [46]
Young’s modulus $E_g$	[Pa]	$1·{10}^{10}$	Reduced modulus [46]
Poisson ratio ${{\nu }_{ }}_{g }$	[–]	0.3	Structural steel [46]
Particle:
Young’s modulus $E_p$	[Pa]	$2.8·{10}^8$	Reduced modulus [40,41]
Poisson ratio ${{\nu }_{ }}_{p }$	[–]	0.4	Abrasive sand [41]
Mean Particle Diameter${ d}_p$	[$\mu$m]	150	Measured
Coarse graining $c_{gr}$	[–]	18	Coarse ratio
Bulk density ${\rho }_{bulk}$	[$kg$/$m^3$]	1780	Measured
Particle density ${\rho }_p$	[$kg$/$m^3$]	3490	Calibrated Figure 3
Contact:
Hertz Mindlin			No Slip
Sliding friction p-p ${{\mu }_{ }}_{p }$	[–]	0.55	Calibrated Figure 3
Sliding friction p-g ${{\mu }_{ }}_{g }$	[–]	0.6	Determined—Inclined plate
Rolling friction p-p ${{{\mu }_{ }}_p^r}_{ }$	[–]	0.1	Calibrated Figure 3
Rolling friction p-g ${{{\mu }_{ }}_g^r}_{ }$	[–]	0.1	Determined—Inclined plate
Coeficient of Restitution p-p $c_{rp}$	[–]	0.44	Assumption based on [41]
Coeficient of Restitution p-g $c_{rg}$	[–]	0.50	Assumption based on [41]
Simulation:
DEM Particle count	[–]	308,609	-
FEM elements count	[–]	2,138,521	4-noded quadratic tetrahedral elements
FEM element size	[mm]	1.5

Table 1. Basic obtained material properties and simulation parameters.

Property	Unit	Value	Note/Reference
Geometry:
Geometry density ${\rho }_g$	[$kg$/$m^3$]	$7800$	Structural steel [46]
Young’s modulus $E_g$	[Pa]	$1·{10}^{10}$	Reduced modulus [46]
Poisson ratio ${{\nu }_{ }}_{g }$	[–]	0.3	Structural steel [46]
Particle:
Young’s modulus $E_p$	[Pa]	$2.8·{10}^8$	Reduced modulus [40,41]
Poisson ratio ${{\nu }_{ }}_{p }$	[–]	0.4	Abrasive sand [41]
Mean Particle Diameter${ d}_p$	[$\mu$m]	150	Measured
Coarse graining $c_{gr}$	[–]	18	Coarse ratio
Bulk density ${\rho }_{bulk}$	[$kg$/$m^3$]	1780	Measured
Particle density ${\rho }_p$	[$kg$/$m^3$]	3490	Calibrated Figure 3
Contact:
Hertz Mindlin			No Slip
Sliding friction p-p ${{\mu }_{ }}_{p }$	[–]	0.55	Calibrated Figure 3
Sliding friction p-g ${{\mu }_{ }}_{g }$	[–]	0.6	Determined—Inclined plate
Rolling friction p-p ${{{\mu }_{ }}_p^r}_{ }$	[–]	0.1	Calibrated Figure 3
Rolling friction p-g ${{{\mu }_{ }}_g^r}_{ }$	[–]	0.1	Determined—Inclined plate
Coeficient of Restitution p-p $c_{rp}$	[–]	0.44	Assumption based on [41]
Coeficient of Restitution p-g $c_{rg}$	[–]	0.50	Assumption based on [41]
Simulation:
DEM Particle count	[–]	308,609	-
FEM elements count	[–]	2,138,521	4-noded quadratic tetrahedral elements
FEM element size	[mm]	1.5

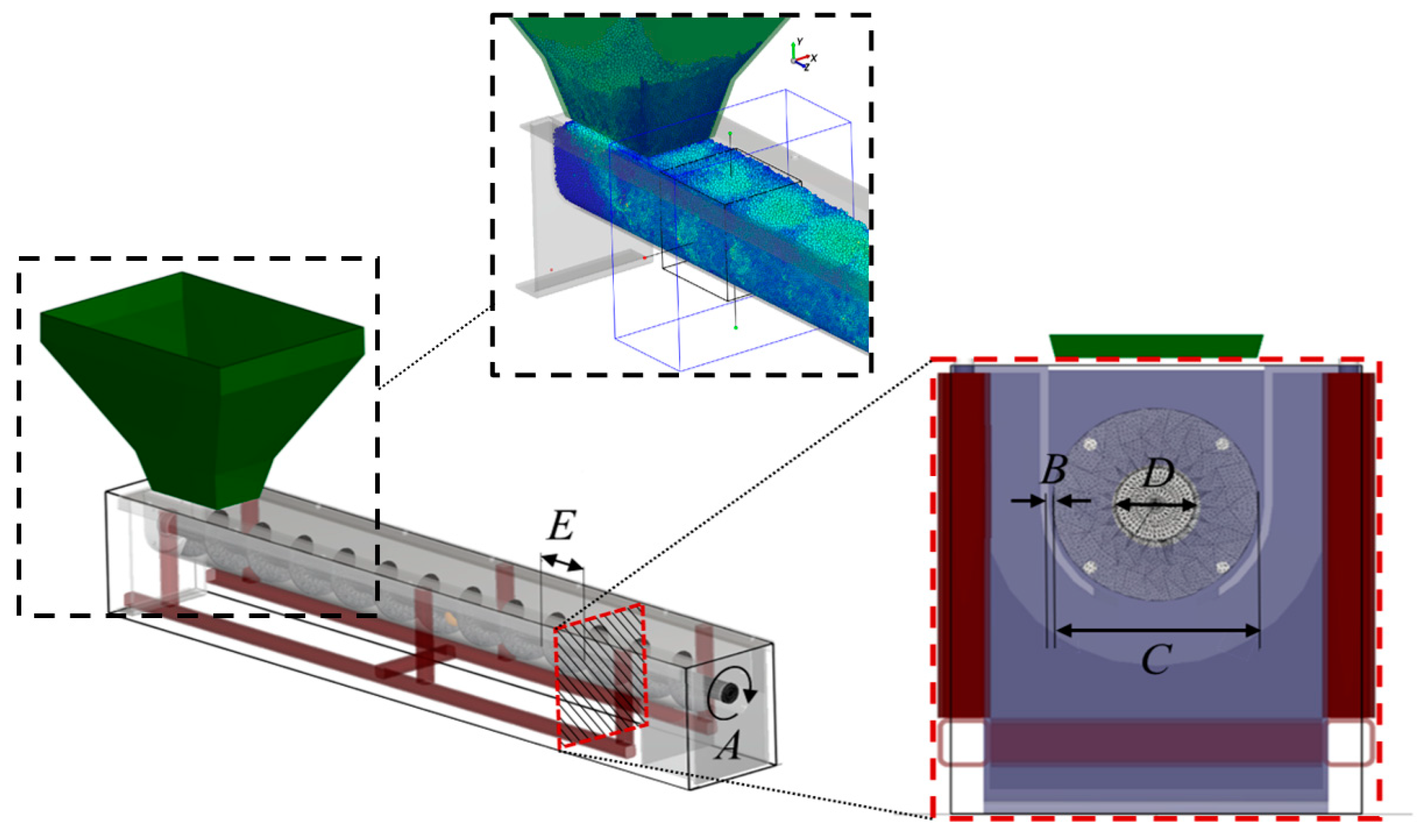
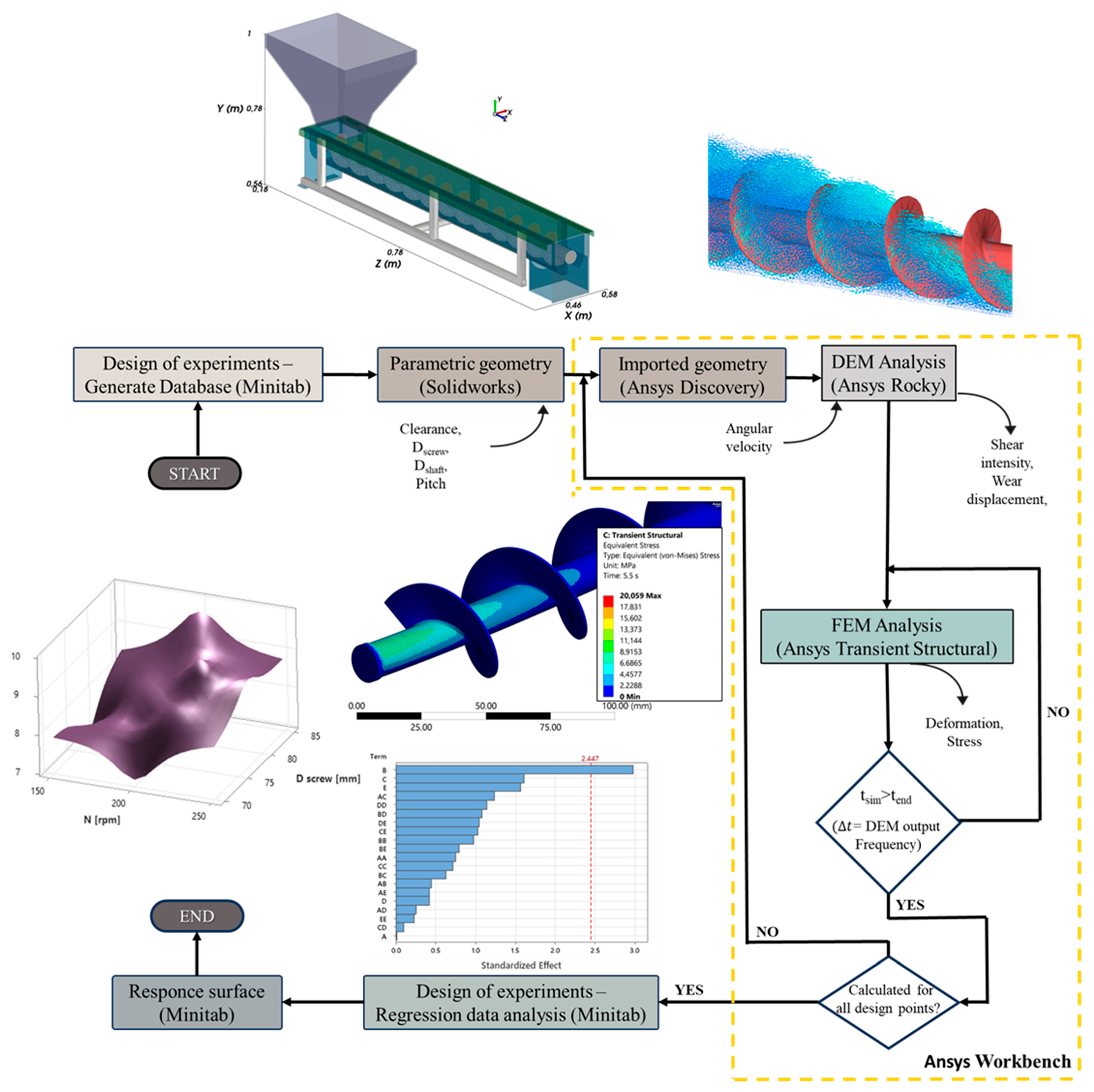
Design of Experiments

Developed in the 1920s, Design of Experiments (DOE) is a statistical theory that gained prominence in engineering and psychology since the 1950s. It efficiently examines the impact of factors on outcomes [47]. In this study, we applied the DOE approach to systematically investigate the performance of a screw conveyor. Our objective extended beyond wear minimization, encompassing a holistic examination that included the assessment of structural integrity and mass flow properties. By methodically varying key parameters shown in Figure 5, such as rotational velocity (A, in rpm), clearance (B in mm), screw diameter (C, in mm), shaft diameter (D, in mm), and Pitch (E in mm), we studied the effects on structural integrity, power consumption, wear and mass flow. Furthermore, to assess the performance of the screw conveyor, control regions delineated in Figure 5. are used to monitor mass flow during stable material flow. Additionally, a specific geometry region is allocated for the calculation of average shear intensity also during stable material flow. Power consumption is quantified as a consequence of particle interaction along the entire length of the screw conveyor, considering that the material fills the entire length of the housing. Stresses and deformations are analyzed on the screw with the shaft, with total deformation evaluated alongside selected stress points. The DOE framework allowed for a thorough exploration of the design space, providing insights into the complex relationships between these parameters and their collective influence on the conveyor system.

Statistical analyses of the data lead to the identification of optimal design configurations that not only minimize wear but also offer insight into structural integrity and efficient mass flow properties. Throughout this study, the investigation of wear and structural integrity was centred on the screw blade of the screw conveyor, while the other components were neglected based on insights from previous studies [48]. As shown in the process flow in Figure 6, the proposed approach initiates with parametric modelling of a screw conveyor, considering already mentioned key parameters. Geometry can be modelled using parametric modelling software (Solidworks 2022). Once the geometry is parametrically modelled, it is essential to ensure seamless integration with Ansys Workbench geometry modellers by accurately importing the defined parameters. The primary workflow is subsequently transferred to Ansys Workbench, where seamless integration facilitates automatic instances between Ansys Rocky (DEM) and Ansys Transient Structural (FEM) modules. Within the Workbench environment, the simulation procedure is automated, streamlining the analysis process and ensuring efficient execution of the coupled DEM/FEM simulations.

Within the framework of discrete element analysis, angular velocity is systematically varied, leading to the extraction of crucial data such as shear intensity and wear displacement from the simulation results. The process begins with an empty screw conveyor. With free-flowing material from the hopper typically horizontal screw conveyors operate with a recommended filling rate of around 40% of the screw channel cross-section which refers to the shape or profile of the internal cavity within the screw conveyor through which material is transported. However, due to the short length (1000 mm) and the absence of additional barriers like bearing holders, the filling rate was not controlled in this study. Sufficient material was present to fill the screw conveyor, and the simulation proceeded until the material exited the bounding box. The analysis extends to the ANSYS Transient module, where, for each timestep defined by the DEM outputs frequency, stresses and deformations are calculated. This iterative procedure is fully automated and continues until all designated design points have undergone evaluation. In DEM, material calibration via real experiments refined model accuracy, with validated mass flow calculations from standard [17] aligning well with simulations.

FEM simulations underwent validation, including Ansys coupling and convergence analyses, supported by custom simulations. The final step involves creating a response surface chart, which visualizes how various variables interact with each other. This step is crucial for optimization. Before this, response surface results are collected and exported to Minitab for regression analysis, complemented by a thorough optimization run aimed at refining and improving the overall performance of the screw conveyor design. When applying the Discrete Element Method (DEM) for numerical simulations, particularly in the optimization of conveying processes, the utilization of the Response Surface Method (RSM) offers various advantages. First, RSM enables the design of a minimal number of simulation runs, thereby enhancing the efficiency of computational time and resources. Additionally, DEM simulations provide a profound understanding of intricate particle interactions during powder conveying, and RSM analysis further enhances comprehension by clarifying how variations in input parameters impact output responses, thereby assisting in the optimization of simulation parameters and maximizing efficiency while minimizing wear. Moreover, RSM enables the iterative refinement of DEM models based on predictions, leading to continuous improvement of predictive capabilities. Central Composite Design (CCD) proves to be a powerful experimental approach to strategically situating points within a design space, enabling researchers to effectively investigate complex systems. CCD’s distinctive configuration of the centre, axis, and factorial points allows for the in-depth study of main effects, interaction effects, and curvature. Its adaptability benefits through design variations such as Face-Centered and Rotatable, adjusting experiments to specific objectives. Especially beneficial in multi-parameter studies, CCD efficiently manages to optimize precision while maintaining practicality, resulting in a reduction in the number of experimental runs without sacrificing the integrity of robust findings [32].

In our study, we implemented DOE based on a set of parameters, as outlined in

Table 2. The provided table encapsulates the design points generated through a central composite design approach, serving as simulation input parameters.

Run Order	Coded Value A B C D E					N [rpm] {150–250}	Clearance [mm] {2–10}	Dscrew [mm] {70–85}	Dshaft [mm] {20–35}	Pitch [mm] {75–90}
1	0	0	0	0	−2	200.0	6.0	77.5	27.5	75.0
2	1	−1	−1	−1	−1	214.2	4.9	75.4	25.4	80.4
3	−1	1	−1	−1	−1	185.8	7.1	75.4	25.4	80.4
4	−1	−1	1	−1	−1	185.8	4.9	79.6	25.4	80.4
5	1	1	1	−1	−1	214.2	7.1	79.6	25.4	80.4
6	−1	−1	−1	1	−1	185.8	4.9	75.4	29.6	80.4
7	1	1	−1	1	−1	214.2	7.1	75.4	29.6	80.4
8	1	−1	1	1	−1	214.2	4.9	79.6	29.6	80.4
9	−1	1	1	1	−1	185.8	7.1	79.6	29.6	80.4
10	0	0	0	−2	0	200.0	6.0	77.5	20.0	82.5
11	0	0	−2	0	0	200.0	6.0	70.0	27.5	82.5
12	0	−2	0	0	0	200.0	2.0	77.5	27.5	82.5
13	−2	0	0	0	0	150.0	6.0	77.5	27.5	82.5
14	0	0	0	0	0	200.0	6.0	77.5	27.5	82.5
15	2	0	0	0	0	250.0	6.0	77.5	27.5	82.5
16	0	2	0	0	0	200.0	10.0	77.5	27.5	82.5
17	0	0	2	0	0	200.0	6.0	85.0	27.5	82.5
18	0	0	0	2	0	200.0	6.0	77.5	35.0	82.5
19	−1	−1	−1	−1	1	185.8	4.9	75.4	25.4	84.6
20	1	1	−1	−1	1	214.2	7.1	75.4	25.4	84.6
21	1	−1	1	−1	1	214.2	4.9	79.6	25.4	84.6
22	−1	1	1	−1	1	185.8	7.1	79.6	25.4	84.6
23	1	−1	−1	1	1	214.2	4.9	75.4	29.6	84.6
24	−1	1	−1	1	1	185.8	7.1	75.4	29.6	84.6
25	−1	−1	1	1	1	185.8	4.9	79.6	29.6	84.6
26	1	1	1	1	1	214.2	7.1	79.6	29.6	84.6
27	0	0	0	0	2	200.0	6.0	77.5	27.5	90.0

. The DOE systematically explored variations in screw conveyor design, including clearance, screw diameter, shaft diameter, pitch, and angular velocity. Each entry in Table 2 represents a unique design point, thoroughly analyzed for shear intensity, wear displacement, stresses, and deformations. The iterative process, encompassing both DEM and FEA, resulted in a response surface chart, guiding subsequent optimization efforts for an enhanced screw conveyor design [49]. An integral step in designing a statistical experiment involves carefully selecting input variables, determining their associated levels, and examining their interactions. The deterministic method’s design points (Table 2), which utilize a central composite design, are exactly chosen in a systematic manner. This systematic approach includes the incorporation of a single centre point, axis points placed at (-α) and (+α) along each input parameter axis, and factorial points distributed at (−1) and (+1) along the diagonals of the parameter space. The quantity of factorial points is determined by the fraction of the factorial design [25].

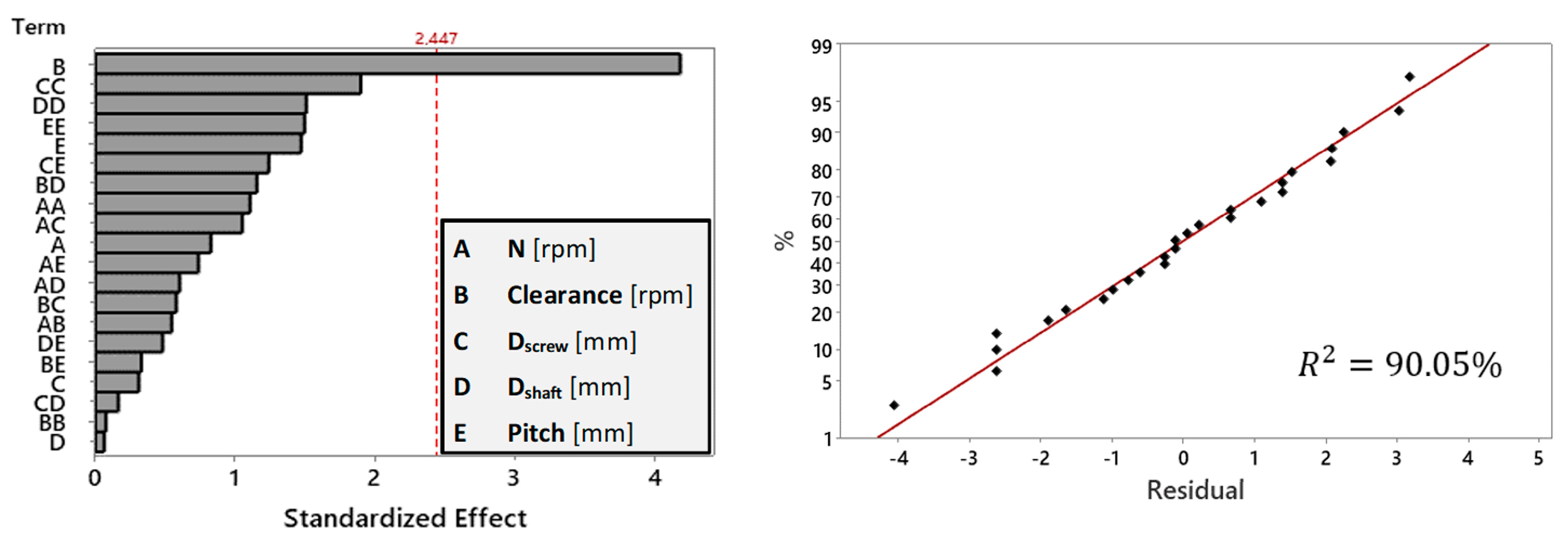
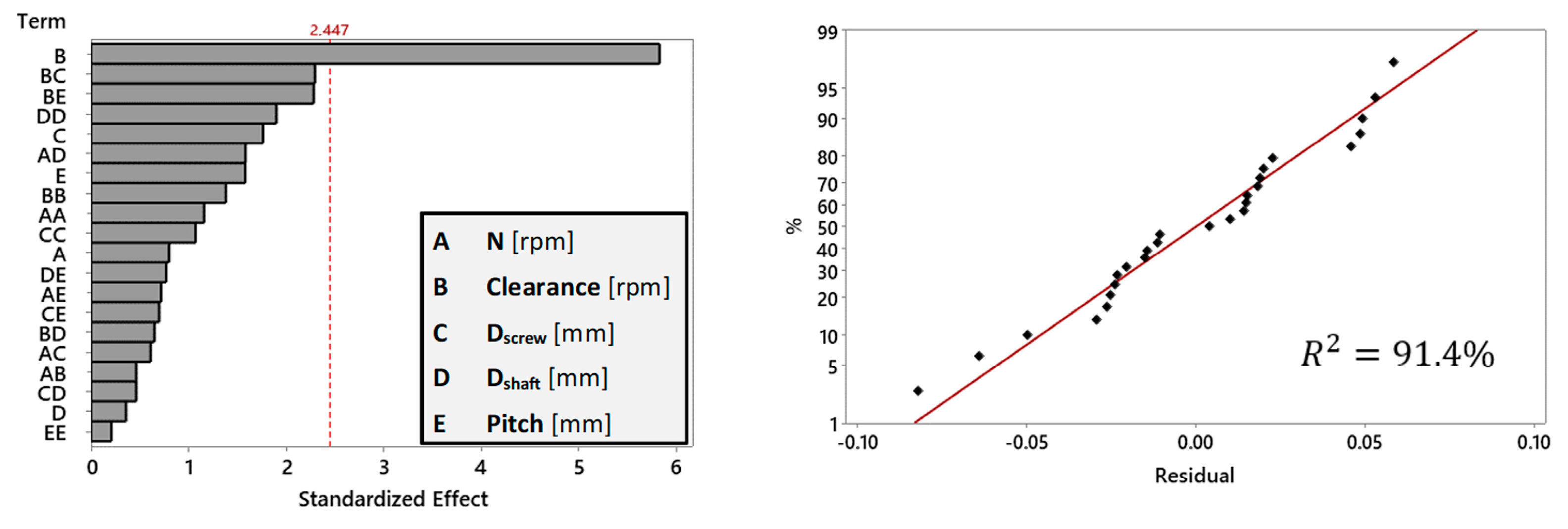
3. Results and Discussion

The MINITAB 21.4.2 software tool was used to evaluate the simulation results [49]. The main objective was to optimize the wear depth at a specific target mass flow of the screw conveyor. The significance of the parameters was evaluated at a 95% confidence level. The method called ANOVA was used to analyze the trial runs and construct a regression model that establishes a connection between the responses and the parameters. The evaluation of the model’s p-value and R-squared values enables the assessment of the model’s predictive accuracy. The variance analysis results for mass are presented in

Table 3. Analysis of Variance for Mass Flow.

Source	DF	Adj SS	Adj MS	F-Value	p-Value
Model	20	2.49783	0.12489	19.94	0.001
Linear	5	2.42307	0.48461	77.39	0
$N$	1	0.04015	0.04015	6.41	0.045
$Clearance$	1	1.02763	1.02763	164.1	0
$D_{screw}$	1	1.12376	1.12376	179.45	0
$D_{shaft}$	1	0.16574	0.16574	26.47	0.002
$Pitch$	1	0.06578	0.06578	10.5	0.018
Square	5	0.0197	0.00394	0.63	0.686
$N^2$	1	0.00012	0.00012	0.02	0.893
${Clearance}^2$	1	0.00003	0.00003	0	0.947
${D_{screw}}^2$	1	0.00012	0.00012	0.02	0.893
${D_{shaft}}^2$	1	0.00052	0.00052	0.08	0.784
${Pitch}^2$	1	0.01398	0.01398	2.23	0.186
2-Way Interaction	10	0.05507	0.00551	0.88	0.592
$N·Clearance$	1	0.00766	0.00766	1.22	0.311
$N·D_{screw}$	1	0.00601	0.00601	0.96	0.365
$N·D_{shaft}$	1	0.00526	0.00526	0.84	0.395
$N·Pitch$	1	0.00331	0.00331	0.53	0.495
$Clearance·D_{screw}$	1	0.00526	0.00526	0.84	0.395
$Clearance·D_{shaft}$	1	0.01156	0.01156	1.85	0.223
$Clearance·Pitch$	1	0.00275	0.00275	0.44	0.532
$D_{screw}·D_{shaft}$	1	0.00766	0.00766	1.22	0.311
$D_{screw}·Pitch$	1	0.00106	0.00106	0.17	0.696
$D_{shaft}·Pitch$	1	0.00456	0.00456	0.73	0.426
Error	6	0.03757	0.00626
Total	26	2.5354

. The ANOVA table is exclusively provided for the mass flow parameter of the screw conveyor. For all other responses such as shear intensity, power, stress, and deformation, ANOVA was similarly used to analyze the trial runs and construct regression models establishing connections between these responses and the parameters. Nevertheless, all examples encompass Pareto charts, regression equations, normal distribution plots and findings concerning the association between the input parameters and the response variable. Overall, the model demonstrates significance, as indicated by a low p-value of 0.001, suggesting that at least one input parameter has a significant impact on the response variable. All terms, including rotational velocity ($N$), Clearance ($Clearance)$, Screw diameter ($D_{screw}$), shaft diameter ($D_{shaft}$), and Pitch ($Pitch$) display distinguished effects on the response variable, supported by their low p-values (<0.05). However, the square terms and 2-way Interactions do not exhibit significant effects. This implies that the majority of the variation in the response variable can be explained by the linear effects of the input parameters.

The regression equations were subsequently derived based on the experimental output responses to establish the relationship between the input and output variables. The relationship representing the mass flow, shear intensity/wear, power consumption, stresses, and deformations on the screw conveyor can be described by the regression equation/model presented in relations (7–11). Next to each association, there is a corresponding parameter (R²) which serves as an indicator of the accuracy of the desired function and its consistency with the observed behaviour of the analyzed parameter. The proximity of this parameter to the value of 100% directly correlates with the accuracy of the function.

The standardized Pareto chart can also effectively demonstrate (Figure 7) the importance of various factors that influence the mass flow response. Notably, the screw blade diameter emerged as the primary factor, applying a substantial impact, and categorizing it as the critical factor. At the same time, the remaining factors were considered as fine adjustment factors. Additionally, the regression model, when presented in uncoded units, enables the prediction of values, as depicted in relation 7. As anticipated, our observations in Figure 7. indicate a direct correlation between the screw blade diameter and shaft angular velocity with variation in mass flow. However, an interesting deviation from expectations occurred in the context of clearance. Upon closer examination, we identified that the material behaved as a moving nut traversing along a thread, and the reduction in clearance translated to a decrease in space and an increase in geometry volume inside the housing. Mass flow increases with a larger clearance due to the expanded volume between the blade and housing which results in higher Mass flow.

$$\begin{gathered} P_{Mass Flow }(A,B,C,D,E)=24.4 -0.0346 A+0.305 B-0.048 C+0.003 D-0.468 E+4·{10}^{-6}{A}^2+ \\ 3·{10}^{-4}{B}^2+1.8·{10}^{-4}{C}^2-3.6·{10}^{-4}{D}^2+0.00186 E^2+0.00136 AB+6.4·{10}^{-4} AC+6·{10}^{-4} AD- \\ 4.7·{10}^{-4} AE-0.00753 BC-0.01116 BD+0.00545 BE-0.00484 CD+0.00180 CE+0.00374 DE \end{gathered}$$

(7)

Considering the coarse-graining employed in our study, it is important to conduct further investigations into the impact of particle size. This is crucial as coarse-graining may yield misleading results, and a better examination of actual particle size could provide a more accurate understanding of the system’s behaviour. Moving to Figure 8, a Pareto Chart reveals that the main effect on power consumption seems to be rotation velocity, with significant rates also observed in terms of clearance and shaft diameter. Concerning shear intensity, stresses, and strains (Figure 9, Figure 10 and Figure 11), clearance emerges as having the most significant effect. At a particular particle size, wear drastically arises because of the “particle entrapment”. Thus, it’s critical to note that coarse-graining may yield misleading results, and further examination of actual particle size should be used in future in order to provide a more comprehensive explanation.

$$\begin{gathered} P_{Power }(A,B,C,D,E) =-2136+1.68 A+3.2 B+28.5 C-0.6 D+21.6 E-0.00130 A^2+ \\ 0.292 B^2-0.0754 C^2+0.0245 D^2-0.0526 E^2-0.0533 AB-0.0321 AC-0.0151 AD+ \\ 0.0285 AE+0.246 BC+0.181 BD-0.286 BE+0.135 CD-0.185 CE-0.099 DE \end{gathered}$$

(8)

$$\begin{gathered} P_{Shear }(A,B,C,D,E)=-3373+2.02 A-15.6 B+44.0 C+11.8 D+33.9 E-0.00151 A^2+ \\ 0.016 B^2-0.1149 C^2-0.0912 D^2-0.0905 E^2-0.0325 AB-0.0335 AC-0.0192 AD+ \\ 0.0235 AE+0.230 BC+0.459 BD-0.131 BE+0.035 CD-0.264 CE-0.102 DE \end{gathered}$$

(9)

$$\begin{gathered} P_{Deformation }(A,B,C,D,E)=22.1+0.0344 A-2.991 B-0.136 C+0.401 D-0.380 E- \\ 3.1·{10}^{-5}{A}^2+0.00571 B^2-0.00126 C^2-0.00223 D^2+2.5·{10}^{-4}{E}^2-5.4·{10}^{-4} AB- \\ 3.8·{10}^{-4} AC-9.8·{10}^{-4} AD+4.4·{10}^{-4} AE+0.01775 BC+0.00503 BD+0.01765 BE+ \\ 0.00191 CD+0.00288 CE-0.00318 DE \end{gathered}$$

(10)

$$\begin{gathered} P_{Stress }(A,B,C,D,E)=724+0.39 A-85.6 B-3.7 C+14.9 D-13.0 E-8.5·{10}^{-4}{A}^2+0.239 B^2- \\ 0.0331 C^2-0.0606 D^2+0.0217 E^2-0.0067 AB-0.0077 AC-0.0264 AD+0.0157 AE+ \\ 0.479 BC+0.094 BD+0.516 BE+0.030 CD+0.078 CE-0.112 DE \end{gathered}$$

(11)

3.1. Parameters Optimization

Response optimization involves the identification of the most beneficial combination of variables to achieve predetermined objectives, such as the reduction of wear depth or power consumption, as well as the optimization or maximization of parameters like mass flow. The application of tools such as Minitab’s Response Optimizer [49] enables users to finely adjust settings to effectively reach the above goals. This iterative process requires the creation of models for each response and the assignment of appropriate weights that reflect their level of importance. Through visual representation and analytical examination, optimal solutions can be determined using the desirability function, where a desired value of (1) indicates highly desirable responses. By concentrating on the target mass flow of the screw conveyor while simultaneously minimizing the shear intensity, the optimization process was successfully applied in our research study. All desirability values met the desired criteria and were considered acceptable (D = 1).

The prediction and simulation results presented in

Table 4. Response optimization data with the comparison of predicted and simulated results.

	Opti. Function	Prediction	Simulation	Error
Mass flow [t/h]	Target value (5.35)	5.35	5.31	0.75%
Shear Intensity [W/m2]	Minimum	14	14.56	4%
Optimum parameters:
N [rpm]	Clearance [mm]	Dscrew [mm]	Dshaft [mm]	Pitch [mm]
167	8.60	80	27	87

indicate a close agreement for the mass flow of the screw conveyor, with only a 0.75% error observed. However, for shear intensity, there is a slightly higher discrepancy, with a 4% error between the predicted and simulated values.

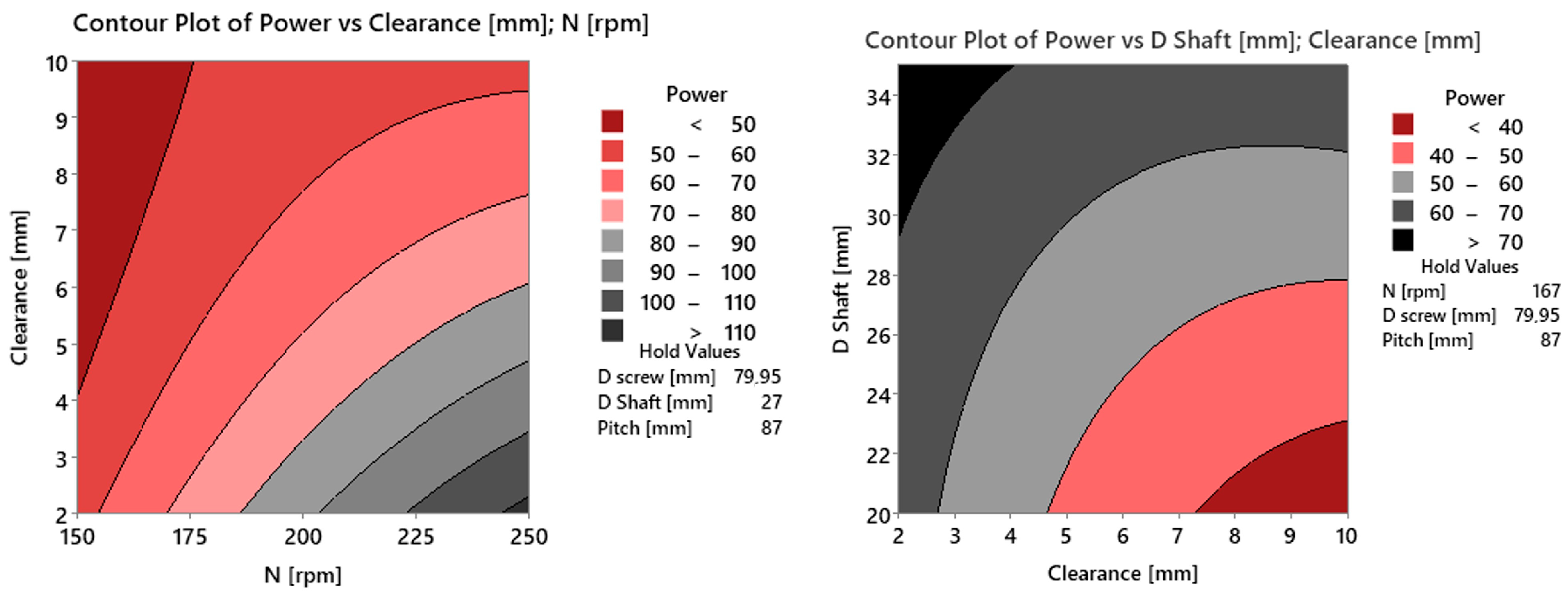
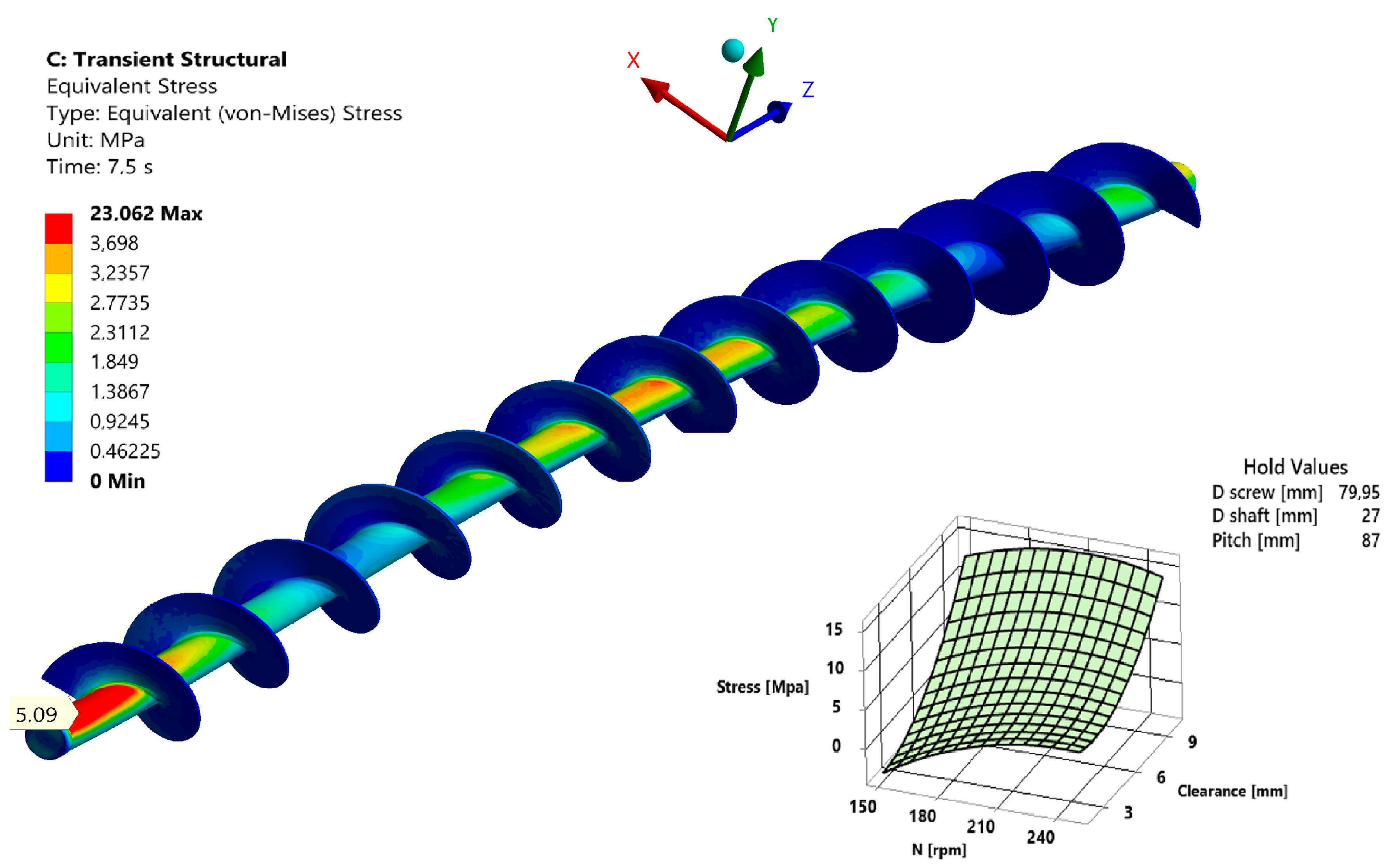
3.2. Response Surface

Contour plots provide valuable visual tools to illustrate the impact of input variables, such as screw blade pitch and screw conveyor angular velocity, on response variables like shear intensity and mass flow. They provide a holistic perspective, allowing engineers to grasp the interconnectedness of various parameters and their effects on system performance. Through the examination of contour plots generated using a fitted model equation, we obtained valuable insights into how variations in these parameters not only influence mass flow, but also influence power consumption, stresses, deformations, and wear in screw conveyors. These plots exposed regions of optimal performance, where various responses were optimized while minimizing undesirable outcomes. The acquisition of such insights is of utmost importance to enhance efficiency in processes involving bulk solids and powders. Furthermore, in the continuation, all parameters that have previously been determined to be significant will be further evaluated through the utilization of response surface analysis, thereby providing a comprehensive understanding of their effects on the system performance. In Figure 12, we present a contour plot illustrating the relationship between mass flow and all input parameters. As clearance increases, mass flow also increases. The material behaved analogous to a threaded nut, with no material left behind on the screw housing. Additionally, we observed that as the screw diameter increases, so does the mass flow. Conversely, an increase in shaft diameter resulted in a decrease in mass flow. Furthermore, we observed that higher pitch values corresponded to higher mass flow rates. These observations highlight the complex relationship between clearance, screw diameter, shaft diameter, and pitch in influencing mass flow dynamics within the system. Similarly, the power needed for driving the screw conveyor demonstrates a rapid increase as clearance decreases and angular velocity increases, as depicted in Figure 13. In addition, the examination of the clearance parameter was conducted to assess its impact on the intensity of shear. This analysis yielded insights into the dissipation of energy during collisions that occurred throughout the simulated period. The quantification of shear intensity, which measures the power transferred per unit area, is of utmost importance in abrasive wear models.

It facilitates the determination of shear wear on geometric surfaces and directly demonstrates wear rates. The shown trend in Figure 14 (right) illustrates an increase in throughput performance with higher angular velocity and reduced clearance. Consequently, this leads to higher wear rates in the screw model. Similarly to the findings in [42], where the vertical screw conveyor was studied we can compare the relationship between the rotation speed and the wear rate of the screw flight. We noted that with the increase in rotation speed, the trend of the wear rate increases, confirming the reported observations. Similarly to the findings, our study also observed that the most severe wear occurs at the outer edge of the screw blade. Interestingly, we found that the amount of wear on the inner side of the screw shaft is relatively small, aligning with the observations.

Conversely, negligible wear on the reverse side of the screw blade was not taken into consideration. To approximate the quantitative wear results, the Archard model was utilized, relying on the predicted wear coefficient as depicted in Figure 14 (left). It’s crucial to emphasize that the wear coefficient was not calibrated but rather assumed based on a literature review. Moving forward, calibration of this coefficient would be essential to ensure accurate quantitative representation in the model. Our investigation expanded beyond the minimization of wear depth to encompass an evaluation of the structural integrity of the screw blade. Figure 15. showcases the stress field data obtained near the support location. The initial conditions involved connecting the screw blade with the shaft to fixed support on specifically created surfaces on each side of the shaft. On one side of the shaft, a cylindrical support was added, with only the radial component fixed. This setup allows rotation and movement in the axial direction while constraining radial movement. In order to apply loading conditions, node forces were employed, which were transferred from DEM simulations. The measuring point is positioned away from the edge of the shaft. Notably, the measurement point is distinctly identified with an additional label. The intention behind this measurement was to avoid any singular points and acquire stress values that are not realistic. By employing FEM analysis at all time steps, we discovered that the highest levels of stress for this specific geometry occur near the support, where the transmission of torque takes place, as well as in the middle of the shaft.

Furthermore, the responsive surface is depicted in Figure 15. demonstrates that as the clearance distances increase, so do the stresses.

During the design phase, the stresses were found to be insignificant, so they were not considered back in the optimization process, which solely focused on the wear depth and mass flow. However, it would be interesting to explore the potential impact of incorporating stress optimization into the analysis. Similarly, our exploration extended to deformation analysis, delving into the structural integrity of the system. Figure 16. display case for the deformation field, particularly emphasizing maximal deformations occurring at the midpoint and increasing with greater clearance distances. Deformations were also negligible and not included in the optimization process. However, considering their potential impact on design, further exploration could provide valuable insights into structural considerations.

4. Conclusions

In summary, the proposed methodological approach, centred on numerical simulations, offers engineers a powerful set of resources for the optimal design of material handling equipment. By implementing parametric numerical analysis, we systematically explore critical parameters and their interdependencies, providing a comprehensive understanding of the screw conveyor system’s behaviour:

• Our research study focused on calibrating the abrasive powder material model to ensure an accurate representation of material behaviour. We successfully approximated and calibrated the abrasive powder material within DEM simulations. This calibration process was crucial for achieving verified material flow, laying a solid foundation for reliable and realistic simulations.
• During the research, we build an advanced numerical model that integrates parametric modelled geometry, DEM, FEM, DOE and response surface optimization to simulate the complex environment of the screw conveyor. The automated parametric numerical model facilitates the exploration of various operating conditions and design parameters, offering valuable insights into the performance of the screw conveyor, wear depth, and structural adequacy of the screw blade.
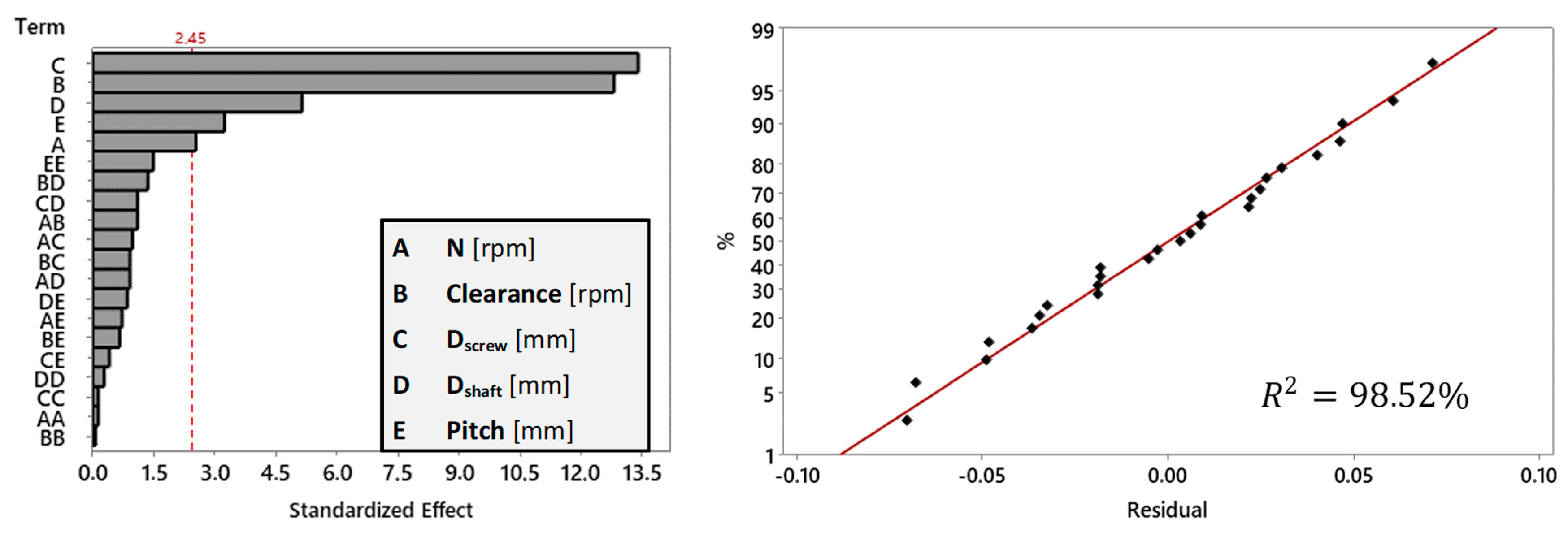
• Clearance has emerged as an important parameter in the optimization process. The mass flow rate demonstrates an increase as the clearance widens, this contributes to the expanded area between the screw blade and the housing. This feature results in a higher mass flow rate. Additionally, as expected, clearance was found to have the most significant influence on power consumption, wear depth, stress, and deformations. Moreover, because of the complexity of the employed material coarse-graining methodology, particle shape and size underwent approximation and adjustment during the calibration process. Consequently, “particle entrapment” between the screw blade and the housing may also occur. Further studies incorporating real particle shape and size are of major importance in order to fully address the clearance effect. It’s crucial to acknowledge that neglecting this aspect may lead to potentially misleading results.
• During the simulations, the stresses on the screw blade were identified to be minor, therefore we have excluded them from further consideration in the optimization phase, which exclusively prioritized wear depth and mass flow.
• Through the utilization of the Design of Experiments, we systematically investigated critical parameters such as screw pitch, clearance, wear depth, rotational velocity, and additional structural factors. We demonstrated how this systematic investigation allows us to not only analyze the individual effects of each parameter but also to consider their interdependencies. The optimization process was a success in focusing on mass flow and reducing wear depth. After carefully studying and applying small adjustments, we achieved our goals. We found an optimal set of factors that would give us a good balance between the mass flow and wear depth. In future studies focusing on screw conveyors where stresses and deformations are higher, it would be beneficial, to include structural parameters in the optimization process (shaft thickness etc.).

Furthermore, through this study, we have acknowledged the necessity of addressing the factors in handling smaller particles and considering the impact of realistic particle shapes. While the present research provides valuable insights for the design of new devices, future studies should prioritize exploring these specific areas to present a more comprehensive analysis. Future research efforts could examine deeper into understanding how factors such as clearance affect the behaviour of real particle-size materials within the system. Additionally, conducting more simulations and exploring a wider range of input parameters could provide more accurate results and better-fitting predictions. The findings demonstrate the effectiveness of DOE analysis in achieving improved performance and provide valuable insights for engineers and researchers involved in the design of material handling systems. Furthermore, this approach clarifies how material handling systems respond to changes in parameters and highlights the interaction between transported particles and the material handling system. By understanding the interactions of these factors, the proposed methodology does not provide only results but also a strategic framework for advancing material handling system design in engineering practices.