Multi-Robot Exploration Employing Harmonic Map Transformations

Abstract

Robot Exploration can be used to autonomously map an area or conduct search missions in remote or hazardous environments. Using multiple robots to perform this task can improve efficiency for time-critical applications. In this work, a distributed method for multi-robot exploration using a Harmonic Map Transformation (HMT) is presented. We employ SLAM to construct a map of the unknown area and utilize map merging to share terrain information amongst robots. Then, a frontier allocation strategy is proposed to increase efficiency. The HMT is used to safely navigate the robots to the frontiers until the exploration task is complete. We validate the efficacy of the proposed strategy via tests in simulated and real-world environments. Our method is compared to other recent schemes for multi-robot exploration and is shown to outperform them in terms of total path distance.

1. Introduction

Robotic Exploration involves the systematic exploration of initially unknown environments, typically achieved by creating a map—either 2D or 3D—using autonomous robots. The process requires three essential components: a mechanism for mapping the environment, knowledge of the robot’s relative position within the map, and a strategy for the robot to autonomously plan its trajectory within the explored area, in order to expand it. The integration of the first two components constitutes the Simultaneous Localization And Mapping (SLAM) problem, a field that has witnessed considerable advancements in recent decades and remains an active area of study [1]. While a straightforward solution for exploration involves teleoperating (remote operation) a robot performing SLAM, the necessity for autonomous exploration arises when direct control becomes impractical due to dangerous environments or substantial time delays. This is particularly relevant in scenarios like search and rescue missions conducted in hazardous settings and space exploration.

While a single robot can effectively explore a designated area of interest, employing multiple robots to cooperatively explore the same setting offers significant advantages. Distributing the exploration task among multiple agents can notably reduce exploration time, computational load, and distance traveled by an individual robot, thereby enhancing the overall operational efficiency. In the realm of multi-robot exploration, two primary architectures are considered: a centralized approach, where a central node possesses all relevant information and coordinates each robot, and a distributed approach, where robots can only periodically exchange information under specific conditions, such as being within communication range.

1.1. Related Works

A vast array of methods have been suggested and implemented for autonomous exploration using a single robot. A well-studied and common approach is that of frontier-based methods. In [2], Yamauchi introduced the idea of frontier detection, i.e., the edges between explored and unknown areas, and then used a depth-first search to navigate to the frontier location, while using reactive obstacle avoidance. In [3], an improved algorithm is proposed for faster frontier detection. In [4], the authors eliminated the need for tuning in frontier clustering with the employment of a histogram. In recent years, artificial intelligence and particularly Deep Reinforcement Learning (DRL) has shown promising results in the field of exploration. Particularly, in [5], DRL is combined with frontier exploration to allow for the exploration of unknown cluttered environments, aiming for use in urban search and rescue missions. In [6], an algorithm that utilizes DRL is used to predict an efficient long-term visiting order for unexplored regions, obtaining knowledge from information derived from a training set of office blueprints.

Another popular approach is using sampling-based algorithms to search and select areas to be explored. In [7], a method called UFOExplorer is proposed that continuously expands a dense undirected graph, optimized for fast and efficient exploration. Rapidly-exploring Random Tree (RRT) and its variants are mainstream among various sampling-based exploration methods. In [8], a novel method is presented where the robot is guided to the unexplored region using multiple RRTs, removing the requirement for frontier exploration. Artificial Potential Fields have been utilized in the field of robotic exploration, such as in [9,10], where a harmonic potential field function is used for navigating to frontiers.

Due to the clear advantages of employing multiple robots for exploration, most methods used in single robot exploration have been extended to multi-robot setups. In [11], Yamauchi first expanded the concept of frontier-based robotic exploration to multiple robots. In this method, each robot exchanged information with others but kept a local copy of its map to maintain robustness. In [12], a more sophisticated approach was taken for multi-robot exploration, as frontier target selection considered both cost and utility. In [13], a modified A* search algorithm for multi-agent exploration is presented that attempts to minimize the energy consumption during the exploration process. Similarly, the RRT approach has been extended to multi-robot systems as well. In [14], local and global RRT-based detectors are used for multi-robot exploration. Additionally, [15] proposes a novel frontier detection algorithm called Hybrid Multi-Strategy RRT to improve the efficiency and reliability of multi-robot exploration. Their method consists of an adaptive incremental distance strategy, a sub-region sampling strategy, and a greedy frontier-based exploration strategy.

In [16], a decentralized and computationally efficient frontier allocation method favoring a well-balanced spatial distribution of robots in the environment was introduced. A wavefront propagation algorithm constructs Artificial Potential Fields used for the path planning process. In [17], multi-robot multi-target Potential Fields are used for exploration, an approach that eliminates local minima for multi-robot Artificial Potential Fields. In the same vein, artificial harmonic potential fields were employed in [18], leading to a reactive algorithm for autonomous exploration for multiple autonomous multi-rotor robots. In [19], a collaborative multi-robot exploration method is proposed. Utilizing Voronoi-based exploration strategies, each robot is assigned a target location for exploration. The robots then navigate to the target location with the use of a DRL collision avoidance algorithm. In [20], a Gaussian Process and relative localization belief information are used to generate a map and determine the unexplored region. The next-best unexplored region is then selected by solving a linearized convex hull optimization problem. In [21], a novel exploration strategy is presented using the Monte Carlo Tree Search algorithm, optimized for multi-robot exploration missions in unknown areas. Navigation is based on a reward function, and a decentralized coordination model is used among multiple robots, resulting in significantly reduced exploration times.

1.2. Contributions

This paper presents a novel method for both single-robot and multi-robot exploration, leveraging a HMT for frontier navigation and obstacle avoidance. This modified version will hereby be referred to as HMT for Exploration. In the proposed approach, a map of the perceived space is obtained and the HMT for Exploration is computed. Employing a greedy frontier allocation strategy, the robot is able to choose its goal and navigate to it safely using the HMT. In the multi-robot case, the exploration process is optimized by sharing the local maps of the robot and constructing a merged map. The key contributions of this work include the following:

• The extension of the concept of HMT to incorporate frontier points on the boundary of the perceived workspace, enabling its use for exploration tasks.
• The design of a comprehensive exploration method that integrates the HMT for effective navigation and mapping in unknown environments.
• The extension of the proposed method to facilitate multi-robot exploration, enabling collaborative exploration efforts with improved efficiency and coverage.

To the best of our knowledge, this is the first time that the HMT has been extended for exploration in a multi-robot framework. This paper is organized as follows: In Section 2, the problem of multi-robot exploration is formally introduced. In Section 3, the proposed methodology is presented. The validity of the proposed methodology is evaluated through both high-fidelity simulations and real-world experiments, the results of which are detailed in Section 4. Finally, conclusions regarding the presented method and future work are shown in Section 5.

2. Problem Formulation

Let $W\subset {\mathbb{R}}^2$ denote the compact and connected workspace of the robot. Within W exists a finite set of inner obstacles $W_j,j\in [1,\dots ,M]$. The workspace is considered static and the only dynamic elements are the robots themselves. The boundaries of the outer and inner curves are denoted as $\partial W_0$ and $\partial W_j$ and the entirety of the workspace’s boundaries can be referred to as $\partial W$ (see Figure 1).

Now, consider a group of N robots, where the position of each robot is described by the state vector $p_i\left(t\right)={[x_i\left(t\right),y_i\left(t\right)]}^T\in {\mathbb{R}}^2,i\in [1,\dots ,N]$, representing the Cartesian coordinates in the workspace. Each robot has a sensing region $r_i,i\in [1,\dots ,N]$ that denotes a disk with a radius equal to maximum distance that can be perceived as unoccupied by the robot’s sensors. The explored region of each robot at time t is noted as ${\epsilon }_i\left(t\right)=(r_i\cap W)\cup {\epsilon }_i(t-T)\subseteq W$, where T is the period that the explored region is updated and the initial explored region is ${\epsilon }_i\left(0\right)=r_i\cap W.$ The boundaries of the explored region $\partial {\epsilon }_i$ can be a part of the workspace boundaries and denoted as $\partial {\epsilon }_{i_O}\subseteq \partial W$ or belong to the workspace and denoted as $\partial {\epsilon }_{i_f}\subset W$. The latter boundaries will henceforth be referred to as frontiers. The total explored region at any given moment t can be defined as follows:

$$\mathcal{E}\left(t\right)=\bigcup _{i=1}^N{\epsilon }_i\left(t\right).$$

(1)

Problem: Our goal is to create a controller that plans the path of each robot so that $\mathcal{E}\left(t_f\right)=W$ with $t_f<\infty$, using the information provided by each of the robots in an efficient manner, while ensuring that each robots’ trajectory remains safe, i.e., $p_i\left(t\right)\in W$ for all $t\ge 0$.

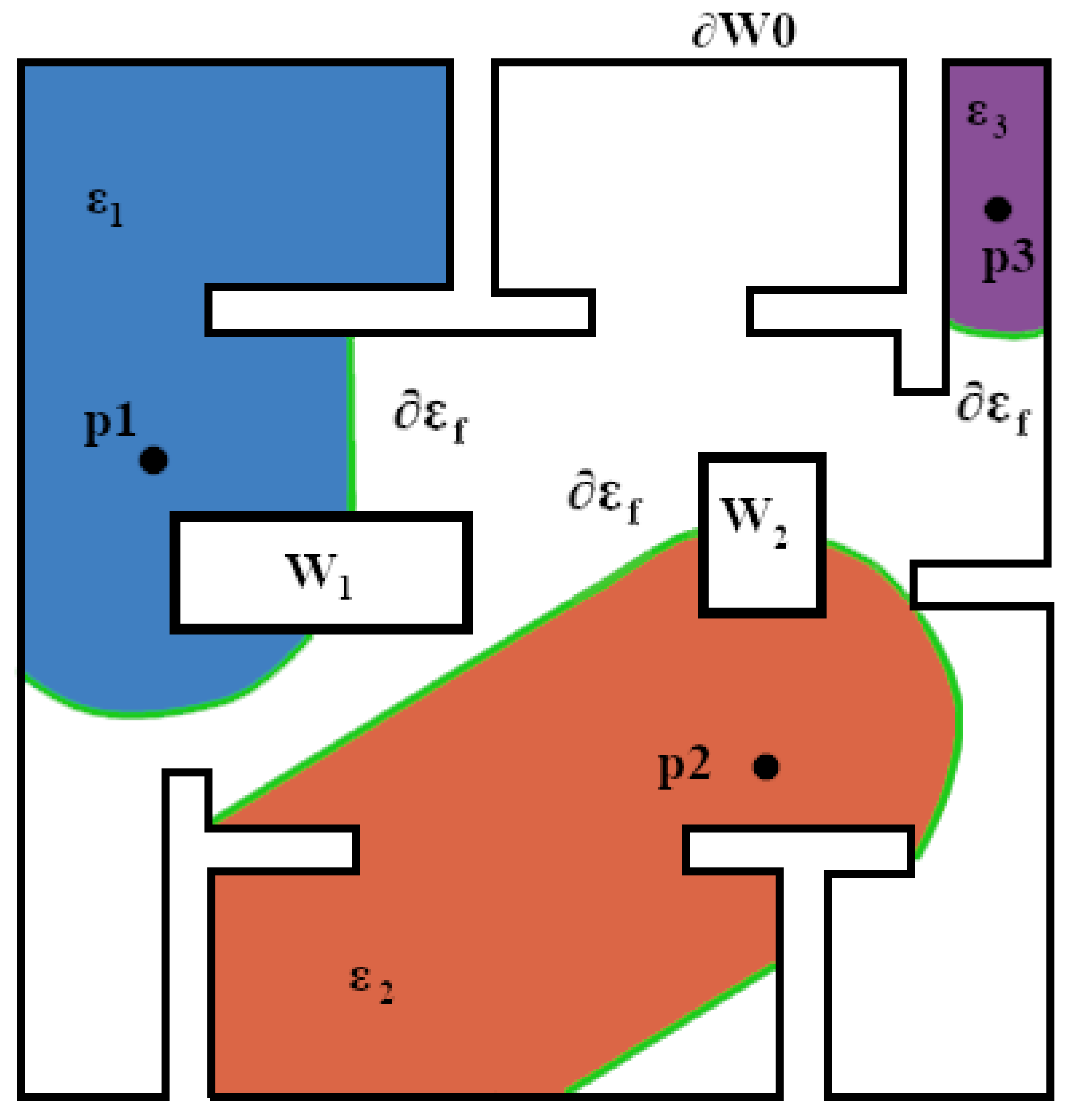
3. Methodology

The methodology proposed in this paper revolves around the computation of a HMT from the data given by the mapping process. To achieve this, the map undergoes a series of preprocessing steps, including filtering and boundary extraction.

3.1. Filtering and Boundary Extraction

Each robot generates a dynamic map of the explored area and its corresponding position using odometry and LIDAR data through SLAM. Subsequently, this map undergoes filtering to eliminate noise or imperfections that may arise during the mapping process, such as small gaps in boundary walls. This filtering primarily involves image processing techniques, including boundary dilation and erosion. To simplify the control process, each robot is considered to be a point, and thus the boundaries are inflated by the robot’s radius. Computer vision algorithms are then employed for edge detection and boundary coordinate extraction. The extraction of the explored region’s boundaries, including the identification of frontiers, is essential for the construction of the HMT.

3.2. Harmonic Maps Transformation for Exploration

To navigate within the explored region while avoiding static obstacles, a modified version of Harmonic Maps for Planar Navigation used in [22] is proposed. The aforementioned method maps the robots’ workspace W into a punctured unit disk $\mathcal{D}$. In contrast, our modified version of the transformation $\mathcal{T}$ maps only the explored region $\epsilon$ into $\mathcal{D}$ and has the following properties:

• Maps the explored region’s outer boundary $\partial \epsilon$ onto the unit circle $\partial \mathcal{D}$
• Maps each of the frontiers $\partial {\epsilon }_f$ of the outer boundary into a single point $q_f\in \partial \mathcal{D}$
• Maps the inner obstacle boundaries $\partial W_j$ that are within the explored region $\epsilon$ to a distinct point $q_j\in int\left(\mathcal{D}\right)$
• The transformation $\mathcal{T}$ is a diffeomorphism for all $p\in int\left(W\right)$.

The modified transformation is visualized in Figure 2. Since no closed-form solutions exist for non-trivial domains of the aforementioned transformation, the inner and outer boundaries are subdivided into a sufficient number of linear elements in order to numerically approximate $\mathcal{T}$ with $\tilde{\mathcal{T}}.$ Thus, the following transformation is given

$$\tilde{\mathcal{T}}\left(p\right)={\left[\tilde{u}\left(p\right),\tilde{v}\left(p\right)\right]}^T=q,p\in \epsilon ,q\in \mathcal{D},$$

(2)

with $\tilde{u}\left(p\right),\tilde{v}\left(p\right)$ being harmonic functions with respect to p, by approximating an ideal harmonic map $\mathcal{T}.$

The HMT for Exploration is particularly useful for navigating inside the explored region while avoiding the static obstacles, since each inner obstacle is mapped to a single point. Thus, in the transformed space $\mathcal{D}$, a line that connects the mapped position to the desired destination may intersect with inner obstacles with zero probability. Furthermore, since frontiers are mapped to points, navigating towards them becomes trivial, as shown in later sections.

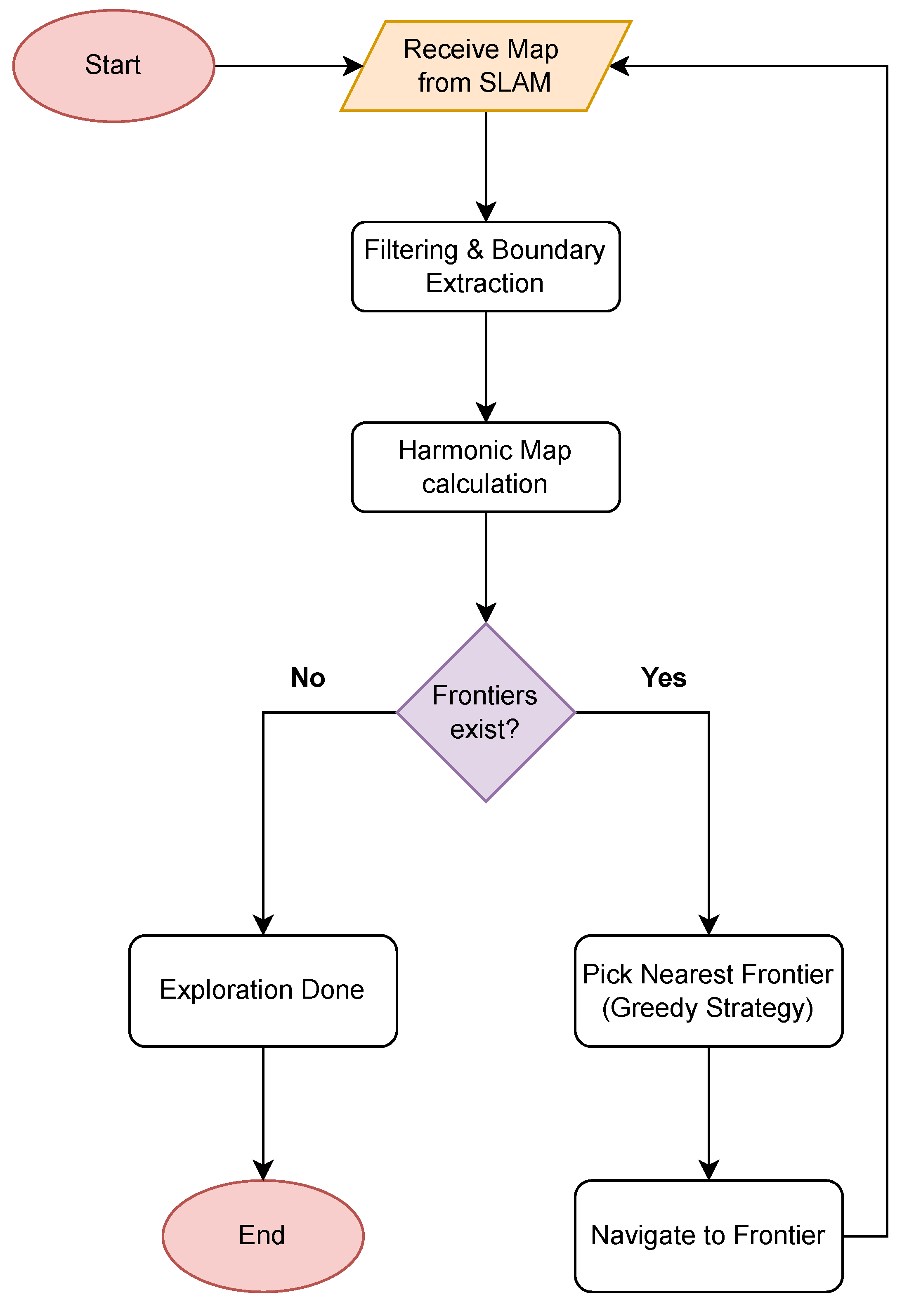
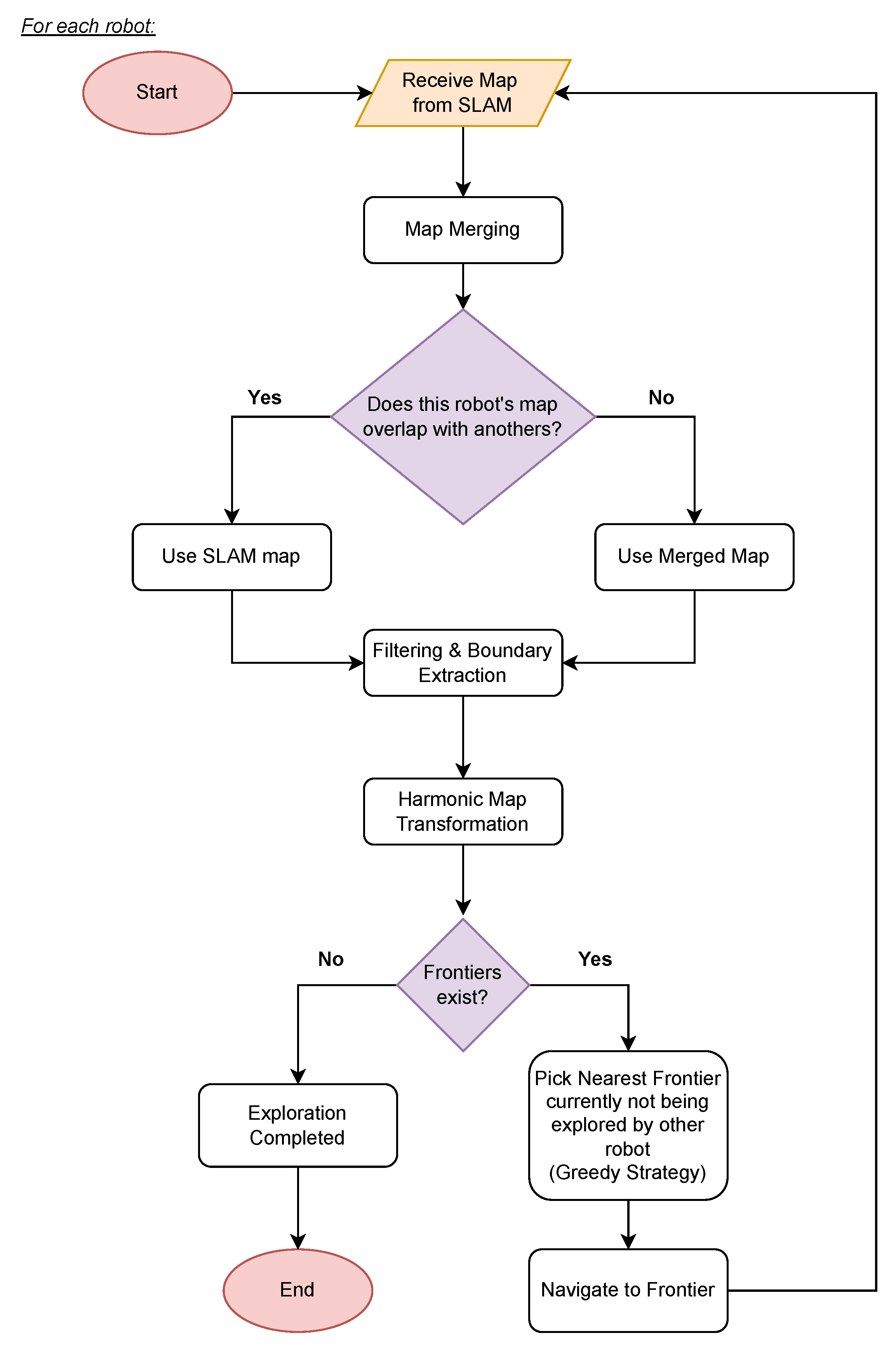
3.3. Robot Exploration

The algorithms followed for both single-robot and multi-robot exploration are presented in this subsection. The proposed method is heavily based on the HMT, since it is used for goal selection, path planning, and terminating exploration.

3.3.1. Single Robot

Single robot exploration follows the algorithm depicted in Figure 3. We propose a simple yet effective approach. First, an occupancy grid map is constructed utilizing SLAM. Then, the boundaries are extracted as previously discussed. Subsequently, the HMT for Exploration is computed using the extracted boundaries. As highlighted in [22], the transformation incurs a computational complexity of $O\left(M^3\right)$, where M denotes the total number of elements (samples of the boundaries) utilized in the computation. Although the mapping process may slow as the size of the map expands, this issue is mitigated by the fact that the map only needs to be updated when the robot is close to a frontier so that new information is added to the map. Thus, the transformation can be calculated at a low frequency. However, if computational demands persist, a solution proposed in [22] involves employing a map atlas, where numerous local HMTs are interconnected within a graph structure.

Following the calculation of the HMT, the presence of frontiers is used as a condition for terminating the exploration process. In the event that frontiers are detected, the single robot selects one to navigate towards. A greedy approach is adopted, wherein the nearest frontier is chosen as the destination. This selection strategy optimizes the exploration process by prioritizing proximity to unexplored regions. After selecting a navigation goal, a controller based on the HMT guides the robot towards the frontier. The robot’s position is denoted as $p={\left[x,y\right]}^T\in {\mathbb{R}}^2$, and the yaw angle is represented as $\theta \in \mathbb{R}$. The mapping of the robot’s position is expressed as $q=\tilde{\mathcal{T}}\left(p\right)\in {\mathbb{R}}^2$, with its corresponding Jacobian matrix denoted as $J\left(q\right)$. The following vector

$$u=-J^{-1}\left(q\right)(q-q_{\mathrm{dest}})$$

(3)

signifies the velocity required for the robot to navigate to the point that maps to $q_{\mathrm{dest}}$. It should be noted that $q_{\mathrm{dest}}$ represents the set of points of the nearest frontier and not a single point in the actual workspace.

The above equations are sufficient to control a single integrator model. A more common case is that of a differential drive model. Although it is possible to map the single integrator dynamics to the differential drive, as shown in [23], a simpler approach is used in this paper. The low-level controllers of differential drive robots often require that linear v and angular $\omega$ velocities be provided to them. The controller chosen is a proportional controller that aims to align the robot with the u vector.

$$v=K_{lin}{K}_t\alpha \parallel u\parallel$$

(4)

$$\omega =K_{ang}\Delta \theta$$

(5)

with $\Delta \theta \in \left[-\pi ,\pi \right]$ denoting the angular error between $\theta$ and ${\theta }_d=arctan(u_y/u_x)$, and with $K_{lin},K_{ang}\in \mathbb{R}$ being the controller gains. The rotation gain

$$K_t(\Delta \theta )=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\Delta \theta \in \left[-\varphi ,\varphi \right]\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(6)

determines whether the robot should be stationary while turning to avoid larger deviations from the single integrator path and ensure that the robot remains within the workspace. The angle $\varphi$ represents the largest acceptable deviation. The gain $\alpha$ is a damping factor that reduces linear velocity near frontiers, assisting in avoiding collisions near unexplored regions, such as sharp corner turns.

Remark 1. 

An issue arises with the inner obstacle’s "shadows". During the exploration process, an obstacle may be detached from $\partial \epsilon$, but the area around it will not be fully explored, thus remaining unknown. Frequently, the above issue is solved by simply continuing the exploration process, but for small areas or obstacles with complex shapes the issue may persist. HMTs can by modified to handle the exploration of such areas. Simply put, the inner obstacle’s frontier is mapped to a single point in the interior of $\mathcal{D}$, similarly to the frontiers belonging to $\partial \mathcal{E}$, but in this case the angle of approach must be taken into account so the correct area is explored. Finding the correct angle of approach can be achieved trivially, since the transformation is orientation preserving. When approaching inner obstacle frontiers, the control law must be altered to guarantee convergence to the correct angle of approach. The HMT is modified by adding a dipolar vector field, as shown in Figure 4. A similar approach is taken in [24]. Since a dipolar vector field is harmonic, no local minima will arise [25]. Hence, when navigating to an inner obstacle frontier, the updated control law for the velocity vector $u\in {\mathbb{R}}^2$ is given by

$$u=J^{-1}\left(q\right)v_{\mathit{dvf}}$$

(7)

where $v_{\mathit{dvf}}$ represents the dipolar vector field direction [24].

Figure 4. An example of inner frontier. (a) a workspace with a singular L-shaped inner obstacle. The explored region is colored in blue and the frontier in green, showing that the inner corner remains unexplored. (b) HMT of the explored region with the dipolar vector field overlayed on top. The inner obstacle is mapped to the green point and the white arrow shows the desired angle of approach. The dipolar vector field guides the robot through the desired angle.

Figure 4. An example of inner frontier. (a) a workspace with a singular L-shaped inner obstacle. The explored region is colored in blue and the frontier in green, showing that the inner corner remains unexplored. (b) HMT of the explored region with the dipolar vector field overlayed on top. The inner obstacle is mapped to the green point and the white arrow shows the desired angle of approach. The dipolar vector field guides the robot through the desired angle.

3.3.2. Multi-Robot Setup

The framework outlined for single robot exploration can be extended to accommodate multiple robots working cooperatively. This extension provides enhanced exploration efficiency and coverage, by leveraging collaborative efforts among multiple agents. The method detailed in Figure 5 is used for multi-robot exploration. First, utilizing SLAM, a local occupancy grid map is constructed. Then, if possible, maps from other robots are merged with the local map. Next, the boundaries are extracted and if frontiers are detected the robot navigates to the nearest frontier as explained previously. To reduce frontier overlap and increase efficiency, a frontier allocation process is used that will be discussed later.

The approach is implemented in a distributed manner, since each robot has limited information about the others and can independently explore the workspace regardless of the state of the other agents. The information shared among robots involves their location, their map of the so far explored workspace, and their currently explored frontier. If the explored region of a robot intersects with another’s, the new information is used to expand their explored region. Finally, overlapping between explored regions is minimized by the goal frontier selection, further optimizing the exploration process. By using a distributed approach, each robot can act autonomously, thus making the system robust to robot failure.

It is important to consider the scalability of the system. Since the approach is distributed, when more agents are added the complexity of the system grows only in the amount of data shared and the number of maps to be merged. If all robots exchange information with each other, then $n(n-1)$ information exchanges would be required, where n is the total number of robots, making the scaling of the system $O\left(n^2\right)$. The complexity is reduced by limiting the inter robot communication to a certain range, reducing the total number of information exchanges to $O\left(nl\right)$, where $l\le n$ is the average number of agents within each robot’s communication range. The amount of data in each exchange is mainly dependent on the size of the map being shared and its resolution.

A big advantage of using multiple robots is the ability to combine many maps to produce a complete mapping of the workspace. This process is called map merging [26]. The merging process facilitates the creation of a unified and comprehensive map, thereby eliminating the need to fully map the workspace with each individual robot. In our approach, when a map is shared, it is aligned with the robot local map and added to the robot’s merged map, as shown in Figure 6. Thus, each robot has an individual local and merged map. This approach ensures that the system does not rely on a central map merging node, although a common frame of reference is selected for all merged maps, so their resulting maps can be comparable. Moreover, the map merger checks if the added area is connected to the local explored region, in the sense that a clear path connecting the two regions exists in the merged explored region. If the two areas overlap, then the new region is added to the HMT. Notable is a fact that during the merging process when the local map overlaps with another, the data of the local map is selected as correct, so as to not interfere with the local explored region when a map is misaligned. The merging of partial maps generated by multiple robots enhances the exploration process significantly as larger areas can be fully mapped in a more efficient manner.

A potential challenge arises post-merging, wherein multiple robots may inadvertently explore the same frontiers simultaneously. To address this issue, a strategy is employed to ensure efficient frontier allocation among robots. At the start of the exploration process, each robot is assigned an arbitrary priority number, with a smaller number indicating higher priority. The priority number assists the frontier allocation process, as constant changes in the goal frontier are avoided when the allocation metric (the distance from the frontier in this case) of two agents is equal. When selecting a frontier to navigate to, the robots with higher priority share a merged map and state their current goal frontier. Then, a check is performed to detect any duplicate frontiers. If duplicates are found, the robot’s current frontier goal is set as a random frontier that no other robot with higher priority has set as a goal. If all other frontiers are taken, then the robot will not pick a goal frontier and stay stationary until a new frontier is discovered. Using the above rule, the inefficient scenario of multiple robots exploring the same frontier is avoided. An exception is made when the robot with higher priority is located outside a certain range, chosen as the laser scanner’s maximum distance. In that case, both robots head to the same goal and it is assumed that a new nearest frontier will be discovered during exploration. This approach minimizes redundancy and maximizes exploration coverage, thereby optimizing the collective exploration efforts of the multi-robot system.

Finally, the inclusion of other robots inside the workspace breaks the earlier assumption that all obstacles are static. Since our approach is distributed, a simple solution such as active collision avoidance is executed using the LIDAR data that overrides the HMT controller to avoid an imminent collision when robots are located close to each other.

4. Results

To verify the validity of the proposed HMT Exploration method, we tested on simulated and real-world environments both the single-robot and multi-robot cases. The results of the multi-robot simulation are compared with recent methods to highlight its advantages and limitations. All experiments presented have supplemental video material available at https://vimeo.com/showcase/11030898 (last accessed 13 March 2024). The calculations and simulations where performed on a computer with an AMD Ryzen 5 5500U CPU @ 2.10 GHz and 8 GB RAM. The software versions used were MATLAB 2023a and Robotic Operating System (ROS) Noetic running on Ubuntu 20.04 LTS.

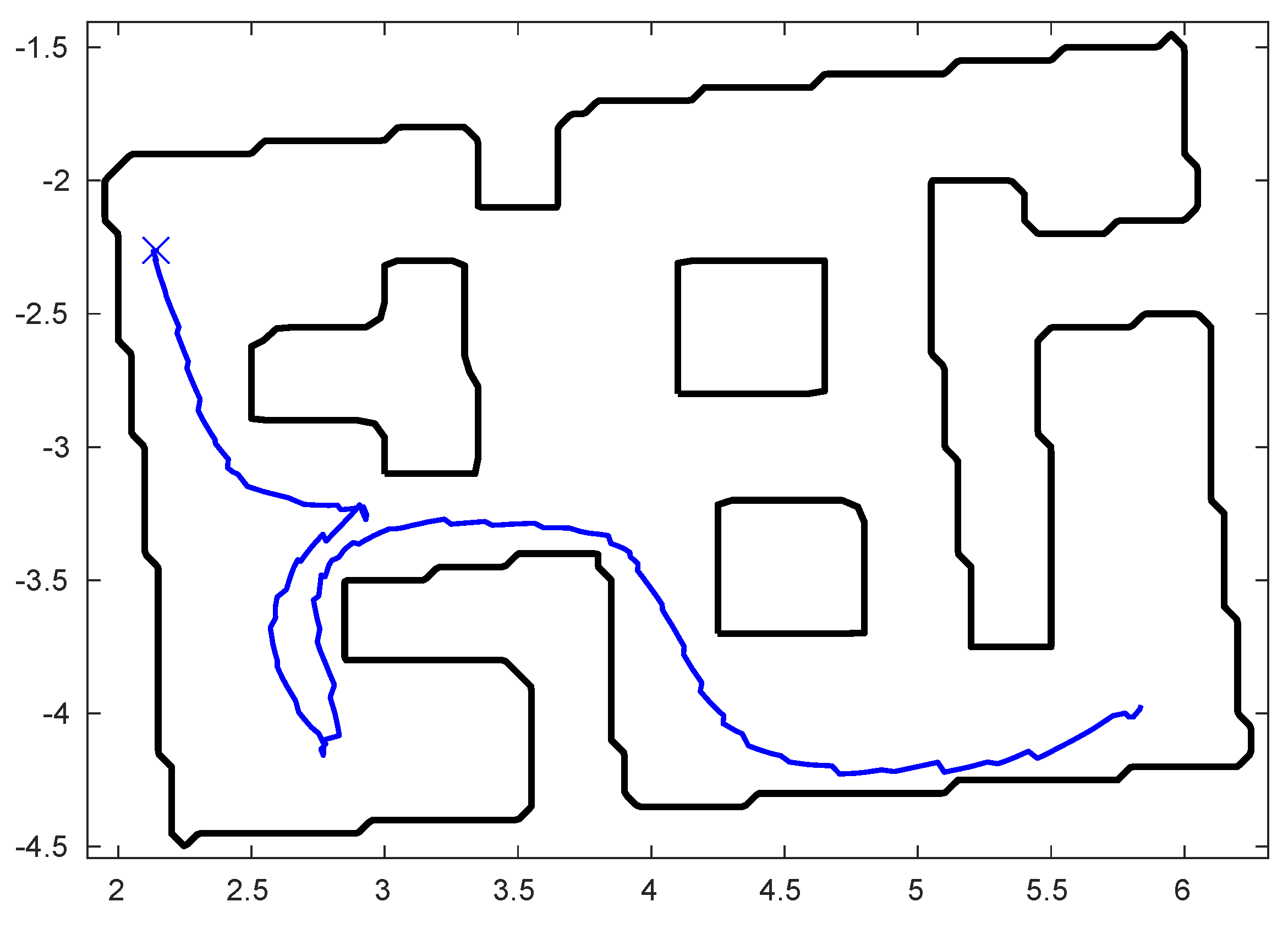
4.1. Single Robot Results

4.1.1. Simulation Results

We simulated the following scenario in the Gazebo simulator. The proposed method was applied on a single TurtleBot3 Burger to explore a 13.5 m × 14.5 m workspace with a large wall as an inner obstacle. For SLAM, a simulated LIDAR with a 5 m laser range is utilized. The resulting path can be seen in Figure 7. The robot manages to explore the workspace covering a path distance (PD) of 51.40 m with an elapsed time (ET) of 276.68 s. It should be noted that ET in simulated experiments refers to the simulated ET.

4.1.2. Experimental Results

A real-world experiment was conducted to validate the simulated results. A rectangular workspace, with approximate dimensions of 2.6 m × 4 m, was constructed and three inner obstacles were placed inside it. The obstacles consist of two rectangular boxes and a T-shaped barrier. The workspace is visible in Figure 8. To explore the workspace, an AmigoBot robot is chosen due to its small size, versatility, and its ROS integration through the RosAria package. The AmigoBot is connected to an ODROID computer to run ROS locally. Additionally, an RPLIDAR A1 and the odometer data provided by the robot are used for SLAM that is provided by the gmapping ROS package. The robot manages to fully explore the workspace. The resulting PD is 7.33 m and the ET 124.2 s. The full path can be observed in Figure 9.

4.2. Multi-Robot Results

The suggested multi-robot method was tested in Gazebo using the same simulated workspace as in the single robot simulation scenario. Three TurtleBot3 Burger robots were used. Multiple simulations were performed to reduce randomness in the results. The mean values and standard divination of ET, PD, and total PD are presented in

Table 1. HMT for Exploration Simulation Results.

	ET (s)	PD Robot 1 (m)	PD Robot 2 (m)	PD Robot 3 (m)	Total PD (m)
Mean Values	168.75	15.10	23.86	17.54	56.50
Std Dev	1.2698	1.9450	2.3356	1.1087	9.1234

. The simulation is designed to replicate the methodology outlined in the simulation scenario 1 from Ning et al. [15], facilitating a direct comparison of results between our method and theirs. The comparative results are shown in

Table 2. Comparison of Multi-Robot Exploration Simulated Experiments.

Algorithm	ET (s)	Total PD (m)	PD (m)	Mean-PD	Std-PD
M-RRTs [8]	244.21	110.30	{32.49, 25.38, 52.43}	36.7667	14.0229
RRT-GFB [27]	234.49	107.82	{27.41, 34.87, 45.54}	35.9400	9.1122
RRT-BFS [28]	202.10	97.34	{26.28, 30.47, 40.59}	32.4467	7.3569
E-RRT [29]	219.07	102.89	{29.70, 27.52, 45.67}	34.2967	9.9097
ID-RRT [30]	194.33	86.26	{17.69, 25.01, 43.56}	28.7533	13.3351
HMS-RRT [15]	144.18	67.28	{21.33, 16.43, 29.52}	22.4267	6.6135
HMT	168.75	56.50	{15.10, 23.86, 17.54}	18.8333	4.5209

The smallest value of each column is denoted with bold.

.

The paths produced by the robot are visualized along with the workspace in Figure 10. The final maps generated by SLAM and the map merging process is presented in Figure 11. Notice that our method outperforms the other in terms of path length, exhibiting slightly longer execution than the best one.

5. Conclusions

This paper proposes a method for robotic exploration, suitable for both single-robot and multi-robot setups. Firstly, we present a Harmonic Map Transformation for Exploration, and introduce a novel approach for frontier detection and navigation. Then, the concept is extended to distributed multi-robot systems, using map merging to effectively exchange information and a greedy frontier allocation strategy. An algorithm to further optimize the frontier allocation by ensuring that each robot heads to a unique frontier is also presented. The proposed approach is verified through both simulations and real-world experiments and the results are compared with recent multi-robot cooperative exploration methods. It is concluded that the proposed method is efficient as it outperforms existing approaches in terms of path distance.

The proposed method is heavily reliant on the accuracy of the maps produced by the SLAM algorithm, since the HMT only uses the boundaries provided by the map. Filtering of the map before boundary extraction does reduce sensitivity to noise and improves accuracy. The issue of added noise in the map during the map merging process is also of concern for the aforementioned reasons. This issue is addressed by assuming that each robot’s local map is accurate and using it unmodified in the merged map, ensuring that the local region of the robot is correct despite possible inaccuracies in the merged global map. Nevertheless, the experiments confirm that the proposed method is able to perform in realistic conditions while retaining the total PD and ET low when compared to other recent methods.

In future work, we are considering improving and extending the proposed method. We aim to incorporate map altasing methodologies to facilitate exploration of expansive spaces and integrate sophisticated heuristics for frontier selection to refine the exploration strategy. Finally, it would be of great interest to explore the efficacy of extending the application of the HMT to three-dimensional environments as it would prove useful for aerial robotic navigation and exploration.