Adaptive Graph Convolutional Network with Deep Sequence and Feature Correlation Learning for Porosity Prediction from Well-Logging Data
Abstract
1. Introduction
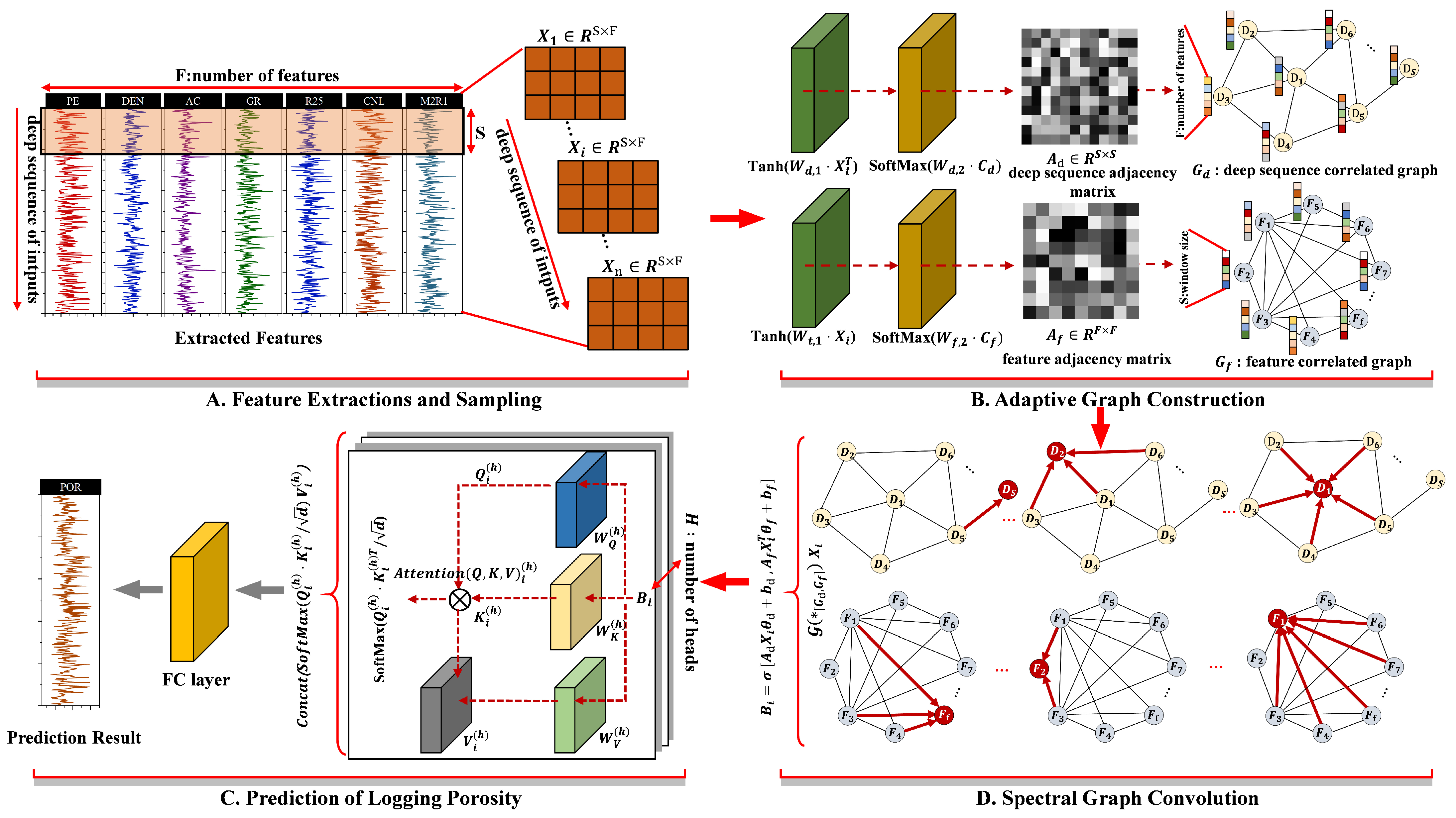
2. Methods
2.1. Adaptive Construction of Deep Sequence and Feature Correlation Graphs
2.2. Spectral Graph Convolution
2.3. Porosity Prediction Based on Multi-Head Attention Mechanism
3. Experimental Data Analysis
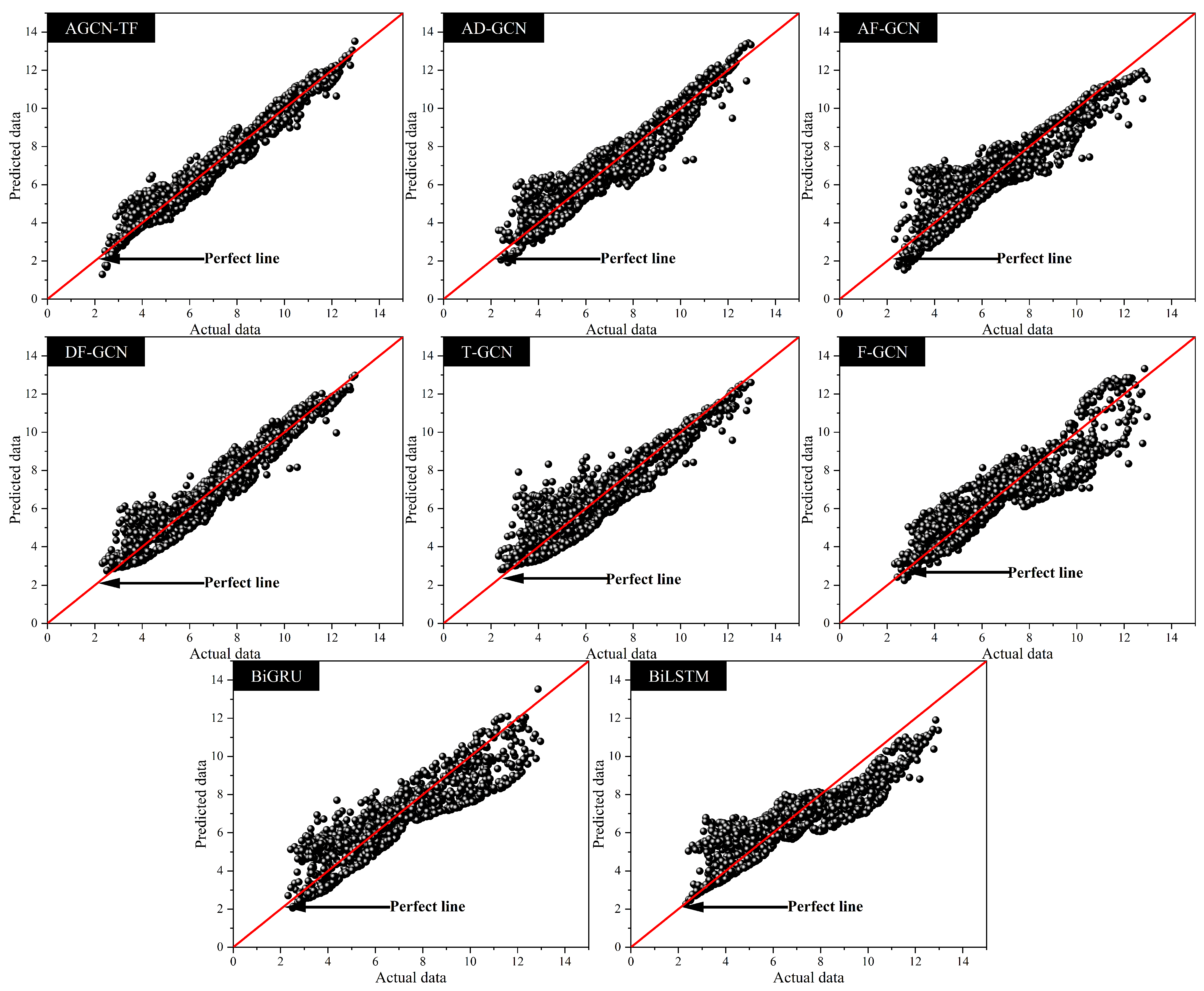
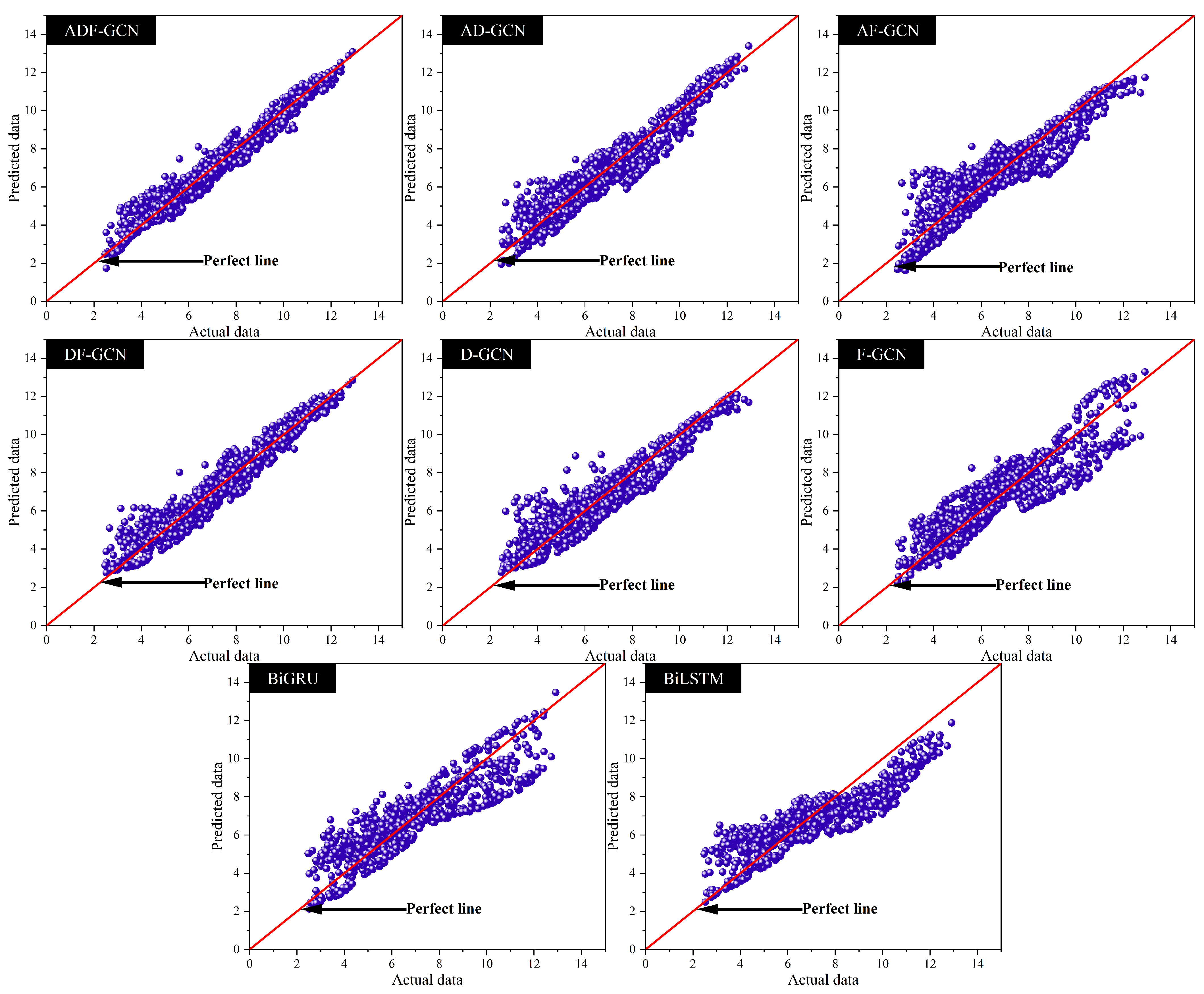
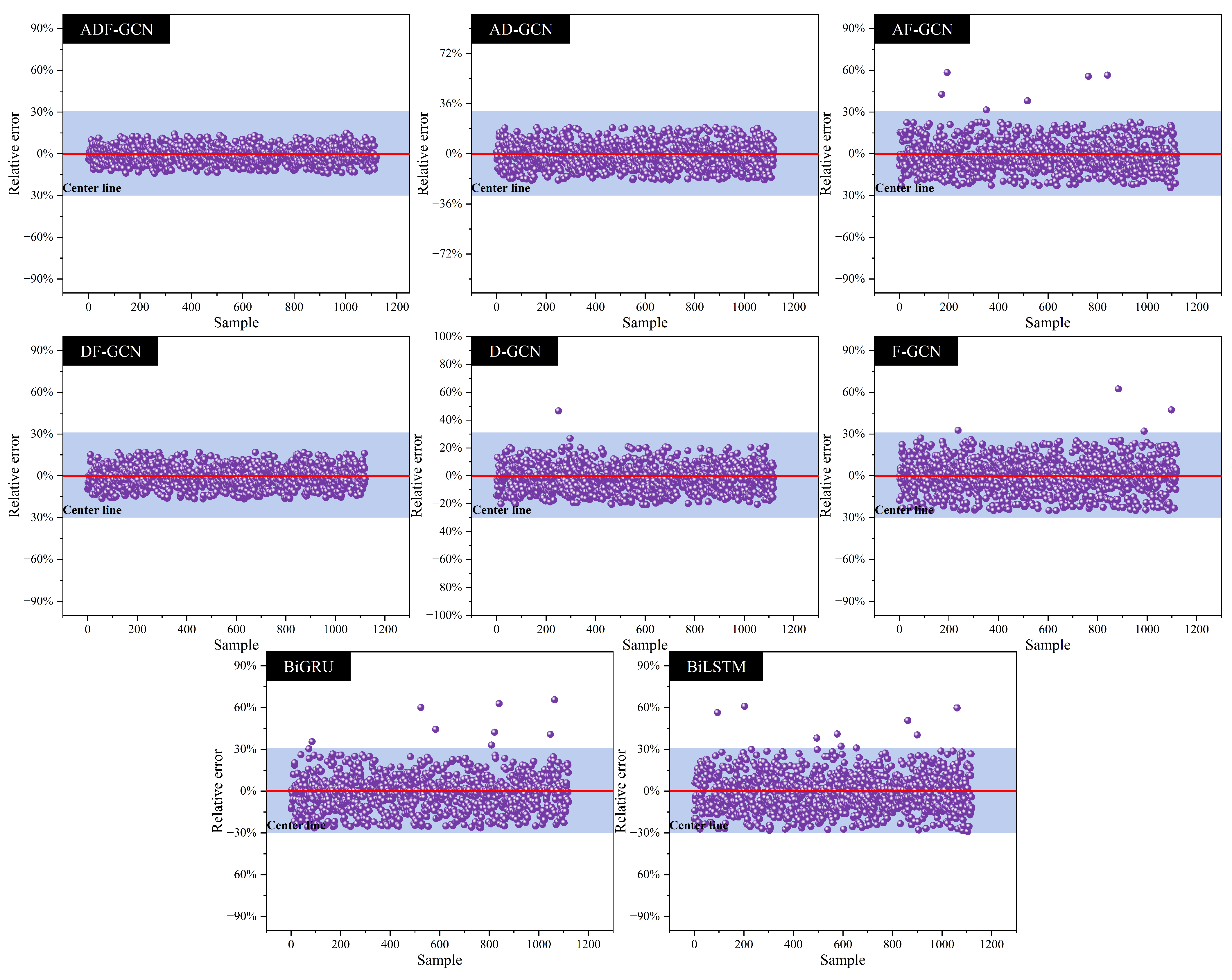
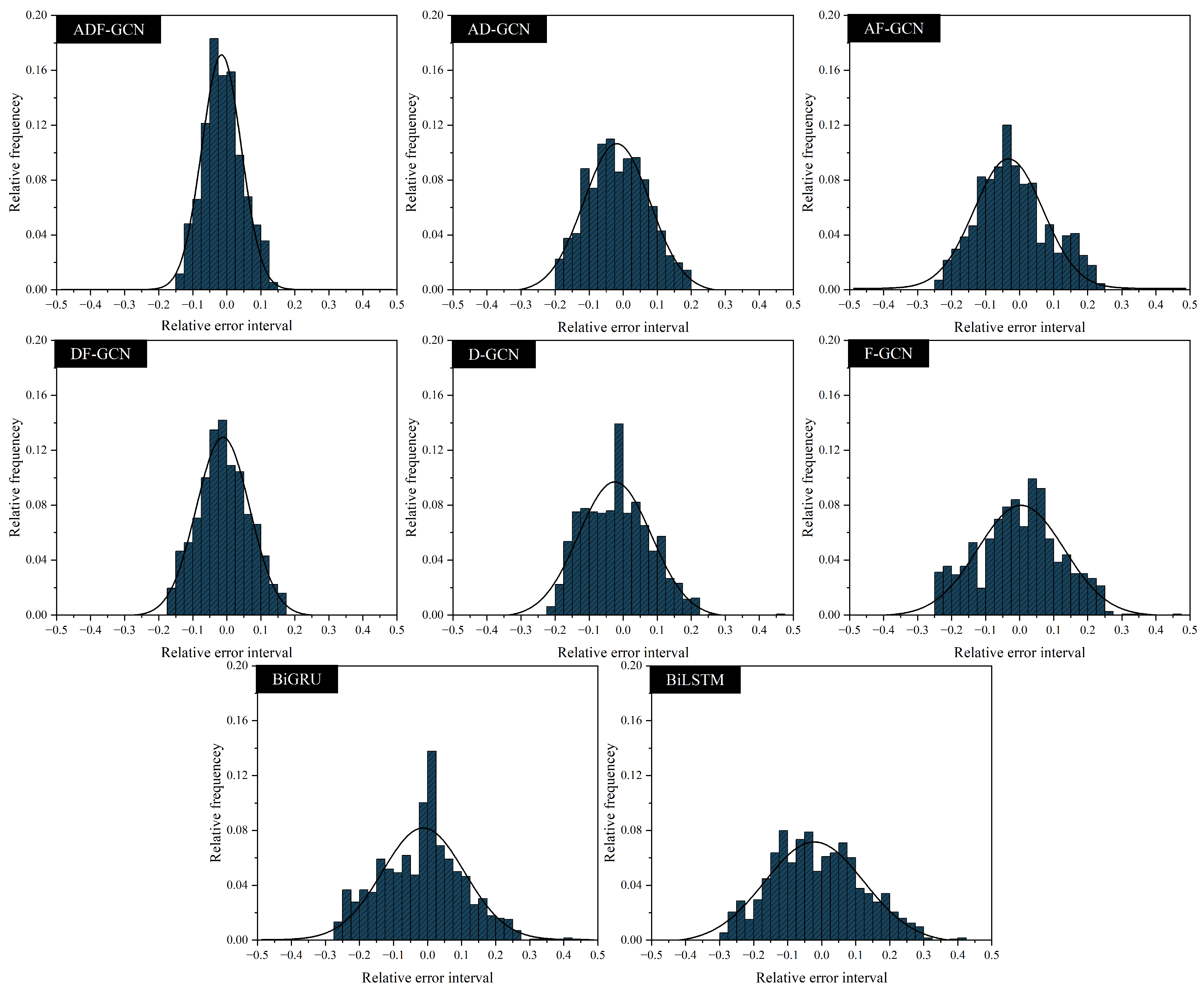
4. Analysis of Prediction Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Definition of Graph Determinacy Entropy
References
- Zhang, F.; Qiu, F.; Fang, Q.; Zhang, X.; Zhang, H.; Tang, F.; Fan, J. An accurately determining porosity method from pulsed-neutron element logging in unconventional reservoirs. In Proceedings of the SPWLA Annual Logging Symposium; OnePetro: Richardson, TX, USA, 2021; p. D041S037R001. [Google Scholar]
- Zhu, L.; Zhang, C.; Guo, C.; Jiao, Y.; Chen, L.; Zhou, X.; Zhang, C.; Zhang, Z. Calculating the total porosity of shale reservoirs by combining conventional logging and elemental logging to eliminate the effects of gas saturation. Petrophysics 2018, 59, 162–184. [Google Scholar] [CrossRef]
- An, P.; Yang, X.; Zhang, M. Porosity prediction and application with multiwell-logging curves based on deep neural network. In Proceedings of the SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2018; pp. 819–823. [Google Scholar]
- Spinelli, R.; Magagnotti, N.; Nati, C. Benchmarking the impact of traditional small-scale logging systems used in Mediterranean forestry. Forest Ecol. Manag. 2010, 260, 1997–2001. [Google Scholar] [CrossRef]
- Zhou, K.; Hu, Y.; Pan, H.; Kong, L.; Liu, J.; Huang, Z.; Chen, T. Fast prediction of reservoir permeability based on embedded feature selection and LightGBM using direct logging data. Meas. Sci. Technol. 2020, 31, 045101. [Google Scholar] [CrossRef]
- Merembayev, T.; Yunussov, R.; Yedilkhan, A. Machine learning algorithms for classification geology data from well logging. In Proceedings of the 14th International Conference on Electronics Computer and Computation (ICECCO), Kaskelen, Kazakhstan, 29 November–1 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 206–212. [Google Scholar]
- Alqahtani, N.; Armstrong, R.T.; Mostaghimi, P. Deep learning convolutional neural networks to predict porous media properties. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 23–25 October 2018; SPE: Calgary, AB, Canada, 2018; p. D012S032R010. [Google Scholar]
- Santos, J.E.; Xu, D.; Jo, H.; Landry, C.J.; Prodanović, M.; Pyrcz, M.J. PoreFlow-Net: A 3D convolutional neural network to predict fluid flow through porous media. Adv. Water Resour. 2020, 138, 103539. [Google Scholar] [CrossRef]
- Zhang, F.; He, X.; Teng, Q.; Wu, X.; Dong, X. 3D-PMRNN: Reconstructing three-dimensional porous media from the two-dimensional image with recurrent neural network. J. Pet. Sci. Eng. 2022, 208, 109652. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J.; Zhou, X. Reservoir porosity prediction based on deep bidirectional recurrent neural network. Prog. Geophys. 2022, 37, 267–274. [Google Scholar]
- Song, X.; Liu, Y.; Xue, L.; Wang, J.; Zhang, J.; Wang, J.; Jiang, L.; Cheng, Z. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Pet. Sci. Eng. 2020, 186, 106682. [Google Scholar] [CrossRef]
- Shi, S.Z.; Shi, G.F.; Pei, J.B.; Zhao, K.; He, Y.Z. Porosity prediction in tight sandstone reservoirs based on a one–dimensional convolutional neural network–gated recurrent unit model. Appl. Geophys. 2023, 1–13. [Google Scholar] [CrossRef]
- Yu, Z.; Sun, Y.; Zhang, J.; Zhang, Y.; Liu, Z. Gated recurrent unit neural network (GRU) based on quantile regression (QR) predicts reservoir parameters through well logging data. Front. Earth Sci. 2023, 11, 1087385. [Google Scholar] [CrossRef]
- Zeng, L.; Ren, W.; Shan, L. Attention-based bidirectional gated recurrent unit neural networks for well logs prediction and lithology identification. Neurocomputing 2020, 414, 153–171. [Google Scholar] [CrossRef]
- Yang, L.; Wang, S.; Chen, X.; Chen, W.; Saad, O.M.; Zhou, X.; Pham, N.; Geng, Z.; Fomel, S.; Chen, Y. High-fidelity permeability and porosity prediction using deep learning with the self-attention mechanism. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 3429–3443. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Yang, L.; Zha, B.; Zhang, M.; Chen, Y. Deep learning reservoir porosity prediction based on multilayer long short-term memory network. Geophysics 2020, 85, WA213–WA225. [Google Scholar] [CrossRef]
- Shan, L.; Liu, Y.; Tang, M.; Yang, M.; Bai, X. CNN-BiLSTM hybrid neural networks with attention mechanism for well log prediction. J. Pet. Sci. Eng. 2021, 205, 108838. [Google Scholar] [CrossRef]
- Ersavas, T.; Smith, M.A.; Mattick, J.S. Novel applications of Convolutional Neural Networks in the age of Transformers. Sci. Rep. 2024, 14, 10000. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Zhang, G.; Xu, L. Dynamic spatio-temporal graph network with adaptive propagation mechanism for multivariate time series forecasting. Expert Syst. Appl. 2023, 216, 119374. [Google Scholar] [CrossRef]
- Yang, J.; Xie, F.; Yang, J.; Shi, J.; Zhao, J.; Zhang, R. Spatial-temporal correlated graph neural networks based on neighborhood feature selection for traffic data prediction. Appl. Intell. 2023, 53, 4717–4732. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 922–929. [Google Scholar]
- Wang, X.; Zhao, J.; Zhu, L.; Zhou, X.; Li, Z.; Feng, J.; Deng, C.; Zhang, Y. Adaptive multi-receptive field spatial-temporal graph convolutional network for traffic forecasting. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–7. [Google Scholar]
- Wang, Y.; Ren, Q.; Li, J. Spatial–temporal multi-feature fusion network for long short-term traffic prediction. Expert Syst. Appl. 2023, 224, 119959. [Google Scholar] [CrossRef]
- Cai, K.; Shen, Z.; Luo, X.; Li, Y. Temporal attention aware dual-graph convolution network for air traffic flow prediction. J. Air Transp. Manag. 2023, 106, 102301. [Google Scholar] [CrossRef]
- Tao, B.; Liu, X.; Zhou, H.; Liu, J.; Lyu, F.; Lin, Y. Porosity prediction based on a structural modeling deep learning method. Geophysics 2024, 89, 1–73. [Google Scholar] [CrossRef]
- Yuan, C.; Wu, Y.; Li, Z.; Zhou, H.; Chen, S.; Kang, Y. Lithology identification by adaptive feature aggregation under scarce labels. J. Pet. Sci. Eng. 2022, 215, 110540. [Google Scholar] [CrossRef]
- Feng, S.; Li, X.; Zeng, F.; Hu, Z.; Sun, Y.; Wang, Z.; Duan, H. Spatiotemporal deep learning model with graph convolutional network for well logs prediction. IEEE Geosci. Remote Sens. Lett. 2023, 20, 7505205. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Multireceptive field graph convolutional networks for machine fault diagnosis. IEEE Trans. Ind. Electron. 2020, 68, 12739–12749. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D. Prediction of state of health and remaining useful life of lithium-ion battery using graph convolutional network with dual attention mechanisms. Reliab. Eng. Syst. Saf. 2023, 230, 108947. [Google Scholar] [CrossRef]
- Lin, Z.; Feng, M.; Santos, C.N.d.; Yu, M.; Xiang, B.; Zhou, B.; Bengio, Y. A structured self-attentive sentence embedding. arXiv 2017, arXiv:1703.03130. [Google Scholar]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef]
- Ellis, D.V.; Singer, J.M. Lithology and Porosity Estimation. In Well Logging for Earth Scientists; Springer: Berlin/Heidelberg, Germany, 2007; pp. 629–652. [Google Scholar]
- Helle, H.B.; Bhatt, A.; Ursin, B. Porosity and permeability prediction from wireline logs using artificial neural networks: A North Sea case study. Geophys. Prospect. 2001, 49, 431–444. [Google Scholar] [CrossRef]
- Soete, J.; Kleipool, L.M.; Claes, H.; Claes, S.; Hamaekers, H.; Kele, S.; Özkul, M.; Foubert, A.; Reijmer, J.J.; Swennen, R. Acoustic properties in travertines and their relation to porosity and pore types. Mar. Pet. Geol. 2015, 59, 320–335. [Google Scholar] [CrossRef]
- de Oliveira, J.M., Jr.; Andreo Filho, N.; Chaud, M.V.; Angiolucci, T.; Aranha, N.; Martins, A.C.G. Porosity measurement of solid pharmaceutical dosage forms by gamma-ray transmission. Appl. Radiat. Isot. 2010, 68, 2223–2228. [Google Scholar] [CrossRef]
- Wu, W.; Tong, M.; Xiao, L.; Wang, J. Porosity sensitivity study of the compensated neutron logging tool. J. Pet. Sci. Eng. 2013, 108, 10–13. [Google Scholar] [CrossRef][Green Version]
- Xu, B.S.; Li, N.; Xiao, L.Z.; Wu, H.L.; Wang, B.; Wang, K.W. Serial structure multi-task learning method for predicting reservoir parameters. Appl. Geophys. 2022, 19, 513–527. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, J.; Yu, Z.; Zhang, Y.; Liu, Z. Bidirectional long short-term neural network based on the attention mechanism of the residual neural network (ResNet–BiLSTM–attention) predicts porosity through well logging parameters. ACS Omega 2023, 8, 24083–24092. [Google Scholar] [CrossRef] [PubMed]
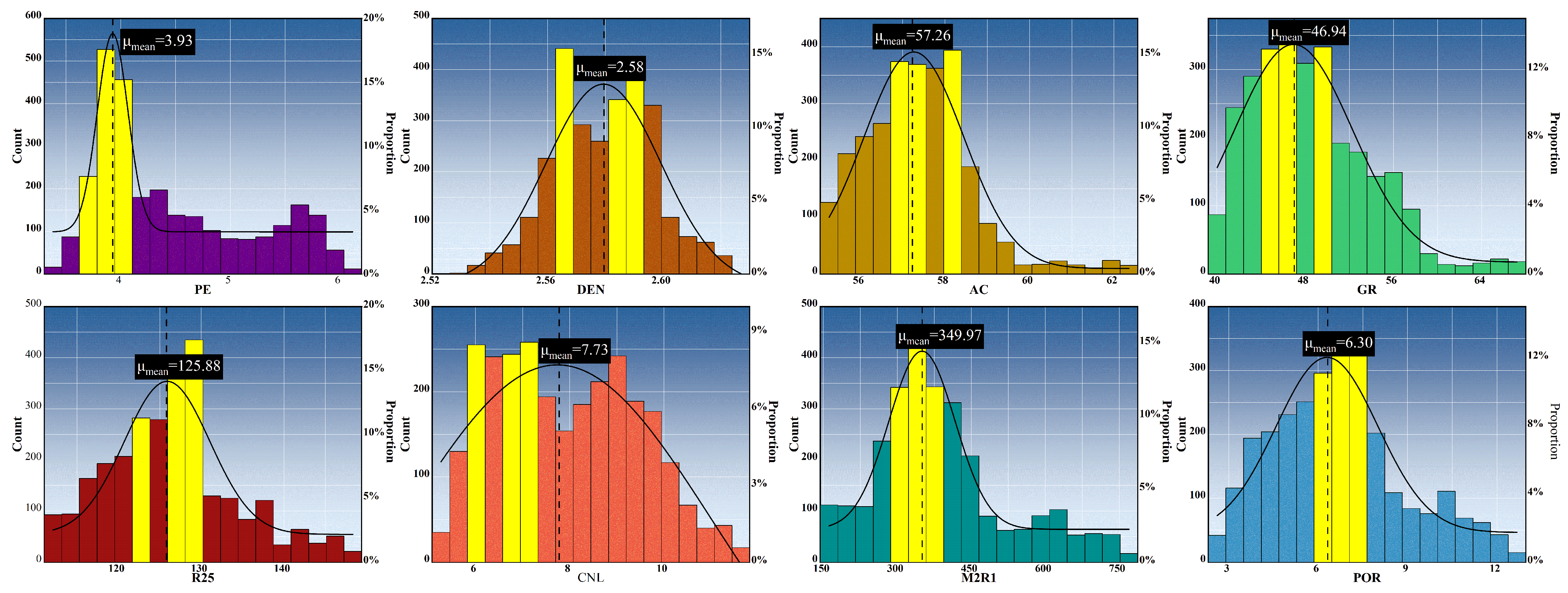

| Logging Parameters | Max | Min | Mean | Median | Standard Deviation | Skewness |
|---|---|---|---|---|---|---|
| PE | ||||||
| DEN | ||||||
| AC | ||||||
| GR | ||||||
| R25 | ||||||
| CNL | ||||||
| M2R1 | ||||||
| POR |
| Experiments | Abbreviations | Particulars |
|---|---|---|
| Ablation Experiments | ADF-GCN | Adaptive GCN for deep sequence and feature correlation graph (ours) |
| AD-GCN | Adaptive GCN for deep sequence correlation graph | |
| AF-GCN | Adaptive GCN for feature correlation graph | |
| DF-GCN | GCN for deep sequence and feature correlation graph | |
| D-GCN | GCN for deep sequence correlation graph | |
| F-GCN | GCN for feature correlation graph | |
| Comparison Experiments | BiGRU [37] | Bidirectional Gated Recurrent Unit |
| BiLSTM [38] | Bidirectional Long Short-Term Memory |
| Models | Parameters | Values |
|---|---|---|
| Ablation Model Ensemble * | Graph convolution layer | 4 |
| The number of heads | 2 | |
| The window size | 12 | |
| Activation function | ReLU | |
| Learning rate | ||
| Optimizer | Adam | |
| Dropout | 0.3 | |
| Maximum iterations | 1000 | |
| Batch size | 32 | |
| BiGRU | The number of GRU units in each layer | 128 |
| Activation function | ReLU | |
| Learning rate | ||
| Optimizer | Adam | |
| Dropout | 0.3 | |
| Maximum iterations | 1000 | |
| Batch size | 32 | |
| BiLSTM | The number of LSTM units in each layer | 128 |
| Activation function | ReLU | |
| Learning rate | ||
| Optimizer | Adam | |
| Dropout | 0.3 | |
| Maximum iterations | 1000 | |
| Batch size | 32 |
| Model | RMSE | R2 | MAE | MAPE | ||||
|---|---|---|---|---|---|---|---|---|
| Dataset | Train | Test | Train | Test | Train | Test | Train | Test |
| ADF-GCN | 0.487 | 0.506 | 0.951 | 0.948 | 0.347 | 0.0.378 | 6.389% | 6.733% |
| AD-GCN | 0.720 | 0.746 | 0.894 | 0.887 | 0.575 | 0.586 | 9.930% | 10.162% |
| AF-GCN | 0.866 | 0.916 | 0.845 | 0.830 | 0.678 | 0.704 | 12.080% | 12.656% |
| DF-GCN | 0.608 | 0.638 | 0.924 | 0.917 | 0.475 | 0.487 | 8.365% | 8.670% |
| D-GCN | 0.786 | 0.851 | 0.872 | 0.854 | 0.608 | 0.642 | 10.743% | 11.596% |
| F-GCN | 0.975 | 0.998 | 0.808 | 0.794 | 0.728 | 0.764 | 11.623% | 12.124% |
| BiGRU | 1.049 | 1.061 | 0.777 | 0.767 | 0.783 | 0.794 | 13.567% | 13.619% |
| BiLSTM | 1.155 | 1.156 | 0.730 | 0.723 | 0.904 | 0.913 | 15.293% | 15.327% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, L.; Wang, X.; Dong, Y.; Zhao, P.; Han, P.; Li, X.; Jing, F.; Zhai, C. Adaptive Graph Convolutional Network with Deep Sequence and Feature Correlation Learning for Porosity Prediction from Well-Logging Data. Appl. Sci. 2025, 15, 4609. https://doi.org/10.3390/app15094609
Hao L, Wang X, Dong Y, Zhao P, Han P, Li X, Jing F, Zhai C. Adaptive Graph Convolutional Network with Deep Sequence and Feature Correlation Learning for Porosity Prediction from Well-Logging Data. Applied Sciences. 2025; 15(9):4609. https://doi.org/10.3390/app15094609
Chicago/Turabian StyleHao, Long, Xun Wang, Yunlong Dong, Peizhi Zhao, Peifu Han, Xue Li, Fengrui Jing, and Chuchu Zhai. 2025. "Adaptive Graph Convolutional Network with Deep Sequence and Feature Correlation Learning for Porosity Prediction from Well-Logging Data" Applied Sciences 15, no. 9: 4609. https://doi.org/10.3390/app15094609
APA StyleHao, L., Wang, X., Dong, Y., Zhao, P., Han, P., Li, X., Jing, F., & Zhai, C. (2025). Adaptive Graph Convolutional Network with Deep Sequence and Feature Correlation Learning for Porosity Prediction from Well-Logging Data. Applied Sciences, 15(9), 4609. https://doi.org/10.3390/app15094609






