Pattern Formation on Alloys by Cluster Ion Beam Irradiation
Abstract
1. Introduction
2. Model
3. Results and Discussion
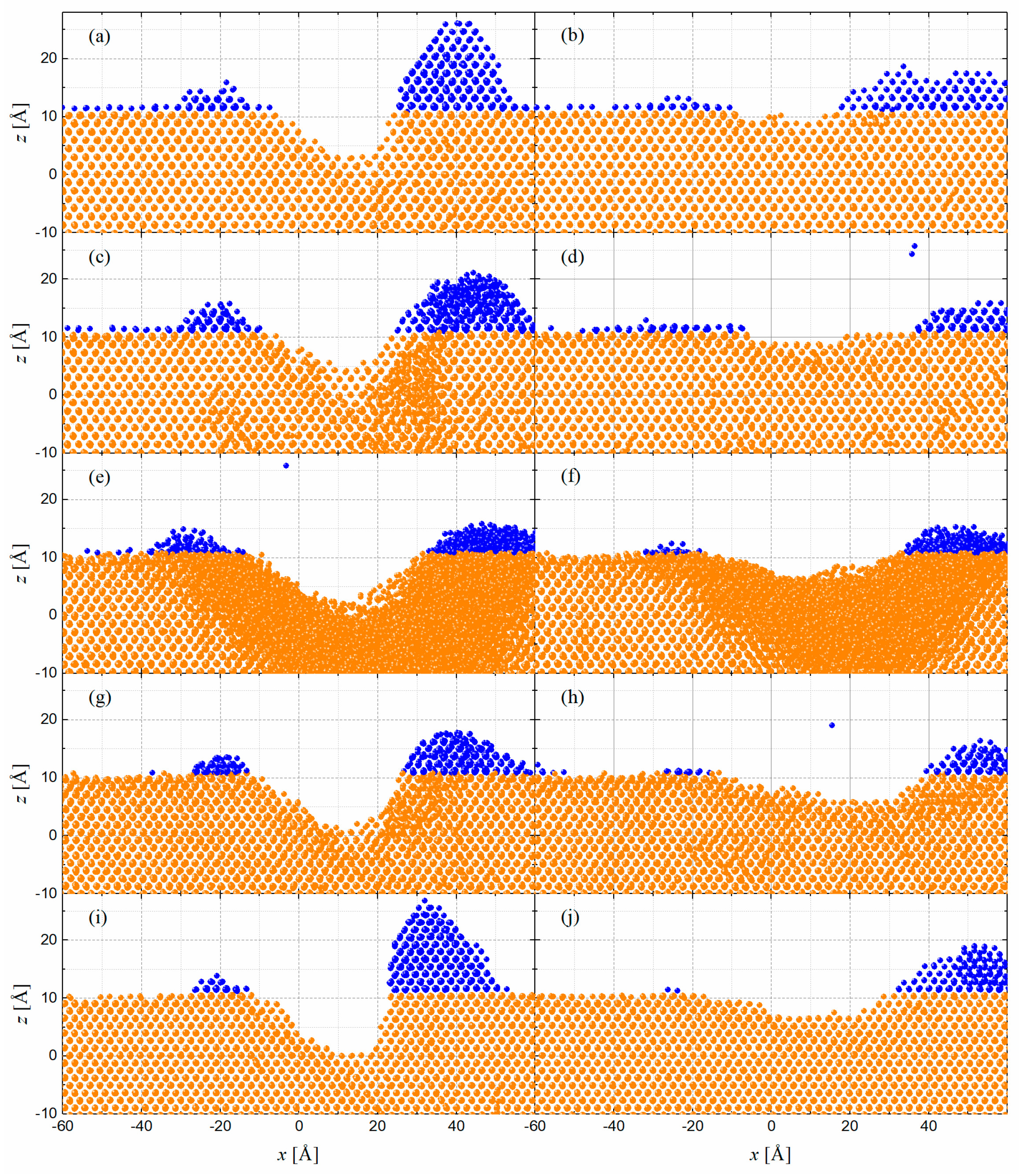
3.1. Atomic Description
3.2. Sputter Yield and Displacement
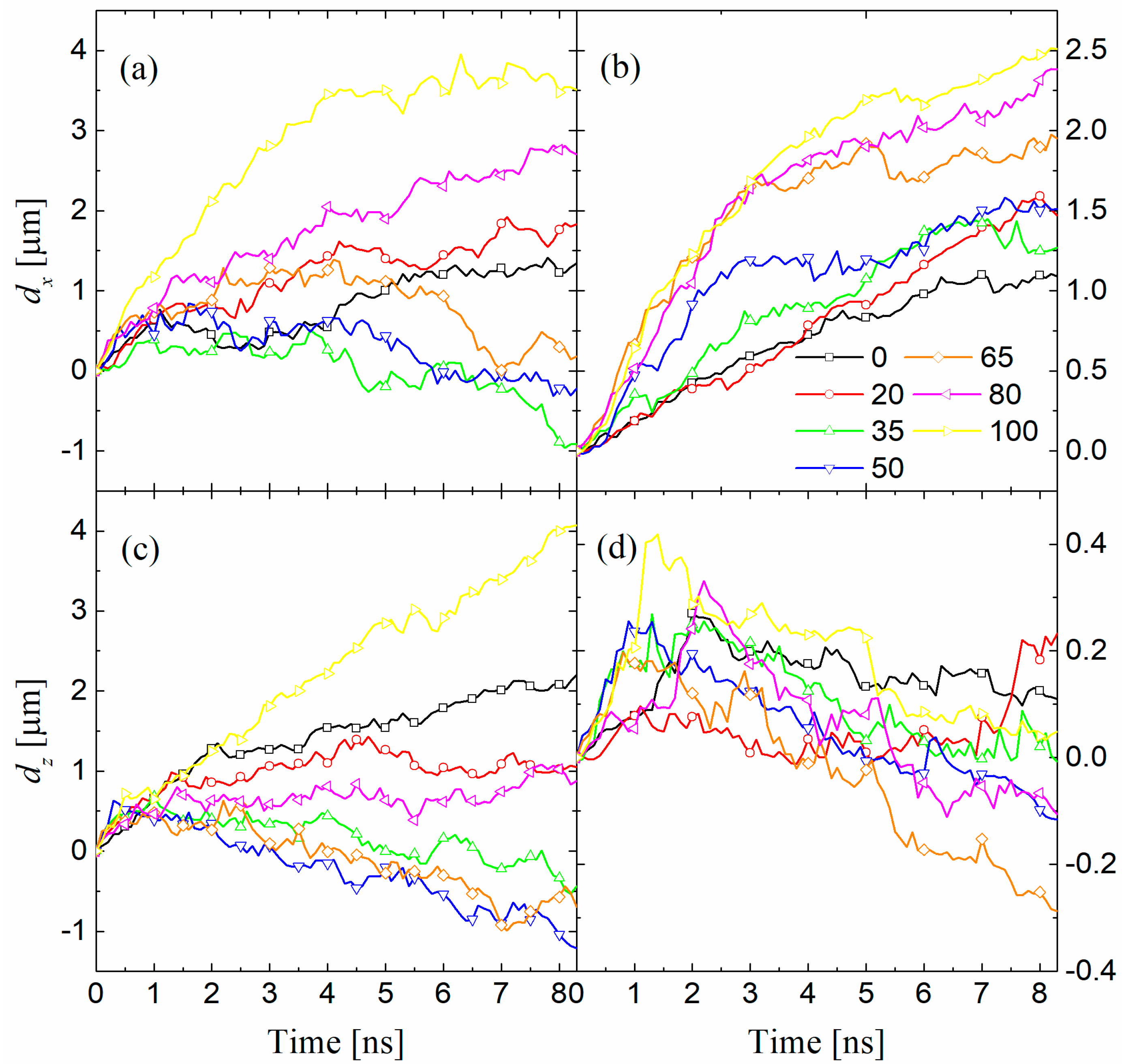
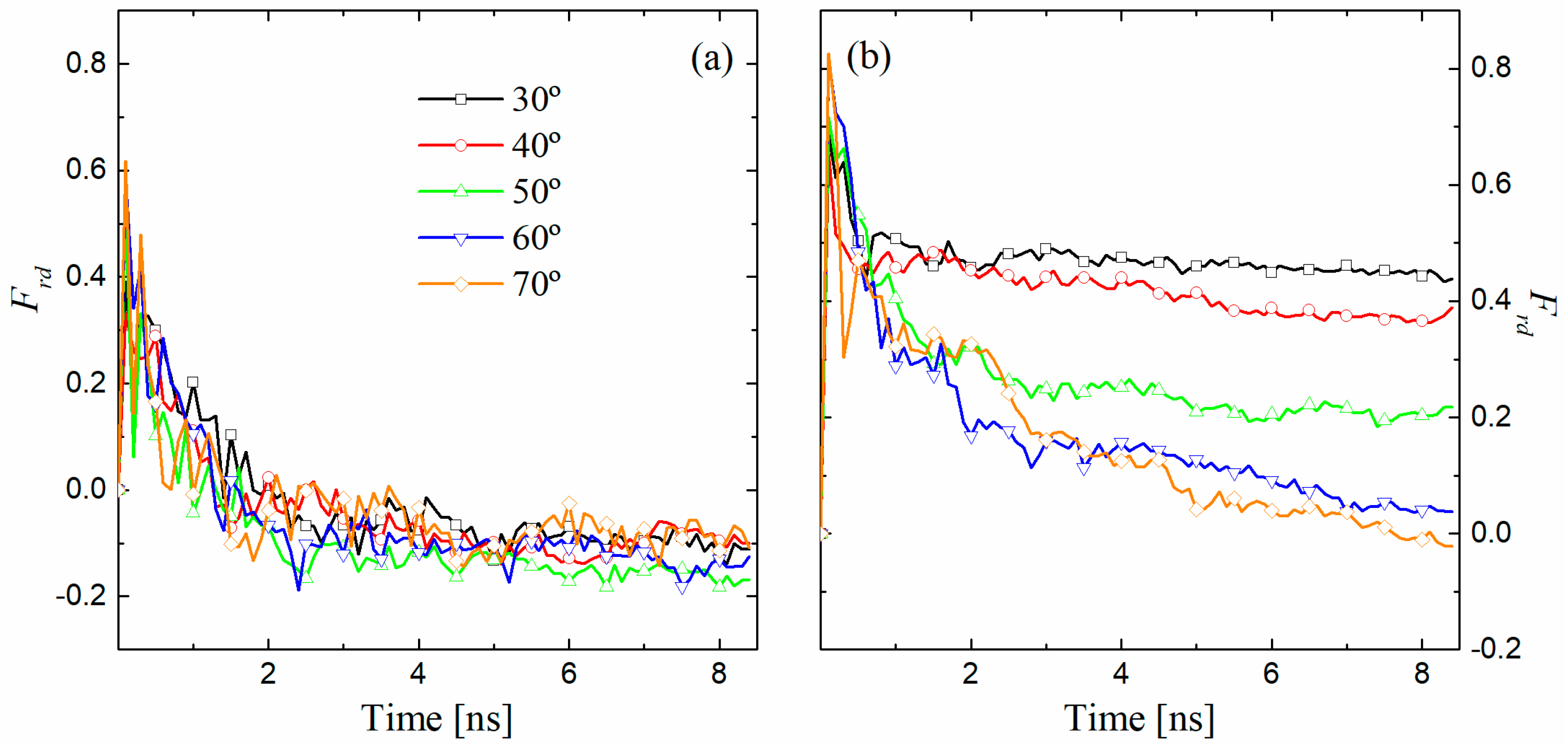
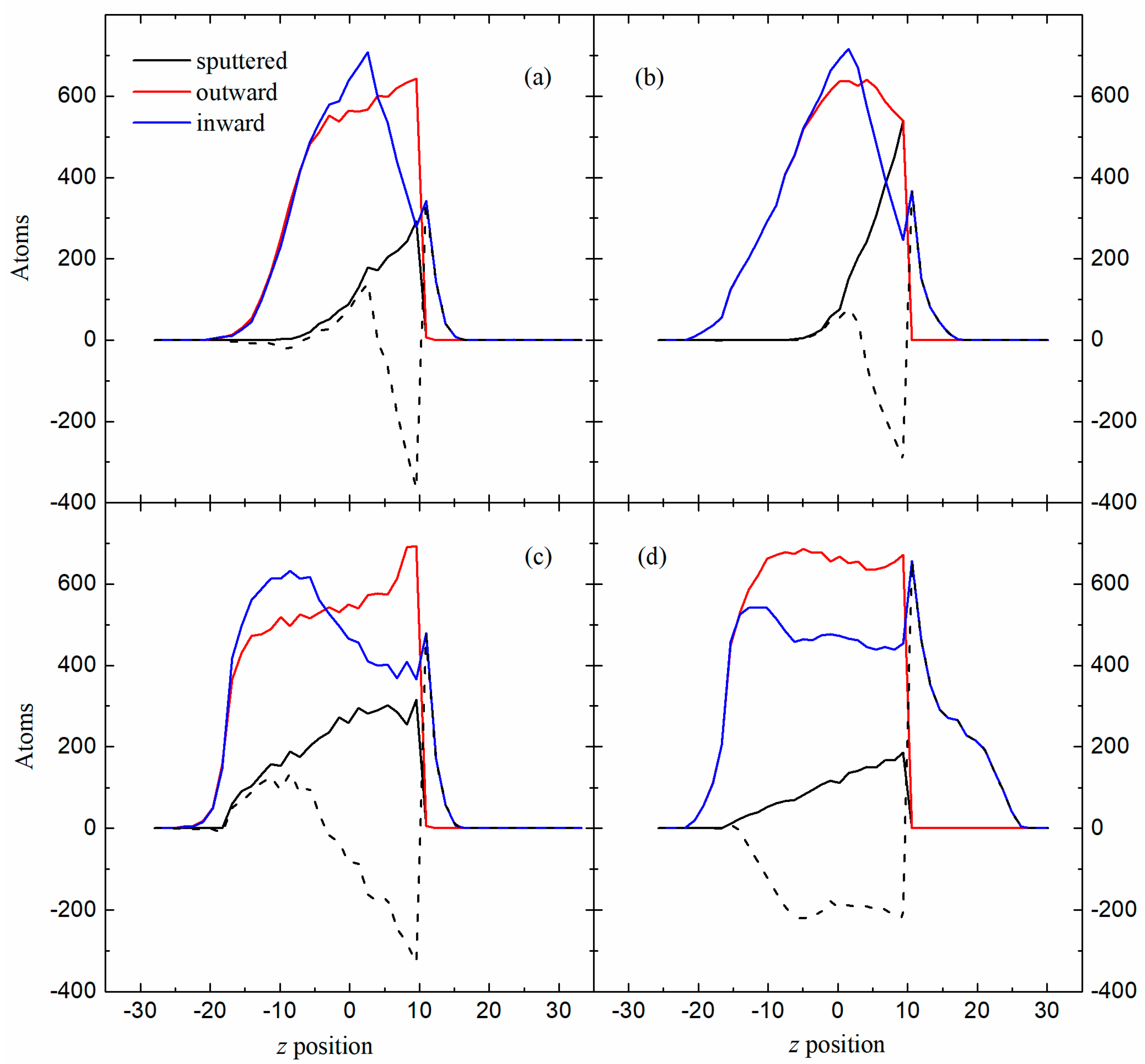
3.3. Volume Exchange
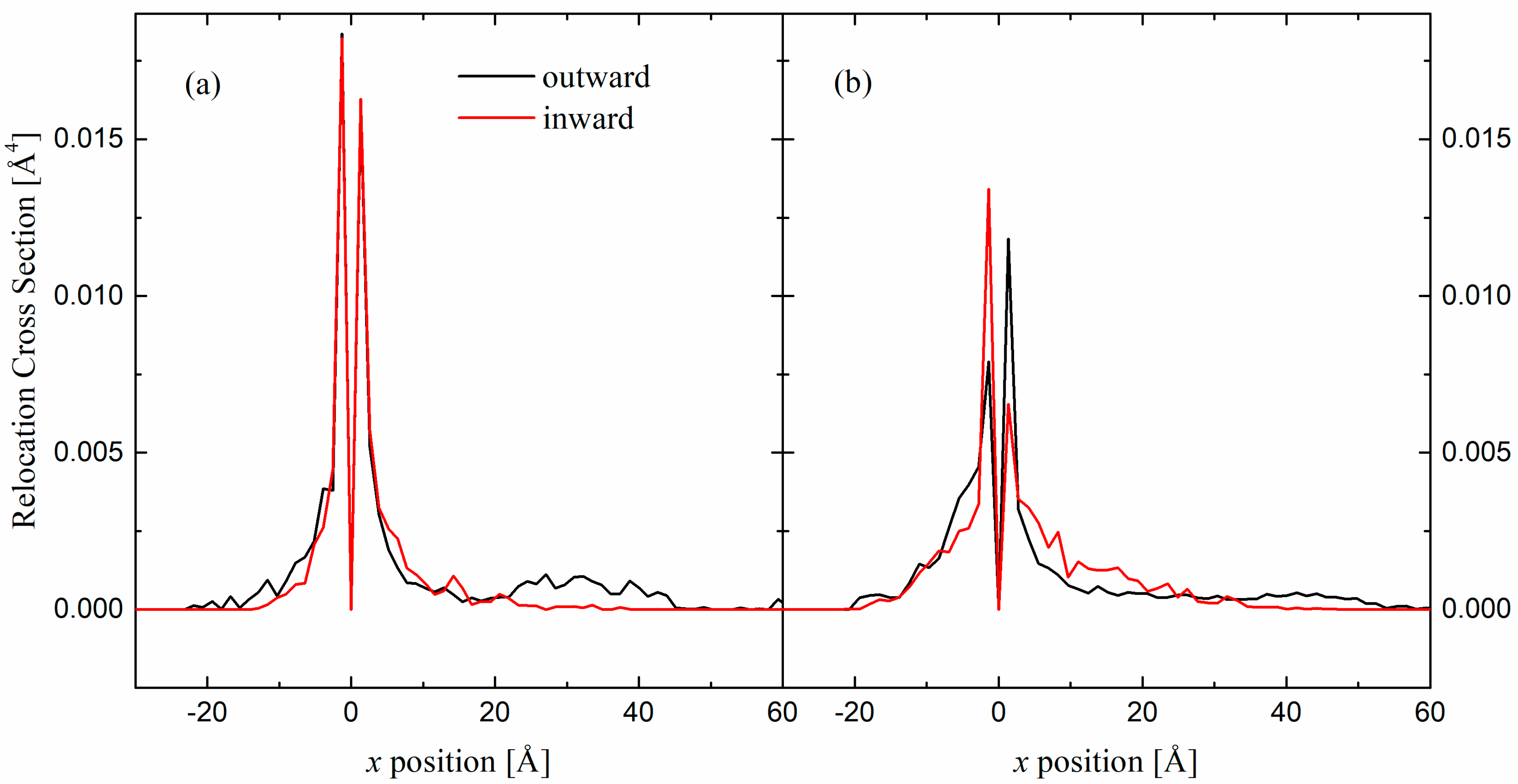
3.4. Relocation Cross-Sections
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.; Ha, N.; Kim, J.; Joe, M.; Lee, K.; Cuerno, R. One-dimensional pattern of Au nanodots by ion-beam sputtering: Formation and mechanism. Nanotechnology 2011, 22, 285301. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, L.; Redondo-Cubero, A.; Lorenz, K.; Palomares, F.J.; Cuerno, R. Surface nanopatterning by ion beam irradiation: Compositional effects. J. Phys. Condens. Matter 2022, 34, 333002. [Google Scholar] [CrossRef]
- Bharathi, M.S.; Ramanarayan, H.; Zhang, Y.W. Pattern formation and nonlinear evolution in alloy surfaces by ion-beam sputtering. Appl. Phys. Lett. 2011, 99, 083103. [Google Scholar] [CrossRef]
- Bradley, R.M.; Harper, J.M.E. Theory of ripple topography induced by ion bombardment. J. Vac. Sci. Technol. A 1988, 6, 2390. [Google Scholar] [CrossRef]
- Cuerno, R.; Barabasi, A.L. Dynamic scaling of ion-sputtered surfaces. Phys. Rev. Lett. 1995, 74, 4746. [Google Scholar] [CrossRef]
- Chason, E.; Aziz, M.J. Spontaneous formation of patterns on sputtered surfaces. Scr. Mater. 2003, 49, 953–959. [Google Scholar] [CrossRef]
- Carter, G.; Vishnyakov, V. Roughening and ripple instabilities on ion-bombarded Si. Phys. Rev. B 1996, 54, 17647. [Google Scholar] [CrossRef] [PubMed]
- Norris, S.A.; Samela, J.; Bukonte, L.; Backman, M.; Djurabekova, F.; Nordlund, K.; Madi, C.S.; Brenner, M.P.; Aziz, M.J. Molecular dynamics of single-particle impacts predicts phase diagrams for large scale pattern formation. Nat. Commun. 2011, 2, 276. [Google Scholar] [CrossRef]
- Lopez-Cazalilla, A.; Ilinov, A.; Nordlund, K.; Chowdhury, D.; Bhattacharyya, S.R.; Ghose, D.; Mondal, S.; Barman, P.; Djurabekova, F.; Norris, S. Pattern formation on ion-irradiated Si surface at energies where sputtering is negligible. J. Appl. Phys. 2018, 123, 235108S. [Google Scholar] [CrossRef]
- Norris, S.A.; Brenner, M.P.; Aziz, M.J. From crater functions to partial differential equations: A new approach to ion bombardment induced nonequilibrium pattern formation. J. Phys. Condens. Matter 2009, 21, 224017. [Google Scholar] [CrossRef]
- Umbach, C.C.; Headrick, R.; Chang, K.C. Spontaneous nanoscale corrugation of ion-eroded SiO2: The role of ion-irradiation-enhanced viscous flow. Phys. Rev. Lett. 2001, 87, 246104. [Google Scholar] [CrossRef] [PubMed]
- Norris, S.A. Stress-induced patterns in ion-irradiated silicon: Model based on anisotropic plastic flow. Phys. Rev. B 2012, 86, 235405. [Google Scholar] [CrossRef]
- Bradley, R.M.; Hofsäss, H. Nanoscale patterns produced by self-sputtering of solid surfaces: The effect of ion implantation. J. Appl. Phys. 2016, 120, 074302. [Google Scholar] [CrossRef]
- Shenoy, V.; Chan, W.; Chason, E. Compositionally modulated ripples induced by sputtering of alloy surfaces. Phys. Rev. Lett. 2007, 98, 256101. [Google Scholar] [CrossRef]
- Bradley, R.M.; Shipman, P.D. Spontaneous pattern formation induced by ion bombardment of binary compounds. Phys. Rev. Lett. 2010, 105, 145501. [Google Scholar] [CrossRef] [PubMed]
- Facsko, S.; Dekorsy, T.; Koerdt, C.; Trappe, C.; Kurz, H.; Vogt, A.; Hartnagel, H.L. Formation of ordered nanoscale semiconductor dots by ion sputtering. Science 1999, 285, 1551–1553. [Google Scholar] [CrossRef]
- Bradley, R.M.; Shipman, P. A surface layer of altered composition can play a key role in nanoscale pattern formation induced by ion bombardment. Appl. Surf. Sci. 2012, 258, 4161–4170. [Google Scholar] [CrossRef]
- Zhou, Z.; Cui, J.; Hou, Q. Role of mass redistribution on nanoripple formation and propagation: A molecular dynamics simulation study. Appl. Surf. Sci. 2022, 585, 152630. [Google Scholar] [CrossRef]
- Lopez-Cazalilla, A.; Nordlund, K.; Djurabekova, F. Formation of parallel and perpendicular ripples on solid amorphous surfaces by ion beam-driven atomic flow on and under the surface. Phys. Rev. Mater. 2023, 7, 036002. [Google Scholar] [CrossRef]
- Jiménez-Sáez, J.C.; Muñoz, S.; Palacios, P. Nanoscale pattern formation on surfaces by cluster ion beam irradiation. Phys. Scr. 2024, 99, 085984. [Google Scholar] [CrossRef]
- Jiménez-Sáez, J.C.; Muñoz, S.; Palacios, P. Cluster ion beam irradiation at low energy and surface pattern formation. Nucl. Instrum. Methods Phys. Res. B 2025, 563, 165707. [Google Scholar] [CrossRef]
- Cuerno, R.; Kim, J.-S. A perspective on nanoscale pattern formation at surfaces by ion-beam irradiation. J. Appl. Phys. 2020, 128, 180902. [Google Scholar] [CrossRef]
- Okamoto, H.; Chakrabarti, D.J.; Laughlin, D.E.; Massalski, T.B. The Au-Cu (gold-copper) system. Bull. Alloy Phase Diagr. 1987, 8, 454–473. [Google Scholar] [CrossRef]
- Adelman, S.A.; Doll, J.D. Generalized Langevin equation approach for atom/solid-surface scattering: General formulation for classical scattering off harmonic solids. J. Chem. Phys. 1976, 64, 2375–2388. [Google Scholar] [CrossRef]
- Ackland, G.J.; Vitek, V. Many-body potentials and atomic-scale relaxations in noble-metal alloys. Phys. Rev. B 1990, 41, 10324–10333. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Bernardes, N. Theory of solid Ne, A, Kr, and Xe at 0 K. Phys. Rev. 1958, 112, 1534–1539. [Google Scholar] [CrossRef]
- Lopez-Cazalilla, A.; Ilinov, A.; Nordlund, K.; Djurabekova, F. Modeling of high-fluence irradiation of amorphous Si and crystalline Al by linearly focused Ar ions. J. Phys. Condens. Matter 2019, 31, 075302. [Google Scholar] [CrossRef]
- Brink, T.; Sopu, D.; Albe, K. Solid-state amorphization of Cu nanolayers embedded in a Cu64Zr36 glass. Phys. Rev. B 2015, 91, 184103. [Google Scholar] [CrossRef]
- Cleveland, C.L.; Luedtke, W.D.; Landman, U. Melting of gold clusters. Phys. Rev. B 1999, 60, 5065–5077. [Google Scholar] [CrossRef]
- Kreth, M.; Entel, P.; Kadau, K.; Meyer, R. Molecular-dynamics study of the local symmetry changes in metallic liquids. Phase Transit. 2004, 77, 89–100. [Google Scholar] [CrossRef]
- Bailey, N.P.; Schiotz, J.; Jacobsen, K.W. Simulation of Cu-Mg metallic glass: Thermodynamics and structure. Phys. Rev. B 2004, 69, 144205. [Google Scholar] [CrossRef]
- Lively, M.A.; Holybee, B.; Toriyama, M.; Facsko, S.; Allain, J.P. Nonlinear compositional and morphological evolution of ion irradiated GaSb prior to nanostructure formation. Sci. Rep. 2020, 10, 8253. [Google Scholar] [CrossRef]
- Jiménez-Rodríguez, J.J.; Pérez-Martín, A.M.C.; Peinador, J.A. Calculation of the ballistic relocation cross-sections. Nucl. Instrum. Methods B 1992, 67, 504–508. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-Sáez, J.C.; Muñoz, S.; Palacios, P. Pattern Formation on Alloys by Cluster Ion Beam Irradiation. Appl. Sci. 2025, 15, 4615. https://doi.org/10.3390/app15094615
Jiménez-Sáez JC, Muñoz S, Palacios P. Pattern Formation on Alloys by Cluster Ion Beam Irradiation. Applied Sciences. 2025; 15(9):4615. https://doi.org/10.3390/app15094615
Chicago/Turabian StyleJiménez-Sáez, José C., Sagrario Muñoz, and Pablo Palacios. 2025. "Pattern Formation on Alloys by Cluster Ion Beam Irradiation" Applied Sciences 15, no. 9: 4615. https://doi.org/10.3390/app15094615
APA StyleJiménez-Sáez, J. C., Muñoz, S., & Palacios, P. (2025). Pattern Formation on Alloys by Cluster Ion Beam Irradiation. Applied Sciences, 15(9), 4615. https://doi.org/10.3390/app15094615





