Recovery Motion Analysis for False Ceiling Inspection Robot
Abstract
1. Introduction
2. Background
2.1. Problems Encountered During Indoor False Ceiling Maintenance
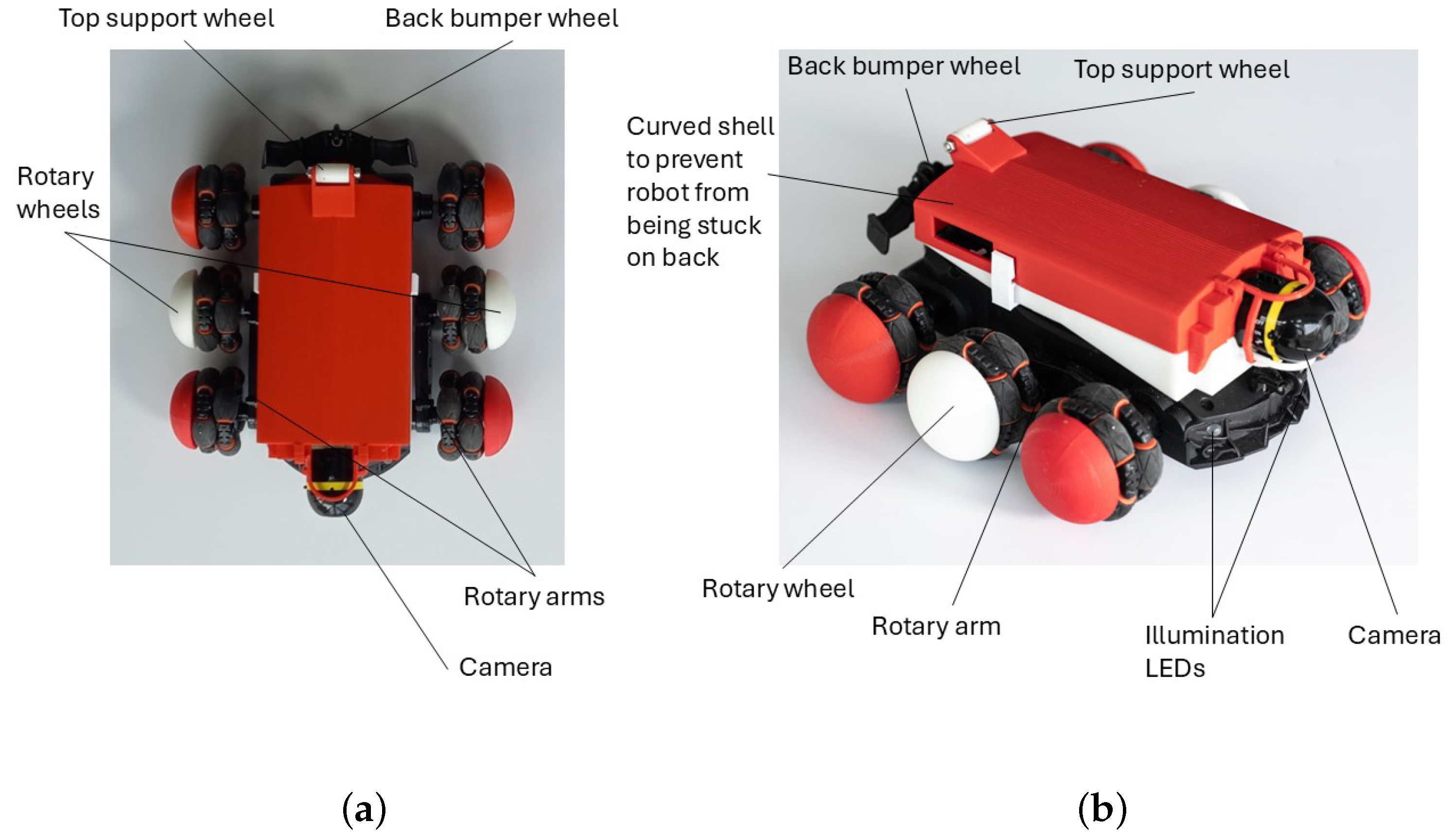
2.2. Using Mobile Robotic Solutions for False Ceiling Inspection
3. Materials and Methods
3.1. Mathematical Formulation: Jump-Start Motion
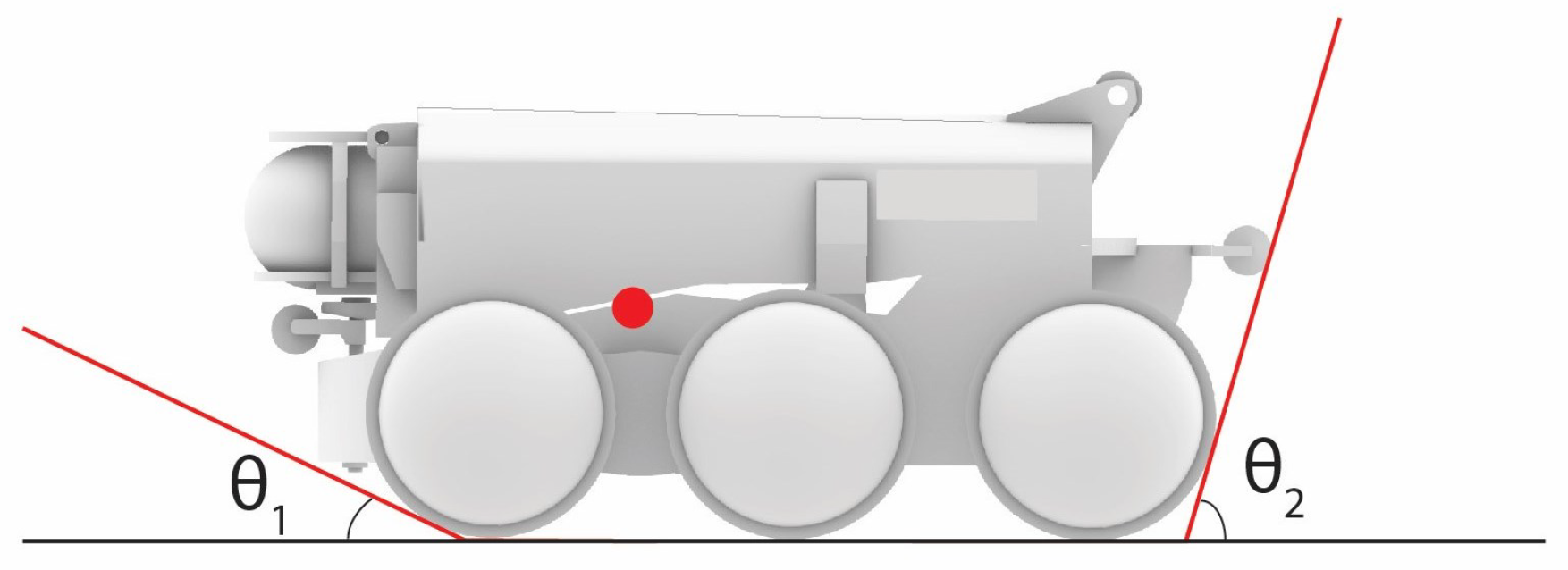
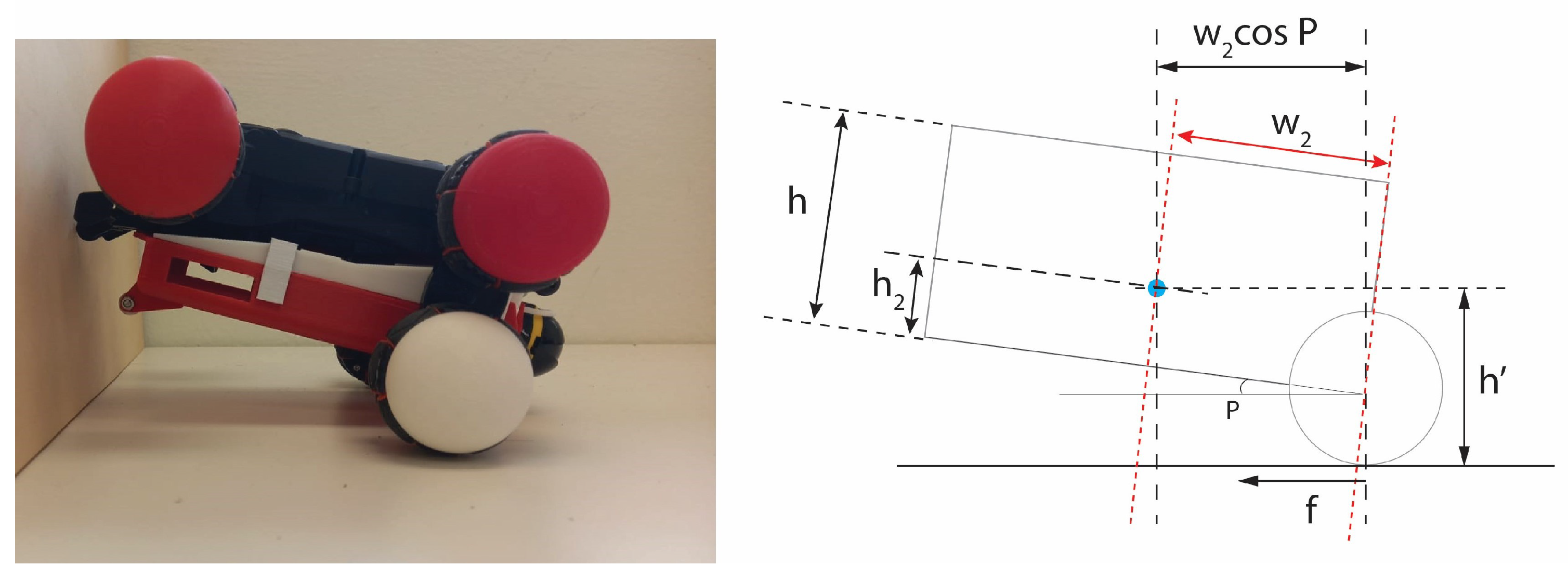
3.2. Mathematical Formulation: Self-Righting
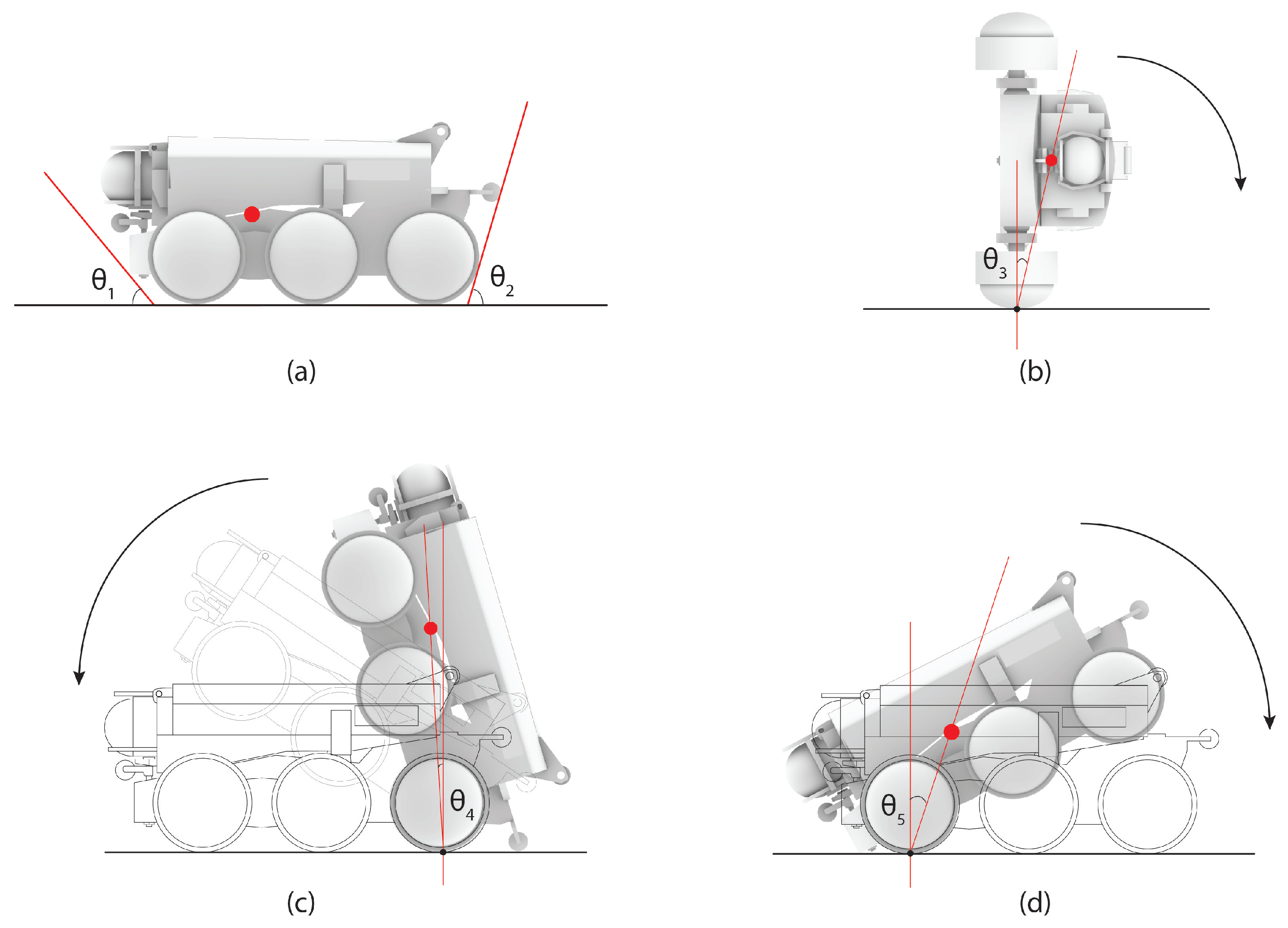
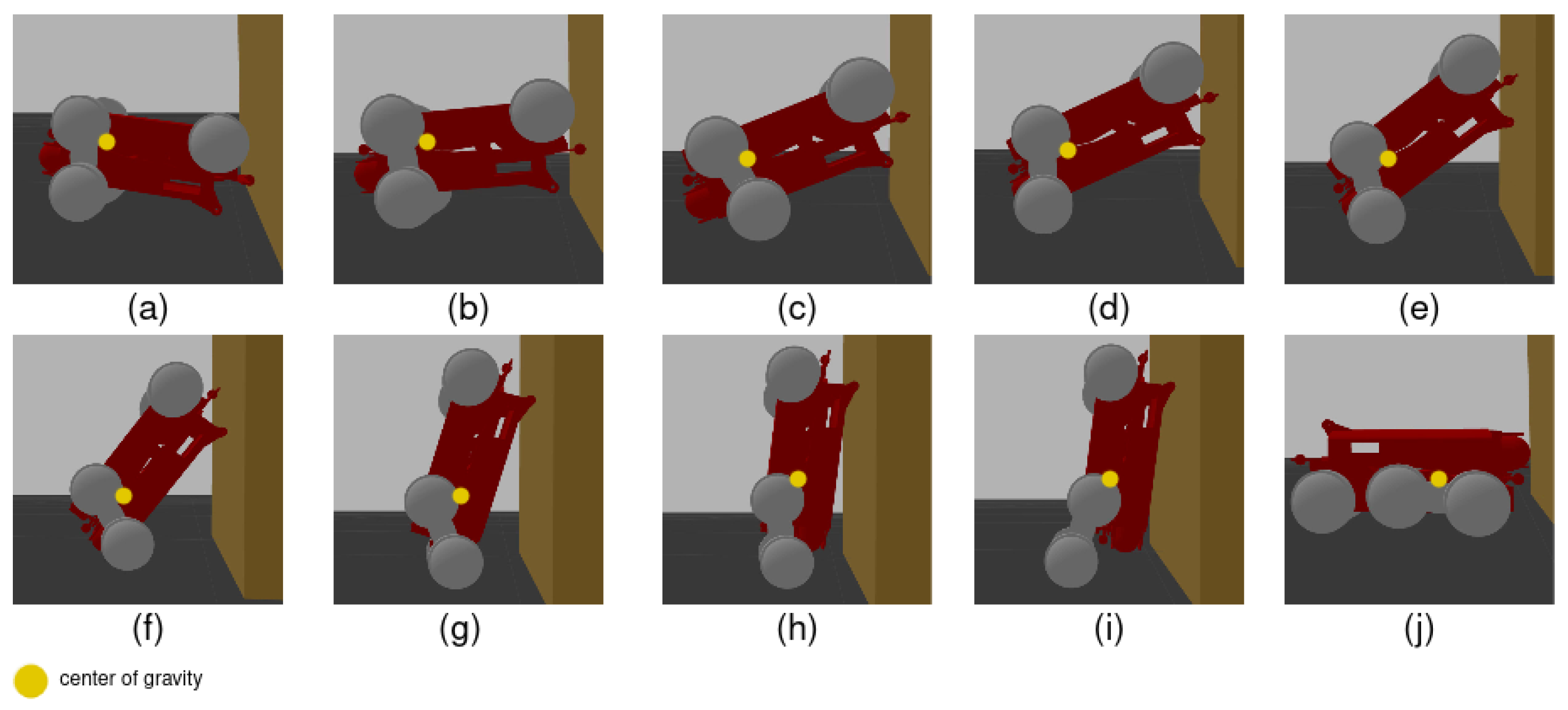
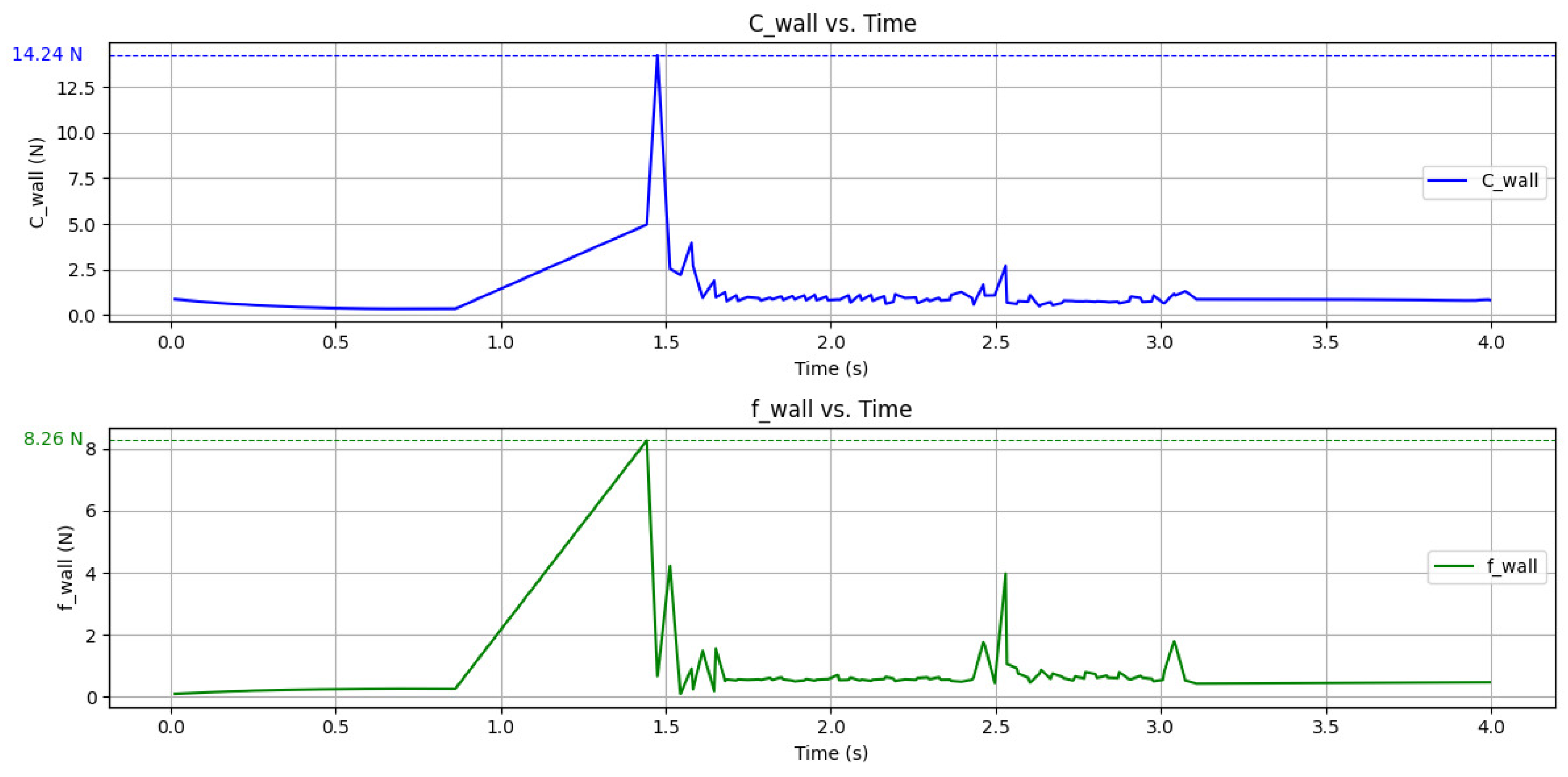
4. Results
- 1.
- Flipped onto side
- 2.
- Flipped onto back edge
- 3.
- Flipped onto front edge
- 4.
- Flipped upside down
4.1. Scenarios Where Robot Falls onto Its Side
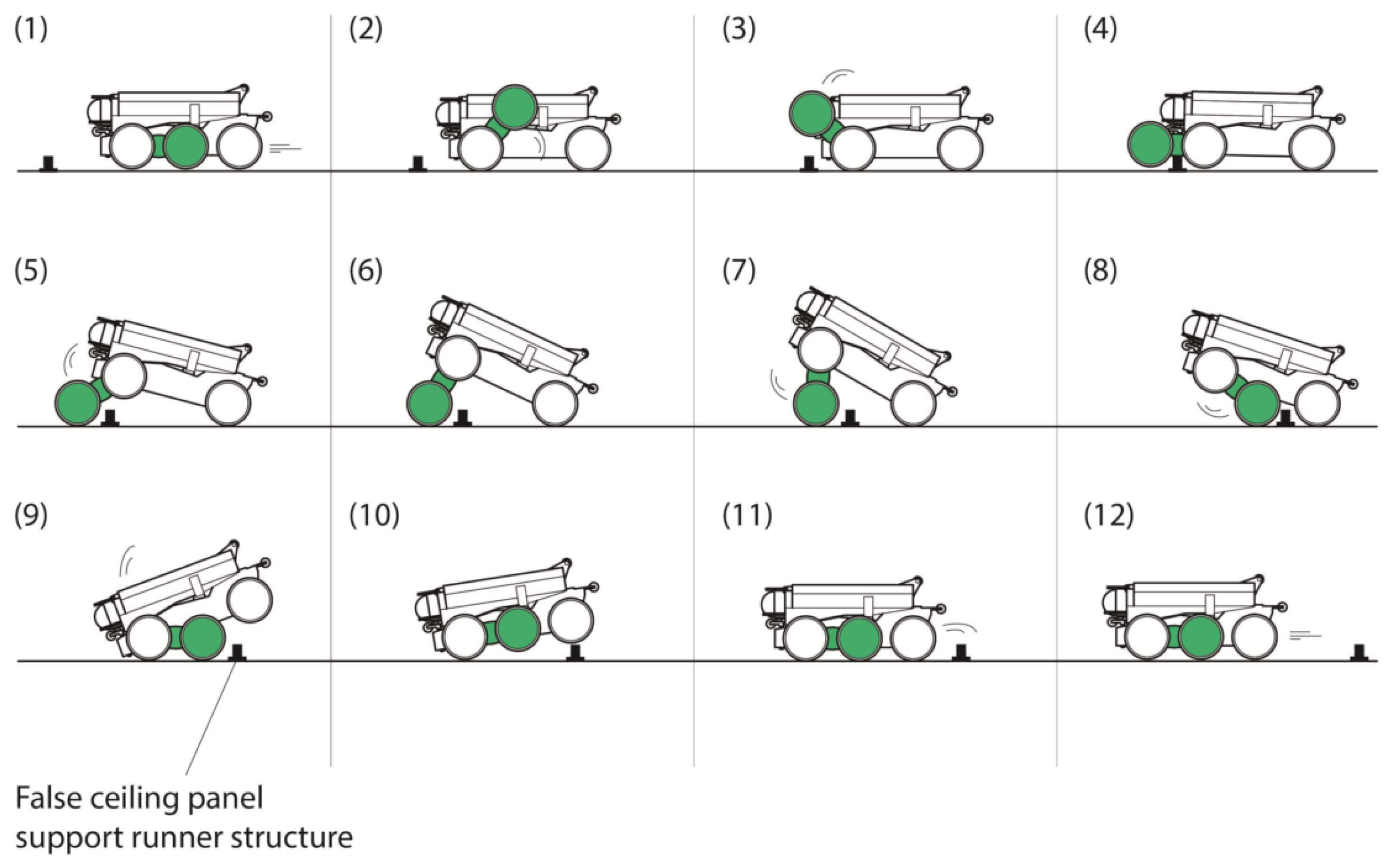
4.2. Scenarios Where Robot Falls onto Its Back Edge
4.3. Scenarios Where Robot Falls onto Its Front Edge
4.4. Scenarios Where Robot Is Flipped Upside Down
4.5. Summary
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sullivan, C.; Horwitz-Bennett, B. Ceiling Designs. 2021. Available online: https://www.bdcuniversity.com/sites/sgc-university/files/AIA_BDC0213.pdf (accessed on 20 January 2025).
- Cha, S.H.; Koo, C.; Kim, T.W.; Hong, T. Spatial perception of ceiling height and type variation in immersive virtual environments. Build. Environ. 2019, 163, 106285. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Zhang, J.P.; Yu, F.Q.; Tian, P.L.; Xiang, X.S. Construction and facility management of large MEP projects using a multi-Scale building information model. Adv. Eng. Softw. 2016, 100, 215–230. [Google Scholar] [CrossRef]
- Beddu, S.; Zainoodin, M.M.; Muda, Z.C.; Kamal, N.L.M.; Mohamad, D.; Nazri, F.M.; Naganathan, S.; Husain, N.M.; Sadon, S.N. Investigation of Natural Fibers as Ceiling Material. In Proceedings of the AWAM International Conference on Civil Engineering, Penang, Malaysia, 21–22 August 2019; pp. 1239–1244. [Google Scholar]
- Michael, M.; Sankar, V.; Paul, A.; Joy, A.; Fainusa, V.; Raju, C.I. Comparative study on the effect of false ceiling materials on the room temperature. In Green Buildings and Sustainable Engineering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 179–187. [Google Scholar]
- Kruger, K. The Effect of Various Parameters on the Sound Isolation between Offices with Suspended Ceilings. Can. Acoust. 1988, 16, 9. [Google Scholar]
- Manglani, P.; Dee, R.; McHugh, J.; Heschong, L. Best Practices for Designing Modular Skylight Systems with Suspended Ceilings. PIER Integrated Ceilings Project. 2003. Available online: https://www.aceee.org/files/proceedings/2004/data/papers/SS04_Panel3_Paper18.pdf (accessed on 20 January 2025).
- Tan, C.Y. Advisory on Good Practices for the Inspection and Maintenance of Suspended Ceilings. 2021. Available online: https://www1.bca.gov.sg/docs/default-source/docs-corp-news-and-publications/circulars/good-practices-for-the-inspection-and-maintenance-of-suspended-ceilings.pdf (accessed on 22 January 2025).
- Min, J.; Kim, Y.; Lee, S.; Jang, T.W.; Kim, I.; Song, J. The fourth industrial revolution and its impact on occupational health and safety, worker’s compensation and labor conditions. Saf. Health Work 2019, 10, 400–408. [Google Scholar] [CrossRef]
- Koh, K.H.; Farhan, M.; Yeung, K.P.C.; Tang, D.C.H.; Lau, M.P.Y.; Cheung, P.K.; Lai, K.W.C. Teleoperated service robotic system for on-site surface rust removal and protection of high-rise exterior gas pipes. Autom. Constr. 2021, 125, 103609. [Google Scholar] [CrossRef]
- Agnisarman, S.; Lopes, S.; Madathil, K.C.; Piratla, K.; Gramopadhye, A. A survey of automation-enabled human-in-the-loop systems for infrastructure visual inspection. Autom. Constr. 2019, 97, 52–76. [Google Scholar] [CrossRef]
- Nitta, Y.; Inai, S.; Matsumura, K.; Ishida, M.; Onai, T.; Nishitani, A. The visual inspection methodology for ceiling utilizing the blimp. Procedia Eng. 2017, 188, 256–262. [Google Scholar] [CrossRef]
- Ko, H.; Yi, H.; Jeong, H.E. Wall and ceiling climbing quadruped robot with superior water repellency manufactured using 3D printing (UNIclimb). Int. J. Precis. Eng. Manuf.-Green Technol. 2017, 4, 273–280. [Google Scholar] [CrossRef]
- Zhang, Y.; Dodd, T.; Atallah, K.; Lyne, I. Design and optimization of magnetic wheel for wall and ceiling climbing robot. In Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation, Singapore, 28–30 June 2010; pp. 1393–1398. [Google Scholar]
- Selvakumaran, S.; Hayat, A.; Elangovan, K.; Manivannan, K.; Elara, M. Design of a Self-reconfigurable Robot with Roll, Crawl, and Climb Features for False Ceiling Inspection Task. In Robotics, Control and Computer Vision: Select Proceedings of ICRCCV 2022; Springer: Berlin/Heidelberg, Germany, 2023; pp. 467–477. [Google Scholar]
- Kessens, C.C.; Smith, D.C.; Osteen, P.R. A framework for autonomous self-righting of a generic robot on sloped planar surfaces. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 4724–4729. [Google Scholar]
- Johnson, A.M.; Libby, T.; Chang-Siu, E.; Tomizuka, M.; Full, R.J.; Koditschek, D.E. Tail assisted dynamic self righting. In Adaptive Mobile Robotics; World Scientific: Singapore, 2012; pp. 611–620. [Google Scholar]
- Casarez, C.S.; Fearing, R.S. Dynamic terrestrial self-righting with a minimal tail. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 314–321. [Google Scholar]
- Chen, K.; Chen, D.; Zhang, Z.; Wang, M. Jumping robot with initial body posture adjustment and a self-righting mechanism. Int. J. Adv. Robot. Syst. 2016, 13, 127. [Google Scholar] [CrossRef]
- Zhang, J.; Song, G.; Li, Z.; Qiao, G.; Sun, H.; Song, A. Self-righting, steering and takeoff angle adjusting for a jumping robot. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2089–2094. [Google Scholar]
- Jani, N.K. Study of False Ceiling Design and Execution Process; Research and Publications Department, National Institute of Construction Management and Research: Pune, India, 2019; p. 296. [Google Scholar]
- Yeo, M.S.K.; Samarakoon, S.M.B.P.; Ng, Q.B.; Ng, Y.J.; Muthugala, M.A.V.J.; Elara, M.R.; Yeong, R.W.W. Robot-Inclusive False Ceiling Design Guidelines. Buildings 2021, 11, 600. [Google Scholar] [CrossRef]
- Horodinca, M.; Doroftei, I.; Mignon, E.; Preumont, A. A simple architecture for in-pipe inspection robots. Proc. Int. Colloq. Mobile Auton. Syst. 2002, 61, 64. [Google Scholar]
- Kroll, A. A survey on mobile robots for industrial inspection. In Proceedings of the International Conference on Intelligent Autonomous Systems IAS10, Baden-Baden, Germany, 15 July 2008; pp. 406–414. [Google Scholar]
- Verma, A.; Kaiwart, A.; Dubey, N.D.; Naseer, F.; Pradhan, S. A review on various types of in-pipe inspection robot. Mater. Today Proc. 2022, 50, 1425–1434. [Google Scholar] [CrossRef]
- Halder, S.; Afsari, K. Robots in inspection and monitoring of buildings and infrastructure: A systematic review. Appl. Sci. 2023, 13, 2304. [Google Scholar] [CrossRef]
- Lattanzi, D.; Miller, G. Review of Robotic Infrastructure Inspection Systems. J. Infrastruct. Syst. 2017, 23, 04017004. [Google Scholar] [CrossRef]
- Ma, W.; Li, B.; Jiang, L.; Wu, Y.; Bai, R.; Chen, G. A Soft, Centimeter-Scaled, Thin-Cable-Crawling Robot for Narrow Space Inspection. Adv. Intell. Syst. 2024, 6, 2300828. [Google Scholar] [CrossRef]
- Cheah, W.; Groves, K.; Martin, H.; Peel, H.; Watson, S.; Marjanovic, O.; Lennox, B. MIRRAX: A reconfigurable robot for limited access environments. IEEE Trans. Robot. 2022, 39, 1341–1352. [Google Scholar] [CrossRef]
- Khan, M.B.; Chuthong, T.; Danh Do, C.; Thor, M.; Billeschou, P.; Larsen, J.C.; Manoonpong, P. iCrawl: An Inchworm-Inspired Crawling Robot. IEEE Access 2020, 8, 200655–200668. [Google Scholar] [CrossRef]
- Leggieri, S.; Canali, C.; Caldwell, D.G. Design, modeling, and experimental analysis of the Crawler Unit for inspection in constrained space. Annu. Rev. Control 2024, 57, 100950. [Google Scholar] [CrossRef]
- Ciszewski, M.; Giergiel, M.; Buratowski, T.; Małka, P. Modeling and Control of a Tracked Mobile Robot for Pipeline Inspection; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Koh, K.; Choi, H.; Kim, J.S.; Ko, K.W.; Cho, H. Sensor-based navigation of air duct inspection mobile robots. Optomechatronic Syst. 2001, 4190, 202–211. [Google Scholar]
- Filipek, P.; Kamiński, T. Remote controlled mobile inspection robot. J. KONES 2011, 18, 129–135. [Google Scholar]
- Ab Rashid, M.Z.; Mohd Yakub, M.F.; Zaki bin Shaikh Salim, S.A.; Mamat, N.; Syed Mohd Putra, S.M.; Roslan, S.A. Modeling of the in-pipe inspection robot: A comprehensive review. Ocean Eng. 2020, 203, 107206. [Google Scholar] [CrossRef]
- Parween, R.; Wen, T.Y.; Elara, M.R. Modelling and Analysis of a Vertical Wall Robot for Ceiling Inspection. In Proceedings of the 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC), Virtual, 26–29 January 2022; pp. 0679–0687. [Google Scholar]
- Scalise, R.; Caglar, E.; Boots, B.; Kessens, C.C. Toward Self-Righting and Recovery in the Wild: Challenges and Benchmarks. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 15329–15335. [Google Scholar]
- King, K.; Revzen, S. Self-Righting Shell for Robotic Hexapod. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 1436–1442. [Google Scholar]
- Teder, E.; Chong, B.; He, J.; Wang, T.; Iaschi, M.; Soto, D.; Goldman, D.I. Effective self-righting strategies for elongate multi-legged robots. arXiv 2024, arXiv:2410.01056. [Google Scholar]
- Li, C.; Kessens, C.C.; Young, A.; Fearing, R.S.; Full, R.J. Cockroach-inspired winged robot reveals principles of ground-based dynamic self-righting. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 2128–2134. [Google Scholar]
- Qian, J.; Cheng, W.; He, Y.; Su, J.; Zhang, Y. A novel mobile robot with a backbone for self up-righting capability. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2000) (Cat. No.00CH37113), Takamatsu, Japan, 31 October–5 November 2000; Volume 3, pp. 2224–2229. [Google Scholar]
- Muthugala, M.V.J.; Apuroop, K.G.S.; Padmanabha, S.G.A.; Samarakoon, S.B.P.; Elara, M.R.; Wen, R.Y.W. Falcon: A false ceiling inspection robot. Sensors 2021, 21, 5281. [Google Scholar] [CrossRef] [PubMed]
- Semwal, A.; Mohan, R.E.; Melvin, L.M.J.; Palanisamy, P.; Baskar, C.; Yi, L.; Pookkuttath, S.; Ramalingam, B. False ceiling deterioration detection and mapping using a deep learning framework and the teleoperated reconfigurable ‘Falcon’Robot. Sensors 2021, 22, 262. [Google Scholar] [CrossRef]
- Pathmakumar, T.; Sivanantham, V.; Anantha Padmanabha, S.G.; Elara, M.R.; Tun, T.T. Towards an optimal footprint based area coverage strategy for a false-ceiling inspection robot. Sensors 2021, 21, 5168. [Google Scholar] [CrossRef]
- Shanmugam, P. Reminder on Good Practices for Design and Installation of Suspended Ceiling Works. BCA. 2018. Available online: https://www1.bca.gov.sg/docs/default-source/docs-corp-news-and-publications/circulars/reminder-on-adoption-of-good-practices-for-design-and-installation-of-suspended-ceilings.pdf (accessed on 22 January 2025).



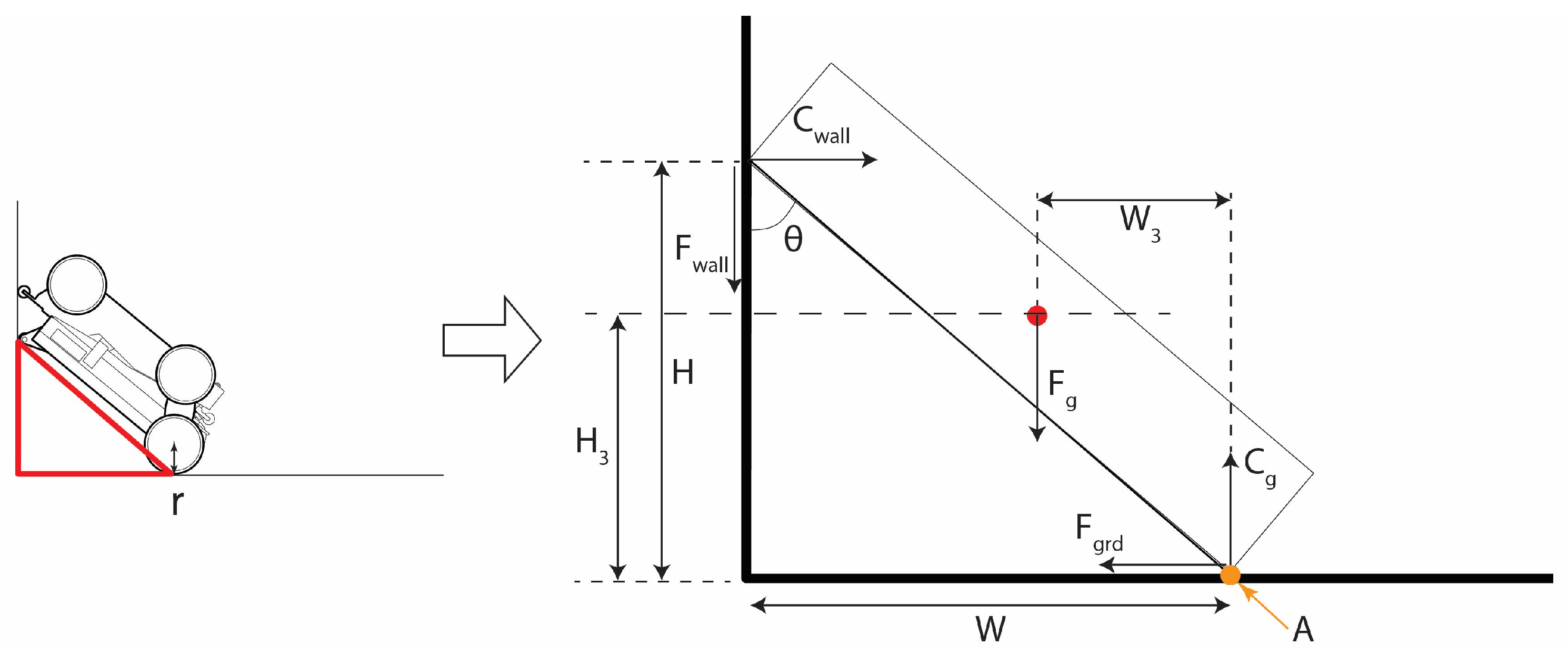


| Explanation | Formula | Calculation with Values |
|---|---|---|
| 1. Horizontal distance between contact point and CG | m | |
| 2. Vertical distance between contact point and CG | = 0.0592 m | |
| 3. Torque balance at contact point | T + mg w′ − f h′ = 0 | – |
| 4. Frictional torque relation | T = f r | – |
| 5. Solve for friction force f | ||
| 6. Final required torque | T = f r | 9.74 ∗ 0.025 = 0.2435 Nm |
| Component | Description |
|---|---|
| Robot model | FalconX robot (a URDF file) |
| Wall | A cube (1.0 × 1.0 × 1.0 m), mass = 10 kg |
| Static friction coefficient of the wall | 1.0 |
| Sliding friction coefficient of the wall | 0.8 |
| Physics engine | Open Dynamics Engine (ODE) |
| Scenario | Recovery Mechanism | Key Features |
|---|---|---|
| Falls onto its side | Rounded wheel caps allow rolling to back; rotary wheels and top support wheel form 3-point contact to let the robot flip upright using vertical surface. | , offset CG enables roll |
| Falls onto its back edge | Offset CG causes natural fall to neutral position; rotary wheels help in further motion or overcoming obstacles. | , offset CG helps recovery |
| Falls onto its front edge | Front bumper wheel stops forwards motion; the robot uses rotary wheels as leverage to reverse. | , uses reverse + rotary wheels |
| Flipped completely upside down | Curved top shell and low storage height allow rotary wheels to touch ground; robot moves to vertical surface, pivots and flips upright. | rotary wheel to support, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeo, M.S.K.; Yang, Z.; Samarakoon, S.M.B.P.; Mohan, R.E. Recovery Motion Analysis for False Ceiling Inspection Robot. Appl. Sci. 2025, 15, 4616. https://doi.org/10.3390/app15094616
Yeo MSK, Yang Z, Samarakoon SMBP, Mohan RE. Recovery Motion Analysis for False Ceiling Inspection Robot. Applied Sciences. 2025; 15(9):4616. https://doi.org/10.3390/app15094616
Chicago/Turabian StyleYeo, Matthew S. K., Zhenyuan Yang, S. M. Bhagya P. Samarakoon, and R. E. Mohan. 2025. "Recovery Motion Analysis for False Ceiling Inspection Robot" Applied Sciences 15, no. 9: 4616. https://doi.org/10.3390/app15094616
APA StyleYeo, M. S. K., Yang, Z., Samarakoon, S. M. B. P., & Mohan, R. E. (2025). Recovery Motion Analysis for False Ceiling Inspection Robot. Applied Sciences, 15(9), 4616. https://doi.org/10.3390/app15094616





