A Coupling Error Compensation Approach Concerning Constrained Space Coordinate Precision of a Heavy-Load Longitudinal and Transversal Swing Table
Abstract
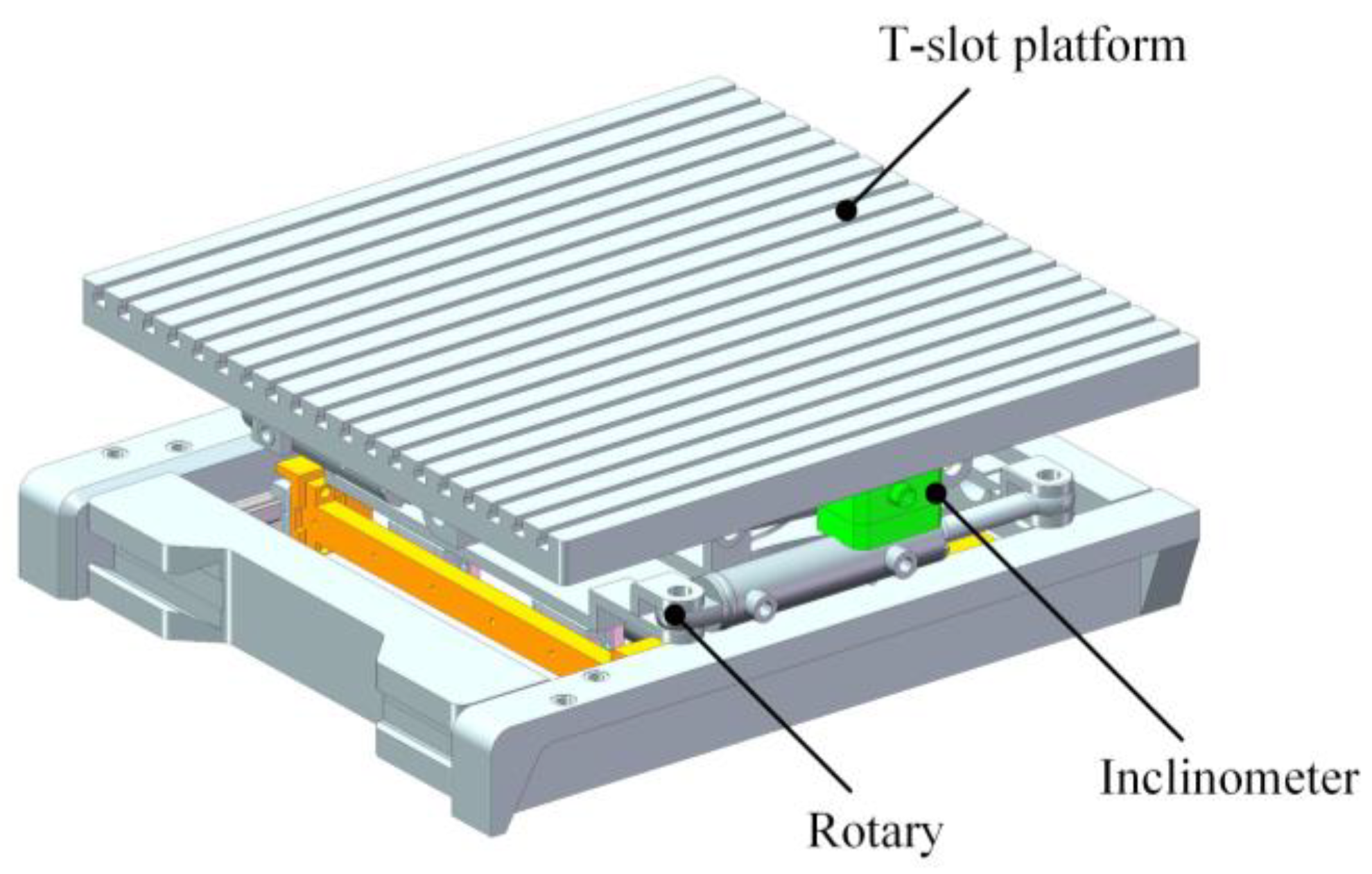
1. Introduction
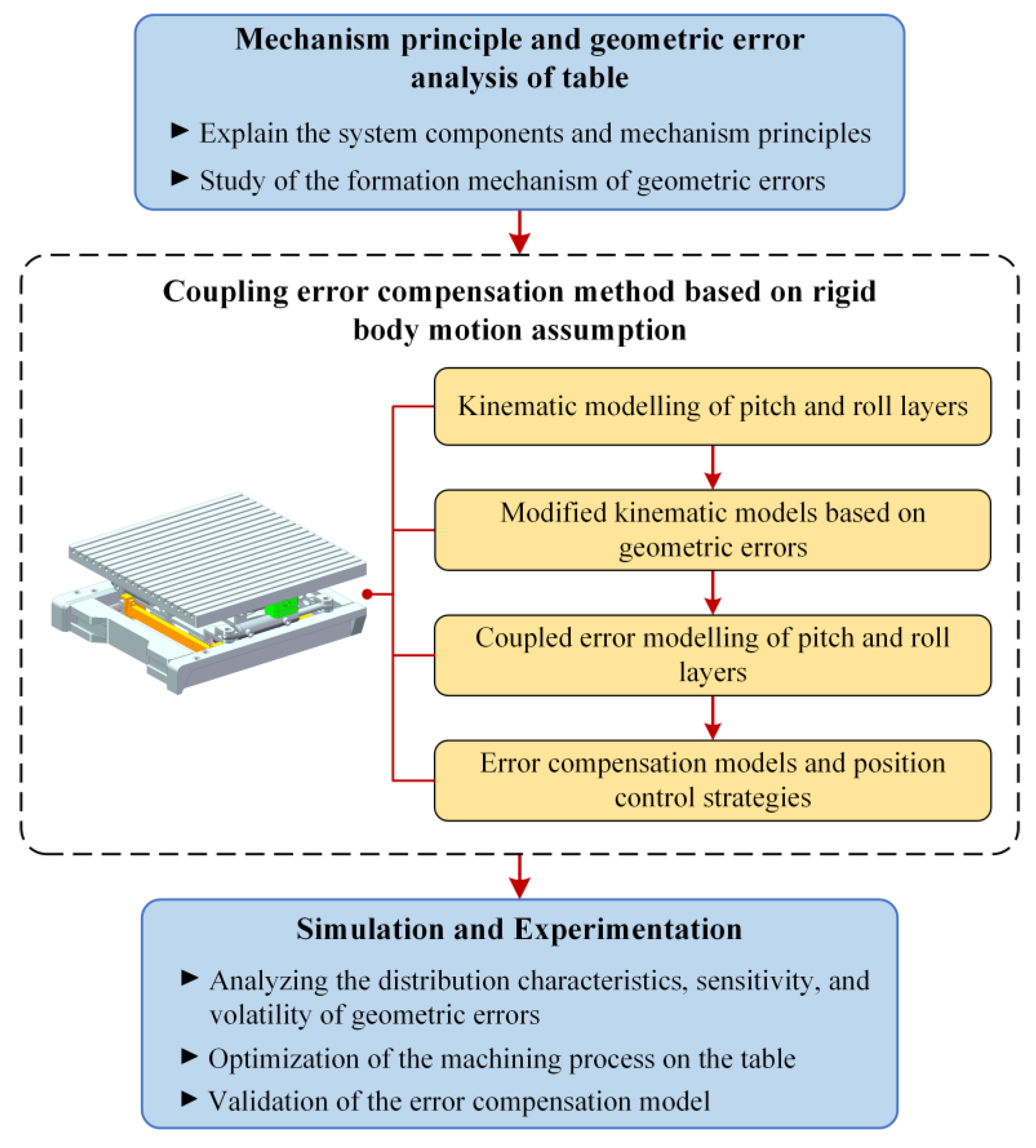
2. Theory and Method
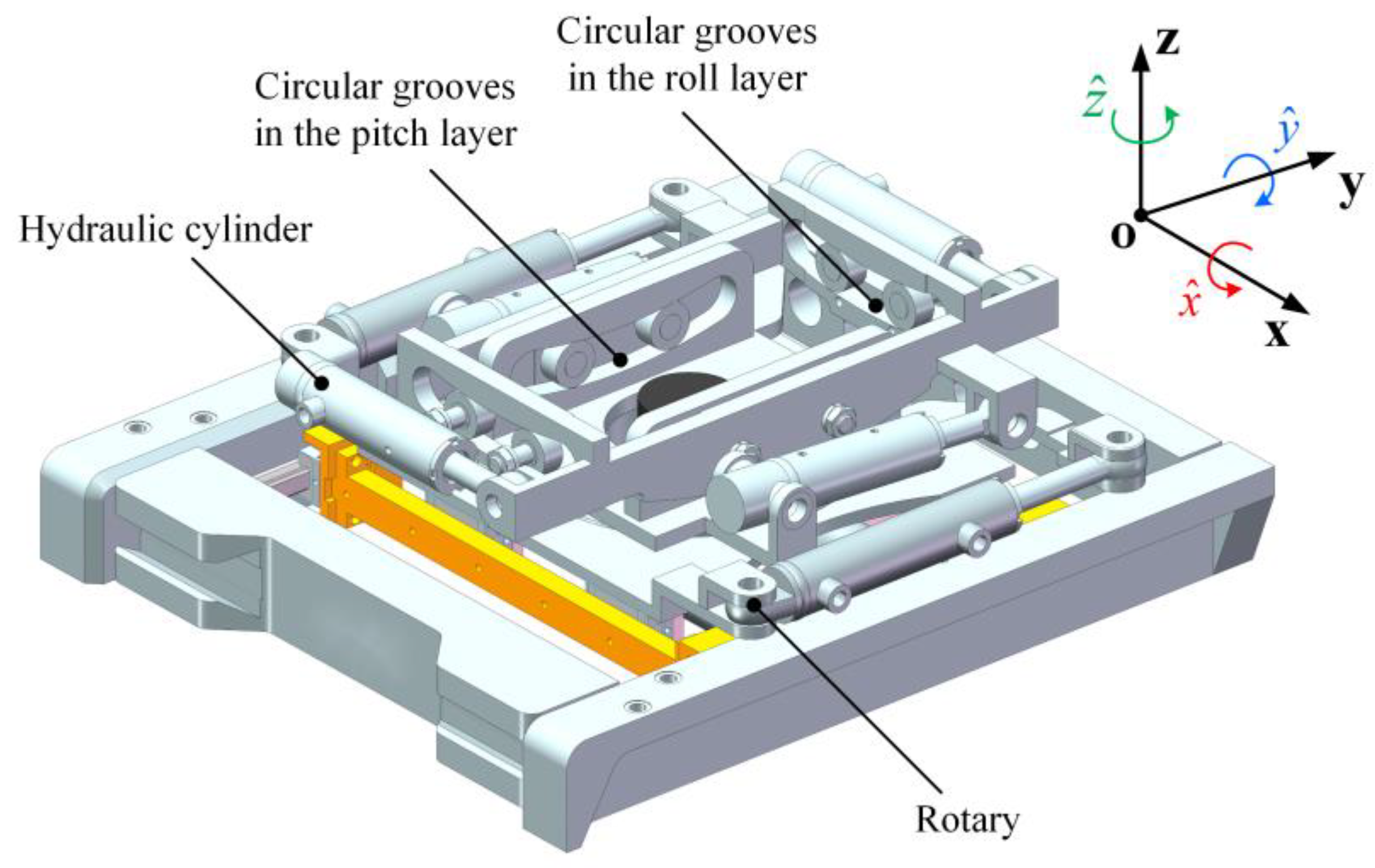
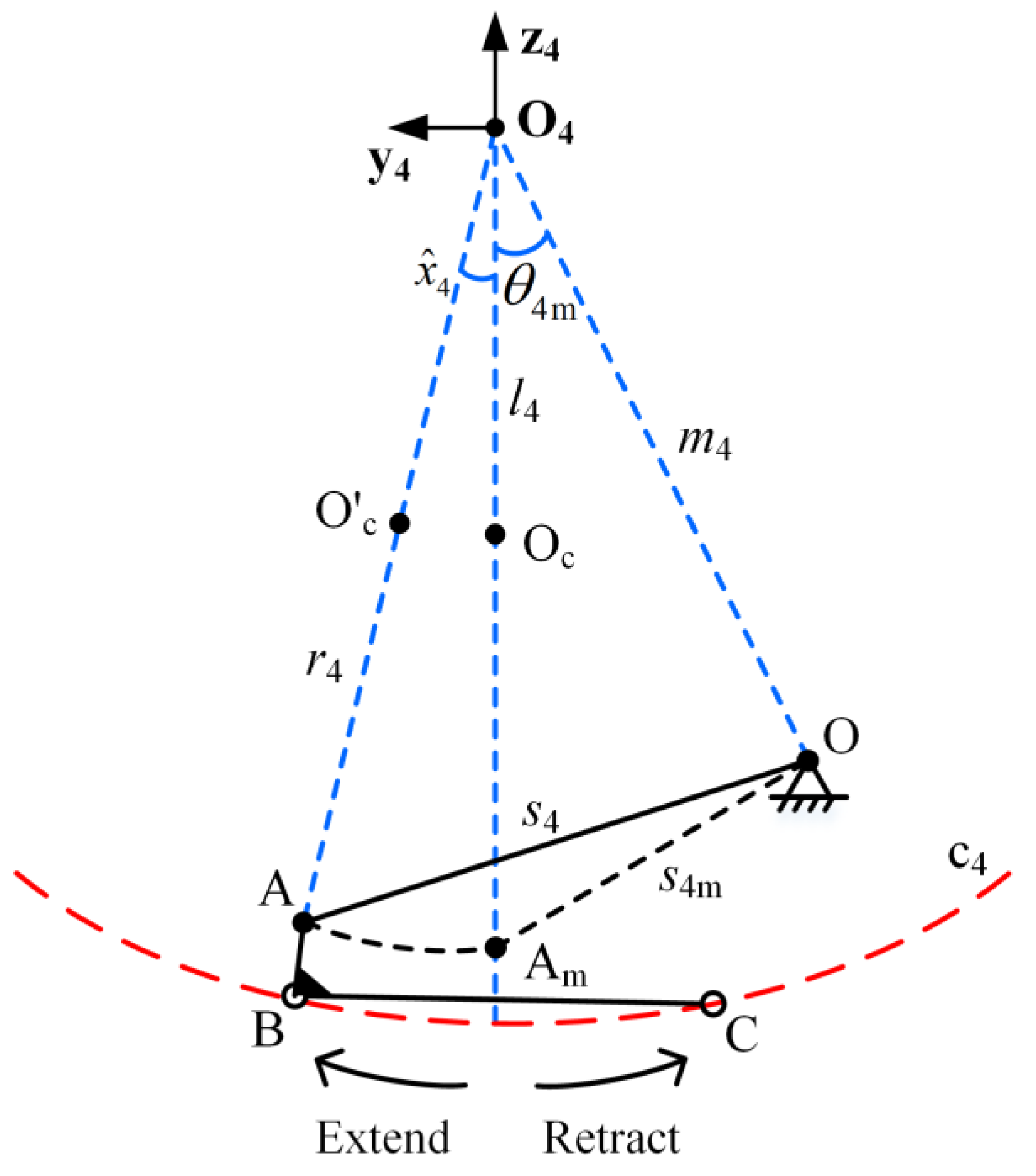
2.1. Kinematics Modelling
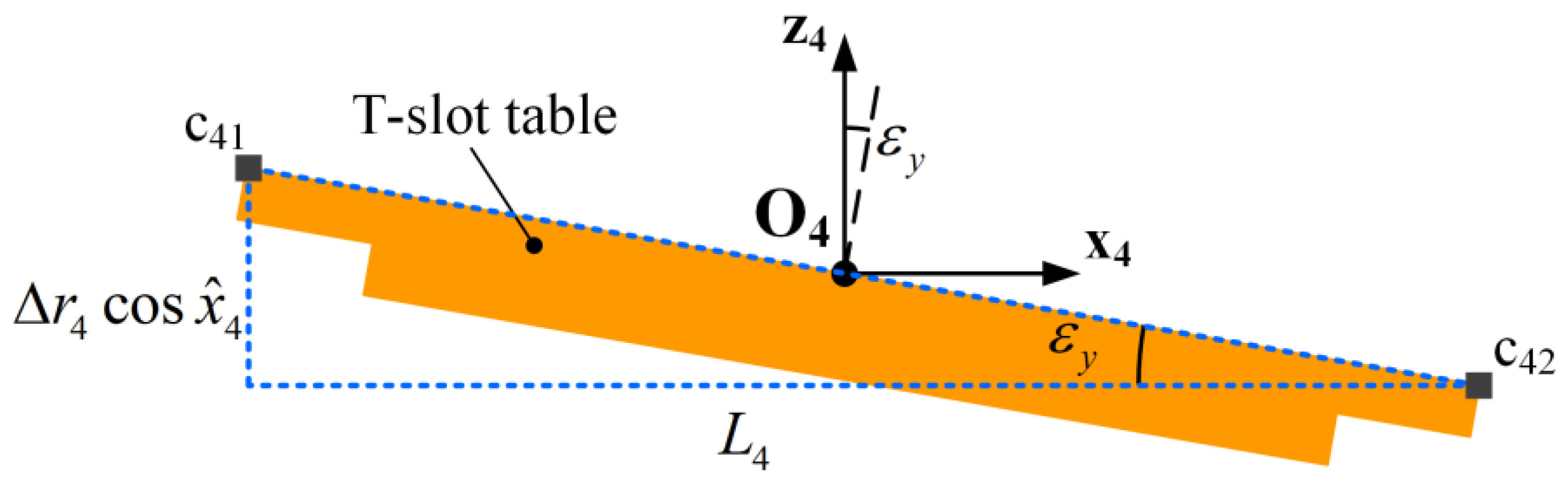
2.2. Correction of Geometric Parameters for Kinematic Models
2.3. Modelling of Coupling Errors
2.4. Error Compensation Model
3. Results and Analysis
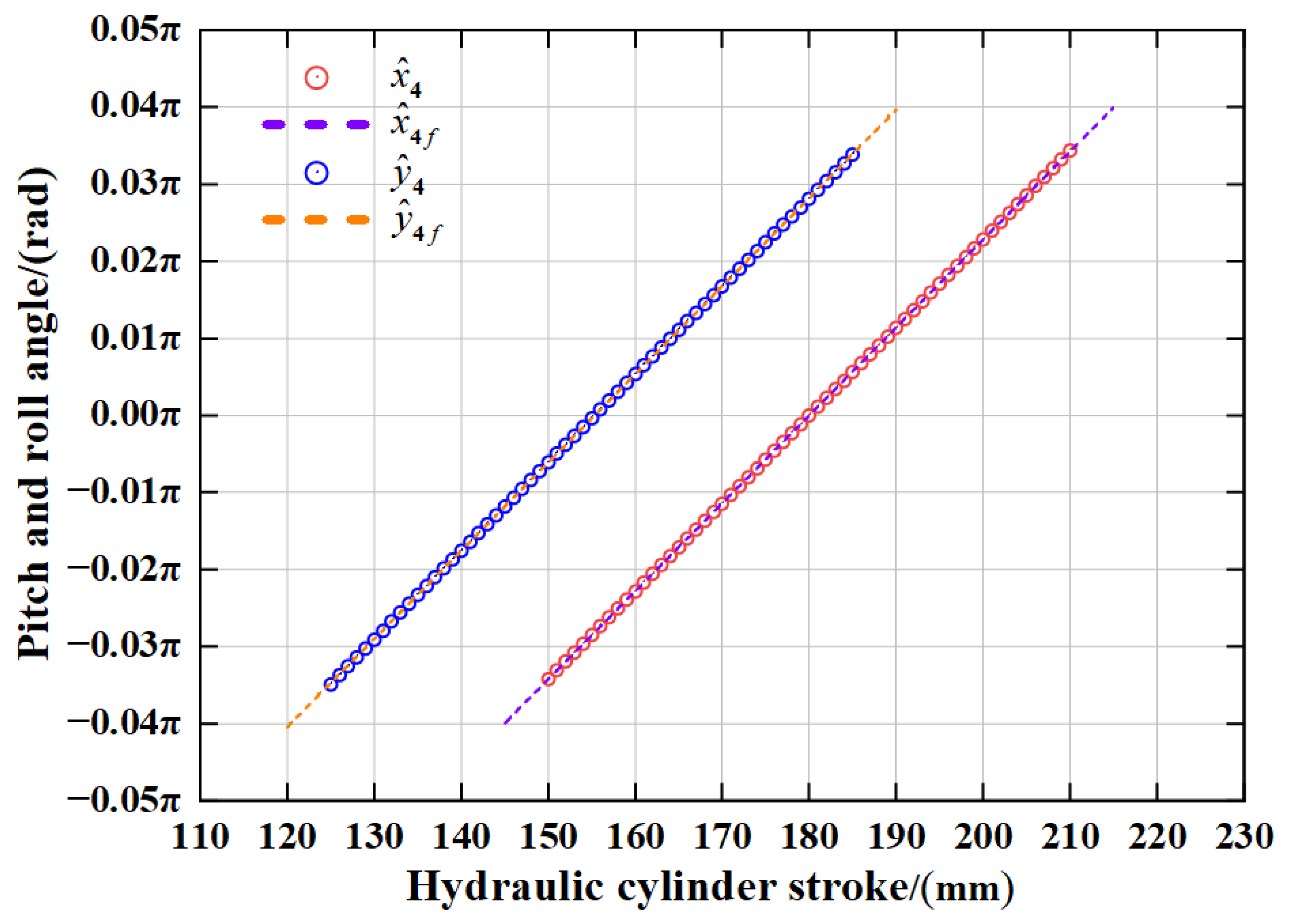
3.1. Kinematic Model Fitting
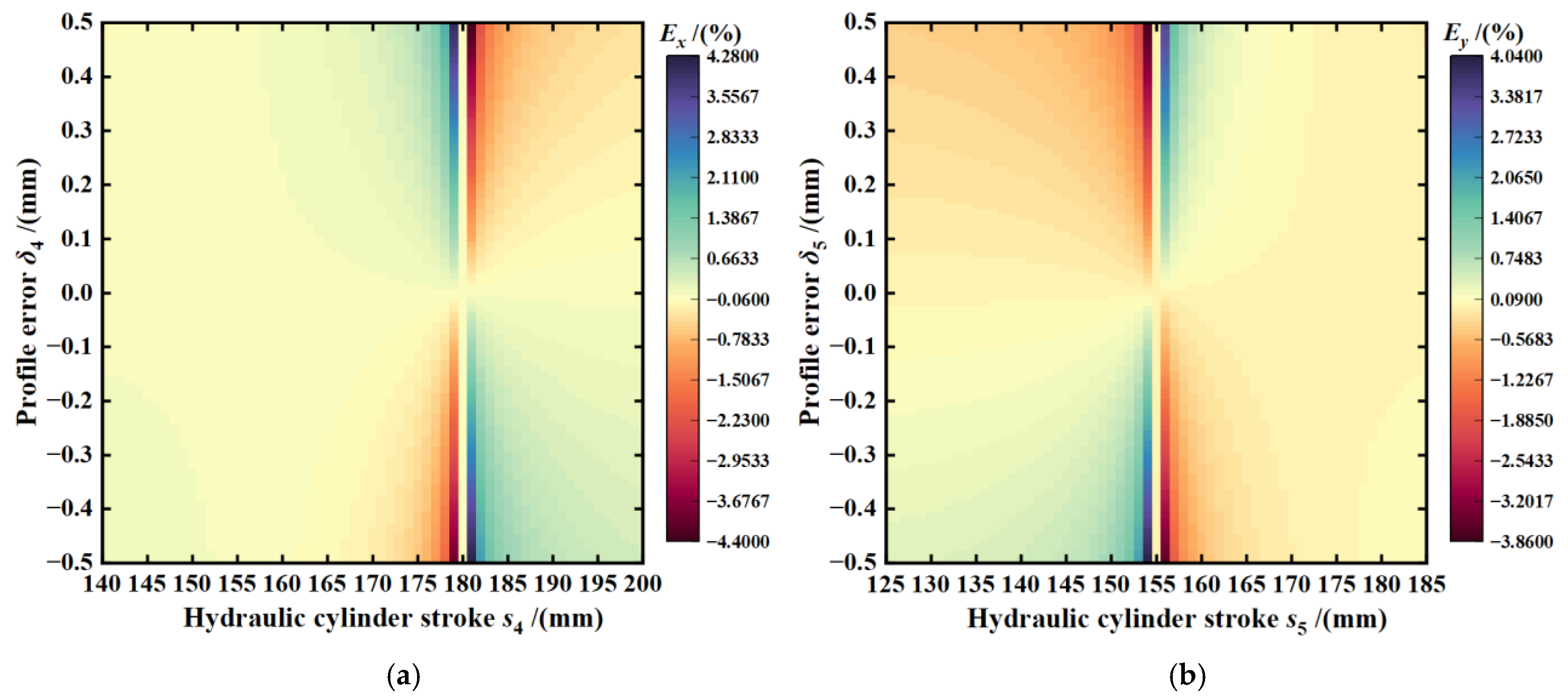
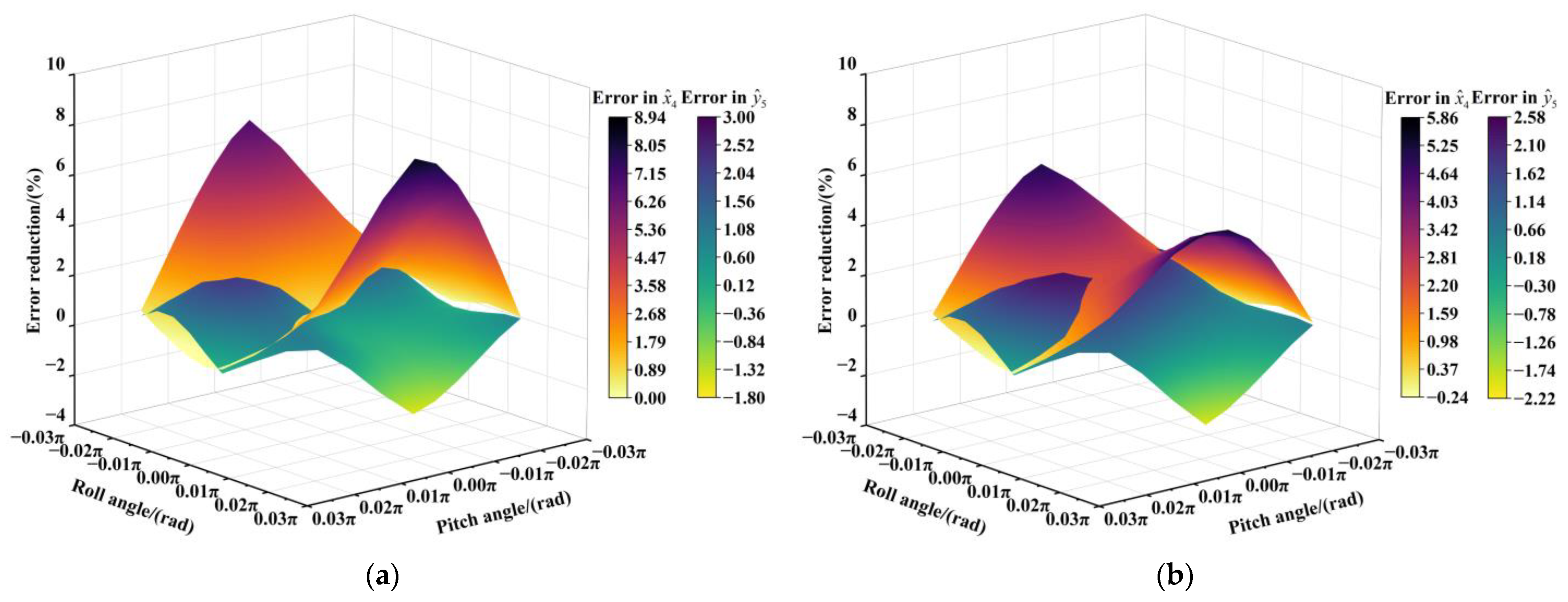
3.2. Numerical Simulation and Process Optimization
3.3. Error Compensation Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, G.; Li, Y.; Weng, S.F.; Wan, H.; Luo, D.B. Design and Simulation of a Novel 6-DOF Hybrid Mechanism Motion Platform for Pose Adjustment of Heavy Equipment. Iran. J. Sci. Technol. Trans. Mech. Eng. 2022, 47, 1055–1078. [Google Scholar] [CrossRef]
- Cui, R.; Ma, M.F.; Liu, H.Q.; Tan, Z.; Huang, X.Z.; Zhang, Y.M. Tolerance analysis of cradle-type double rotary table using the local parallel dimension chain method. Int. J. Adv. Manuf. Technol. 2024, 134, 1–18. [Google Scholar] [CrossRef]
- Liu, Y.; Yi, W.M.; Feng, Z.Q.; Yao, J.T.; Zhao, Y.S. Design and motion planning of a 7-DOF assembly robot with heavy load in spacecraft module. Robot. Comput. Integr. Manuf. 2024, 86, 102645. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Gao, H. Modeling and simulation of the assembly accuracy of aero-engine rotors in the docking processes using a specially designed novel multi-DOF NC motion platform. Aerosp. Sci. Technol. 2021, 113, 106648. [Google Scholar] [CrossRef]
- Wang, R.; Xiong, X.Y.; Liang, H.S.; Zhang, J.Z. Optimization Design of Redundant Parallel Posture Adjustment Mechanism for Solar Wing Docking Based on Response Surface Methodology. Appl. Sci. 2024, 14, 8059. [Google Scholar] [CrossRef]
- Tang, X.X.; Zhou, H.B.; Jiang, X.N. Monocular vision-based online kinematic calibration method for five-axis motion platform. Meas. Sci. Technol. 2024, 35, 015033. [Google Scholar] [CrossRef]
- Tang, G.; Lei, J.M.; Li, F.R.; Zhu, W.D.; Xu, X.Z.; Yao, B.H.; Claramunt, C.; Hu, X. A modified 6-DOF hybrid serial–parallel platform for ship wave compensation. Ocean. Eng. 2023, 280, 114336. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, R.; Cheng, H.L. Calculation method for military aircraft’s turnaround time. J. Beijing Univ. Aeronaut. Astronaut. 2008, 34, 1415–1418. [Google Scholar]
- Wang, H.; Chen, G.L. Research progress and perspective of robotic equipment applied in aviation assembly. Acta Aeronaut. Astronaut. Sin. 2022, 43, 49–71. [Google Scholar]
- Zhang, Z.; Jiang, F.; Luo, M.; Wu, B.H.; Zhang, D.H.; Tang, K. Geometric error measuring, modeling, and compensation for CNC machine tools: A review. Chin. J. Aeronaut. 2024, 37, 163–198. [Google Scholar] [CrossRef]
- Ramesh, R.; Mannan, A.M.; Poo, N.A. Error compensation in machine tools—A review Part I: Geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manuf. Des. Res. Appl. 2000, 40, 1235–1256. [Google Scholar] [CrossRef]
- Fan, Y.C.; Fan, K.C.; Huang, Y.B. Modeling and compensation of enhanced volumetric error of machine tools containing crosstalk errors. Precis. Eng. 2024, 86, 252–264. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, T.M.; Wang, L.P.; Chen, F.F. Kinematic error modeling and identification of the over-constrained parallel kinematic machine. Robot. Comput. Integr. Manuf. 2018, 49, 105–119. [Google Scholar] [CrossRef]
- Liao, Z.Y.; Wu, J.Z.; Wu, H.M.; Xie, H.L.; Wang, Q.H.; Zhou, X.F. Profile Error Estimation and Hierarchical Compensation Method for Robotic Surface Machining. IEEE Robot. Autom. Lett. 2024, 9, 3195–3202. [Google Scholar] [CrossRef]
- Tang, H.; Duan, J.A.; Lu, S.Q. Stream-of-Variation (SOV) Theory Applied in Geometric Error Modeling for Six-Axis Motion Platform. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 762–770. [Google Scholar] [CrossRef]
- Zheng, Y.; Duan, J.A. A geometric and kinematic error model and compensation of a 6-axis motorized optical fiber alignment stage. Adv. Mech. Eng. 2015, 7, 1–12. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, H.B.; Ju, X.; Li, Z.Q. Vision-based measurement for decoupling identification of geometric errors of rotating axes for five-axis platform. Meas. Sci. Technol. 2022, 33, 045007. [Google Scholar]
- Yu, J.; Yang, Y.L.; Cai, J.H.; Li, D.S. Coupling error model for the contact probe of a three-dimensional screw thread-measuring machine. Meas. Sci. Technol. 2022, 33, 055012. [Google Scholar] [CrossRef]
- Zhang, H.N.; Xiang, S.T.; Wu, C.; Yang, J.G. Optimal proportion compensation method of key geometric errors for five-axis machine tools considering multiple-direction coupling effects. J. Manuf. Process. 2024, 110, 447–461. [Google Scholar] [CrossRef]
- He, S.; Shi, T.L. Sensitivity analysis of surface contour error to geometric errors for four-axis ultra-precision machine tools. J. Manuf. Process. 2024, 131, 569–588. [Google Scholar] [CrossRef]
- Luo, Y.H.; Gao, J.; Chen, D.S.; Zhang, L.Y.; Liu, Y.C.; Zhong, Y.B. Accurate error compensation method for multi-axis parallel machine via singularized jacobi geometric parameter correction and coupling error evaluation. Robot. Comput. Integr. Manuf. 2024, 89, 102771. [Google Scholar] [CrossRef]
- Shen, H.Y.; Zhou, H.G.; Jin, Y.Y.; Li, L.; Deng, B.; Xu, J.W. Research on Pose Error Modeling and Compensation of Posture Adjustment Mechanism Based on WOA-RBF Neural Network. Machines 2024, 12, 782. [Google Scholar] [CrossRef]
- Nguyen, K.Q.; Khim, G.; Oh, S.J.; Ro, S.K. A unified geometric error model applicable to all configurations of three-axis machine tools. Int. J. Adv. Manuf. Technol. 2024, 134, 2653–2673. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, H.; Yonezawa, H.; Yongezawa, A.; Kajiwara, I.; Jiang, T.; He, J.J. Geometric and dynamic error compensation of dual-drive machine tool based on mechanism-data hybrid method. Mech. Syst. Signal Process. 2025, 224, 112041. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, X.; Yang, M.; Liu, Z.H.; Cai, C.G. A deep learning approach for pose error prediction in parallel robots. Measurement 2025, 242, 115815. [Google Scholar] [CrossRef]
- Fang, S.P.; Liu, Y.S.; Otsubo, H.; Sumida, T. An automatic leveling method for the stage of precision machining center. Int. J. Adv. Manuf. Technol. 2012, 61, 303–309. [Google Scholar] [CrossRef]
- Li, Y.; Yu, M.L.; Bai, Y.M.; Hou, Z.Y.; Wu, W.W. A Review of Thermal Error Modeling Methods for Machine Tools. Appl. Sci. 2021, 11, 5216. [Google Scholar] [CrossRef]
- Peng, W.C.; Huang, J.F.; Wan, K.; Xia, H.J. A novel identification method for all geometric errors of rotary axis based on boundaryless constraint optimization method. Measurement. 2024, 234, 114876. [Google Scholar] [CrossRef]
- Chen, Y.P.; Wang, J.C.; Tang, Q.C.; Li, J. A Study on the Coarse-to-Fine Error Decomposition and Compensation Method of Free-Form Surface Machining. Appl. Sci. 2024, 14, 9044. [Google Scholar] [CrossRef]
- Liu, C.H.; Song, Z.J.; Sang, Y.C.; He, G.Y. An Improved Measurement Uncertainty Calculation Method of Profile Error for Sculptured Surfaces. Chin. J. Mech. Eng. 2019, 32, 1–10. [Google Scholar] [CrossRef]
- Shi, H.L.; Jiang, P.Y. Quality control in multistage machining processes based on a machining error propagation event-knowledge graph. Adv. Manuf. 2024, 12, 679–697. [Google Scholar] [CrossRef]
- Song, C.Y.; Li, Y.F.; Sui, J.H. Auxiliary model nonlinear innovation least squares algorithm for identification ship 4-DOF via full-scale test data. Sci. Rep. 2024, 14, 25861. [Google Scholar] [CrossRef] [PubMed]




| Pitch Layer | Roll Layer | ||
|---|---|---|---|
| Parameters | Value/(mm) | Parameters | Value/(mm) |
| Radius of turn, r4 | 280 | Radius of turn, r5 | 280 |
| Hinge point radius, m4 | 320 | Hinge point radius, m5 | 330 |
| Initial stroke, s4m | 180 | Initial stroke, s5m | 155 |
| Maximum stroke, s4max | 204.3 | Maximum stroke, s5max | 179.4 |
| Minimum stroke, s4min | 155.6 | Minimum stroke, s5min | 130.8 |
| Center radius, l4 | 210 | Center radius, l5 | 220 |
| Rotation Layer | δ/(mm) | μE | σE |
|---|---|---|---|
| Pitch layer | −0.03 | 0.0067% | 0.0577 |
| −0.02 | 0.0045% | 0.0384 | |
| −0.01 | 0.0022% | 0.0192 | |
| 0.01 | −0.0022% | 0.0192 | |
| 0.02 | −0.0045% | 0.0385 | |
| 0.03 | −0.0067% | 0.0678 | |
| Roll layer | −0.03 | 0.0121% | 0.0518 |
| −0.02 | 0.0081% | 0.0345 | |
| −0.01 | 0.004% | 0.0172 | |
| 0.01 | −0.004% | 0.0172 | |
| 0.02 | −0.0081% | 0.0344 | |
| 0.03 | 0.0121% | 0.0516 |
| Experiment No. | Targeted /(rad) | Targeted /(rad) | Actual /(rad) | Actual /(rad) | Error in | s4/(mm) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | −0.0003π | 0 | 180.021 |
| 2 | 0.0056π | 0 | 0.0056π | −0.0003π | 0 | 184.847 |
| 3 | 0.0111π | 0 | 0.0115π | −0.0004π | 3.6036% | 190.016 |
| 4 | 0.0167π | 0 | 0.0172π | −0.0004π | 2.9940% | 195.047 |
| 5 | 0.0222π | 0 | 0.0222π | −0.0004π | 0 | 199.374 |
| 6 | 0.0278π | 0 | 0.0278π | −0.0004π | 0 | 204.311 |
| 7 | 0.0222π | 0 | 0.0224π | 0.0001π | 0.9009% | 199.603 |
| 8 | 0.0167π | 0 | 0.0172π | 0.0001π | 2.9940% | 195.044 |
| 9 | 0.0111π | 0 | 0.0115π | 0.0001π | 3.6036% | 190.039 |
| 10 | 0.0056π | 0 | 0.0062π | 0.0001π | 10.7143% | 185.454 |
| 11 | 0 | 0 | 0 | 0.0001π | 0 | 179.972 |
| 12 | −0.0056π | 0 | −0.0060π | 0.0001π | 7.1429% | 174.751 |
| 13 | −0.0111π | 0 | −0.0116π | 0.0001π | 4.5045% | 169.809 |
| 14 | −0.0167π | 0 | −0.0172π | 0 | 2.9940% | 164.916 |
| 15 | −0.0222π | 0 | −0.0223π | 0 | 0.4505% | 160.421 |
| 16 | −0.0278π | 0 | −0.0279π | 0 | 0.3597% | 155.594 |
| 17 | −0.0222π | 0 | −0.0224π | −0.0001π | 0.9009% | 160.409 |
| 18 | −0.0167π | 0 | −0.0170π | −0.0001π | 1.7964% | 165.129 |
| 19 | −0.0111π | 0 | −0.0118π | −0.0002π | 6.3063% | 169.687 |
| 20 | −0.0056π | 0 | −0.0056π | −0.0003π | 0 | 175.077 |
| 21 | 0 | 0 | 0 | −0.0003π | 0 | 180.017 |
| Experiment No. | Targeted /(rad) | Targeted /(rad) | Actual /(rad) | Actual /(rad) | Error in | s5/(mm) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | −0.0001π | 0 | 0 | 155.387 |
| 2 | 0 | 0.0056π | −0.0008π | 0.0055π | −1.7857% | 160.187 |
| 3 | 0 | 0.0111π | −0.0008π | 0.0115π | 3.6036% | 165.371 |
| 4 | 0 | 0.0167π | −0.0007π | 0.0167π | 0 | 169.945 |
| 5 | 0 | 0.0222π | −0.0008π | 0.0223π | 0.4505% | 174.834 |
| 6 | 0 | 0.0278π | −0.0007π | 0.0278π | 0 | 179.639 |
| 7 | 0 | 0.0222π | −0.0008π | 0.0224π | 0.9009% | 174.894 |
| 8 | 0 | 0.0167π | −0.0010π | 0.0170π | 1.7964% | 170.193 |
| 9 | 0 | 0.0111π | −0.0010π | 0.0114π | 2.7027 | 165.348 |
| 10 | 0 | 0.0056π | −0.0010π | 0.0055π | −1.7857 | 160.191 |
| 11 | 0 | 0 | −0.0010π | −0.0007π | 0 | 154.725 |
| 12 | 0 | −0.0056π | −0.0010π | −0.0056π | 0 | 150.463 |
| 13 | 0 | −0.0111π | −0.0010π | −0.0111π | 0 | 145.647 |
| 14 | 0 | −0.0167π | −0.0010π | −0.0167π | 0 | 140.752 |
| 15 | 0 | −0.0222π | −0.0009π | −0.0224π | 0.9009% | 135.811 |
| 16 | 0 | −0.0278π | −0.0008π | −0.0278π | 0 | 131.085 |
| 17 | 0 | −0.0222π | −0.0009π | −0.0219π | −1.3514% | 136.201 |
| 18 | 0 | −0.0167π | −0.0009π | −0.0172π | 2.9940% | 140.279 |
| 19 | 0 | −0.0111π | −0.0009π | −0.0112π | 0.9009% | 145.601 |
| 20 | 0 | −0.0056π | −0.0009π | −0.0056π | 0 | 150.477 |
| 21 | 0 | 0 | −0.0009π | 0.0002π | 0 | 155.555 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Bao, R.; Li, S.; Ji, L.; Li, S.; Yan, X.; Li, W. A Coupling Error Compensation Approach Concerning Constrained Space Coordinate Precision of a Heavy-Load Longitudinal and Transversal Swing Table. Appl. Sci. 2025, 15, 4693. https://doi.org/10.3390/app15094693
Liu M, Bao R, Li S, Ji L, Li S, Yan X, Li W. A Coupling Error Compensation Approach Concerning Constrained Space Coordinate Precision of a Heavy-Load Longitudinal and Transversal Swing Table. Applied Sciences. 2025; 15(9):4693. https://doi.org/10.3390/app15094693
Chicago/Turabian StyleLiu, Manxian, Rui Bao, Shuo Li, Liang Ji, Suozhuang Li, Xiaoqiang Yan, and Wei Li. 2025. "A Coupling Error Compensation Approach Concerning Constrained Space Coordinate Precision of a Heavy-Load Longitudinal and Transversal Swing Table" Applied Sciences 15, no. 9: 4693. https://doi.org/10.3390/app15094693
APA StyleLiu, M., Bao, R., Li, S., Ji, L., Li, S., Yan, X., & Li, W. (2025). A Coupling Error Compensation Approach Concerning Constrained Space Coordinate Precision of a Heavy-Load Longitudinal and Transversal Swing Table. Applied Sciences, 15(9), 4693. https://doi.org/10.3390/app15094693







