Nonlinear Dynamic Analysis of Tall Bridge Piers Under Multidimensional Pulse Earthquakes Considering Varying Damping Ratios
Abstract
:1. Introduction
2. Dynamic Time History Analysis of the Structure
3. Model of a Tall Bridge Pier with Multidimensional Ground Motion Input
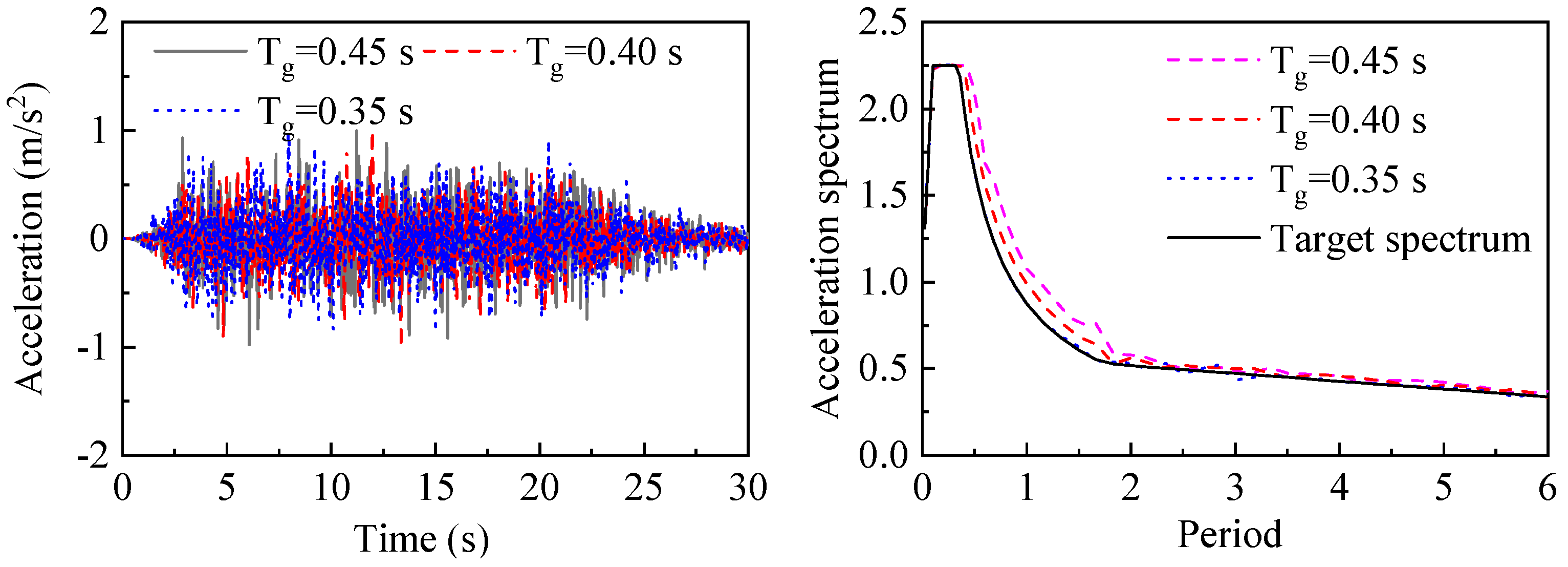
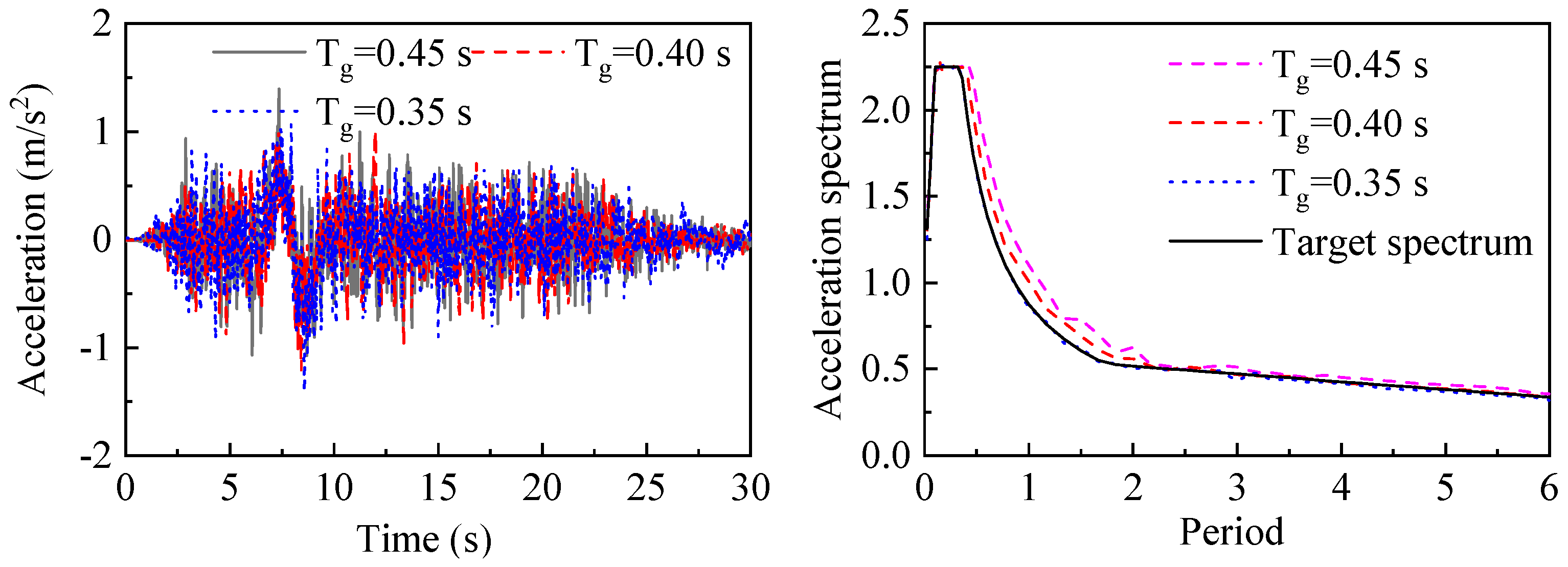
4. Synthesis of Seismic Waves
5. Results Analysis
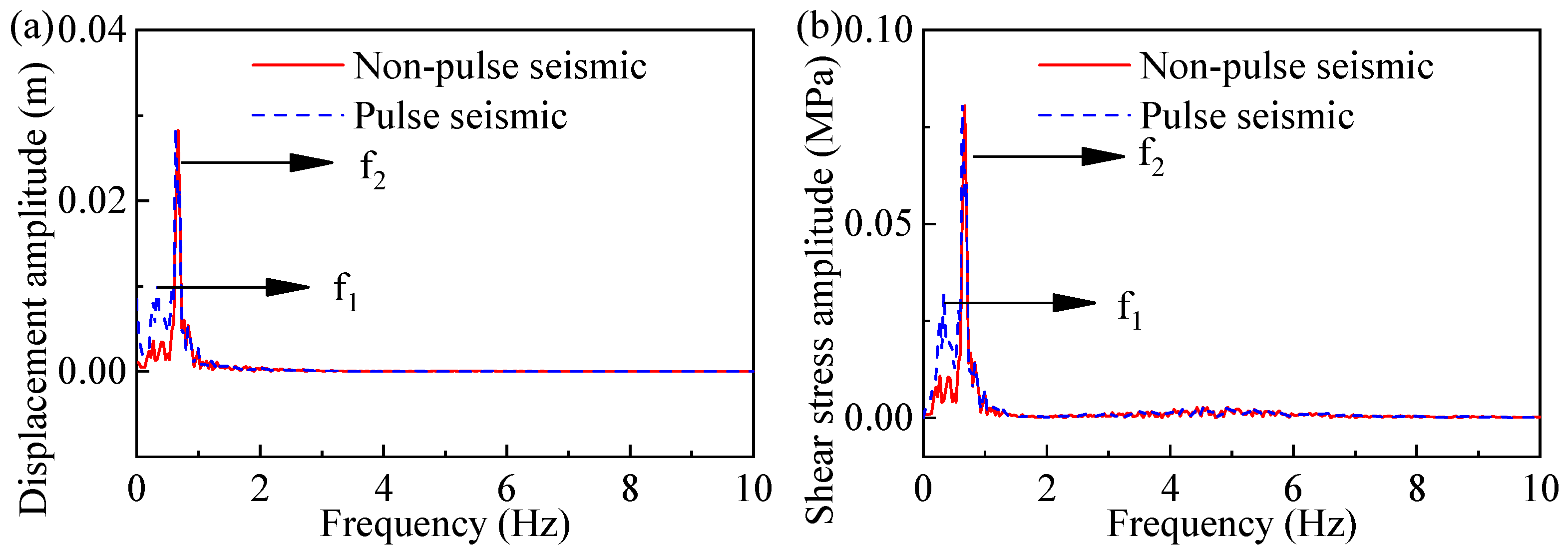
5.1. Tall Bridge Pier Under Pulse Ground Motion
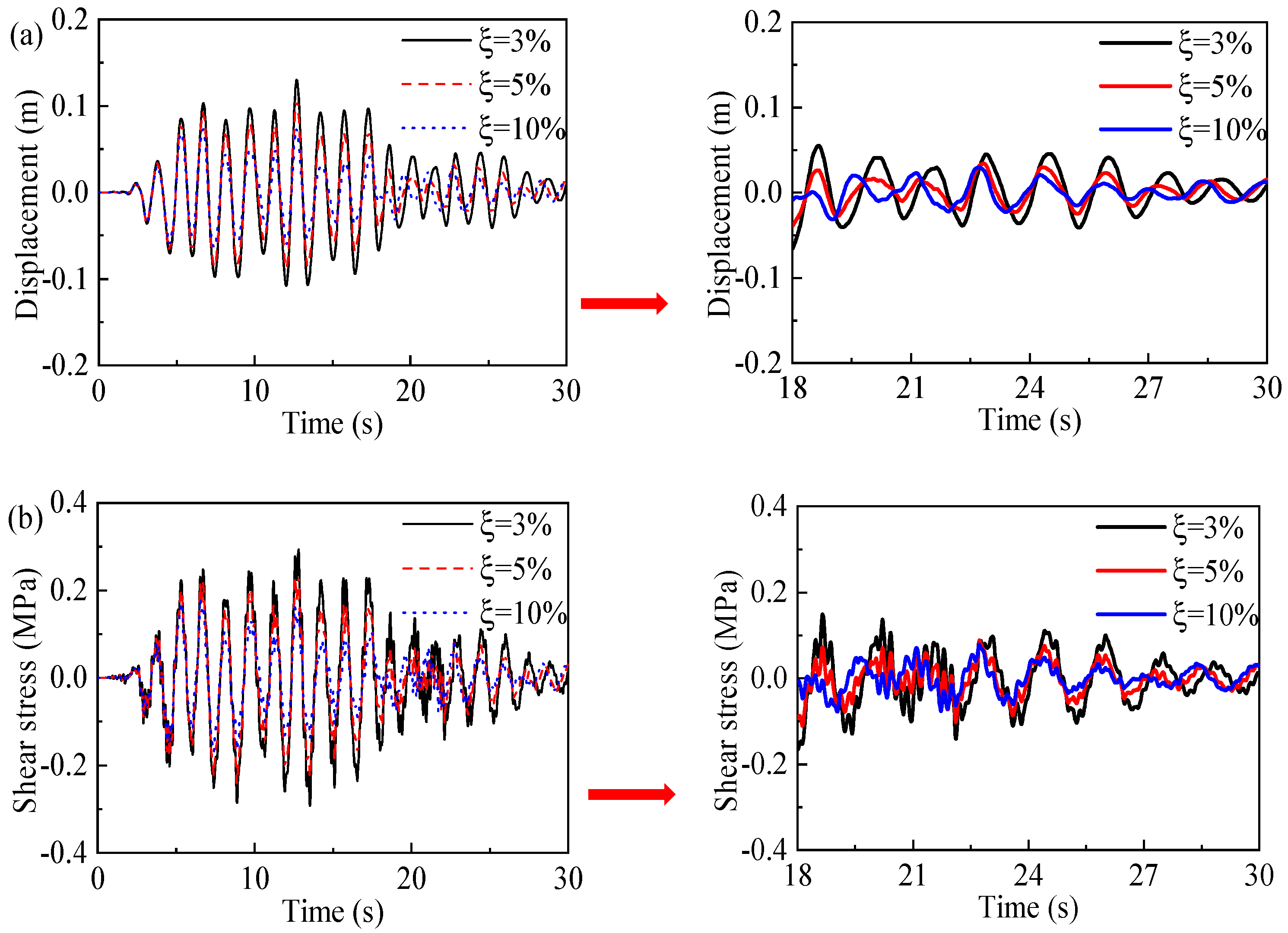
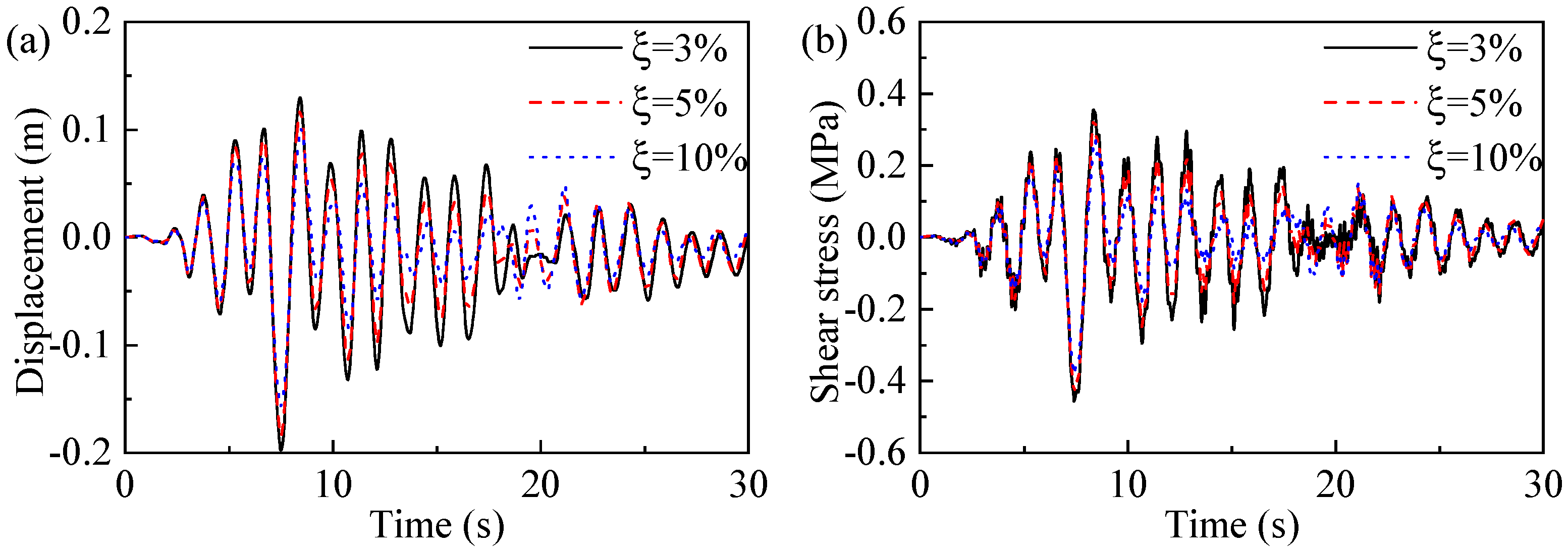
5.2. Varying Damping Ratios Affect the Dynamic Response
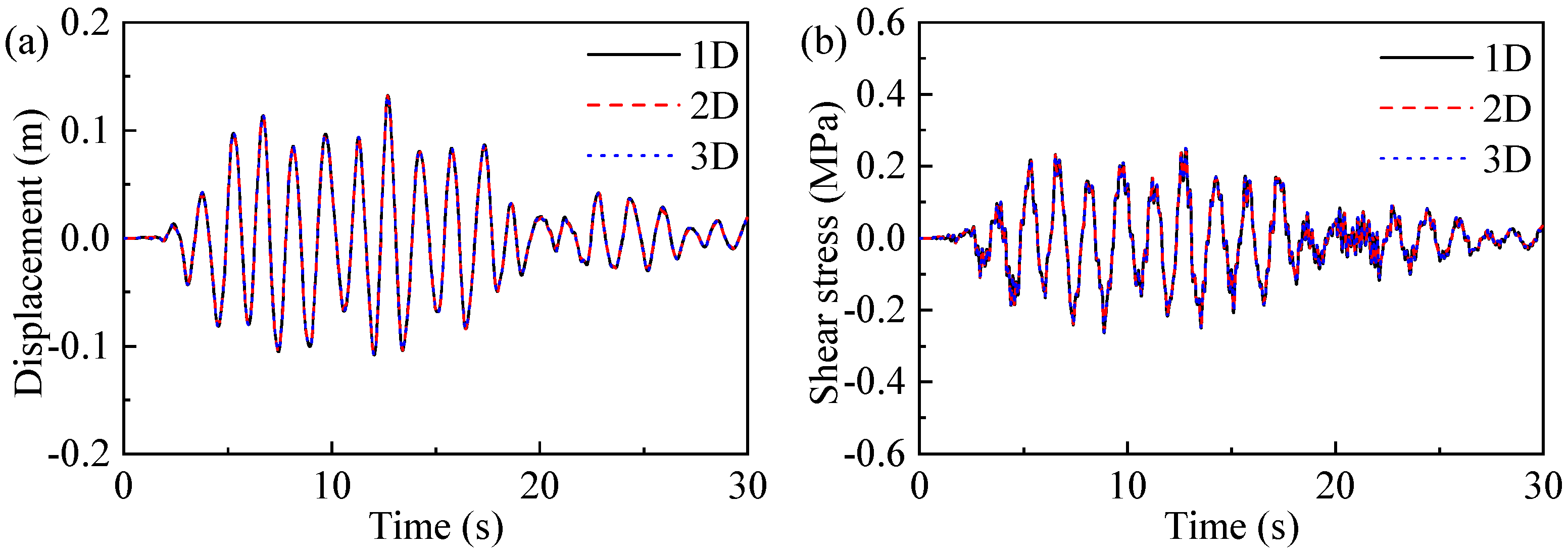
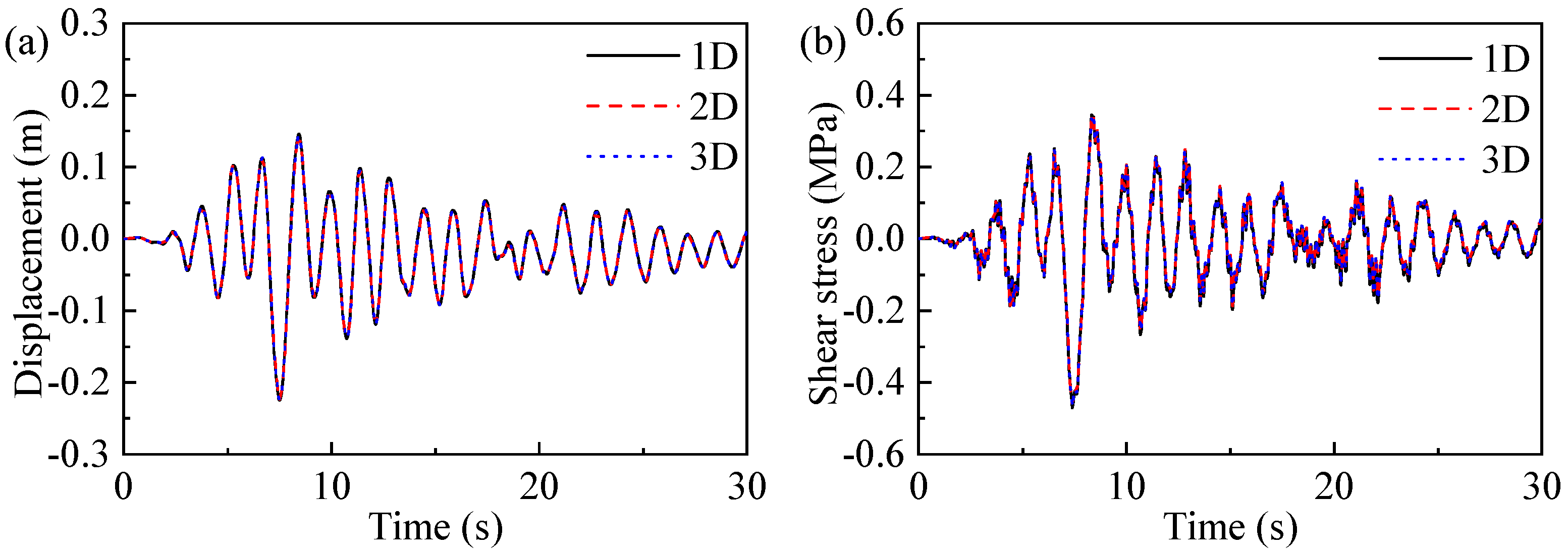
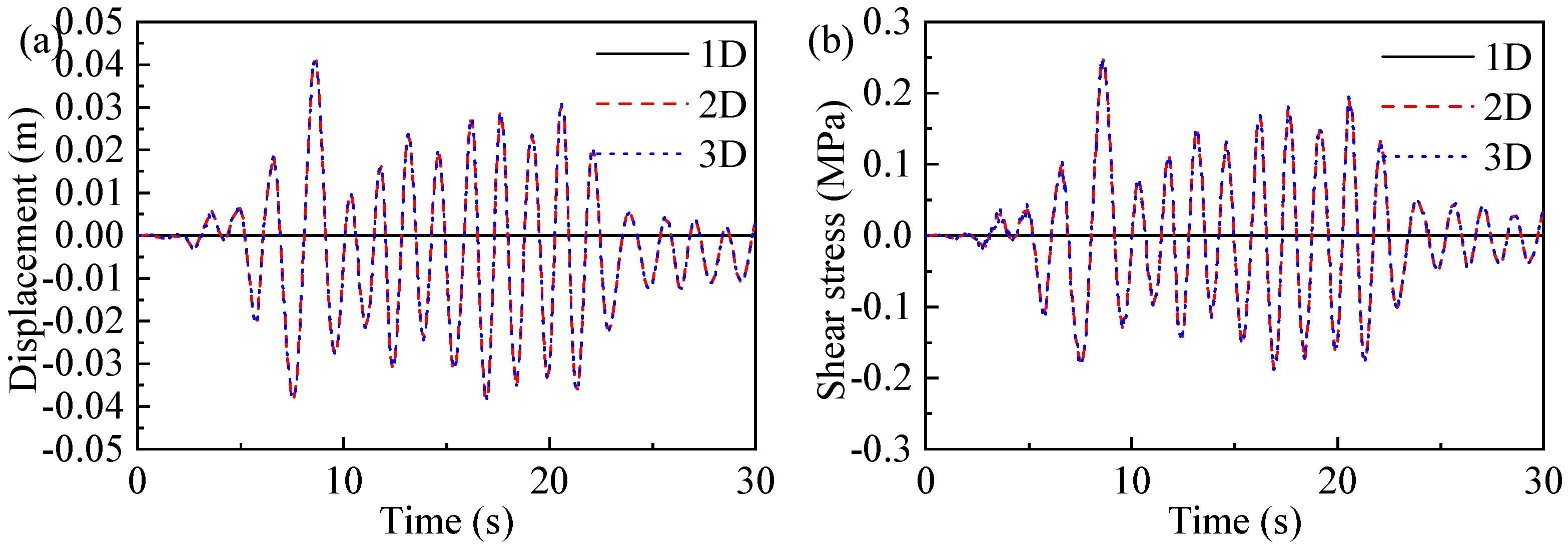
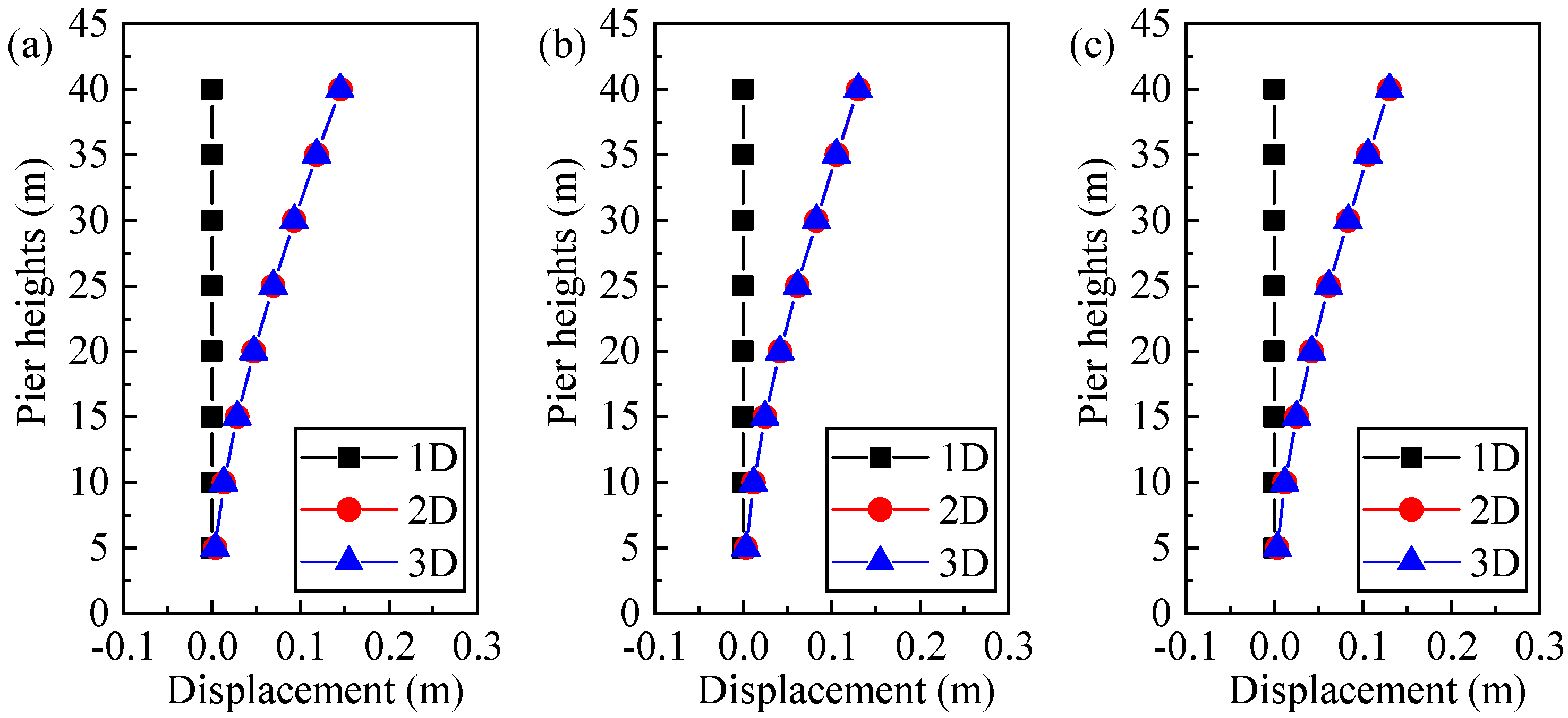
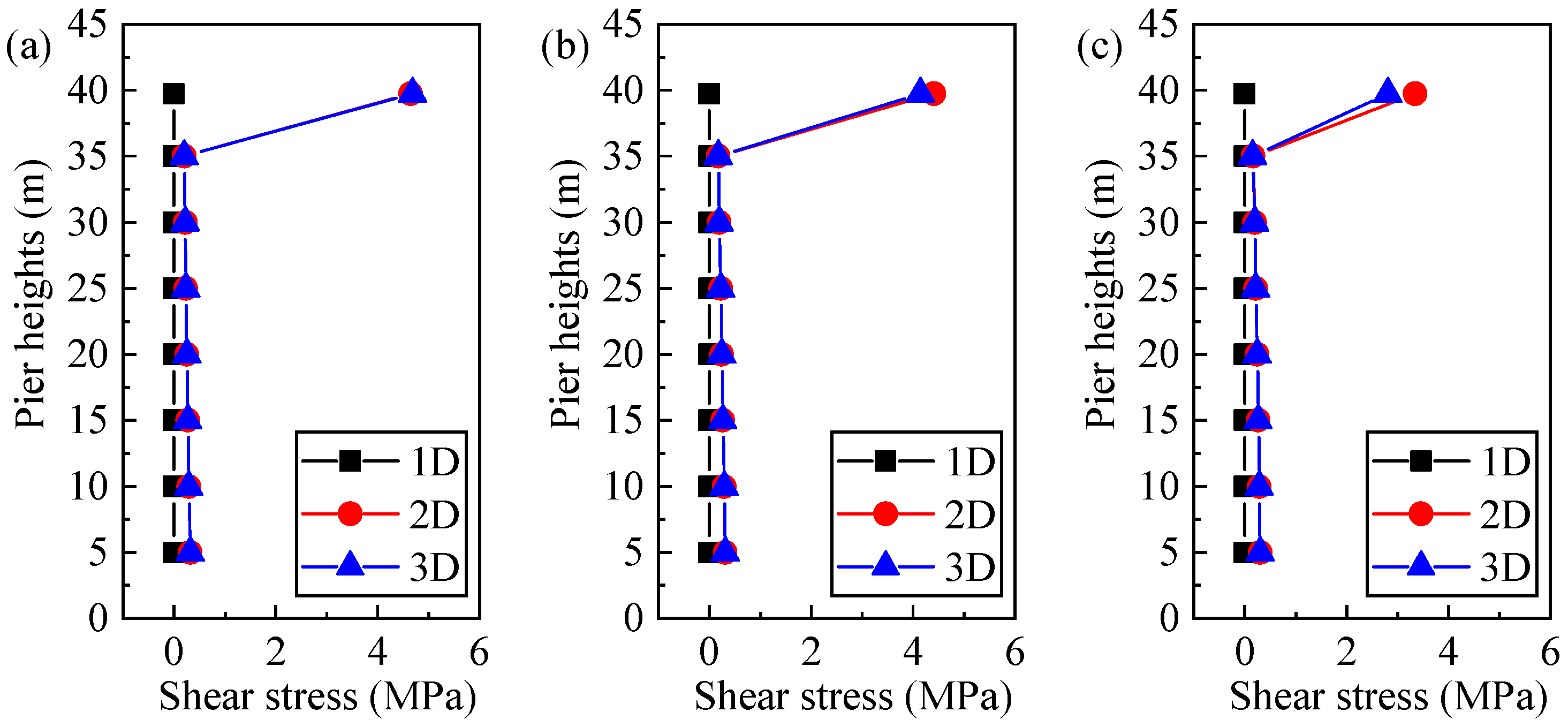
5.3. Tall Bridge Pier Under Multidimensional Ground Motions
6. Conclusions and Discussion
- (1)
- Compared with those under non-pulse ground motion, the displacement and shear stress behaviour of a tall bridge pier under pulse ground motion are significantly greater. In the time range of 0–5 s, the displacement and shear stress time histories exhibit more intricate variations when the ground motion is in the form of pulse ground motion. This is particularly evident in the case of tall bridge piers.
- (2)
- When under pulse ground motion, the peak displacement and shear stress errors of tall bridge pier structures, incorporating three different damping ratios, are notably smaller than those under non-pulse ground motion conditions. When the time t on the displacement and shear stress time history curves exceeds 18 s, the influence of pulse ground motion on the variations in the curves becomes more significant than the impact of the damping ratio itself. In contrast, for non-pulse ground motion, the influence of the damping ratio on the changes in the displacement and shear stress time histories is more pronounced than that of the ground motion.
- (3)
- When subjected to two-dimensional and three-dimensional non-pulse ground motions, the displacement at the Z section and the shear stress at the YZ section of a tall bridge pier are found to be smaller than those under one-dimensional ground motion. When the tall bridge pier is under the influence of two-dimensional and three-dimensional pulse ground motion, both the peak displacement at the Z section and the peak shear stress at the YZ section of the bridge pier are reduced compared with the response under one-dimensional motion. However, when the tall bridge pier is subjected to two-dimensional and three-dimensional pulse ground motion, the displacement at the X section and the shear stress at the XY section are considerably greater than the corresponding response under one-dimensional ground motion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Collura, D.; Nascimbene, R. Comparative assessment of variable loads and seismic actions on bridges: A case study in italy using a multimodal approach. Appl. Sci. 2023, 13, 2771. [Google Scholar] [CrossRef]
- Huang, Z.; Bai, S.; Lai, M. A review of damping in time-course analysis of structural seismic response. Earthq. Eng. Eng. Vib. 1996, 16, 95–105. (In Chinese) [Google Scholar]
- An, D.; Zhou, J. Influence law of high-rise structure damping ratio on seismic response and design discussion of seismic energy dissipation. Build. Struct. 2022, 52, 123–128. (In Chinese) [Google Scholar]
- Lee, D.H.; Choi, E.; Zi, G. Evaluation of earthquake deformation and performance for rc bridge piers. Eng. Struct. 2005, 27, 1451–1464. [Google Scholar] [CrossRef]
- Solberg, K.; Mashiko, N.; Mander, J.B.; Dhakal, R.P. Performance of a damage-protected highway bridge pier subjected to bidirectional earthquake attack. J. Struct. Eng. 2009, 135, 469–478. [Google Scholar] [CrossRef]
- Zhu, S.; Li, Y.; Togbenou, K.; Xiang, T. An advanced algorithm to study the effect of uncertainties on the stochastic performance of high-pier bridge under earthquake. Soil Dyn. Earthq. Eng. 2019, 126, 105805. [Google Scholar] [CrossRef]
- Chen, X.; Li, C. Seismic performance of tall pier bridges retrofitted with lead rubber bearings and rocking foundation. Eng. Struct. 2020, 212, 110529. [Google Scholar] [CrossRef]
- Soleimani, F. Pattern recognition of the seismic demands for tall pier bridge systems. J. Earthq. Eng. 2022, 26, 6548–6566. [Google Scholar] [CrossRef]
- Qi, Q.; Shao, C.; Wei, W.; Xiao, Z.; He, J. Seismic performance of railway rounded rectangular hollow tall piers using the shaking table test. Eng. Struct. 2020, 220, 110968. [Google Scholar] [CrossRef]
- Yun, G.; Liu, C. Shaking table tests on a deep-water high-pier whole bridge under joint earthquake, wave and current action. Appl. Ocean. Res. 2020, 103, 102329. [Google Scholar] [CrossRef]
- Yun, G.; Liu, C. A model for underwater shaking table tests on the basis of different similar criteria. Appl. Ocean. Res. 2022, 118, 103010. [Google Scholar] [CrossRef]
- Li, Z.X.; Wu, K.; Shi, Y.; Li, N.; Ding, Y. Coordinative similitude law considering fluid-structure interaction for underwater shaking table tests. Earthq. Eng. Struct. Dyn. 2018, 47, 2315–2332. [Google Scholar] [CrossRef]
- Han, Q.; Wen, J.; Du, X.; Zhong, Z.; Hao, H. Nonlinear seismic response of a base isolated single pylon cable-stayed bridge. Eng. Struct. 2018, 175, 806–821. [Google Scholar] [CrossRef]
- Lin, W.; Chen, S.H.; Yu, J.X.; Qi, A. Seismic behavior of long-span connected structures under multi-supported and multi-dimensional-earthquake excitations. Adv. Struct. Eng. 2013, 16, 1579–1586. [Google Scholar] [CrossRef]
- Meng, S.; Ding, Y. Stochastic response of a coastal cable-stayed bridge subjected to multi-dimensional and multi-supported earthquake and waves. J. Earthq. Tsunami 2020, 15, 2150006. [Google Scholar] [CrossRef]
- Yun, G.; Liu, C. Nonlinear dynamic analysis of the deep-water bridge piers under combined earthquakes and wave actions. Ocean. Eng. 2022, 261, 112076. [Google Scholar] [CrossRef]
- Zhou, G.; Zhu, Z.; Tang, Y.; Xu, W.; Li, X.; Jiang, L. Seismic scenario reproduction and damage mechanism analysis of liuhuanggou bridge under near-fault earthquake. Bull. Earthq. Eng. 2023, 21, 6091–6120. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Guan, Z. Fragility analysis of tall pier bridges subjected to near-fault pulse-like ground motions. Struct. Infrastruct. Eng. 2020, 16, 1082–1095. [Google Scholar] [CrossRef]
- Srivastava, C.; Pandikkadavath, M.S.; Mangalathu, S.; AlHamaydeh, M. Seismic response of rc bridges under near-fault ground motions: A parametric investigation. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; p. 106033. [Google Scholar]
- Chen, X.; Xiang, N.; Li, J.; Guan, Z. Influence of near-fault pulse-like motion characteristics on seismic performance of tall pier bridges with fragility analysis. J. Earthq. Eng. 2022, 26, 2001–2022. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; Wu, K.; Li, Z. Experimental research on dynamic responses and hydrodynamic pressures of deep-water bridge piers under seismic and wave actions. Eng. Struct. 2024, 313, 118276. [Google Scholar] [CrossRef]
- Akitoku, S. Structural Seismic Analysis; Industrial Building Press: Beijing, China, 2020. (In Chinese) [Google Scholar]
- GB50011-2010; China Academy of Building Research. Seismic Design Code of Building. China Building Industry Press: Beijing, China, 2010. (In Chinese)
- Yun, G.; Liu, C. Dynamic analysis of bridge structures under combined earthquakes and wave loadings based on a simplified nonlinear Morison equation considering limit wave steepness. Ocean. Eng. 2022, 265, 112690. [Google Scholar] [CrossRef]
- Yun, G.; Liu, C. Nonlinear dynamic analysis of high-strength concrete bridge under post-fire earthquakes considering hydrodynamic effects. Sustainability 2024, 16, 6486. [Google Scholar] [CrossRef]
- Yun, G.; Liu, C. Study on the hydrodynamic effects of bridge piers under velocity-type pulse ground motion based on different characteristic periods. Appl. Sci. 2024, 14, 10709. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R.; Luo, H.; Shen, H. Baseline correction of vibration acceleration signals with inconsistent initial velocity and displacement. Adv. Mech. Eng. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R.; Luo, H.; Shen, H. Target-based algorithm for baseline correction of inconsistent vibration signals. J. Vib. Control. 2018, 24, 2562–2575. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, L.; Pan, C.; Chen, Q.; Wang, Y. Generating high spectral consistent endurance time excitations by a modified time-domain spectral matching method. Soil Dyn. Earthq. Eng. 2021, 145, 106708. [Google Scholar] [CrossRef]
- Kim, S.J.; Holub, C.J.; Elnashai, A.S. Analytical assessment of the effect of vertical earthquake motion on rc bridge piers. J. Struct. Eng. 2011, 137, 252–260. [Google Scholar] [CrossRef]
- Sengupta, A.; Quadery, L.; Sarkar, S.; Roy, R. Influence of bidirectional near-fault excitations on rc bridge piers. J. Bridge Eng. 2016, 21, 04016034. [Google Scholar] [CrossRef]
- JTG/T2231-01-2020; China Merchants Chongqing Transportation Research and Design Institute Co., Ltd., Specifications for Seismic Design of Highway Bridges. China Communications Press: Beijing, China, 2020. (In Chinese)




| Physical Parameters | Values |
|---|---|
| Density | 2430 kg/m3 |
| Elastic modulus | 3.2 × 1010 N/m2 |
| Poisson’s ratio | 0.191 |
| Damping ratio | 3%; 5%; 10% |
| Pier Heights (m) | Displacement (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| = 3% | = 5% | = 10% | |||||||
| 1D | 2D | 3D | 1D | 2D | 3D | 1D | 2D | 3D | |
| 5 | 0.0062 | 0.0062 | 0.0037 | 0.0058 | 0.0058 | 0.0058 | 0.0049 | 0.0049 | 0.0049 |
| 10 | 0.0229 | 0.0229 | 0.0139 | 0.0213 | 0.0212 | 0.0212 | 0.0182 | 0.0181 | 0.0181 |
| 15 | 0.0480 | 0.0479 | 0.0297 | 0.0446 | 0.0444 | 0.0444 | 0.0381 | 0.0379 | 0.0379 |
| 20 | 0.0795 | 0.0793 | 0.0501 | 0.0740 | 0.0736 | 0.0736 | 0.0631 | 0.0628 | 0.0628 |
| 25 | 0.1159 | 0.1155 | 0.0743 | 0.1078 | 0.1072 | 0.1071 | 0.0920 | 0.0915 | 0.0915 |
| 30 | 0.1556 | 0.1549 | 0.1012 | 0.1448 | 0.1438 | 0.1437 | 0.1235 | 0.1228 | 0.1228 |
| 35 | 0.1973 | 0.1962 | 0.1299 | 0.1836 | 0.1823 | 0.1822 | 0.1566 | 0.1557 | 0.1556 |
| 40 | 0.2421 | 0.2408 | 0.1608 | 0.2248 | 0.2234 | 0.2233 | 0.1915 | 0.1904 | 0.1904 |
| Pier Heights (m) | Shear Stress (MPa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| = 3% | = 5% | = 10% | |||||||
| 1D | 2D | 3D | 1D | 2D | 3D | 1D | 2D | 3D | |
| 5 | 0.4928 | 0.4853 | 0.3200 | 0.4709 | 0.4635 | 0.4631 | 0.4198 | 0.4160 | 0.4158 |
| 10 | 0.4557 | 0.4458 | 0.2935 | 0.4307 | 0.4236 | 0.4233 | 0.3806 | 0.3759 | 0.3758 |
| 15 | 0.4240 | 0.4136 | 0.2761 | 0.3987 | 0.3901 | 0.3899 | 0.3484 | 0.3425 | 0.3424 |
| 20 | 0.3891 | 0.3830 | 0.2651 | 0.3659 | 0.3587 | 0.3587 | 0.3189 | 0.3121 | 0.3122 |
| 25 | 0.3608 | 0.3517 | 0.2666 | 0.3367 | 0.3295 | 0.3291 | 0.2887 | 0.2850 | 0.2849 |
| 30 | 0.3185 | 0.3118 | 0.2553 | 0.2970 | 0.2912 | 0.2907 | 0.2539 | 0.2496 | 0.2495 |
| 35 | 0.2698 | 0.2627 | 0.2280 | 0.2512 | 0.2455 | 0.2455 | 0.2135 | 0.2099 | 0.2098 |
| 39.75 | 5.2428 | 5.2090 | 4.8242 | 5.0922 | 5.0050 | 4.8623 | 4.6830 | 4.1019 | 3.8914 |
| Pier Heights (m) | Displacement (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| = 3% | = 5% | = 10% | |||||||
| 1D | 2D | 3D | 1D | 2D | 3D | 1D | 2D | 3D | |
| 5 | 2.3783 × 10−13 | 0.0036 | 0.0036 | 1.8606 × 10−13 | 0.0032 | 0.0032 | 1.1612 × 10−13 | 0.0032 | 0.0032 |
| 10 | 8.8947 × 10−13 | 0.0135 | 0.0135 | 6.9469 × 10−13 | 0.0117 | 0.0117 | 4.9610 × 10−13 | 0.0119 | 0.0118 |
| 15 | 1.8826 × 10−12 | 0.0285 | 0.0284 | 1.4681 × 10−12 | 0.0248 | 0.0248 | 1.0479 × 10−12 | 0.0250 | 0.0250 |
| 20 | 3.1468 × 10−12 | 0.0473 | 0.0472 | 2.4497 × 10−12 | 0.0416 | 0.0416 | 1.7494 × 10−12 | 0.0419 | 0.0419 |
| 25 | 4.6151 × 10−12 | 0.0691 | 0.0690 | 3.5862 × 10−12 | 0.0612 | 0.0612 | 2.5625 × 10−12 | 0.0615 | 0.0615 |
| 30 | 6.2258 × 10−12 | 0.0931 | 0.0929 | 4.8297 × 10−12 | 0.0828 | 0.0828 | 3.4522 × 10−12 | 0.0831 | 0.0831 |
| 35 | 7.9231 × 10−12 | 0.1186 | 0.1183 | 6.1375 × 10−12 | 0.1057 | 0.1056 | 4.3875 × 10−12 | 0.1059 | 0.1059 |
| 40 | 9.6923 × 10−12 | 0.1454 | 0.1451 | 7.4841 × 10−12 | 0.1301 | 0.1301 | 5.3736 × 10−12 | 0.1300 | 0.1300 |
| Pier Heights (m) | Shear Stress (MPa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| = 3% | = 5% | = 10% | |||||||
| 1D | 2D | 3D | 1D | 2D | 3D | 1D | 2D | 3D | |
| 5 | 3.0518 × 10−11 | 0.3232 | 0.3225 | 2.2880 × 10−11 | 0.3162 | 0.3153 | 1.5259 × 10−11 | 0.3054 | 0.3050 |
| 10 | 3.0518 × 10−11 | 0.2956 | 0.2952 | 1.5259 × 10−11 | 0.2908 | 0.2900 | 1.1444 × 10−11 | 0.2826 | 0.2821 |
| 15 | 1.9074 × 10−11 | 0.2751 | 0.2747 | 1.5259 × 10−11 | 0.2672 | 0.2667 | 1.5259 × 10−11 | 0.2624 | 0.2620 |
| 20 | 1.9074 × 10−11 | 0.2499 | 0.2496 | 1.5259 × 10−11 | 0.2470 | 0.2468 | 1.1444 × 10−11 | 0.2412 | 0.2412 |
| 25 | 1.7166 × 10−11 | 0.2311 | 0.2310 | 1.5259 × 10−11 | 0.2243 | 0.2240 | 1.5259 × 10−11 | 0.2178 | 0.2176 |
| 30 | 1.5259 × 10−11 | 0.2232 | 0.2231 | 1.5259 × 10−11 | 0.1978 | 0.1975 | 9.5367 × 10−12 | 0.1917 | 0.1914 |
| 35 | 1.4305 × 10−11 | 0.2017 | 0.2009 | 1.3351 × 10−11 | 0.1726 | 0.1722 | 9.5367 × 10−12 | 0.1601 | 0.1599 |
| 39.75 | 7.8125 × 10−9 | 4.6484 | 4.6849 | 7.8125 × 10−9 | 4.4148 | 4.1414 | 7.8125 × 10−9 | 3.3451 | 2.8067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, G.; Liu, C. Nonlinear Dynamic Analysis of Tall Bridge Piers Under Multidimensional Pulse Earthquakes Considering Varying Damping Ratios. Appl. Sci. 2025, 15, 4754. https://doi.org/10.3390/app15094754
Yun G, Liu C. Nonlinear Dynamic Analysis of Tall Bridge Piers Under Multidimensional Pulse Earthquakes Considering Varying Damping Ratios. Applied Sciences. 2025; 15(9):4754. https://doi.org/10.3390/app15094754
Chicago/Turabian StyleYun, Gaojie, and Chunguang Liu. 2025. "Nonlinear Dynamic Analysis of Tall Bridge Piers Under Multidimensional Pulse Earthquakes Considering Varying Damping Ratios" Applied Sciences 15, no. 9: 4754. https://doi.org/10.3390/app15094754
APA StyleYun, G., & Liu, C. (2025). Nonlinear Dynamic Analysis of Tall Bridge Piers Under Multidimensional Pulse Earthquakes Considering Varying Damping Ratios. Applied Sciences, 15(9), 4754. https://doi.org/10.3390/app15094754





