3-D Point Cloud Registration Using Convolutional Neural Networks

Abstract

This paper develops a registration architecture for the purpose of estimating relative pose including the rotation and the translation of an object in terms of a model in 3-D space based on 3-D point clouds captured by a 3-D camera. Particularly, this paper addresses the time-consuming problem of 3-D point cloud registration which is essential for the closed-loop industrial automated assembly systems that demand fixed time for accurate pose estimation. Firstly, two different descriptors are developed in order to extract coarse and detailed features of these point cloud data sets for the purpose of creating training data sets according to diversified orientations. Secondly, in order to guarantee fast pose estimation in fixed time, a seemingly novel registration architecture by employing two consecutive convolutional neural network (CNN) models is proposed. After training, the proposed CNN architecture can estimate the rotation between the model point cloud and a data point cloud, followed by the translation estimation based on computing average values. By covering a smaller range of uncertainty of the orientation compared with a full range of uncertainty covered by the first CNN model, the second CNN model can precisely estimate the orientation of the 3-D point cloud. Finally, the performance of the algorithm proposed in this paper has been validated by experiments in comparison with baseline methods. Based on these results, the proposed algorithm significantly reduces the estimation time while maintaining high precision.

1. Introduction

Automated assembly systems capable of repeatedly performing assembly tasks with high-precision and high-speed play an indispensable role in modern manufacturing lines. Intuitively, to perform these automated assembly tasks, cameras are employed for the purpose of providing vision feedback to estimate the pose (position and orientation) of objects to the system. Based on the feedback, the system controls manipulators to perform object picking and assembly tasks in order to interact with the environment. In recent years, much of the work related to the vision-based automated assembly was published. S. Huang et al. [1,2] proposed the dynamic compensation to realize a fast peg-in-hole alignment in the case of a large position and attitude uncertainty based on vision information provided by high-speed cameras. In References [3,4], 3-D scenes used to estimate the pose of objects were reconstructed from multiple images acquired by several cameras. Nonetheless, these algorithms encountered some problems when extracting features as well as reconstructing 3-D feature points from images in the case of general objects that have no distinctly geometric and color features. Thus, in order to address these problems, in Reference [2], color features were added to objects which are not real in general automated assembly systems. Besides, in Reference [3], B. Wang et al. reconstructed 3-D point clouds of the object surface by employing two Charge-Coupled Device (CCD) cameras integrated with a laser beam to sweep over objects which increased the complexity in the configuration of these systems. Chang [4] proposed a vision-based control algorithm for automatic back shell assembly related to smartphone assembly based on 3-D reconstruction by two uniocular fields of view of two cameras. In Reference [5], T. R. Savarimuthu et al. developed a three-level cognitive system to perform a complex assembly task, Cranfield benchmark, based on learning by demonstration using 3-D point clouds extracted from BumbleBee2 stereo camera for the purpose of detecting the object and estimating its pose and a Kinect sensor with the aim of tracking the object in real-time, respectively.

With the aforementioned explanations, 3-D point cloud data brings reliability and capability applied for most categories of objects without demanding special features. Moreover, based on great breakthroughs in manufacturing technology, 3-D cameras or 3-D scanners become increasingly common in automation fields because of redeeming features such as the precision, speed and reliability provided by these 3-D cameras. As a result, applications such as 3-D pose estimation, 3-D object detection and segmentation and 3-D point cloud matching based 3-D spatial information were focused in recent years. In particular, regarding 3-D pose estimation, K. Chan et al. [6] developed a 3-D point cloud system with the aim of estimating human pose by using a depth sensor whilst a fusion framework for the purpose of 3-D modeling, object detection and pose estimation from a given set of point clouds in the case of occlusion and clutter is proposed in Reference [7]. Besides, a generic 3-D detection VoxelNet network was developed in Reference [8] to accurately detect objects in 3-D point clouds whereas R. Q. Charles et al. [9] proposed a unified architecture, PointNet, that directly employs 3-D point clouds as the input to carry out object classification, part segmentation and scene semantic parsing. Moreover, in Reference [10], 3-D point clouds and 2-D images were fused to segment complicated 3-D urban scenes in the case of a large scale by using deep learning. When it comes to point cloud matching, in our previous research [11], we proposed to apply a learning-based algorithm to resolve 2-D point cloud matching by using a deep neural network. Therefore, a very challenging task, 3-D point cloud matching, also known as 3-D point cloud registration, that is really meaningful in estimating the pose of objects using convolutional neural networks in automated assembly systems, has been addressed in this paper.

2. Related Work

Basically, point cloud registration consists of two stages including rough registration and precise registration stage for algorithms based on Iterative Closest Point (ICP) approach and its variants. In particular, the rough registration is performed to give an initial estimation about the transformation between two point clouds, followed by the precise registration to refine this estimation to best align these two point clouds. On the one hand, to address the rough registration problem, a well-known algorithm, RANdom Sample Consensus (RANSAC) approach, was proposed in Reference [12] to roughly estimate the rotation and translation between two point clouds. Because of slow computational speed, several variants of the RANSAC algorithm were developed to address this problem such as IMPSAC [13], Preemptive RANSAC [14], Distributed RANSAC [15] and Recursive-RANSAC [16]. Besides, Han et al. [17] proposed an improved RANSAC algorithm based on 3-D Region Covariance (RC) descriptor, RC–RANSAC method, to enhance the successful percentage of point cloud registration in a single repetition when describing region covariance of each point. Additionally, other global registration algorithms in the case of arbitrary initial poses between two point clouds were also published in recent years. In Reference [18], Aiger et al. developed a robust and fast alignment principle, 4-Points Congruent Sets (4PCS) algorithm, employing wide bases robust to outliers and noise for 3-D point clouds based on extracting all sets of coplanar four-points from a 3-D point cloud. Moreover, similarity and affine transform problems were taken into account in their research. However, a drawback existed in their method because 4PCS approach took approximately a quadratic time complexity according to the quantity of data points. Hence, they presented an improvement of 4PCS method, called Super 4PCS approach [19], that degraded the quadratic complexity to linear complexity and confined the volume of candidate conjugate pairs created to tackle this negative point. Super 4PCS approach appeared to be an effective solution to handle 3-D point cloud registration when existing a low overlap and outliers. The other existing approach, the Iterative Closest Point method integrated with the Normal Distribution Transform approach (NDT-ICP), was proposed in Reference [20] with the aim of accelerating the registration speed. In addition, Liu et al. [21] developed a point cloud registration algorithm based on improved digital image correlation approach, followed by the ICP method with a high accuracy, anti-noise capability and efficiency. Moreover, Chang et al. proposed the candidate-based axially switching (CBAS) computed closer point (CCP) algorithm [22] to effectively and robustly address rough registration problem in the case of an arbitrarily initial pose between two point clouds.

On the other hand, as regards the precise registration fulfilled after the rough registration, the most common registration algorithm is the ICP approach proposed by Besl et al. in Reference [23] that minimizes the distance between two point clouds. In addition, many variants of the ICP method were presented in recent years with the aim of improving the original method in some aspects such as high accuracy, high speed, robust registration, scale registration, affine registration and globally-optimal solution. Particularly, dual interpolating point-to-surface algorithm adopting surface fitting by using B-spline to establish correspondences between two point clouds was proposed in Reference [24] to address the precise registration for two point clouds with a partial overlap. Chen et al. [25] developed the Hong-Tan based ICP method (HT-ICP) for the purpose of improving the speed and precision of registration for partially overlapping point clouds. Additionally, a registration algorithm by using the hand and soft assignments to improve the robustness and accuracy for partially overlapping point cloud registration was proposed in Reference [26]. To extend the robustness to noise and/or outliers, the Trimmed ICP approach was presented in Reference [27] that applied the Least Trimmed Squares algorithm in all stages of the operation. In Reference [28], Phillips et al. presented the Fraction ICP method that can robustly identify and discard outliers and guarantee the convergence to a locally optimal solution. The other existing approach, Efficient Sparse ICP method, using sparsity-inducing norms to considerably improve robust registration caused by noise and outliers whilst employing a Simulated Annealing search in order to efficiently resolve the underlying optimization problem was proposed in Reference [29]. Yang et al. [30] developed the ICP-based algorithm integrating with a branch-and-bound (BnB) principle to figure out the globally optimal solution for Euclidean registration between two 3-D surfaces or 3-D point clouds starting from any initialization. Scale-ICP approach integrating a scale factor with the original ICP method was proposed in Reference [31] so as to accurately perform the registration between two 3-D point clouds in the case of large-scale stretches and noises. Wang et al. [32] developed a multi-directional affine registration (MDAR) algorithm by using the statistical characteristics and shape features of point clouds for affine registration problem. In addition to the aforementioned distance-minimization-based registration algorithms, another registration approach using distinct features extracted from 3-D point cloud data sets was also presented in References [33,34,35,36], to robustly and efficiently enhance the registration problem. Particularly, many feature descriptors including local-based descriptor, global-based descriptor and hybrid-based descriptor were presented in recent years and a comprehensive review of the existing algorithms can be sought in Reference [37].

Nevertheless, the aforementioned existing algorithms all are based on randomly selecting different points in two 3-D point clouds to form a pair of corresponding bases in rough registration phase whilst iteratively minimizing the distance between two 3-D point clouds until the convergence within the desired tolerance of ICP-based methods in the precise registration phase. These are the reasons why those algorithms cannot be employed in real-time closed-loop object picking and assembly systems due to their slow computation. In addition to the aforementioned algorithms, there are some approaches related to point cloud registration using deep learning which were developed in recent years. In Reference [38], a point cloud registration method using a deep neural network auto-encoder for outdoor localization between a close-proximity scanned point cloud and a large-scale point cloud was proposed. Specially, Aoki et al. [39] developed an efficient and robust point cloud registration architecture, PointNetLK architecture, based on an iterative image registration approach [40] and PointNet architecture [9]. However, the PointNetLK architecture involved iterative computation with the number of iterations in accordance with a minimum threshold of the optimal twist parameters. In this paper, a seemingly novel efficient algorithm using deep learning is proposed to accelerate the estimation time while maintaining the required accuracy.

The key contributions of this research can be summarized as follows:

• We propose a seemingly novel registration architecture including 3-D convolutional neural networks (3-D CNNs) for the rough registration stage and 2-D CNNs for the precise registration stage that transforms the 3-D point cloud registration problem to a regression problem with estimated outputs as angular disparities between the model point cloud and a data point cloud.
• We propose two descriptors in order to extract distinct features such as Simplified Spatial Point Distribution and 8-Corner-Based Closest Points from a given 3-D point cloud as data sets for the purpose of training the proposed 3-D convolutional neural network (3-D CNN) model and the proposed 2-D CNN model, respectively. After training, the trained CNN models can quickly estimate the rotation between two 3-D point clouds, followed by the translation estimation based on computing average values of these two point cloud data sets in fixed time with high precision.

The remainder of this paper is organized as follows. Section 3 shows the problem formulation and the strategy of 3-D point cloud registration using CNNs. In Section 4, two categories of descriptors employed to extract coarse and detailed features in terms of the orientation of a 3-D point cloud are proposed with the aim of generating training data sets. Section 5 develops the proposed registration architecture which consists of two stages including the rough and precise registration based on 3-D CNN and 2-D CNN architecture, respectively. Finally, Section 6 provides experimental results whilst conclusions of this paper are drawn in Section 7.

3. Problem Formulation

Given the model point cloud P and a data point cloud Q, point cloud registration is to estimate the transformation including the rotation matrix R and the translation vector t between these two point clouds.

$$\begin{array}{c}\hfill \mathit{P}=\{{\mathit{p}}_1,{\mathit{p}}_2,\dots ,{\mathit{p}}_n\},\\ \hfill \mathit{Q}=\{{\mathit{q}}_1,{\mathit{q}}_2,\dots ,{\mathit{q}}_m\}\end{array}$$

(1)

where ${\mathit{p}}_i$ and ${\mathit{q}}_j$ stand for the $i^{th}$ point and $j^{th}$ point in the model and data point cloud, respectively. To fulfill this task, ICP-based approaches minimize an objective function, the mean squared error, based on corresponding closest point pairs $({\mathit{p}}_i,{\mathit{q}}_j)$ in two point clouds as follows.

$$\xi (\mathit{R},\mathit{t})=\frac{1}{m}\sum _{j=1}^m\left|\right|{\mathit{p}}_i-\mathit{R}{\mathit{q}}_j-\mathit{t}{\left|\right|}^2$$

(2)

where m is the number of points in the data point cloud. Because the ICP algorithm can only successfully match if the uncertainty between two point clouds is small enough, an initial registration stage is necessary to address a large uncertainty problem based on the well-known RANSAC approach. Thus, inspired by this two-stage registration process, we propose a deep CNN framework with two consecutive CNN models including the first model for the rough registration and the second model for the precise registration. In the proposed architecture, only rotation angles are estimated instead of estimating both rotation and translation because the translation can be computed by subtracting coordinate values of two corresponding center points of two point clouds. In addition, because of arbitrary translations between two point clouds in 3-D space, it is not reasonable to use the translation vector as ground truth for the purpose of training. Moreover, the limitation of rotations is confined in the range from $-{180}^{\circ }$ to $+{180}^{\circ }$ that make rotation angles potential ground truths for the convergence of the learning process. Figure 1 shows a block diagram of the proposed architecture for 3-D point cloud registration.

Hence, point clouds of an object with different rotation angles in the $xyz$ coordinate system and these corresponding rotation angles are collected with the aim of creating a data set. As regards the CNN architecture, the first CNN model in the rough registration stage is to cover an arbitrary initial rotation in a full range of uncertainty from $-{180}^{\circ }$ to ${180}^{\circ }$ whilst the second CNN model is used in order to refine the rotation estimation in covering a smaller range with a higher angular resolution in the precise registration stage. In particular, in this precise registration stage, a trade-off about selecting the range of the uncertainty of the data set should be satisfied in a such way that this uncertainty is small enough to make the CNN model learn deep characteristics and large enough to cover errors existing after the rough registration stage. In this research, the range of this uncertainty is selected from $-{15}^{\circ }$ to ${15}^{\circ }$ based on experiments. Ideally, only one CNN model can be considered to handle the registration problem if the number of samples for training is large enough to cover the full range of uncertainty with a high resolution of rotation angles. Nonetheless, it is impossible to realize this idea as a huge data set is required in this case that leads to a difficulty in the convergence of solutions and the time-consuming problem during the training process due to using too much training data. Thus, the precision of the rotation estimation is reasonably guaranteed by using this two-stage CNN model. To demonstrate this estimation process, a simple representation of the model and data point cloud in a plane is visualized in Figure 2. Initially, the arbitrarily angular disparity $\alpha$ is witnessed between model and data which is covered in the full range of uncertainty from $-{180}^{\circ }$ to ${180}^{\circ }$. After the first stage, data can be transformed to $dat{a}_1$ based on a rough estimation ${\alpha }_1$ that exists an error $\alpha -{\alpha }_1$ compared with the ground truth $\alpha$. Then, the second CNN model seemingly precise estimates the disparity ${\alpha }_2$ between model and $dat{a}_1$ to finalize the whole angular disparity ${\alpha }_1+{\alpha }_2$ between model and data.

In addition, because points in a general 3-D point cloud are not in order and the number of points is not fixed according to different viewpoints for the same object, a descriptor extracting distinct features from a point cloud is employed to tackle these problems. In this case, a powerful descriptor must be able to capture the geometric structure of a data point cloud that can precisely describe the orientation of this point cloud in the coordinate frame and be invariant to translation. Thereby, instead of directly inputting 3-D point cloud data sets, features extracted from 3-D point clouds based on the descriptors are employed as the input of these CNN models. By using features, every sample in the data set has the same format such as the same order and the same finite size, which is good for the learning process. In accordance with using these descriptors, a comprehensive architecture of the proposed algorithm is illustrated in Figure 3.

4. The Proposed Descriptors for 3-D Point Clouds

In this section, two types of descriptors used to extract features in the rough and precise registration stage, respectively, with the aim of generating the training data sets are given. Intuitively, the first descriptor should extract coarse features roughly describing the orientation of an object to ensure the fast convergence in the learning process whilst detailed features precisely expressing the orientation of the object should be captured by the second descriptor. Before showing procedures to compute these two descriptors, two corresponding data sets in the case of a large uncertainty of rotation angles from $-{180}^{\circ }$ to ${180}^{\circ }$ and a small uncertainty from $-{15}^{\circ }$ to ${15}^{\circ }$, need to be created in advance.

4.1. Point Cloud Data Set Preparation

In order to generate the data set, several 3-D point clouds with different orientations of an object need to be collected. Nevertheless, it is not suitable to collect a large number of 3-D point clouds of an object when using a 3-D scanner to capture these point cloud data sets. Therefore, the data set can be obtained by randomly rotating and downsampling the model point cloud of the object. Particularly, the box grid filter algorithm provided by Matlab is used to downsample the rotated model point cloud to low-resolution point clouds with the different number of points and distribution characteristics. Based on this approach, the created point clouds can simulate disparities among point clouds that would exist in real 3-D point clouds captured by a 3-D camera. The principal difference between two kinds of data sets of an object is that each rotation angle with respect to an axis is randomly initialized with 80 different values in the range from $-{180}^{\circ }$ to ${180}^{\circ }$ for the first data set whereas the second data set is generated based on 80 random values of each rotation angle in the range from $-{15}^{\circ }$ to ${15}^{\circ }$. Totally, there are 3 rotation angles with respect to x, y, and z axis that results in generating ${80}^3$ = 512,000 point clouds with different orientations. Each data set is divided into 3 subsets including training set (392,000 samples), validation set (60,000 samples) and test set (60,000 samples). Algorithm 1 shows procedures step by step in order to generate these data sets.

Algorithm 1 Data set generation

4.2. Simplified Spatial Point Distribution Descriptor

A 3-D data point cloud Q employed as an input of the descriptors can be given as follows

$$\mathit{Q}=\left[\begin{array}{c}{\mathit{q}}_1\\ {\mathit{q}}_2\\ ⋮\\ {\mathit{q}}_m\end{array}\right]=\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ & ⋮& \\ x_m& y_m& z_m\end{array}\right]$$

(3)

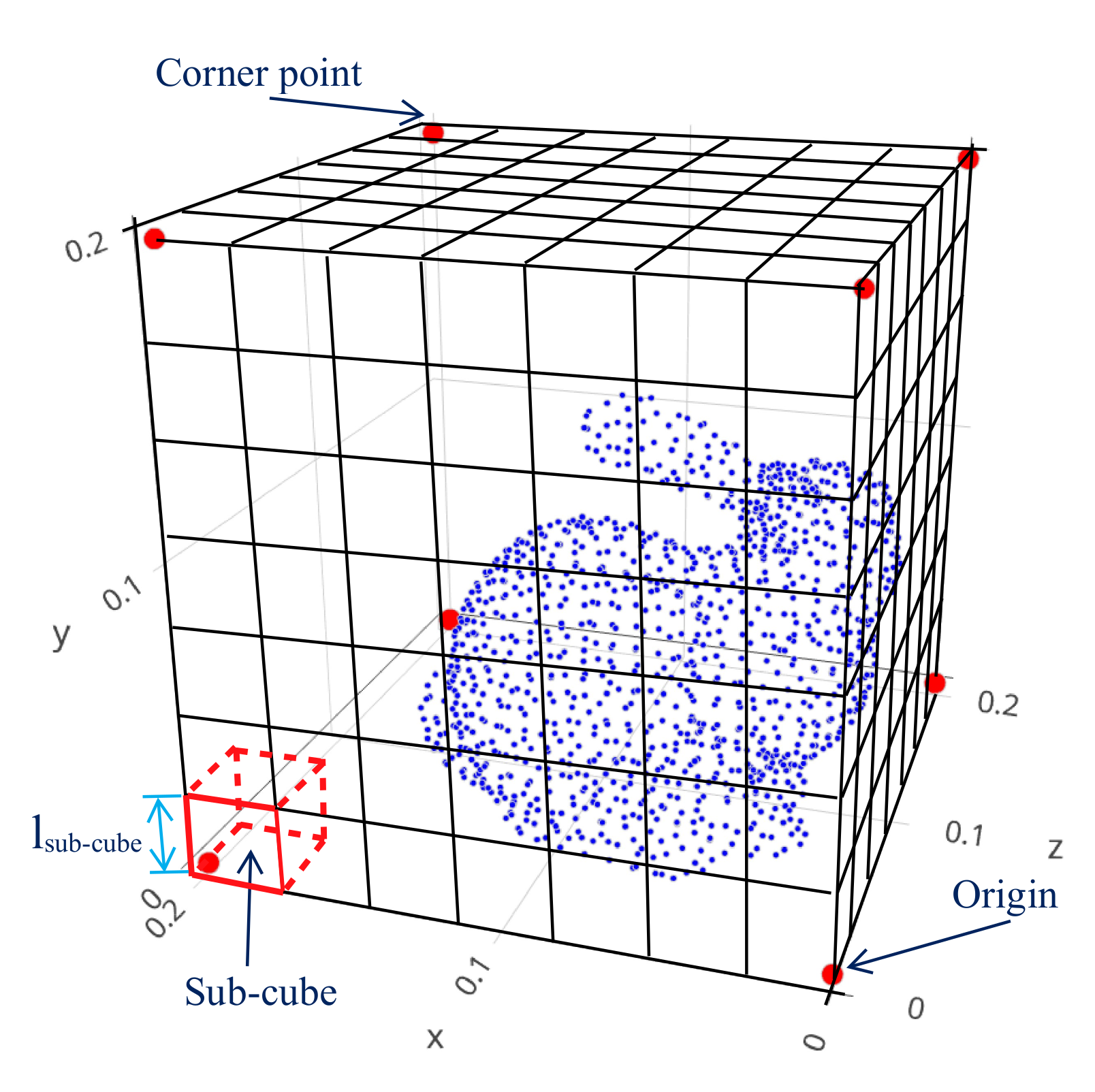
where ${\mathit{q}}_j$ denotes the $j^{th}$ data point. In the first stage, the rough registration stage, features extracted from the point set Q should generally describe the orientation of Q such that a successful and fast convergence in the learning process can be guaranteed. Because the rough registration covers a full range of uncertainty from $-{180}^{\circ }$ to ${180}^{\circ }$ that leads to significant disparities in characteristics of these features, it is hard to obtain optimal weights with a small enough loss for a CNN model after training. Therefore, a Simplified Spatial Point Distribution (SSPD) descriptor is proposed in this paper to describe coarse characteristics of the orientation of a 3-D data point cloud in 3-D space. The key point is to divide a spatial region involving the point set into several sub-regions and count the number of points in each sub-region, followed by a normalization with the total quantity of points of the point cloud. To begin with, a cubic bounding box with the length of an edge $l_{cube}$ is created that consists of the point set.

$$l_{cube}=max\left\{{norm}_2\left({\mathit{q}}_i,{\mathit{q}}_j\right)|i\ne j\right\}$$

(4)

where $nor{m}_2$ denotes the Euclidean distance between two points ${\mathit{q}}_i$ and ${\mathit{q}}_j$. Secondly, this cube is divided into several sub-cubes as shown in Figure 4 with the size of s x s x s where the length of an edge of a sub-cube can be computed as follows.

$$l_{sub-cube}=\frac{l_{cube}}{s}$$

(5)

Finally, the quantity of points in each sub-cube is counted and then divided by the total number of points of the point cloud. Because each sub-cube has one value, SSPD is a 3-D matrix with the size of s × s × s where the parameter $s=15$ is selected based on experiments. Algorithm 2 illustrates steps in details to compute SSPD based on a given 3-D point cloud.

Algorithm 2 Offline computations of SSPD

4.3. 8-Corner-Based Closest Points Descriptor

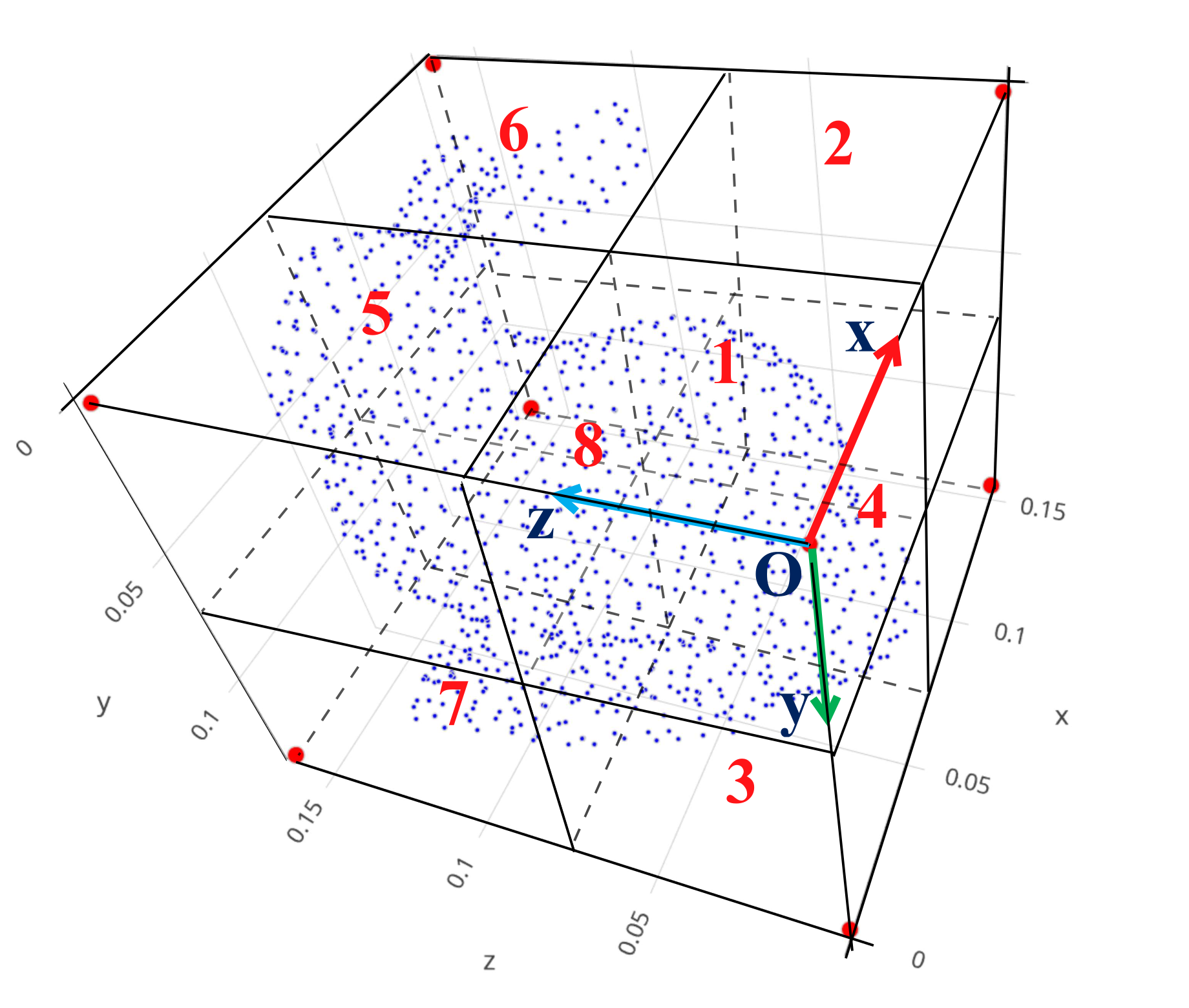
In comparison with the SSPD descriptor for the rough registration, features employed for training a CNN model to precisely estimate the spatial orientation of a given 3-D point cloud should be able to thoroughly describe the characteristics of this point set in details. Thereby, 8-Corner-Based Closest Points (8CBCP) descriptor is proposed in this paper for the purpose of extracting oriented characteristics of a 3-D point cloud in 3-D space. As shown in the name of this descriptor, the main point is to find d closest points according to each corner of the Axis-Aligned Bounding Box (AABB) [41] of a data point cloud. Based on considering each corner of AABB as a viewpoint when observing the point cloud, the 8CBCP descriptor possesses the robustness in describing oriented features of this point cloud and a simple format because only key points can be collected. In addition, by numbering corners and arranging closest points with a suitably predetermined order, the problem without a specific order of a general point cloud can be effectively addressed. Moreover, to tackle the problem about the disparity in the point distribution among point clouds, the coordinate values of these closest points are normalized with the total number of points of the corresponding point cloud. Hence, the result of 8CBCP is a 2-D matrix with the size of $8d$× 3 because $8d$ corresponding closest points can be obtained based on 8 corners. In this research, d is selected based on a trade-off between the total number of points of a point cloud at approximately 1000 points after downsampling and the necessary number of points according to each corner for the purpose of describing orientation features of a point set. Thus, by testing in experiments, d is chosen at 40 points. Although this paper focuses on whole point cloud registration, 8CBCP can be a potential descriptor when resolving partial point cloud registration problem due to multiple different observations applied for one object. Algorithm 3 shows computation procedures in details to generate 8CBCP features of a given 3-D point cloud.

Algorithm 3 Offline computations of 8CBCP

Input: Data point cloud $\mathit{Q}$;

1: Compute $AABB$ and use these parameters to make a cube that bounds of the data point cloud;

$w=max\left\{x_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\}-min\left\{x_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\};$

$d=max\left\{y_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\}-min\left\{y_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\};$

$h=max\left\{z_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\}-min\left\{z_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\};$

2: Shift all points to the first quadrant;

$x_{{\mathit{q}}_i}=x_{{\mathit{q}}_i}-min\left\{x_{{\mathbf{q}}_i}|i=1,2,\dots ,m\right\};y_{{\mathit{q}}_i}=y_{{\mathit{q}}_i}-min\left\{y_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\};$

$z_{{\mathit{q}}_i}=z_{{\mathit{q}}_i}-min\left\{z_{{\mathit{q}}_i}|i=1,2,\dots ,m\right\};$

3: Divide the cube into 8 sub-cubes numbered from 1 to 8 and bin points into the according sub-cube as shown in Figure 5;

4: Based on 8 corner points, red points, of the cube, scan d closest points in the corresponding sub-cube of each corner as illustrated in Figure 6;

5: According to the closest points in terms of each corner in the corresponding sub-cube, consider each corner as a local origin $O_k(k=1,2,\dots ,8)$ and transfer coordinate values of these closest points with respect to the corresponding local frame (Figure 7), followed by a normalization by the total number of points m of the data point cloud;

$$\left[\begin{array}{c}{}^{\left\{k\right\}}{\alpha }_i\\ {}^{\left\{k\right\}}{\beta }_i\\ {}^{\left\{k\right\}}{\gamma }_i\end{array}\right]=\frac{1}{m}\left|\left[\begin{array}{c}{x}_{{\mathit{q}}_i}\hfill \\ y_{{\mathit{q}}_i}\hfill \\ z_{{\mathit{q}}_i}\hfill \end{array}\right]-\left[\begin{array}{c}{x}_{O_k}\\ y_{O_k}\\ z_{O_k}\end{array}\right]\right|;$$

where ${}^{\left\{k\right\}}{\alpha }_i$, ${}^{\left\{k\right\}}{\beta }_i$, ${}^{\left\{k\right\}}{\gamma }_i$ stand for three coordinates according to three axes of point $q_i$ with respect to the local frame $\left\{k\right\}$;

6: Compute 8CBCP, a 2-D matrix with the size of $8d$ x 3;

$$\mathit{8}\mathit{CBCP}={\left[\begin{array}{c}{}^{\left\{1\right\}}{\alpha }_1\cdots {}^{\left\{1\right\}}{\alpha }_d{}^{\left\{2\right\}}{\alpha }_1\cdots {}^{\left\{2\right\}}{\alpha }_d\cdots {}^{\left\{8\right\}}{\alpha }_1\cdots {}^{\left\{8\right\}}{\alpha }_d\\ {}^{\left\{1\right\}}{\beta }_1\cdots {}^{\left\{1\right\}}{\beta }_d{}^{\left\{2\right\}}{\beta }_1\cdots {}^{\left\{2\right\}}{\beta }_d\cdots {}^{\left\{8\right\}}{\beta }_1\cdots {}^{\left\{8\right\}}{\beta }_d\\ {}^{\left\{1\right\}}{\gamma }_1\cdots {}^{\left\{1\right\}}{\gamma }_d{}^{\left\{2\right\}}{\gamma }_1\cdots {}^{\left\{2\right\}}{\gamma }_d\cdots {}^{\left\{8\right\}}{\gamma }_1\cdots {}^{\left\{8\right\}}{\gamma }_d\end{array}\right]}^T;$$

Output: 8CBCP of a data point cloud.

5. The Proposed CNN Architectures

Based on two kinds of features including SSPD and 8CBCP shown in Section 4, the corresponding CNN architectures are developed in this section with the aim of estimating the orientation of a 3-D point cloud on the generated point cloud data set. Related to the first stage, the rough registration, because the input of CNN model is SSPD, a 3-D matrix with the size of s × s × s, a 3-D CNN model is selected. When it comes to the second stage, the precise registration, a 2-D CNN model is employed in accordance with the size of the input 8CBCP in the case of a 2-D matrix. Figure 8 shows the proposed 3-D architecture for the rough registration whilst the proposed 2-D architecture for the precise registration is demonstrated in Figure 9.

5.1. 3-D CNN Architecture for Rough Registration

As shown in Figure 8, to start with, SSPD with the size of s × s × s extracted from an input point cloud is convoluted with each of 16 kernels with the size of 2 × 2 × 2 that results in 16 feature maps in the layer C1. Then, to continuously increase the number of feature maps, we apply 3-D convolutions with the same kernel size 2 × 2 × 2 as the first convolutional layer for the layer C2 and C3. Consequently, the layer C2 has 32 feature maps while there are 64 feature maps in the layer C3. Additionally, in these layers C1, C2 and C3, zero padding is used in convolutional operations such that the output of feature maps has the same size as the original input. Moreover, after the convolutional operation, the result is added with a bias and then passed through a hyperbolic tangent activation function $tanh(.)$ to generate the output of each feature map as follows.

$${\chi }_k=tanh(b_k+\sum _i{w}_{ki}\ast x_i)$$

(6)

where ${\chi }_k$ stands for the output of the $k^{th}$ feature map, $b_k$ is a bias of the $k^{th}$ feature map, $w_{ki}$ denotes the weight of kernel connected from the $i^{th}$ input map, $x_i$ means the $i^{th}$ input map and * denotes the convolutional operation. In the subsequent layer, the 3-D max-pooling layer S1 with a window size of 2 × 2 × 2 is applied to each of the feature maps in the layer C3 that results in the same quantity of feature maps but a reduced spatial dimension, which is two times smaller. Next, the output of the max-pooling layer S1 is flattened to become a feature vector such that each element in this vector is fully connected to each of 2048 neurons in the layer H1. Similarly, the output of the layer H1 is fully connected to the layer H2 with 1024 neurons whilst the fully connected layer H3 has 512 neurons connected from the output of the layer H2. Finally, neurons of the last fully connected layer H3 are connected to 3 neurons representative for the estimation of Euler angles in the output layer. The activation function used in each neuron in these fully connected layers is $tanh(.)$ function.

5.2. 2-D CNN Architecture for Precise Registration

With the explanations in the previous section, because the 8CBCP descriptor collects d closest points according to each corner of AABB to generate one sample, there are totally 8 closest point groups that play an equal role in describing the orientation of a 3-D point cloud. Inspired by this idea, the proposed architecture of the 2-D CNN model employs 8 sub-models in parallel in order to independently estimate Euler angles, followed by an average computation of these estimated Euler angles. As shown in Figure 9, as regards the first sub-model, the first part with the size of d × 3 of 8CBCP extracted from an input point cloud is convoluted with each of 8 kernels with the size of 5 × 1 that results in 8 feature maps in the layer C1. Then, the quantity of feature maps is continuously grown in the sequential layers by applying 2-D convolutional operations with a kernel size of 5 × 1 similar to the previous layer C1. As a result, the layer C2 and C3 have 16 feature maps and 32 feature maps, respectively. Similar to 3-D CNN architecture used in the rough registration, zero padding is applied in convolutional operations so as to make no modification about the size of the output of feature maps compared with the original input. Additionally, before being connected to the next layers, the output of the convolutional operation is added by a bias and then delivered to the activation function $tanh(.)$ to create the output of feature maps. Next, the output of feature maps in the layer C3 is passed through the 2-D max-pooling layer S1 with a window size of 2 × 1 that leads to a reduced spatial dimension, which is two times smaller but the same number of feature maps. Then, the output of the max-pooling layer S1 is flattened as a feature vector and elements in this vector is fully connected to each of 1024 neurons in the layer H1. In the same way, the output of the layer H1 is fully connected to 512 neurons in the layer H2 and the outputs of the layer H2 are fully connected to the layer H3 with 256 neurons. Eventually, neurons in the layer H3 are connected to 3 neurons in the output layer $Output1$ which figures out a more precise estimation of Euler angles ${\psi }_1,{\theta }_1,{\varphi }_1$ in comparison with the estimation in the rough registration stage. Besides, the activation function applied for neurons in fully connected layers is $tanh(.)$ function. Similar to the first sub-model, 7 sub-models left from the second sub-model to the eighth sub-model possess the same 2-D CNN architecture with the output from ${\psi }_2,{\theta }_2,{\varphi }_2$ to ${\psi }_8,{\theta }_8,{\varphi }_8$, respectively. After all estimations of 8 sub-models, an average computation of these Euler angles is required to obtain the mean estimation of the orientation of a data point cloud as the output of the whole 2-D CNN model as follows.

$${\left[\begin{array}{ccc}\psi & \theta & \varphi \end{array}\right]}^T=\frac{1}{8}{\left[\begin{array}{ccc}{\displaystyle \sum _{k=1}^8{\psi }_k}& {\displaystyle \sum _{k=1}^8{\theta }_k}& {\displaystyle \sum _{k=1}^8{\varphi }_k}\end{array}\right]}^T$$

(7)

6. Experiments

In this section, experimental results for 3-D point cloud registration are provided to validate the proposed registration algorithm based on CNN architectures. In particular, when it comes to point cloud data, open data including “Bunny”, “Dragon” & “Buddha”, “Armadillo” and “Horse” from the Stanford 3-D Scanning Repository [42,43,44] and NTU CSIE [45], respectively, are employed. Besides, two algorithms such as the “RANSAC then ICP” (RANSAC+ICP) algorithm using Fast Point Feature Histograms (FPFH) [46] to describe features for point clouds and the “Fast Global Registration” (FGR) algorithm [47] provided in Open3D [48,49], a modern library for 3-D data processing, are applied to evaluate the performance of the proposed algorithm. Moreover, in order to give the quantitative evaluation, in addition to the computation time, the mean squared error (MSE) value used to compare the matching rate among these methods is given as follows [22].

$$MSE=\frac{1}{m}\sum _{j=1}^m\left|\right|{\mathit{p}}_i-{\mathit{q}}_j\left|\right|$$

(8)

where m is the number of points in the data point cloud and ${\mathit{p}}_i$ and ${\mathit{q}}_j$ stand for the corresponding closest points in the model point cloud and the data point cloud, respectively. All programs performing these approaches are programmed in Python on an Intel Core i9-9900K CPU @3.6GHz PC equipped with a GeForce RTX 2080 Ti SEA HAWK X Graphics Processing Unit (GPU). In the training process, for each of point cloud data, it takes about 6 hours and 3 hours to train a 3-D CNN model for the rough registration and a 2-D CNN model for the precise registration, respectively. Nevertheless, transfer learning can be employed to reduce the training time of CNN models for a new 3-D point cloud data.

After training, 20 unforeseen samples which are generated by randomly rotating and translating, followed by downsampling the model point cloud, according to each of these five data sets including Bunny, Horse, Dragon, Buddha and Armadillo are employed to validate the performance of the trained CNN models as well as two other approaches such as RANSAC+ICP and FGR approach.

Table 1. The comparisons about mean squared error (MSE) and computation time of “Bunny” data for test samples from 1 to 10.

Test Sample	1		2		3		4		5		6		7		8		9		10
Points (n, m)	(1116, 1015)		(1116, 990)		(1116, 1032)		(1116, 1012)		(1116, 1001)		(1116, 979)		(1116, 1025)		(1116, 982)		(1116, 985)		(1116, 1015)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	3.219	0.025	3.172	0.027	3.418	0.026	3.192	0.025	2.948	0.026	2.957	0.024	3.150	0.025	2.851	0.023	3.096	0.025	3.040	0.025
RANdom SAmple Consensus
then Iterative Closest Point
(RANSAC then ICP)	3.113	0.327	3.036	0.214	3.750	0.140	3.100	0.173	2.979	0.291	2.933	0.459	2.879	0.437	2.845	0.465	2.917	0.451	2.812	0.411
Fast Global Registration	3.266	0.045	3.297	0.032	13.450	0.032	3.420	0.033	3.042	0.043	3.518	0.048	2.880	0.048	3.286	0.055	2.917	0.048	3.000	0.070

shows a comparison on the MSE and computation time for test samples from 1 to 10 of Bunny data whilst the similar comparison for test samples from 11 to 20 is given

Table 2. The comparisons about MSE and computation time of “Bunny” data for test samples from 11 to 20.

Test Sample	11		12		13		14		15		16		17		18		19		20
Points (n, m)	(1116, 1005)		(1116, 1002)		(1116, 973)		(1116, 1001)		(1116, 1011)		(1116, 1004)		(1116, 1016)		(1116, 997)		(1116, 993)		(1116, 993)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	3.045	0.024	2.957	0.025	2.934	0.025	3.141	0.026	3.048	0.025	2.989	0.027	3.183	0.025	2.974	0.024	3.155	0.024	3.057	0.024
RANSAC then ICP	2.904	0.645	3.357	0.128	2.875	0.288	3.875	0.118	3.522	0.221	2.867	0.307	2.923	0.277	2.889	0.392	2.976	0.145	2.827	0.255
Fast Global Registration	3.135	0.076	3.459	0.031	2.883	0.046	14.322	0.028	12.704	0.030	3.050	0.037	2.941	0.040	2.914	0.049	3.106	0.032	3.124	0.039

where n and m stand for the number of points in the model and data point cloud, respectively. When it comes to the MSE, the smaller MSE is, the better registration result is. Generally, it is noticeable that from all the three algorithms, FGR algorithm gives the worst result in terms of MSE value whereas the results of the proposed approach are a little bit worse than RANSAC+ICP method. Particularly, although FGR method shows the smaller computation time compared with RANSAC+ICP method, MSE values according to this method are quite large with three imprecise estimations observed in samples 3, 14 and 15. Besides, the maximum MSE value at approximately 3.418 mm in sample 3 and the minimum MSE at around 2.851 mm in sample 8 experienced in the proposed algorithm shows the lowest disparity, nearly 0.567 mm, in all estimations of 20 test samples while these differences are witnessed at around 1.063 mm and 11.442 mm in accordance with RANSAC+ICP and FGR approach, respectively. This shows that the developed registration architecture possesses the best stable result in estimating the transformation between two 3-D point clouds in the case of Bunny data. In addition to this advantage, obviously, the smallest computation time is also experienced in the proposed algorithm with the largest value at around 0.027 s whilst it takes approximately 0.140 s and 0.028 s (an imprecise estimation) for the fastest estimation in the case of RANSAC+ICP and FGR approach, respectively. Similar to Bunny data, comparable results on two benchmarks including the MSE and computation time for these three algorithms are shown in

Table 3. The comparisons about MSE and computation time of “Horse” data for test samples from 1 to 10.

Test Sample	1		2		3		4		5		6		7		8		9		10
Points (n, m)	(1009, 971)		(1009, 962)		(1009, 962)		(1009, 948)		(1009, 988)		(1009, 952)		(1009, 957)		(1009, 964)		(1009, 943)		(1009, 960)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	2.559	0.021	2.573	0.022	2.765	0.022	2.330	0.022	2.419	0.022	2.467	0.022	2.333	0.022	2.926	0.022	2.461	0.022	2.528	0.022
RANSAC then ICP	2.332	0.784	3.365	0.527	2.636	0.465	2.381	0.337	2.457	0.422	2.488	0.183	2.310	0.795	2.374	0.749	2.490	0.452	2.553	0.271
Fast Global Registration	2.418	0.131	10.138	0.049	3.537	0.041	3.779	0.036	2.612	0.047	4.917	0.033	2.420	0.112	2.471	0.126	3.567	0.035	4.345	0.031

,

Table 4. The comparisons about MSE and computation time of “Horse” data for test samples from 11 to 20.

Test Sample	11		12		13		14		15		16		17		18		19		20
Points (n, m)	(1009, 965)		(1009, 965)		(1009, 962)		(1009, 968)		(1009, 984)		(1009, 964)		(1009, 963)		(1009, 976)		(1009, 976)		(1009, 970)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	2.647	0.022	2.659	0.022	2.444	0.022	2.588	0.022	2.354	0.023	4.565	0.022	2.520	0.022	2.607	0.022	2.468	0.023	2.513	0.022
RANSAC then ICP	2.363	0.704	2.385	0.984	2.439	0.692	2.485	0.417	2.544	0.241	2.476	0.324	2.369	0.754	2.994	0.296	2.509	0.290	2.351	0.651
Fast Global Registration	2.577	0.125	2.496	0.073	2.695	0.053	4.754	0.038	8.123	0.033	3.311	0.033	2.463	0.127	7.756	0.038	5.001	0.033	3.148	0.051

,

Table 5. The comparisons about MSE and computation time of “Dragon” data for test samples from 1 to 10.

Test Sample	1		2		3		4		5		6		7		8		9		10
Points (n, m)	(1041, 990)		(1041, 1020)		(1041, 1010)		(1041, 1011)		(1041, 1014)		(1041, 992)		(1041, 973)		(1041, 992)		(1041, 995)		(1041, 1003)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	3.350	0.021	3.565	0.023	3.462	0.022	3.425	0.022	3.320	0.024	3.440	0.022	3.662	0.022	3.459	0.022	3.430	0.021	3.437	0.023
RANSAC then ICP	6.608	0.127	4.201	0.105	3.489	0.288	3.837	0.118	5.092	0.104	4.274	0.107	4.350	0.115	3.293	0.365	3.264	0.827	3.615	0.110
Fast Global Registration	12.770	0.042	11.011	0.040	3.694	0.044	4.693	0.040	19.807	0.042	21.254	0.040	12.617	0.039	3.395	0.063	3.277	0.104	5.337	0.039

,

Table 6. The comparisons about MSE and computation time of “Dragon” data for test samples from 11 to 20.

Test Sample	11		12		13		14		15		16		17		18		19		20
Points (n, m)	(1041, 999)		(1041, 998)		(1041, 1010)		(1041, 978)		(1041, 970)		(1041, 984)		(1041, 997)		(1041, 1012)		(1041, 1015)		(1041, 1005)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	3.611	0.022	3.471	0.022	3.427	0.022	3.332	0.024	9.643	0.022	3.348	0.021	3.431	0.022	3.368	0.021	3.568	0.023	3.564	0.022
RANSAC then ICP	4.374	0.128	5.802	0.107	3.576	0.111	4.474	0.122	3.889	0.122	3.823	0.105	4.232	0.120	4.992	0.110	6.352	0.110	3.558	0.190
Fast Global Registration	4.895	0.041	13.340	0.039	3.914	0.043	12.717	0.039	19.966	0.041	21.143	0.038	4.364	0.040	10.031	0.040	9.287	0.040	3.543	0.043

,

Table 7. The comparisons about MSE and computation time of “Buddha” data for test samples from 1 to 10.

Test Sample	1		2		3		4		5		6		7		8		9		10
Points (n, m)	(1045, 963)		(1045, 926)		(1045, 975)		(1045, 984)		(1045, 986)		(1045, 965)		(1045, 956)		(1045, 935)		(1045, 949)		(1045, 941)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	2.836	0.025	3.072	0.024	2.795	0.024	2.898	0.023	3.189	0.024	2.776	0.024	2.871	0.024	2.815	0.024	2.794	0.024	3.192	0.023
RANSAC then ICP	2.880	0.329	3.188	0.398	2.773	0.784	3.203	0.269	2.772	0.336	2.887	0.459	3.107	0.271	3.931	0.258	2.921	0.378	3.563	0.300
Fast Global Registration	2.924	0.048	6.434	0.045	3.167	0.088	6.619	0.040	3.487	0.047	4.040	0.054	3.299	0.044	8.494	0.044	4.252	0.053	9.496	0.055

,

Table 8. The comparisons about MSE and computation time of “Buddha” data for test samples from 11 to 20.

Test Sample	11		12		13		14		15		16		17		18		19		20
Points (n, m)	(1045, 963)				(1045, 989)		(1045, 934)		(1045, 973)		(1045, 931)		(1045, 976)		(1045, 975)		(1045, 934)		(1045, 1007)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	3.140	0.025	2.961	0.024	2.812	0.024	2.808	0.023	2.928	0.024	2.848	0.023	2.868	0.025	2.874	0.025	2.847	0.024	2.943	0.025
RANSAC then ICP	2.808	0.465	2.761	0.525	2.876	0.270	2.739	0.305	3.469	0.263	2.796	0.665	3.334	0.400	2.867	0.542	3.066	0.163	2.931	0.263
Fast Global Registration	3.152	0.046	3.205	0.053	4.283	0.042	3.875	0.048	6.827	0.042	4.094	0.062	7.933	0.043	3.355	0.060	5.291	0.038	4.720	0.041

,

Table 9. The comparisons about MSE and computation time of “Armadillo” data for test samples from 1 to 10.

Test Sample	1		2		3		4		5		6		7		8		9		10
Points (n, m)	(1046, 984)		(1046, 969)		(1046, 937)		(1046, 966)		(1046, 961)		(1046, 939)		(1046, 958)		(1046, 968)		(1046, 949)		(1046, 952)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	2.632	0.025	2.738	0.024	2.689	0.024	2.507	0.024	2.412	0.023	2.899	0.025	2.479	0.024	2.733	0.026	2.784	0.024	2.678	0.024
RANSAC then ICP	2.376	0.658	3.056	0.741	2.473	0.357	2.631	0.261	2.472	0.562	2.381	0.365	2.340	0.924	3.226	0.743	2.342	0.543	3.308	0.704
Fast Global Registration	2.404	0.131	10.075	0.091	2.887	0.040	10.415	0.039	3.368	0.040	5.443	0.044	2.387	0.129	9.998	0.086	2.943	0.054	9.824	0.106

and

Table 10. The comparisons about MSE and computation time of “Armadillo” data for test samples from 11 to 20.

Test Sample	11		12		13		14		15		16		17		18		19		20
Points (n, m)	(1046, 966)		(1046, 977)		(1046, 955)		(1046, 978)		(1046, 963)		(1046, 963)		(1046, 956)		(1046, 949)		(1046, 965)		(1046, 974)
Benchmark	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time	MSE	Time
3-D CNNs then 2-D CNNs	2.862	0.024	2.900	0.024	2.713	0.024	2.635	0.026	2.887	0.024	2.786	0.024	2.671	0.023	2.954	0.024	2.780	0.024	2.638	0.026
RANSAC then ICP	2.392	0.514	2.367	0.631	3.162	0.328	2.551	0.808	2.554	0.198	3.281	0.260	2.444	0.503	2.471	0.230	2.699	0.206	2.788	0.388
Fast Global Registration	3.156	0.042	2.522	0.130	9.796	0.039	9.875	0.115	12.566	0.038	10.099	0.037	3.637	0.040	6.806	0.037	12.101	0.034	10.938	0.040

for Horse, Dragon, Buddha and Armadillo data, respectively.

In order to draw thorough comparisons and reinforce an efficient improvement on reducing the computation time but maintaining the high precision when estimating the pose of a 3-D data point cloud of the proposed algorithm, average values in terms of the MSE and computation time of all tested samples for 5 objects are figured out and visualized into two bar charts as shown in Figure 10 and Figure 11. In fact, it is obvious that FGR method witnesses the strongest fluctuation as well as the highest error of MSE values that lead to the worst performance in terms of the precision of this method. Particularly, the average MSE value of 5 tested objects of this approach is approximately two times as high as the average MSE value of the proposed and RANSAC+ICP approach as illustrated in the last column group in Figure 10. In addition, the lowest discrepancy among the average MSE values of 5 tested objects at roughly 1.130 mm, followed by a larger disparity at approximately 1.840 mm according to RANSAC+ICP approach, draws that our CNNs-based algorithm achieves the robust performance for a variety of objects. Moreover, the proposed approach matches the comparable precision with a slightly smaller average MSE value at around 0.108 mm in comparison with RANSAC+ICP algorithm as given in the column group “Average” in Figure 10. As regards the computation time, the presented algorithm significantly outperforms with approximately 15 times and 2 times as fast as RANSAC+ICP and FGR method, respectively, as shown in the last column group in Figure 11.

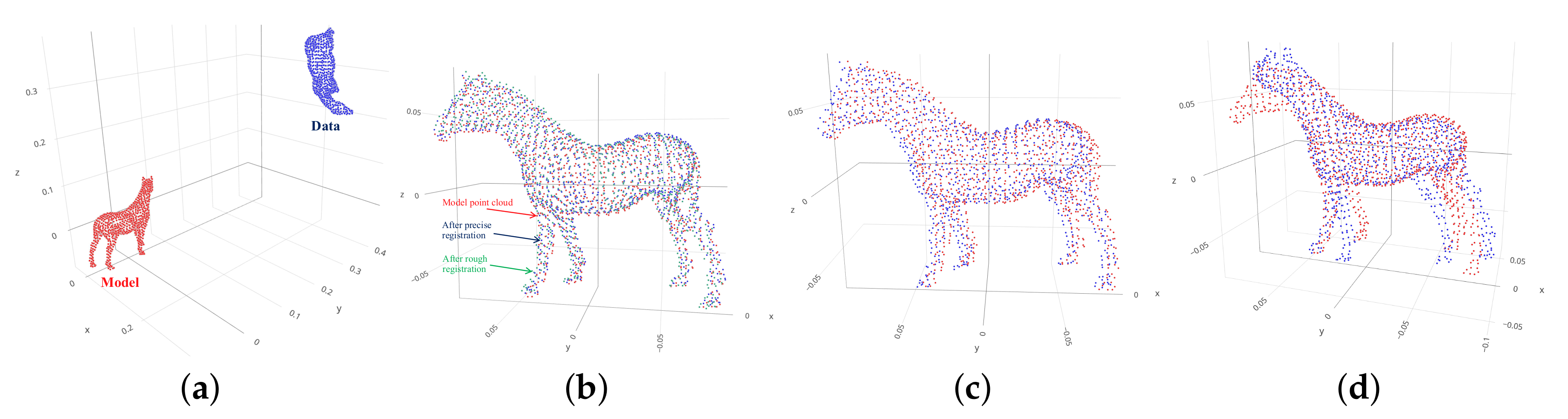
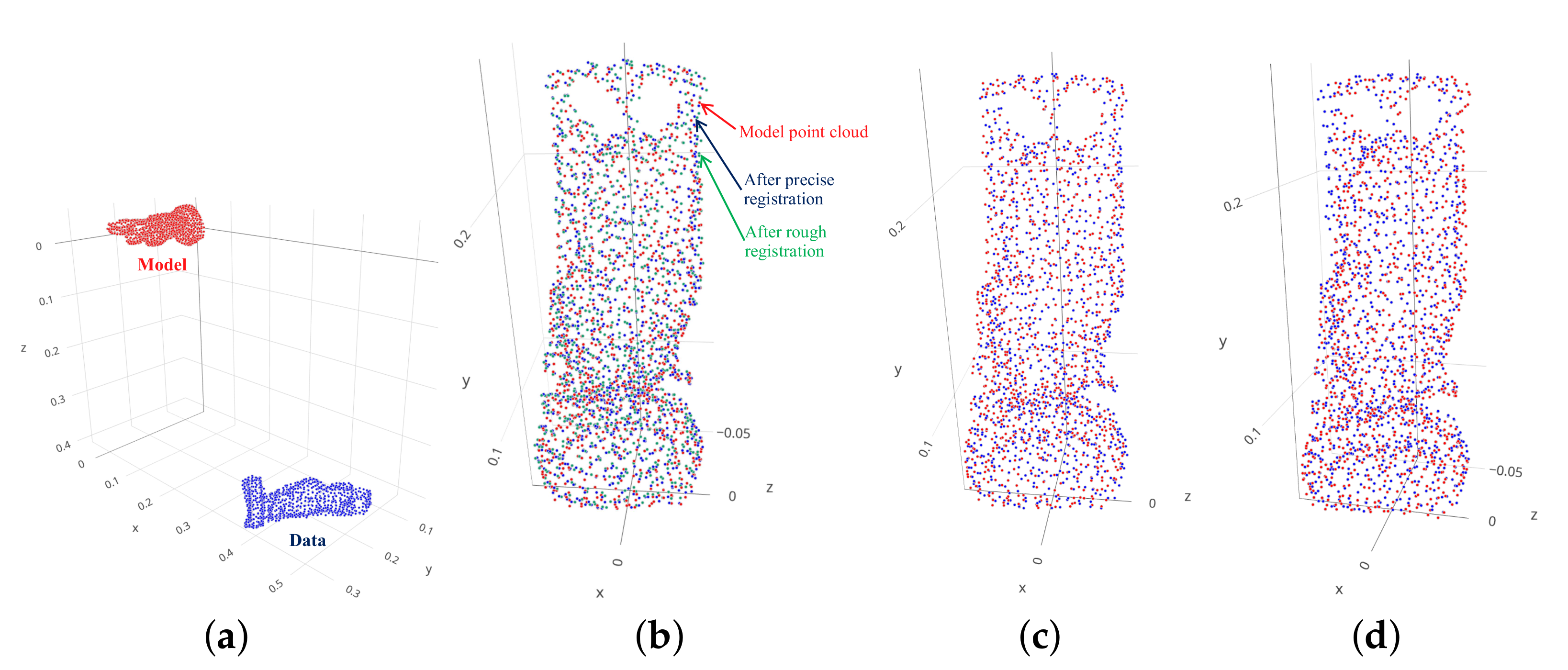
To conclude these comparisons, registration results of these three algorithms with specific samples are visualized in Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 for Bunny, Horse, Dragon, Buddha and Armadillo data, respectively. It is noticeable that data point clouds transformed by the proposed and RANSAC+ICP algorithm are closer to the model point clouds than FGR approach. Additionally, as shown in Figure 12b, Figure 13b, Figure 14b, Figure 15b and Figure 16b, the registration result in the precise stage (blue point cloud) is better than the result in the rough stage (green point cloud) because the 2-D CNN model covers a smaller uncertainty from $-{15}^{\circ }$ to ${15}^{\circ }$ than the 3-D CNN model with the full range of uncertainty from $-{180}^{\circ }$ to ${180}^{\circ }$. Therefore, based on 3-D point clouds of an object captured by a 3-D camera, the pose of the object can be precisely estimated in fixed time that is sufficient for the application of real-time closed-loop object picking and assembly systems because of two redeeming features such as the high accuracy and fast estimation.

7. Conclusions

This paper resolves the time-consuming problem of 3-D point cloud registration. The estimation time is significantly shortened by using the proposed two-stage CNN architecture, 3-D CNN model and 2-D CNN model. To generate the training data sets, firstly, the model point cloud of a specific object is randomly rotated in the full range from $-{180}^{\circ }$ to ${180}^{\circ }$ and the small range from $-{15}^{\circ }$ to ${15}^{\circ }$ and then downsampled several times. Then, these two point cloud data sets, according to the full range and the small range of rotation angles, are passed through two descriptors, SSPD and 8CBCP, respectively. Based on these training data sets, CNN models are independently trained for each specific object to update optimal weights with the aim of estimating the relative orientation between the 3-D model point cloud and a 3-D data point cloud. Specifically, to guarantee comparable accuracy with existing algorithms such as RANSAC then ICP approach, the 2-D CNN model is trained on the labeled data set created by the 8CBCP descriptor. Hence, in the training process, this 2-D CNN model can thoroughly learn distinct characteristics of several point clouds with different orientations in the case of the small uncertainty. After training, the proposed two-stage CNN architecture can quickly estimate the transformation between the model point cloud and a data point cloud in which the translation is estimated based on the average values of these two point cloud data sets. The experimental results show that the proposed algorithm can precisely and quickly estimate the relative transformation between the model point cloud and a data point cloud in fixed time. This leads to potential significance and applicability of the proposed algorithm for the purpose of estimating the pose of an object based on 3-D point clouds in automated assembly systems. Additionally, according to the results of this research, 3-D partial point cloud registration employing CNNs appears to be an important direction of future research.