Pore Water Conversion Characteristics during Methane Hydrate Formation: Insights from Low-Field Nuclear Magnetic Resonance (NMR) Measurements
Abstract
:1. Introduction
2. Experiment
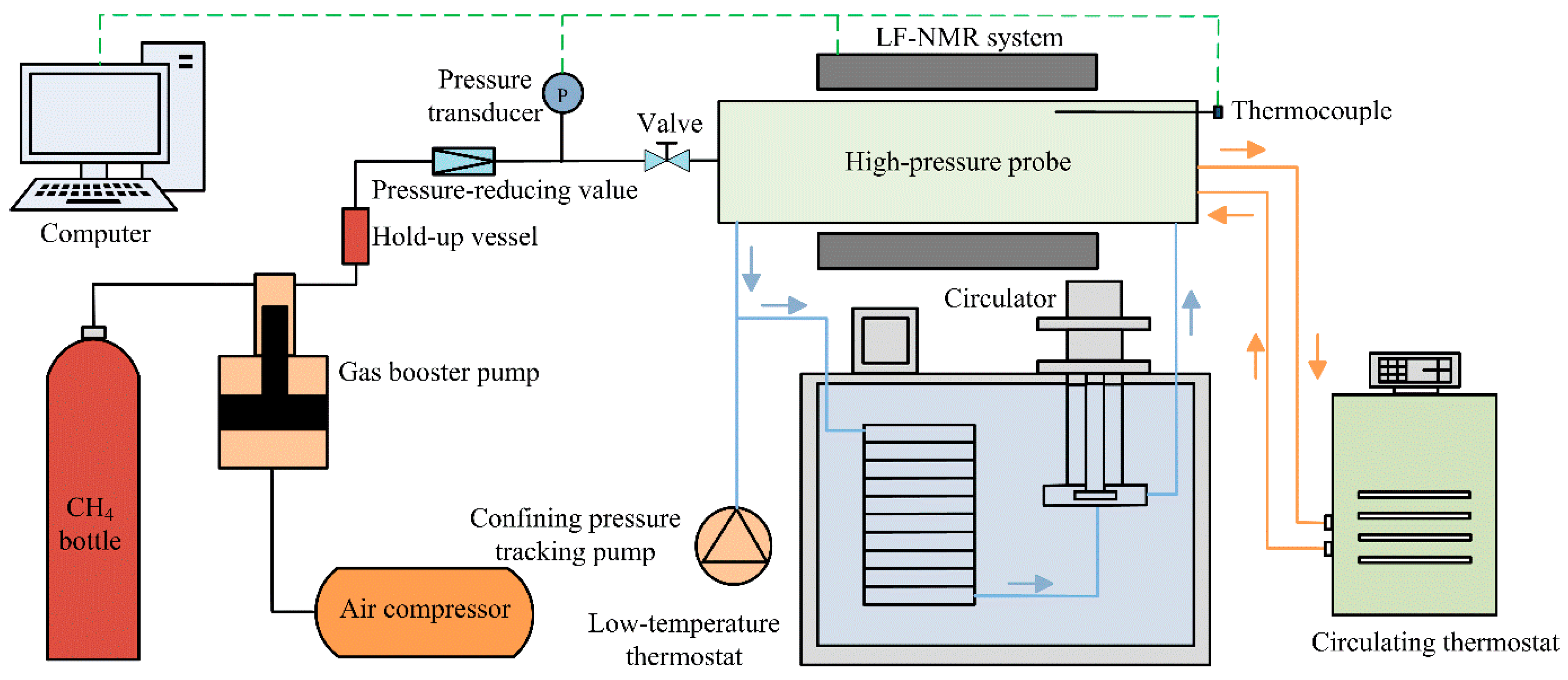
2.1. Experimental Equipment
2.2. Experimental Materials
2.3. Experimental Procedures
- (1)
- The sand weight was calculated based on the filling volume of the sample chamber, the sand density, and the sand sample porosity. The deionized water weight was calculated according to the water saturation. Sand and water were mixed thoroughly, sealed, and placed in a cool place for 24 h.
- (2)
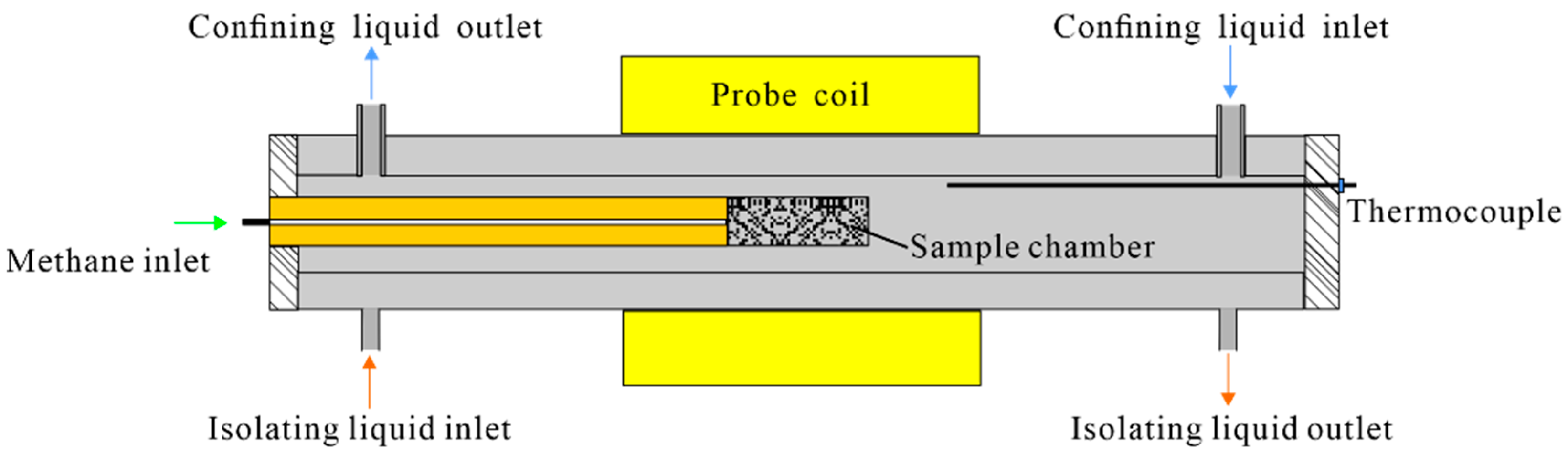
- The sand sample was loaded into the low-temperature and high-pressure probe module (Figure 2). The measurement parameters of T2 distribution were determined.
- (3)
- The sand sample was removed from the low-temperature and high-pressure probe module and sealed for storage. The standard samples with different water contents (Suzhou Niumag Analytical Instrument Corp., Suzhou, China) were cooled to 275.65 K in the thermostat. Next, these standard samples were loaded into the low-temperature and high-pressure probe module one by one. The measurement parameters in the procedure (2) were used to obtain T2 distributions corresponding to standard samples with different water contents at the experimental temperature. Based on these data, the calibration curve was obtained. Based on the calibration curve and the NMR signal intensity of T2 distribution, the water content in the sand sample could be determined.
- (4)
- The sand sample was reloaded into the low-temperature and high-pressure probe module. After connecting all experimental components, the confining pressure was adjusted to exceed the pore pressure by 0.4 MPa. The temperature of the sample chamber was controlled at 275.65 K. After the temperature was stabilized, the measurement parameters in the procedure (2) were used to measure T2 distribution of the sand sample at the experimental temperature. Next, the initial water content (mw0 in Table 1) in the sand sample was determined by the calibration curve obtained in the procedure (3). Based on the above data, the initial water saturation Sw0, porosity φNMR, and other parameters of each experimental group were obtained (shown in Table 1). In addition, the initial pore water distribution characteristics of the sand sample at this temperature were obtained using the MRI.
- (5)
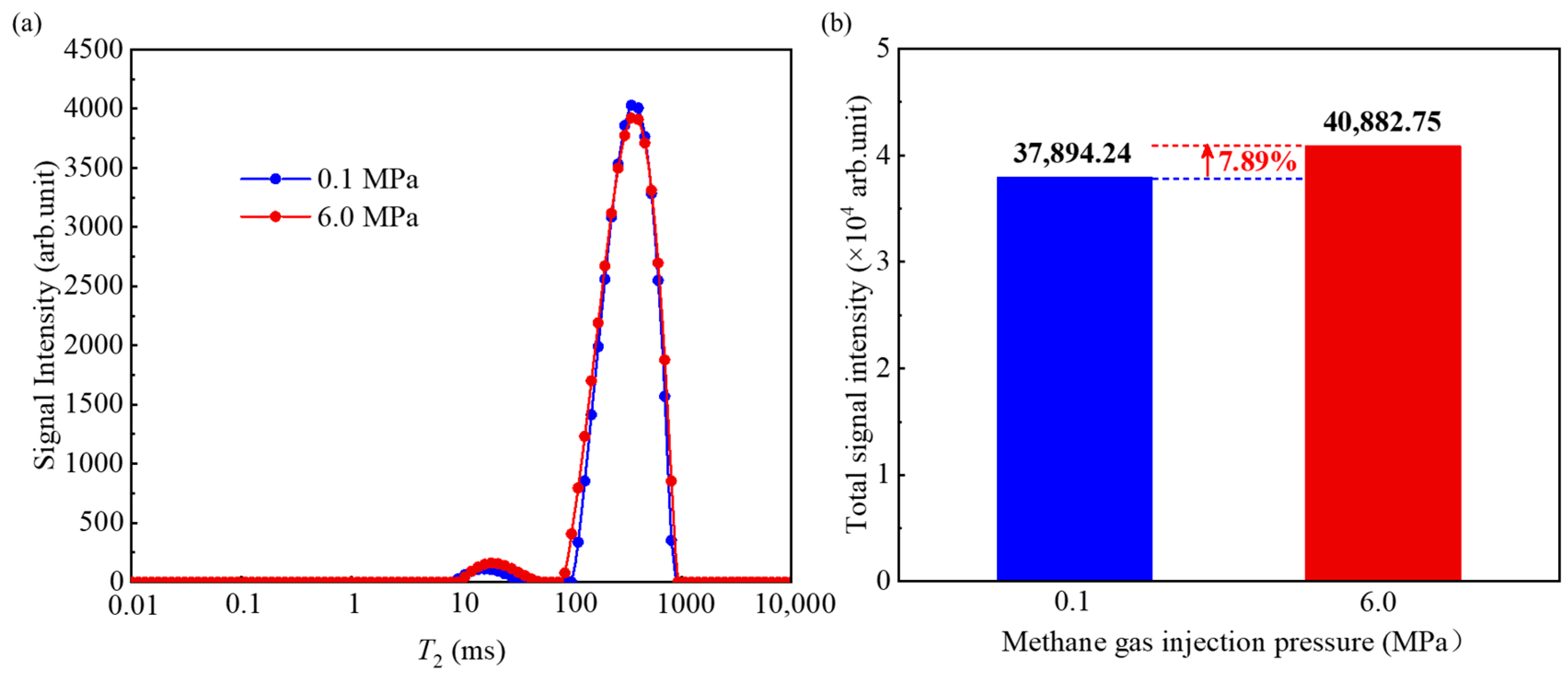
- On the premise of safety, the pore pressure was raised to 6.0 MPa in approximately 45 s using the gas injection module. During the methane hydrate formation, the pore pressure remained constant. After the methane gas injection, the initial T2 distribution was immediately measured. Afterward, T2 distribution measurement and MRI were conducted alternately. The test interval was adjusted according to the experimental progress. The methane hydrate formation was completed when the T2 distribution remained unchanged.
- (6)
- After the experiment, the sand sample was removed from the sample chamber and completely dried (120 °C, 12 h). The initial water content in the sand sample was once again determined by the weight method (mwa in Table 1).
3. Methodology
3.1. T2 Distribution Measurement
3.2. MRI Measurement
3.3. Data Processing Methods
4. Result and Discussion
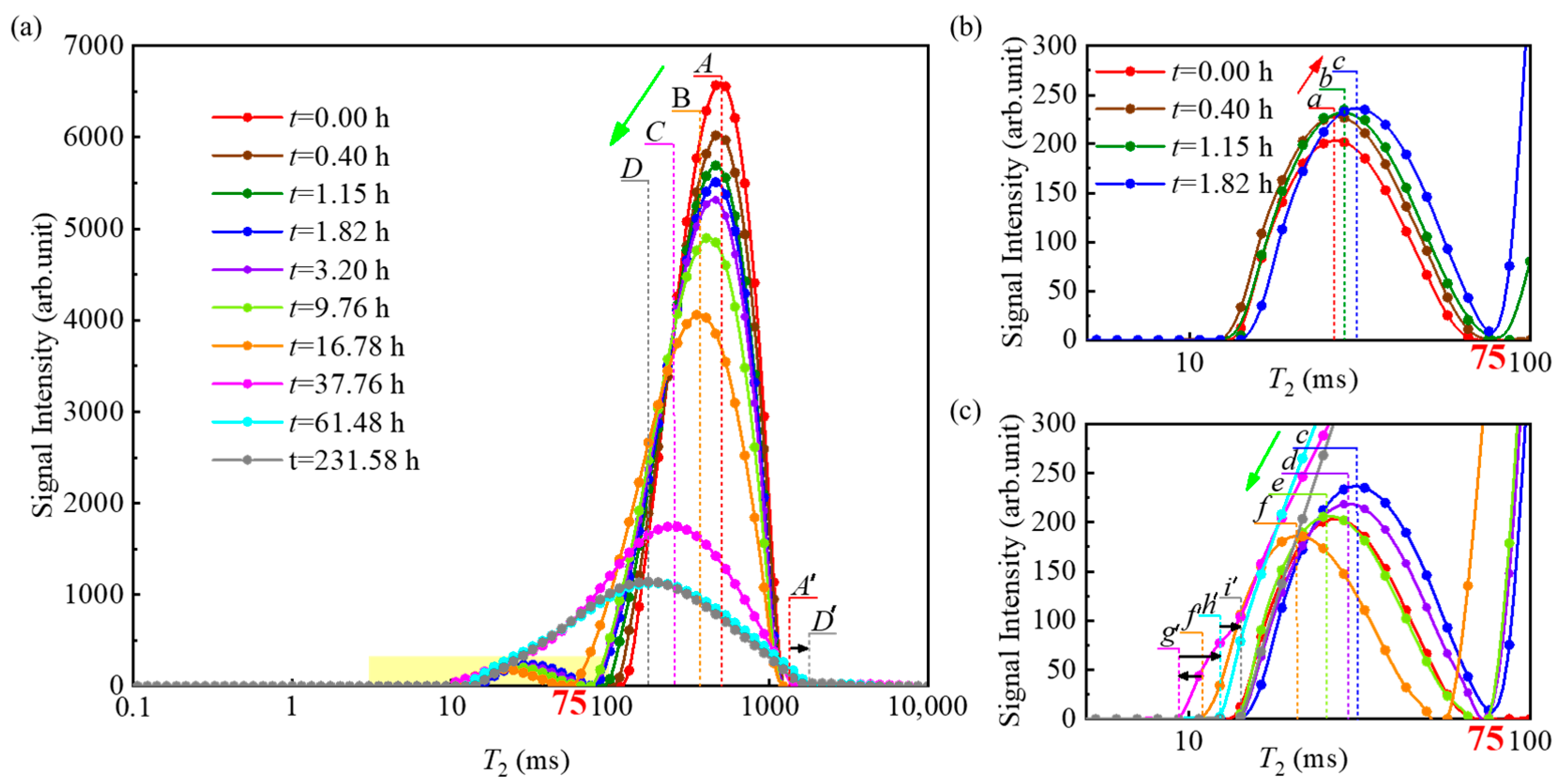
4.1. Variation Characteristics of T2 Distribution
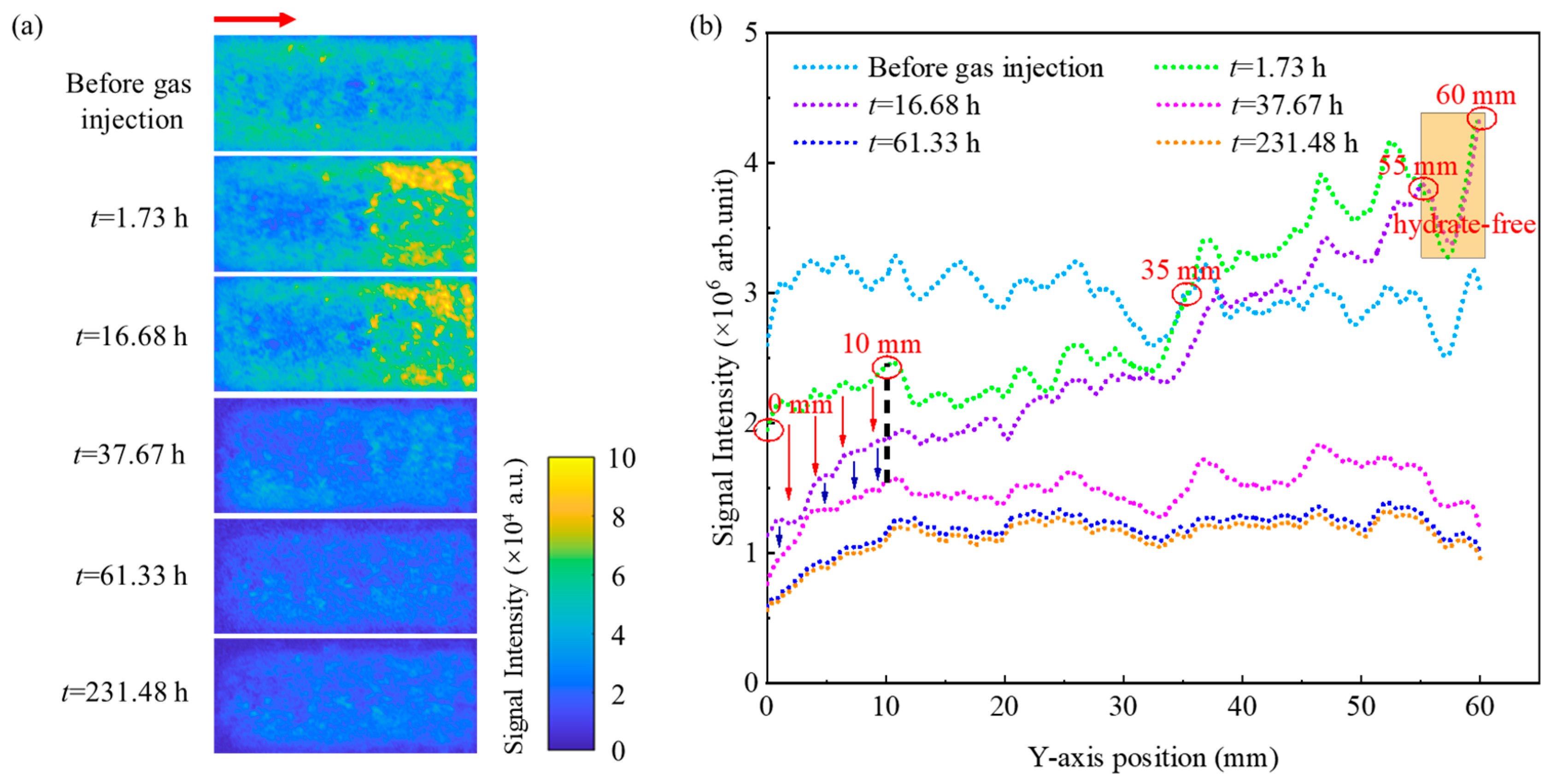
4.2. Variation Characteristics of Pore Water Spatial Distribution
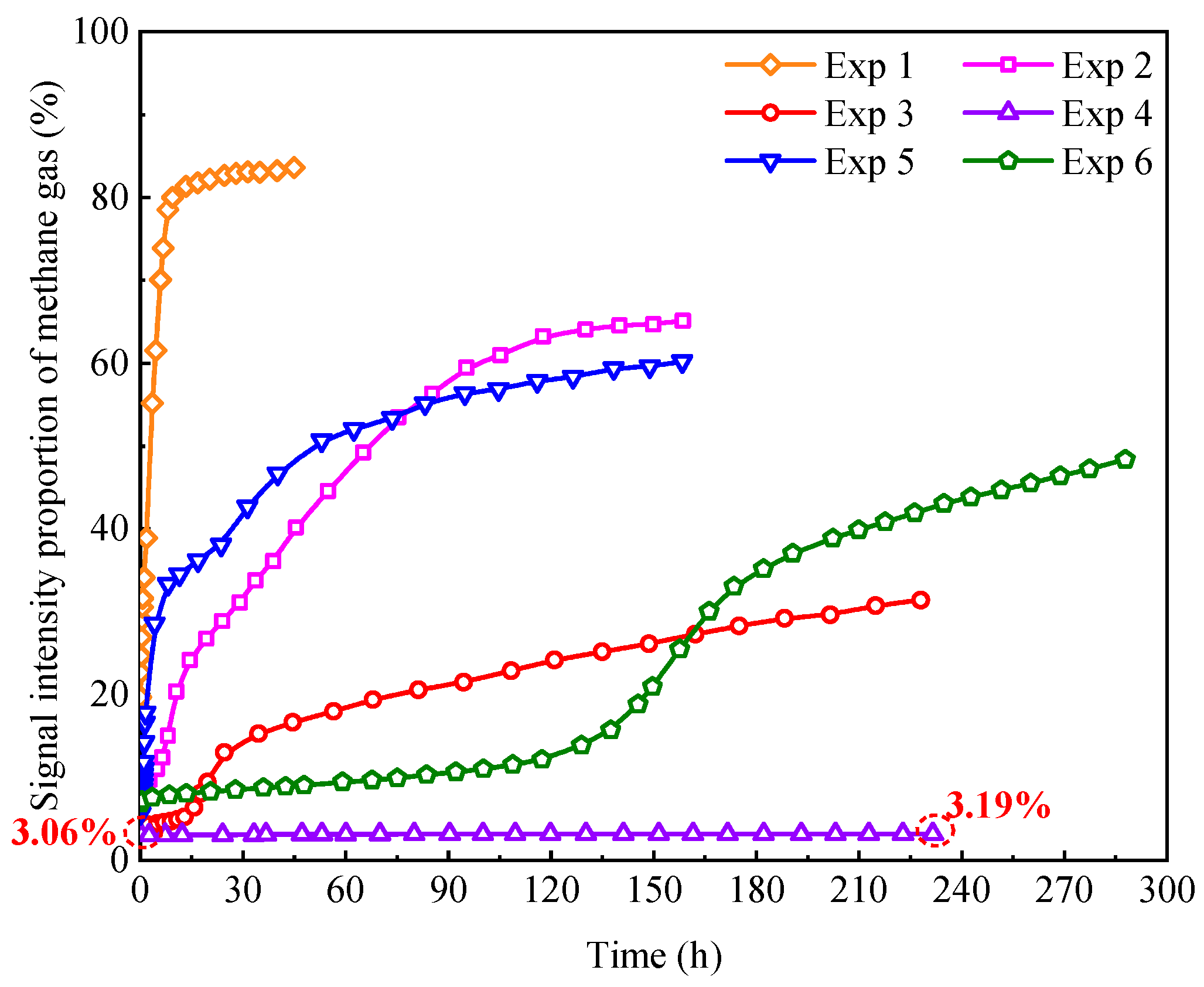
4.3. Analysis of Influence Factors on Pore Water Conversion
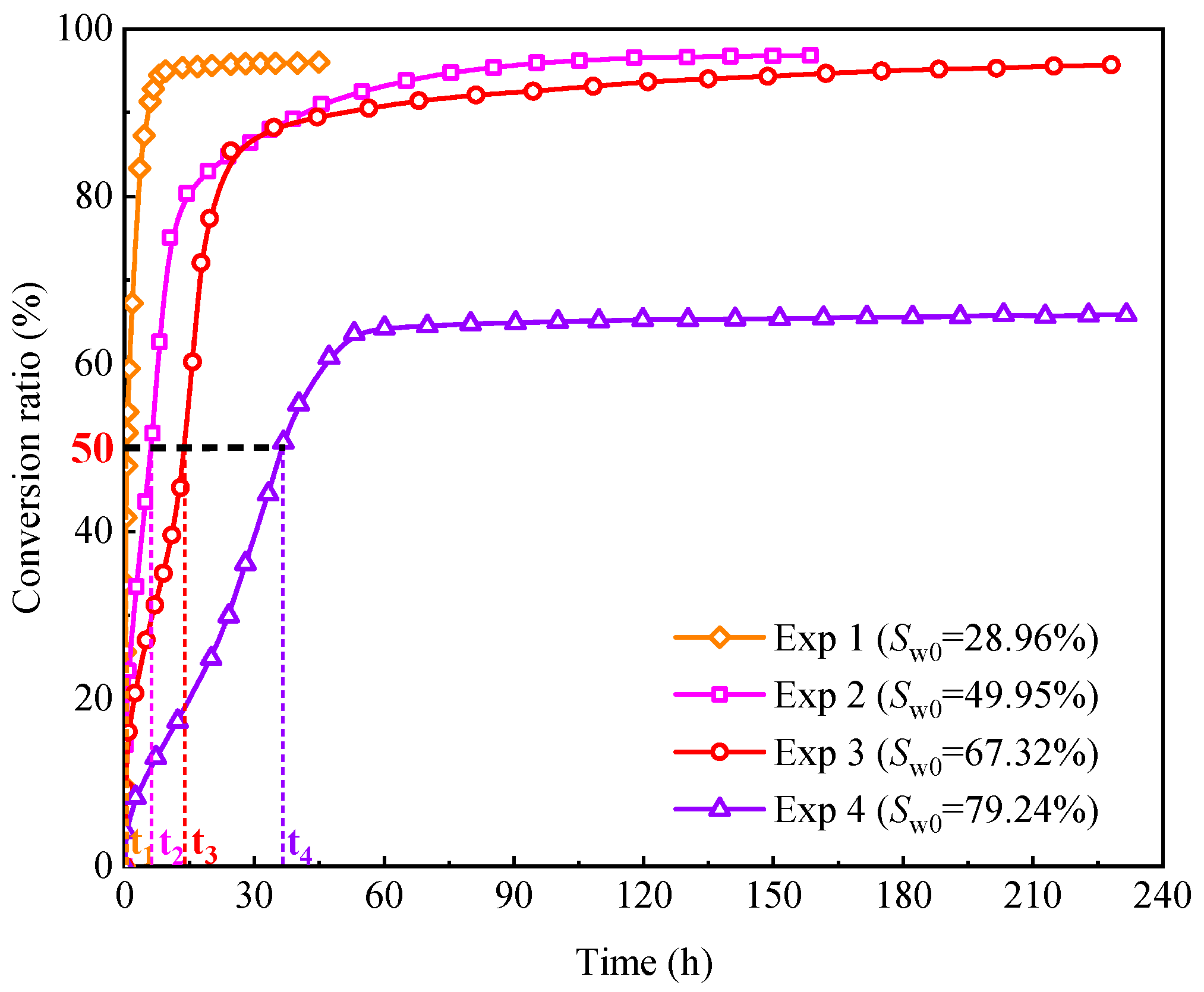
4.3.1. Effect of Initial Water Saturation
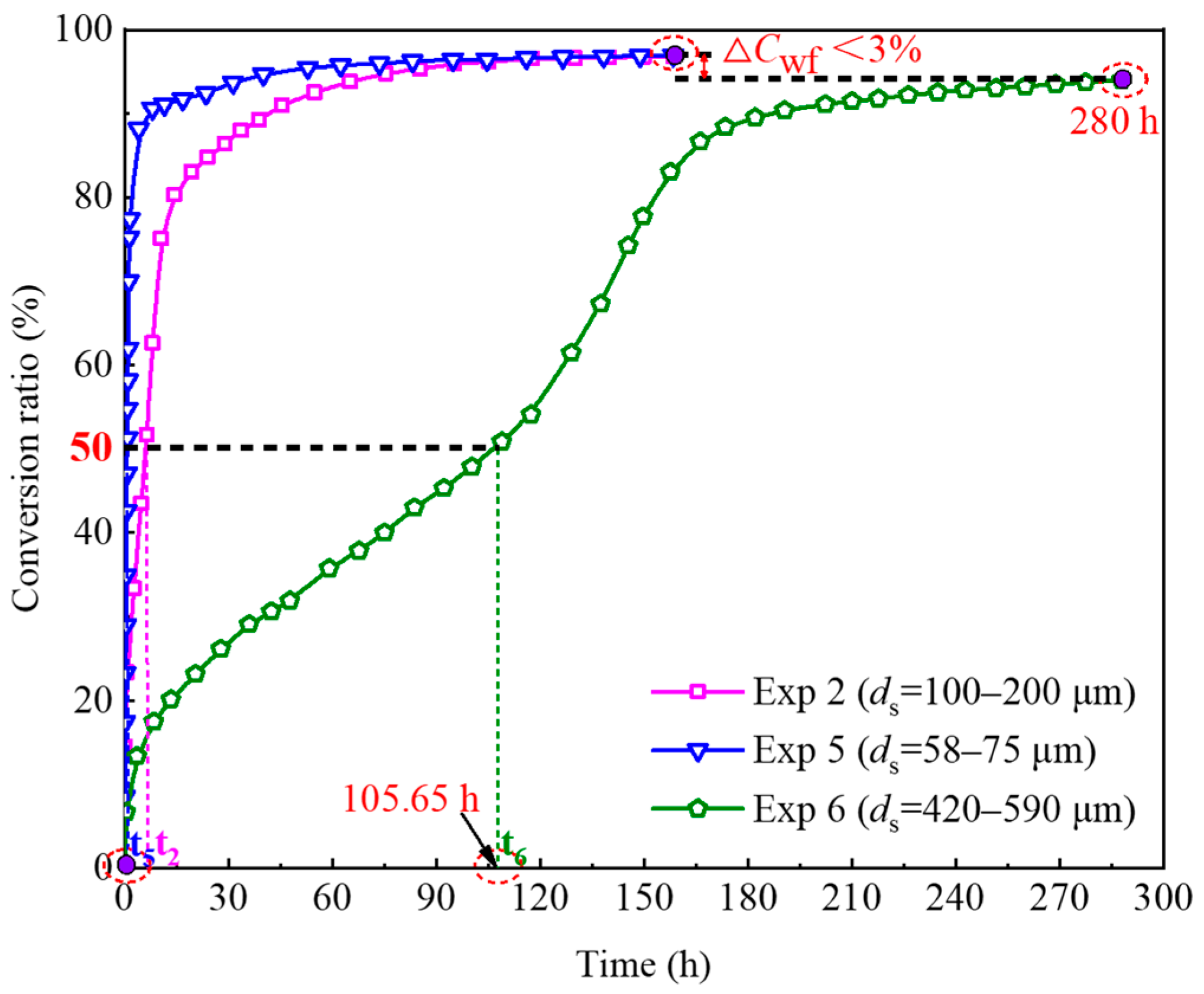
4.3.2. Effect of Sand Particle Size
5. Conclusions
- (1)
- Methane hydrate formation occurs in both large and small pores within unconsolidated sands. The hydrate formation process leads to the transformation of large pores into small pores, and contributes to enhancing the homogeneity of the effective pore structure within the samples.
- (2)
- Variations in heat and mass transfer capacity significantly influence the conversion rate of pore water across different regions within unconsolidated sands. The thickening of the hydrate film increases mass transfer resistance between methane gas and water, thereby causing an early termination of the pore water conversion process. The distribution of hydrate within unconsolidated sands is primarily controlled by the initial distribution of pore water, especially when utilizing the excess-gas method for methane hydrate formation.
- (3)
- Increased initial water saturation reduces the contact area between methane gas and water, leading to a decline in the conversion rate of pore water. Moreover, large-sized sand particles with a small specific surface area and fewer nucleation sites also contribute to decreased pore water conversion rates. For instance, it takes over 100 h to achieve a 50% conversion ratio of pore water in unconsolidated sands with particle sizes of 420–590 μm.
- (4)
- Pore water cannot be completely converted into hydrates within unconsolidated sands. The final conversion ratio of pore water in water-poor sands across different particle sizes exceeds 94% but remains below 97%. However, in water-rich sand samples, the final conversion ratio is only 65.80% due to the barrier effect of the hydrate film on gas–water contact.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Li, X. Recent advances on natural gas hydrate exploration and development in the South China Sea. Energy Fuels 2021, 35, 7528–7552. [Google Scholar] [CrossRef]
- Hassanpouryouzband, A.; Joonaki, E.; Farahani, M.V.; Takeya, S.; Ruppel, C.; Yang, J.H.; English, N.J.; Schicks, J.M.; Edlmann, K.; Mehrabian, H. Gas hydrates in sustainable chemistry. Chem. Soc. Rev. 2020, 49, 5225–5309. [Google Scholar]
- Wu, X.; Guo, G.; Ye, H.; Miao, Y.; Li, D. Application of dual horizontal well systems in the Shenhu area of the South China Sea: Analysis of productivity improvement. J. Mar. Sci. Eng. 2023, 11, 1443. [Google Scholar] [CrossRef]
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Zhan, L.; Wang, Y.; Li, X. Experimental study on characteristics of methane hydrate formation and dissociation in porous medium with different particle sizes using depressurization. Fuel 2018, 230, 37–44. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T.S. Current perspectives on gas hydrate resources. Eng. Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Sloan, E. Gas hydrates: Review of physical/chemical properties. Energy Fuels 1998, 12, 191–196. [Google Scholar] [CrossRef]
- He, J.; Huang, X.; Cao, P. Fine particle migration in a gas hydrate sand: Single-and two-phase fluid using a device for observation at the pore scale. J. Mar. Sci. Eng. 2024, 12, 109. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, X.; Liu, J.; Lee, Y.; Li, X. Natural gas hydrate resources and hydrate technologies: A review and analysis of the associated energy and global warming challenges. Eng. Environ. Sci. 2021, 14, 5611–5668. [Google Scholar] [CrossRef]
- Liang, Y.; Tan, Y.; Luo, Y.; Zhang, Y.; Li, B. Progress and challenges on gas production from natural gas hydrate-bearing sediment. J. Clean. Prod. 2020, 261, 121061. [Google Scholar] [CrossRef]
- Zhan, L.; Liu, B.; Zhang, Y.; Lu, H. Rock physics modeling of acoustic properties in gas hydrate-bearing sediment. J. Mar. Sci. Eng. 2022, 10, 1076. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Y.; Sun, X.; Chen, M.; Bu, Q.; Gong, B. Integrating test device and method for creep failure and ultrasonic response of methane hydrate-bearing sediments. Rev. Sci. Instrum. 2023, 94, 025105. [Google Scholar] [CrossRef]
- Peng, C.; Zou, C.; Lu, Z.; Yu, C.; Liu, A.; Tang, Y.; Hu, X.; Zhang, S.; Wen, H.; Li, Y.; et al. Characteristics of gas hydrate reservoirs and their effect on petrophysical properties in the Muli area, Qinghai-Tibetan plateau permafrost. J. Nat. Gas Sci. Eng. 2018, 57, 266–283. [Google Scholar] [CrossRef]
- Liu, C.; Jing, J.; Zhao, Q.; Luo, X.; Chen, K.; Wang, M.; Deng, M. High-resolution resistivity imaging of a transversely uneven gas hydrate reservoir: A case in the Qiongdongnan basin, South China Sea. Remote Sens. 2023, 15, 2000. [Google Scholar] [CrossRef]
- Yuan, Q.; Kong, L.; Liang, Q.; Liang, J.; Yang, L.; Dong, Y.; Wang, Z.; Wu, X. Mechanical characteristics of gas hydrate-bearing sediments: An experimental study from the South China Sea. J. Mar. Sci. Eng. 2024, 12, 301. [Google Scholar] [CrossRef]
- Zhao, Y.; Kong, L.; Liu, L.; Hu, G.; Ji, Y.; Bu, Q.; Bai, C.; Zhao, J.; Li, J.; Liu, J. Mechanical behaviors of natural gas hydrate-bearing clayey-silty sediments: Experiments and constitutive modeling. Ocean Eng. 2024, 294, 116791. [Google Scholar] [CrossRef]
- Li, Y.; Hu, W.; Tang, H.; Wu, P.; Liu, T.; You, Z.; Yu, T.; Song, Y. Mechanical properties of the interstratified hydrate-bearing sediment in permafrost zones. Energy 2023, 282, 128970. [Google Scholar] [CrossRef]
- Li, N.; Fan, Z.; Ma, H.; Jia, S.; Kan, J.; Sun, C.; Liu, S. Permeability of hydrate-bearing sediment formed from CO2-N2 mixture. J. Mar. Sci. Eng. 2023, 11, 376. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Sang, S.; Hua, L.; Kong, L.; Zeng, Z.; Yuan, Q. Experimental investigation on the permeability characteristics of methane hydrate-bearing clayey-silty sediments considering various factors. Energy 2023, 269, 126811. [Google Scholar] [CrossRef]
- Handa, Y.P.; Stupin, D. Thermodynamic properties and dissociation characteristics of methane and propane hydrates in 70-. ANG.-radius silica gel pores. J. Phys. Chem. 1992, 96, 8599–8603. [Google Scholar] [CrossRef]
- Chuvilin, E.M.; Istomin, V.A.; Safonov, S.S. Residual nonclathrated water in sediments in equilibrium with gas hydrate: Comparison with unfrozen water. Cold. Reg. Sci. Technol. 2011, 68, 68–73. [Google Scholar] [CrossRef]
- Ji, Y.; Hou, J.; Cui, G.; Lu, N.; Zhao, E.; Liu, Y.; Du, Q. Experimental study on methane hydrate formation in a partially saturated sandstone using low-field NMR technique. Fuel 2019, 251, 82–90. [Google Scholar] [CrossRef]
- Feng, Y.; Qu, A.; Han, Y.; Shi, C.; Liu, Y.; Zhang, L.; Zhao, J.; Yang, L.; Song, Y. Effect of gas hydrate formation and dissociation on porous media structure with clay particles. Appl. Eng. 2023, 349, 121694. [Google Scholar] [CrossRef]
- Ge, X.; Liu, J.; Fan, Y.; Xing, D.; Deng, S.; Cai, J. Laboratory investigation into the formation and dissociation process of gas hydrate by low-field NMR technique. J. Geophys. Res. Solid Earth 2018, 123, 3339–3346. [Google Scholar] [CrossRef]
- Zhan, J.; Zhang, P.; Wang, Y.; Wu, Q. Experimental research on methane hydrate formation in porous media based on the low-field NMR technique. Chem. Eng. Sci. 2021, 244, 116804. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Lei, X.; Yang, M.; Zhang, Y.; Song, Y. Quantitatively study on methane hydrate formation/decomposition process in hydrate-bearing sediments using low-field MRI. Fuel 2020, 262, 116555. [Google Scholar] [CrossRef]
- Ji, Y.; Hou, J.; Zhao, E.; Lu, N.; Bai, Y.; Zhou, K.; Liu, Y. Study on the effects of heterogeneous distribution of methane hydrate on permeability of porous media using low-field NMR technique. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018572. [Google Scholar] [CrossRef]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.H.; Tohidi, B. Insights into the climate-driven evolution of gas hydrate-bearing permafrost sediments: Implications for prediction of environmental impacts and security of energy in cold regions. RSC Adv. 2021, 11, 14334–14346. [Google Scholar] [CrossRef] [PubMed]
- Farahani, M.V.; Guo, X.W.; Zhang, L.X.; Yang, M.Z.; Hassanpouryouzband, A.; Zhao, J.F.; Yang, J.H.; Song, Y.C.; Tohidi, B. Effect of thermal formation/dissociation cycles on the kinetics of formation and pore-scale distribution of methane hydrates in porous media: A magnetic resonance imaging study. Sustain. Energy Fuels 2021, 5, 1567–1583. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Q.; Li, Y.; Yang, M.; Liu, W.; Yao, L.; Wang, S.; Zhang, Y.; Song, Y. In-situ visual observation for the formation and dissociation of methane hydrates in porous media by magnetic resonance imaging. Magn. Reson. Imaging 2015, 33, 485–490. [Google Scholar] [CrossRef]
- Linga, P.; Haligva, C.; Nam, S.C.; Ripmeester, J.A.; Englezos, P. Gas hydrate formation in a variable volume bed of silica sand particles. Energy Fuels 2009, 23, 5496–5507. [Google Scholar] [CrossRef]
- Lv, J.; Jiang, L.; Mu, H.; Xue, K.; Cheng, Z.; Wang, S.; Liu, Y. MRI investigation of hydrate pore habits and dynamic seepage characteristics in natural gas hydrates sand matrix. Fuel 2021, 303, 121287. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, X.; Sun, M.; Zhao, Y.; Yang, L.; Song, Y. N2O hydrate formation in porous media: A potential method to mitigate N2O emissions. Chem. Eng. J. 2019, 361, 12–20. [Google Scholar] [CrossRef]
- Ren, J.; Yin, Z.; Li, Q.; Wu, F.; Chen, D.; Li, S. Pore-scale investigation of CH4 hydrate kinetics in clayey-silty sediments by low-field NMR. Energy Fuels 2022, 36, 14874–14887. [Google Scholar] [CrossRef]
- Bello-Palacios, A.; Almenningen, S.; Fotland, P.; Ersland, G. Experimental and numerical analysis of the effects of clay content on CH4 hydrate formation in sand. Energy Fuels 2021, 35, 9836–9846. [Google Scholar] [CrossRef]
- Sun, X.; Qin, X.; Lu, H.; Wang, J.; Xu, J.; Ning, Z. Gas hydrate in-situ formation and dissociation in clayey-silt sediments: An investigation by low-field NMR. Eng. Explor. Exploit. 2021, 39, 256–272. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Li, C.; Liu, C.; Ning, F.; Liu, Z.; Meng, Q. A testing assembly for combination measurements on gas hydrate-bearing sediments using x-ray computed tomography and low-field nuclear magnetic resonance. Rev. Sci. Instrum. 2021, 92, 085108. [Google Scholar] [CrossRef]
- Liu, B.; Zhan, L.; Lu, H.; Zhang, J. Advances in characterizing gas hydrate formation in sediments with NMR transverse relaxation time. Water 2022, 14, 330. [Google Scholar] [CrossRef]
- Kleinberg, R.L.; Flaum, C.; Griffin, D.D.; Brewer, P.G.; Malby, G.E.; Peltzer, E.T.; Yesinowski, J.P. Deep sea NMR: Methane hydrate growth habit in porous media and its relationship to hydraulic permeability, deposit accumulation, and submarine slope stability. J. Geophys. Res. Solid Earth 2003, 108, 2508. [Google Scholar] [CrossRef]
- Coates, G.R.; Xiao, L.; Prammer, M.G. NMR Logging: Principles and Applications; Halliburton Energy Services: Huston, TX, USA, 1999. [Google Scholar]
- Zhao, Y.; Liu, T.; Lin, B.Q.; Sun, Y. Evaluation of compressibility of multiscale pore-fractures in fractured low-rank coals by low-field nuclear magnetic resonance. Energy Fuels 2021, 35, 13133–13143. [Google Scholar] [CrossRef]
- Duschl, M.; Pohlmeier, A.; Brox, T.I.; Galvosas, P.; Vereecken, H. Effect of magnetic pore surface coating on the NMR relaxation and diffusion signal in quartz sand. Magn. Reson. Chem. 2016, 54, 975–984. [Google Scholar] [CrossRef]
- Kleinberg, R.L. Nuclear Magnetic Resonance Pore-Scale Investigation of Permafrost and Gas Hydrate Sediments; Geological Society: London, UK, 2006; pp. 179–192. [Google Scholar]
- Weng, L.; Wu, Z.; Liu, Q.; Chu, Z.; Zhang, S. Evolutions of the unfrozen water content of saturated sandstones during freezing process and the freeze-induced damage characteristics. Int. J. Rock. Mech. Min. 2021, 142, 104757. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef]
- Kuang, Y.; Lei, X.; Yang, L.; Zhao, Y.; Zhao, J. Observation of in situ growth and decomposition of carbon dioxide hydrate at gas-water interfaces using magnetic resonance imaging. Energy Fuels 2018, 32, 6964–6969. [Google Scholar] [CrossRef]
- Wu, Z.; Gu, Q.; Li, G.; Zhao, Z.; Li, Y. Effect of decomposition water content of natural gas hydrate on permeability and gas production of clay sediments based on numerical simulation. J. Nat. Gas Sci. Eng. 2022, 108, 104826. [Google Scholar] [CrossRef]
- Ji, Y.; Liu, C.; Zhang, Z.; Meng, Q.; Liu, L.; Zhang, Y.; Wu, N. Experimental study on characteristics of pore water conversion during methane hydrates formation in unsaturated sand. China Geol. 2022, 5, 276–284. [Google Scholar] [CrossRef]
- Ma, S.; Zheng, J.; Tian, M.; Tang, D.; Yang, M. NMR quantitative investigation on methane hydrate formation characteristics under different driving forces. Fuel 2020, 261, 116364. [Google Scholar] [CrossRef]
- Li, M.; Wu, P.; Zhou, S.; Zhang, L.; Yang, L.; Li, Y.; Liu, Y.; Zhao, J.; Song, Y. Permeability Analysis of Hydrate-Bearing Sediments during the Hydrate Formation Process. Energy Fuels 2021, 35, 19606–19613. [Google Scholar] [CrossRef]
- Kar, A.; Bhati, A.; Acharya, P.V.; Mhadeshwar, A.; Venkataraman, P.; Barckholtz, T.A.; Bahadur, V. Diffusion-based modeling of film growth of hydrates on gas-liquid interfaces. Chem. Eng. Sci. 2021, 234, 116456. [Google Scholar] [CrossRef]
- Kneafsey, T.J.; Tomutsa, L.; Moridis, G.J.; Seol, Y.; Freifeld, B.M.; Taylor, C.E.; Gupta, A. Methane hydrate formation and dissociation in a partially saturated core-scale sand sample. J. Pet. Sci. Eng. 2007, 56, 108–126. [Google Scholar] [CrossRef]
- Davies, S.R.; Sloan, E.D.; Sum, A.K.; Koh, C.A. In Situ Studies of the Mass Transfer Mechanism across a Methane Hydrate Film Using High-Resolution Confocal Raman Spectroscopy. J. Phys. Chem. C 2010, 114, 1173–1180. [Google Scholar] [CrossRef]
- Mori, Y.H.; Mochizuki, T. Mass transport across clathrate hydrate films—A capillary permeation model. Chem. Eng. Sci. 1997, 52, 3613–3616. [Google Scholar] [CrossRef]
- Tian, M.; Song, Y.; Zheng, J.; Gong, G.; Yang, M. Effects of temperature gradient on methane hydrate formation and dissociation processes and sediment heat transfer characteristics. Energy 2022, 261, 125220. [Google Scholar] [CrossRef]
- Song, Y.; Wang, S.; Cheng, Z.; Huang, M.; Zhang, Y.; Zheng, J.; Jiang, L.; Liu, Y. Dependence of the hydrate-based CO2 storage process on the hydrate reservoir environment in high-efficiency storage methods. Chem. Eng. J. 2021, 415, 128937. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Moudrakovski, I.L.; Ripmeester, J.A.; Englezos, P. Magnetic resonance imaging of gas hydrate formation in a bed of silica sand particles. Energy Fuels 2011, 25, 3083–3092. [Google Scholar] [CrossRef]
- Grünberg, B.; Emmler, T.; Gedat, E.; Shenderovich, I.; Findenegg, G.H.; Limbach, H.H.; Buntkowsky, G. Hydrogen bonding of water confined in mesoporous silica MCM-41 and SBA-15 studied by 1H solid-state NMR. Chem. A Eur. J. 2004, 10, 5689–5696. [Google Scholar] [CrossRef]
- Aladko, E.Y.; Dyadin, Y.A.; Fenclonov, V.B.; Larionov, E.G.; Mel’gunov, M.S.; Manakov, A.Y.; Nesterov, A.N.; Zhurko, F.V. Dissociation conditions of methane hydrate in mesoporous silica gels in wide ranges of pressure and water content. J. Phys. Chem. B 2004, 108, 16540–16547. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Chen, Z.; Li, G.; Wang, Y. Effects of particle and pore sizes on the formation behaviors of methane hydrate in porous silica gels. J. Nat. Gas Sci. Eng. 2016, 35, 1463–1471. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, Y.; Li, G.; Chen, Z.; Li, X.; Wu, H. Experimental study on formation behavior of methane hydrate in sea mud from South China Sea. Geoscience 2013, 27, 1373. [Google Scholar]
- Smirnov, V.G.; Manakov, A.Y.; Ukraintseva, E.A.; Villevald, G.V.; Karpova, T.D.; Dyrdin, V.V.; Lyrshchikov, S.Y.; Ismagilov, Z.R.; Terekhova, I.S.; Ogienko, A.G. Formation and decomposition of methane hydrate in coal. Fuel 2016, 166, 188–195. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, S.; Li, S.; Wang, X.; Peng, S. Hydrate formation from clay bound water for CO2 storage. Chem. Eng. J. 2021, 406, 126872. [Google Scholar] [CrossRef]



| Experiment No. | ds (μm) | Vs (cm3) | mw0 (g) | mwa (g) | Sw0 (%) | φNMR (%) |
|---|---|---|---|---|---|---|
| Exp 1 | 100–200 | 42.41 ± 0.12 | 5.50 ± 0.06 | 5.52 ± 0.02 | 28.96 ± 0.29 | 44.79 ± 0.06 |
| Exp 2 | 100–200 | 42.41 ± 0.12 | 9.53 ± 0.10 | 9.54 ± 0.06 | 49.95 ± 0.43 | 44.99 ± 0.10 |
| Exp 3 | 100–200 | 42.41 ± 0.12 | 12.68 ± 0.11 | 12.71 ± 0.06 | 67.32 ± 0.45 | 44.42 ± 0.10 |
| Exp 4 | 100–200 | 42.41 ± 0.12 | 15.06 ± 0.16 | 15.09 ± 0.11 | 79.24 ± 0.59 | 44.81 ± 0.14 |
| Exp 5 | 58–75 | 42.41 ± 0.12 | 9.19 ± 0.03 | 9.26 ± 0.04 | 48.49 ± 0.14 | 44.69 ± 0.02 |
| Exp 6 | 420–590 | 42.41 ± 0.12 | 9.48 ± 0.09 | 9.53 ± 0.03 | 49.77 ± 0.39 | 44.91 ± 0.08 |
| Experiment No. | Φgf (%) | t50 (h) | Cwf (%) |
|---|---|---|---|
| Exp 1 | 83.60 | 0.58 | 96.19 |
| Exp 2 | 65.13 | 6.04 | 96.82 |
| Exp 3 | 31.37 | 14.35 | 95.68 |
| Exp 4 | 3.19 | 37.73 | 65.80 |
| Exp 5 | 60.48 | 0.72 | 96.99 |
| Exp 6 | 48.38 | 105.65 | 94.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ji, Y.; Liu, C.; Meng, Q.; Zhao, Y.; Zhang, Z.; Sun, J.; Liu, L.; Ning, F. Pore Water Conversion Characteristics during Methane Hydrate Formation: Insights from Low-Field Nuclear Magnetic Resonance (NMR) Measurements. J. Mar. Sci. Eng. 2024, 12, 619. https://doi.org/10.3390/jmse12040619
Wang J, Ji Y, Liu C, Meng Q, Zhao Y, Zhang Z, Sun J, Liu L, Ning F. Pore Water Conversion Characteristics during Methane Hydrate Formation: Insights from Low-Field Nuclear Magnetic Resonance (NMR) Measurements. Journal of Marine Science and Engineering. 2024; 12(4):619. https://doi.org/10.3390/jmse12040619
Chicago/Turabian StyleWang, Jiaxian, Yunkai Ji, Changling Liu, Qingguo Meng, Yapeng Zhao, Zhun Zhang, Jianye Sun, Lele Liu, and Fulong Ning. 2024. "Pore Water Conversion Characteristics during Methane Hydrate Formation: Insights from Low-Field Nuclear Magnetic Resonance (NMR) Measurements" Journal of Marine Science and Engineering 12, no. 4: 619. https://doi.org/10.3390/jmse12040619
APA StyleWang, J., Ji, Y., Liu, C., Meng, Q., Zhao, Y., Zhang, Z., Sun, J., Liu, L., & Ning, F. (2024). Pore Water Conversion Characteristics during Methane Hydrate Formation: Insights from Low-Field Nuclear Magnetic Resonance (NMR) Measurements. Journal of Marine Science and Engineering, 12(4), 619. https://doi.org/10.3390/jmse12040619








