Accuracy of Selection in Early Generations of Field Pea Breeding Increases by Exploiting the Information Contained in Correlated Traits
Abstract
1. Introduction
2. Results
2.1. Re-Analysis of 2015 Data (Cycle 2) and Mating Design for Cycle 3
2.2. 2019(Cycle 3) Trial Data Preparation
2.3. Univariate Linear Mixed Model Analyses of 2019 Data (Cycle 3)
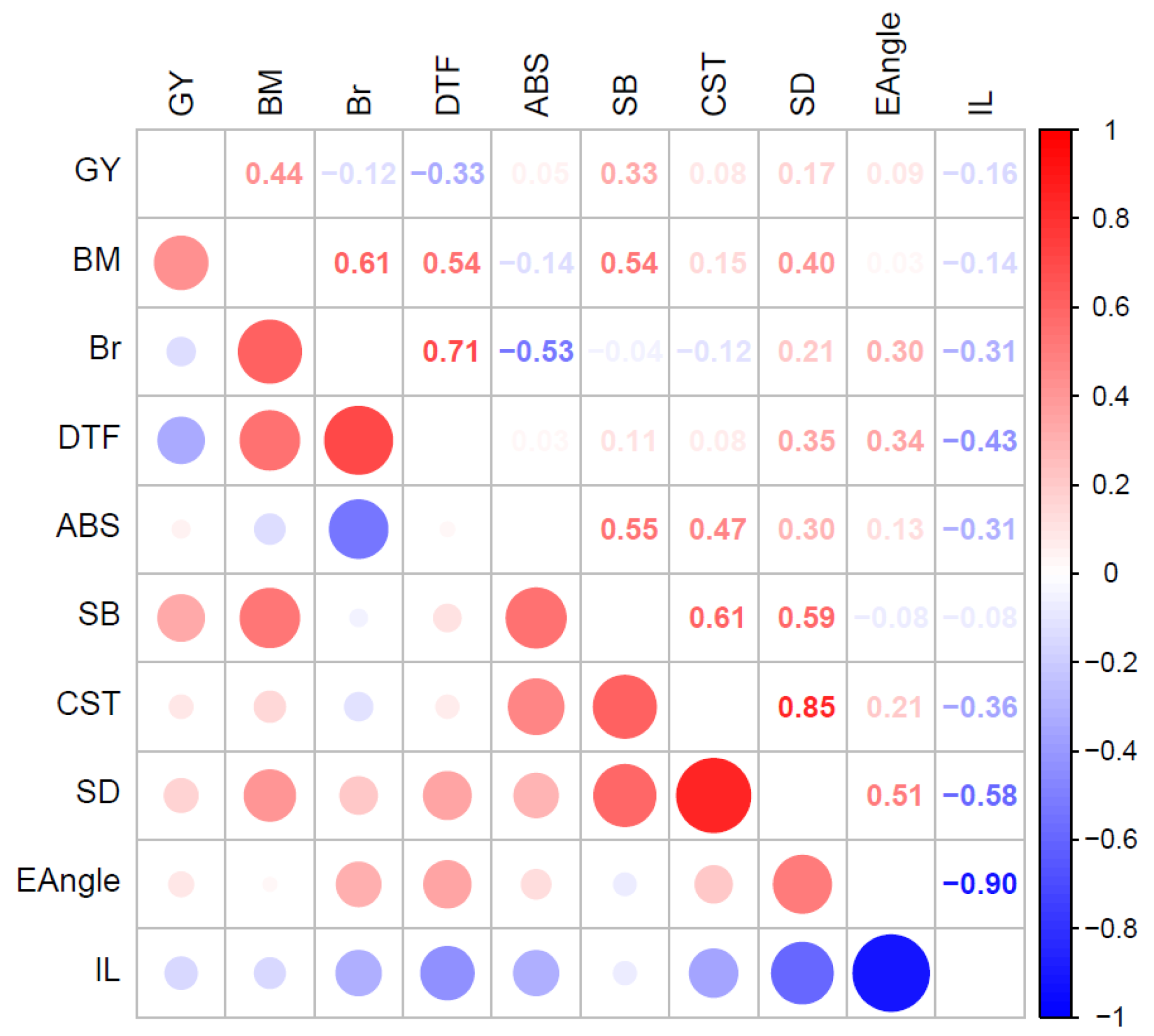
2.4. Multivariate Linear Mixed Model Analyses
2.4.1. 10-Trait Model
2.4.2. Trait Correlations
2.5. Accuracy of Predicted Breeding Values
2.6. Prediction of Genetic Gain in the Next Cycle with OCS
3. Discussion
4. Materials and Methods
4.1. Crossing to Begin Cycle 3
4.2. Field Trial and Trait Assessment
4.3. Statistical Methods
4.3.1. Univariate Linear Mixed Model
4.3.2. Multivariate Linear Mixed Model
4.3.3. Model Accuracy
4.4. Prediction of Progeny Performance in Cycle 4
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cobb, J.N.; Juma, R.U.; Biswas, P.S.; Arbelaez, J.D.; Rutkoski, J.; Atlin, G.; Hagen, T.; Quinn, M.; Ng, E.H. Enhancing the rate of genetic gain in public-sector plant breeding programs: Lessons from the breeder’s equation. Theor. Appl. Genet. 2019, 132, 627–645. [Google Scholar] [CrossRef] [PubMed]
- Falconer, D.S.; Mackay, T.F.C. Introduction to Quantitative Genetics, 4th ed.; Pearson/Longman: Harlow, UK, 1996. [Google Scholar]
- Walsh, B.; Lynch, M. Evolution and Selection of Quantitative Traits; Oxford University Press: New York, NY, USA, 2018; p. 1496. [Google Scholar]
- Wricke, G.; Weber, E. Quantitative Genetics and Selection in Plant Breeding; W. de Gruyter: Berlin, Germany, 1986. [Google Scholar]
- Food and Agriculture Organization of the United Nations. FAOSTAT Statistical Database; FAO: Rome, Italy, 2023. [Google Scholar]
- Foyer, C.H.; Lam, H.M.; Nguyen, H.T.; Siddique, K.H.; Varshney, R.K.; Colmer, T.D.; Cowling, W.; Bramley, H.; Mori, T.A.; Hodgson, J.M.; et al. Neglecting legumes has compromised human health and sustainable food production. Nat. Plants 2016, 2, 16112. [Google Scholar] [CrossRef] [PubMed]
- Khan, T.N.; Mdeldrum, A.; Croser, J.S. Pea: Overview. In Encyclopedia of Food Grains, 2nd ed.; Wrigley, C., Corke, H., Seetharaman, K., Faubion, J., Eds.; Academic Press: Oxford, UK, 2016; Volume 1, pp. 324–333. [Google Scholar]
- Adhikari, K.N.; Khan, T.N.; Stefanova, K.; Pritchard, I. Recurrent breeding method enhances the level of blackspot (Didymella pinodes (Berk. & Blox.) Vestergr.) resistance in field pea (Pisum sativum L.) in southern Australia. Plant Breed. 2014, 133, 508–514. [Google Scholar] [CrossRef]
- Beeck, C.P.; Wroth, J.M.; Falk, D.E.; Khan, T.; Cowling, W.A. Two cycles of recurrent selection lead to simultaneous improvement in black spot resistance and stem strength in field pea. Crop Sci. 2008, 48, 2235–2244. [Google Scholar] [CrossRef]
- Salam, M.; MacLeod, W.; Maling, T.; Prichard, I.; Seymour, M.; Barbetti, M. A meta-analysis of severity and yield loss from ascochyta blight on field pea in Western Australia. Australas. Plant Pathol. 2011, 40, 591–600. [Google Scholar] [CrossRef]
- Khan, T.N.; Timmerman-Vaughan, G.M.; Rubiales, D.; Warkentin, T.D.; Siddique, K.H.M.; Erskine, W.; Barbetti, M.J. Didymella pinodes and its management in field pea: Challenges and opportunities. Field Crop Res. 2013, 148, 61–77. [Google Scholar] [CrossRef]
- Martins, L.B.; Balint-Kurti, P.; Reberg-Horton, S.C. Genome-wide association study for morphological traits and resistance to Peryonella pinodes in the USDA pea single-plant plus collection. G3-Genes Genom. Genet. 2022, 12, jkac168. [Google Scholar] [CrossRef]
- Parihar, A.K.; Kumar, J.; Gupta, D.S.; Lamichaney, A.; Naik Sj, S.; Singh, A.K.; Dixit, G.P.; Gupta, S.; Toklu, F. Genomics Enabled Breeding Strategies for Major Biotic Stresses in Pea (Pisum sativum L.). Front. Plant Sci. 2022, 13, 861191. [Google Scholar] [CrossRef]
- Fondevilla, S.; Almeida, N.F.; Satovic, Z.; Rubiales, D.; Vaz Patto, M.C.; Cubero, J.I.; Torres, A.M. Identification of common genomic regions controlling resistance to Mycosphaerella pinodes, earliness and architectural traits in different pea genetic backgrounds. Euphytica 2011, 182, 43–52. [Google Scholar] [CrossRef]
- Siddique, K.H.M.; Erskine, W.; Hobson, K.; Knights, E.J.; Leonforte, A.; Khan, T.N.; Paull, J.G.; Redden, R.; Materne, M. Cool-season grain legume improvement in Australia—Use of genetic resources. Crop Pasture Sci. 2013, 64, 347–360. [Google Scholar] [CrossRef]
- Jha, A.B.; Gali, K.K.; Tar’an, B.; Warkentin, T.D. Fine Mapping of QTLs for Ascochyta Blight Resistance in Pea Using Heterogeneous Inbred Families. Front. Plant Sci. 2017, 8, 765. [Google Scholar] [CrossRef]
- Wroth, J.M. Possible role for wild genotypes of Pisum spp. to enhance ascochyta blight resistance in pea. Aust. J. Exp. Agric. 1998, 38, 469–479. [Google Scholar] [CrossRef]
- Cowling, W.A.; Stefanova, K.T.; Beeck, C.P.; Nelson, M.N.; Hargreaves, B.L.; Sass, O.; Gilmour, A.R.; Siddique, K.H. Using the animal model to accelerate response to selection in a self-pollinating crop. G3-Genes Genom. Genet. 2015, 5, 1419–1428. [Google Scholar] [CrossRef]
- Carpenter, M.A.; Goulden, D.S.; Woods, C.J.; Thomson, S.J.; Kenel, F.; Frew, T.J.; Cooper, R.D.; Timmerman-Vaughan, G.M. Genomic Selection for Ascochyta Blight Resistance in Pea. Front. Plant Sci. 2018, 9, 1878. [Google Scholar] [CrossRef]
- Smitchger, J.; Weeden, N. Quantitative trait loci controlling lodging resistance and other important agronomic traits in dry field peas. Crop Sci. 2019, 59, 1442–1456. [Google Scholar] [CrossRef]
- Tar’an, B.; Warkentin, T.; Somers, D.J.; Miranda, D.; Vandenberg, A.; Blade, S.; Woods, S.; Bing, D.; Xue, A.; DeKoeyer, D.; et al. Quantitative trait loci for lodging resistance, plant height and partial resistance to mycosphaerella blight in field pea (Pisum sativum L.). Theor. Appl. Genet. 2003, 107, 1482–1491. [Google Scholar] [CrossRef]
- Warkentin, T.D.; Smýkal, P.; Coyne, C.J.; Weeden, N.; Domoney, C.; Bing, D.-J.; Leonforte, A.; Xuxiao, Z.; Dixit, G.P.; Boros, L.; et al. Grain Legumes; De Ron, A.M., Ed.; Springer: New York, NY, USA, 2015; pp. 37–83. [Google Scholar]
- Mikić, A.; Mihailović, V.; Ćupina, B.; Kosev, V.; Warkentin, T.; McPhee, K.; Ambrose, M.; Hofer, J.; Ellis, N. Genetic background and agronomic value of leaf types in pea (Pisum sativum). Ratar. i Povrt. 2011, 48, 275–284. [Google Scholar] [CrossRef]
- Skubisz, G.; Kravtsova, T.I.; Velikanov, L.P. Analysis of the strength properties of pea stems. Int. Agrophys. 2007, 21, 189–197. [Google Scholar]
- Beeck, C.P.; Wroth, J.M.; Cowling, W.A. Additive genetic variance for stem strength in field pea (Pisum sativum). Aust. J. Agric. Res. 2008, 59, 80–85. [Google Scholar] [CrossRef]
- Lenaerts, B.; Collard, B.C.Y.; Demont, M. Review: Improving global food security through accelerated plant breeding. Plant Sci. 2019, 287, 110207. [Google Scholar] [CrossRef]
- Hickey, J.M.; Chiurugwi, T.; Mackay, I.; Powell, W.; Implementing Genomic Selection in CGIAR Breeding Programs Workshop Participants. Genomic prediction unifies animal and plant breeding programs to form platforms for biological discovery. Nat. Genet. 2017, 49, 1297–1303. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Rasheed, A.; Hickey, L.T.; He, Z. Fast-forwarding genetic gain. Trends Plant Sci. 2018, 23, 184–186. [Google Scholar] [CrossRef] [PubMed]
- Voss-Fels, K.P.; Stahl, A.; Hickey, L.T. Q&A: Modern crop breeding for future food security. BMC Biol. 2019, 17, 18. [Google Scholar] [CrossRef]
- Liu, H.; Zwer, P.; Wang, H.; Liu, C.; Lu, Z.; Wang, Y.; Yan, G.; Miedaner, T. A fast generation cycling system for oat and triticale breeding. Plant Breed. 2016, 135, 574–579. [Google Scholar] [CrossRef]
- Watson, A.; Ghosh, S.; Williams, M.J.; Cuddy, W.S.; Simmonds, J.; Rey, M.D.; Asyraf Md Hatta, M.; Hinchliffe, A.; Steed, A.; Reynolds, D.; et al. Speed breeding is a powerful tool to accelerate crop research and breeding. Nat. Plants 2018, 4, 23–29. [Google Scholar] [CrossRef]
- Bauer, A.M.; Léon, J. Multiple-trait breeding values for parental selection in self-pollinating crops. Theor. Appl. Genet. 2008, 116, 235–242. [Google Scholar] [CrossRef]
- Piepho, H.P.; Möhring, J.; Melchinger, A.E.; Büchse, A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica 2007, 161, 209–228. [Google Scholar] [CrossRef]
- Thompson, R.; Meyer, K. A review of theoretical aspects in the estimation of breeding values for multi-trait selection. Livest. Prod. Sci. 1986, 15, 299–313. [Google Scholar] [CrossRef]
- Hardner, C.M.; Healey, A.L.; Downes, G.; Herberling, M.; Gore, P.L. Improving prediction accuracy and selection of open-pollinated seed-lots in Eucalyptus dunnii Maiden using a multivariate mixed model approach. Ann. For. Sci. 2016, 73, 1035–1046. [Google Scholar] [CrossRef]
- Montesinos-López, A.; Runcie, D.E.; Ibba, M.I.; Pérez-Rodríguez, P.; Montesinos-López, O.A.; Crespo, L.A.; Bentley, A.R.; Crossa, J. Multi-trait genomic-enabled prediction enhances accuracy in multi-year wheat breeding trials. G3-Genes Genom. Genet. 2021, 11, jkab270. [Google Scholar] [CrossRef]
- Schulthess, A.W.; Zhao, Y.; Longin, C.F.H.; Reif, J.C. Advantages and limitations of multiple-trait genomic prediction for Fusarium head blight severity in hybrid wheat (Triticum aestivum L.). Theor. Appl. Genet. 2018, 131, 685–701. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Montesinos-López, J.C.; Montesinos-López, A.; Ramírez-Alcaraz, J.M.; Poland, J.; Singh, R.; Dreisigacker, S.; Crespo, L.; Mondal, S.; Govidan, V.; et al. Bayesian multitrait kernel methods improve multienvironment genome-based prediction. G3-Genes Genom. Genet. 2022, 12, jkab406. [Google Scholar] [CrossRef]
- Neyhart, J.L.; Lorenz, A.J.; Smith, K.P. Multi-trait improvement by predicting genetic correlations in breeding crosses. G3-Genes Genom. Genet. 2019, 9, 3153–3165. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Montesinos-López, A.; Crossa, J.; Toledo, F.H.; Pérez-Hernández, O.; Eskridge, K.M.; Rutkoski, J. A genomic bayesian multi-trait and multi-environment model. G3-Genes Genom. Genet. 2016, 6, 2725–2744. [Google Scholar] [CrossRef]
- Lado, B.; Vázquez, D.; Quincke, M.; Silva, P.; Aguilar, I.; Gutiérrez, L. Resource allocation optimization with multi-trait genomic prediction for bread wheat (Triticum aestivum L.) baking quality. Theor. Appl. Genet. 2018, 131, 2719–2731. [Google Scholar] [CrossRef]
- Jia, Y.; Jannink, J.L. Multiple-trait genomic selection methods increase genetic value prediction accuracy. Genetics 2012, 192, 1513–1522. [Google Scholar] [CrossRef]
- Ganesalingam, A.; Smith, A.B.; Beeck, C.P.; Cowling, W.A.; Thompson, R.; Cullis, B.R. A bivariate mixed model approach for the analysis of plant survival data. Euphytica 2013, 190, 371–383. [Google Scholar] [CrossRef]
- Kinghorn, B.P. An algorithm for efficient constrained mate selection. Genet. Sel. Evol. 2011, 43, 4–9. [Google Scholar] [CrossRef]
- Kinghorn, B.P.; Kinghorn, A.J. Instructions for MateSel ver 7.6. 2022. Available online: https://www.matesel.com/Website/Support (accessed on 5 January 2023).
- Strik, B.C.; Davis, A.J.; Bryla, D.R.; Orr, S.T. Individual and Combined Use of Sawdust and Weed Mat Mulch in a New Planting of Northern Highbush Blueberry I. Impacts on Plant Growth and Soil and Canopy Temperature. HortScience 2020, 55, 1280–1287. [Google Scholar] [CrossRef]
- Beeck, C.P.; Wroth, J.M.; Cowling, W.A. Genetic variation in stem strength in field pea (Pisum sativum L.) and its association with compressed stem thickness. Aust. J. Agric. Res. 2006, 57, 193–199. [Google Scholar] [CrossRef]
- Smitchger, J.; Weeden, N.; Akin, I.; Warkentin, T. Stress equation for a cantilever beam: A model of lodging resistance in field pea. Int. Agrophys. 2020, 34, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Niklas, K.J. Plant Biomechanics: An Engineering Approach to Plant Form and Function; University of Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Shah, D.U.; Reynolds, T.P.S.; Ramage, M.H. The strength of plants: Theory and experimental methods to measure the mechanical properties of stems. J. Exp. Bot. 2017, 68, 4497–4516. [Google Scholar] [CrossRef] [PubMed]
- Spatz, H.C.; Niklas, K.J. Modes of failure in tubular plant organs. Am. J. Bot. 2013, 100, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Semagn, K.; Crossa, J.; Cuevas, J.; Iqbal, M.; Ciechanowska, I.; Henriquez, M.A.; Randhawa, H.; Beres, B.L.; Aboukhaddour, R.; McCallum, B.D.; et al. Comparison of single-trait and multi-trait genomic predictions on agronomic and disease resistance traits in spring wheat. Theor. Appl. Genet. 2022, 135, 2747–2767. [Google Scholar] [CrossRef] [PubMed]
- Cowling, W.A.; Li, L.; Siddique, K.H.M.; Henryon, M.; Berg, P.; Banks, R.G.; Kinghorn, B.P. Evolving gene banks: Improving diverse populations of crop and exotic germplasm with optimal contribution selection. J. Exp. Bot. 2017, 68, 1927–1939. [Google Scholar] [CrossRef]
- Cowling, W.A.; Li, L.; Siddique, K.H.M.; Banks, R.G.; Kinghorn, B.P. Modeling crop breeding for global food security during climate change. Food Energy Secur. 2019, 8, e00157. [Google Scholar] [CrossRef]
- Cowling, W.A.; Castro-Urrea, F.A.; Stefanova, K.T.; Li, L.; Banks, R.G.; Saradadevi, R.; Sass, O.; Kinghorn, B.P.; Siddique, K.H.M. Optimal Contribution Selection Improves the Rate of Genetic Gain in Grain Yield and Yield Stability in Spring Canola in Australia and Canada. Plants 2023, 12, 383. [Google Scholar] [CrossRef]
- Gaynor, R.C.; Gorjanc, G.; Bentley, A.R.; Ober, E.S.; Howell, P.; Jackson, R.; Mackay, I.J.; Hickey, J.M. A two-part strategy for using genomic selection to develop inbred lines. Crop Sci. 2017, 57, 2372–2386. [Google Scholar] [CrossRef]
- Krause, M.R.; Mondal, S.; Crossa, J.; Singh, R.P.; Pinto, F.; Haghighattalab, A.; Shrestha, S.; Rutkoski, J.; Gore, M.A.; Sorrells, M.E.; et al. Aerial high-throughput phenotyping enables indirect selection for grain yield at the early generation, seed-limited stages in breeding programs. Crop Sci. 2020, 60, 3096–3114. [Google Scholar] [CrossRef]
- Gorjanc, G.; Gaynor, R.C.; Hickey, J.M. Optimal cross selection for long-term genetic gain in two-part programs with rapid recurrent genomic selection. Theor. Appl. Genet. 2018, 131, 1953–1966. [Google Scholar] [CrossRef]
- Hayes, B.J.; Wei, X.; Joyce, P.; Atkin, F.; Deomano, E.; Yue, J.; Nguyen, L.; Ross, E.M.; Cavallaro, T.; Aitken, K.S.; et al. Accuracy of genomic prediction of complex traits in sugarcane. Theor. Appl. Genet. 2021, 134, 1455–1462. [Google Scholar] [CrossRef]
- Michel, S.; Löschenberger, F.; Sparry, E.; Ametz, C.; Bürstmayr, H. Multi-year dynamics of single-step genomic prediction in an spplied wheat breeding program. Agronomy 2020, 10, 1591. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, P.; Crossa, J.; Rutkoski, J.; Poland, J.; Singh, R.; Legarra, A.; Autrique, E.; Campos, G.d.L.; Burgueño, J.; Dreisigacker, S. Single-step genomic and pedigree genotype x environment interaction models for predicting wheat lines in international environments. Plant Genome 2017, 10, plantgenome2016.09.0089. [Google Scholar] [CrossRef]
- Ratcliffe, B.; El-Dien, O.G.; Cappa, E.P.; Porth, I.; Klapste, J.; Chen, C.; El-Kassaby, Y.A. Single-Step BLUP with varying genotyping effort in open-pollinated Picea glauca. G3-Genes Genom. Genet. 2017, 7, 935–942. [Google Scholar] [CrossRef]
- Velazco, J.G.; Malosetti, M.; Hunt, C.H.; Mace, E.S.; Jordan, D.R.; van Eeuwijk, F.A. Combining pedigree and genomic information to improve prediction quality: An example in sorghum. Theor. Appl. Genet. 2019, 132, 2055–2067. [Google Scholar] [CrossRef]
- Bonnett, D.; Li, Y.; Crossa, J.; Dreisigacker, S.; Basnet, B.; Pérez-Rodríguez, P.; Alvarado, G.; Jannink, J.L.; Poland, J.; Sorrells, M. Response to Early Generation Genomic Selection for Yield in Wheat. Front. Plant Sci. 2022, 12, 718611. [Google Scholar] [CrossRef]
- Saradadevi, R.; Mukankusi, C.; Li, L.; Amongi, W.; Mbiu, J.P.; Raatz, B.; Ariza, D.; Beebe, S.; Varshney, R.K.; Huttner, E.; et al. Multivariate genomic analysis and optimal contributions selection predicts high genetic gains in cooking time, iron, zinc, and grain yield in common beans in East Africa. Plant Genome 2021, 14, e20156. [Google Scholar] [CrossRef]
- Mortimer, S.I.; van der Werf, J.H.; Jacob, R.H.; Hopkins, D.L.; Pannier, L.; Pearce, K.L.; Gardner, G.E.; Warner, R.D.; Geesink, G.H.; Edwards, J.E.; et al. Genetic parameters for meat quality traits of Australian lamb meat. Meat Sci. 2014, 96, 1016–1024. [Google Scholar] [CrossRef]
- Woolliams, J.A.; Berg, P.; Dagnachew, B.S.; Meuwissen, T.H. Genetic contributions and their optimization. J. Anim. Breed. Genet. 2015, 132, 89–99. [Google Scholar] [CrossRef]
- Akdemir, D.; Beavis, W.; Fritsche-Neto, R.; Singh, A.K.; Isidro-Sanchez, J. Multi-objective optimized genomic breeding strategies for sustainable food improvement. Heredity 2019, 122, 672–683. [Google Scholar] [CrossRef]
- Allier, A.; Teyssedre, S.; Lehermeier, C.; Moreau, L.; Charcosset, A. Optimized breeding strategies to harness genetic resources with different performance levels. BMC Genom. 2020, 21, 349. [Google Scholar] [CrossRef] [PubMed]
- Labroo, M.R.; Studer, A.J.; Rutkoski, J.E. Heterosis and hybrid crop breeding: A multidisciplinary review. Front. Genet. 2021, 12, 643761. [Google Scholar] [CrossRef] [PubMed]
- Varshney, R.K.; Roorkiwal, M.; Sun, S.; Bajaj, P.; Chitikineni, A.; Thudi, M.; Singh, N.P.; Du, X.; Upadhyaya, H.D.; Khan, A.W.; et al. A chickpea genetic variation map based on the sequencing of 3366 genomes. Nature 2021, 599, 622–627. [Google Scholar] [CrossRef] [PubMed]
- Coombes, N.E. DiGGer, a Spatial Design Program. Biometric Bulletin; NSW Department of Primary Industries: Orange, Australia, 2009; Available online: https://www.nswdpibiom.org/austatgen/software/ (accessed on 1 August 2022).
- Gilmour, A.R.; Cullis, B.R.; Verbyla, A.P. Accounting for natural and extraneous variation in the analysis of field experiments. J. Agric. Biol. Environ. Stat. 1997, 2, 269–293. [Google Scholar] [CrossRef]
- De Faveri, J.; Verbyla, A.P.; Cullis, B.R.; Pitchford, W.S.; Thompson, R. Residual variance–covariance modelling in analysis of multivariate data from variety selection trials. J. Agric. Biol. Environ. Stat. 2016, 22, 1–22. [Google Scholar] [CrossRef]
- Butler, D.; Cullis, B.; Gilmour, A.; Gogel, B.; Thompson, R. ASReml-R Reference Manual Version 4; VSN International Ltd.: Hemel Hempstead, UK, 2018; Available online: https://asreml.kb.vsni.co.uk/article-categories/asreml-r-resources (accessed on 23 August 2022).
- Gilmour, A.R.; Gogel, B.J.; Cullis, B.R.; Welham, S.J.; Thompson, R. ASReml User Guide Release 4.2 Functional Specification; VSN International Ltd.: Hemel Hempstead, UK, 2021; Available online: https://asreml.kb.vsni.co.uk/article-categories/asreml-documentation (accessed on 23 August 2022).
- Mrode, R.A. Linear Models for the Prediction of Animal Breeding Values, 2nd ed.; CAB International: Wallingford, UK, 2005. [Google Scholar]
- Brascamp, E.W. Selection indices with constraints. Anim. Breed. Abstr. 1984, 52, 645–654. [Google Scholar]
- Kinghorn, B.P. DESIRE ver. 2.42. 2013. Available online: https://bkinghor.une.edu.au/desire.htm (accessed on 5 January 2023).


| Trait Abbreviation | Univariate LMM Variance Components ± SE | h2 ± SE | ||
|---|---|---|---|---|
| Additive | Non-Additive | Residual | ||
| GY | 22.79 ± 8.15 | 103.77 ± 14.64 | 79.60 ± 10.98 | 0.11 ± 0.04 |
| BM | 77.79 ± 26.55 | 232.02 ± 46.36 | 279.74 ± 37.21 | 0.13 ± 0.04 |
| Br | 0.08 ± 0.01 | ns | 0.14 ± 0.01 | 0.36 ± 0.05 |
| DTF | 24.14 ± 3.89 | 11.05 ± 1.34 | 8.46 ± 0.72 | 0.55 ± 0.05 |
| ABS | 0.62 ± 0.16 | ns | 5.81 ± 0.24 | 0.10 ± 0.02 |
| SB | 2.01 ± 0.71 | ns | 31.39 ± 1.46 | 0.06 ± 0.02 |
| CST | 0.04 ± 0.01 | 0.07 ± 0.03 | 0.19 ± 0.03 | 0.13 ± 0.04 |
| SD | 0.04 ± 0.01 | ns | 0.23 ± 0.02 | 0.15 ± 0.04 |
| EAngle | 98.76 ± 21.05 | ns | 327.06 ± 13.44 | 0.23 ± 0.04 |
| IL | 0.48 ± 0.08 | 0.11 ± 0.04 | 0.31 ± 0.03 | 0.53 ± 0.05 |
| Trait Abbreviation | MLMM Variance Components ± SE | h2 ± SE | ||
|---|---|---|---|---|
| Additive | Non-Additive | Residual | ||
| GY | 35.90 ± 10.23 | 18.78 ± 4.62 | 245.70 ± 12.16 | 0.12 ± 0.03 |
| BM | 99.43 ± 29.24 | ns | 797.45 ± 54.54 | 0.11 ± 0.03 |
| Br | 0.09 ± 0.02 | ns | 0.17 ± 0.01 | 0.35 ± 0.04 |
| DTF | 32.22 ± 4.50 | 7.51 ± 1.20 | 10.00 ± 0.82 | 0.65 ± 0.04 |
| ABS | 0.61 ± 0.14 | ns | 5.90 ± 0.24 | 0.09 ± 0.02 |
| SB | 1.81 ± 0.61 | ns | 32.96 ± 1.46 | 0.05 ± 0.02 |
| CST | 0.04 ± 0.01 | ns | 0.28 ± 0.01 | 0.12 ± 0.03 |
| SD | 0.04 ± 0.01 | ns | 0.28 ± 0.01 | 0.14 ± 0.03 |
| EAngle | 125.04 ± 21.52 | ns | 146.15 ± 62.46 | 0.46 ± 0.12 |
| IL | 0.62 ± 0.09 | ns | 0.39 ± 0.02 | 0.61 ± 0.04 |
| Trait | S0 | S2+ | ||
|---|---|---|---|---|
| Univariate | Multivariate | Univariate | Multivariate | |
| GY | 0.75 ± 0.06 | 0.80 ± 0.04 | 0.79 ± 0.08 | 0.84 ± 0.06 |
| BM | 0.77 ± 0.05 | 0.81 ± 0.04 | 0.80 ± 0.08 | 0.84 ± 0.05 |
| Br | 0.86 ± 0.03 | 0.88 ± 0.02 | 0.89 ± 0.05 | 0.91 ± 0.04 |
| DTF | 0.88 ± 0.02 | 0.90 ± 0.02 | 0.92 ± 0.04 | 0.94 ± 0.03 |
| ABS | 0.77 ± 0.05 | 0.83 ± 0.04 | 0.81 ± 0.07 | 0.86 ± 0.05 |
| SB | 0.71 ± 0.06 | 0.77 ± 0.05 | 0.74 ± 0.09 | 0.81 ± 0.06 |
| CST | 0.76 ± 0.05 | 0.81 ± 0.04 | 0.80 ± 0.07 | 0.84 ± 0.05 |
| SD | 0.78 ± 0.05 | 0.83 ± 0.04 | 0.82 ± 0.07 | 0.86 ± 0.04 |
| EAngle | 0.84 ± 0.04 | 0.88 ± 0.02 | 0.88 ± 0.04 | 0.92 ± 0.02 |
| IL | 0.87 ± 0.03 | 0.90 ± 0.02 | 0.91 ± 0.03 | 0.93 ± 0.02 |
| Average | 0.799 | 0.841 | 0.835 | 0.875 |
| Parameter | Units | Selection Goal | Selection Index Weights | Mean PBV in Candidates | Prediction of Mean PBV in Next Cycle | Change in Mean PBV in Next Cycle | Change in Mean PBV in Next Cycle as % of Phenotypic Mean |
|---|---|---|---|---|---|---|---|
| Index | Increase | 2.30 | 4.55 | 2.25 | |||
| GY | g | Increase | −0.028 | 2.87 | 5.46 | 2.60 | +9.4 |
| BM | g | Increase | 0.150 | 2.21 | 2.76 | 0.55 | +1.0 |
| Br | number | Decrease | −6.000 | 0.12 | 0.14 | 0.02 | +0.9 |
| DTF | days | Decrease | −0.200 | −2.26 | −4.04 | −1.79 | −2.5 |
| ABS | number | Decrease | −2.900 | −0.51 | −0.71 | −0.20 | −3.8 |
| SB | N | Increase | 1.200 | 0.13 | 0.26 | 0.13 | +1.4 |
| CST | mm | Increase | 1.700 | 0.02 | 0.13 | 0.11 | +5.0 |
| SD | mm | Increase | 2.000 | 0.08 | 0.22 | 0.14 | +5.1 |
| EAngle | degrees | Increase | 0.150 | 3.24 | 8.43 | 5.19 | +7.8 |
| IL | cm | Maintain | −0.030 | −0.05 | −0.33 | −0.28 | −10.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro-Urrea, F.A.; Urricariet, M.P.; Stefanova, K.T.; Li, L.; Moss, W.M.; Guzzomi, A.L.; Sass, O.; Siddique, K.H.M.; Cowling, W.A. Accuracy of Selection in Early Generations of Field Pea Breeding Increases by Exploiting the Information Contained in Correlated Traits. Plants 2023, 12, 1141. https://doi.org/10.3390/plants12051141
Castro-Urrea FA, Urricariet MP, Stefanova KT, Li L, Moss WM, Guzzomi AL, Sass O, Siddique KHM, Cowling WA. Accuracy of Selection in Early Generations of Field Pea Breeding Increases by Exploiting the Information Contained in Correlated Traits. Plants. 2023; 12(5):1141. https://doi.org/10.3390/plants12051141
Chicago/Turabian StyleCastro-Urrea, Felipe A., Maria P. Urricariet, Katia T. Stefanova, Li Li, Wesley M. Moss, Andrew L. Guzzomi, Olaf Sass, Kadambot H. M. Siddique, and Wallace A. Cowling. 2023. "Accuracy of Selection in Early Generations of Field Pea Breeding Increases by Exploiting the Information Contained in Correlated Traits" Plants 12, no. 5: 1141. https://doi.org/10.3390/plants12051141
APA StyleCastro-Urrea, F. A., Urricariet, M. P., Stefanova, K. T., Li, L., Moss, W. M., Guzzomi, A. L., Sass, O., Siddique, K. H. M., & Cowling, W. A. (2023). Accuracy of Selection in Early Generations of Field Pea Breeding Increases by Exploiting the Information Contained in Correlated Traits. Plants, 12(5), 1141. https://doi.org/10.3390/plants12051141







