Smoothness of Graph Energy in Chemical Graphs

Abstract

The energy of a graph G as a chemical concept leading to HMO theory was introduced by Hückel in 1931 and developed into a mathematical interpretation many years later when Gutman in 1978 gave his famous definition of the graph energy as the sum of the absolute values of the eigenvalues of the adjacency matrix of G. One of the general requirements for any topological index is that similar molecules have close TI values, which is called smoothness. To explore this property, we consider two variants of structure sensitivity and abruptness as introduced by Furtula et al. in 2013 and 2019, for hydrocarbons with up to 20 carbon atoms. Finally, we investigate the relationships between graph energies of acyclic hydrocarbons compared to their cyclic versions.

1. Introduction

In graph theory and chemical graph theory, graph invariants are quantitative measures that preserve the structural properties of graphs under isomorphism. Graph energy is one of the graph invariants which is associated with the physico-chemical properties of the selected molecules. The origin of this research field goes back 50 years when the famous graph energy was introduced in [1].

Countless papers and some monographs have been written on graph energy; for some of them, see [1,2,3]. The monograph [3] is an excellent compilation of results on graph energy, historical background of the subject and methodological approaches, which can serve as a guide for the reader who wishes to know more about this field.

Let G be a (simple) graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. Let the number of vertices of the graph G be n and let them be denoted by $v_1$, $v_2$, …, $v_n$. The adjacency matrix $A\left(G\right)$ of the graph G is a square matrix of order n whose $(i,j)$ entry is equal to 1 if the vertices $v_i$ and $v_j$ are adjacent and zero otherwise. The eigenvalues ${\lambda }_1$, ${\lambda }_2$, …, ${\lambda }_n$ of the adjacency matrix $A\left(G\right)$ are called the eigenvalues of the graph G [4].

In [4], Gutman et al. state that for molecular graph G of a conjugated hydrocarbon with eigenvalues ${\lambda }_1$, ${\lambda }_2$, …, ${\lambda }_n$, in the so-called Hückel molecular orbital (HMO) [5] approximation, the energy of the i-th molecular orbital is given by

$$E_i=\alpha +{\lambda }_i\beta ,$$

where $\alpha$ and $\beta$ are constants. To simplify the formalism, it is common to set $\alpha =0$ and $\beta =1$ so that the $\pi$-electron orbital energies and the graph eigenvalues coincide. It follows that the total $\pi$-electron energy (E) is equal to the sum of all $\pi$-electron energies present in the molecule, i.e., $E={\sum }_{i=1}^n{g}_i{E}_i={\sum }_{i=1}^n{g}_i{\lambda }_i$, where $g_i$ is the number of electrons in the i-th molecular orbital with energy $E_i$. In [4], it is explained that because of restrictions presented in [6], $g_i$ is 2, 1 or 0. It is important for us to note that in most chemically relevant cases $g_i=2$ when ${\lambda }_i>0$ and $g_i=0$ when ${\lambda }_i<0$, which implies that energy is equal to summation over positive eigenvalues $(E=2{\sum }_{+}{\lambda }_i$, where ${\sum }_{+}$ is summation over positive eigenvalues). However, since the sum of all eigenvalues is zero, it follows that

$$E=E\left(G\right)=\sum _{i=1}^n\left|{\lambda }_i\right|.$$

The total of $\pi$-electron energy and the right-hand side of the previous equation were studied by Coulson [7] back in the pioneering days of quantum chemistry. In the 1970s, Gutman [1] came up with the idea of defining the energy of a graph G as the sum of the absolute values of its eigenvalues.

In [2], Gutman describes a large number of lower and upper bounds for the graph energy, but the first to write a theorem for lower and upper bounds for the graph energy was McClelland in 1971 [8]. Koolen, Moulton and Gutman introduced an improvement to McClelland’s inequality for the total $\pi$-electron energy in [9].

Estrada and Benzi wrote in [10] that the graph energy is a weighted sum of the traces of the even powers of the adjacency matrix. They saw the potential benefit of this finding in new techniques that can be developed to constrain the graph energy where the specific contribution of subgraphs can be determined. This is very important in chemistry, where the search for additional rules for molecular properties contributes to the understanding of such properties in structural terms.

Gutman and Furtula in [11] outline basic principles and facts for the study of graph energies and point out their main applications. A comprehensive research on the subject did not begin until twenty-five years after graph energy was introduced. Over a hundred variants of graph energy have been proposed, based on various matrices rather than the adjacency matrix as in our case. Research on these graph energies is very active nowadays and has led to well over a thousand publications. This has led to a rapid increase in the number of published papers, which is now more than two per week. Graph energies have found unexpected applications in fields of science and engineering such as crystallography, air transport, satellite communication, face recognition, protein sequence comparison, spacecraft construction and high-resolution satellite image processing. Some applications have also been tested in medicine.

The aim of this paper is to study the smoothness of graph energy of certain acyclic and cyclic hydrocarbons. We calculate the graph energies and give linear relations for their prediction. We also compare the graph energies of acyclic molecules with those of their cyclic versions. We then establish measures of smoothness—the (modified) structure sensitivity and (modified) abruptness for 135 molecular graphs in our dataset.

The structure of the paper is the following: In the next section we introduce graph edit distance (GED), structure sensitivity and abruptness, as well as modified structure sensitivity and modified abruptness. The computational details and results are presented in Section 3. First, linear regression analysis of graph energy and correlations is considered and second (modified) structure sensitivity and (modified) abruptness is examined with respect to graph energy. The graph energies of acyclic and cyclic molecules from our dataset are compared finally. A discussion is presented in Section 4 and in Section 5 conclusions are presented. All the calculated data are gathered at the end of the paper.

2. Preliminaries

The concept of smoothness of a molecular descriptor (or topological index) can be viewed as an answer to the question of whether a slight change in the structure of a molecule leads to a slight change in the molecular descriptor. Furtula et al. approached this problem in [12] and introduced the structure sensitivity and the abruptness of a topological index. A sensitive topological index should have a high structure sensitivity, but needs to keep the abruptness as low as possible. The graph edit distance GED can be used to compare graphs with a small structural change. Graph edit distance is defined as the cost of the least expensive sequence of edit operations required to transform one graph into another; for a survey on GED, see [13]. Our goal is to compare molecules of the same size and order. More precisely, for a graph G, let $\mathcal{S}\left(G\right)$ be a set of graphs obtained from G by adding an edge together with its endpoint. Consequently, the graph edit distance between G and any graph from $\mathcal{S}\left(G\right)$ is equal to two. For a molecular descriptor $TI$ of the graph G, the structure sensitivity $S{S}_G\left(TI\right)$ and the abruptness ${\mathrm{Abr}}_G\left(TI\right)$ are defined as follows:

$${\displaystyle S{S}_G\left(TI\right)=\frac{1}{\left|\mathcal{S}\right(G\left)\right|}\sum _{H\in \mathcal{S}\left(G\right)}\left|\frac{TI\left(G\right)-TI\left(H\right)}{TI\left(G\right)}\right|}$$

and

$${\mathrm{Abr}}_G\left(TI\right)=\underset{H\in \mathcal{S}\left(G\right)}{max}\left|\frac{TI\left(G\right)-TI\left(H\right)}{TI\left(G\right)}\right|.$$

In [14], a new method for quantifying the structure sensitivity and abruptness of a molecular descriptor is presented that outperforms the first method. Instead of comparing graphs based on a fixed graph edit distance, we chose a molecule M represented by a molecular graph G and then formed a set of all molecules in our dataset that are similar to M. The set of molecular graphs of these molecules is denoted by $\mathcal{M}\left(G\right)$. Then, a modified structure sensitivity $S{S}_G^{*}\left(TI\right)$ and a modified abruptness ${\mathrm{Abr}}_G^{*}\left(TI\right)$ of a molecular descriptor $TI$ for a molecular graph G were assessed with the following formulas:

$${\displaystyle S{S}_G^{*}\left(TI\right)=\sqrt{{\displaystyle \frac{1}{\left|\mathcal{M}\right(G\left)\right|}\sum _{H\in \mathcal{M}\left(G\right)}{(TI\left(G\right)-TI\left(H\right))}^2}}}$$

and

$${\mathrm{Abr}}_G^{*}\left(TI\right)=\underset{H\in \mathcal{M}\left(G\right)}{max}\left|TI\left(G\right)-TI\left(H\right)\right|.$$

The average values of a modified structure sensitivity and a modified abruptness of a molecular descriptor $TI$ over molecular graphs in the set $\mathcal{M}$ were calculated as follows:

$${\displaystyle \overline{S{S}^{*}}\left(TI\right)=\frac{{\displaystyle \sum _{G\in \mathcal{M}}S{S}_G^{*}\left(TI\right)}}{\left|\mathcal{M}\right|\left({\displaystyle \underset{G\in \mathcal{M}}{max}TI\left(G\right)-\underset{G\in \mathcal{M}}{min}TI\left(G\right)}\right)}}$$

and

$${\displaystyle \overline{{\mathrm{Abr}}^{*}}\left(TI\right)=\frac{{\displaystyle \sum _{G\in \mathcal{M}}{\mathrm{Abr}}_G^{*}\left(TI\right)}}{\left|\mathcal{M}\right|\left({\displaystyle \underset{G\in \mathcal{M}}{max}TI\left(G\right)-\underset{G\in \mathcal{M}}{min}TI\left(G\right)}\right)}.}$$

3. Computational Details and Results

Our dataset $\mathcal{M}$ is composed of four sets of hydrocarbons with up to 20 carbon atoms. The first set $M_1$ consists of 19 acyclic alkanes from ethane to icosane and the second set $M_2$ is formed of 18 cyclic versions of the molecules in the first set. The third and the fourth set, $M_3$ and $M_4$, were obtained by adding the methyl group to the cycloalkanes and alkanes of the sets $M_2$ and $M_1$, respectively (see Figure 1). So in the set $M_3$ there are 17 methyl-cycloalkanes and in the set $M_4$ there are 82 methyl-alkanes. The cardinality of $M_4$ is larger due to the structural isomers of methyl-alkanes. For all 135 molecules in the dataset $\mathcal{M}$, the eigenvalues and then the graph energies are calculated; see

Table A5. The graph energy of considered molecular graphs.

Set	Molecule	E(G)	Set	Molecule	E(G)	Set	Molecule	E(G)
$M_1$	ethane	2.00000	$M_3$	methylcycloundecane	15.07008	$M_4$	2-methyltetradecane	17.86281
$M_1$	propane	2.82843	$M_3$	methylcyclododecane	16.17966	$M_4$	3-methyltetradecane	18.16937
$M_1$	butane	4.47214	$M_3$	methylcyclotridecane	17.61161	$M_4$	4-methyltetradecane	17.98224
$M_1$	pentane	5.46410	$M_3$	methylcyclotetradecane	18.83458	$M_4$	5-methyltetradecane	18.11767
$M_1$	hexane	6.98792	$M_3$	methylcyclopentadecane	20.15434	$M_4$	6-methyltetradecane	18.03991
$M_1$	heptane	8.05468	$M_3$	methylcyclohexadecane	21.30986	$M_4$	7-methyltetradecane	18.07995
$M_1$	octane	9.51754	$M_3$	methylcycloheptadecane	22.69787	$M_4$	2-methylpentadecane	19.02873
$M_1$	nonane	10.62750	$M_3$	methylcyclooctadecane	23.92413	$M_4$	3-methylpentadecane	19.55275
$M_1$	decane	12.05335	$M_3$	methylcyclononadecane	25.24196	$M_4$	4-methylpentadecane	19.13426
$M_1$	undecane	13.19151	$M_4$	2-methyilpropane	3.46410	$M_4$	5-methylpentadecane	19.51960
$M_1$	dodecane	14.59246	$M_4$	2-methylbutane	5.22625	$M_4$	6-methylpentadecane	19.17167
$M_1$	tridecane	15.75049	$M_4$	2-methylpentane	6.15537	$M_4$	7-methylpentadecane	19.50812
$M_1$	tetradecane	17.13354	$M_4$	3-methylpentane	6.89898	$M_4$	8-methylpentadecane	19.18177
$M_1$	pentadecane	18.30634	$M_4$	2-methylhexane	7.72741	$M_4$	2-methylhexadecane	20.40459
$M_1$	hexadecane	19.67590	$M_4$	3-methylhexane	7.87846	$M_4$	3-methylhexadecane	20.72530
$M_1$	heptadecane	20.86010	$M_4$	2-methylheptane	8.76257	$M_4$	4-methylhexadecane	20.52275
$M_1$	octadecane	22.21913	$M_4$	3-methylheptane	9.40926	$M_4$	5-methylhexadecane	20.67691
$M_1$	nonadecane	23.41241	$M_4$	4-methylheptane	8.82843	$M_4$	6-methylhexadecane	20.57827
$M_1$	icosane	24.76298	$M_4$	2-methyloktane	10.25166	$M_4$	7-methylhexadecane	20.64463
$M_2$	cyclopropane	4.00000	$M_4$	3-methyloktane	10.47214	$M_4$	8-methylhexadecane	20.61452
$M_2$	cyclobutane	4.00000	$M_4$	4-methyloktane	10.38398	$M_4$	2-methylheptadecane	21.58344
$M_2$	cyclopentane	6.47214	$M_4$	2-methylnonane	11.34256	$M_4$	3-methylheptadecane	22.09506
$M_2$	cyclohexane	8.00000	$M_4$	3-methylnonane	11.93751	$M_4$	4-methylheptadecane	21.69103
$M_2$	cycloheptane	8.98792	$M_4$	4-methylnonane	11.42991	$M_4$	5-methylheptadecane	22.06053
$M_2$	cyclooctane	9.65685	$M_4$	5-methylnonane	11.91801	$M_4$	6-methylheptadecane	21.73174
$M_2$	cyclononane	11.51754	$M_4$	2-methyldecane	12.78491	$M_4$	7-methylheptadecane	22.04685
$M_2$	cyclodecane	12.94427	$M_4$	3-methyldecane	13.04588	$M_4$	8-methylheptadecane	21.74737
$M_2$	cycloundecane	14.05335	$M_4$	4-methyldecane	12.90997	$M_4$	9-methylheptadecane	22.04302
$M_2$	cyclododecane	14.92820	$M_4$	5-methyldecane	12.97890	$M_4$	2-methyloctadecane	22.94743
$M_2$	cyclotridecane	16.59246	$M_4$	2-methylundecane	13.91031	$M_4$	3-methyloctadecane	23.27911
$M_2$	cyclotetradecane	17.97584	$M_4$	3-methylundecane	14.47285	$M_4$	4-methyloctadecane	23.06473
$M_2$	cyclopentadecane	19.13354	$M_4$	4-methylundecane	14.00741	$M_4$	5-methyloctadecane	23.23289
$M_2$	cyclohexadecane	20.10936	$M_4$	5-methylundecane	14.44570	$M_4$	6-methyloctadecane	23.11891
$M_2$	cycloheptadecane	21.67590	$M_4$	6-methylundecane	14.02929	$M_4$	7-methyloctadecane	23.20394
$M_2$	cyclooctadecane	23.03508	$M_4$	2-methyldodecane	15.32260	$M_4$	8-methyloctadecane	23.15298
$M_2$	cyclononadecane	24.21913	$M_4$	3-methyldodecane	15.61023	$M_4$	9-methyloctadecane	23.17929
$M_2$	cycloicosane	25.25501	$M_4$	4-methyldodecane	15.44407	$M_4$	2-methylnonadecane	24.13641
$M_3$	methylcyclopropane	4.96239	$M_4$	5-methyldodecane	15.55311	$M_4$	3-methylnonadecane	24.63826
$M_3$	methylcyclobutane	5.34831	$M_4$	6-methyldodecane	15.50548	$M_4$	4-methylnonadecane	24.24541
$M_3$	methylcyclopentane	7.46588	$M_4$	2-methyltridecane	16.47148	$M_4$	5-methylnonadecane	24.60280
$M_3$	methylcyclohexane	8.72057	$M_4$	3-methyltridecane	17.01176	$M_4$	6-methylnonadecane	24.28829
$M_3$	methylcycloheptane	9.99435	$M_4$	4-methyltridecane	16.57385	$M_4$	7-methylnonadecane	24.58774
$M_3$	methylcyclooctane	11.00351	$M_4$	5-methyltridecane	16.98080	$M_4$	8-methylnonadecane	24.30726
$M_3$	methylcyclononane	12.53047	$M_4$	6-methyltridecane	16.60578	$M_4$	9-methylnonadecane	24.58171
$M_3$	methylcyclodecane	13.75486	$M_4$	7-methyltridecane	16.97315	$M_4$	10-methylnonadecane	24.31279

in Appendix A.

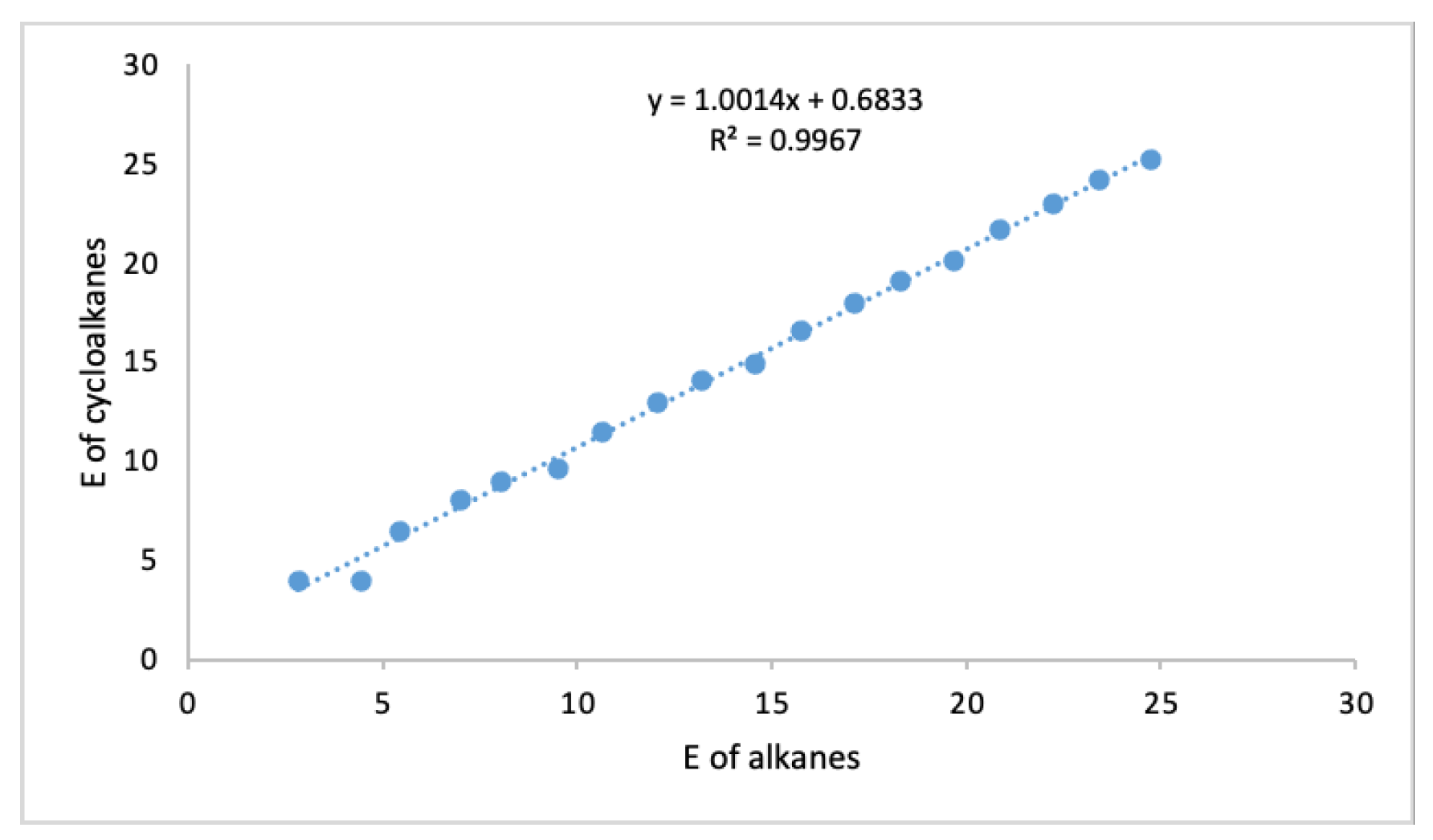
3.1. Linear Regression Analysis of Graph Energy and Correlations

First, we compare the values of the calculated graph energies as a linear function of the number of vertices in a molecular graph, denoted by n. Each of the four subsets $M_1,\dots ,M_4$ is considered separately. In the subset $M_4$, we have structural isomers with the same number of vertices, so in this case the average of the graph energies is considered in the regression analysis. Linear regressions for predicting the graph energy for alkanes (1), cycloalkanes (2), methyl-cycloalkanes (3) and the average value of graph energy for methyl-alkanes (4) are:

$$\begin{array}{c}\hfill E\left(M_1\right)=1.2782n-0.8149,R^2=0.9996\end{array}$$

(1)

$$\begin{array}{c}\hfill E\left(M_2\right)=1.2806n-0.1406,R^2=0.9976\end{array}$$

(2)

$$\begin{array}{c}\hfill E\left(M_3\right)=1.2827n+0.8792,R^2=0.9991\end{array}$$

(3)

$$\begin{array}{c}\hfill E\left(M_4\right)=1.2825n+0.0682,R^2=0.9993\end{array}$$

(4)

As we can observe, the correlations are very good, since the coefficients of determination are all higher than $0.99$.

Second, we are interested in the connection between the graph energies of acyclic and cyclic molecules and so we compare the values of graph energies between molecular graphs in the sets $M_1$ and $M_2$. More specifically, we perform the correlation analysis between alkanes and cycloalkanes with the same number of vertices. The results are gathered in Figure 2. We proceed similarly with the molecules in the subsets $M_3$ and $M_4$, i.e., with methyl-alkanes and methyl-cycloalkanes. As in the linear regressions for the prediction of graph energies, because of the structural isomers of methyl-alkanes with the same number of vertices, the average value of graph energies of isomers is included in the calculation. The results can be seen in Figure 3.

Again, the correlations between graph energies of acyclic and cyclic molecules are very good, as the coefficients of determination are both above 0.99.

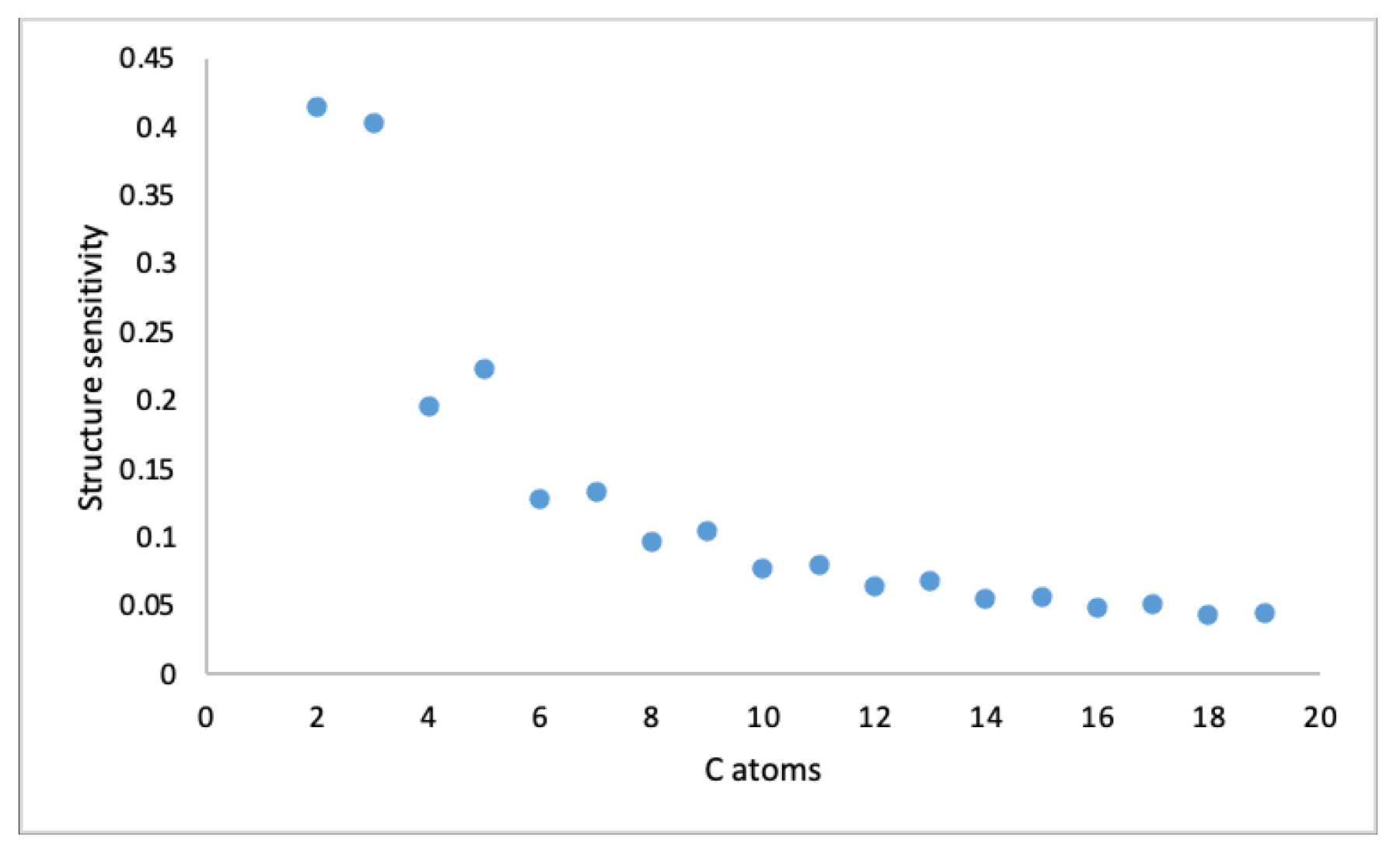
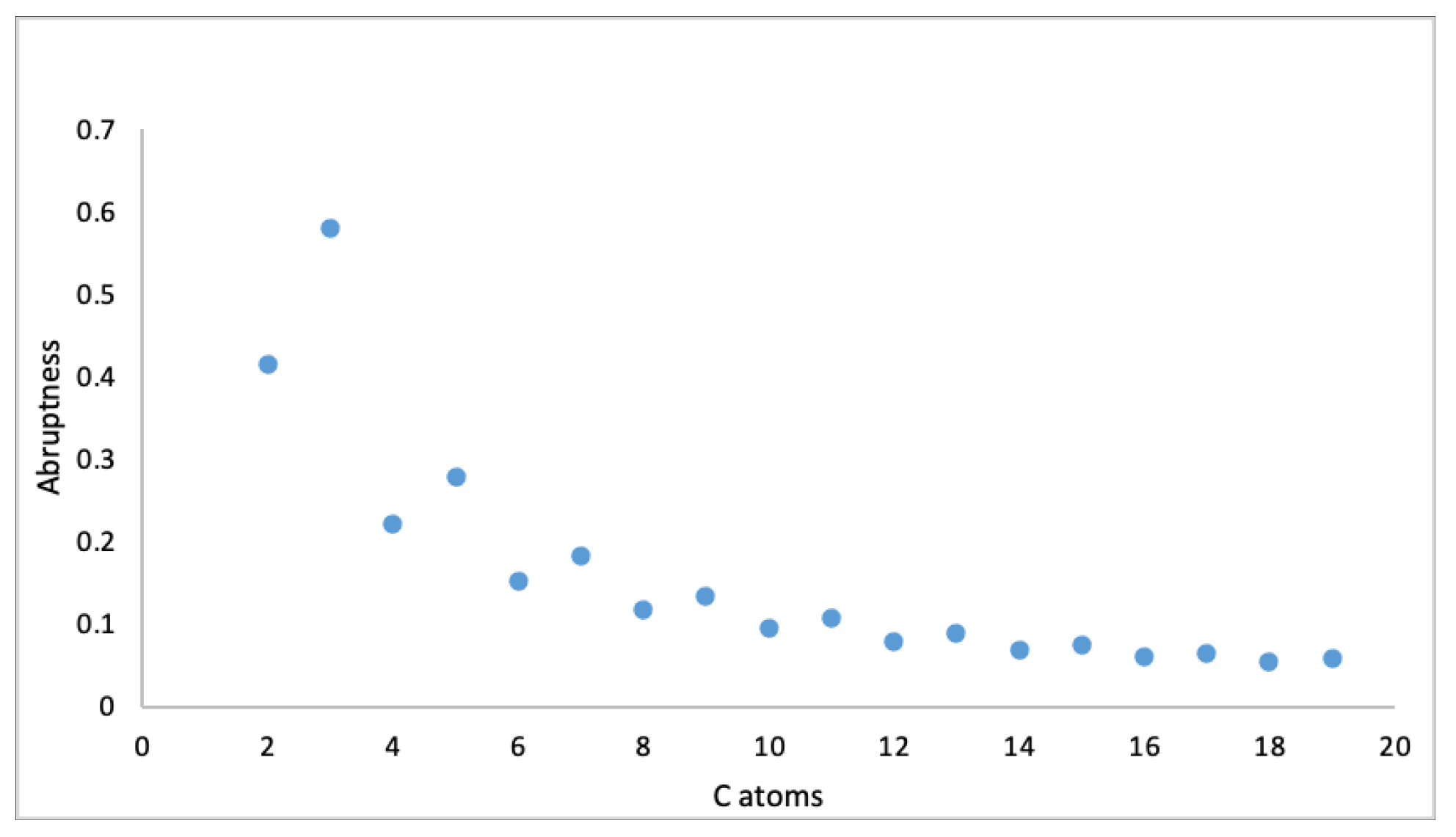
3.2. Structure Sensitivity and Abruptness of Graph Energy

We now consider the structure sensitivity and the abruptness of the graph energy of alkanes and molecular graphs in the dataset $\mathcal{M}$, which has a graph edit distance equal to 2. More precisely, for an alkane G, let $\mathcal{S}\left(G\right)$ be the set of all molecular graphs resulting from G with the addition of an edge and its endpoint. For example, for hexane G, there are three molecular graphs from our dataset with GED = 2, that is, the molecular graphs of 2-methylhexane, 3-methylhexane and heptane form the set $\mathcal{S}\left(G\right)$ (see Figure 4). The structure sensitivity and abruptness of graph energy are then calculated for each alkane G. The obtained values are shown in

Table A1. The structure sensitivity and the abruptness of graph energy of alkanes with up to 19 vertices with regard to the molecular graphs in the dataset with GED = 2.

G	$\left|\mathcal{S}\right(\mathit{G}\left)\right|$	${\mathit{SS}}_{\mathit{G}}\left(\mathit{E}\right)$	${\mathbf{Abr}}_{\mathit{G}}\left(\mathit{E}\right)$
ethane	1	0.41421	0.41421
propane	2	0.40294	0.58114
butane	2	0.19522	0.22181
pentane	3	0.22266	0.27888
hexane	3	0.12864	0.15266
heptane	4	0.13343	0.18162
octane	4	0.09627	0.11662
nonane	5	0.10433	0.13417
decane	5	0.07706	0.09443
undecane	6	0.07971	0.10620
dodecane	6	0.06432	0.07936
tridecane	7	0.06800	0.08781
tetradecane	7	0.05523	0.06845
pentadecane	8	0.05683	0.07481
hexadecane	8	0.04841	0.06019
heptadecane	9	0.05048	0.06515
octadecane	9	0.04310	0.05371
nonadecane	10	0.04416	0.05769

in Appendix A.

Visualisation of the data from Table A1 from Appendix A is shown in Figure 5 for structure sensitivity and in Figure 6 for abruptness of graph energy. It can be seen that both structure sensitivity and abruptness of graph energy decrease with the order of a molecule.

Finally, we consider the modified structure sensitivity $S{S}^{*}$ and the modified abruptness ${\mathrm{Abr}}^{*}$ as introduced by Furtula et al. in [14], where the authors aim to determine the structure sensitivity of molecular descriptors by grouping similar molecules using the Tanimoto index and the Morgan circular fingerprints. The same concept is also applied in [15], where the authors investigated structural sensitivity of some eigenvalue-based topological indices, including the graph energy. In this way we now consider isomeric molecules in the database instead of using the concept of graph edit distance.

Our dataset is again the set $\mathcal{M}$ without the smallest molecule ethane. The dataset is divided into 18 subsets of mutually isomeric molecules with respect to the number of carbon atoms, so the smallest subset contains molecules with 3 carbon atoms and the last subset contains molecules with 20 carbon atoms. The modified structure sensitivity and modified abruptness are considered separately in 18 subsets. For example, in Figure 7 we see isomers with five carbon atoms: pentane, 2-methylbutane, cyclopentane and methylcyclobutane. In each of these subsets, each molecule is set once as a referent molecule G and then the modified structure sensitivity and modified abruptness are computed for G, so that the calculations must be performed for all 134 molecules from $\mathcal{M}$. Moreover, the average values are calculated for modified structure sensitivity and modified abruptness in each of the 18 subgroups of isomers. Due to the complexity of the calculations, an algorithm was developed in the Python programming language. The results are summarised in

Table A2. Modified structure sensitivity and modified abruptness with average values, Part I.

# C	G	${\mathit{SS}}_{\mathit{G}}^{*}\left(\mathit{E}\right)$	${\mathbf{Abr}}_{\mathit{G}}^{*}\left(\mathit{E}\right)$	$\overline{{\mathit{SS}}^{*}}\left(\mathit{E}\right)$	$\overline{{\mathbf{Abr}}^{*}}\left(\mathit{E}\right)$
3	propane	0.82843	1.17157	0.70711	1.00000
	cyclopropane	0.82843	1.17157
4	butane	0.60815	1.00804	0.51271	0.82878
	2-methylpropane	0.94183	1.49829
	cyclobutane	0.59923	0.96239
	methylcyclopropane	0.92350	1.49829
5	pentane	0.52109	1.00804	0.60176	1.02855
	2-methylbutane	0.63713	1.24589
	cyclopentane	0.97870	1.24589
	methylcyclobutane	0.56818	1.12383
6	hexane	0.62511	1.01208	0.45578	0.77120
	2-methylpentane	1.12838	1.84463
	3-methylpentane	0.64722	1.10102
	cyclohexane	1.08853	1.84463
	methylcyclopentane	0.71450	1.31051
7	heptane	0.53898	0.93324	0.54555	0.88169
	2-methylhexane	0.73555	1.26051
	3-methylhexane	0.63149	1.10946
	cycloheptane	0.86743	1.26051
	methylcyclohexane	0.66489	0.99316
8	octane	0.46607	0.75497	0.49261	0.80174
	2-methylheptane	0.74269	1.23178
	3-methylheptane	0.44176	0.64669
	4-methylheptane	0.69068	1.16592
	cyclooctane	0.52925	0.89428
	methylcycloheptane	0.77031	1.23178
9	nonane	0.43936	0.89004	0.46611	0.83639
	2-methyloktane	0.62917	1.26588
	3-methyloktane	0.49257	1.04540
	4-methyloktane	0.54058	1.13356
	cyclononane	0.91621	1.26588
	methylcyclooctane	0.52234	0.75185
10	decane	0.52739	0.89092	0.44980	0.78752
	2-methylnonane	0.85978	1.60171
	3-methylnonane	0.53326	1.00676
	4-methylnonane	0.79253	1.51436
	5-methylnonane	0.53671	1.02626
	cyclodecane	1.06170	1.60171
	methylcyclononane	0.73172	1.18791
11	undecane	0.44258	0.86184	0.47531	0.85526
	2-methyldecane	0.63656	1.26844
	3-methyldecane	0.48254	1.00747
	4-methyldecane	0.55282	1.14338
	5-methyldecane	0.51390	1.07445
	cycloundecane	0.91944	1.26844
	methylcyclodecane	0.67251	0.96995

,

Table A3. Modified structure sensitivity and modified abruptness with average values, Part II.

# C	G	${\mathit{SS}}_{\mathit{G}}^{*}\left(\mathit{E}\right)$	${\mathbf{Abr}}_{\mathit{G}}^{*}\left(\mathit{E}\right)$	$\overline{{\mathit{SS}}^{*}}\left(\mathit{E}\right)$	$\overline{{\mathbf{Abr}}^{*}}\left(\mathit{E}\right)$
12	dodecane	0.43322	0.68215	0.47928	0.79161
	2-methylundecane	0.65890	1.15977
	3-methylundecane	0.40449	0.59723
	4-methylundecane	0.58503	1.06267
	5-methylundecane	0.40266	0.62438
	6-methylundecane	0.56934	1.04079
	cyclododecane	0.63885	1.01789
	methylcycloundecane	0.75435	1.15977
13	tridecane	0.40136	0.84197	0.42822	0.83628
	2-methyldodecane	0.58248	1.26986
	3-methyldodecane	0.42327	0.98223
	4-methyldodecane	0.50147	1.14839
	5-methyldodecane	0.44474	1.03935
	6-methyldodecane	0.46724	1.08698
	cyclotridecane	0.93790	1.26986
	methylcyclododecane	0.59177	0.85706
14	tetradecane	0.47516	0.84230	0.42032	0.79215
	2-methyltridecane	0.73279	1.50436
	3-methyltridecane	0.46608	0.96408
	4-methyltridecane	0.65694	1.40199
	5-methyltridecane	0.46881	0.99504
	6-methyltridecane	0.63480	1.37006
	7-methyltridecane	0.46980	1.00269
	cyclotetradecane	1.04737	1.50436
	methylcyclotridecane	0.73900	1.14013
15	pentadecane	0.40023	0.82720	0.42503	0.84107
	2-methyltetradecane	0.57807	1.27073
	3-methyltetradecane	0.41464	0.96417
	4-methyltetradecane	0.49861	1.1513
	5-methyltetradecane	0.43140	1.01587
	6-methyltetradecane	0.46638	1.09363
	7-methyltetradecane	0.44703	1.05359
	cyclopentadecane	0.94172	1.27073
	methylcyclotetradecane	0.68286	0.97177
16	hexadecane	0.41172	0.64717	0.45513	0.78507
	2-methylpentadecane	0.60447	1.12561
	3-methylpentadecane	0.37716	0.60159
	4-methylpentadecane	0.52563	1.02008
	5-methylpentadecane	0.37429	0.63474
	6-methylpentadecane	0.50004	0.98267
	7-methylpentadecane	0.37398	0.64622
	8-methylpentadecane	0.49340	0.97257
	cyclohexadecane	0.71180	1.08063
	methylcyclopentadecane	0.75050	1.12561

and

Table A4. Modified structure sensitivity and modified abruptness with average values, Part III.

# C	G	${\mathit{SS}}_{\mathit{G}}^{*}\left(\mathit{E}\right)$	${\mathbf{Abr}}_{\mathit{G}}^{*}\left(\mathit{E}\right)$	$\overline{{\mathit{SS}}^{*}}\left(\mathit{E}\right)$	$\overline{{\mathbf{Abr}}^{*}}\left(\mathit{E}\right)$
17	heptadecane	0.37776	0.81578	0.25875	0.83038
	2-methylhexadecane	0.54462	1.27131
	3-methylhexadecane	0.38081	0.95060
	4-methylhexadecane	0.46564	1.15315
	5-methylhexadecane	0.39333	0.99899
	6-methylhexadecane	0.43471	1.09763
	7-methylhexadecane	0.40470	1.03127
	8-methylhexadecane	0.41728	1.06138
	cycloheptadecane	0.95089	1.27131
	methylcyclohexadecane	0.63079	0.90527
18	octadecane	0.44099	0.81595	0.39023	0.79306
	2-methylheptadecane	0.65567	1.45164
	3-methylheptadecane	0.42065	0.94002
	4-methylheptadecane	0.57727	1.34405
	5-methylheptadecane	0.42136	0.97455
	6-methylheptadecane	0.55018	1.30334
	7-methylheptadecane	0.42243	0.98823
	8-methylheptadecane	0.54024	1.28771
	9-methylheptadecane	0.42280	0.99206
	cyclooctadecane	1.03767	1.45164
	methylcycloheptadecane	0.74203	1.11443
19	nonadecane	0.37550	0.80672	0.38681	0.83130
	2-methyloctadecane	0.53800	1.27170
	3-methyloctadecane	0.37328	0.94002
	4-methyloctadecane	0.45958	1.15440
	5-methyloctadecane	0.38349	0.98624
	6-methyloctadecane	0.42938	1.10022
	7-methyloctadecane	0.39253	1.01519
	8-methyloctadecane	0.41291	1.06615
	9-methyloctadecane	0.40171	1.03984
	cyclononadecane	0.95361	1.27170
	methylcyclooctadecane	0.69097	0.97670
20	icosane	0.39502	0.62657	0.42462	0.77814
	2-methylnonadecane	0.56515	1.11860
	3-methylnonadecane	0.35491	0.61675
	4-methylnonadecane	0.48431	1.00960
	5-methylnonadecane	0.35084	0.65221
	6-methylnonadecane	0.45574	0.96672
	7-methylnonadecane	0.35019	0.66727
	8-methylnonadecane	0.44384	0.94775
	9-methylnonadecane	0.35011	0.67330
	10-methylnonadecane	0.44046	0.94222
	cycloicosane	0.76036	1.11860
	methylcyclononadecane	0.74880	1.10555

in Appendix A.

In Figure 8 and Figure 9, it can be seen that the modified sensitivity decreases with the order of the isomers considered, while the modified abruptness also decreases, but more slowly and depending on the parity of the vertices.

4. Discussion

The calculated graph energies allow us to establish a very good linear relationship for predicting the graph energies of (methyl)-(cyclo)alkanes. All four types of molecular groups are treated separately, as is common in chemical graph theory, to obtain more accurate predictions. Very high correlations ensure reliable prediction of graph energies obtained in a simple way from the order of a molecular graph. There is also a high correlation between the graph energies of cyclic molecular graphs compared to acyclic graphs.

According to [12], from a practical point of view, the desirable property of a topological index is that the structure sensitivity is as large as possible, but the abruptness is as small as possible. As for many of the topological indices considered therein, our results also show that the structure sensitivity and abruptness of graphs clustered with respect to the graph edit distance both decrease with the order of the molecular graphs, tending towards zero.

In our study, the structure sensitivity behaves similarly to the modified structure sensitivity. The modified abruptness also decreases with the number of vertices of the molecular graph, but at a slower rate. We also found that abruptness and modified abruptness behave similarly in graphs with even order and graphs with odd order. However, we must take into account that the sets of “similar” molecules are defined differently in these two cases. In the first case, we considered molecular graphs with the same graph edit distance and in the second case similar molecules were grouped together in terms of isomerism and therefore cannot be compared numerically.

5. Conclusions

This research gives us an insight into the relationship between graph energies of cyclic and acyclic structures and establishes the linear formulae for a very good prediction of this topological index from the order of the molecular graph.

The measures of smoothness of graph energy are provided and their behaviour is studied. The next line of work is to compare the data provided here with other molecular descriptors to derive how smooth the graph energy behaves compared to other topological indices.