Multi-Objective Optimization in Support of Life-Cycle Cost-Performance-Based Design of Reinforced Concrete Structures
Abstract
1. Introduction
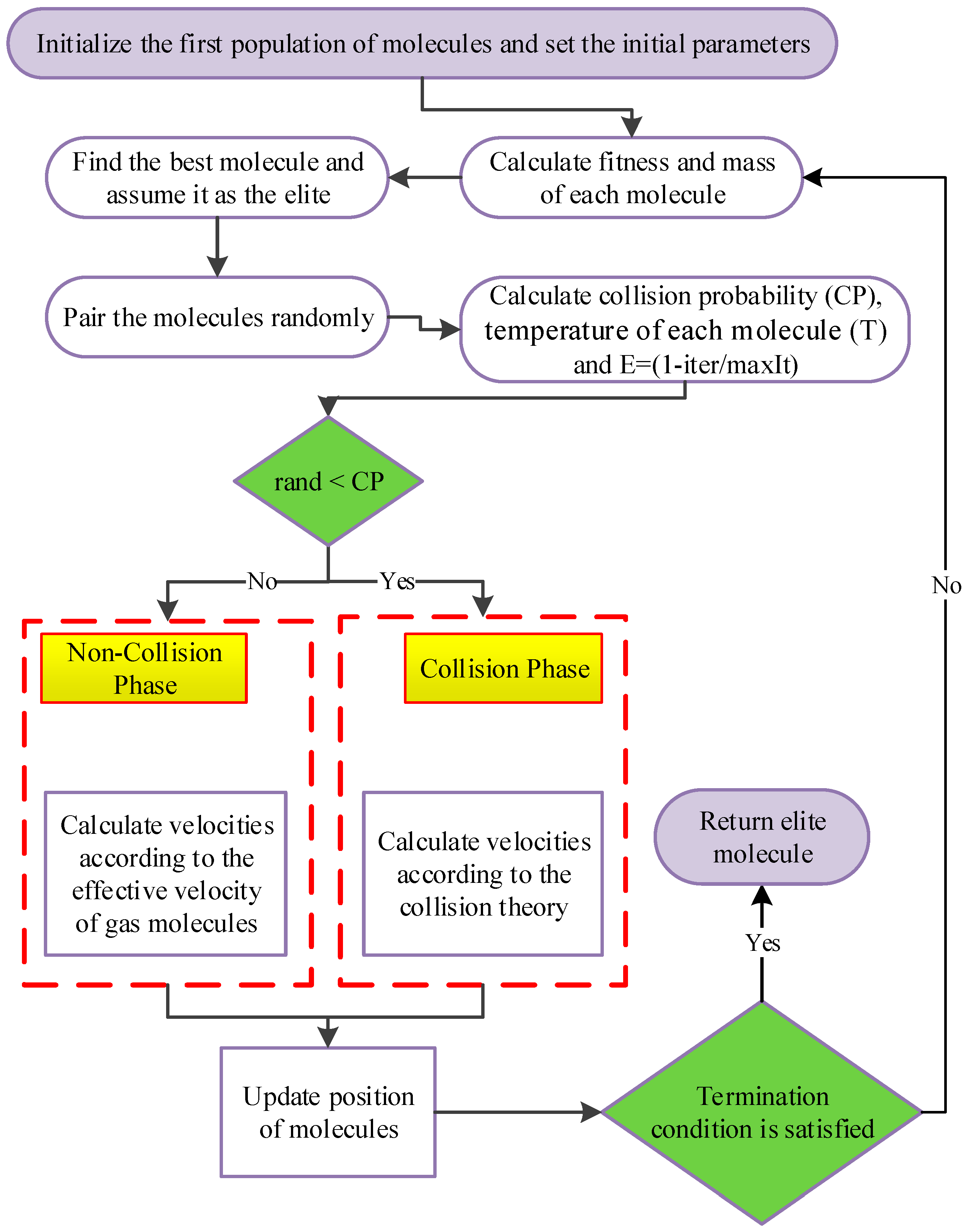
2. Optimization Algorithm
2.1. Mono-Objective IGMM-Based Algorithm
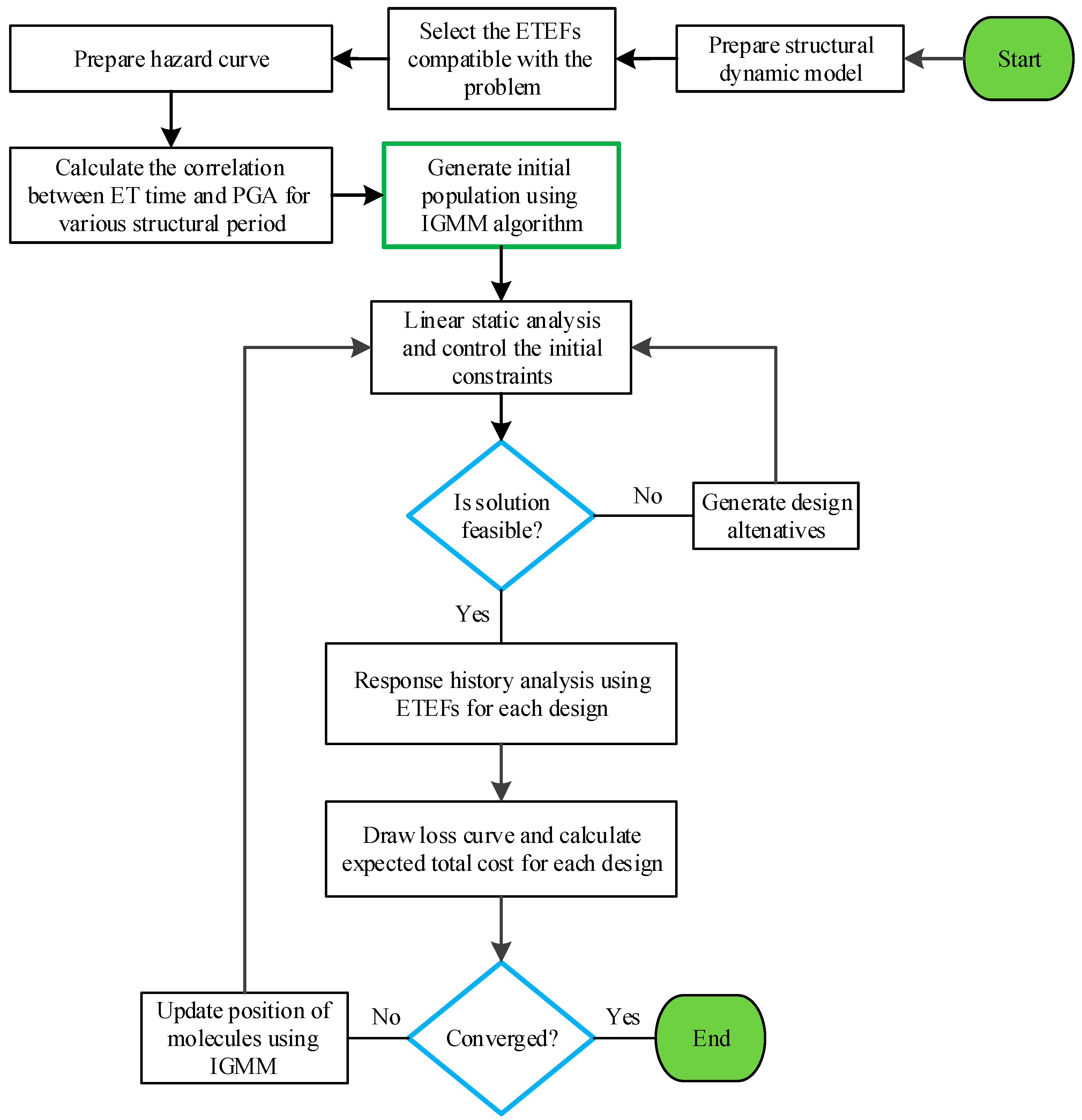
2.2. IGMM-Based Multi-Objective Optimization Algorithm
3. Endurance Time Method
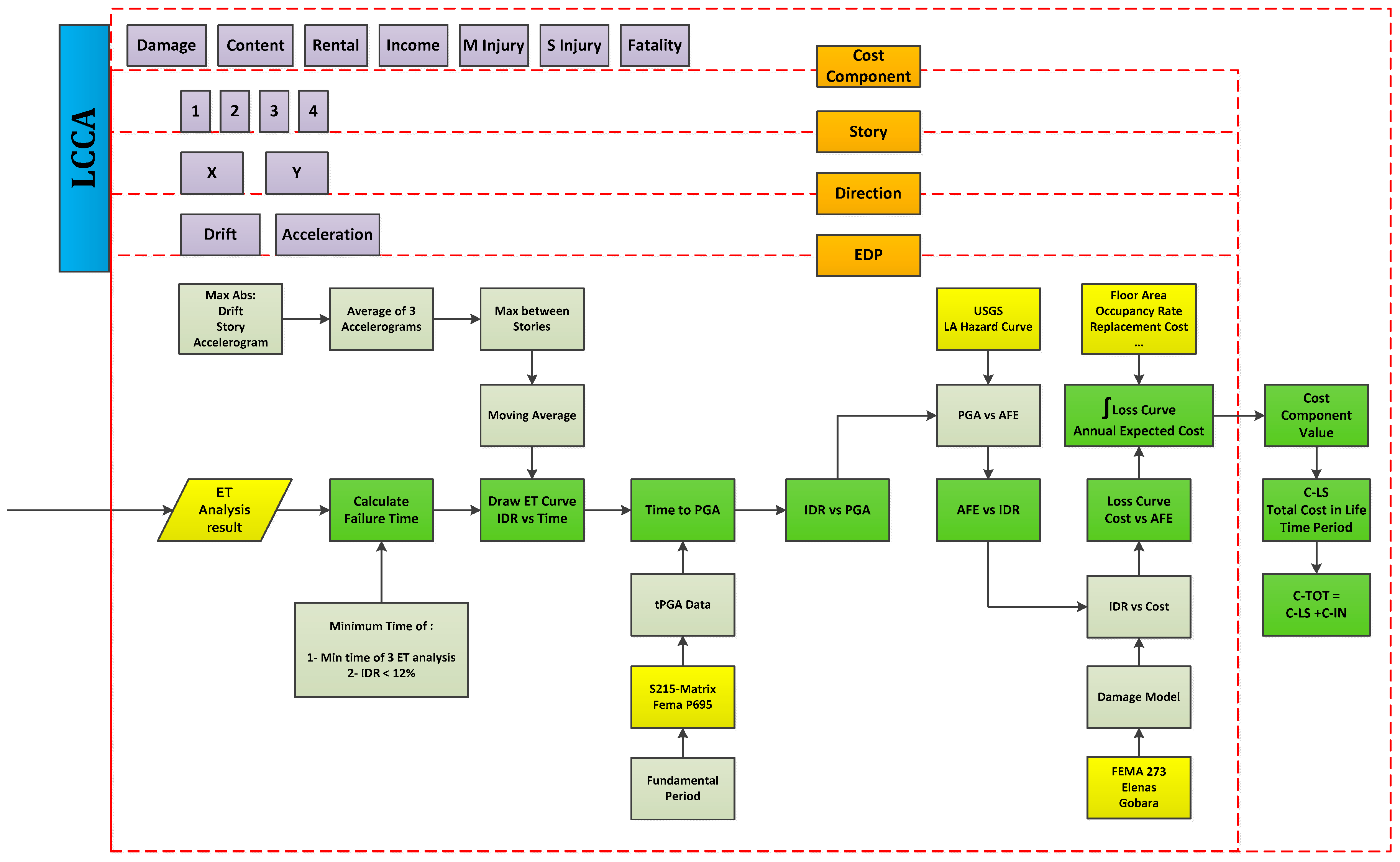
4. Design Based on the Life-Cycle Cost
4.1. Initial Cost
4.2. Lifetime Cost
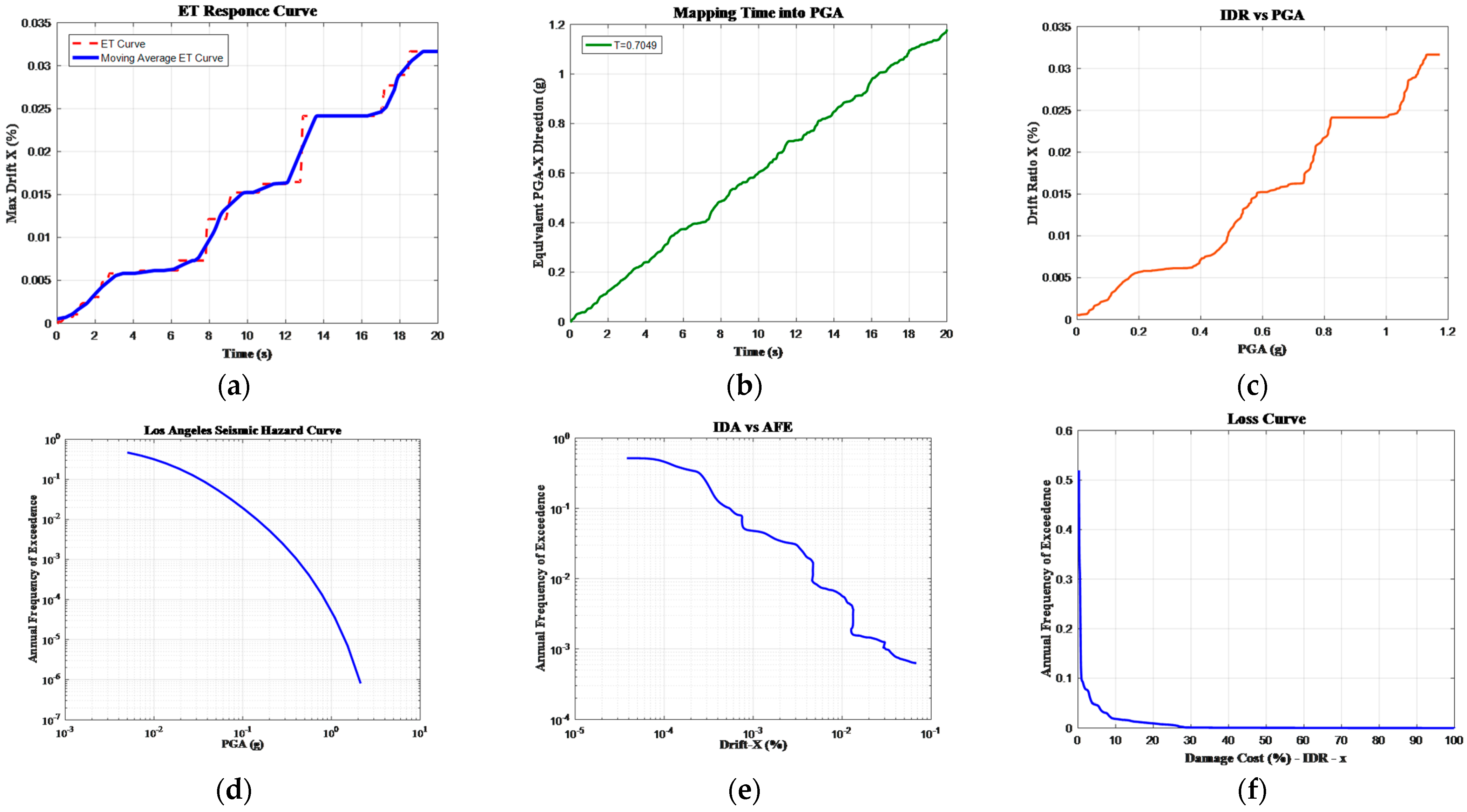
4.3. LCC Calculations Based on the ET Approach
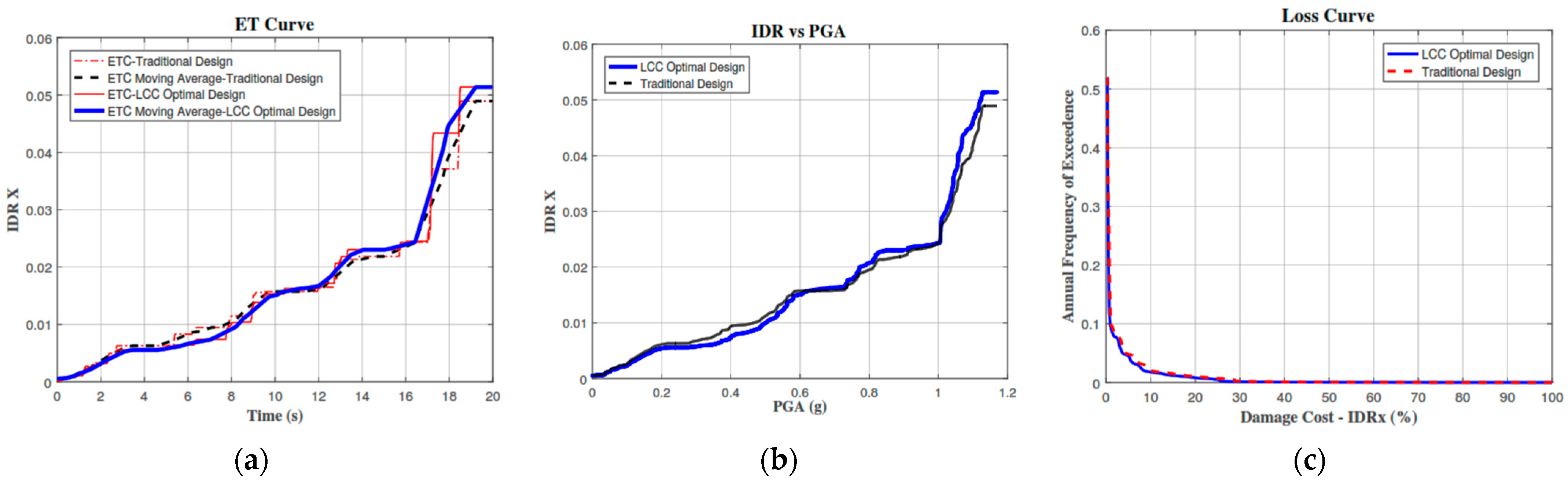
5. Numerical Example
5.1. Structural Model
- -
- The floor diaphragms are assumed to be rigid in their planes, and the masses and the moments of inertia are lumped at the center of gravity.
- -
- The elastic elements connect all joints at the story level to the center of mass. They are used to model the rigid diaphragm at the story level, where the mass can be represented in one point. Columns contain the P-delta effect.
- -
- One-component lumped plasticity elements, consisting of an elastic beam and two inelastic rotational hinges (defined by the moment–rotation relationship), are used to model the beam and column flexural behaviors. The element’s formulation is based on the concept of a point of inflection at the element’s midpoint. The plastic hinge is only used for the main axis bending in beams. For columns, two independent plastic hinges are used for bending about the two principal axes [53].
- -
- In the present study, the elastic beam-column elements and zero-length-section elements are used to create the model. At each elevation, “rigid” elements linked all of the nodes. The TakedaDAsym uniaxial material, designed in the software OpenSees_1.7.4, is used for plastic hinges in beams and columns [49].
- -
- A bi-linear or tri-linear relationship is used to model the moment–rotation relationship. When determining the moment–rotation relationship for beams or columns, zero axial force and axial strain due to gravity loads are considered, respectively. After the maximum moment, a linear negative post-capping stiffness is assumed.
- -
- The gravity load was modeled on beams as a uniformly distributed load and on columns as point loads. The self-weight of the slab and beams and the permanent load on the slab result in an evenly distributed load on the beams. Only the self-weight of columns is modeled using the point loads at the top of the columns.
5.2. Defining the Optimization Problem
5.3. Mono-Objective Optimization
- Load calculation based on ASCE 7 and determination of the base shear force using seismic hazard maps and building response factors.
- Preliminary sizing and performing of the initial sizing of structural elements (beams, columns, etc.) to resist the calculated seismic loads.
- Checking for compliance with strength and stiffness requirements.
- Structural analysis using linear static analysis to determine internal forces and moments. In this step, we ensure that all structural elements meet the required safety margins against yielding and buckling.
- Design iteration and adjustment of element sizes and configurations iteratively to optimize material usage while maintaining safety. In this step, we verify the design through detailed checks, such as ensuring proper detailing of reinforcement in concrete structures.
5.4. Multi-Objective Optimization
Computational Time
6. Conclusions
- -
- The mono-objective optimization procedure led to a 13% reduction in the useful lifetime costs by merely increasing a 1% initial cost.
- -
- In total, a 10% reduction in all structural Life-Cycle Costs was attained by mono-objective optimization.
- -
- The use of LCC-based optimization could cause a significant effect on reducing minor injury, rental, and income costs by 22%, 16%, and 16%, respectively.
- -
- Using multi-objective IGMM-based optimization resulted in performing a set of optimum responses for the 3D four-story concrete building under study, which could assist engineering designers in making a decision to perform an optimum design.
- -
- As a result, the accessible methodology here, including the ET method as an analysis tool and IGMM algorithm as an optimizer, provides a numerical tool with a considerable computational saving for the quantitative estimation of the Life-Cycle Cost and the vulnerability assessment of any real-scale reinforced concrete building.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mitropoulou, C.C.; Lagaros, N.D.; Papadrakakis, M. Life-Cycle Cost Assessment of Optimally Designed Reinforced Concrete Buildings under Seismic Actions. Reliab. Eng. Syst. Saf. 2011, 96, 1311–1331. [Google Scholar] [CrossRef]
- Varaee, H.; Safaeian Hamzehkolaei, N.; Safari, M. A Hybrid Generalized Reduced Gradient-Based Particle Swarm Optimizer for Constrained Engineering Optimization Problems. J. Soft Comput. Civ. Eng. 2021, 5, 86–119. [Google Scholar]
- Noori, F.; Varaee, H. Nonlinear Seismic Response Approximation Of Steel Moment Frames Using Artificial Neural Networks. Jordan J. Civ. Eng. 2022, 16, 108. [Google Scholar]
- Basim, M.C.; Estekanchi, H.E. Application of Endurance Time Method in Performance-Based Optimum Design of Structures. Struct. Saf. 2015, 56, 52–67. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Moradi, S.; Burton, H. V Performance-Based Design Optimization of Structures: State-of-the-Art Review. J. Struct. Eng. 2024, 150, 03124001. [Google Scholar] [CrossRef]
- Kleingesinds, S.; Lavan, O.; Venanzi, I. Life-Cycle Cost-Based Optimization of MTMDs for Tall Buildings under Multiple Hazards. Struct. Infrastruct. Eng. 2021, 17, 921–940. [Google Scholar] [CrossRef]
- Chen, A.; Ruan, X.; Frangopol, D.M.; Tsompanakis, Y. Life-Cycle, Reliability and Sustainability of Civil Infrastructure. Struct. Infrastruct. Eng. 2022, 18, 893–894. [Google Scholar] [CrossRef]
- Ganzerli, S.; Pantelides, C.P.; Reaveley, L.D. Performance-Based Design Using Structural Optimization. Earthq. Eng. Struct. Dyn. 2000, 29, 1677–1690. [Google Scholar] [CrossRef]
- Liu, Z.; Atamturktur, S.; Juang, C.H. Performance Based Robust Design Optimization of Steel Moment Resisting Frames. J. Constr. Steel. Res. 2013, 89, 165–174. [Google Scholar] [CrossRef]
- Pan, P.; Ohsaki, M.; Kinoshita, T. Constraint Approach to Performance-Based Design of Steel Moment-Resisting Frames. Eng. Struct. 2007, 29, 186–194. [Google Scholar] [CrossRef]
- Asadi, P.; Hajirasouliha, I. A Practical Methodology for Optimum Seismic Design of RC Frames for Minimum Damage and Life-Cycle Cost. Eng. Struct. 2020, 202, 109896. [Google Scholar] [CrossRef]
- Wen, Y.-K.; Kang, Y.J. Minimum Building Life-Cycle Cost Design Criteria. I: Methodology. J. Struct. Eng. 2001, 127, 330–337. [Google Scholar] [CrossRef]
- Basim, M.C.; Estekanchi, H.E. Application of Endurance Time Method in Value Based Seismic Design of Structures. In Proceedings of the Second European Conference on Earthquake Engineering and Seismology, Istanbul, Turkey, 25–29 August 2014. [Google Scholar]
- Salgado, R.A.; Apul, D.; Guner, S. Life Cycle Assessment of Seismic Retrofit Alternatives for Reinforced Concrete Frame Buildings. J. Build. Eng. 2020, 28, 101064. [Google Scholar] [CrossRef]
- Kappos, A.J.; Dimitrakopoulos, E.G. Feasibility of Pre-Earthquake Strengthening of Buildings Based on Cost-Benefit and Life-Cycle Cost Analysis, with the Aid of Fragility Curves. Nat. Hazards 2008, 45, 33–54. [Google Scholar] [CrossRef]
- Varaee, H.; Shishegaran, A.; Ghasemi, M.R. The Life-Cycle Cost Analysis Based on Probabilistic Optimization Using a Novel Algorithm. J. Build. Eng. 2021, 43, 103032. [Google Scholar] [CrossRef]
- Mirfarhadi, S.A.; Estekanchi, H.E. Value Based Seismic Design of Structures Using Performance Assessment by the Endurance Time Method. Struct. Infrastruct. Eng. 2020, 16, 1397–1415. [Google Scholar] [CrossRef]
- Mirfarhadi, S.A.; Estekanchi, H.E.; Sarcheshmehpour, M. On Optimal Proportions of Structural Member Cross-Sections to Achieve Best Seismic Performance Using Value Based Seismic Design Approach. Eng. Struct. 2021, 231, 111751. [Google Scholar] [CrossRef]
- Sarcheshmehpour, M.; Estekanchi, H.E. Life Cycle Cost Optimization of Earthquake-Resistant Steel Framed Tube Tall Buildings. Proc. Struct. 2021, 30, 585–601. [Google Scholar] [CrossRef]
- Fragiadakis, M.; Lagaros, N.D.; Papadrakakis, M. Performance-Based Multiobjective Optimum Design of Steel Structures Considering Life-Cycle Cost. Struct. Multidiscip. Optim. 2006, 32, 1–11. [Google Scholar] [CrossRef]
- Estekanchi, H.E.; Vafai, H.A. Seismic Analysis and Design Using the Endurance Time Method; CRC Press: Boca Raton, FL, USA, 2021; ISBN 1003217478. [Google Scholar]
- Estekanchi, H.E.; Valamanesh, V.; Vafai, A. Application of Endurance Time Method in Linear Seismic Analysis. Eng. Struct. 2007, 29, 2551–2562. [Google Scholar] [CrossRef]
- Estekanchi, H.E.; Riahi, H.T.; Vafai, A. Application of Endurance Time Method in Seismic Assessment of Steel Frames. Eng. Struct. 2011, 33, 2535–2546. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Sattar, S.; Estekanchi, H.E. Performance-Based Seismic Assessment of Steel Frames Using Endurance Time Analysis. Eng. Struct. 2014, 69, 216–234. [Google Scholar] [CrossRef]
- Takahashi, Y.; Der Kiureghian, A.; Ang, A.H.S. Life-Cycle Cost Analysis Based on a Renewal Model of Earthquake Occurrences. Earthq. Eng. Struct. Dyn. 2004, 33, 859–880. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Ghiasi, R.; Varaee, H. Probability-Based Damage Detection Using Kriging Surrogates and Enhanced Ideal Gas Molecular Movement Algorithm. In Proceedings of the ICAVMS 2017: 19th International Conference on Acoustics and Vibration of Mechanical Structures, Timisoara, Romania, 25–26 May 2017; Volume 4. [Google Scholar]
- Ghasemi, M.R.; Ghiasi, R.; Varaee, H. Probability-Based Damage Detection of Structures Using Kriging Surrogates and Enhanced Ideal Gas Molecular Movement Algorithm. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2017, 11, 628–636. [Google Scholar]
- Varaee, H.; Ghasemi, M.R. An Improved Chaotic Ideal Gas Molecular Movement Algorithm for Engineering Optimization Problems. Expert Syst. 2022, 39, e12913. [Google Scholar] [CrossRef]
- Varaee, H.; Ghasemi, M.R. Engineering Optimization Based on Ideal Gas Molecular Movement Algorithm. Eng. Comput. 2017, 33, 71–93. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of Multi-Objective Optimization Methods for Engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Yang, X. Multiobjective Firefly Algorithm for Continuous Optimization. Eng. Comput. 2013, 29, 175–184. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. Novel Performance Metrics for Robust Multi-Objective Optimization Algorithms. Swarm Evol. Comput. 2015, 21, 1–23. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly Algorithm: A New Meta-Heuristic Optimization Technique for Solving Single-Objective, Discrete, and Multi-Objective Problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling Multiple Objectives with Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Varaee, H. A Fast Multi-Objective Optimization Using an Efficient Ideal Gas Molecular Movement Algorithm. Eng. Comput. 2017, 33, 477–496. [Google Scholar] [CrossRef]
- Coello Coello, C.A. Evolutionary Multi-Objective Optimization: Some Current Research Trends and Topics That Remain to Be Explored. Front. Comput. Sci. China 2009, 3, 18–30. [Google Scholar] [CrossRef]
- Reyes-Sierra, M.; Coello, C.A.C. Multi-Objective Particle Swarm Optimizers: A Survey of the State-of-the-Art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Nozari, A.; Estekanchi, H.E. Optimization of Endurance Time Acceleration Functions for Seismic Assessment of Structures. Int. J. Optim. Civ. Eng. 2011, 1, 257–277. [Google Scholar]
- Mirzaee, A.; Estekanchi, H.E. Performance-Based Seismic Retrofitting of Steel Frames by the Endurance Time Method. Earthq. Spectra 2015, 31, 383–402. [Google Scholar] [CrossRef]
- Endurance Time Method. Available online: https://sites.google.com/site/etmethod/ (accessed on 1 June 2014).
- FEMA-440 Improvement of Nonlinear Static Seismic Analysis Procedures; Federal Emergency Management Agency: Washington, DC, USA, 2005.
- Camp, C.V.; Huq, F. CO2 and Cost Optimization of Reinforced Concrete Frames Using a Big Bang-Big Crunch Algorithm. Eng. Struct. 2013, 48, 363–372. [Google Scholar] [CrossRef]
- Mitropoulou, C.C.; Lagaros, N.D.; Papadrakakis, M. Building Design Based on Energy Dissipation: A Critical Assessment. Bull. Earthq. Eng. 2010, 8, 1375–1396. [Google Scholar] [CrossRef]
- Ghobarah, A. On Drift Limits Associated with Different Damage Levels. In Proceedings of the International Workshop on Performance-Based Seismic Design, Bled, Slovenia, 28 June–1 July 2004; Department of Civil Engineering, McMaster University: Hamilton, ON, Canada, 2004; Volume 28. [Google Scholar]
- Elenas, A.; Meskouris, K. Correlation Study between Seismic Acceleration Parameters and Damage Indices of Structures. Eng. Struct. 2001, 23, 698–704. [Google Scholar] [CrossRef]
- A Benefit-Cost Model for the Seismic Rehabilitation of Buildings; FEMA-227; Federal Emergency Management Agency: Washington, DC, USA, 1992; Volume 2.
- Applied Technology Council. ATC-13: Earthquake Damage Evaluation Data for California; Applied Technology Council: Redwood City, CA, USA, 1985. [Google Scholar]
- U.S. Geological Survey. Available online: https://www.usgs.gov/ (accessed on 1 June 2024).
- Dolsek, M. Development of Computing Environment for the Seismic Performance Assessment of Reinforced Concrete Frames by Using Simplified Nonlinear Models. Bull. Earthq. Eng. 2010, 8, 1309–1329. [Google Scholar] [CrossRef]
- Code, P. Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Fajfar, P. A Nonlinear Analysis Method for Performance-Based Seismic Design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Peruš, I.; Fajfar, P.; Dolšek, M. Simplified Nonlinear Seismic Assessment of Structures Using Approximate Sdof-Ida Curves. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- PBEE TOOLBOX—Examples of Application Version 1.0. Matjaž Dolšek. 2008. Available online: https://dokumen.tips/documents/pbee-toolbox-examples-of-application-version-1.html (accessed on 1 June 2008).
- Dolsek, M. Summary of the Toolbox and Methodology for PBEE. In Proceedings of the Earthquake Engineering by the Beach Workshop, Anacapri, Italy, 2–4 July 2009. [Google Scholar]
- Dolšek, M. Seismic Risk Assessment of Reinforced Concrete Frame with Consideration of Aleatory and Epistemic Uncertainty. Procedia Eng. 2011, 14, 982–988. [Google Scholar] [CrossRef]
- American Concrete Institute. ACI 318-14: Building Code Requirements for Structural Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Varaee, H.; Ahmadi-Nedushan, B. Minimum Cost Design of Concrete Slabs Using Particle Swarm Optimization with Time Varying Acceleration Coefficients. World Appl. Sci. J. 2011, 13, 2484–2494. [Google Scholar]
- Ahmadi-Nedushan, B.; Varaee, H. Optimal Design of Reinforced Concrete Retaining Walls Using a Swarm Intelligence Technique. In Proceedings of the First International Conference on Soft Computing Technology in Civil, Structural and Environmental Engineering, Madeira, Portugal, 1–4 September 2009. [Google Scholar]
- Hoseini, Z.; Varaee, H.; Rafieizonooz, M.; Kim, J.-H.J. A New Enhanced Hybrid Grey Wolf Optimizer (GWO) Combined with Elephant Herding Optimization (EHO) Algorithm for Engineering Optimization. J. Soft Comput. Civ. Eng. 2022, 6, 1–42. [Google Scholar]
- Gholizadeh, S.; Kamyab, R.; Dadashi, H. Performance-Based Design Optimization of Steel Moment Frames. Int. J. Optim. Civ. Eng. 2013, 3, 327–343. [Google Scholar]
- McKenna, F. OpenSees: A Framework for Earthquake Engineering Simulation. Comput. Sci. Eng. 2011, 13, 58–66. [Google Scholar] [CrossRef]




| Study | Methodology | Focus | Key Contributions |
|---|---|---|---|
| Liu et al. [9] | Genetic Algorithm | Multi-objective optimization under uncertainties | Introduced a Pareto-optimal design set for multi-objective optimization. |
| Pan et al. [10] | Constraint-based Multi-objective Method | Design constraints integration | Developed a new formulation based on the constraint approach for multi-objective optimization. |
| Wen and Kang [12] | Long-term cost–benefit analysis | Life-Cycle Cost evaluation under multiple hazards | Early formulation of LCC in engineering systems considering multiple hazards. |
| Takahashi et al. [25] | Renewal model for earthquake occurrence | Life-Cycle Cost of construction alternatives | Estimated LCC of construction alternatives using a temporal relationship model. |
| Mitropoulou et al. [1] | Cost–benefit analysis and LCCA | Safety and economy in RC buildings design | Examined the influence of behavior factors and analysis methods on LCC assessment of RC buildings. |
| Asadi and Hajirasouliha [11] | Uniform Damage Distribution (UDD) | Minimizing damage and Life-Cycle Cost | Developed a practical methodology for optimal seismic design based on uniform damage distribution. |
| Mirfarhadi and Estekanchi [17,18] | Value-based seismic design | Comprehensive set of performance indicators | Compared conventional code-based design with value-based design in terms of seismic response and consequences. |
| This Study | IGMM Algorithm and Endurance Time (ET) Method | LCC-based mono- and multi-objective optimization | Integrated ET method with IGMM algorithm for efficient LCC-based seismic design, achieving significant LCC reduction. |
| Performance Level | Damage States | Drift Ratio Limit (%) Ghobarah [44] | Floor Acceleration Limit (g) Elenas and Meskouris [46] |
|---|---|---|---|
| I | None | ||
| II | Slight | ||
| III | Light | ||
| IV | Moderate | ||
| V | Heavy | ||
| VI | Major | ||
| VII | Destroyed |
| Cost Category | Calculation Formula | Basic Cost |
|---|---|---|
| Damage/repair () | Replacement cost × floor area × mean damage index | 1500 |
| Loss of content () | Unit content cost × floor area × mean damage index | 500 |
| Rental () | Rental rate × gross leasable area × loss of function | 10 |
| Income () | Rental rate × gross leasable area × down time | 2000 |
| Minor Injury () | Minor injury cost per person × floor area × occupancy rate × expected minor injury rate | 2000 |
| Serious Injury () | serious injury cost per person × floor area × occupancy rate × expected serious injury rate | |
| Human fatality () | Human fatality cost per person × floor area × occupancy rate × expected death rate |
| Limit State | FEMA-227 [46] | ATC-13 [47] | ||||
|---|---|---|---|---|---|---|
| Mean Damage Index (%) | Expected Minor Injury Rate | Expected Serious Injury Rate | Expected Death Rate | Loss of Function (%) | Down Time (%) | |
| None | 0 | 0 | 0 | 0 | 0 | 0 |
| Slight | 0.5 | 3.0 × 10−5 | 4.0 × 10−6 | 1.0 × 10−6 | 0.9 | 0.9 |
| Light | 5 | 3.0 × 10−4 | 4.0 × 10−5 | 1.0 × 10−5 | 3.33 | 3.33 |
| Moderate | 20 | 3.0 × 10−3 | 4.0 × 10−4 | 1.0 × 10−4 | 12.4 | 12.4 |
| Heavy | 45 | 3.0 × 10−2 | 4.0 × 10−3 | 1.0 × 10−3 | 34.8 | 34.8 |
| Major | 80 | 3.0 × 10−1 | 4.0 × 10−2 | 1.0 × 10−2 | 65.4 | 65.4 |
| Destroyed | 100 | 4.0 × 10−1 | 4.0 × 10−1 | 2.0 × 10−1 | 100 | 100 |
| Number | Name | n | (mm) | (cm) | (cm) | (cm2) | (cm2) | (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | C30x30-8T16 | 8 | 16 | 30 | 30 | 16.08 | 900 | 1.79% |
| 2 | C30x30-8T18 | 8 | 18 | 30 | 30 | 20.36 | 900 | 2.26% |
| … | … | … | … | … | … | … | … | … |
| 27 | C45x45-16T20 | 16 | 20 | 45 | 45 | 50.26 | 2025 | 2.48% |
| 28 | C45x45-16T22 | 16 | 22 | 45 | 45 | 60.82 | 2025 | 3.00% |
| … | … | … | … | … | … | … | … | … |
| 65 | C60x60-24-22 | 24 | 22 | 60 | 60 | 91.23 | 3600 | 2.53% |
| 66 | C60x60-24-25 | 24 | 25 | 60 | 60 | 117.81 | 3600 | 3.27% |
| Element | Variable | Permissible Values |
|---|---|---|
| Column | Column section | 28 first section of Table 1 |
| Beam | Height (cm) | 30, 35, 40, 45 |
| Beam | Relative section areas of the upper bars (%) | 0.35, 0.5, 0.7, 0.8, 1.0, 1.2, 1.4, 1.6, 2.0 |
| Category | Description |
|---|---|
| Objective | Minimize sum of the initial construction cost and the expected lifetime cost of the structure. |
| Constraints | 1. The selected sections for columns in each story cannot be weaker than those in the upper story. |
| 2. All code-based limitations imposed by the ACI318-14 design recommendations must be met. | |
| 3. Inter-story drift ratio limits at both operational and ultimate levels must be maintained. | |
| Design Variables | Predefined sections from Table 6. |
| Parameter | IGMM | PSO [60] | GA [60] |
|---|---|---|---|
| Population Size | 20 | 20 | 20 |
| Max Iterations | 100 | 100 | 100 |
| Crossover Rate | N/A | N/A | 0.9 |
| Mutation Rate | N/A | N/A | 0.001 |
| Start Weight | N/A | 0.9 | N/A |
| End Weight | N/A | 0.4 | N/A |
| Cognitive Component | N/A | 1 | N/A |
| Social Component | N/A | 3 | N/A |
| Initial Temperature | 1000 | N/A | N/A |
| Cooling Schedule | Linear Cooling | N/A | N/A |
| Selection Mechanism | N/A | N/A | Roulette Wheel Selection |
| Mutation Mechanism | N/A | N/A | Random Perturbation |
| Velocity Limits | N/A | [−1, 1] | N/A |
| Termination Condition | Max Iterations | Max Iterations | Max Iterations |
| Initialization Method | Random Initialization | Random Initialization | Random Initialization |
| Column Type | Stories 1 and 2 | Stories 3 and 4 |
|---|---|---|
| C1 | 40x40-12T20 | 40x40-8T18 |
| C2 | 40x40-12T20 | 40x40-8T20 |
| C3 | 40x40-12T20 | 40x40-8T20 |
| C4 | 45x45-12T20 | 40x40-8T20 |
| C5 | 40x40-12T20 | 40x40-8T16 |
| C6 | 40x40-12T20 | 40x40-8T20 |
| No. | Story 1 | Story 2 | Story 3 | Story 4 |
|---|---|---|---|---|
| 1 | 40x40-B8-T16 | 40x40-B6.4-T12.8 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 2 | 40x40-B6.4-T12.8 | 40x40-B5.6-T11.2 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 3 | 40x40-B8-T16 | 40x40-B8-T16 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 4 | 40x40-B8-T16 | 40x40-B6.4-T12.8 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 5 | 40x40-B9.6-T19.2 | 40x40-B8-T16 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 6 | 40x40-B9.6-T19.2 | 40x40-B9.6-T19.2 | 40x40-B6.4-T12.8 | 35x40-B4.9-T4.9 |
| 7 | 40x40-B8-T16 | 40x40-B8-T16 | 40x40-B6.4-T12.8 | 35x40-B4.9-T4.9 |
| 8 | 40x40-B9.6-T19.2 | 40x40-B8-T16 | 40x40-B6.4-T12.8 | 35x40-B4.9-T4.9 |
| 9 | 40x40-B8-T16 | 40x40-B6.4-T12.8 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 10 | 40x40-B8-T16 | 40x40-B8-T16 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 11 | 40x40-B9.6-T19.2 | 40x40-B9.6-T19.2 | 40x40-B6.4-T12.8 | 35x40-B4.9-T4.9 |
| 12 | 40x40-B9.6-T19.2 | 40x40-B9.6-T19.2 | 40x40-B6.4-T12.8 | 35x40-B4.9-T4.9 |
| 13 | 40x40-B8-T16 | 40x40-B8-T16 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| 14 | 40x40-B8-T16 | 40x40-B6.4-T12.8 | 40x40-B5.6-T11.2 | 35x40-B4.9-T4.9 |
| Column Type | Stories 1 and 2 | Stories 3 and 4 |
|---|---|---|
| C1 | 40x40-12T18 | 40x40-8T16 |
| C2 | 45x45-12T20 | 35x35-8T16 |
| C3 | 40x40-8T25 | 40x40-8T22 |
| C4 | 45x45-12T16 | 35x35-8T22 |
| C5 | 40x40-12T16 | 40x40-8T20 |
| C6 | 35x35-8T22 | 35x35-8T18 |
| No. | Story 1 | Story 2 | Story 3 | Story 4 |
|---|---|---|---|---|
| 1 | 45x40-B9-T18 | 45x40-B7.2-T14.4 | 40x35-B4.9-T9.8 | 35x35-B4.2875-T6.125 |
| 2 | 45x40-B9-T18 | 45x40-B7.2-T14.4 | 40x35-B4.9-T9.8 | 35x35-B4.2875-T8.575 |
| 3 | 45x40-B10.8-T21.6 | 45x40-B7.2-T14.4 | 40x40-B5.6-T11.2 | 35x40-B4.9-T7 |
| 4 | 45x40-B12.6-T25.2 | 45x40-B12.6-T25.2 | 40x40-B8-T16 | 35x40-B5.6-T11.2 |
| 5 | 45x45-B10.125-T20.25 | 45x45-B8.1-T16.2 | 40x35-B5.6-T11.2 | 35x35-B4.9-T9.8 |
| 6 | 45x45-B10.125-T20.25 | 45x45-B10.125-T20.25 | 40x35-B4.9-T9.8 | 35x35-B4.2875-T4.2875 |
| 7 | 45x40-B12.6-T25.2 | 45x40-B6.3-T9 | 40x35-B4.9-T9.8 | 35x35-B4.2875-T6.125 |
| 8 | 45x40-B7.2-T14.4 | 45x40-B6.3-T9 | 40x35-B4.9-T7 | 35x35-B4.2875-T6.125 |
| 9 | 45x40-B12.6-T25.2 | 45x40-B12.6-T25.2 | 40x40-B8-T16 | 35x40-B5.6-T11.2 |
| 10 | 45x40-B9-T18 | 45x40-B7.2-T14.4 | 40x40-B6.4-T12.8 | 35x40-B5.6-T11.2 |
| 11 | 45x35-B7.875-T15.75 | 45x35-B7.875-T15.75 | 40x35-B4.9-T9.8 | 35x35-B4.2875-T4.2875 |
| 12 | 45x35-B9.45-T18.9 | 45x35-B6.3-T12.6 | 40x35-B5.6-T11.2 | 35x35-B4.2875-T6.125 |
| 13 | 45x35-B9.45-T18.9 | 45x35-B7.875-T15.75 | 40x35-B7-T14 | 35x35-B4.2875-T6.125 |
| 14 | 45x35-B9.45-T18.9 | 45x35-B5.5125-T7.875 | 40x35-B4.9-T7 | 35x35-B4.2875-T4.2875 |
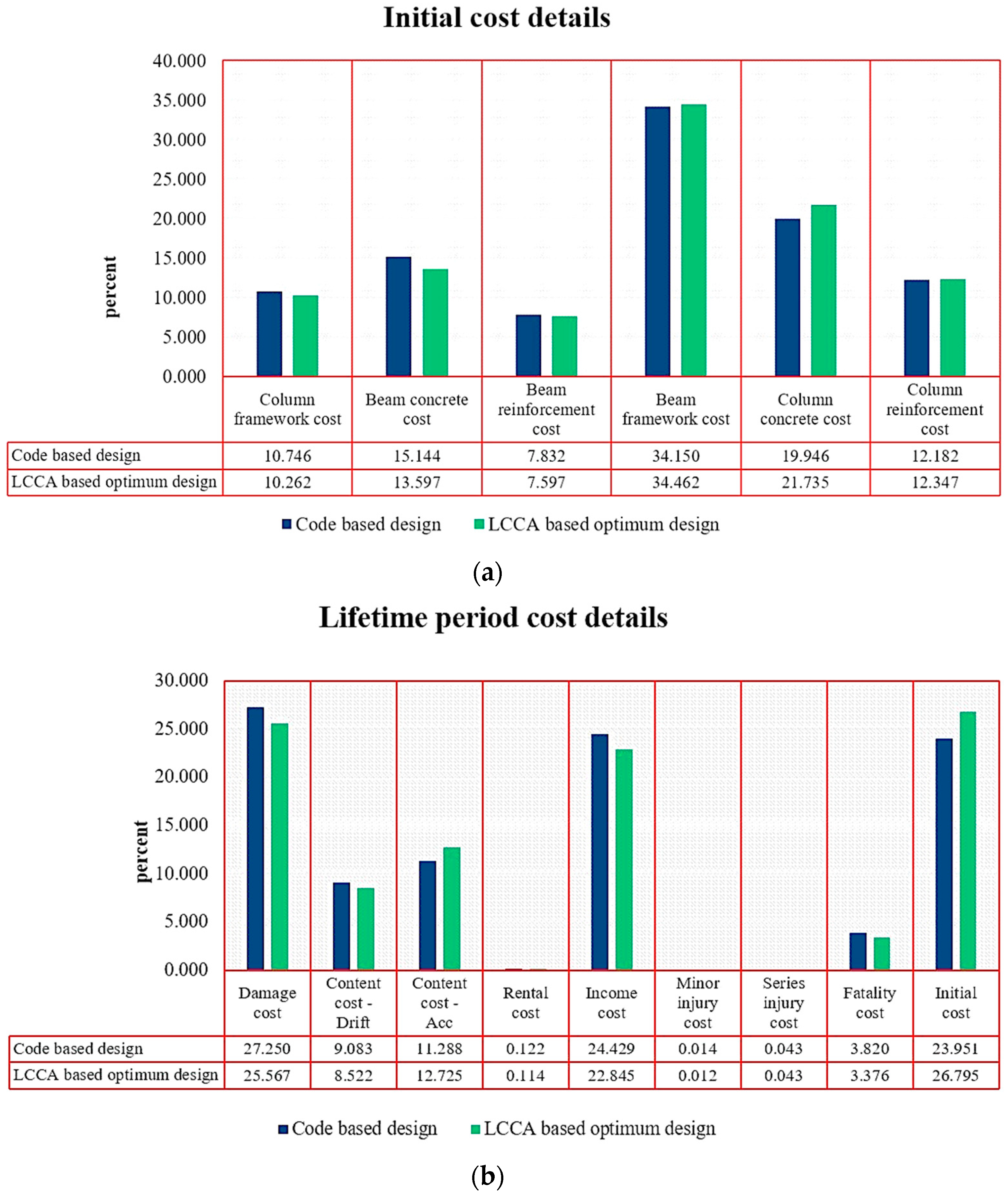
| Initial Cost Components | Traditional Design (USD) | LCC-Based Optimal Design (USD) | Percentage of Variation |
|---|---|---|---|
| Column Reinforcement | 13,433 | 12,961 | −4% |
| Column Concrete | 18,931 | 17,173 | −9% |
| Column Formwork | 9790.2 | 9595.8 | −2% |
| Beam Reinforcement | 42,689 | 43,527 | +2% |
| Beam Concrete | 24,933 | 27,451 | +10% |
| Beam Formwork | 15,228 | 15,595 | +2% |
| Sum | 125,004 | 126,302 | +1% |
| Lifetime Cost Components | Traditional Design (USD) | LCC-Based Optimal Design (USD) | Percentage of Variation |
|---|---|---|---|
| 1.42 × 105 | 1.21 × 105 | −15% | |
| 47,408 | 40,171 | −15% | |
| 58,914 | 59,981 | +2% | |
| 637.49 | 538.41 | −16% | |
| 1.28 × 105 | 1.08 × 105 | −16% | |
| 71.728 | 55.702 | −22% | |
| 223.76 | 204.26 | −9% | |
| 19,937 | 15,915 | −20% | |
| Sum | 397,192 | 345,865 | −13% |
| Total Cost | Initial Cost (USD) | Lifetime Cost (USD) | Total Life-Cycle Cost (USD) |
|---|---|---|---|
| Traditional Design | 1.25 × 105 | 3.97 × 105 | 5.22 × 105 |
| LCC-Based Optimal Design | 1.26 × 105 | 3.45 × 105 | 4.71 × 105 |
| Percentage of Improvement | +1% | −13% | −10% |
| Code Based Design | LCCA-Based Design | |||||
|---|---|---|---|---|---|---|
| First Mode (s) | Second Mode (s) | Third Mode (s) | First Mode (s) | Second Mode (s) | Third Mode (s) | |
| Period | 0.736 | 0.730 | 0.602 | 0.722 | 0.693 | 0.569 |
| Mode shape | UX | UY | RZ | UX | UY | RZ |
| Story 1 | 0.4563 | 0.4535 | 0.4669 | 0.2986 | 0.3031 | 0.2247 |
| Story 2 | 0.7051 | 0.7014 | 0.7162 | 0.5667 | 0.5716 | 0.4242 |
| Story 3 | 0.8968 | 0.8954 | 0.9046 | 0.8205 | 0.8252 | 0.5983 |
| Story 4 | 1 | 1 | 1 | 1 | 1 | 1 |
| Category | Description |
|---|---|
| Objective | Minimize both the initial construction cost and the expected lifetime cost of the structure. |
| Constraints | 1. The selected sections for columns in each story cannot be weaker than those in the upper story. |
| 2. All code-based limitations imposed by ACI318-14 design recommendations must be met. | |
| 3. Inter-story drift ratio limits at both operational and ultimate levels must be maintained. | |
| Design Variables | 1. Column sections: Predefined sections from Table 9 |
| 2. Beam heights: Permissible values are 30, 35, 40, 45, 50, 55, 60 cm | |
| 3. Relative section areas of the upper bars: Permissible values are 0.35%, 0.40%, 0.45%, 0.50%, 0.60%, 0.65%, 0.70%, 0.75%, 0.80%, 0.85%, 0.90%, 0.95%, 1.00%, 1.10%, 1.20%, 1.30%, 1.40%, 1.50%, 1.60%, 1.80%, 2.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabbaghzade Feriz, A.; Varaee, H.; Ghasemi, M.R. Multi-Objective Optimization in Support of Life-Cycle Cost-Performance-Based Design of Reinforced Concrete Structures. Mathematics 2024, 12, 2008. https://doi.org/10.3390/math12132008
Sabbaghzade Feriz A, Varaee H, Ghasemi MR. Multi-Objective Optimization in Support of Life-Cycle Cost-Performance-Based Design of Reinforced Concrete Structures. Mathematics. 2024; 12(13):2008. https://doi.org/10.3390/math12132008
Chicago/Turabian StyleSabbaghzade Feriz, Ali, Hesam Varaee, and Mohammad Reza Ghasemi. 2024. "Multi-Objective Optimization in Support of Life-Cycle Cost-Performance-Based Design of Reinforced Concrete Structures" Mathematics 12, no. 13: 2008. https://doi.org/10.3390/math12132008
APA StyleSabbaghzade Feriz, A., Varaee, H., & Ghasemi, M. R. (2024). Multi-Objective Optimization in Support of Life-Cycle Cost-Performance-Based Design of Reinforced Concrete Structures. Mathematics, 12(13), 2008. https://doi.org/10.3390/math12132008









