Design of Static Output Feedback Integrated Path Tracking Controller for Autonomous Vehicles
Abstract
1. Introduction
- An SOF controller that does not use a side-slip angle is designed. Two sets of sensor outputs, (ey, eψ) and (ey, eψ, γ), are composed from the lateral offset error, ey, heading error, eψ, and yaw rate, γ. An LQOC and SMC are applied as control methods.
- Three IPCs and nine actuator combinations, consisting of FWS, RWS, 4WS, 4WIB, and 4WID, are proposed and tested for path tracking and lateral stability. The SOF controllers with the three IPCs are tested on high- and low-friction roads. From the simulation results, the effects of these IPCs on control performance are discussed.
- From the simulation, the best SOF controller, among the LQ SOF and SOF SMC, is determined, as well as the best actuator combination from various options for path tracking.
2. Design of Integrated Path Tracking Control
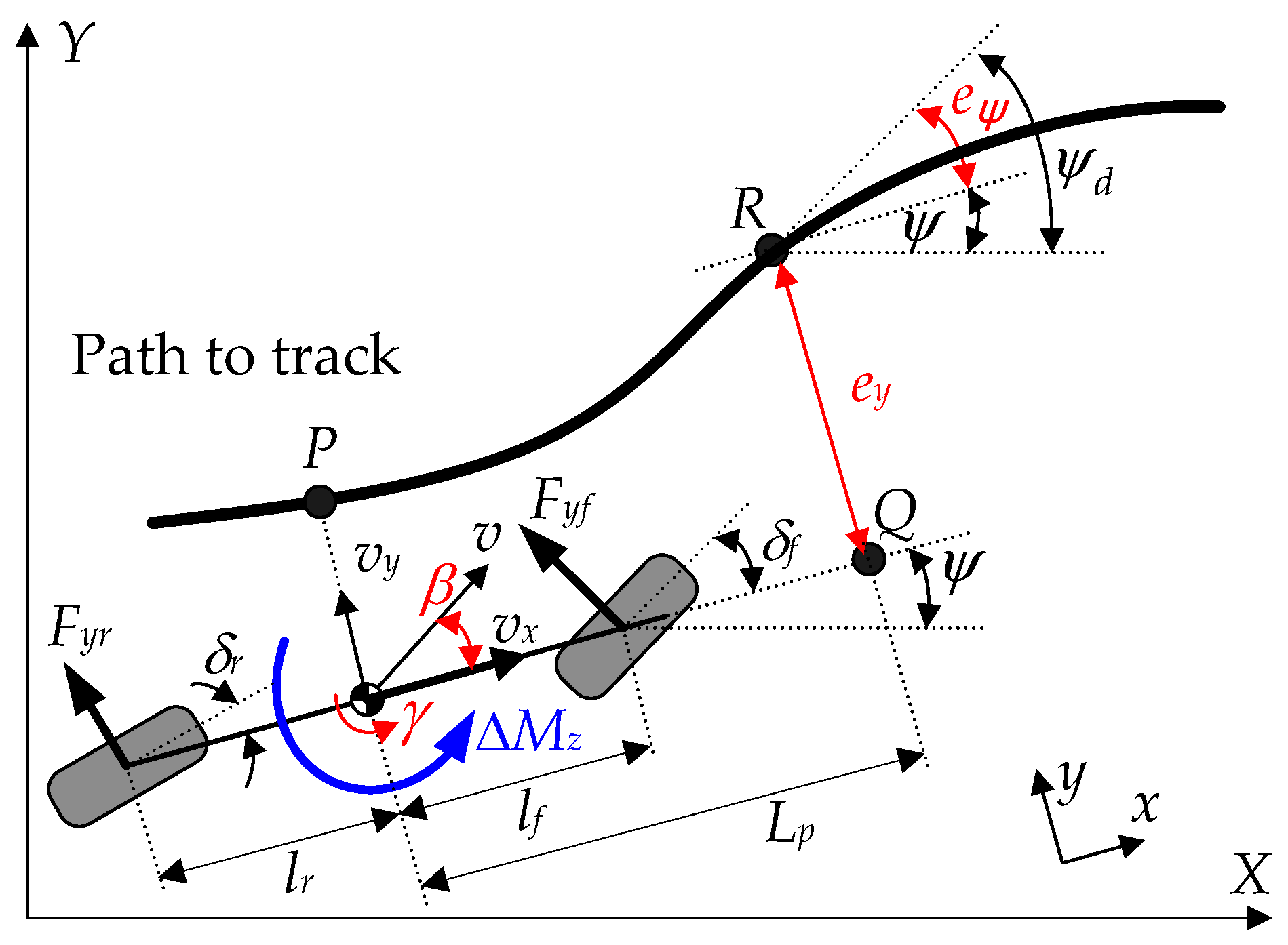
2.1. Derivation of State–Space Model
2.2. Design of LQR for Path Tracking
2.3. Design of LQ SOF Controllers for Path Tracking
2.4. Design of SOF SMC
2.5. Constraints Related to Tire Slip Angle
2.6. Control Allocation for LQR, LQ SOF Controllers, and SOF SMC
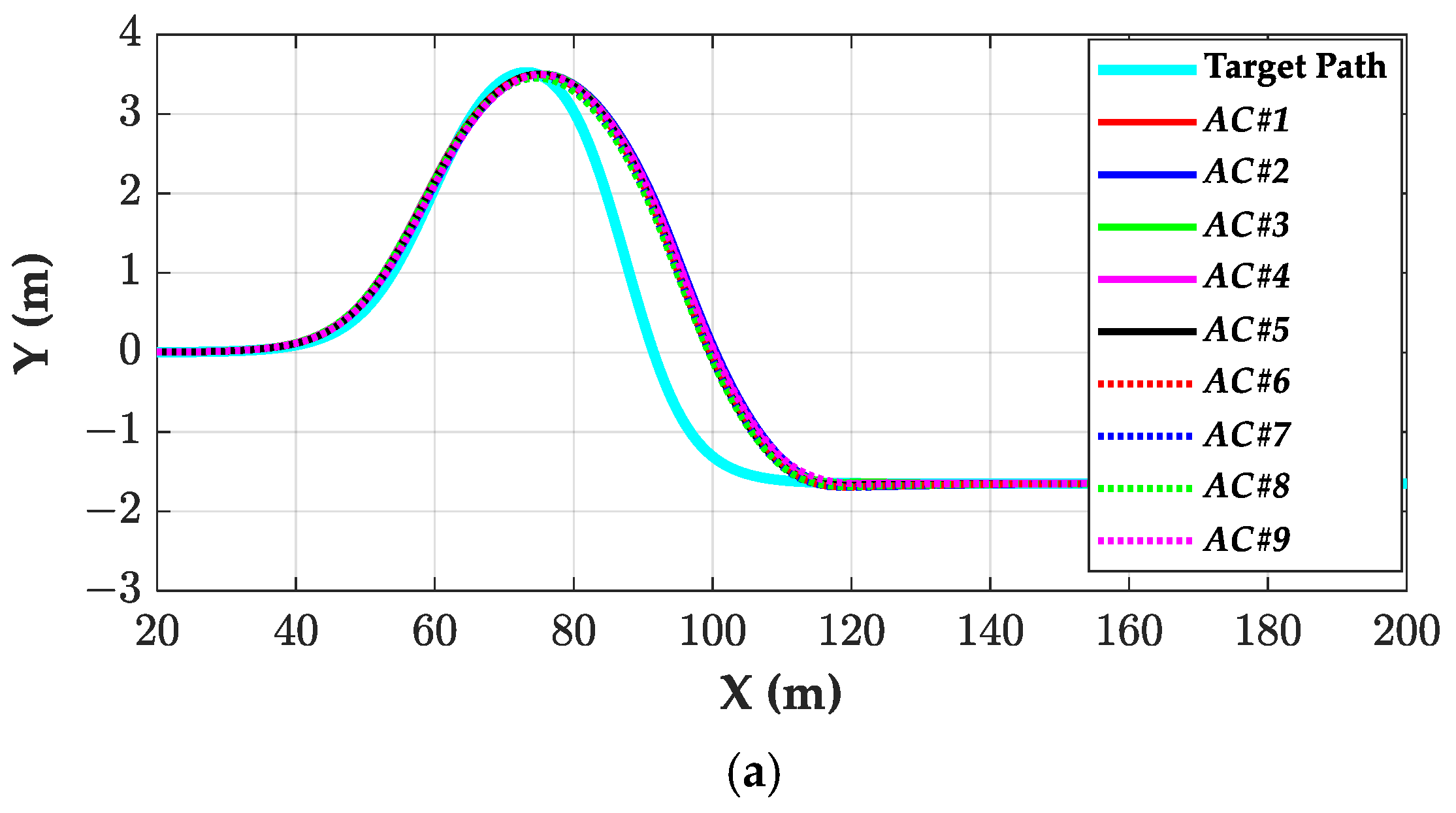
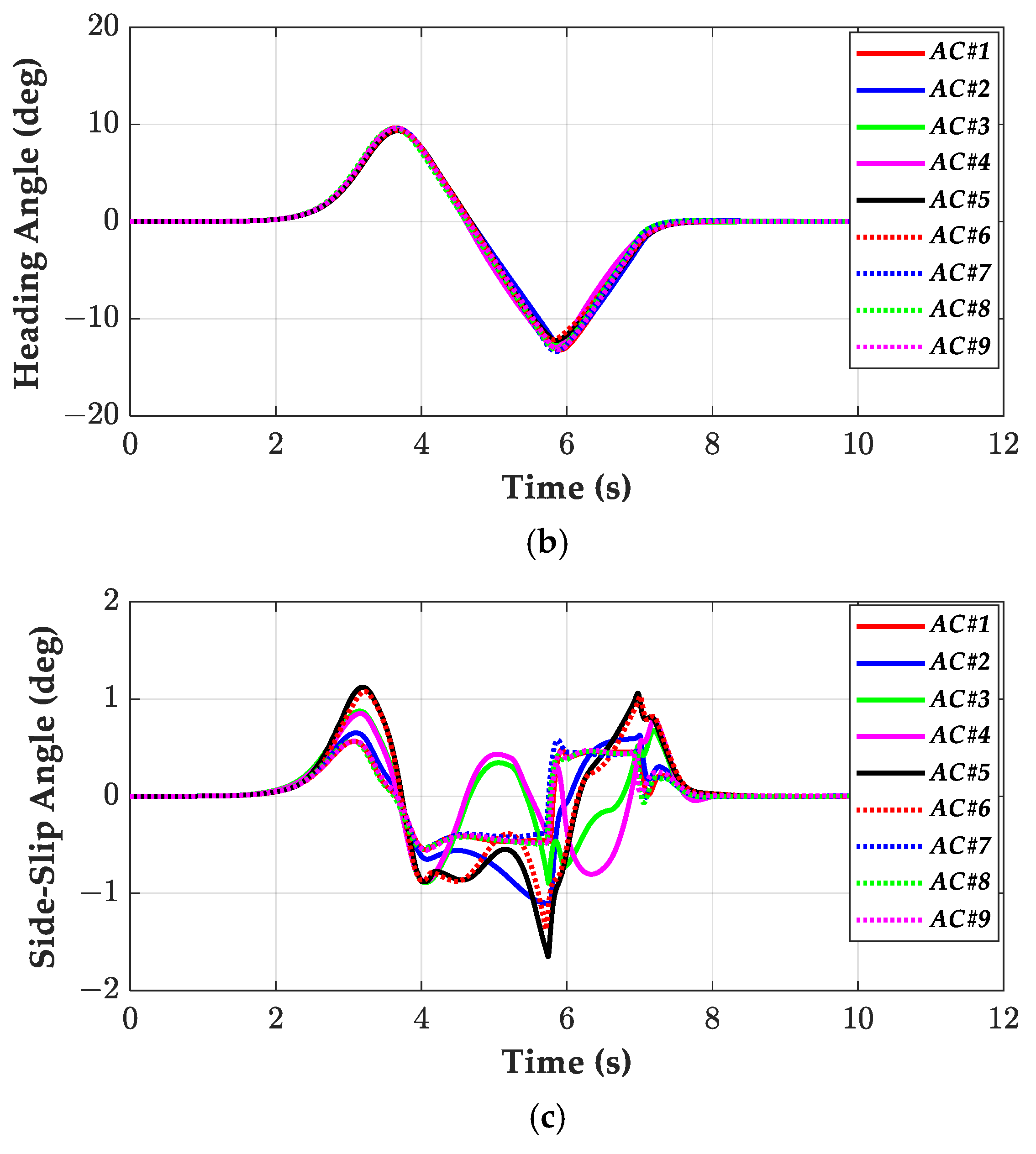
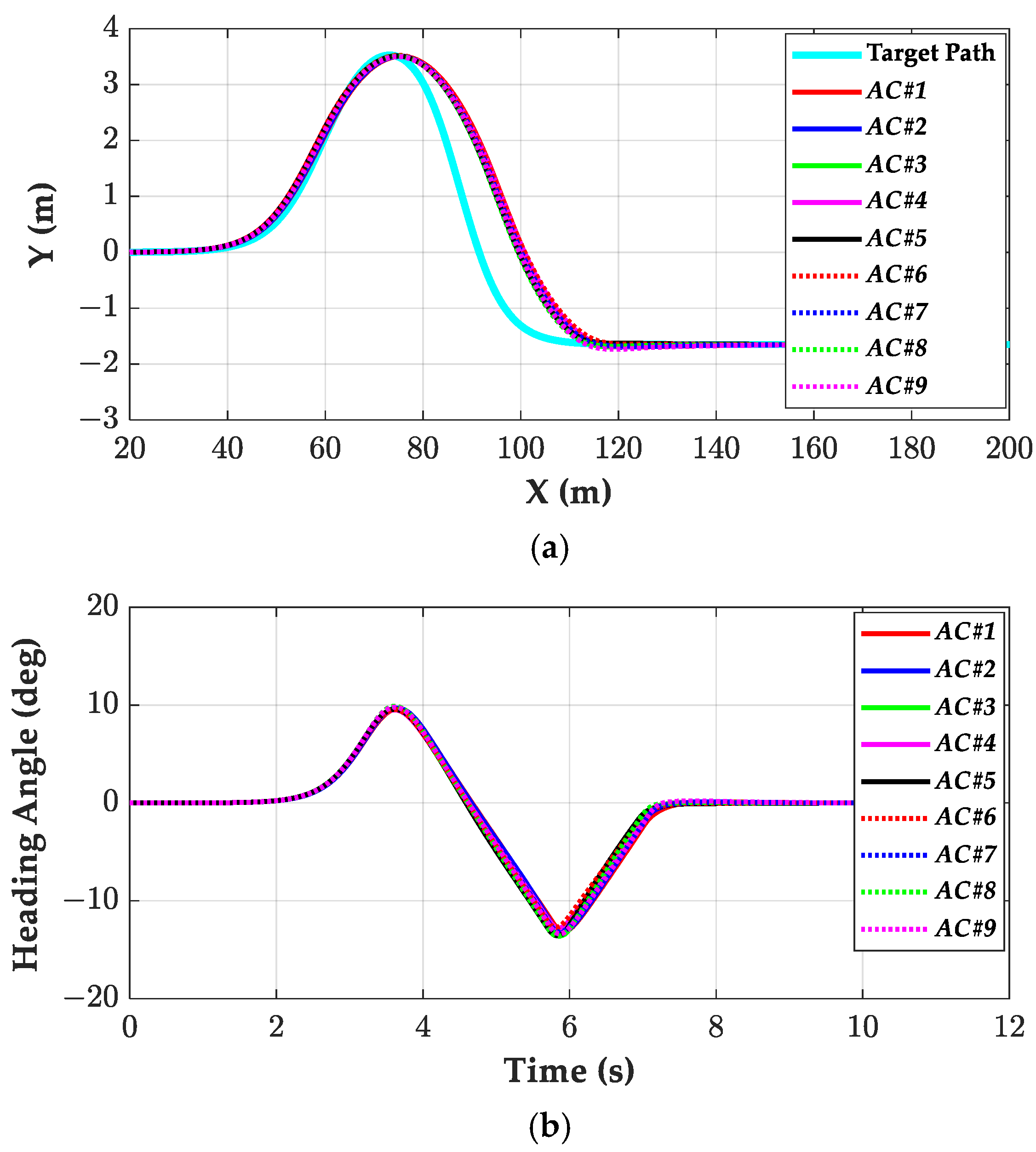
3. Performance Evaluation for Path Tracking Control
4. Simulation and Discussion
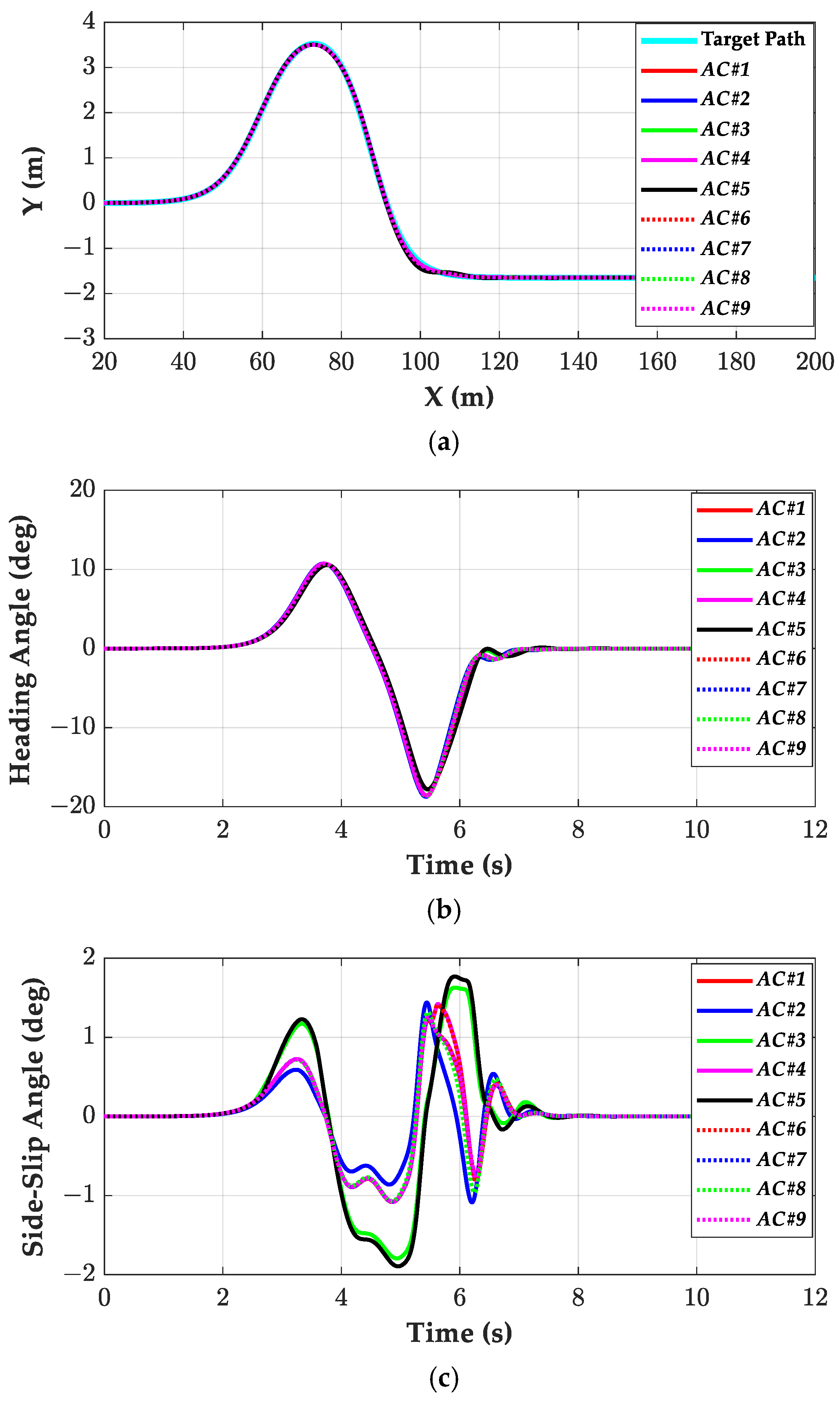
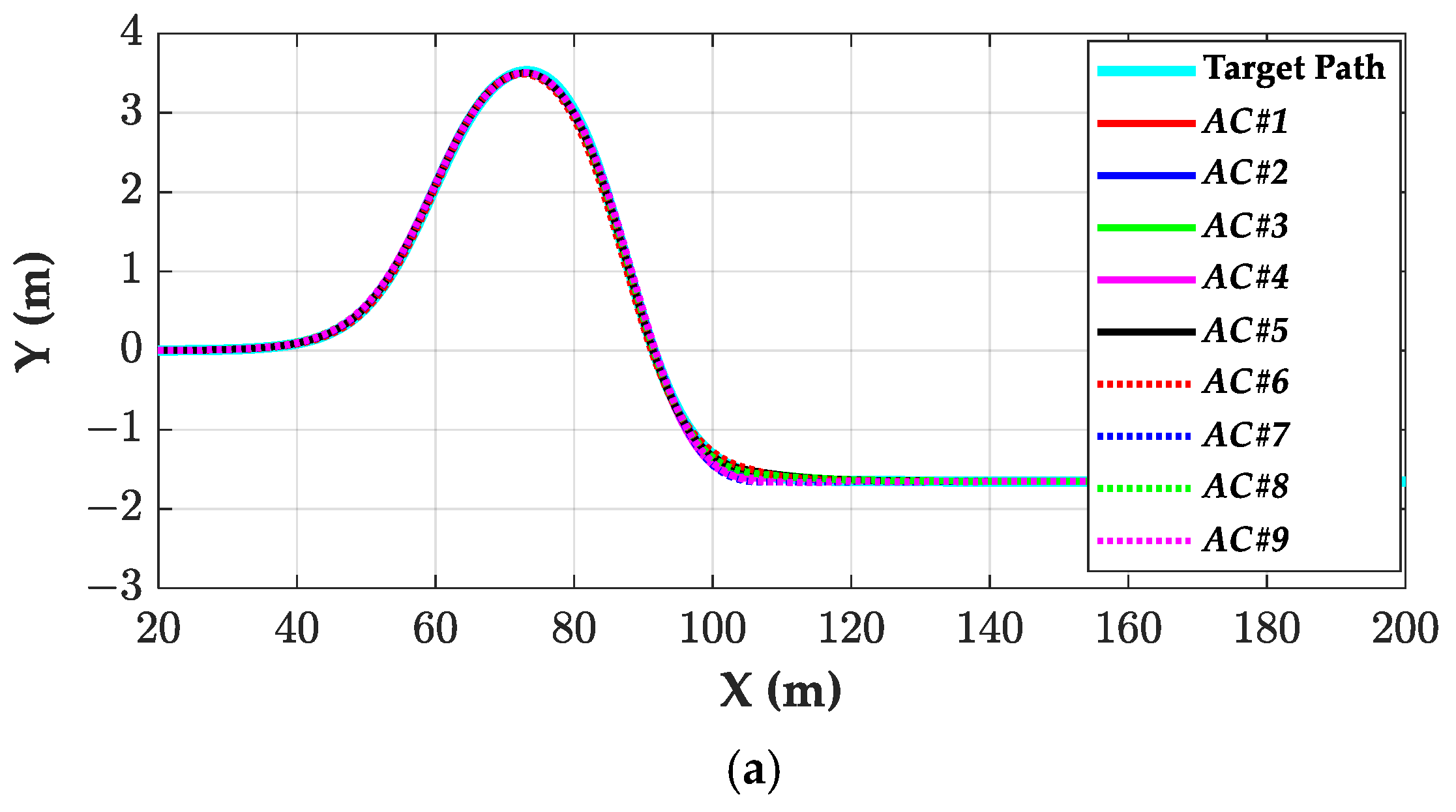
4.1. Simulation on High-Friction Surfaces
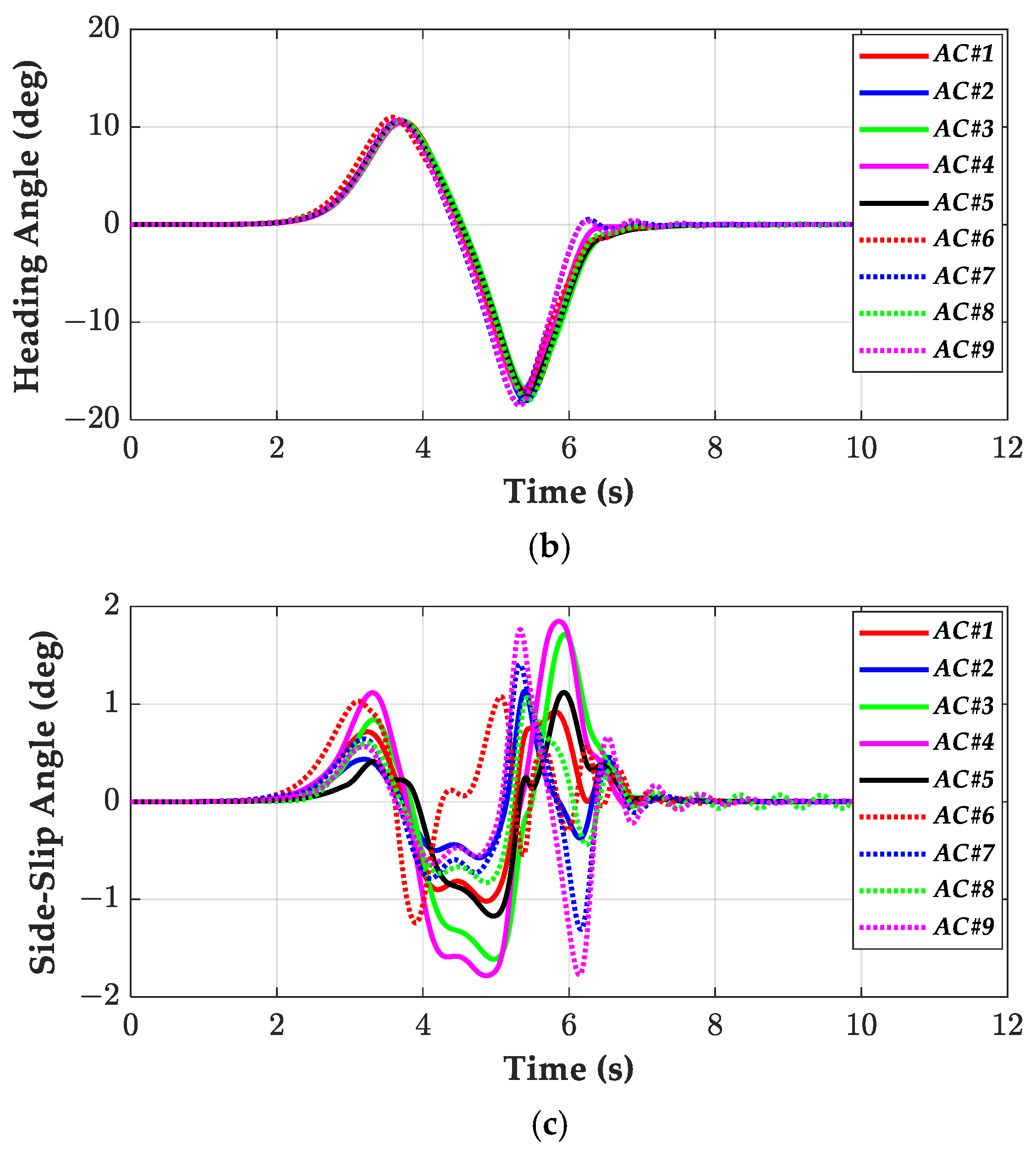
4.2. Simulation on Low-Friction Surfaces
4.3. Discussion on Simulation Results
5. Conclusions
- The LQ SOF and SOF SMC controllers, using three sensor outputs, can give equivalent performances as the full-state feedback controls, LQR, and SMC. In other words, the LQ SOF and SOF SMC show nearly identical performance to the LQR and SMC if the yaw rate is used for the control, respectively. On the contrary, the SOF controllers using two sensor signals show the smallest D1 and the largest side-slip angle because the side-slip angle is not used in the control. From the simulation results, small differences in terms of path tracking performance can be identified. This means that the side-slip angle and the yaw-rate signals are not needed for path tracking. In other words, the LQ SOF and SOF SMC controllers with two sensor signals, i.e., the LQSOF2 and SMCSOF2, are recommended for path tracking.
- In view of the actuator combination, it was shown that there are small differences among actuator combinations derived from three input configurations. This is caused by the fact that each tire can generate a larger lateral force on high-friction surfaces, and that each tire can generate a very small lateral force on low-friction surfaces. On high-friction surfaces, the simplest actuator, i.e., FWS, is recommended among the actuator combinations. If collision avoidance is critical, then the LQSOF2 and SOFSMC2 are recommended because they can reduce D1. On low-friction surfaces, IPC#3 (FWS+RWS) is recommended for the LQR and LQSOF3, and IPC#3 (FWS+4WIB) is recommended for the SOFSMC2.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 4WIB | four-wheel independent braking |
| 4WID | four-wheel independent driving |
| 4WS | four-wheel steer = FWS + RWS |
| CoG | center of gravity |
| ESC | electronic stability control |
| EV | electric vehicle |
| FWS | front wheel steering |
| IPC | input configuration |
| LQOC | linear quadratic optimal control |
| LQR | linear quadratic regulator |
| LSC | lateral stability control |
| MPC | model predictive control |
| RWS | rear wheel steering |
| SMC | sliding mode control |
| SOF | static output feedback |
| TVF | torque vectoring function |
| VSC | vehicle stability control |
| WLSs | weighted least squares |
| YRT | yaw rate tracking |
| Nomenclature | |
| Cf, Cr | cornering stiffness of front/rear tires (N/rad) |
| D1, D2 | longitudinal and lateral offsets (m) |
| D3, D4 | response and settling delays (m) |
| DOS | percentage overshoot |
| ey, eψ | lateral offset error (m) and heading error (rad) |
| Fyf, Fyr | lateral tire forces of front and rear wheels (N) |
| Fzi | vertical tire force of wheel i (N) |
| g | gravitational acceleration constant (=9.81 m/s2) |
| Iz | yaw moment of inertia (kg·m2) |
| kv | velocity gain or preview period in the lookahead distance (s) |
| Lp | lookahead or preview distance (m) |
| lf, lr | distance from C.G. to front and rear axles (m) |
| m | vehicle total mass (kg) |
| v | vehicle speed (m/s) |
| vx, vy | longitudinal and lateral velocities at CoG of a vehicle (m/s) |
| y | lateral displacement (m) from the preview point to the target path |
| β | side-slip angle (rad) |
| ΔFxi | control longitudinal tire force of wheel i (N) |
| ΔFyr | control lateral tire force of rear wheels (N) |
| ΔMz | control yaw moment (N·m) |
| δf, δr | front and rear steering angles (rad) |
| ε | very small value, 10−4 |
| χ | curvature (1/m) |
| κi | virtual weight on i-th term in the objective function of control allocation |
| κ | vector of virtual weights |
| γ | yaw rate (rad/s) |
| ξi | maximum allowable value (MAV) of weight in LQ objective function |
| μ | tire–road friction coefficient |
| ψ | heading angle (rad) |
| ψd | target heading angle (rad) |
| ρi | weight in LQ objective function |
| σmax | maximum steering angle used to limit the lateral tire force (rad) |
| θf, θr | tire slip angles of front and rear wheels (rad) |
| θmax | maximum tire slip angle used to limit the lateral tire force (rad) |
References
- Montanaro, U.; Dixit, S.; Fallaha, S.; Dianatib, M.; Stevensc, A.; Oxtobyd, D.; Mouzakitisd, A. Towards connected autonomous driving: Review of use-cases. Veh. Syst. Dyn. 2019, 57, 779–814. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A survey of autonomous driving: Common practices and emerging technologies. IEEE Access. 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Omeiza, D.; Webb, H.; Jirotka, M.; Kunze, M. Explanations in autonomous driving: A survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10142–10162. [Google Scholar] [CrossRef]
- Paden, B.; Cap, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Sorniotti, A.; Barber, P.; De Pinto, S. Path tracking for automated driving: A tutorial on control system formulations and ongoing research. In Automated Driving; Watzenig, D., Horn, M., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Amer, N.H.; Hudha, H.Z.K.; Kadir, Z.A. Modelling and control strategies in path tracking control for autonomous ground vehicles: A review of state of the art and challenges. J. Intell. Robot. Syst. 2017, 86, 225–254. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Liu, L. Review and comparison of path tracking based on model predictive control. Electronics 2019, 8, 1077. [Google Scholar] [CrossRef]
- Yao, Q.; Tian, Y.; Wang, Q.; Wang, S. Control strategies on path tracking for autonomous vehicle: State of the art and future challenges. IEEE Access. 2020, 8, 161211–161222. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2022, 55, 194–236. [Google Scholar] [CrossRef]
- Yakub, F.; Mori, Y. Comparative study of autonomous path-following vehicle control via model predictive control and linear quadratic control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 1695–1714. [Google Scholar] [CrossRef]
- Wang, R.; Yin, G.; Zhuang, J.; Zhang, N.; Chen, J. The path tracking of four-wheel steering autonomous vehicles via sliding mode control. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016. [Google Scholar]
- Lee, K.; Jeon, S.; Kim, H.; Kum, D. Optimal path tracking control of autonomous vehicle: Adaptive full-state linear quadratic gaussian (LQG) control. IEEE Access 2019, 7, 109120–109133. [Google Scholar] [CrossRef]
- Hang, P.; Chen, X. Path tracking control of 4-wheel steering autonomous ground vehicles based on linear parameter-varying system with experimental verification. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2021, 235, 411–423. [Google Scholar] [CrossRef]
- Barari, A.; Afshari, S.S.; Liang, X. Coordinated control for path-following of an autonomous four in-wheel motor drive electric vehicle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 6335–6346. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.; Zhu, C.; Li, Q.; Tian, B.; Li, L. Optimal path tracking control for intelligent four-wheel steering vehicles based on MPC and state estimation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 1964–1976. [Google Scholar] [CrossRef]
- Lee, J.; Yim, S. comparative study of path tracking controllers on low friction roads for autonomous vehicles. Machines 2023, 11, 403. [Google Scholar] [CrossRef]
- Wang, R.; Yin, G.; Jin, X. Robust adaptive sliding mode control for nonlinear four-wheel steering autonomous Vehicles path tracking systems. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016; pp. 2999–3006. [Google Scholar]
- Hang, P.; Luo, F.; Fang, S.; Chen, X. path tracking control of a four-wheel-independent-steering electric vehicle based on model predictive control. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017. [Google Scholar]
- Hang, P.; Chen, X.; Luo, F. Path-Tracking Controller Design for a 4WIS and 4WID Electric Vehicle with Steer-By-Wire System; SAE Technical Paper 2017-01-1954; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Guo, J.; Luo, Y.; Li, K. An adaptive hierarchical trajectory following control approach of autonomous four-wheel independent drive electric vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2482–2492. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K.; Dai, Y. Coordinated path-following and direct yaw-moment control of autonomous electric vehicles with sideslip angle estimation. Mech. Syst. Sig. Proc. 2018, 105, 183–199. [Google Scholar] [CrossRef]
- Hang, P.; Chen, X.; Luo, F. LPV/H∞ controller design for path tracking of autonomous ground vehicles through four-wheel steering and direct yaw-moment control. Int. J. Automot. Technol. 2019, 20, 9. [Google Scholar] [CrossRef]
- Ren, Y.; Zheng, L.; Khajepour, A. Integrated model predictive and torque vectoring control for path tracking of 4-wheeldriven autonomous vehicles. IET Intell. Transp. Syst. 2019, 13, 98–107. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Zhou, Q.; Tian, Y. A model predictive controller with switched tracking error for autonomous vehicle path tracking. IEEE Access 2019, 7, 53103–53114. [Google Scholar] [CrossRef]
- Chen, X.; Peng, Y.; Hang, P.; Tang, T. Path tracking control of four-wheel independent steering electric vehicles based on optimal control. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–30 July 2020; pp. 5436–5442. [Google Scholar]
- Wu, H.; Si, Z.; Li, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control. IEEE Access 2020, 8, 73071–73081. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Xiang, C.; Peng, H.; Wang, W.; Li, L.; An, Q.; Cheng, S. Path tracking coordinated control strategy for autonomous four in-wheel-motor independent-drive vehicles with consideration of lateral stability. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 1023–1036. [Google Scholar] [CrossRef]
- Yang, K.; Tang, X.; Qin, Y.; Huang, Y.; Wang, H.; Pu, H. Comparative study of trajectory tracking control for automated vehicles via model predictive control and robust H-infinity state feedback control. Chin. J. Mech. Eng. 2021, 34, 74. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Meng, Y.; Gu, Q.; Bai, G. Integrated path tracking control of steering and braking based on holistic MPC. IFAC PapersOnLine 2021, 54, 45–50. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Wang, F.; Tang, Z.; Chen, L. Coordinated control based path following of distributed drive autonomous electric vehicles with yaw-moment control. Cont. Eng. Prac. 2021, 106, 104659. [Google Scholar] [CrossRef]
- Ahn, T.; Lee, Y.; Park, K. Design of integrated autonomous driving control system that incorporates chassis controllers for improving path tracking performance and vehicle stability. Electronics 2021, 10, 144. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Meng, Y.; Gu, Q.; Bai, G. Integrated path tracking control of steering and differential braking based on tire force distribution. Int. J. Control Autom. Syst. 2022, 20, 536–550. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Yang, C.; Qie, T.; Ma, M. Adaptive model predictive control-based path following control for four-wheel independent drive automated vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14399–14412. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. comparative study on coordinated control of path tracking and vehicle stability for autonomous vehicles on low-friction roads. Actuators 2023, 12, 398. [Google Scholar] [CrossRef]
- Lee, J.; Yim, S. path tracking control with constraint on tire slip angles under low-friction road conditions. Appl. Sci. 2024, 14, 1066. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. Design of a path-tracking controller with an adaptive preview distance scheme for autonomous vehicles. Machines 2024, 12, 764. [Google Scholar] [CrossRef]
- Syrmos, V.L.; Abdallah, C.T.; Dorato, P.; Grigoriadis, K. Static output feedback—A survey. Automatica 1997, 33, 125–137. [Google Scholar] [CrossRef]
- Benton, R.E.; Smith, D. A static-output-feedback design procedure for robust emergency lateral control of a highway vehicle. IEEE Trans. Control. Syst. Technol. 2005, 13, 618–623. [Google Scholar] [CrossRef]
- Hu, C.; Jing, H.; Wang, R.; Yan, F.; Chadli, M. Robust H∞ output-feedback control for path following of autonomous ground vehicles. Mech. Syst. Signal Process. 2016, 70–71, 414–427. [Google Scholar] [CrossRef]
- Chen, J.; Lin, C.; Chen, B. An improved path-following method for solving static output feedback control problems. Optim. Control. Appl. Methods 2016, 37, 1193–1206. [Google Scholar] [CrossRef]
- Nguyen, A.; Sentouh, C.; Zhang, H.; Popieul, J. Fuzzy static output feedback control for path following of autonomous vehicles with transient performance improvements. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3069–3079. [Google Scholar] [CrossRef]
- Liang, Y.; Li, Y.; Zheng, L.; Yu, Y.; Ren, Y. Yaw rate tracking-based path-following control for four-wheel independent driving and four-wheel independent steering autonomous vehicles considering the coordination with dynamics stability. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 260–272. [Google Scholar] [CrossRef]
- Kennouche, A.; Saifia, D.; Chadli, M.; Labiod, S. Multi-objective H2/H∞ saturated non-PDC static output feedback control for path tracking of autonomous vehicle. Trans. Inst. Meas. Control. 2022, 44, 2235–2247. [Google Scholar] [CrossRef]
- Xue, W.; Lian, B.; Fan, J.; Chai, T.; Lewis, F.L. Inverse reinforcement learning for trajectory imitation using static output feedback control. IEEE Trans. Cybern. 2024, 54, 1695–1707. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.; Si, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control and sliding mode control. Adv. Mech. Eng. 2021, 13, 1–17. [Google Scholar] [CrossRef]
- Liang, J.; Tian, Q.; Feng, J.; Pi, D.; Yin, G. Polytopic model-based robust predictive control scheme for path tracking of autonomous vehicles. IEEE Trans. Intell. Veh. 2024, 9, 3928–3939. [Google Scholar] [CrossRef]
- Wong, H.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley and Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere: New York, NY, USA, 1975. [Google Scholar]
- da Silva, A.P.A.; Falcão, D.M. Fundamentals of genetic algorithms. In Modern Heuristic Optimization Techniques: Theory and Applications to Power Systems, 1st ed.; Lee, K.Y., El-Sharkawi, M.A., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2008; Chapter 2; pp. 25–42. [Google Scholar]
- Bozorg-Haddad, O.; Solgi, M.; Loáiciga, H.A. Meta-Heuristic and Evolutionary Algorithms for Engineering Optimization; John Wiley and Sons: Hoboken, NJ, USA, 2008; Chapter 4; pp. 53–67. [Google Scholar]
- Hansen, N.; Muller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Jeong, Y.; Sohn, Y.; Chang, S.; Yim, S. Design of static output feedback controllers for an active suspension system. IEEE Access 2022, 10, 26948–26964. [Google Scholar] [CrossRef]
- Rezaeian, A.; Zarringhalam, R.; Fallah, S.; Melek, W.; Khajepour, A.; Chen, S.-K.; Moshchuck, N.; Litkouhi, B. Novel tire force estimation strategy for real-time implementation on vehicle applications. IEEE Trans. Veh. Technol. 2015, 64, 2231–2241. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Wang, F.; Dong, H.; Yan, Y.; Ren, Y.; Zhou, C.; Yin, G. Tire road friction coefficient estimation: Review and research perspectives. Chin. J. Mech. Eng. 2022, 35, 6. [Google Scholar] [CrossRef]
- Mechanical Simulation Corporation. VS Browser: Reference Manual, The Graphical User Interfaces of BikeSim, CarSim, and TruckSim; Mechanical Simulation Corporation: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Heredia, G.; Ollero, A. Stability of autonomous vehicle path tracking with pure delays in the control loop. Adv. Robot. 2007, 21, 23–50. [Google Scholar] [CrossRef]
- Oya, H.; Hagino, K. Trajectory-based design of robust non-fragile controllers for a class of uncertain linear continuous-time systems. Int. J. Control. 2007, 80, 1849–1862. [Google Scholar] [CrossRef]
- Liu, S.; Li, Z.; Luo, X.; Zhang, M.; Zhang, Z. Non-fragile adaptive sliding tracking control for a nonlinear uncertain robotic system with unknown actuator nonlinearities. Int. J. Robust Nonlinear Control. 2025. early access. [Google Scholar] [CrossRef]





| Actuator Combinations | Vector of Virtual Weights | ||
|---|---|---|---|
| IPC#1 | AC#1 | FWS | |
| IPC#2 | AC#2 | 4WS | |
| IPC#3 FWS | AC#3 | +RWS | |
| AC#4 | +RWS+4WID | ||
| AC#5 | +RWS+4WIB | ||
| AC#6 | +RWS+4WID+4WIB | ||
| AC#7 | +4WID | ||
| AC#8 | +4WIB | ||
| AC#9 | +4WID+4WIB | ||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ms | 1823 kg | Iz | 6286 kg-m2 |
| lf | 1.27 m | lr | 1.90 m |
| tf | 42,000 N/rad | tr | 62,000 N/rad |
| Cf | 1.6 m | Cr | 1.6 m |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 0.31 | −0.021 | 0.3 | 0.91 | −2.69 | 0.95 | 7.3 |
| IPC#2 | AC#2 | 4WS | 0.33 | −0.020 | 0.3 | 0.93 | −2.77 | 1.01 | 7.61 |
| IPC#3 FWS | AC#3 | +RWS | 0.46 | −0.021 | 0.6 | 1.07 | −2.31 | 1.44 | 8.02 |
| AC#4 | +RWS+4WID | 0.47 | −0.021 | 0.6 | 1.07 | −2.32 | 1.43 | 8.01 | |
| AC#5 | +RWS+4WIB | 0.47 | −0.020 | 0.6 | 1.13 | −2.21 | 1.42 | 7.99 | |
| AC#6 | +RWS+4WID+4WIB | 0.48 | −0.020 | 0.6 | 1.08 | −2.36 | 1.42 | 8.01 | |
| AC#7 | +4WID | 0.32 | −0.020 | 0.4 | 1.30 | −3.28 | 0.80 | 7.28 | |
| AC#8 | +4WIB | 0.18 | −0.021 | 0.5 | 1.19 | −2.47 | 1.09 | 7.60 | |
| AC#9 | +4WID+4WIB | 0.18 | −0.020 | 0.6 | 1.15 | −2.80 | 1.03 | 7.60 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | −0.15 | −0.021 | 0.0 | −0.08 | 0.77 | 1.23 | 9.57 |
| IPC#2 | AC#2 | 4WS | −0.13 | −0.021 | 0.0 | −0.05 | 0.47 | 1.44 | 9.32 |
| IPC#3 FWS | AC#3 | +RWS | −0.30 | −0.021 | 0.0 | −0.18 | 2.29 | 1.79 | 8.65 |
| AC#4 | +RWS+4WID | −0.15 | −0.021 | 0.0 | −0.06 | 0.74 | 1.42 | 9.57 | |
| AC#5 | +RWS+4WIB | −0.30 | −0.020 | 0.1 | −0.18 | 2.45 | 1.89 | 8.79 | |
| AC#6 | +RWS+4WID+4WIB | −0.15 | −0.021 | 0.0 | −0.06 | 0.77 | 1.41 | 9.51 | |
| AC#7 | +4WID | −0.16 | −0.020 | 0.0 | −0.07 | 0.79 | 1.25 | 9.61 | |
| AC#8 | +4WIB | −0.15 | −0.021 | 0.0 | −0.08 | 0.77 | 1.23 | 9.57 | |
| AC#9 | +4WID+4WIB | −0.13 | −0.021 | 0.0 | −0.05 | 0.47 | 1.44 | 9.32 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 0.57 | −0.021 | 0.9 | 0.98 | −3.81 | 0.98 | 4.28 |
| IPC#2 | AC#2 | 4WS | 0.58 | −0.020 | 0.9 | 0.99 | −3.15 | 1.75 | 5.76 |
| IPC#3 FWS | AC#3 | +RWS | 0.30 | −0.021 | 0.2 | 0.52 | −3.30 | 1.44 | 8.36 |
| AC#4 | +RWS+4WID | 0.30 | −0.020 | 0.2 | 0.45 | −3.26 | 1.79 | 9.19 | |
| AC#5 | +RWS+4WIB | 0.29 | −0.020 | 0.2 | 0.55 | −2.89 | 1.10 | 4.01 | |
| AC#6 | +RWS+4WID+4WIB | 0.30 | −0.020 | 0.2 | 0.57 | −3.32 | 1.07 | 4.38 | |
| AC#7 | +4WID | 0.47 | −0.020 | 0.7 | 1.07 | −3.71 | 0.88 | 7.12 | |
| AC#8 | +4WIB | 0.41 | −0.021 | 0.5 | 0.73 | −3.37 | 1.16 | 4.71 | |
| AC#9 | +4WID+4WIB | 0.40 | −0.021 | 0.6 | 0.73 | −3.63 | 1.07 | 4.91 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | −0.18 | −0.020 | 0.0 | 0.31 | −3.82 | 0.97 | 7.50 |
| IPC#2 | AC#2 | 4WS | −0.06 | −0.020 | 0.0 | 0.62 | −3.24 | 1.51 | 12.55 |
| IPC#3 FWS | AC#3 | +RWS | 0.07 | −0.020 | 0.1 | 0.67 | −1.36 | 1.07 | 6.77 |
| AC#4 | +RWS+4WID | 0.19 | −0.020 | 0.9 | 1.17 | −3.75 | 1.09 | 8.29 | |
| AC#5 | +RWS+4WIB | 0.07 | −0.020 | 0.1 | 0.67 | −1.36 | 1.07 | 6.77 | |
| AC#6 | +RWS+4WID+4WIB | 0.06 | −0.020 | 0.0 | 0.68 | −1.22 | 1.12 | 6.68 | |
| AC#7 | +4WID | 0.25 | −0.021 | 0.7 | 1.49 | −3.91 | 1.05 | 11.27 | |
| AC#8 | +4WIB | 0.10 | −0.020 | 0.0 | 0.73 | −2.73 | 0.81 | 6.68 | |
| AC#9 | +4WID+4WIB | 0.11 | −0.020 | 0.0 | 0.73 | −3.03 | 0.97 | 7.17 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | −0.26 | −0.020 | 0.0 | 0.02 | 2.26 | 1.02 | 6.73 |
| IPC#2 | AC#2 | 4WS | −0.25 | −0.020 | 0.0 | 0.05 | 1.65 | 1.13 | 6.19 |
| IPC#3 FWS | AC#3 | +RWS | −0.42 | −0.020 | 0.0 | −0.15 | 4.56 | 1.72 | 6.41 |
| AC#4 | +RWS+4WID | −0.42 | −0.021 | 0.0 | −0.06 | −5.52 | 1.85 | 7.87 | |
| AC#5 | +RWS+4WIB | −0.36 | −0.021 | 0.0 | −0.14 | 3.98 | 1.17 | 6.50 | |
| AC#6 | +RWS+4WID+4WIB | −0.49 | −0.020 | 0.3 | −0.29 | 0.37 | 1.43 | 10.05 | |
| AC#7 | +4WID | −0.23 | −0.020 | 0.2 | 0.20 | −6.13 | 1.41 | 9.13 | |
| AC#8 | +4WIB | −0.27 | −0.020 | 0.0 | 0.03 | 3.21 | 1.06 | 7.10 | |
| AC#9 | +4WID+4WIB | −0.26 | −0.020 | 0.2 | 0.02 | 1.97 | 1.02 | 6.61 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 0.08 | −0.020 | 0.0 | 0.37 | −1.44 | 0.99 | 5.97 |
| IPC#2 | AC#2 | 4WS | −0.04 | −0.020 | 0.0 | 0.29 | 0.06 | 1.01 | 5.48 |
| IPC#3 FWS | AC#3 | +RWS | −0.13 | −0.020 | 0.0 | 0.16 | 0.22 | 1.30 | 5.92 |
| AC#4 | +RWS+4WID | −0.15 | −0.020 | 0.0 | 0.21 | −2.43 | 1.69 | 8.11 | |
| AC#5 | +RWS+4WIB | −0.17 | −0.020 | 0.0 | 0.11 | 1.24 | 1.36 | 6.08 | |
| AC#6 | +RWS+4WID+4WIB | −0.70 | −0.021 | 0.7 | −0.06 | −2.72 | 1.31 | 12.89 | |
| AC#7 | +4WID | 0.02 | −0.021 | 0.0 | 0.52 | −4.15 | 1.36 | 9.13 | |
| AC#8 | +4WIB | −0.04 | −0.020 | 0.0 | 0.29 | −0.06 | 0.95 | 6.71 | |
| AC#9 | +4WID+4WIB | −0.03 | −0.020 | 0.1 | 0.28 | −0.61 | 1.00 | 6.15 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 1.82 | −0.021 | 0.5 | 8.05 | 4.61 | 0.58 | 12.66 |
| IPC#2 | AC#2 | 4WS | 1.82 | −0.020 | 0.9 | 7.99 | 3.89 | 1.64 | 13.46 |
| IPC#3 FWS | AC#3 | +RWS | 1.74 | −0.021 | 0.5 | 7.90 | 3.93 | 1.65 | 12.16 |
| AC#4 | +RWS+4WID | 1.72 | −0.021 | 0.5 | 7.94 | 4.14 | 1.46 | 12.04 | |
| AC#5 | +RWS+4WIB | 1.87 | −0.021 | 0.8 | 8.60 | 4.29 | 1.53 | 12.13 | |
| AC#6 | +RWS+4WID+4WIB | 1.79 | −0.020 | 0.6 | 8.21 | 4.28 | 1.32 | 12.11 | |
| AC#7 | +4WID | 1.91 | −0.020 | 0.9 | 8.90 | 5.23 | 0.63 | 12.52 | |
| AC#8 | +4WIB | 2.10 | −0.021 | 0.7 | 8.91 | 4.23 | 0.66 | 13.06 | |
| AC#9 | +4WID+4WIB | 1.99 | −0.020 | 0.9 | 8.45 | 4.44 | 0.63 | 12.84 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 2.22 | −0.021 | 0.9 | 9.11 | 5.35 | 0.57 | 13.19 |
| IPC#2 | AC#2 | 4WS | 2.27 | −0.020 | 0.9 | 9.11 | 5.37 | 1.11 | 13.34 |
| IPC#3 FWS | AC#3 | +RWS | 2.17 | −0.021 | 0.4 | 8.52 | 4.39 | 1.07 | 8.25 |
| AC#4 | +RWS+4WID | 2.30 | −0.021 | 0.6 | 9.11 | 5.09 | 0.85 | 9.93 | |
| AC#5 | +RWS+4WIB | 2.04 | −0.021 | 0.8 | 8.24 | 3.67 | 1.69 | 10.74 | |
| AC#6 | +RWS+4WID+4WIB | 2.12 | −0.020 | 0.6 | 9.15 | 5.54 | 1.89 | 11.64 | |
| AC#7 | +4WID | 2.38 | −0.021 | 0.7 | 10.35 | 7.51 | 0.60 | 12.97 | |
| AC#8 | +4WIB | 2.51 | −0.021 | 0.8 | 10.29 | 6.31 | 0.66 | 13.40 | |
| AC#9 | +4WID+4WIB | 2.37 | −0.021 | 0.9 | 9.57 | 6.13 | 0.62 | 13.34 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 1.54 | −0.021 | 0.4 | 7.76 | 4.36 | 0.58 | 12.46 |
| IPC#2 | AC#2 | 4WS | 1.74 | −0.020 | 0.9 | 8.11 | 4.33 | 1.56 | 15.92 |
| IPC#3 FWS | AC#3 | +RWS | 1.52 | −0.021 | 0.7 | 7.59 | 3.28 | 1.00 | 12.38 |
| AC#4 | +RWS+4WID | 1.74 | −0.021 | 0.6 | 9.00 | 5.46 | 0.76 | 11.59 | |
| AC#5 | +RWS+4WIB | 1.42 | −0.021 | 0.0 | 7.39 | 4.76 | 1.58 | 12.51 | |
| AC#6 | +RWS+4WID+4WIB | 1.72 | −0.020 | 0.8 | 9.36 | 6.66 | 1.50 | 11.42 | |
| AC#7 | +4WID | 2.22 | −0.021 | 1.0 | 10.07 | 6.95 | 0.57 | 12.31 | |
| AC#8 | +4WIB | 1.34 | −0.020 | 0.8 | 7.18 | 2.61 | 0.73 | 11.57 | |
| AC#9 | +4WID+4WIB | 1.41 | −0.021 | 0.6 | 7.60 | 3.37 | 0.62 | 12.13 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 0.81 | −0.020 | 0.4 | 7.69 | 3.53 | 0.59 | 10.89 |
| IPC#2 | AC#2 | 4WS | 0.65 | −0.021 | 0.7 | 7.60 | 3.25 | 1.20 | 13.16 |
| IPC#3 FWS | AC#3 | +RWS | 0.51 | −0.021 | 0.2 | 7.04 | 3.03 | 0.57 | 10.59 |
| AC#4 | +RWS+4WID | 0.37 | −0.021 | 0.9 | 7.56 | 3.58 | 0.87 | 10.68 | |
| AC#5 | +RWS+4WIB | −0.32 | −0.020 | 0.0 | 5.79 | 2.13 | 0.88 | 11.61 | |
| AC#6 | +RWS+4WID+4WIB | −0.17 | −0.021 | 0.9 | 7.13 | 3.47 | 0.94 | 11.29 | |
| AC#7 | +4WID | 0.65 | −0.020 | 1.0 | 7.09 | 2.41 | 0.60 | 11.09 | |
| AC#8 | +4WIB | 0.63 | −0.020 | 0.6 | 6.82 | 2.14 | 0.64 | 10.85 | |
| AC#9 | +4WID+4WIB | 0.58 | −0.021 | 0.6 | 6.92 | 2.46 | 0.64 | 11.12 | |
| Actuator Combinations | D1 (m) | D2 (m) | DOS (%) | D3 (m) | D4 (m) | (deg) | |||
|---|---|---|---|---|---|---|---|---|---|
| IPC#1 | AC#1 | FWS | 2.32 | −0.020 | 0.8 | 9.23 | 5.70 | 0.56 | 13.33 |
| IPC#2 | AC#2 | 4WS | 2.02 | −0.020 | 0.9 | 8.55 | 4.68 | 1.02 | 14.38 |
| IPC#3 FWS | AC#3 | +RWS | 1.61 | −0.021 | 0.8 | 7.99 | 3.48 | 0.83 | 12.01 |
| AC#4 | +RWS+4WID | 1.66 | −0.020 | 0.6 | 8.88 | 5.43 | 0.87 | 11.53 | |
| AC#5 | +RWS+4WIB | 1.44 | −0.021 | 0.0 | 7.56 | 4.90 | 0.79 | 11.89 | |
| AC#6 | +RWS+4WID+4WIB | 1.49 | −0.021 | 0.4 | 8.45 | 5.43 | 0.90 | 11.42 | |
| AC#7 | +4WID | 1.69 | −0.021 | 0.3 | 8.17 | 4.97 | 0.58 | 12.47 | |
| AC#8 | +4WIB | 1.55 | −0.020 | 0.5 | 7.54 | 3.61 | 0.73 | 11.70 | |
| AC#9 | +4WID+4WIB | 1.82 | −0.021 | 0.3 | 8.73 | 5.32 | 0.62 | 12.38 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, M.; Yim, S. Design of Static Output Feedback Integrated Path Tracking Controller for Autonomous Vehicles. Processes 2025, 13, 1335. https://doi.org/10.3390/pr13051335
Park M, Yim S. Design of Static Output Feedback Integrated Path Tracking Controller for Autonomous Vehicles. Processes. 2025; 13(5):1335. https://doi.org/10.3390/pr13051335
Chicago/Turabian StylePark, Manbok, and Seongjin Yim. 2025. "Design of Static Output Feedback Integrated Path Tracking Controller for Autonomous Vehicles" Processes 13, no. 5: 1335. https://doi.org/10.3390/pr13051335
APA StylePark, M., & Yim, S. (2025). Design of Static Output Feedback Integrated Path Tracking Controller for Autonomous Vehicles. Processes, 13(5), 1335. https://doi.org/10.3390/pr13051335







