Multivariable Fractional-Order Controller Design for a Nonlinear Dual-Tank Device
Abstract
:1. Introduction
2. Mathematical Preparation
2.1. Fractional Calculus
2.2. Newmark- Method
3. Modeling
3.1. Fractional Heat Exchange Process
3.2. Fractional Liquid Process
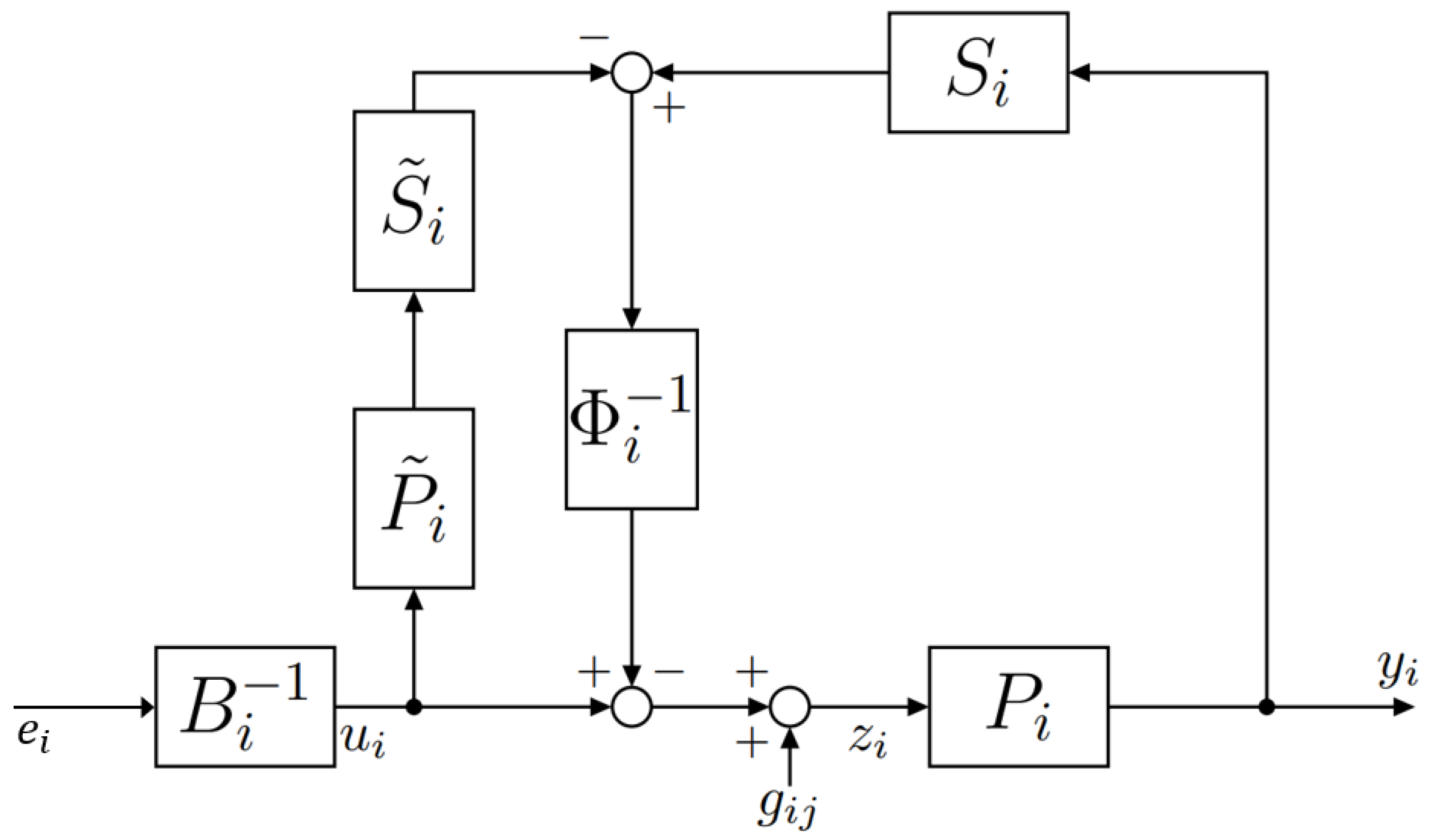
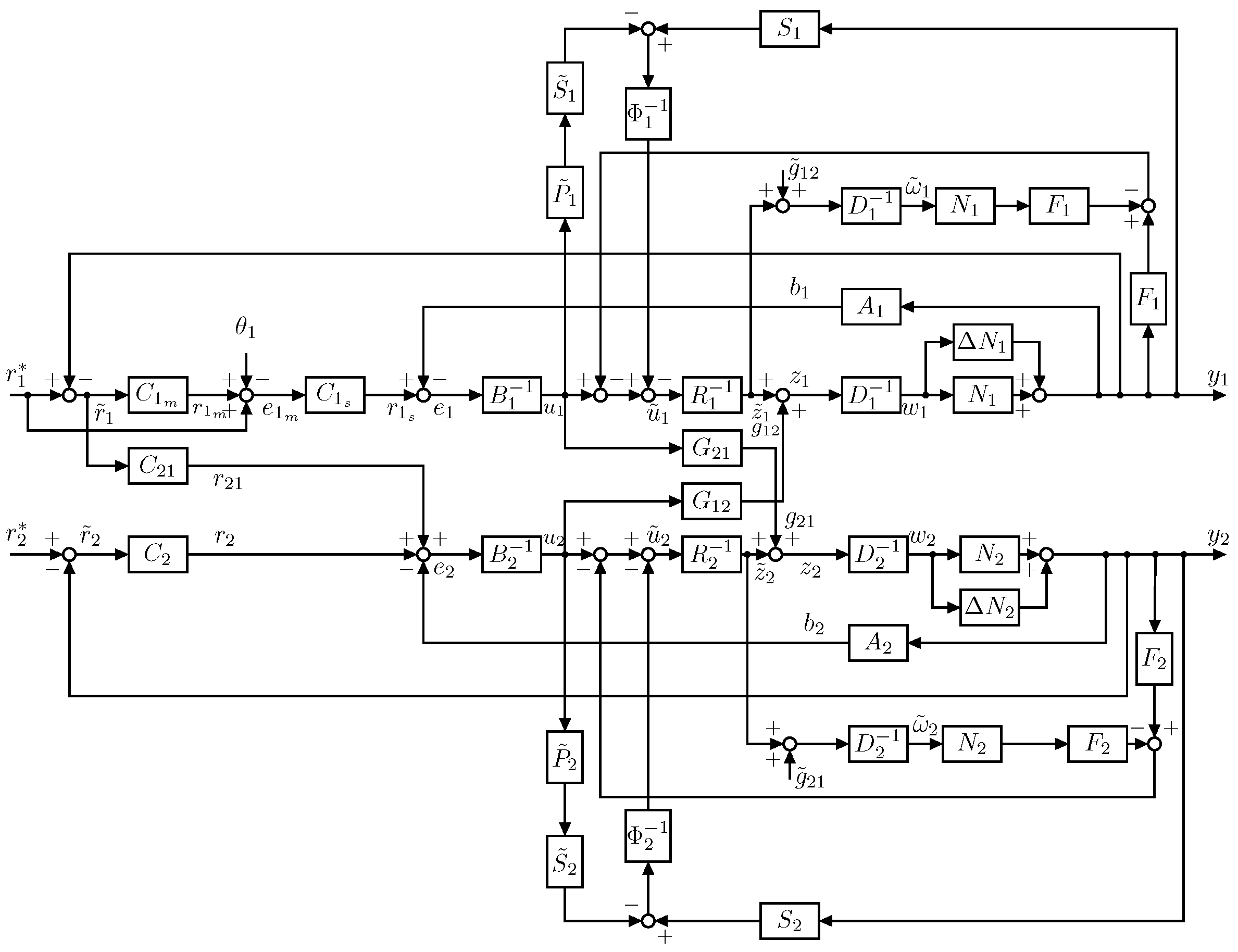
4. Multivariable Fractional-Order Nonlinear Control Feedback System Design
4.1. Fractional Liquid Temperature Control Design
4.2. Fractional Liquid Level Control Design
4.3. Interference Design
4.4. Uncertainty Compensation Design
4.5. Coupling Effect Elimination Design
4.6. Control System Design Details
5. Results and Discussion
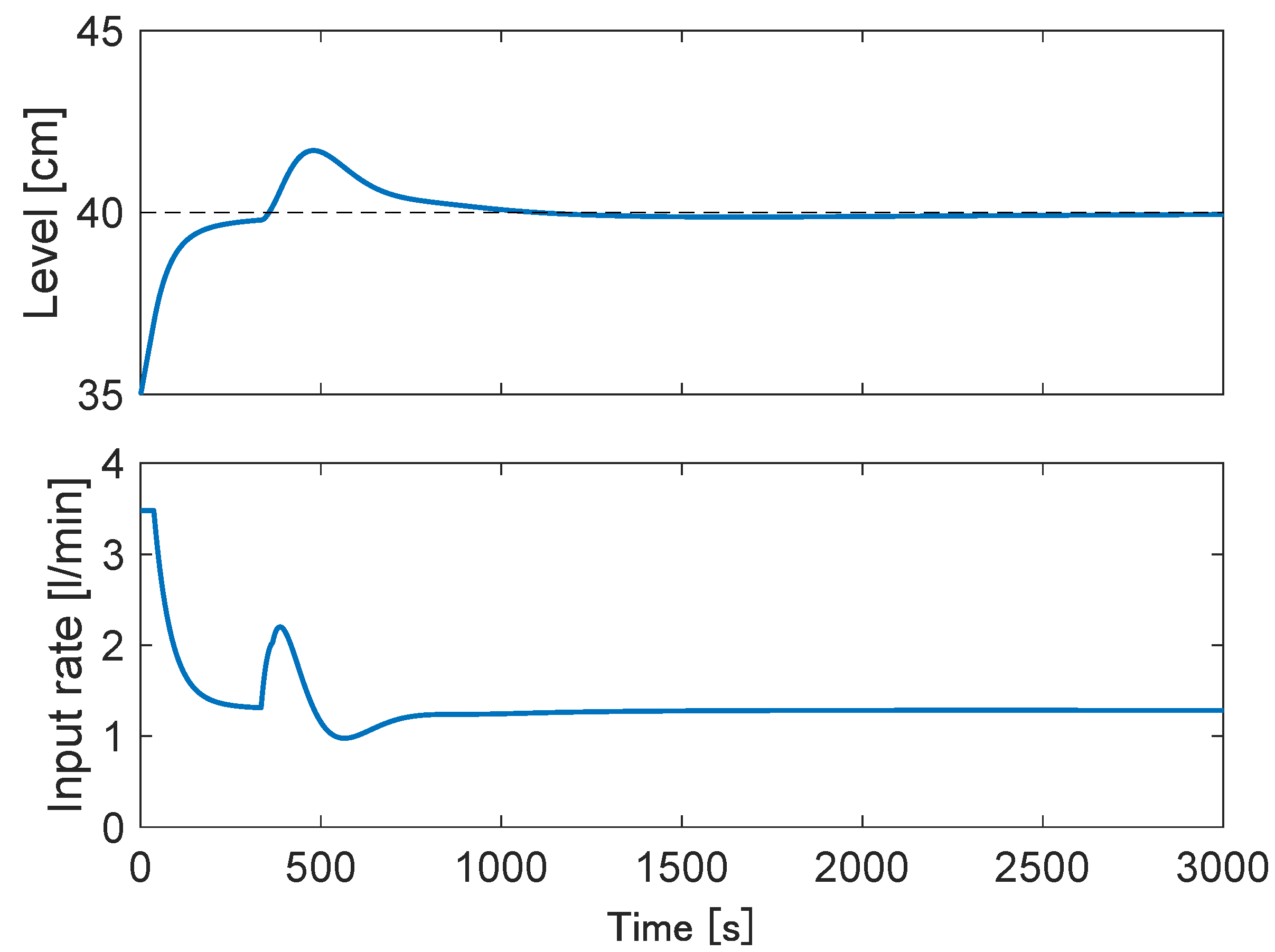
5.1. Simulation Results
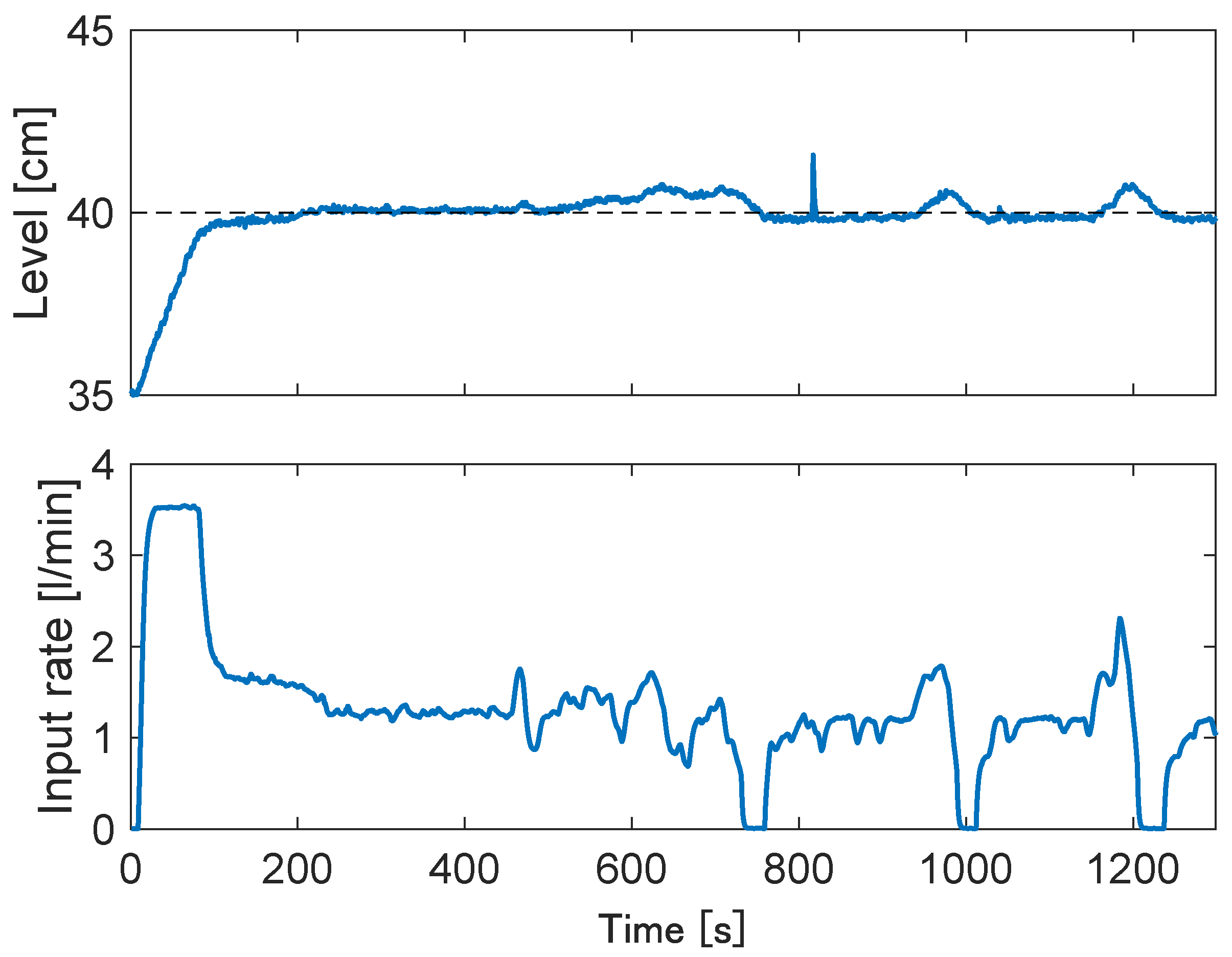
5.2. Exprimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, M.; Iwai, Z.; Mizumoto, I. Robust parallel compensator design for output feedback stabilization of plants with structured uncertainty. Syst. Control. Lett. 1999, 36, 193–198. [Google Scholar] [CrossRef]
- Shah, S.L.; Iwai, Z.; Mizumoto, I.; Deng, M. Simple adaptive control of processes with time-delay. J. Process. Control 1997, 7, 439–449. [Google Scholar] [CrossRef]
- Matsumoto, K.; Saito, D.; Wakui, S. Comparison of Connection Methods of One-axis Tracking Filters and Implementation for Pneumatic Anti-Vibration Apparatus. In Proceedings of the 2018 International Conference on Advanced Mechatronic Systems, Zhengzhou, China, 29 August–2 September 2018. [Google Scholar]
- Ishii, H.; Wakui, S. Performance improvement of PDD2 compensator embedded in position control for pneumatic stage. In Proceedings of the 2019 International Conference on Advanced Mechatronic Systems, Kusatsu, Japan, 26–28 August 2019. [Google Scholar]
- Patra, A.K.; Nanda, A. Automated micro insulin dispenser system based on the model predictive control algorithm. Int. J. Adv. Mechatron. Syst. 2020, 8, 144–154. [Google Scholar] [CrossRef]
- Wen, S.; Liang, T.; Wang, P. Adaptive position estimation and control for permanent magnet synchronous motor. In Proceedings of the 2018 International Conference on Advanced Mechatronic Systems, Zhengzhou, China, 29 August–2 September 2018. [Google Scholar]
- Shafieenejad, I. Novel method for bang-bang optimal control of starship soft landing. Int. J. Adv. Mechatron. Syst. 2023, 10, 146–155. [Google Scholar] [CrossRef]
- Wang, C.; Man, Z.; Jin, J.; Ye, W. Hash-Based Convolutional Deep-thinking Pattern Classifier. In Proceedings of the 2023 International Conference on Advanced Mechatronic Systems, Melbourne, Australia, 4–7 September 2023. [Google Scholar]
- Cheng, W.; Liu, T.; Liang, S. Temperatrue Control of Microwave Heating System by Adaptive Dynamic Programming. In Proceedings of the 2020 International Conference on Advanced Mechatronic Systems, Hanoi, Vietnam, 10–13 December 2020. [Google Scholar]
- Rsetam, K.; Cao, Z.; Man, Z. Design of Robust Terminal Sliding Mode Control for Underactuated Flexible Joint Robot. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4272–4285. [Google Scholar] [CrossRef]
- Man, Z.; Paplinski, A.P.; Wu, H.R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control 1994, 39, 2464–2469. [Google Scholar]
- Wang, H.; Man, Z.; Kong, H.; Zhao, Y.; Yu, M.; Cao, Z.; Zheng, J.; Do, M.T. Design and Implementation of Adaptive Terminal Sliding-Mode Control on a Steer-by-Wire Equipped Road Vehicle. IEEE Trans. Ind. Electron. 2016, 63, 5774–5785. [Google Scholar] [CrossRef]
- Yu, X.; Man, Z. Model reference adaptive control systems with terminal sliding modes. Int. J. Control 1996, 64, 1165–1176. [Google Scholar] [CrossRef]
- Chen, J.; Qian, D. Three controllers via 2nd-order sliding mode for leader-following formation control of multi-robot systems. Int. J. Adv. Mechatron. Syst. 2021, 9, 85–101. [Google Scholar] [CrossRef]
- Deng, M. Operator-Based Nonlinear Control Systems: Design and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 5–26. [Google Scholar]
- Chen, G.; Han, Z. Robust right coprime factorization and robust stabilization of nonlinear feedback control systems. IEEE Trans. Autom. Control 1998, 43, 1505–1509. [Google Scholar] [CrossRef]
- Gao, X.; Yang, Q.; Zhang, J. Multi-objective optimisation for operator-based robust nonlinear control design for wireless power transfer systems. Int. J. Adv. Mechatron. Syst. 2022, 9, 203–210. [Google Scholar] [CrossRef]
- Bu, N.; Zhang, Y.; Li, X. Robust tracking control for uncertain micro-hand actuator with Prandtl-Ishlinskii hysteresis. Int. J. Robust Nonlinear Control 2023, 33, 9391–9405. [Google Scholar] [CrossRef]
- Bu, N.; Liu, H.; Li, W. Robust passive tracking control for an uncertain soft actuator using robust right coprime factorization. Int. J. Robust Nonlinear Control 2021, 31, 6810–6825. [Google Scholar] [CrossRef]
- Bu, N.; Wang, X. Swing-up design of double inverted pendulum by using passive control method based on operator theory. Int. J. Adv. Mechatron. Syst. 2023, 10, 1–7. [Google Scholar] [CrossRef]
- Wang, A.; Deng, M. Robust nonlinear multivariable tracking control design to a manipulator with unknown uncertainties using operator-based robust right coprime factorization. Trans. Inst. Meas. Control 2013, 35, 788–797. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Goto, S. Operator based thermal control of an aluminum plate with a peltier device. Int. J. Innov. Comput. Inf. Control 2008, 4, 3219–3229. [Google Scholar]
- Furukawa, K.; Deng, M. Operator based fault detection and compensation design of an unknown multivariable tank process. In Proceedings of the 2013 International Conference on Advanced Mechatronic Systems, Luoyang, China, 25–27 September 2013. [Google Scholar]
- Keith, B.O.; Jerome, S. The Fractional Calculus; Dover Publications: Mineola, NY, USA, 2006; pp. 107–117. [Google Scholar]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011; pp. 149–152. [Google Scholar]
- Fractional Calculus: What Is It? Available online: https://igor.podlubny.website.tuke.sk/fc.html (accessed on 24 December 2023).
- Zhang, T.; Li, Y. Exponential Euler scheme of multi-delay Caputo-Fabrizio fractional-order differential equations. Appl. Math. Lett. 2022, 124, 107709. [Google Scholar] [CrossRef]
- Nasuno, H.; Shimizu, N. Numerical Integration Algorithm for Nonlinear Fractional Differential Equation. Trans. Jpn. Soc. Mech. Eng. Ser. C 2006, 72, 3193–3200. [Google Scholar] [CrossRef]
- Mehta, U.; Aryan, P.; Raja, G.L. Tri-Parametric Fractional-Order Controller Design for Integrating Systems with Time Delay. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4166–4170. [Google Scholar] [CrossRef]
- Arya, Y. A new optimized fuzzy FOPI-FOPD controller for automatic generation control of electric power systems. J. Frankl. Inst. 2019, 356, 16–32. [Google Scholar] [CrossRef]
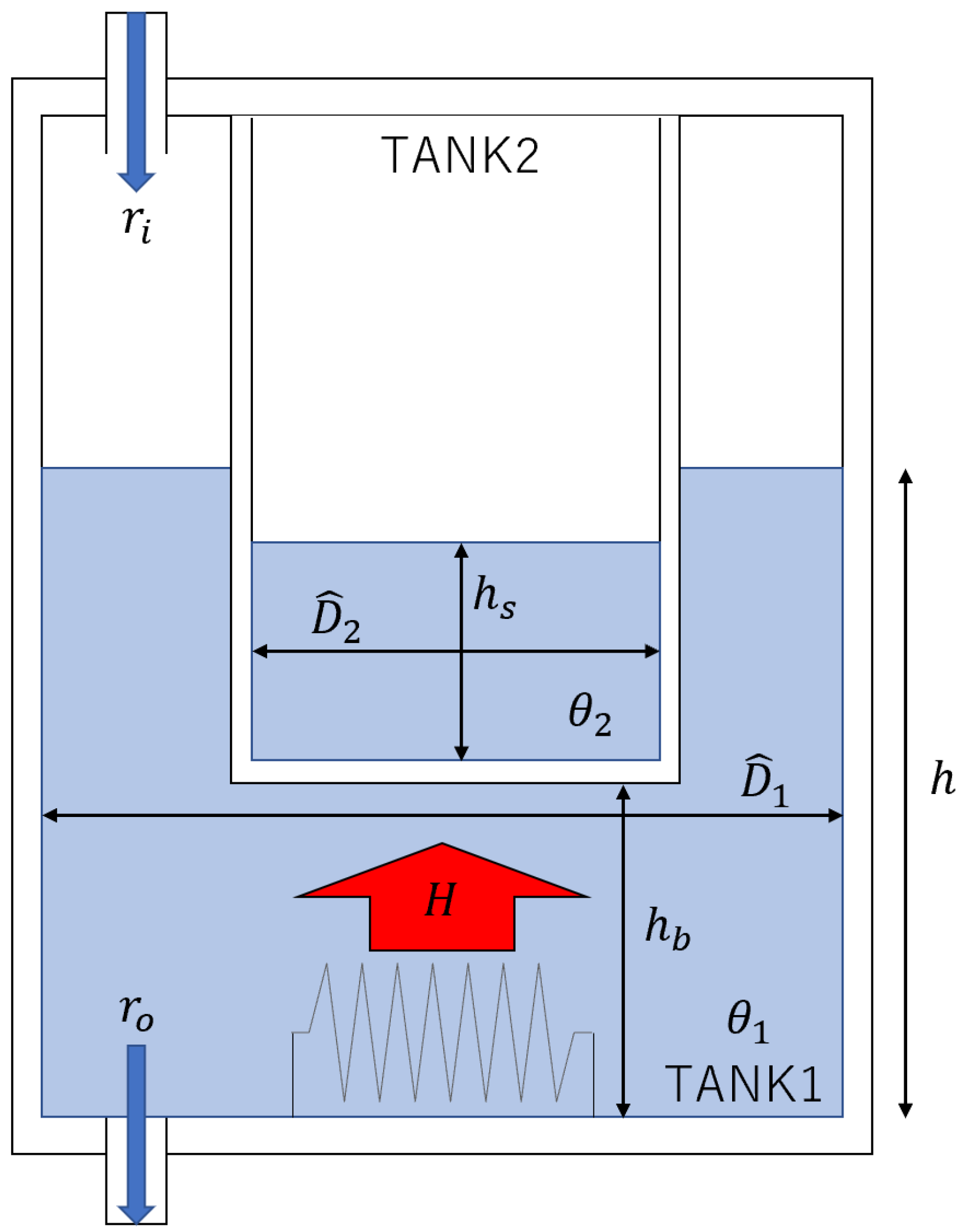
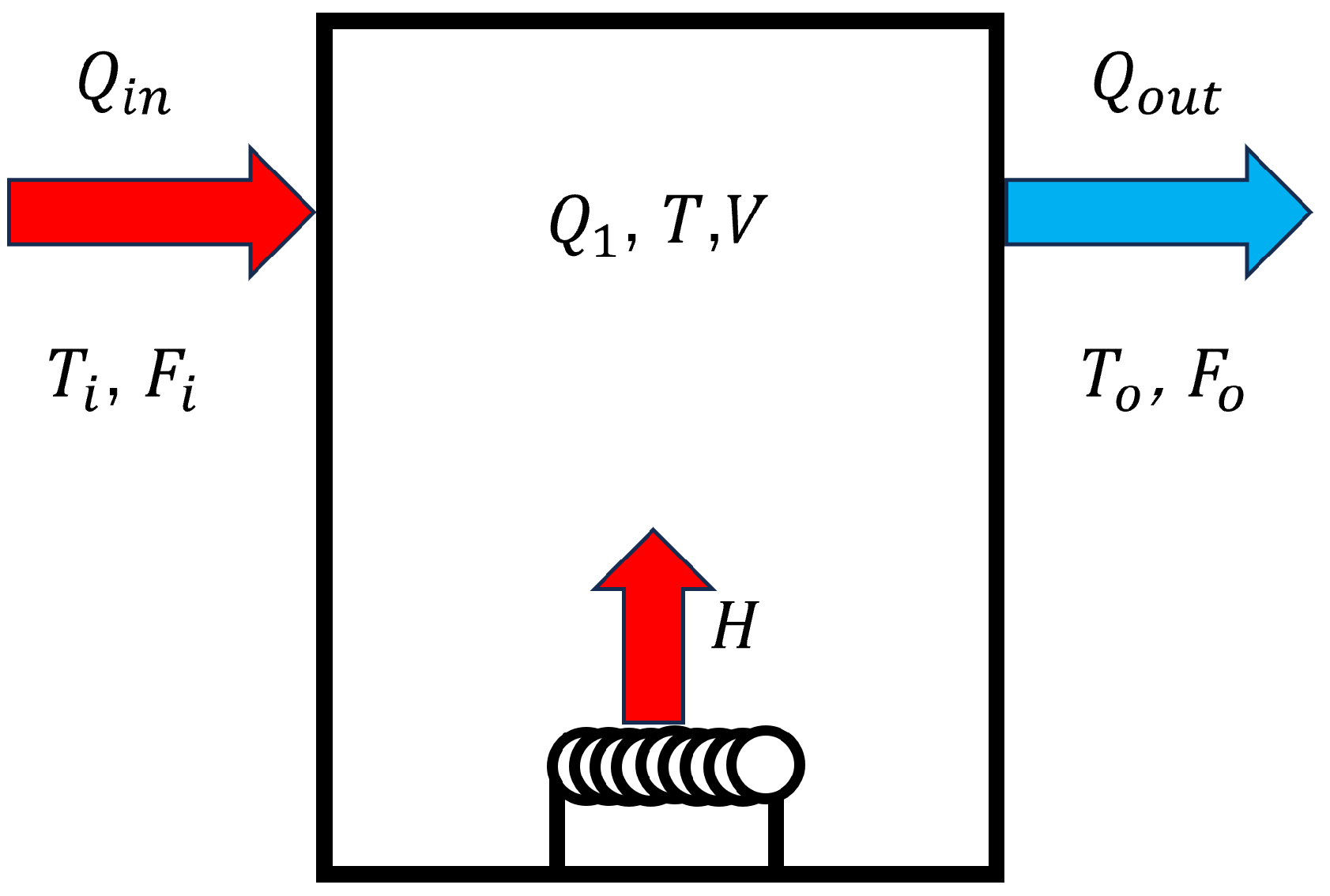




| Parameter | Definition | Value |
|---|---|---|
| Inside diameter (TANK1) | 32 cm | |
| Inside diameter (TANK2) | 11 cm | |
| Inner diameter | 4.0 cm | |
| Thickness of wall | 2.0 cm | |
| Distance between botttoms of TANK1 and TANK2 | 20 cm | |
| Water level (TANK2) | 35 cm | |
| Heat transfer coefficient | °C) | |
| Heat transfer coefficient | °C) | |
| k | Thermal conductivity of TANK wall | °C) |
| TANK1 wall heat capacity | 47 | |
| Heat capacity of water in TANK2 | ||
| TANK2 wall heat capacity | 10 | |
| Specific heat of water | ||
| Density of water | ||
| g | acceleration of gravity | |
| Temperature of influent liquid | 18 | |
| Liquid temperature (TANK1) | ||
| Liquid temperature (TANK2) | ||
| Outer wall temperature | ||
| Inner wall temperature | ||
| h | Water level (TANK1) | |
| Heat capacity of water in TANK1 | ||
| Liquid volume of effluent | ||
| Liquid volume of influent | ||
| H | Heat supplied by heater | |
| Thermal conductivity |
| Parameter | Definition | Value |
|---|---|---|
| Simulation time | 3500 s | |
| Sampling time | s | |
| Target liquid level | 40 | |
| Target liquid temperature | 26 | |
| Initial value | 35 | |
| Initial value | 25 | |
| Proportional gain | 3.0 | |
| Integral gain | 0.0015 | |
| Proportional gain | 1.0 | |
| Integral gain | 0.003 | |
| Proportional gain | 50 | |
| Integral gain | 0.02 | |
| p | Differential factorial | |
| q | Differential factorial | |
| Differential factorial | ||
| Gain | ||
| Gain | ||
| Angular frequency | ||
| Angular frequency |
| Parameter | Definition | Value |
|---|---|---|
| Sampling time | s | |
| Outside temperature | 22 | |
| Target liquid level | 40 | |
| Target liquid temperature | 26 | |
| Initial value | 35 | |
| Initial value | 25 | |
| Inflow liquid temperature | 20 | |
| Proportional gain | 1.8 | |
| Integral gain | 0.0024 | |
| Proportional gain | 1.1 | |
| Integral gain | 0.003 | |
| Proportional gain | 15 | |
| Integral gain | 0.001 | |
| p | Differential factorial | |
| q | Differential factorial | |
| Differential factorial | ||
| Gain | ||
| Gain | ||
| Angular frequency | ||
| Angular frequency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kochi, R.; Deng, M. Multivariable Fractional-Order Controller Design for a Nonlinear Dual-Tank Device. Fractal Fract. 2024, 8, 27. https://doi.org/10.3390/fractalfract8010027
Kochi R, Deng M. Multivariable Fractional-Order Controller Design for a Nonlinear Dual-Tank Device. Fractal and Fractional. 2024; 8(1):27. https://doi.org/10.3390/fractalfract8010027
Chicago/Turabian StyleKochi, Ryota, and Mingcong Deng. 2024. "Multivariable Fractional-Order Controller Design for a Nonlinear Dual-Tank Device" Fractal and Fractional 8, no. 1: 27. https://doi.org/10.3390/fractalfract8010027
APA StyleKochi, R., & Deng, M. (2024). Multivariable Fractional-Order Controller Design for a Nonlinear Dual-Tank Device. Fractal and Fractional, 8(1), 27. https://doi.org/10.3390/fractalfract8010027








