Analytical Solutions of the Fractional Hirota–Satsuma Coupled KdV Equation along with Analysis of Bifurcation, Sensitivity and Chaotic Behaviors
Abstract
:1. Introduction
2. Proposal of the Logistic Method
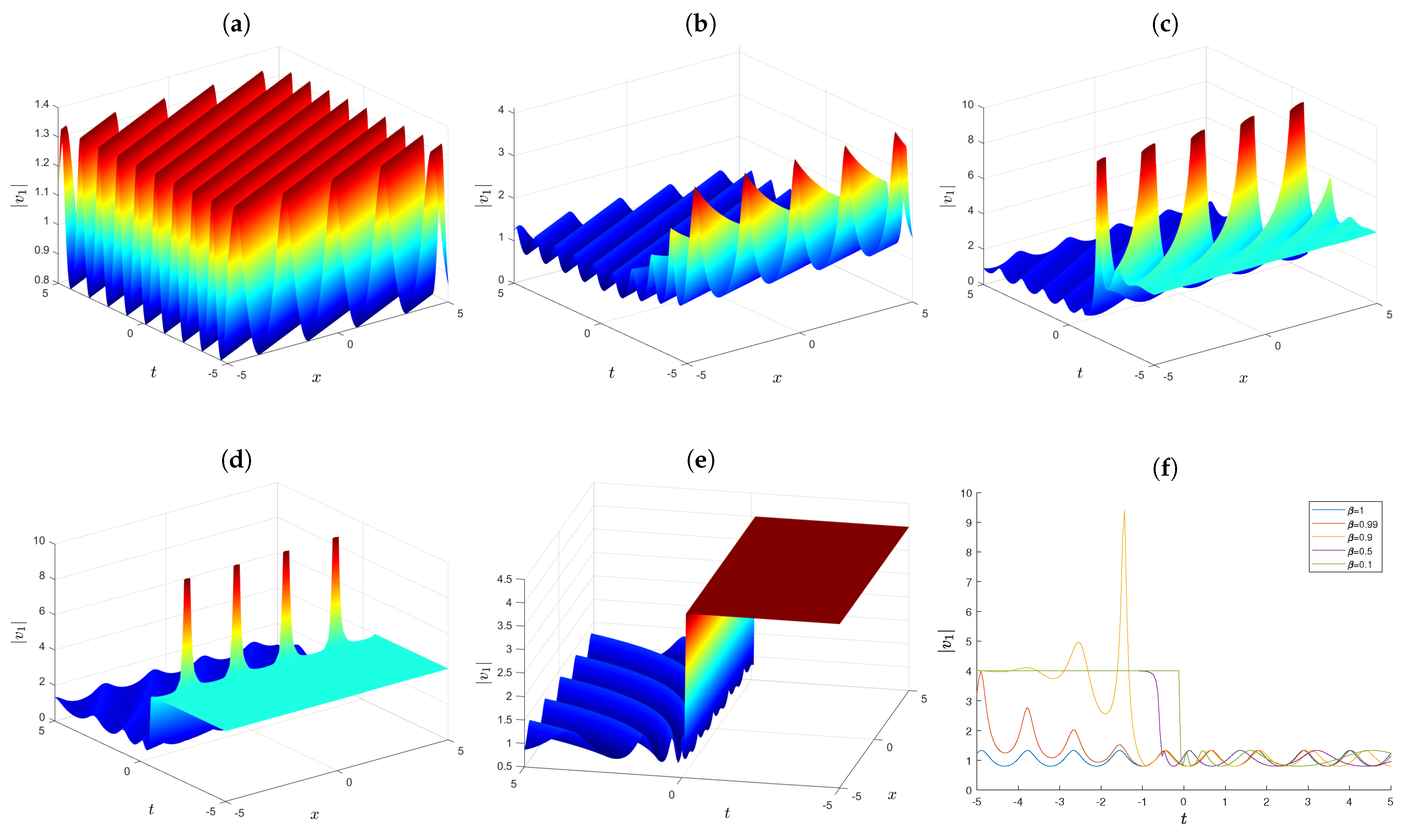
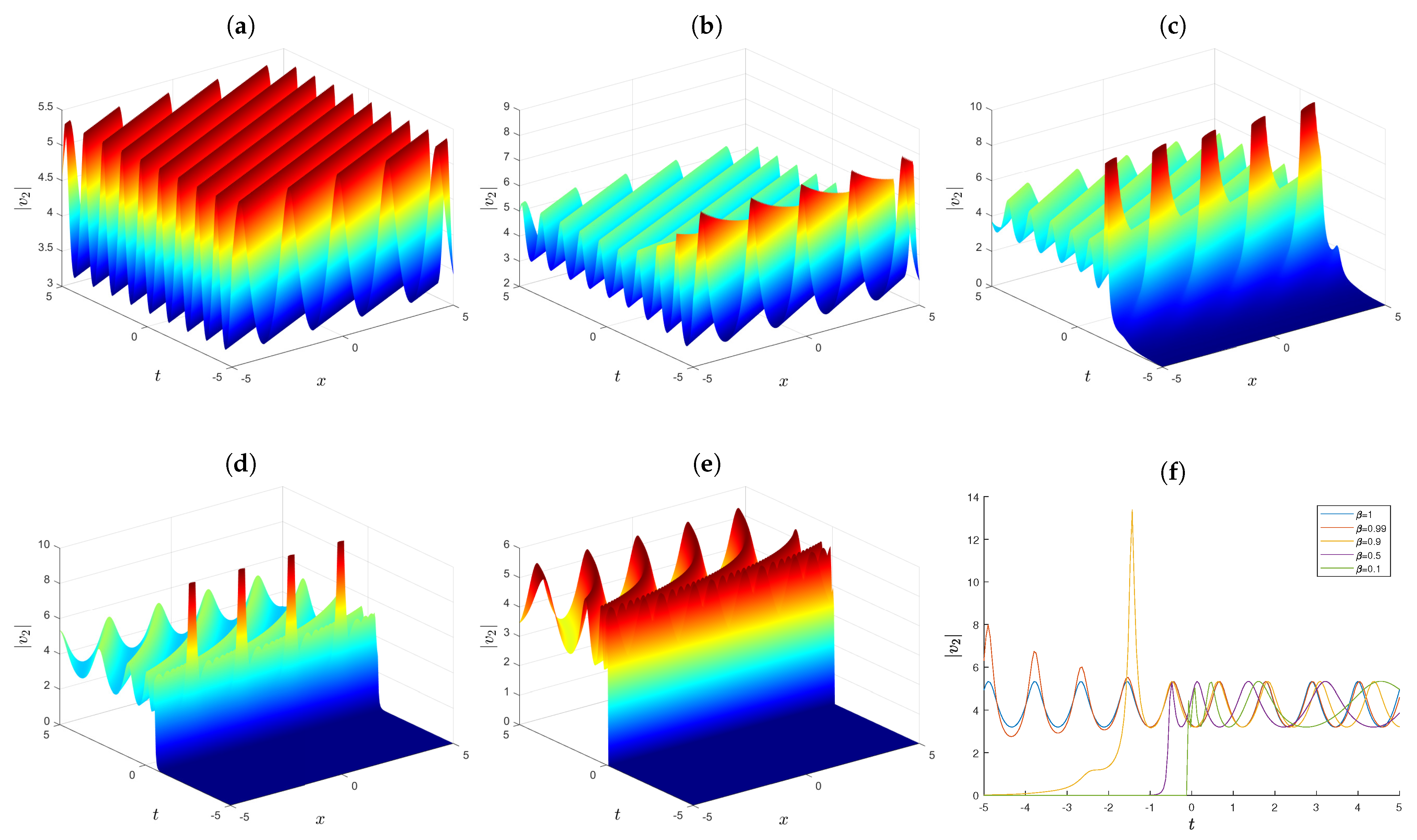
3. Applications to the fHScKdV Equation
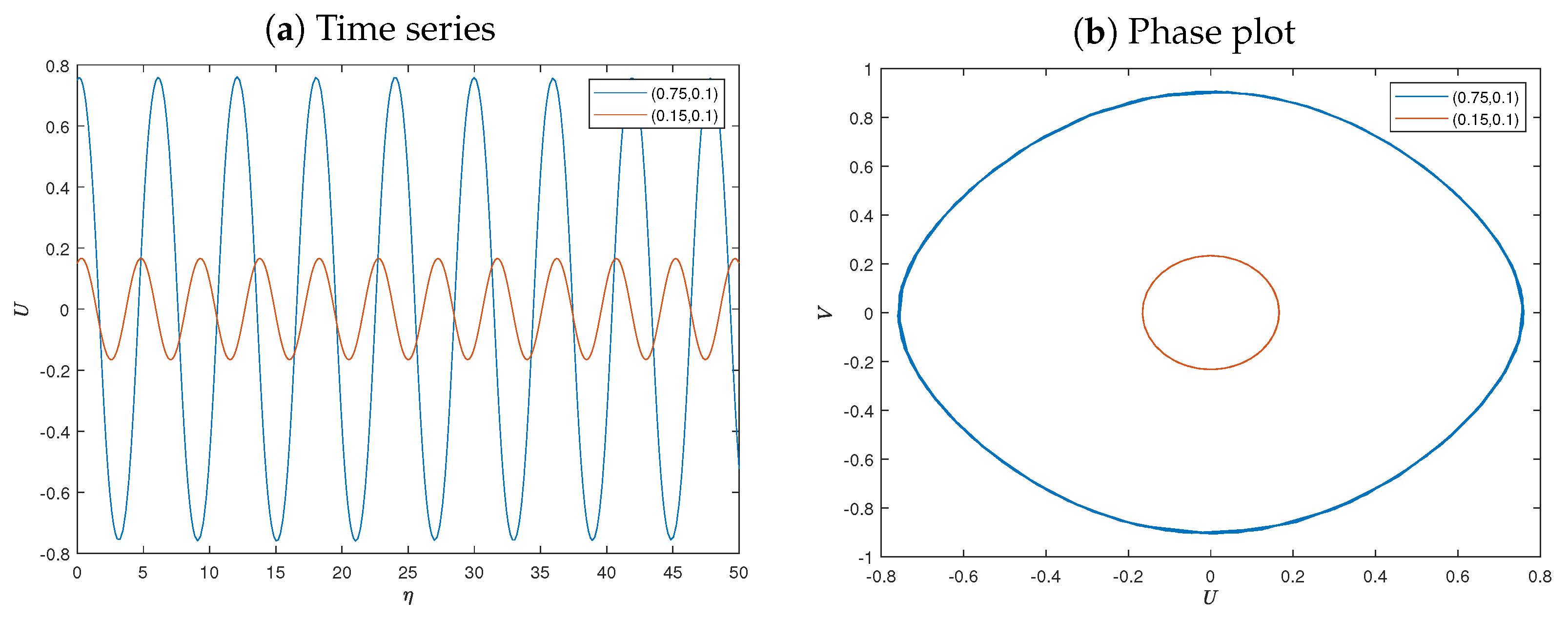
4. Phase Portraits and Bifurcation Behaviors
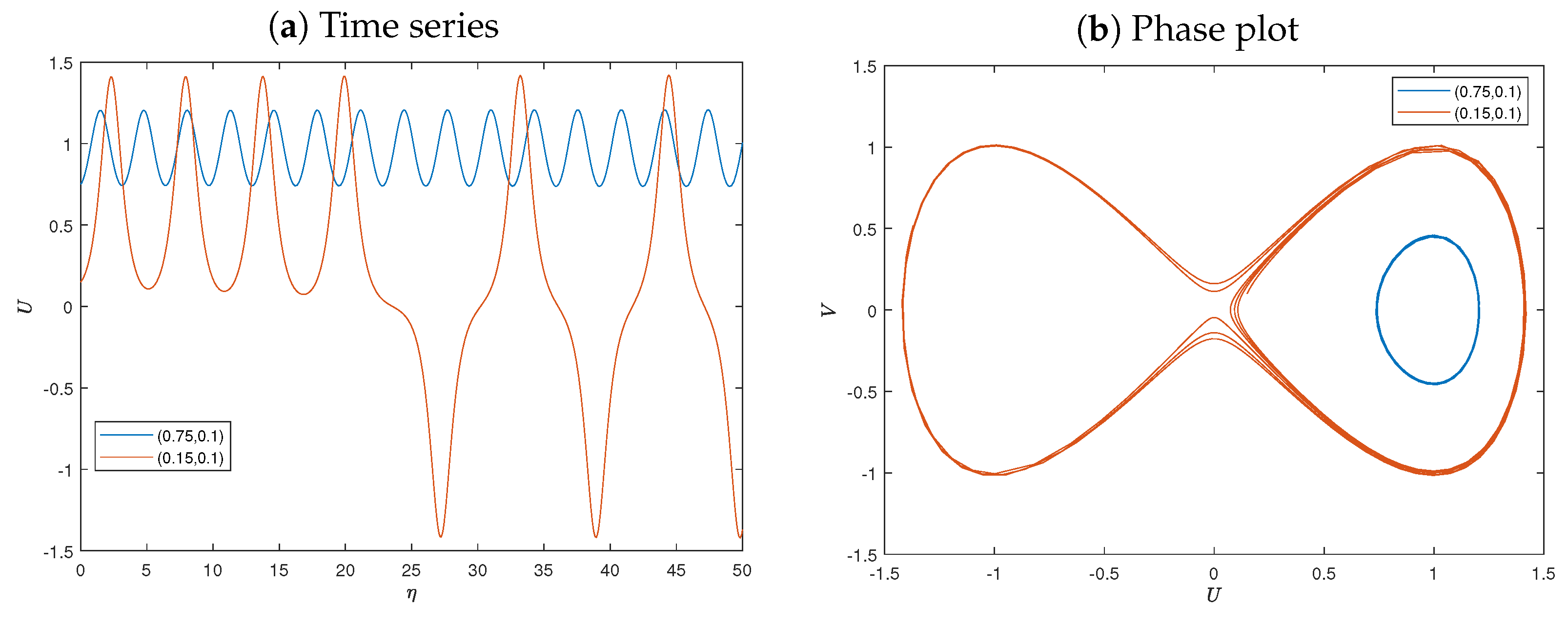
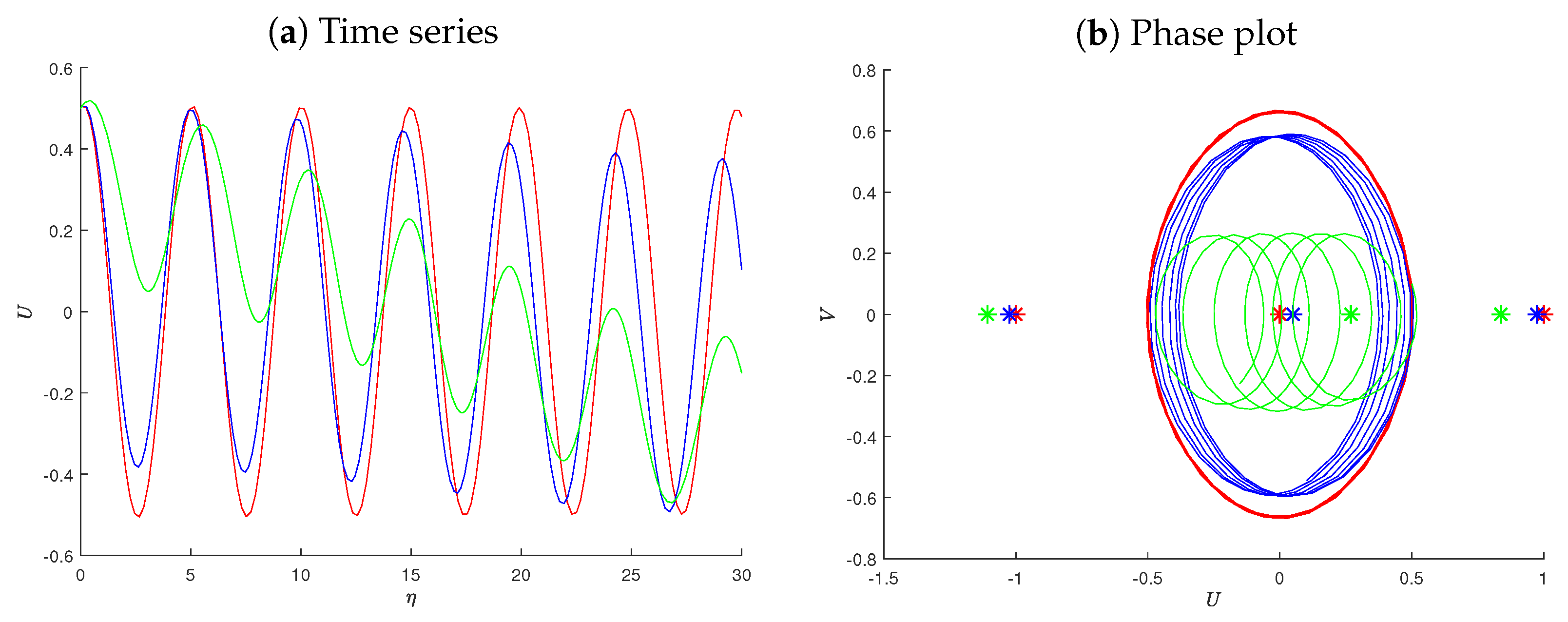
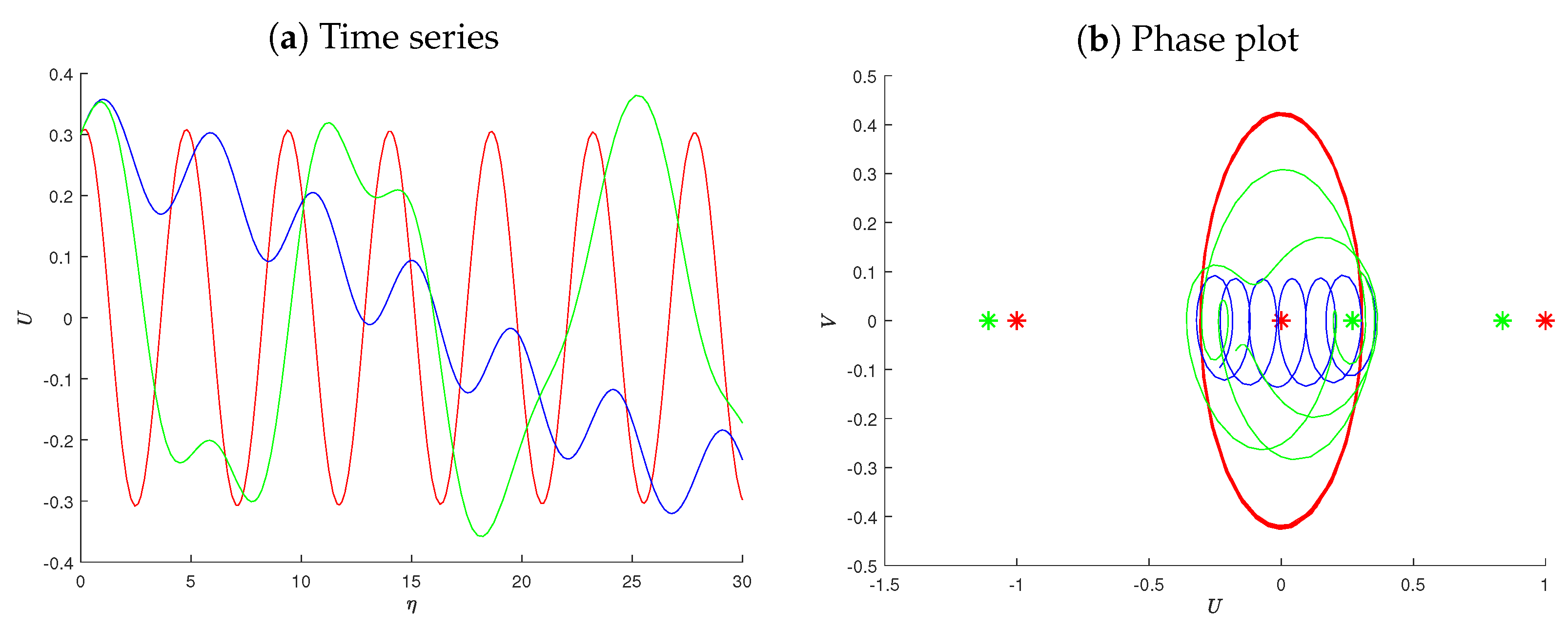
5. Sensitive Analysis
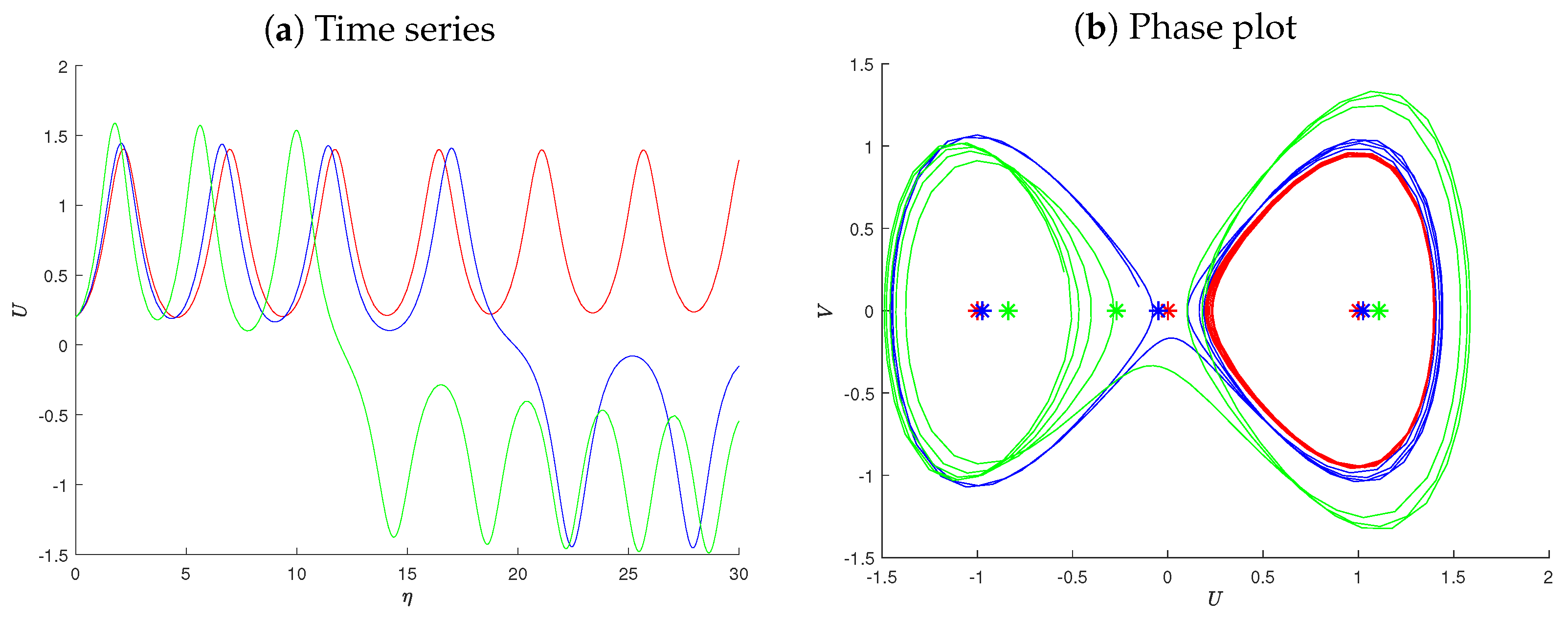
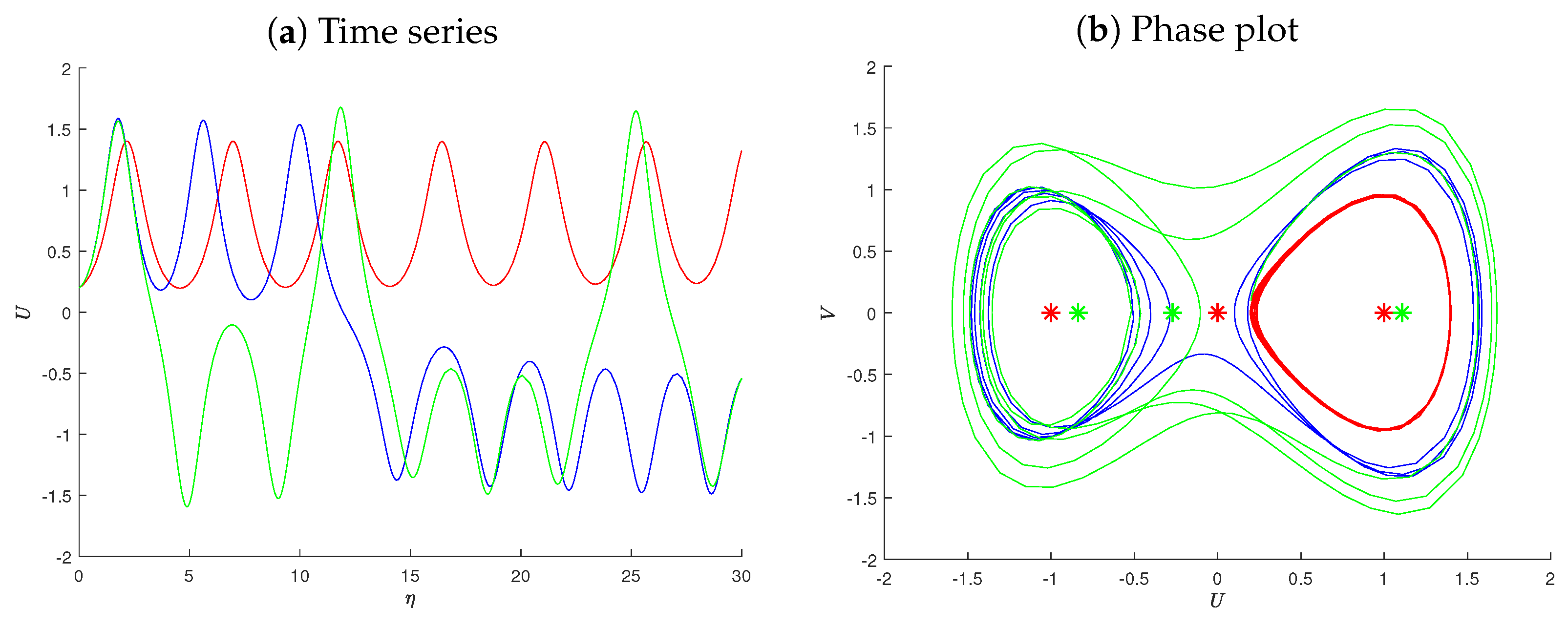
6. Chaotic Behavior
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ullah, M.S.; Ali, M.Z.; Roshid, H.-O.; Seadawy, A.; Baleanu, D. Collision phenomena among lump, periodic and soliton solutions to a (2+1)-dimensional bogoyavlenskii’s breaking soliton model. Phys. Lett. A 2021, 397, 127263. [Google Scholar] [CrossRef]
- Wu, X.-S.; Liu, J.-G. Solving the variable coefficient nonlinear partial differential equations based on the bilinear residual network method. Nonlinear Dyn. 2024, 112, 8329–8340. [Google Scholar] [CrossRef]
- Kumar, D.; Seadawy, A.R.; Haque, M.R. Multiple soliton solutions of the nonlinear partial differential equations describing the wave propagation in nonlinear low-pass electrical transmission lines. Chaos Solitons Fractals 2018, 115, 62–76. [Google Scholar] [CrossRef]
- Tuan, N.H.; Mohammadi, H.; Rezapour, S. A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos Solitons Fractals 2020, 140, 110107. [Google Scholar] [CrossRef]
- Machado, J.A.T. The bouncing ball and the Grünwald-Letnikov definition of fractional derivative. Fract. Calc. Appl. Anal. 2021, 24, 1003–1014. [Google Scholar] [CrossRef]
- Hilfer, R. Fractional diffusion based on Riemann-Liouville fractional derivatives. J. Phys. Chem. B 2000, 104, 3914–3917. [Google Scholar] [CrossRef]
- Bagheri, M.; Khani, A. Analytical method for solving the fractional order generalized KdV equation by a Beta-fractional derivative. Adv. Math. Phys. 2020, 2020, 8819183. [Google Scholar] [CrossRef]
- Ozkan, E.M. New exact solutions of some important nonlinear fractional partial differential equations with beta derivative. Fractal Fract. 2022, 6, 173. [Google Scholar] [CrossRef]
- Tang, B.; He, Y.; Wei, L.; Zhang, X. A generalized fractional sub-equation method for fractional differential equations with variable coefficients. Phys. Lett. A 2012, 376, 2588–2590. [Google Scholar] [CrossRef]
- Bekir, A.; Aksoy, E.; Cevikel, A. Exact solutions of nonlinear time fractional partial differential equations by sub-equation method. Math. Methods Appl. Sci. 2014, 38, 2779–2784. [Google Scholar] [CrossRef]
- Nisar, K.S.; Inan, I.E.; Inc, M.; Rezazadeh, H. Properties of some higher-dimensional nonlinear schrödinger equations. Results Phys. 2021, 31, 105073. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Jhangeer, A.; Rezazadeh, H.; Akinyemi, L.; Akbar, M.A.; Inc, M. Propagation of new dynamics of longitudinal bud equation among a magneto-electro-elastic round rod. Mod. Phys. Lett. B 2021, 35, 2150381. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Eslami, M.; Biswas, A. Solitons and periodic solutions to a couple of fractional nonlinear evolution equations. Pramana 2014, 82, 465–476. [Google Scholar] [CrossRef]
- Eslami, M.; Fathi-Vajargah, B.; Mirzazadeh, M.; Biswas, A. Application of first integral method to fractional partial differential equations. Indian J. Phys. 2014, 88, 177–184. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Baleanu, D.; Raza, N.; Park, C.; Ahmadian, A.; Salahshour, S. The generalized complex Ginzburg-Landau model and its dark and bright soliton solutions. Eur. Phys. J. Plus 2021, 136, 709. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Salahshour, S.; Baleanu, D.; Zafar, A. Specific wave structures of a fifth-order nonlinear water wave equation. J. Ocean Eng. Sci. 2022, 7, 462–466. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A. A novel analytical method for time-fractional differential equations. Optik 2016, 127, 8209–8214. [Google Scholar] [CrossRef]
- Hosseini, K.; Bekir, A.; Ansari, R. Exact solutions of nonlinear conformable time-fractional boussinesq equations using the exp(-φ(ϵ))-expansion method. Opt. Quantum Electron. 2017, 49, 131. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A.; Koppelaar, H. Study of coupled nonlinear partial differential equations for finding exact analytical solutions. R. Soc. Open Sci. 2015, 2, 140406. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Asif, M.; Hosseini, K.; Mirzazadeh, M.; Akinyemi, L. Some novel integration techniques to explore the conformable m-fractional schrödinger-hirota equation. J. Ocean Eng. Sci. 2022, 7, 337–344. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ali, K.K.; Inc, M.; Mehanna, M.S.; Rezazadeh, H.; Akinyemi, L. New solutions for the generalized resonant nonlinear schrödinger equation. Results Phys. 2022, 33, 105153. [Google Scholar] [CrossRef]
- Nisar, K.S.; Inan, I.E.; Yepez-Martinez, H.; Inc, M. Some new type optical and the other soliton solutions of coupled nonlinear hirota equation. Results Phys. 2022, 35, 105388. [Google Scholar] [CrossRef]
- Hu, H.; Li, X. New interaction solutions of the similarity reduction for the integrable (2+1)-dimensional boussinesq equation. Int. J. Mod. Phys. B 2022, 36, 2250001. [Google Scholar] [CrossRef]
- Raslan, K.R.; Ali, K.K.; Shallal, M.A. The modified extended tanh method with the riccati equation for solving the space-time fractional EW and MEW equations. Chaos Solitons Fractals 2017, 103, 404–409. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A.; Aksoy, E. The modified simple equation method for nonlinear fractional differential equations. Rom. J. Phys. 2015, 60, 1374. [Google Scholar]
- Kaplan, M.; Koparan, M.; Bekir, A. Regarding on the exact solutions for the nonlinear fractional differential equations. Open Phys. 2016, 14, 478–482. [Google Scholar] [CrossRef]
- Rahman, Z.; Abdeljabbar, A.; Harun-Or-Roshid; Ali, M.Z. Novel precise solitary wave solutions of two time fractional nonlinear evolution models via the MSE scheme. Fractal Fract. 2022, 6, 444. [Google Scholar] [CrossRef]
- Kumar, D.; Hosseini, K.; Kaabar, M.K.A.; Kaplan, M.; Salahshour, S. On some novel solution solutions to the generalized Schrödinger-Boussinesq equations for the interaction between complex short wave and real long wave envelope. J. Ocean Eng. Sci. 2022, 7, 353–362. [Google Scholar] [CrossRef]
- Gu, Y.; Yuan, W.; Aminakbari, N.; Lin, J. Meromorphic solutions of some algebraic differential equations related Painlevé equation IV and its applications. Math. Methods Appl. Sci. 2018, 41, 3832–3840. [Google Scholar] [CrossRef]
- Gu, Y.; Wu, C.; Yao, X.; Yuan, W. Characterizations of all real solutions for the KdV equation and WR. Appl. Math. Lett. 2020, 107, 106446. [Google Scholar] [CrossRef]
- Gu, Y.; Liao, L. Closed form solutions of Gerdjikov-Ivanov equation in nonlinear fiber optics involving the beta derivatives. Int. J. Mod. Phys. B 2022, 36, 2250116. [Google Scholar] [CrossRef]
- Hirota, R.; Satsuma, J. Soliton solutions of a coupled Korteweg-de Vries equation. Phys. Lett. A 1981, 85, 407–408. [Google Scholar] [CrossRef]
- Alam, M.N.; Seadawy, A.R.; Baleanu, D. Closed-form wave structures of the space-time fractional Hirota-Satsuma coupled KdV equation with nonlinear physical phenomena. Open Phys. 2020, 18, 555–565. [Google Scholar] [CrossRef]
- Yin, Q.; Gao, B. New solutions of the time-fractional Hirota-Satsuma coupled KdV equation by three distinct methods. Int. J. Geom. Methods Mod. Phys. 2023, 20, 2350170. [Google Scholar] [CrossRef]
- Kurt, A.; Rezazadeh, H.; Senol, M.; Neirameh, A.; Tasbozan, O.; Eslami, M.; Mirzazadeh, M. Two effective approaches for solving fractional generalized Hirota-Satsuma coupled KdV system arising in interaction of long waves. J. Ocean Eng. Sci. 2019, 4, 24–32. [Google Scholar] [CrossRef]
- Yan, Z. The extended jacobian elliptic function expansion method and its application in the generalized Hirota-Satsuma coupled KdV system. Chaos Solitons Fractals 2003, 15, 575–583. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A. Construction of exact solutions to the space-time fractional differential equations via new approach. Optik 2017, 132, 1–8. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional hunter-saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Atangana, A.; Goufo, E.F.D. Extension of matched asymptotic method to fractional boundary layers problems. Math. Probl. Eng. 2014, 2014, e107535. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Modelling the spread of river blindness disease via the Caputo fractional derivative and the beta-derivative. Entropy 2016, 18, 40. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Gómez-Aguilar, J.F. Soliton solutions of the Sasa-Satsuma equation in the monomode optical fibers including the beta-derivatives. Optik 2020, 224, 165425. [Google Scholar] [CrossRef]
- Hosseini, K.; Kaur, L.; Mirzazadeh, M.; Baskonus, H.M. 1-Soliton solutions of the (2+1)-dimensional Heisenberg ferromagnetic spin chain model with the beta time derivative. Opt. Quantum Electron. 2021, 53, 125. [Google Scholar] [CrossRef]
- Neishtadt, A.I.; Vasiliev, A.A.; Artemyev, A.V. Capture into resonance and escape from it in a forced nonlinear pendulum. Regul. Chaotic Dyn. 2013, 18, 686–696. [Google Scholar] [CrossRef]
- Bazzani, A.; Capoani, F.; Giovannozzi, M.; Tomás, R. Nonlinear cooling of an annular beam distribution. Phys. Rev. Accel. Beams 2024, 26, 024001. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Y.; Jiang, C.; Lai, Y. Analytical Solutions of the Fractional Hirota–Satsuma Coupled KdV Equation along with Analysis of Bifurcation, Sensitivity and Chaotic Behaviors. Fractal Fract. 2024, 8, 585. https://doi.org/10.3390/fractalfract8100585
Gu Y, Jiang C, Lai Y. Analytical Solutions of the Fractional Hirota–Satsuma Coupled KdV Equation along with Analysis of Bifurcation, Sensitivity and Chaotic Behaviors. Fractal and Fractional. 2024; 8(10):585. https://doi.org/10.3390/fractalfract8100585
Chicago/Turabian StyleGu, Yongyi, Chunling Jiang, and Yongkang Lai. 2024. "Analytical Solutions of the Fractional Hirota–Satsuma Coupled KdV Equation along with Analysis of Bifurcation, Sensitivity and Chaotic Behaviors" Fractal and Fractional 8, no. 10: 585. https://doi.org/10.3390/fractalfract8100585





