The Investigation of Nonlinear Time-Fractional Models in Optical Fibers and the Impact Analysis of Fractional-Order Derivatives on Solitary Waves
Abstract
:1. Introduction
- .
- .
- .
- .
- .
2. The Extended Generalized Kudryashov Method
3. Determination of Soliton Solutions
3.1. The Time-Fractional Cubic-Quintic-Septic-Nonic Equation
3.2. The Time-Fractional Davey–Stewartson (DS) Equation
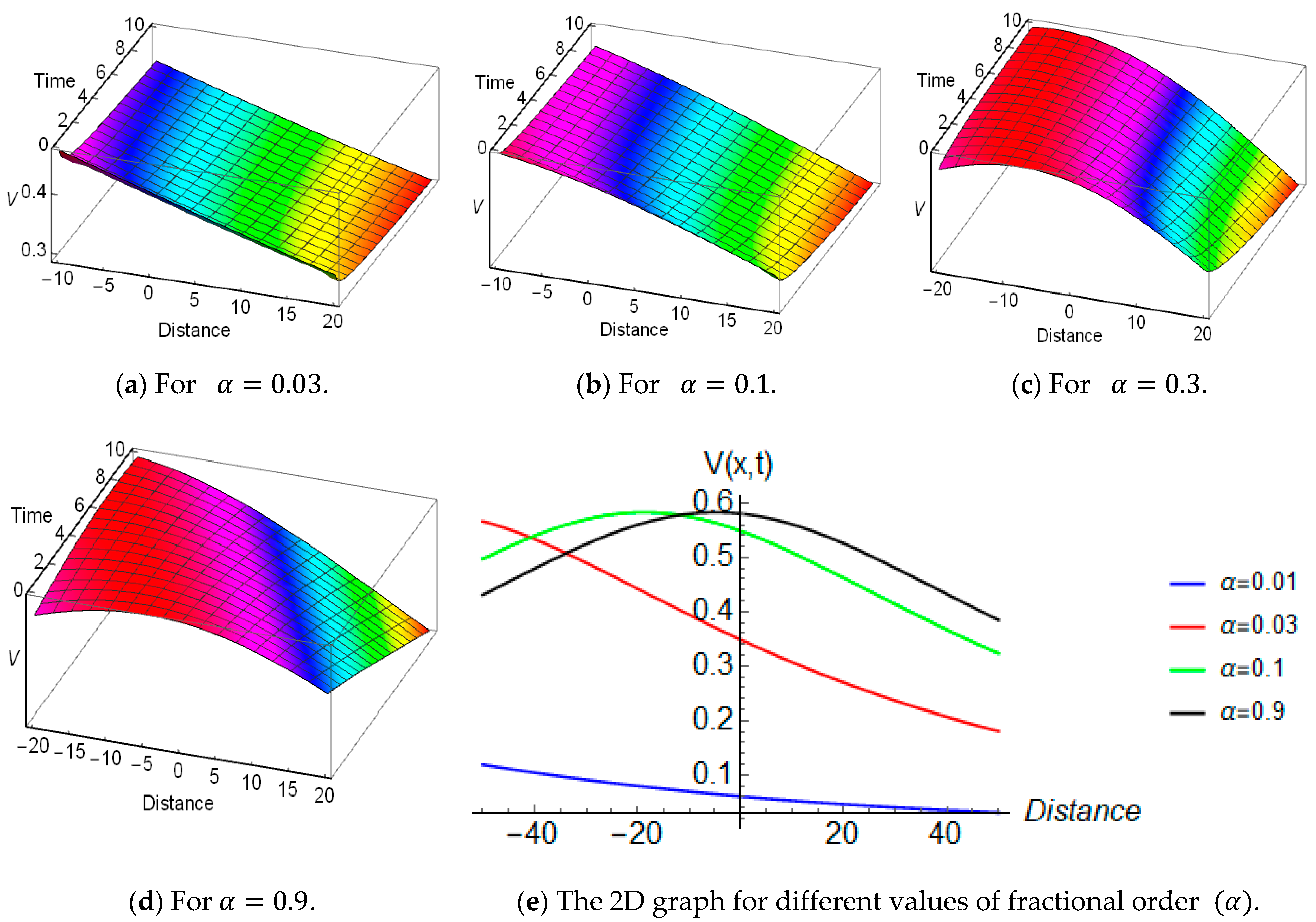
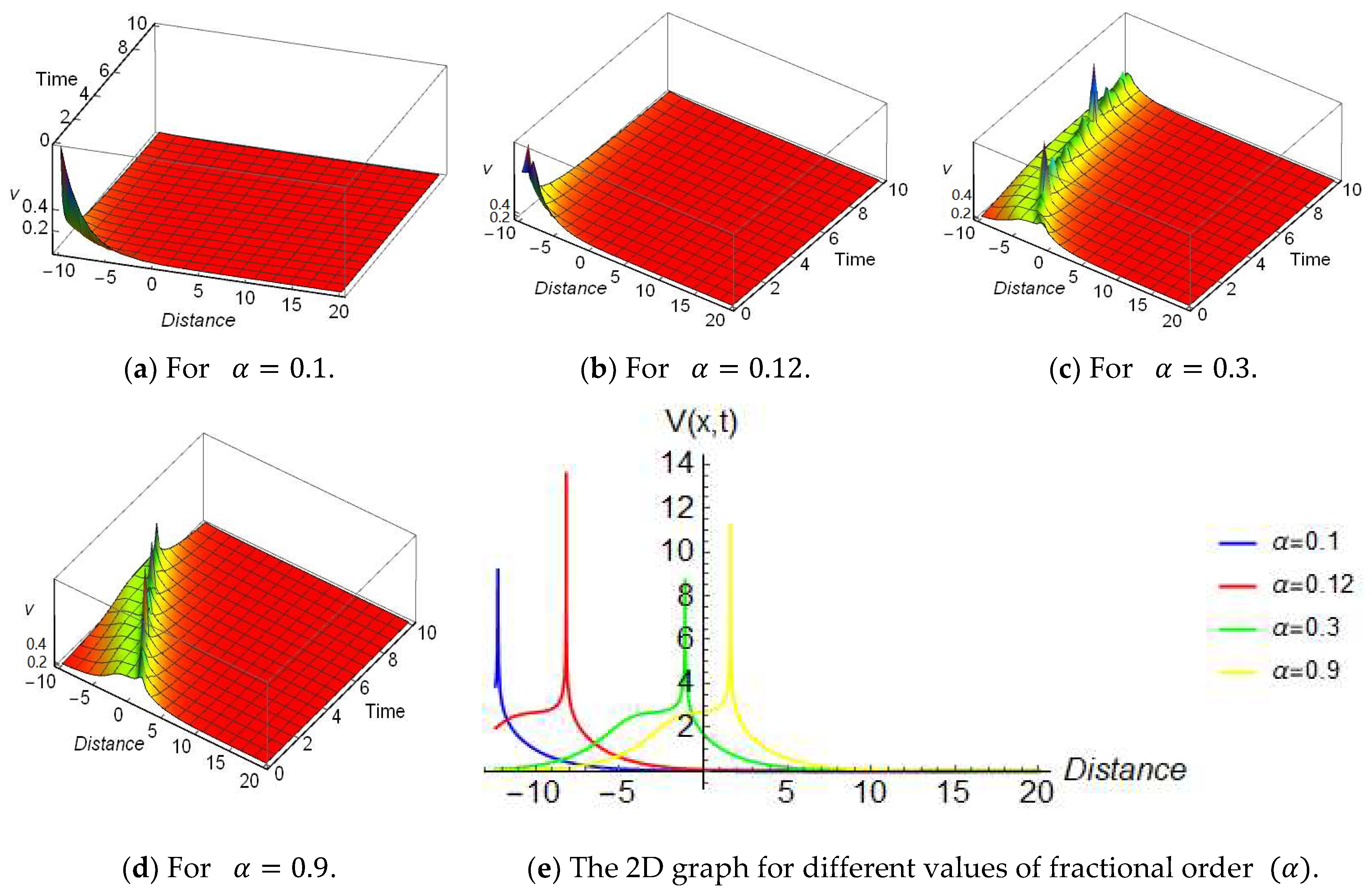
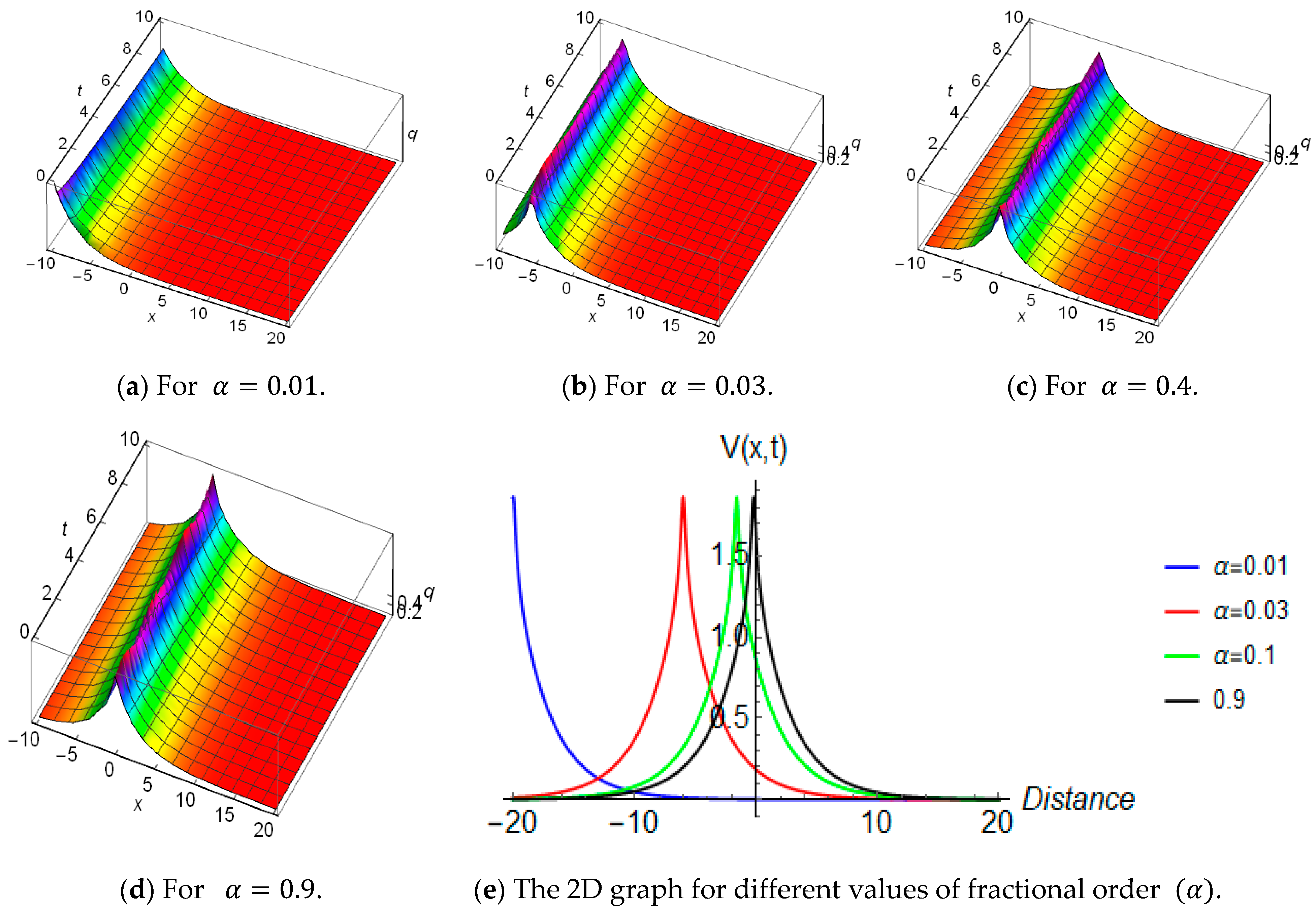
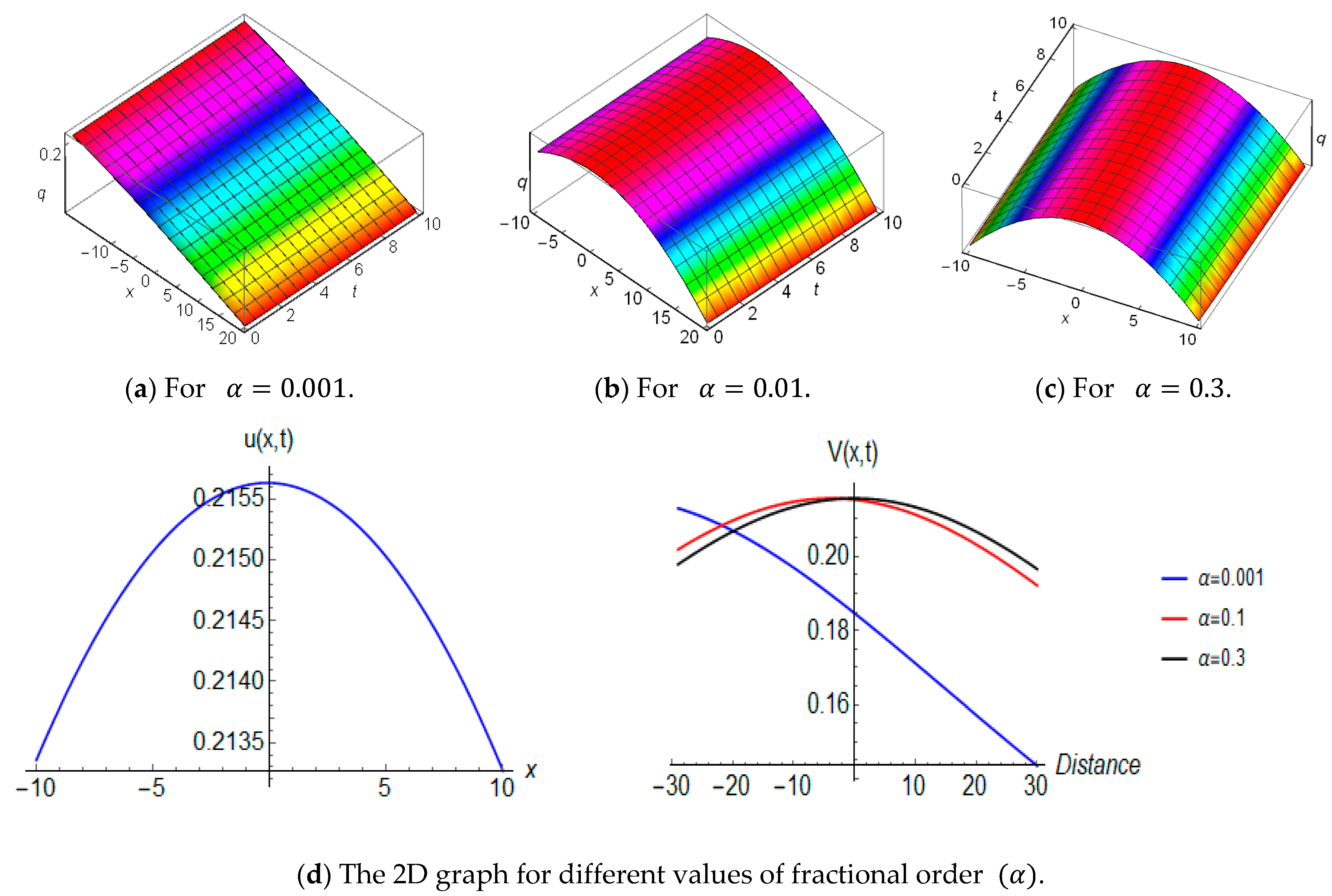
4. Graphical Representations and Physical Explanations
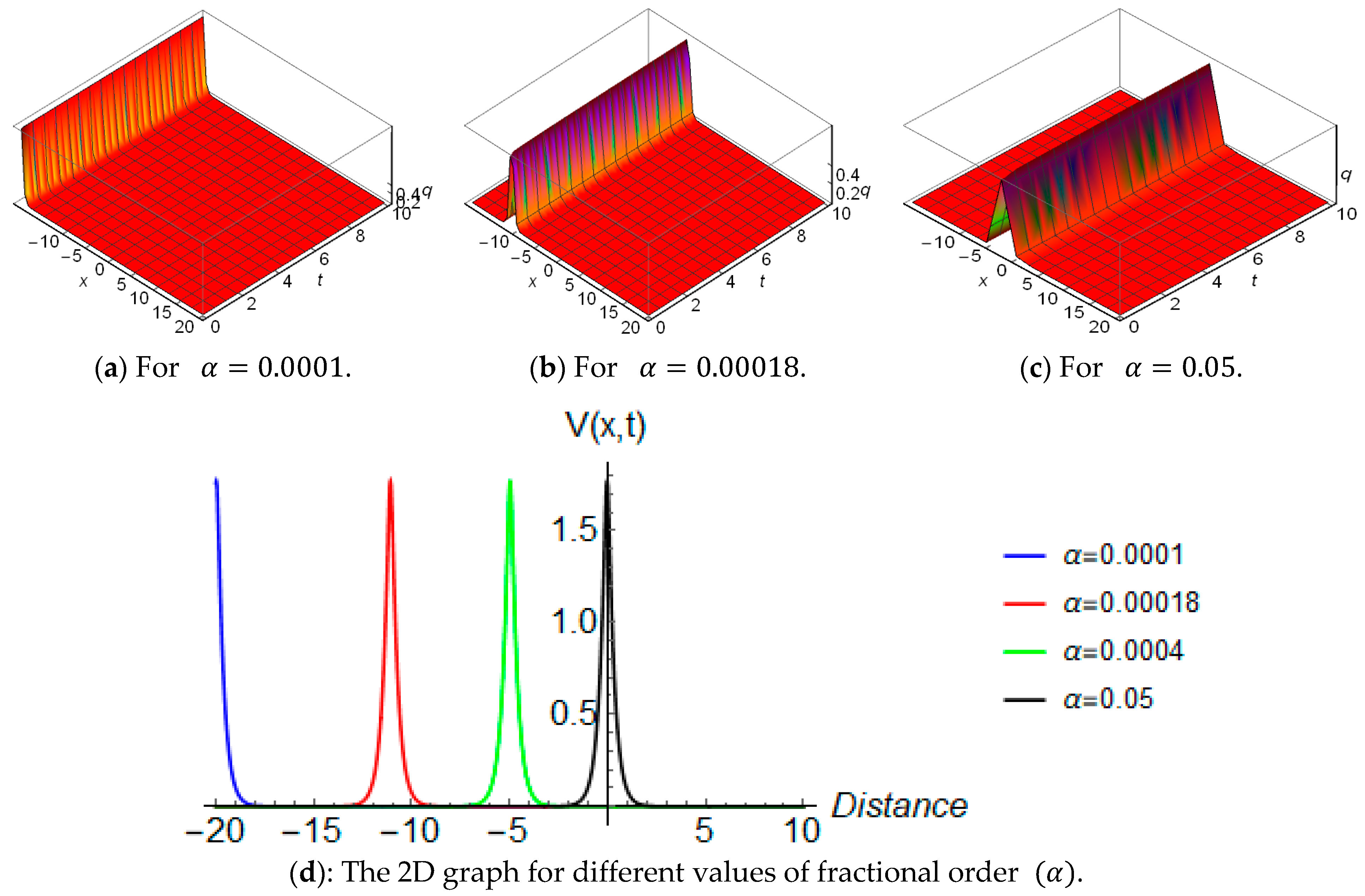
4.1. The Nonlinear Time-Fractional Cubic-Quantic-Septic-Nonic Equation
4.2. The Nonlinear Time Fractional Davey–Stewartson Equation
5. Comparison of the Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Samir, I.; Arnous, A.H.; Yıldırım, Y.; Biswas, A.; Moraru, L.; Moldovanu, S. Optical solitons with cubic-quantic-septic-nonic nonlinear and quadrupled power-law nonlinearity: An observation. Mathematics 2022, 10, 4085. [Google Scholar] [CrossRef]
- Ding, C.C.; Zhou, Q.; Triki, H.; Sun, Y.; Biswas, A. Dynamics of dark and anti-dark solitons for the x-nonlocal Davey-Stewartson II equation. Nonlinear Dyn. 2023, 111, 2621–2629. [Google Scholar] [CrossRef]
- Ross, B. Fractional Calculus: An Introduction to the Theory and Applications of Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Jumarie, G. Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions. Appl. Math. Lett. 2009, 22, 378–385. [Google Scholar] [CrossRef]
- Raza, N.; Osman, M.S.; Abdel-Aty, A.H.; Abdel-Khalek, S.; Besbes, H.R. Optical solitons of space-time fractional Fokas–Lenells equation with two versatile integration architectures. Adv. Differ. Equ. 2020, 2020, 517. [Google Scholar] [CrossRef]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. Modeling the spread of Rubella disease using the concept of with local derivative with fractional parameter: Beta-derivative. Complexity 2016, 21, 442–451. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Modelling the spread of River blindness disease via the Caputo fractional derivative and the β-derivative. Entropy 2016, 18, 40. [Google Scholar] [CrossRef]
- Volkan, A. Exact solutions of nonlinear time fractional Schrödinger equation with beta-derivative. Fundam. Contemp. Math. Sci. 2023, 4, 1–8. [Google Scholar]
- Mahak, N.; Akram, G. The modified auxiliary equation method to investigate solutions of the perturbed nonlinear Schrödinger equation with Kerr law nonlinearity. Optik 2020, 207, 164467. [Google Scholar] [CrossRef]
- Islam, M.E.; Barman, H.K.; Akbar, M.A. Search for interactions of phenomena described by the coupled Higgs field equation through analytical solutions. Opt. Quant. Electron. 2020, 52, 468. [Google Scholar] [CrossRef]
- Haq, E.U.; Ali, M.; Khan, A.S. On the solution of fractional Riccati differential equations with variation of parameters method. Engg. Appl. Sci. Lett. 2020, 3, 1–9. [Google Scholar]
- Fadugba, S.E.; Oluwayemi, M.O.; Ajayi, A.O.; Faweya, O.; Okunlola, J.T.; Kekana, M. Fractional reduced differential transform method for solving fractional order measles model. In Proceedings of the 2023 International Conference on Science, Engineering and Business for Sustainable Development Goals (SEB-SDG), Omu-Aran, Nigeria, 5–7 April 2023. [Google Scholar]
- Ali, R.; Tag-eldin, E. A comparative analysis of generalized and extended (G′/G)-expansion methods for travelling wave solutions of fractional Maccari’s system with complex structure. Alex. Eng. J. 2023, 79, 508–530. [Google Scholar] [CrossRef]
- Çulha Ünal, S. Exact solutions of the Landau-Ginzburg-Higgs equation utilizing the Jacobi elliptic functions. Opt. Quant. Electron. 2024, 56, 1027. [Google Scholar] [CrossRef]
- Korkmaz, A.; Hepson, O.E.; Hosseini, K.; Rezazadeh, H.; Eslami, M. Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class. J. King Saud. Univ. Sci. 2020, 32, 567–574. [Google Scholar] [CrossRef]
- Mamun, A.A.; Lu, C.; Ananna, S.N.; Uddin, M.M. Rational sine-Gordon expansion method to analyze the dynamical behavior of the time-fractional Phi-four and (2+1)- dimensional CBS equations. Sci. Rep. 2024, 14, 9473. [Google Scholar] [CrossRef]
- Kumar, S.; Dhiman, S.K.; Baleanu, D.; Osman, M.S.; Wazwaz, A.M. Lie symmetries, closed-form solutions, and various dynamical profiles of solitons for the variable coefficient (2 + 1)-dimensional KP equations. Symmetry 2022, 14, 597. [Google Scholar] [CrossRef]
- Akinyemi, L.; Şenol, M.; Osman, M.S. Analytical and approximate solutions of nonlinear Schrödinger equation with higher dimension in the anomalous dispersion regime. J. Ocean Eng. Sci. 2022, 7, 143–154. [Google Scholar] [CrossRef]
- Umar, T.; Hosseini, K.; Kaymakamzade, B.; Boulaaras, S.; Osman, M.S. Hirota D-operator forms, multiple soliton waves, and other nonlinear patterns of a 2D generalized Kadomtsev–Petviashvili equation. Alex. Eng. J. 2024, 108, 999–1010. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, E.; Yuen, M. The Hopf-Cole transformation, topological solitons and multiple fusion solutions for the n-dimensional Burgers system. Phys. Lett. A 2016, 380, 9–14. [Google Scholar] [CrossRef]
- Tasnim, F.; Akbar, M.A.; Osman, M.S. The extended direct algebraic method for extracting analytical solitons solutions to the cubic nonlinear Schrödinger equation involving beta derivatives in space and time. Fractal Fract. 2023, 7, 426. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M. The improved F-expansion method with Riccati equation and its applications in mathematical physics. Cogent Math. 2017, 4, 1282577. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients. Cent. Eur. J. Eng. 2014, 4, 64–71. [Google Scholar] [CrossRef]
- Irshad, A.; Mohyud-Din, S.T.; Ahmed, N.; Khan, U. A new modification in simple equation method and its applications on nonlinear equations of physical nature. Results Phys. 2017, 7, 4232–4240. [Google Scholar] [CrossRef]
- Hasan, F.L. First integral method for constructing new exact solutions of the important nonlinear evolution equations in physics. J. Phys. Conf. Ser. 2020, 1530, 012109. [Google Scholar] [CrossRef]
- Elsaid, A. Adomian polynomials: A powerful tool for iterative methods of series solution of nonlinear equations. J. Appl. Anal. Comput. 2012, 2, 381–394. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, Y.; Li, S. Improved fractional subequation method and exact solutions to fractional partial differential equations. J. Funct. Spaces 2020, 2020, 5840920. [Google Scholar] [CrossRef]
- Liu, F.; Feng, Y. The modified generalized Kudryashov method for nonlinear space-time fractional partial differential equations of Schrödinger type. Results Phys. 2023, 53, 106914. [Google Scholar] [CrossRef]
- Bekir, A.; Guner, O.; Cevikel, A. The exp-function method for some time-fractional differential equations. IEEE/CAA J. Autom. Sin. 2017, 4, 315–321. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar]
- Bhalekar, S. Fractional Calculus: Theory and Applications, 1st ed.; Chaos in fractional order systems; Narosa Publishing House: New Delhi, India, 2013; Chapter 4. [Google Scholar]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, V.E. Remark to history of fractional derivatives on complex plane: Sonine-Letnikov and Nishimoto derivatives. Fract. Diff. Cal. 2016, 6, 147–149. [Google Scholar] [CrossRef]
- Luchko, Y. Fractional derivatives and the fundamental theorem of fractional calculus. Fract. Calc. Appl. Anal. 2020, 23, 939–966. [Google Scholar] [CrossRef]
- Jisha, C.R.; Jang, B. Novel insights into the exact solutions of the modified (3 + 1) dimensional fractional KS equation with variable coefficients. Nonlinear Dyn. 2024, 112, 7325–7345. [Google Scholar] [CrossRef]
- Mirzazadeh, M. Soliton solutions of Davey-Stewartson equation by trial equation method and ansatz approach. Nonlinear Dyn. 2015, 82, 1775–1780. [Google Scholar] [CrossRef]





| Solutions Obtained by the Present Study | Solutions Obtained by Samir et al. [1] |
|---|---|
. | |
. | |
. | |
. |
| Solutions Obtained by the Present Study | Solutions Obtained by Mirzazadeh [39] |
|---|---|
| No such solution found. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afridi, M.I.; Islam, T.; Akbar, M.A.; Osman, M.S. The Investigation of Nonlinear Time-Fractional Models in Optical Fibers and the Impact Analysis of Fractional-Order Derivatives on Solitary Waves. Fractal Fract. 2024, 8, 627. https://doi.org/10.3390/fractalfract8110627
Afridi MI, Islam T, Akbar MA, Osman MS. The Investigation of Nonlinear Time-Fractional Models in Optical Fibers and the Impact Analysis of Fractional-Order Derivatives on Solitary Waves. Fractal and Fractional. 2024; 8(11):627. https://doi.org/10.3390/fractalfract8110627
Chicago/Turabian StyleAfridi, Muhammad Idrees, Tamanna Islam, Md Ali Akbar, and Mohamed S. Osman. 2024. "The Investigation of Nonlinear Time-Fractional Models in Optical Fibers and the Impact Analysis of Fractional-Order Derivatives on Solitary Waves" Fractal and Fractional 8, no. 11: 627. https://doi.org/10.3390/fractalfract8110627
APA StyleAfridi, M. I., Islam, T., Akbar, M. A., & Osman, M. S. (2024). The Investigation of Nonlinear Time-Fractional Models in Optical Fibers and the Impact Analysis of Fractional-Order Derivatives on Solitary Waves. Fractal and Fractional, 8(11), 627. https://doi.org/10.3390/fractalfract8110627







