Riemann–Hilbert Method Equipped with Mixed Spectrum for N-Soliton Solutions of New Three-Component Coupled Time-Varying Coefficient Complex mKdV Equations

Abstract

This article extends the celebrated Riemann–Hilbert (RH) method equipped with mixed spectrum to a new integrable system of three-component coupled time-varying coefficient complex mKdV equations (ccmKdVEs for short) generated by the mixed spectral equations (msEs). Firstly, the ccmKdVEs and the msEs for generating the ccmKdVEs are proposed. Then, based on the msEs, a solvable RH problem related to the ccmKdVEs is constructed. By using the constructed RH problem with mixed spectrum, scattering data for the recovery of potential formulae are further determined. 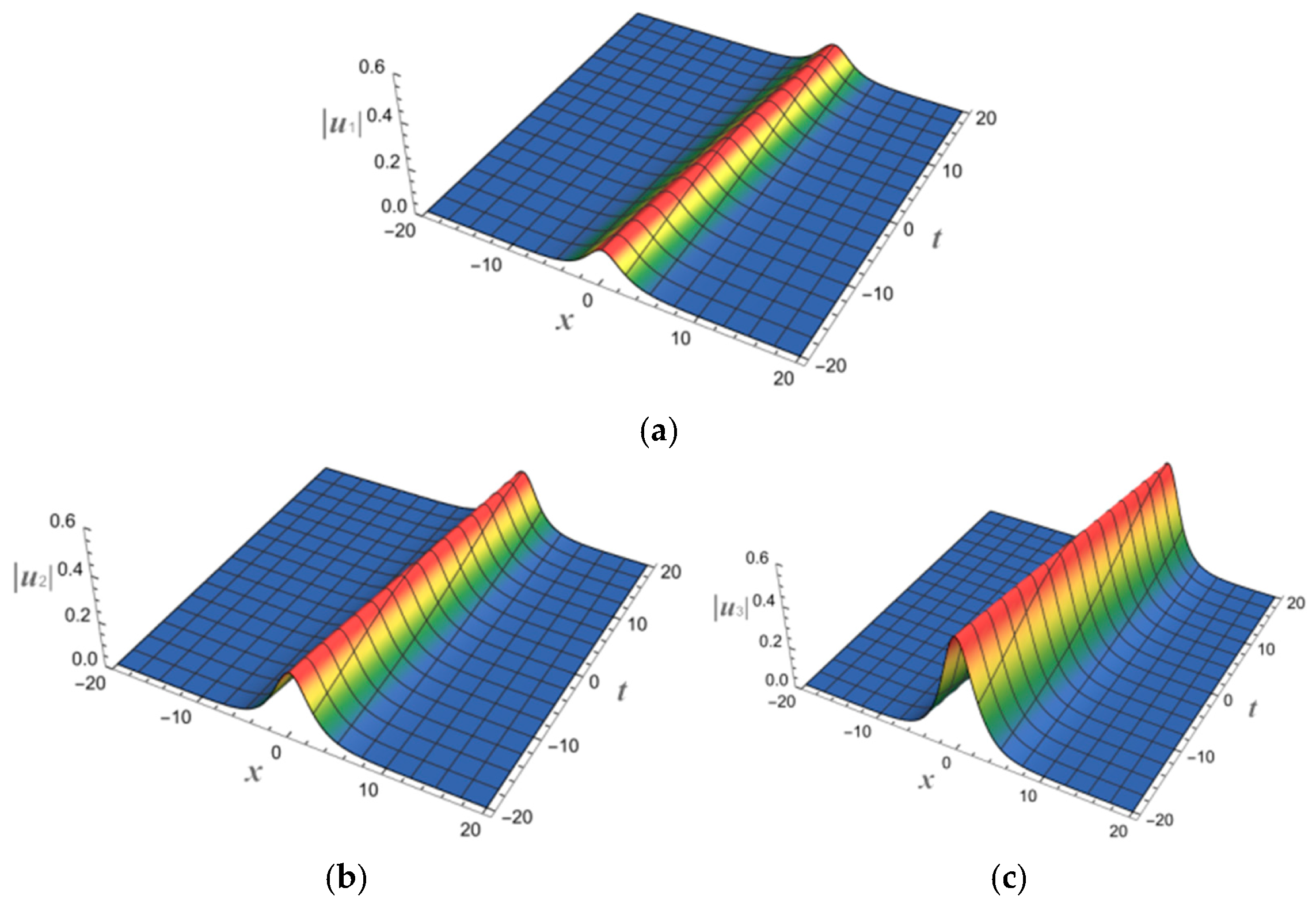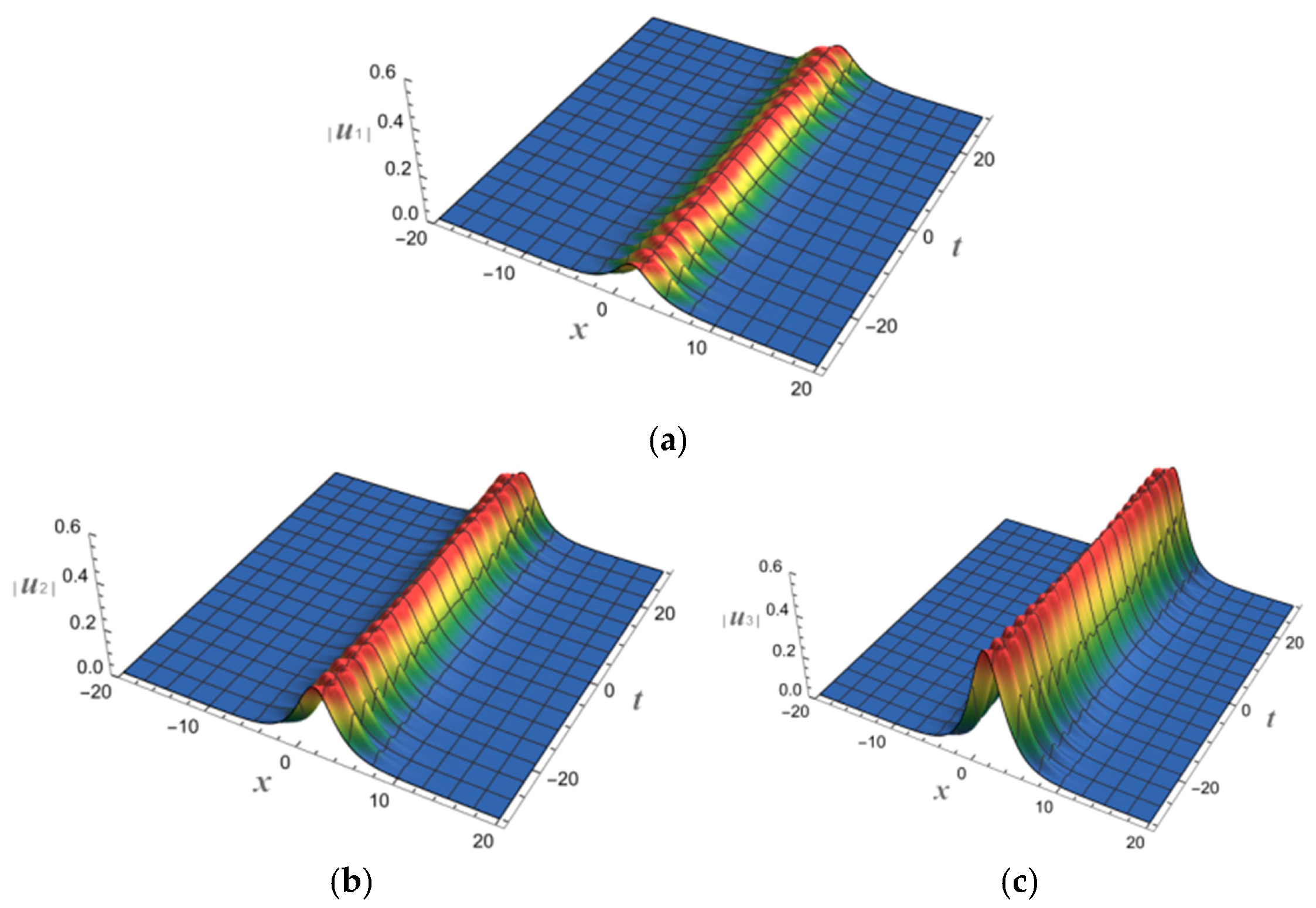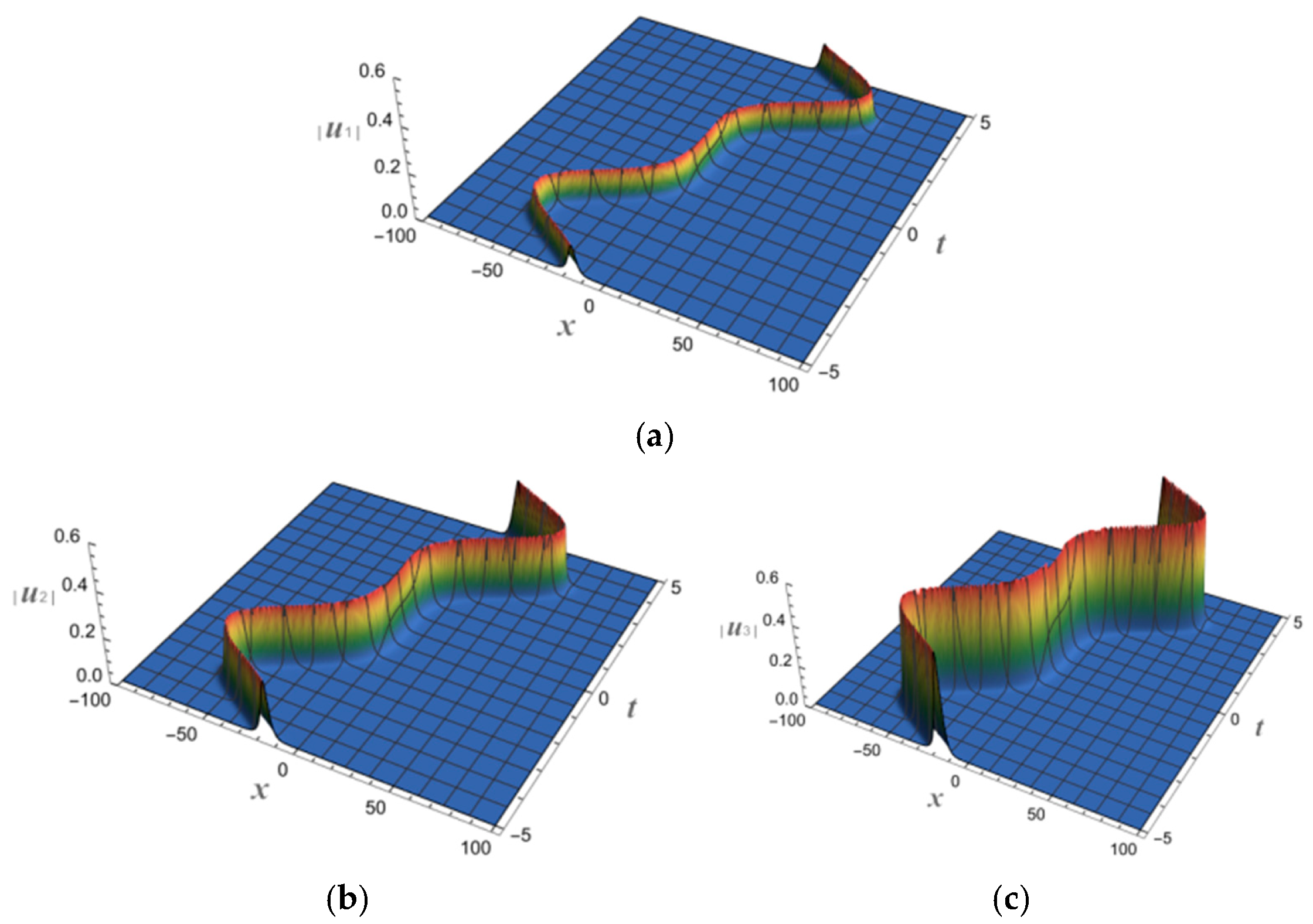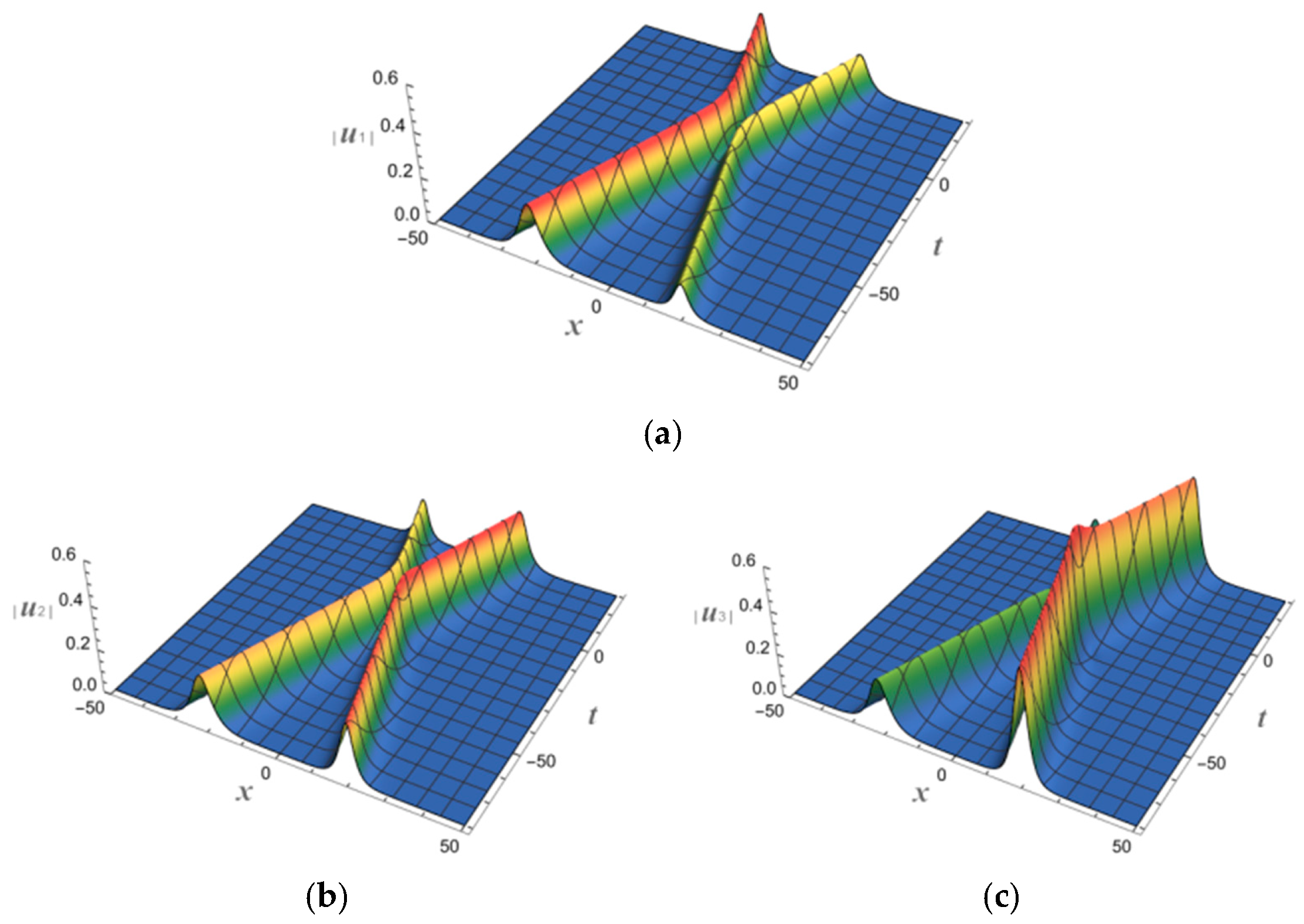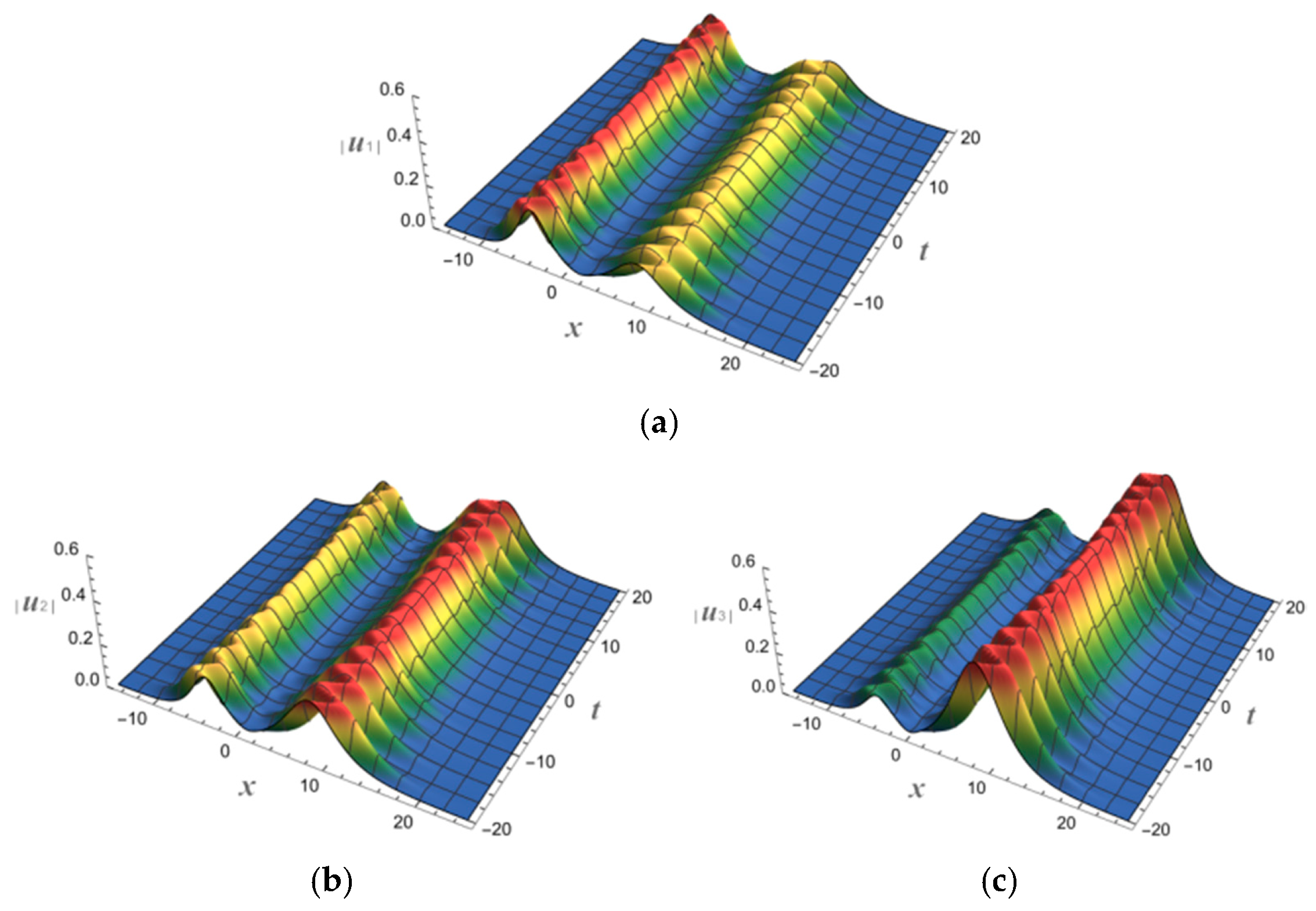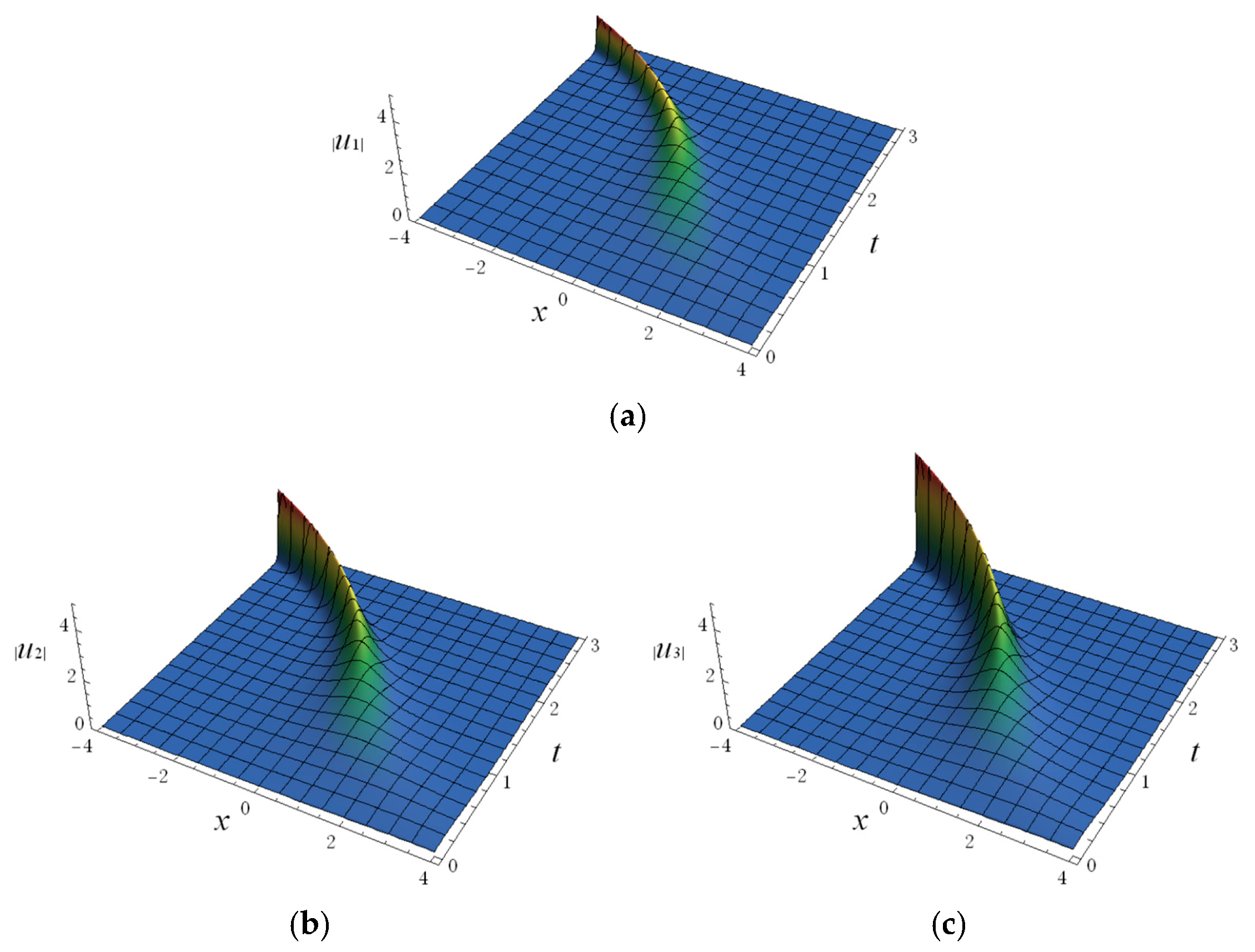In the case of reflectionless coefficients, explicit N-soliton solutions of the ccmKdVEs are ultimately obtained. Taking N equal to 1 and 2 as examples, this paper reveals that the spatiotemporal solution structures with time-varying nonlinear dynamic characteristics localized in the ccmKdVEs is attributed to the multiple selectivity of mixed spectrum and time-varying coefficients. 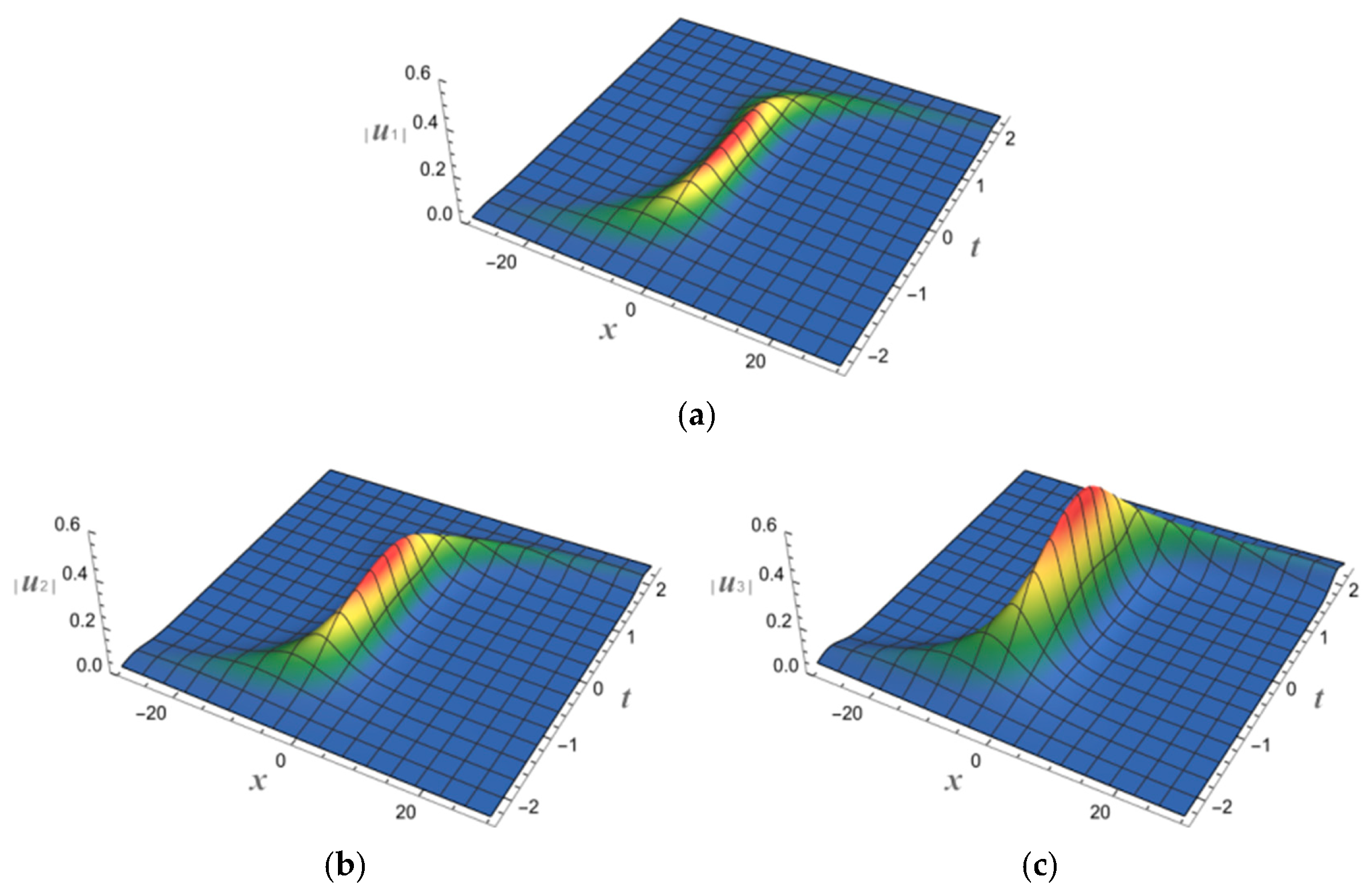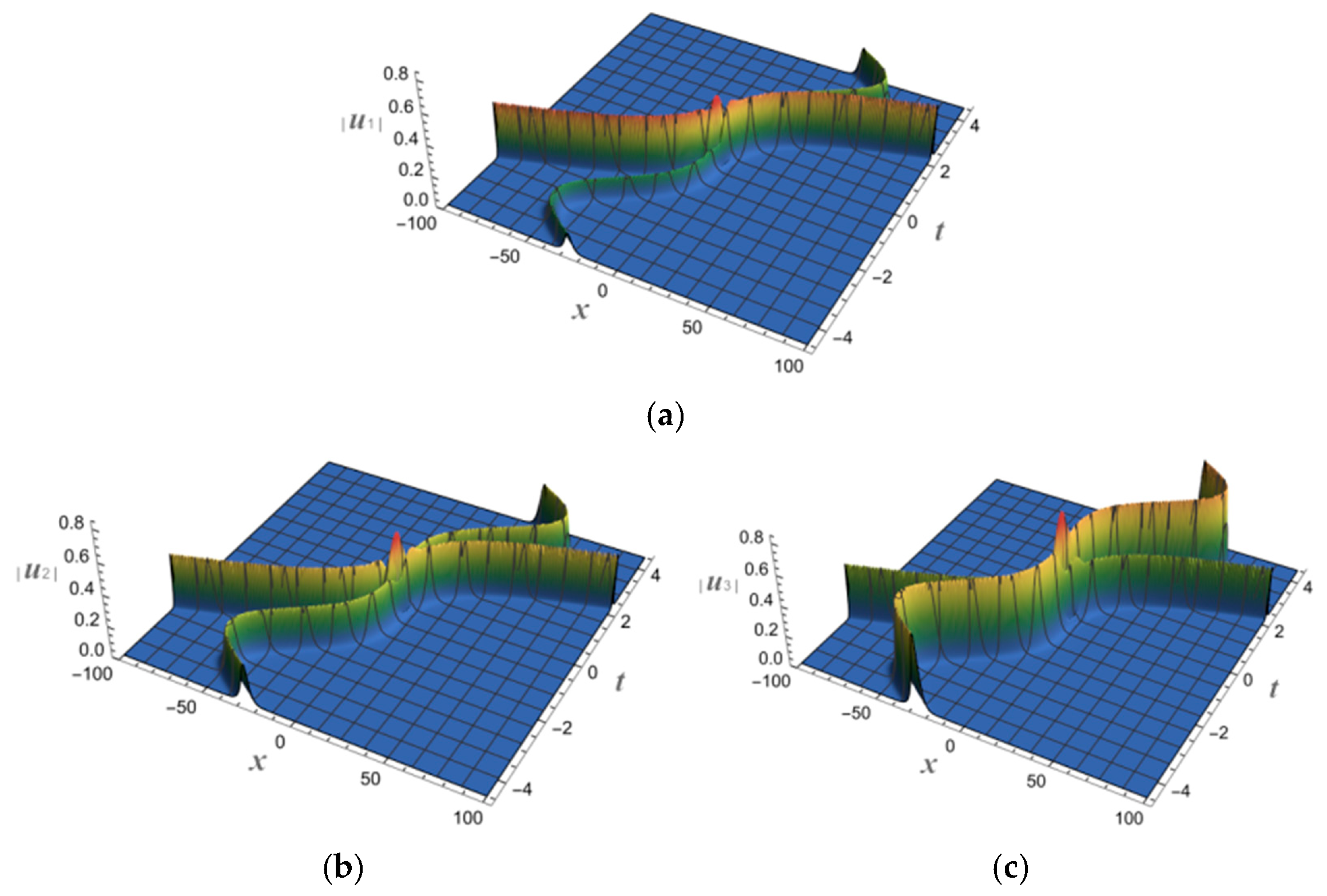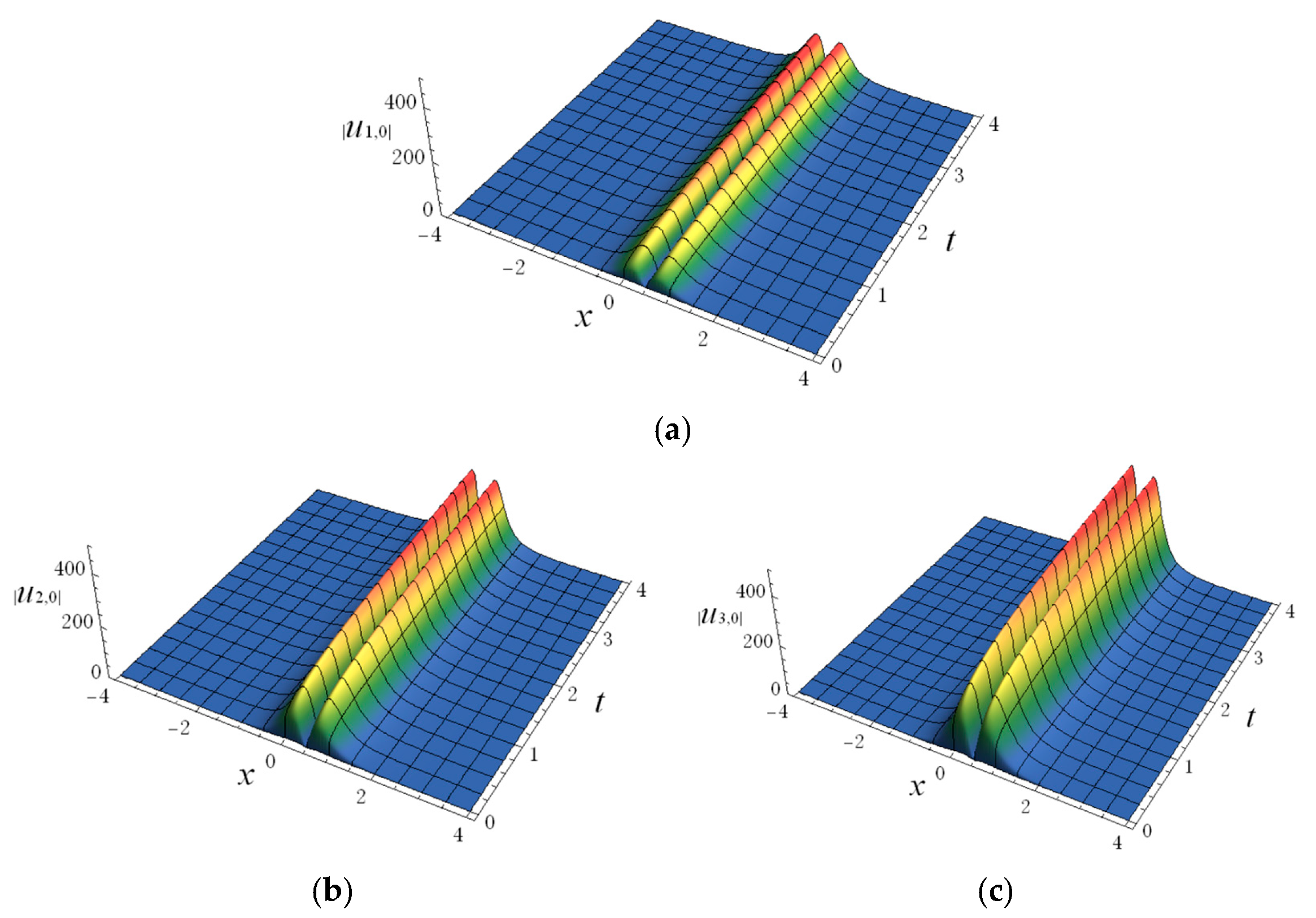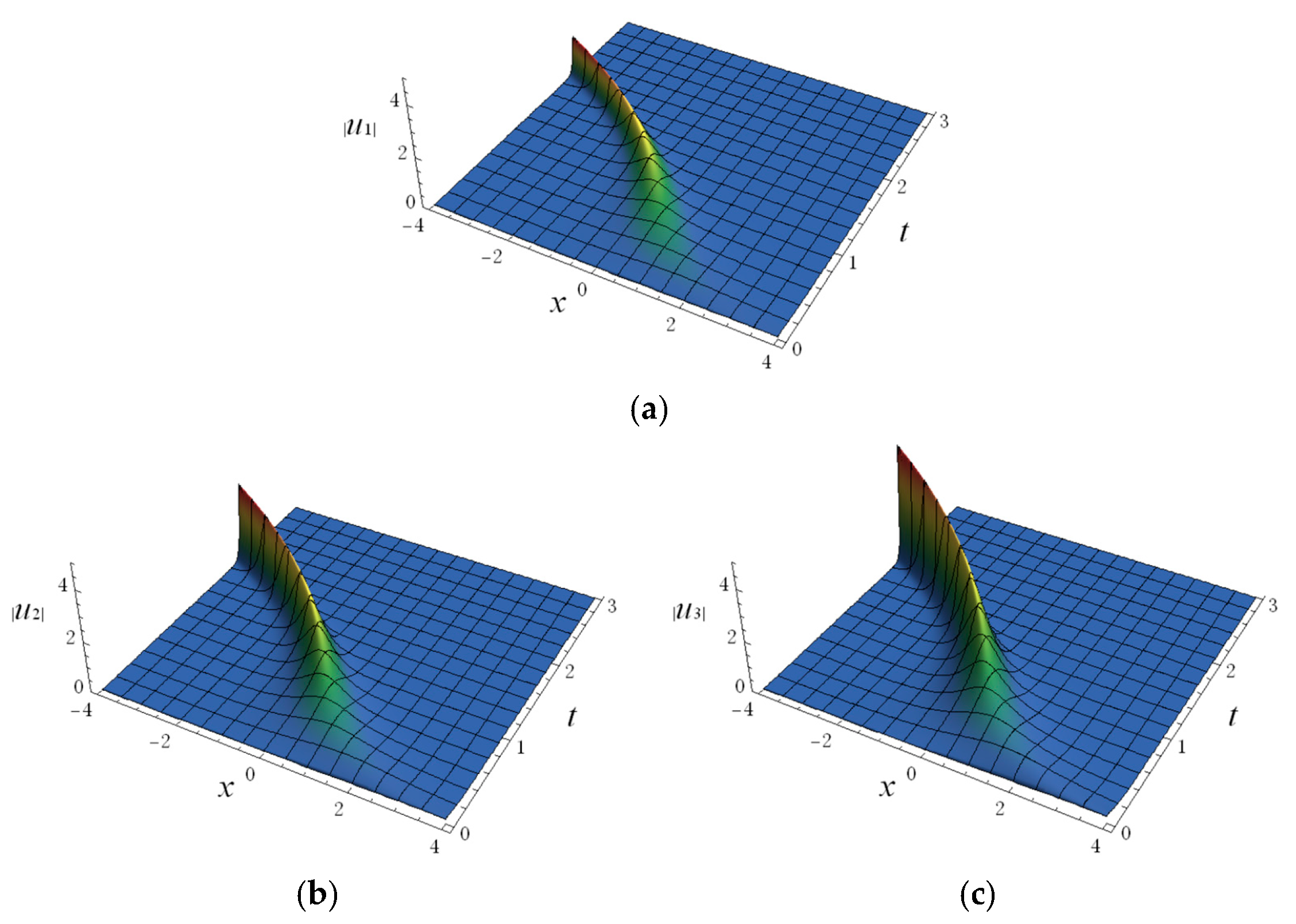In addition, to further highlight the application of our work in fractional calculus, by appropriately selecting these time-varying coefficients, the ccmKdVEs are transformed into a conformable time-fractional order system of three-component coupled complex mKdV equations. Based on the obtained one-soliton solutions, a set of initial values are assigned to the transformed fractional order system, and the N-th iteration formulae of approximate solutions for this fractional order system are derived through the variational iteration method (VIM).

1. Introduction

The RH method introduced in Yang’s monographs [1] has received much attention in recent years [2,3,4,5,6]. It is an analytical tool with complex analysis characteristics that originated from the classical inverse scattering transform (IST) in soliton theory [7] and gradually developed independently. Compared to the existing analytical methods such as Darboux transformation [8], Hirota bilinear method [9], simplified Hirota’s method [10,11,12], and others [13,14,15,16,17] in the same research field, the RH method, which benefited the pioneering contributions of Zakharov and Shabat [18], requires constructing a solvable RH problem that connects the solution of the initial value problem (IVP) of the nonlinear evolution equation being solved. It is worth mentioning that, based on the analysis of the RH problem that occurs in integrable systems, the nonlinear steepest descent method proposed by Deift and Zhou [19] provides a theoretical evaluation of the long-term asymptotic behavior of integrable equations in the sense of IST solvability.

Since the pioneering work [7] of Gardner, Greene, Kruskal and Miura, the scope of IST solvable systems has been extended from the isospectral KdV equation [20] to non-isospectral equations [21,22,23,24] and mixed spectral systems [25,26]. However, the models solved by the RH method are basically isospectral, such as [27,28,29,30,31]. There is little research on the RH method for variable-coefficient equations [32,33,34,35], and even fewer cases [36,37] of non-isospectral or mixed spectral equations. Throughout all the existing literature, we know that Chen, Zhang, and Ye [36] successfully solved a non-isospectral Gross–Pitaevskii equation in 2021 by extending the RH method, followed by Zhang and Zhou [37] solving the variable-coefficient mixed spectral complex mKdV equation in 2023. For all the isospectral equations with variable coefficients that have been studied by RH method, specifically, Li, Tian, Zhang, and Yang [32] obtained multi-soliton solutions containing distinct poles of arbitrary order to the fifth-order nonlinear Schrödinger equation (NLS); Xu and Zhang [33] derived N-soliton solutions of the generalized NLS equation; Zhou and Chen [34] gained high-order soliton solutions and analyzed their long-term asymptotic properties of the inhomogeneous Hirota equation; Ma, Li, Wang, Xie, and Du [35] constructed multi-soliton solutions and gave the corresponding asymptotic analysis for the coupled Lakshmanan–Porsezian–Daniel equations.

When the physical background of nonlinear waves is a non-uniform medium that is not suitable to be described by isospectral equations and constant-coefficient equations, researchers often associate it with non-isospectral equations or variable-coefficient equations. On the other hand, the multi-component coupled models have important applications. For example, as pointed out by Jiang and Qu [38], when describing nonlinear phenomena in fibers such as birefringence, arrays, and multimode, a single NLS equation appears insufficient, and the coupled NLS equations should be adopted to meet the interactions between field components caused by different frequencies or polarizations. Based on this practical background, this article proposes and studies the following ccmKdVEs:

$$u_{1,t}=\alpha (t)[u_{1,xxx}+6{\left|u_1\right|}^2{u}_{1,x}+3{(u_1{u}_2)}_x{u}_2^{\ast }+3{(u_1{u}_3)}_x{u}_3^{\ast }]+\beta (t)(u_1+x{u}_{1,x})-i\delta (t)x{u}_1-i\gamma (t)u_1,$$

(1)

$$u_{2,t}=\alpha (t)[u_{2,xxx}+6{\left|u_2\right|}^2{u}_{2,x}+3{(u_1{u}_2)}_x{u}_1^{\ast }+3{(u_2{u}_3)}_x{u}_3^{\ast }]+\beta (t)(u_2+x{u}_{2,x})-i\delta (t)x{u}_2-i\gamma (t)u_2,$$

(2)

$$u_{3,t}=\alpha (t)[u_{3,xxx}+6{\left|u_3\right|}^2{u}_{3,x}+3{(u_1{u}_3)}_x{u}_1^{\ast }+3{(u_2{u}_3)}_x{u}_2^{\ast }]+\beta (t)(u_3+x{u}_{3,x})-i\delta (t)x{u}_3-i\gamma (t)u_3,$$

(3)

where $u_j=u_j(x,t)$ assigned with values $j=1,2,3$ are all the complex functions related to the spatiotemporal independent variables contained within them. Furthermore, when $\left|x\right|\to \infty$, it is assumed that $u_j$, along with all its partial derivatives, quickly decays to zero. Besides, $\alpha (t)$, $\beta (t)$, $\gamma (t)$, and $\delta (t)$ are real valued functions. In the case of $u_2=0$ and $u_3=0$, Equations (1)–(3) degenerate to the complex mKdV equation [37]:

$$u_{1,t}=\alpha (t)(u_{1,xxx}+6{\left|u_1\right|}^2{u}_{1,x})+\beta (t)(u_1+x{u}_{1,x})-i\delta (t)x{u}_1-i\gamma (t)u_1.$$

(4)

The prototype model of Equation (4) is the known complex mKdV equation [39]:

$$u_t+u_{xxx}+6{\left|u\right|}^2{u}_x=0,$$

(5)

which helps to characterize the nonlinear wave propagation of short pulses in optical fibers [39,40,41]. It is obvious that a special case of Equation (5) gives the famous mKdV equation [42]:

$$u_t+u_{xxx}+6u^2{u}_x=0,$$

(6)

whose extensive applications [43] are not limited to ocean dynamics but also encompass traffic flow, size quantized films, and so on.

In many fields, fractal and fractional calculus have attached much attention [44,45,46,47,48]. Besides the non-isospectral or variable-coefficient equations, it has been shown [49,50,51] that fractional differential equations are also suitable for descripting the nonlinear dynamics in non-uniform physical backgrounds, such as fractal and porous materials. As an application of the ccmKdVEs (1)–(3) and their soliton solutions to be obtained, in this paper, we will reduce a fractional order system from Equations (1)–(3) and use the VIM method to derive the N-th iteration formulae of approximate solutions.

The structure arrangement of the remaining part of this article is as follows. In Section 2, we propose the Lax pair of the ccmKdVEs (1)–(3) and establish the relevant RH problem. In Section 3, we determine the time-dependences of scattering data in the relevant RH problem. In Section 4, we derive N-soliton solutions of the ccmKdVEs (1)–(3) by considering the case of reflectionless coefficients. Besides, the spatiotemporal structures of one- and two-soliton solutions reveal the dominant roles of mixed spectrum and time-varying coefficients on the time-varying nonlinear dynamic characteristics localized in the ccmKdVEs (1)–(3). In Section 5, we select appropriate time-varying coefficients to reduce a conformable time-fractional order system from the ccmKdVEs (1)–(3) and obtain its N-th iteration formulae of approximate solutions. In Section 6, we address the conclusion of this article.

2. Lax Pair and the Relevant RH Problem

Firstly, we propose in this section the Lax pair of the ccmKdVEs (1)–(3) as follows:

$${\zeta }_x+i\eta \Lambda \zeta =P\zeta ,\Lambda =\mathrm{diag}(1,-1,-1,-1),$$

(7)

$${\zeta }_t-i\{4{\eta }^3\alpha (t)-[\eta \beta (t)+\frac{1}{2}\delta (t)]x-\frac{1}{2}\gamma (t)\}\Lambda \zeta =Q\zeta ,$$

(8)

where $\zeta =\zeta (x,t,\eta )$ is the eigenfunction, and $\eta$ determines the mixed spectral parameter by the following:

$$\frac{d\eta }{dt}=\eta \beta (t)+\frac{1}{2}\delta (t),$$

(9)

while $P$ and $Q$ are two auxiliary matrices:

$$P=\left(\begin{array}{cccc}0& u_1& u_2& u_3\\ -u_1^{\ast }& 0& 0& 0\\ -u_2^{\ast }& 0& 0& 0\\ -u_3^{\ast }& 0& 0& 0\end{array}\right),$$

(10)

$$Q=\eta \alpha (t)[2i\Lambda (P^2-P_x)-4\eta P]+\alpha (t)(P_{xx}+P{P}_x-P_{x}P-2P^3)+\beta (t)xP.$$

(11)

Due to $u_j$ and all its partial derivatives quickly decaying to zero when $\left|x\right|\to \infty$, as previously assumed, we can gain the Jost solution of Lax pair (7) and (8):

$$\zeta =e^{-\Lambda \varphi },\left|x\right|\to \infty ,$$

(12)

where

$$\varphi =i\{\eta x-{\displaystyle {\int }_0^t[4\alpha (\tau ){\eta }^3(\tau )}-\frac{1}{2}\gamma (\tau )]d\tau \}.$$

(13)

We adopt a transformation in the following form:

$$K=\zeta e^{\Lambda \varphi },$$

(14)

then one has the following:

$$K\to I,\left|x\right|\to \infty ,$$

(15)

where $I$ is the $4\times 4$ identity matrix.

Substitute Equation (14) into Equations (7) and (8), and then rewrite the resulting expressions as follows:

$$K_x+i\eta [\Lambda ,K]=PK,$$

(16)

$$K_t-i\{4{\eta }^3\alpha (t)-[\eta \beta (t)+\frac{1}{2}\delta (t)]x-\frac{1}{2}\gamma (t)\}[\Lambda ,K]=QK.$$

(17)

By integrating Equation (16) through two different pathways, $(x,t)\to (-\infty ,t)$ and $(x,t)\to (+\infty ,t)$, we can obtain the following:

$$K_{-}=I+{\displaystyle {\int }_{-\infty }^x{e}^{-i\eta (x-y)\Lambda }P(y,t,\eta )K_{-}(y,t,\eta )e^{i\eta (x-y)\Lambda }dy,}$$

(18)

$$K_{+}=I-{\displaystyle {\int }_x^{+\infty }{e}^{-i\eta (x-y)\Lambda }P(y,t,\eta )K_{-}(y,t,\eta )e^{i\eta (x-y)\Lambda }dy.}$$

(19)

With the help of $\Omega =e^{i\Lambda \eta x}$, we set ${\xi }_1=K_{-}\Omega$ and ${\xi }_2=K_{+}\Omega$. Then, it is not difficult to check that the matrices ${\xi }_1$ and ${\xi }_2$ satisfy the Lax pair (7) and (8), and they can be connected by the scattering matrix $S(\eta )$ as follows:

$${\xi }_1={\xi }_{2}S(\eta ),$$

(20)

where

$$S(\eta )=\left(\begin{array}{cccc}{s}_{11}(\eta )& s_{12}(\eta )& s_{13}(\eta )& s_{14}(\eta )\\ s_{21}(\eta )& s_{22}(\eta )& s_{23}(\eta )& s_{24}(\eta )\\ s_{31}(\eta )& s_{32}(\eta )& s_{33}(\eta )& s_{34}(\eta )\\ s_{41}(\eta )& s_{42}(\eta )& s_{43}(\eta )& s_{44}(\eta )\end{array}\right).$$

(21)

By using Abel’s identity and the fact that the trace of $P$ is equal to zero, we can prove that $\det K_{\pm }=1$ [1] always holds for all $x$. Then, from Equation (20), one obtains $\det S(\eta )=1$. This ensures that the inverse matrices of $K_{\pm }$ and $S(\eta )$ both exist. Meanwhile, $K_{\pm }$ and $S(\eta )$ have the following symmetry properties [1]:

$$K_{\pm }^H(x,t,{\eta }^{*})=K_{\pm }^{-1}(x,t,\eta ),S^H({\eta }^{*})=S^{-1}(\eta ),$$

(22)

under the Hermitian transformation $H$. For convenience, we assume the following:

$$S^{-1}(\eta )=\left(\begin{array}{cccc}{\widehat{s}}_{11}(\eta )& {\widehat{s}}_{12}(\eta )& {\widehat{s}}_{13}(\eta )& {\widehat{s}}_{14}(\eta )\\ {\widehat{s}}_{21}(\eta )& {\widehat{s}}_{22}(\eta )& {\widehat{s}}_{23}(\eta )& {\widehat{s}}_{24}(\eta )\\ {\widehat{s}}_{31}(\eta )& {\widehat{s}}_{32}(\eta )& {\widehat{s}}_{33}(\eta )& {\widehat{s}}_{34}(\eta )\\ {\widehat{s}}_{41}(\eta )& {\widehat{s}}_{42}(\eta )& {\widehat{s}}_{43}(\eta )& {\widehat{s}}_{44}(\eta )\end{array}\right).$$

(23)

Then, the relationship $s_{11}^{*}({\eta }^{*})={\widehat{s}}_{11}(\eta )$ can be derived from the second expression of Equation (22).

By utilizing Equations (18) and (19), we have the following:

$$e^{-i\eta (x-y)\Lambda }P(y,t,\eta )e^{i\eta (x-y)\Lambda }=\left(\begin{array}{cccc}0& u_1{e}^{-2i\eta (x-y)}& u_2{e}^{-2i\eta (x-y)}& u_3{e}^{-2i\eta (x-y)}\\ -u_1^{\ast }{e}^{2i\eta (x-y)}& 0& 0& 0\\ -u_2^{\ast }{e}^{2i\eta (x-y)}& 0& 0& 0\\ -u_3^{\ast }{e}^{2i\eta (x-y)}& 0& 0& 0\end{array}\right).$$

(24)

We divide the matrices $K_{-}$, $K_{+}$, $K_{-}^{-1}$ and $K_{+}^{-1}$ into blocks:

$$K_{-}=({[K_{-}]}^1,{[K_{-}]}^2,{[K_{-}]}^3,{[K_{-}]}^4),$$

(25)

$$K_{+}=({[K_{+}]}^1,{[K_{+}]}^2,{[K_{+}]}^3,{[K_{+}]}^4),$$

(26)

$$K_{-}^{-1}=\left(\begin{array}{c}{[K_{-}^{-1}]}^1\\ {[K_{-}^{-1}]}^2\\ {[K_{-}^{-1}]}^3\\ {[K_{-}^{-1}]}^4\end{array}\right),K_{+}^{-1}=\left(\begin{array}{c}{[K_{+}^{-1}]}^1\\ {[K_{+}^{-1}]}^2\\ {[K_{+}^{-1}]}^3\\ {[K_{+}^{-1}]}^4\end{array}\right),$$

(27)

where ${[K_{\pm }]}^j$ and ${[K_{\pm }^{-1}]}^j$, $j=1,2,3,4$, are the corresponding column and row vectors.

In order to construct the relevant RH problem, we define two matrices $X^{+}$ and $X^{-}$ as follows:

$$X^{+}=({[K_{-}]}^1,{[K_{+}]}^2,{[K_{+}]}^3,{[K_{+}]}^4)=K_{-}{D}_1+K_{+}{D}_2,$$

(28)

$$X^{-}=\left(\begin{array}{c}{[K_{+}^{-1}]}^1\\ {[K_{-}^{-1}]}^2\\ {[K_{-}^{-1}]}^3\\ {[K_{-}^{-1}]}^4\end{array}\right)=D_1{K}_{-}^{-1}+D_2{K}_{+}^{-1}.$$

(29)

where $D_1=\mathrm{diag}(1,0,0,0)$ and $D_2=\mathrm{diag}(0,1,1,1)$.

In view of Equation (24), we can verify that $X^{+}$ and $X^{-}$ have the properties of analytic extension to the upper half plane $\eta \in C_{+}$ and lower half plane $\eta \in C_{-}$, respectively. In this way, when $\eta \in C_{\pm }\to \infty$, the asymptotic property of $X^{\pm }\to I$ is supported. We thus reach the RHP problem established as below:

(a) $X^{+}(x,t,\eta )$ and $X^{-}(x,t,\eta )$ are analytic in $\eta \in {ℂ}_{+}$ and $\eta \in C_{-}$, respectively;

(b)

$$X^{-}(x,t,\eta )X^{+}(x,t,\eta )=J(x,t,\eta );$$

(30)

(c) $X^{\pm }\to I$, when $\eta \in C_{\pm }\to \infty$;

with the use of jump matrix $J(x,t,\eta )$:

$$J(x,t,k)=\Omega (D_1+D_{2}S)(D_1+S^{-1}{D}_2){\Omega }^{-1}=\Omega \left(\begin{array}{cccc}1& {\widehat{s}}_{12}(\eta )& {\widehat{s}}_{13}(\eta )& {\widehat{s}}_{14}(\eta )\\ s_{21}(\eta )& 1& 0& 0\\ s_{31}(\eta )& 0& 1& 0\\ s_{41}(\eta )& 0& 0& 1\end{array}\right){\Omega }^{-1}.$$

(31)

By using Equations (15), (28) and (29), the following can be concluded:

$$X_x^{+}+i\eta [\Lambda ,X^{+}]=P{X}^{+},$$

(32)

$$X_x^{-}+i\eta [\Lambda ,X^{-}]=P{X}^{-}.$$

(33)

Further implementation of Taylor expansion on $X^{\pm }$ can yield the following:

$$X^{\pm }=X_0^{\pm }+\frac{1}{\eta }{X}_1^{\pm }+O(\frac{1}{{\eta }^2}),\eta \to \infty .$$

(34)

Substituting Equation (34) into Equation (32) and comparing the same power coefficients of $\eta$ in the resulting equation yields the following:

$$O(\eta ):i[\Lambda ,X_0]=0,$$

(35)

$$O({\eta }^0):X_{0,x}^{\pm }+i[\Lambda ,X_1^{\pm }]=P{X}_0^{\pm }.$$

(36)

Then, it is easy to see from Equations (35) and (36) that $X_0^{\pm }=I$ and the following results:

$$u_1=2i{(X_1^{+})}_{12}=2i\underset{\eta \to \infty }{\lim }\eta {(X^{+})}_{12},$$

(37)

$$u_2=2i{(X_1^{+})}_{13}=2i\underset{\eta \to \infty }{\lim }\eta {(X^{+})}_{13},$$

(38)

$$u_3=2i{(X_1^{+})}_{14}=2i\underset{\eta \to \infty }{\lim }\eta {(X^{+})}_{14}.$$

(39)

3. Solvability of Relevant RH Problem and Time-Dependences of Scattering Data

Due to the use of $\Omega =e^{i\Lambda \eta x}$ as mentioned earlier and the obvious results $\Omega D_1{\Omega }^{-1}=D_1$ and $\Omega D_2{\Omega }^{-1}=D_2$, the following two determinants are easy to obtain:

$$\det (X^{+})=\det (K_{-}{D}_1+K_{+}{D}_2)=s_{11}(\eta ),$$

(40)

$$\det (X^{-})=\det (D_1{K}_{-}^{-1}+D_2{K}_{+}^{-1})={\widehat{s}}_{11}(\eta )=s_{11}^{*}({\eta }^{*}).$$

(41)

Theorem 1. 

Regardless of whether it is the regular case at  $\det (X^{\pm })\ne 0$ or the non-regular case at  $\det (X^{\pm })=0$ , the relevant RH problem (30) always has a unique solution.

Proof of Theorem 1. 

The specific proof is similar to the proofs in [1,2], except that $X^{\pm }$ are four-component, see Equations (28) and (29), rather than two-component [2], but the embedded $\eta$ related to the corresponding spectral parameter is a mixed spectrum that satisfies Equation (9) rather than an isospectral case [1]. For the regular case, i.e., $\det (X^{\pm })\ne 0$, the formula proposed by Plemlj [52] help us to obtain a unique solution [1] of the RH problem (30):

$${(X^{+})}^{-1}(\eta )=I+\frac{1}{2\pi i}{\displaystyle {\int }_{-\infty }^{+\infty }\frac{(I-J)(s){(X^{+})}^{-1}(s)}{s-\eta }ds},\eta \in C_{+}.$$

(42)

Next, we consider the non-regular RH problem (30) when $\det (X^{\pm })=0$. The following can be seen from Equations (40) and (41):

$$\det (X^{+})=s_{11}(\eta )=s_{11}^{*}({\eta }^{*})=\det (X^{-})=0,$$

(43)

$$s_{11}(\eta )=s_{11}({\eta }^{*})=0.$$

(44)

Consequently, we know that $\det X^{+}(\eta )$ and $\det X^{-}(\eta )$ have the same number of conjugate zeros, denoted as $\{{\eta }_j\in C_{+};j=1,2,\cdots ,N\}$ and $\{{\eta }_j^{\ast }\in C_{-};j=1,2,\cdots ,N\}$, respectively.

For any integer $j\in \{1,2,\cdots ,N\}$, considering the following linear algebraic equations:

$$X^{+}({\eta }_j)v_j({\eta }_j)=0,$$

(45)

$$v_j^{\ast }({\eta }_j^{*})X^{-}({\eta }_j^{*})=0,$$

(46)

and noting the fact $\det X^{\pm }({\eta }_j)=0$, we can see that in Equations (45) and (46) exist non-zero column and row vector solutions $v_j$ and $v_j^{\ast }$, respectively. From Equations (22), (28) and (29), we obtain the following:

$${(X^{\pm })}^H(x,t,{\eta }^{\ast })=(X^{\mp })(x,t,\eta ),$$

(47)

which supports the relationship $v_j^H({\eta }_j)=v_j^{*}({\eta }_j^{*})$ by taking the conjugate of Equation (46) and transposing it simultaneously.

Furthermore, the conclusion [1] that the non-regular RH problem (30) can be converted into a regular case ensures the existence of a unique solution:

$$X_1^{+}(\eta )={\displaystyle \sum _{l,j=1}^N{v}_l{(Z^{-1})}_{lj}{v}_j^{\ast }+\frac{1}{2\pi i}{\displaystyle {\int }_{-\infty }^{+\infty }P(s)(I-J)(s)P^{-1}(s){({\widehat{X}}^{+})}^{-1}}(s)ds},$$

(48)

which supports Equations (38)–(40) for obtaining solution of the ccmKdVEs (1)–(3), with the help of the following notations:

$${({\widehat{X}}^{+})}^{-1}(\eta )=I+\frac{1}{2\pi i}{\displaystyle {\int }_{-\infty }^{+\infty }\frac{P(s)(I-J)(s){({\widehat{X}}^{+})}^{-1}(s)}{s-\eta }ds},\eta \in C,$$

(49)

$$P(\eta )=I+{\displaystyle \sum _{l,j=1}^N\frac{v_l{(Z^{-1})}_{lj}{v}_j^{*}}{\eta -{\eta }_j^{*}}},$$

(50)

$$P^{-1}(\eta )=I-{\displaystyle \sum _{l,j=1}^N\frac{v_l{(Z^{-1})}_{lj}{v}_j^{*}}{\eta -{\eta }_l}},$$

(51)

$$Z={(z_{lj})}_{N\times N},z_{lj}=\frac{v_l^{*}{v}_j}{{\eta }_l^{*}-{\eta }_j}.$$

(52)

□

Theorem 2. 

In the absence of reflection coefficients, the time-dependences of scattering data:

$$\{k_j,k_j^{*},v_j,v_j^{*};j=1,2,\cdots ,N\},$$

(53)

have the following explicit forms:

$${\eta }_j=e^{{\displaystyle {\int }_0^t\beta (\tau )d\tau }}[{\eta }_j(0)+\frac{1}{2}{\displaystyle {\int }_0^t\delta (\tau )e^{-{\displaystyle {\int }_0^{\tau }\beta (\omega )d\omega }}d\tau }],$$

(54)

$${\eta }_j^{*}=e^{{\displaystyle {\int }_0^t\beta (\tau )d\tau }}[{\eta }_j^{*}(0)+\frac{1}{2}{\displaystyle {\int }_0^t\delta (\tau )e^{-{\displaystyle {\int }_0^{\tau }\beta (\omega )d\omega }}d\tau }],$$

(55)

$$v_j(x,t,{\eta }_j)=e^{-i\Lambda \{{\eta }_{j}x-{\displaystyle {\int }_0^t[4{\eta }_j^3(\tau )\alpha (\tau )-\frac{1}{2}\gamma (\tau )]d\tau \}}}{v}_{j,0},$$

(56)

$$v_j^{*}(x,t,{\eta }_j^{*})=v_{j,0}^{*}{e}^{i\Lambda \{{\eta }_j^{*}x-{\displaystyle {\int }_0^t[4{\eta }_j^{*3}(\tau )\alpha (\tau )-\frac{1}{2}\gamma (\tau )]d\tau \}}},$$

(57)

where  ${\eta }_j(0)$ and  ${\eta }_j^{*}(0)$ are arbitrary complex constants,  $v_{j,0}$ is a four-dimensional constant column vector.

Proof of Theorem 2. 

To determine the time-dependences of $v_j$ and $v_j^{*}$, we take the partial derivatives of Equation (45) about $t$ and $x$, and then arrive at the following:

$$X_x^{+}{v}_j+X^{+}{v}_{j,x}=0,$$

(58)

$$X_t^{+}{v}_j+X^{+}{v}_{j,t}=0.$$

(59)

From Equations (13), (14) and (29) we obtain the following:

$$X_x^{+}=-i{\eta }_j[\Lambda ,X^{+}]+P{X}^{+},$$

(60)

$$X_t^{+}=Q{X}^{+}+i\{4{\eta }_j^3\alpha (t)-[{\eta }_j\beta (t)+\frac{\delta (t)}{2}]x-\frac{1}{2}\gamma (t)\}[\Lambda ,X^{+}].$$

(61)

Inserting Equation (60) into Equation (61) yields the following:

$$X^{+}(v_{j,x}+i{\eta }_j\Lambda v_j)=0.$$

(62)

Similarly, substituting Equation (61) into Equation (59) we obtain the following:

$$X^{+}(v_{j,t}-i\{4{\eta }_j^3\alpha (t)-[{\eta }_j\beta (t)+\frac{\delta (t)}{2}]x-\frac{1}{2}\gamma (t)\}\Lambda v_j)=0.$$

(63)

Thus, from Equations (62) and (63) we gain the following:

$$v_{j,x}+i{\eta }_j\Lambda v_j=0,$$

(64)

$$v_{j,t}-i\{4{\eta }_j^3\alpha (t)-[{\eta }_j\beta (t)+\frac{\delta (t)}{2}]x-\frac{i}{2}\gamma (t)\}\Lambda v_j=0.$$

(65)

By solving Equations (64) and (65), we can reach Equation (56). Additionally, the establishment of Equation (57) is confirmed by using the relationship $v_j^H({\eta }_j)=v_j^{\ast }({\eta }_j^{\ast })$.

As for the time-dependences of ${\eta }_j$ and ${\eta }_j^{*}$, we consider Equation (9) with the discrete spectrum ${\eta }_j$:

$$\frac{d{\eta }_j}{dt}={\eta }_j\beta (t)+\frac{1}{2}\delta (t).$$

(66)

Then, Equations (54) and (55) can be derived from Equation (66) and its conjugate form. It should be noted that Equation (66) and its conjugate form also solve Equations (64) and (65). □

4. N-Soliton Solutions and Their Spatial Structures

Under the case of reflectionless coefficients, that is, $s_{21}=s_{31}=s_{41}=0$ and ${\widehat{s}}_{12}={\widehat{s}}_{13}={\widehat{s}}_{14}=0$, it can be seen from Equation (31) that $J=I$. In this case, Equation (48) degenerates to the following:

$$X_1^{+}(\eta )={\displaystyle \sum _{l,j=1}^N{v}_l{(Z^{-1})}_{lj}{v}_j^{*}}.$$

(67)

Therefore, Equations (37)–(39) become the following:

$$u_1=2i{\left({\displaystyle \sum _{l,j=1}^N{v}_l{(Z^{-1})}_{lj}{v}_j^{*}}\right)}_{12},$$

(68)

$$u_2=2i{\left({\displaystyle \sum _{l,j=1}^N{v}_l{(Z^{-1})}_{lj}{v}_j^{*}}\right)}_{13},$$

(69)

$$u_3=2i{\left({\displaystyle \sum _{l,j=1}^N{v}_l{(Z^{-1})}_{lj}{v}_j^{*}}\right)}_{14}.$$

(70)

When we further take $v_{j,0}={(1,a_j,b_j,c_j)}^T$ combined with complex constants $a_j$, $b_j$ and $c_j$, Equations (56) and (57) can provide the following:

$$v_j=\left(\begin{array}{c}{e}^{-{\varphi }_j}\\ a_j{e}^{{\varphi }_j}\\ b_j{e}^{{\varphi }_j}\\ c_j{e}^{{\varphi }_j}\end{array}\right),$$

(71)

$$v_j^{*}=(e^{-{\varphi }_j^{*}},a_j^{*}{e}^{{\varphi }_j^{*}},b_j^{*}{e}^{{\varphi }_j^{*}},c_j^{*}{e}^{{\varphi }_j^{*}}),$$

(72)

where ${\varphi }_j=i\{{\eta }_{j}x-{\displaystyle {\int }_0^t[4{\eta }_j^3(\tau )\alpha (\tau )-\gamma (\tau )/2]d\tau \}}$.

Finally, we can obtain N-soliton solutions of the ccmKdVEs (1)–(3) as follows:

$$u_1=-2i\frac{\det R_1}{\det Z},$$

(73)

$$u_2=-2i\frac{\det R_2}{\det Z},$$

(74)

$$u_3=-2i\frac{\det R_3}{\det Z},$$

(75)

where $R_1$, $R_2$, and $R_3$ are three $(N+1)\times (N+1)$ matrices:

$$R_1=\left(\begin{array}{cccc}0& e^{-{\varphi }_1}& \cdots & e^{-{\varphi }_N}\\ a_1{e}^{{\varphi }_1^{*}}& z_{11}& \cdots & z_{1N}\\ ⋮& ⋮& \ddots & ⋮\\ a_N{e}^{{\varphi }_N^{*}}& z_{N1}& \cdots & z_{NN}\end{array}\right),$$

(76)

$$R_2=\left(\begin{array}{cccc}0& e^{-{\varphi }_1}& \cdots & e^{-{\varphi }_N}\\ b_1{e}^{{\varphi }_1^{*}}& z_{11}& \cdots & z_{1N}\\ ⋮& ⋮& \ddots & ⋮\\ b_N{e}^{{\varphi }_N^{*}}& z_{N1}& \cdots & z_{NN}\end{array}\right),$$

(77)

$$R_3=\left(\begin{array}{cccc}0& e^{-{\varphi }_1}& \cdots & e^{-{\varphi }_N}\\ c_1{e}^{{\varphi }_1^{*}}& z_{11}& \cdots & z_{1N}\\ ⋮& ⋮& \ddots & ⋮\\ c_N{e}^{{\varphi }_N^{*}}& z_{N1}& \cdots & z_{NN}\end{array}\right).$$

(78)

In the case of $N=1$, Equations (73)–(75) reduce to the one-soliton solutions:

$$u_1=2i\frac{a_1{e}^{-{\varphi }_1+{\varphi }_1^{*}}({\eta }_1^{*}-{\eta }_1)}{({\left|a_1\right|}^2+{\left|b_1\right|}^2+{\left|c_1\right|}^2)e^{{\varphi }_1^{*}+{\varphi }_1}+e^{-{\varphi }_1^{*}-{\varphi }_1}},$$

(79)

$$u_2=2i\frac{b_1{e}^{-{\varphi }_1+{\varphi }_1^{*}}({\eta }_1^{*}-{\eta }_1)}{({\left|a_1\right|}^2+{\left|b_1\right|}^2+{\left|c_1\right|}^2)e^{{\varphi }_1^{*}+{\varphi }_1}+e^{-{\varphi }_1^{*}-{\varphi }_1}},$$

(80)

$$u_3=2i\frac{c_1{e}^{-{\varphi }_1+{\varphi }_1^{*}}({\eta }_1^{*}-{\eta }_1)}{({\left|a_1\right|}^2+{\left|b_1\right|}^2+{\left|c_1\right|}^2)e^{{\varphi }_1^{*}+{\varphi }_1}+e^{-{\varphi }_1^{*}-{\varphi }_1}},$$

(81)

where ${\varphi }_1=i\{{\eta }_{1}x-{\displaystyle {\int }_0^t[4{\eta }_1^3(\tau )\alpha (\tau )-\gamma (\tau )/2]d\tau \}}$, ${\eta }_1$ is determined by Equation (54).

In Figure 1, we show the spatial solution structures of the uniformly propagating bell-shaped one-solitons along the positive x-axis determined by Equations (79)–(81) under the conditions of isospectrum and constant coefficients $\alpha (t)=1$, $\beta (t)=0$, $\gamma (t)=1$, and $\delta (t)=0$.

In the case of isospectrum and variable coefficients $\alpha (t)=t\sin t\cos t$, $\beta (t)=0$, $\gamma (t)=t$, and $\delta (t)=0$, we can see from Figure 2 that the bell-shaped one-solitons determined by Equations (79)–(81) propagate along the x-axis and exhibit periodic reciprocating motion.

For the case of non-isospectral and variable coefficients $\alpha (t)=1$, $\beta (t)=0.01$, $\gamma (t)=1$, and $\delta (t)=\sin t$, we show in Figure 3 the bell-shaped one-solitons determined by Equations (79)–(81), which propagate at varying velocities along the x-axis.

In another case of non-isospectral and variable coefficients $\alpha (t)=t\sin t$, $\beta (t)=-t$, $\gamma (t)=\cos t$, and $\delta (t)=e^t$, the propagating bell-shaped one-solitons with variable velocity propagation determined by Equations (79)–(81) are shown in Figure 4.

In the case of $N=2$, from Equations (73)–(75) we obtain the following two-soliton solutions:

$$u_1=-2i\frac{a_1{e}^{{\varphi }_1^{*}-{\varphi }_2}{z}_{21}+a_2{e}^{{\varphi }_2^{*}-{\varphi }_1}{z}_{12}-a_1{e}^{{\varphi }_1^{*}-{\varphi }_1}{z}_{22}-a_2{e}^{{\varphi }_2^{*}-{\varphi }_2}{z}_{11}}{z_{11}{z}_{22}-z_{12}{z}_{21}},$$

(82)

$$u_2=-2i\frac{b_1{e}^{{\varphi }_1^{*}-{\varphi }_2}{z}_{21}+b_2{e}^{{\varphi }_2^{*}-{\varphi }_1}{z}_{12}-b_1{e}^{{\varphi }_1^{*}-{\varphi }_1}{z}_{22}-b_2{e}^{{\varphi }_2^{*}-{\varphi }_2}{z}_{11}}{z_{11}{z}_{22}-z_{12}{z}_{21}},$$

(83)

$$u_3=-2i\frac{c_1{e}^{{\varphi }_1^{*}-{\varphi }_2}{z}_{21}+c_2{e}^{{\varphi }_2^{*}-{\varphi }_1}{z}_{12}-c_1{e}^{{\varphi }_1^{*}-{\varphi }_1}{z}_{22}-c_2{e}^{{\varphi }_2^{*}-{\varphi }_2}{z}_{11}}{z_{11}{z}_{22}-z_{12}{z}_{21}},$$

(84)

with

$$z_{11}=\frac{e^{-{\varphi }_1^{*}-{\varphi }_1}+{\left|a_1\right|}^2{e}^{{\varphi }_1^{*}+{\varphi }_1}+{\left|b_1\right|}^2{e}^{{\varphi }_1^{*}+{\varphi }_1}+{\left|c_1\right|}^2{e}^{{\varphi }_1^{*}+{\varphi }_1}}{{\eta }_1^{*}-{\eta }_1},$$

(85)

$$z_{12}=\frac{e^{-{\varphi }_1^{*}-{\varphi }_2}+a_1^{*}{a}_2{e}^{{\varphi }_1^{*}+{\varphi }_2}+b_1^{*}{b}_2{e}^{{\varphi }_1^{*}+{\varphi }_2}+c_1^{*}{c}_2{e}^{{\varphi }_1^{*}+{\varphi }_2}}{{\eta }_1^{*}-{\eta }_2},$$

(86)

$$z_{21}=\frac{e^{-{\varphi }_2^{*}-{\varphi }_1}+a_2^{*}{a}_1{e}^{{\varphi }_2^{*}+{\varphi }_1}+b_2^{*}{b}_1{e}^{{\varphi }_2^{*}+{\varphi }_1}+c_2^{*}{c}_1{e}^{{\varphi }_2^{*}+{\varphi }_1}}{{\eta }_2^{*}-{\eta }_1},$$

(87)

$$z_{22}=\frac{e^{-{\varphi }_2^{*}-{\varphi }_2}+{\left|a_2\right|}^2{e}^{{\varphi }_2^{*}+{\varphi }_2}+{\left|b_2\right|}^2{e}^{{\varphi }_2^{*}+{\varphi }_2}+{\left|c_2\right|}^2{e}^{{\varphi }_2^{*}+{\varphi }_2}}{{\eta }_2^{*}-{\eta }_2},$$

(88)

where ${\varphi }_1=i\{{\eta }_{1}x-{\displaystyle {\int }_0^t[4{\eta }_1^3(\tau )\alpha (\tau )-\gamma (\tau )/2]d\tau \}}$, ${\varphi }_2=i\{{\eta }_{2}x-{\displaystyle {\int }_0^t[4{\eta }_2^3(\tau )\alpha (\tau )-\gamma (\tau )/2]d\tau \}}$, ${\eta }_1$ and ${\eta }_2$ are determined by Equation (54).

In the case of isospectral and constant coefficients $\alpha (t)=1$, $\beta (t)=0$, $\delta (t)=1$, and $\gamma (t)=\cos t$, the bell-shaped two-solitons determined by Equations (82)–(84) propagate in opposite directions and then backward along the x-axis, as shown in Figure 5.

In Figure 6, the bell-shaped two-solitons determined by Equations (82)–(84) are shown in the case of isospectral and variable coefficients $\alpha (t)=t\sin t\cos t$, $\beta (t)=0$, $\delta (t)=1$, and $\gamma (t)=\cos t$, which periodically move back and forth along the x-axis in the same direction.

For the case of non-isospectral and variable coefficients $\alpha (t)=t\sin t$, $\beta (t)=-t$, $\gamma (t)=\cos t$ and $\delta (t)=e^t$, the bell-shaped two-solitons with variable-velocity propagation determined by Equations (82)–(84) are shown in Figure 7. We can see that the left soliton propagates first to the right and then to the left along the x-axis, while the right soliton always propagates to the right.

In another case of non-isospectral and variable coefficients $\alpha (t)=1$, $\beta (t)=0.01$, $\gamma (t)=1$, and $\delta (t)=\sin t$, Figure 8 shows that the bell-shaped two-solitons with variable-velocity propagation determined by Equations (82)–(84) interact with each other during their periodic reciprocating motion along the x-axis.

5. Application to Fractional Order System

As an application of the ccmKdVEs (1)–(3) and their solutions (73)–(75), we give in this section the reduced time-fractional order system of Equations (1)–(3) and apply the VIM [53,54,55] for constructing the N-th iteration formulae of approximate solutions.

If we suppose that $\alpha (t)$, $\beta (t)$, $\gamma (t)$, and $\delta (t)$ as $t^{\theta -1}$, together with $0<\theta <1$ and $t\in [0,+\infty )$, the ccmKdVEs (1)–(3) can be transformed into a novel time-fractional order system of three-component coupled mKdV equations:

$$D_t^{\theta }{u}_1=u_{1,xxx}+6{\left|u_1\right|}^2{u}_{1,x}+3{(u_1{u}_2)}_x{u}_2^{\ast }+3{(u_1{u}_3)}_x{u}_3^{\ast }+u_1+x{u}_{1,x}-ix{u}_1-i{u}_1,$$

(89)

$$D_t^{\theta }{u}_2=u_{2,xxx}+6{\left|u_2\right|}^2{u}_{2,x}+3{(u_1{u}_2)}_x{u}_1^{\ast }+3{(u_2{u}_3)}_x{u}_3^{\ast }+u_2+x{u}_{2,x}-ix{u}_2-i{u}_2,$$

(90)

$$D_t^{\theta }{u}_3=u_{3,xxx}+6{\left|u_3\right|}^2{u}_{3,x}+3{(u_1{u}_3)}_x{u}_1^{\ast }+3{(u_2{u}_3)}_x{u}_2^{\ast }+u_3+x{u}_{3,x}-ix{u}_3-i{u}_3,$$

(91)

where $D_t^{\theta }$ is the partial differential operator of conformable derivative [56].

Considering the VIM [53,54,55], we applied solutions (79)–(81) to attach Equations (89)–(91) with the initial conditions:

$$u_{1,0}=\frac{4}{6e^{-2x}+e^{2x}},$$

(92)

$$u_{2,0}=\frac{8}{6e^{-2x}+e^{2x}},$$

(93)

$$u_{3,0}=\frac{12}{6e^{-2x}+e^{2x}},$$

(94)

Here, the one-soliton solutions (79)–(81) have been substituted by the following:

$${\eta }_1=i,a_1=1,b_1=2,c_1=3,{\varphi }_1=-x.$$

(95)

It is not difficult to optimally identify the Lagrange multiplier $\lambda (\xi )=-1$ for Equations (89)–(91). We then have the N-th iteration formulae of approximate solutions for any $N\ge 0$:

$$\begin{gathered} u_{1,N+1}=u_{1,N}+I_{0,t}^{\theta }\{u_{1,N,\xi \xi \xi }(x,\xi )+6{\left|u_{1,N}(x,\xi )\right|}^2{u}_{1,N,\xi }(x,\xi )+3{[u_{1,N}(x,\xi )u_{2,N}(x,\xi )]}_{\xi }{u}_{2,N}^{\ast }(x,\xi ) \\ +3{[u_{1,N}(x,\xi )u_{3,N}(x,\xi )]}_{\xi }{u}_{3,N}^{\ast }(x,\xi )+u_{1,N}(x,\xi )+x{u}_{1,N,\xi }(x,\xi )-ix{u}_{1,N}(x,\xi )-i{u}_{1,N}(x,\xi )\}, \end{gathered}$$

(96)

$$\begin{gathered} u_{2,N+1}=u_{2,N}+I_{0,t}^{\theta }\{u_{2,N,\xi \xi \xi }(x,\xi )+6{\left|u_{2,N}(x,\xi )\right|}^2{u}_{2,N,\xi }(x,\xi )+3{[u_{1,N}(x,\xi )u_{2,N}(x,\xi )]}_{\xi }{u}_{1,N}^{\ast }(x,\xi ) \\ +3{[u_{2,N}(x,\xi )u_{3,N}(x,\xi )]}_{\xi }{u}_{3,N}^{\ast }(x,\xi )+u_{2,N}(x,\xi )+x{u}_{2,N,\xi }(x,\xi )-ix{u}_{2,N}(x,\xi )-i{u}_{2,N}(x,\xi )\}, \end{gathered}$$

(97)

$$\begin{gathered} u_{3,N+1}=u_{3,N}+I_{0,t}^{\theta }\{u_{3,N,\xi \xi \xi }(x,\xi )+6{\left|u_{3,N}(x,\xi )\right|}^2{u}_{3,N,\xi }(x,\xi )+3{[u_{1,N}(x,\xi )u_{3,N}(x,\xi )]}_{\xi }{u}_{1,N}^{\ast }(x,\xi ) \\ +3{[u_{2,N}(x,\xi )u_{3,N}(x,\xi )]}_{\xi }{u}_{2,N}^{\ast }(x,\xi )+u_{3,N}(x,\xi )+x{u}_{3,N,x}(x,\xi )-ix{u}_{3,N}(x,\xi )-i{u}_{3,N}(x,\xi )\}, \end{gathered}$$

(98)

where $I_{0,t}^{\theta }$ represents the conformable fractional variable upper bound integral operator [56] acting on the affected functions with respect to $\xi$ from $0$ to $t$.

Substituting the initial conditions (92)–(94) into Equations (96)–(98), we obtain the first iteration approximate solutions:

$$\begin{gathered} u_{1,1}=\frac{4}{6e^{-2x}+e^{2x}}-\frac{(7776-864i)e^{2x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }-\frac{(38448-432i)e^{6x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }+\frac{(6264+72i)e^{10x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }+\frac{(28+4i)e^{14x}{t}^{\theta }}{{(6+e^{4x})}^4\theta } \\ -\frac{(1728-864i)e^{2x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }-\frac{(288-432i)e^{6x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }+\frac{(48+72i)e^{10x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }+\frac{(8+4i)e^{14x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }, \end{gathered}$$

(99)

$$\begin{gathered} u_{2,1}=\frac{8}{6e^{-2x}+e^{2x}}-\frac{(15552-1728i)e^{2x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }-\frac{(76896-864i)e^{6x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }+\frac{(12528+144i)e^{10x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }+\frac{(56+8i)e^{14x}{t}^{\theta }}{{(6+e^{4x})}^4\theta } \\ -\frac{(3456-1728i)e^{2x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }-\frac{(576-864i)e^{6x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }+\frac{(96+144i)e^{10x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }+\frac{(16+8i)e^{14x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }, \end{gathered}$$

(100)

$$\begin{gathered} u_{3,1}=\frac{12}{6e^{-2x}+e^{2x}}-\frac{(23328-2592i)e^{2x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }-\frac{(115344-1296i)e^{6x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }+\frac{(18792+216i)e^{10x}{t}^{\theta }}{{(6+e^{4x})}^4\theta }+\frac{(84+12i)e^{14x}{t}^{\theta }}{{(6+e^{4x})}^4\theta } \\ -\frac{(5184-2592i)e^{2x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }-\frac{(864-1296i)e^{6x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }+\frac{(144+216i)e^{10x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }+\frac{(24+12i)e^{14x}{t}^{\theta }x}{{(6+e^{4x})}^4\theta }. \end{gathered}$$

(101)

In Figure 9, we show the spatial structures of the first iteration approximate solutions (99)–(101) with $\theta =0.8$.

The second-, third-, and other higher-order iteration approximate solutions of Equations (89)–(91) can be obtained from Equations (96)–(98), and they are omitted here. However, we are unable to obtain an exact solution through this process. We note here that the results obtained earlier regarding the ccmKdVEs (1)–(3) also satisfy Equations (89)–(91) when $\alpha (t)=\beta (t)=\gamma (t)=\delta (t)=t^{\theta -1}$ and $t$ is constrained to the interval $[0,+\infty )$. As for the N-soliton solutions of Equations (89)–(91), we need to adjust those ${\varphi }_j$, $j=1,2,\cdots ,N$, involved in Equations (73)–(78) to the following:

$${\varphi }_j=i\{{\eta }_j(0)e^{\frac{t^{\theta }}{\theta }}x-\frac{4}{3}{e}^{\frac{3t^{\theta }}{\theta }}{\eta }_j^3(0)+\frac{t^{\theta }}{2\theta }+\frac{4}{3}{\eta }_j^3(0)\}.$$

(102)

When $\theta =0.8$ and $\theta =0.5$, the corresponding one-soliton solutions (79)–(81) for Equations (89)–(91) are shown in Figure 10 and Figure 11. By comparing Figure 10 and Figure 11, we can see that the one-solitons with small fractional order value $\theta =0.5$ actually have greater speeds than those with $\theta =0.8$.

6. Conclusions

This paper shows, through the ccmKdVEs (1)–(3) proposed for the first time, the feasibility of solving multi-component coupled time-varying coefficient soliton equations equipped with mixed spectrum by the extension of RH method [1]. The construction of N-soliton solutions (73)–(75) benefits from the derived Lax pair (7) and (8), RH problem (30), and time-dependences of scattering data (54)–(57). This paper is the earliest attempt to extend the RH method [1] to the mixed spectral multi-component integrable systems using the ccmKdVEs (1)–(3) as an example, with the aim of further expanding the applicability of the RH method. Although the proof of Theorem 1 depends mostly on [1,2], and that of Theorem 2 on simple calculi, the proofs of these two Theorems cannot be separated from some crucial preliminary preparations. On the one hand, constructing the ccmKdVEs (1)–(3) requires embedding the time-varying spectrum determined by Equation (9), which makes the calculus operations involved in the proof of Theorems 1 and 2 fully consider the impact of the time-varying spectrum. On the other hand, due to the need to handle the ccmKdVEs (1)–(3), the Lax pair (7) and (8) have $4\times 4$ matrices $P$ and $Q$, as well as the scattering matrix $S(\eta )$ and its inverse matrix $S^{-1}(\eta )$ in Equations (21) and (23), which are all fourth-order. These make the RH problem (30) we established a fourth-order matrix problem, while all of these matrix problems involved in the corresponding single-component systems are all second-order. The above are the main mathematical advantages of this article.

To investigate the nonlinear dynamic characteristics of the obtained soliton solutions under the dual influences of spectral parameter $\eta$ and variable coefficients $\alpha (t)$, $\beta (t)$, $\gamma (t)$ and $\delta (t)$, we provide explicit expressions for the one-soliton solutions (79)–(81) and two-soliton solutions (82)–(84) and simulate their spatial solution structures. The common feature of the nonlinear dynamics shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 is that the solitons in the isospectral case always maintain their amplitudes and widths unchanged during propagation, while the amplitudes and widths of those solitons in the non-isospectral case change over time. At the same time, the coefficient functions have an impact on the velocity of soliton propagation. Whether the coefficient functions are constant determines whether the motion of isospectral solitons is uniform, while the motion of non-isospectral solitons is always variable. Of course, the coefficient functions not only cause periodicity but also affect velocity. Similar nonlinear characteristics of solitons have also been reported in [37], but the difference is that the model dealt with in this article is a three-component coupled system, which leads to computational differences and the earliest extension of the RH method [1] to the mixed spectral multi-component coupled equations with variable coefficients. There are various studies [57,58,59] on the effect of potentials on N-soliton solutions of nonlinear systems, such as the q-deformed Rosen–Morse type potential [59], which has caused scaling of soliton amplitude and spatial shift of soliton peak position. Therefore, this work is beneficial in enriching insights into the factors that affect the N-soliton solutions of nonlinear systems from the perspectives of coefficient functions and time-varying spectra. In the special case of these coefficient functions are taken as $t^{\theta -1}$, the ccmKdVEs (1)–(3) transform into a conformable time-fractional system of three-component coupled mKdV Equations (89)–(91). Based on the VIM [53,54,55] and the assigned initial conditions (89)–(91) inspired by the one-soliton solutions (79)–(81), we obtain the N-th iteration formulae of approximate solutions (96)–(98). This can be seen as a specific application of the ccmKdVEs (1)–(3) and their N-soliton solutions (73)–(75) in fractional calculus. Due to the time memory of nonlocal fractional order derivatives with integral kernels, such as Riemann–Liouville fractional derivative and Caputo fractional derivative, this goes beyond local fractional derivatives. Therefore, we have reason to believe that the numerical and analytical methods, extensions to spatiotemporal fractional orders:

$$D_t^{\theta }{u}_1=D_x^{3\vartheta }{u}_1+6{\left|u_1\right|}^2{D}_x^{\vartheta }{u}_1+3D_x^{\vartheta }(u_1{u}_2)u_2^{\ast }+3D_x^{\vartheta }(u_1{u}_3)u_3^{\ast }+u_1+x{D}_x^{\vartheta }{u}_1-ix{u}_1-i{u}_1,$$

(103)

$$D_t^{\theta }{u}_2=D_x^{3\vartheta }{u}_2+6{\left|u_2\right|}^2{D}_x^{\vartheta }{u}_2+3D_x^{\vartheta }(u_1{u}_2)u_1^{\ast }+3D_x^{\vartheta }(u_2{u}_3)u_3^{\ast }+u_2+x{D}_x^{\vartheta }{u}_2-ix{u}_2-i{u}_2,$$

(104)

$$D_t^{\theta }{u}_3=D_x^{3\vartheta }{u}_3+6{\left|u_3\right|}^2{D}_x^{\vartheta }{u}_x+3D_x^{\vartheta }(u_1{u}_3)u_1^{\ast }+3D_x^{\vartheta }(u_2{u}_3)u_2^{\ast }+u_3+x{D}_x^{\vartheta }{u}_3-ix{u}_3-i{u}_3,$$

(105)

where $D_x^{3\vartheta }$ represents $D_x^{\vartheta }{D}_x^{\vartheta }{D}_x^{\vartheta }$, $0<\vartheta <1$, and applications in related fields of the time-fractional system of three-component coupled mKdV Equations (89)–(91) combined with such nonlocal fractional derivatives deserve further research.

In Section 5, a special case of the ccmKdVEs (1)–(3) with $\alpha (t)$, $\beta (t)$, $\gamma (t)$, and $\delta (t)$ all being $t^{\theta -1}$, $0<\theta <1$, and $t\ge 0$ is used to transform into the time-fractional Equations (89)–(91). In such a special case, the results obtained in Section 1, Section 2, Section 3 and Section 4 can be adjusted accordingly to satisfy Equations (89)–(91), which is attributed to the properties of the comfortable fractional derivative [56]. However, there are very few fractional derivatives with such properties, and our research on the numerical algorithm of Equations (89)–(91) is not deep enough. Nevertheless, we believe that the introduction of the time-fractional Equations (89)–(91) has the following three benefits. Firstly, it not only highlights the importance of the ccmKdVEs (1)–(3) but also contributes to the exploration of the RH method [1] for nonlocal fractional integrable systems. Secondly, it can further remind us of nonlocal fractional systems, making it easier for us to naturally propose the nonlocal time-fractional Equations (89)–(91) or nonlocal spatiotemporal fractional Equations (103)–(105). Thirdly, we all know that for solving nonlocal fractional nonlinear differential systems, numerical algorithms are generally chosen by researchers, but often, as in this article, only approximate solutions can be obtained instead of exact solutions in closed forms, and waiting for N-soliton solutions is even more unrealistic. Numerical algorithms cannot do without the initial values of the system to be solved. The initial values given in Equations (92)–(94) are derived from the one-soliton solutions (79)–(81) obtained by the analytical RH method. Therefore, in the process of searching for the application of the obtained results in fractional calculus, two fractional systems of Equations (89)–(91) and Equations (103)–(105) are proposed in this paper. This can enrich the research content of numerical algorithms and also provide clues and references for the selection of initial values and error estimation of numerical algorithms, thereby achieving complementary advantages between numerical and analytical methods.