Modeling the Creep Behavior of Sliding Zone Carbonaceous Shale Subjected to Dry–Wet Cycles Using a Fractional Derivative Approach
Abstract
:1. Introduction
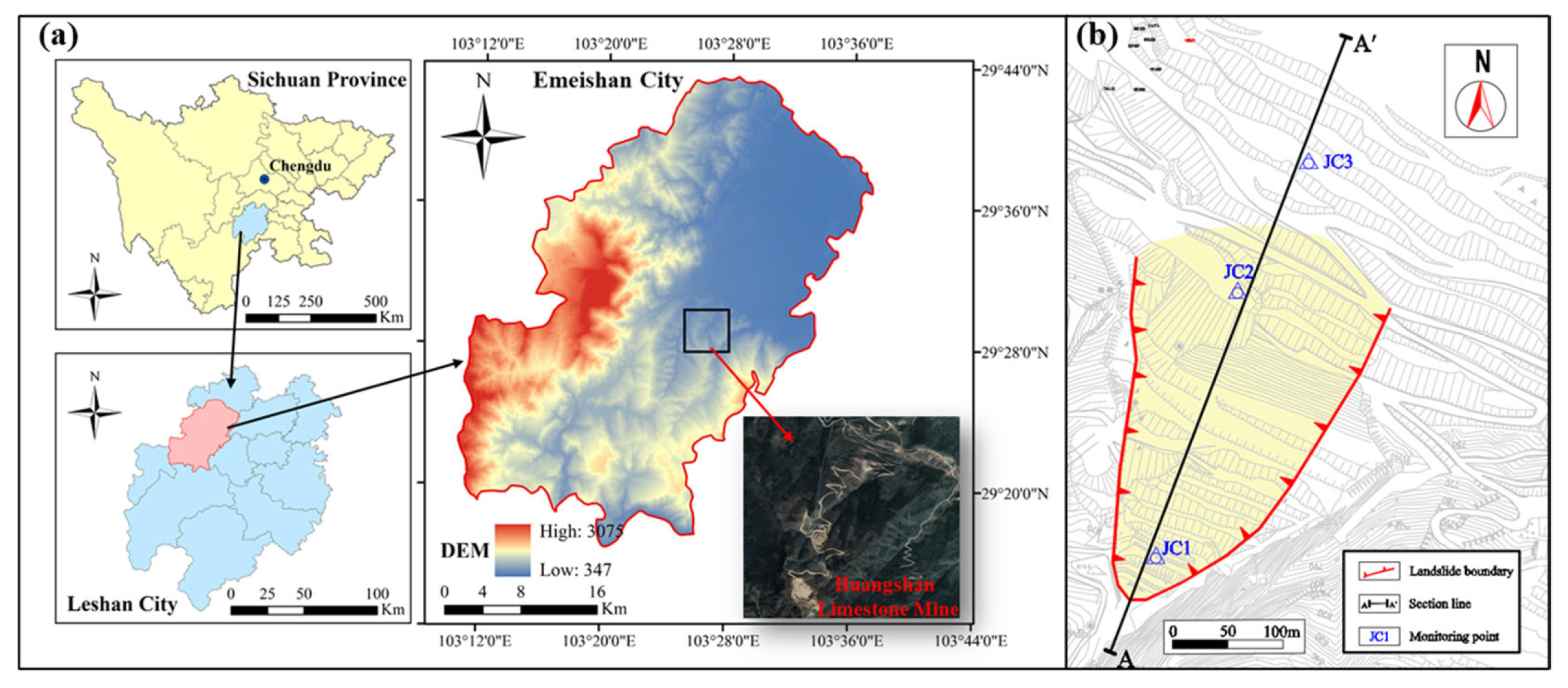
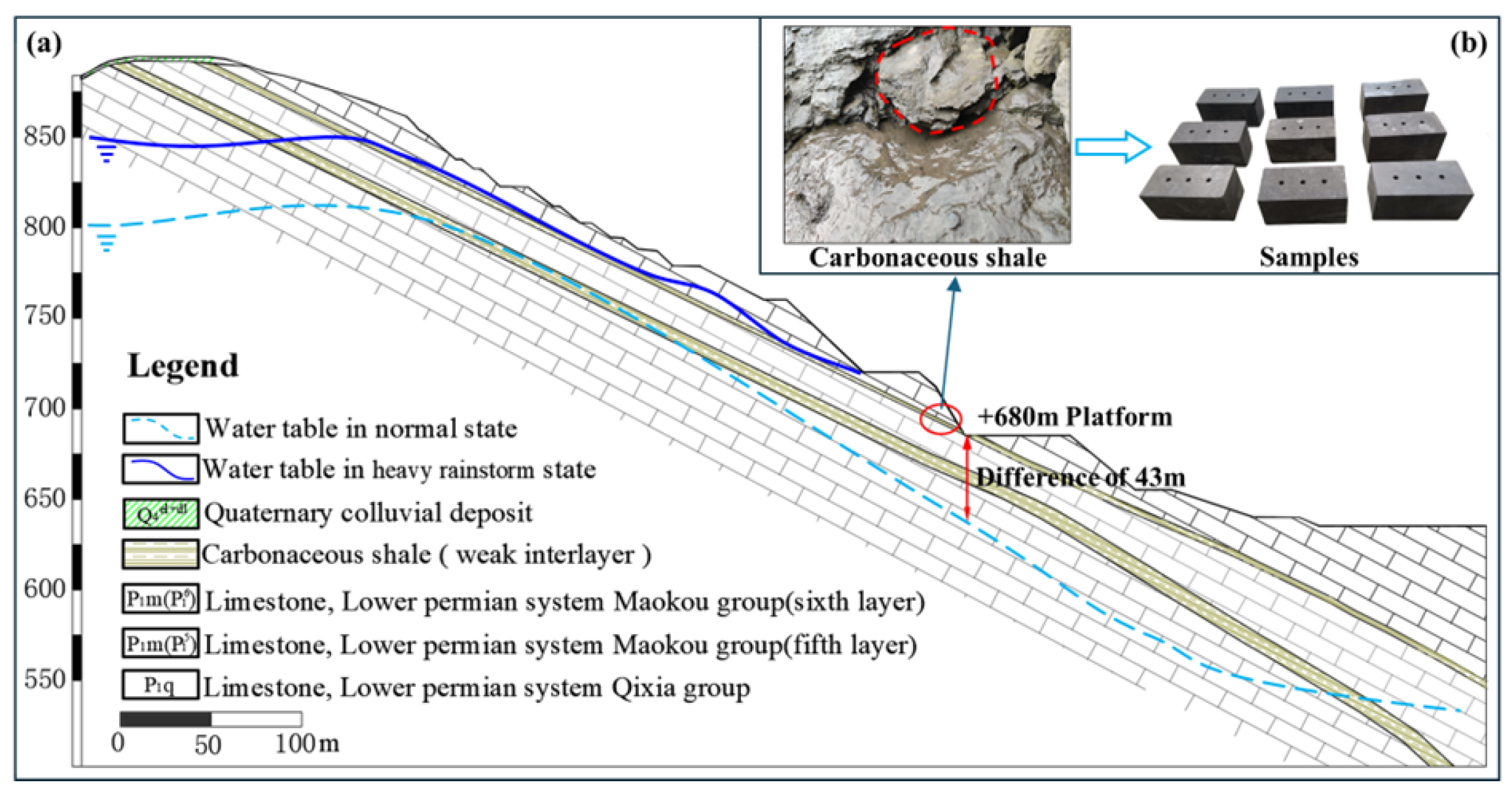
2. Experimental Study on Sliding Zone Rock Creep Behavior Under Dry–Wet Cycles
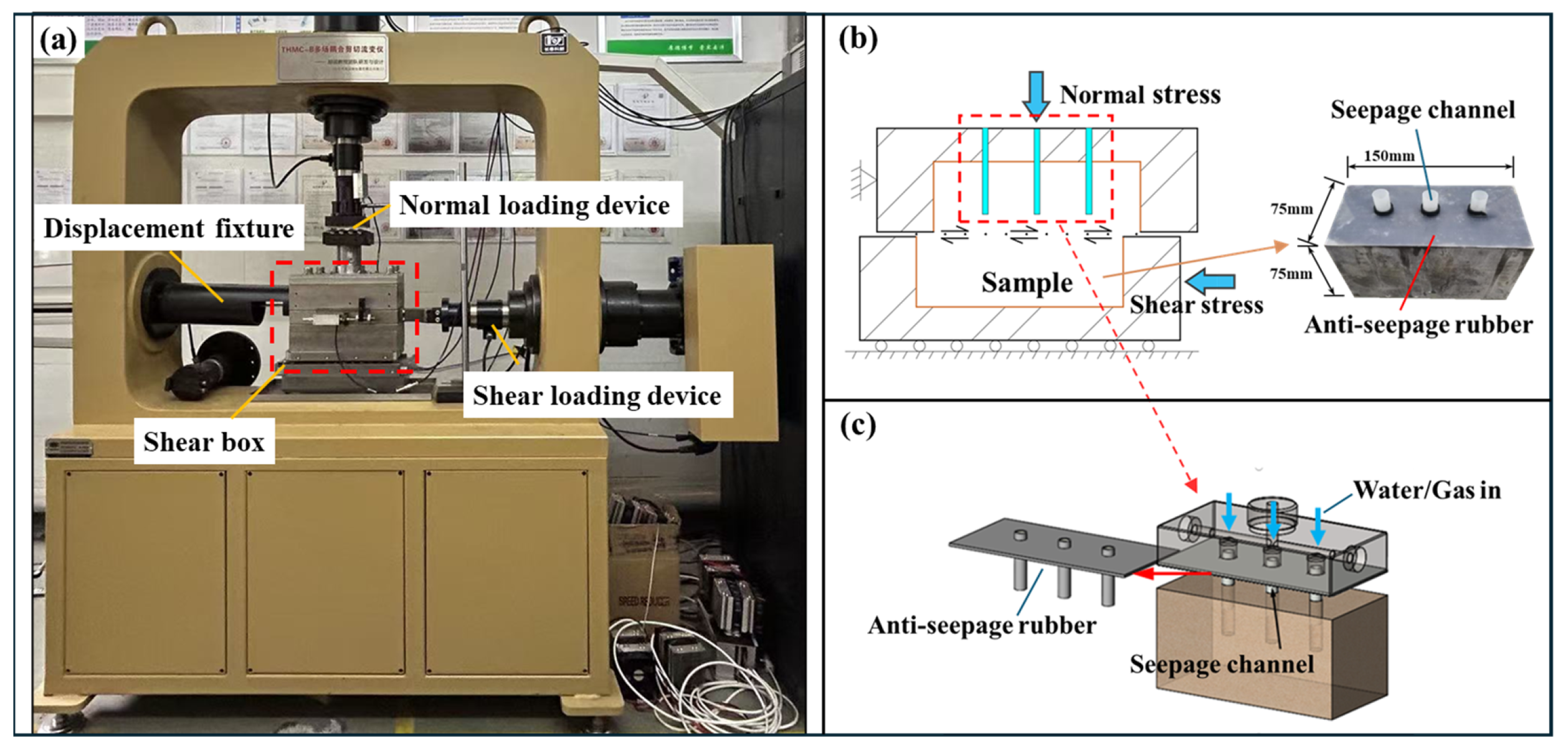
2.1. Experimental Tests
2.2. Analysis of Experimental Results
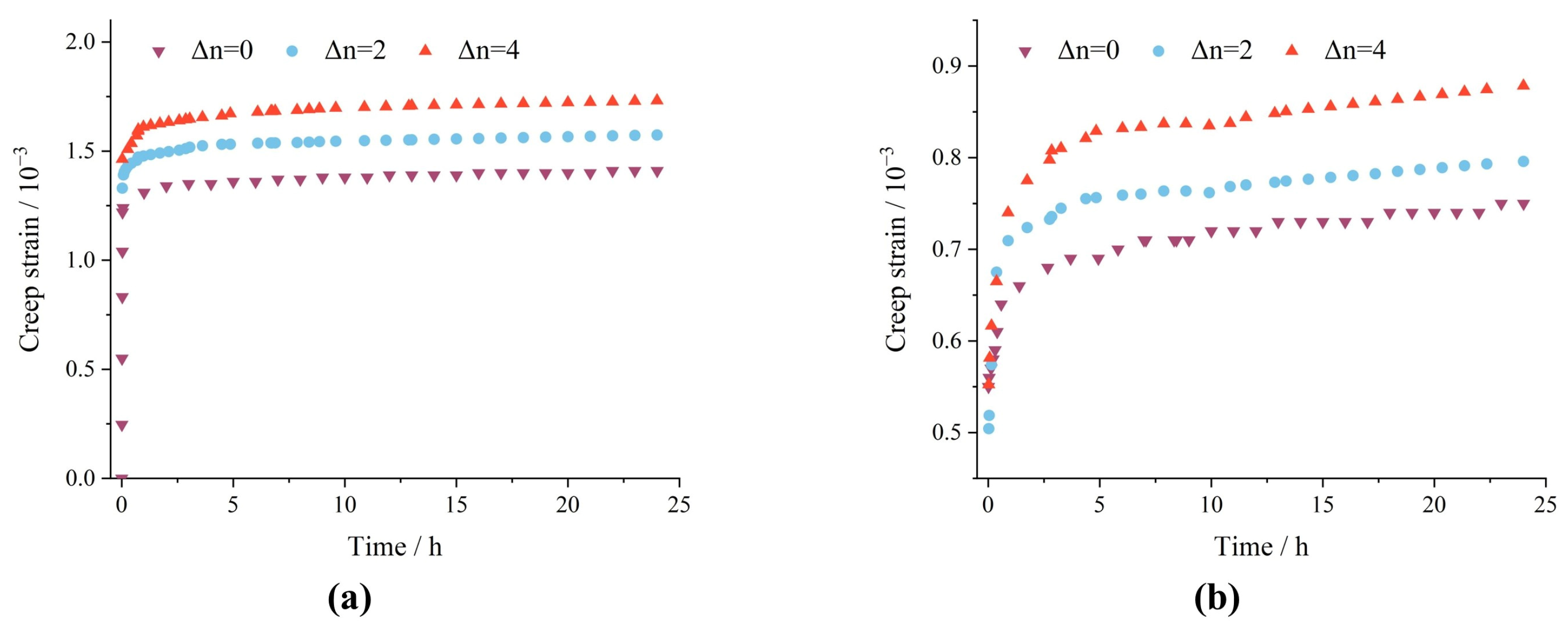
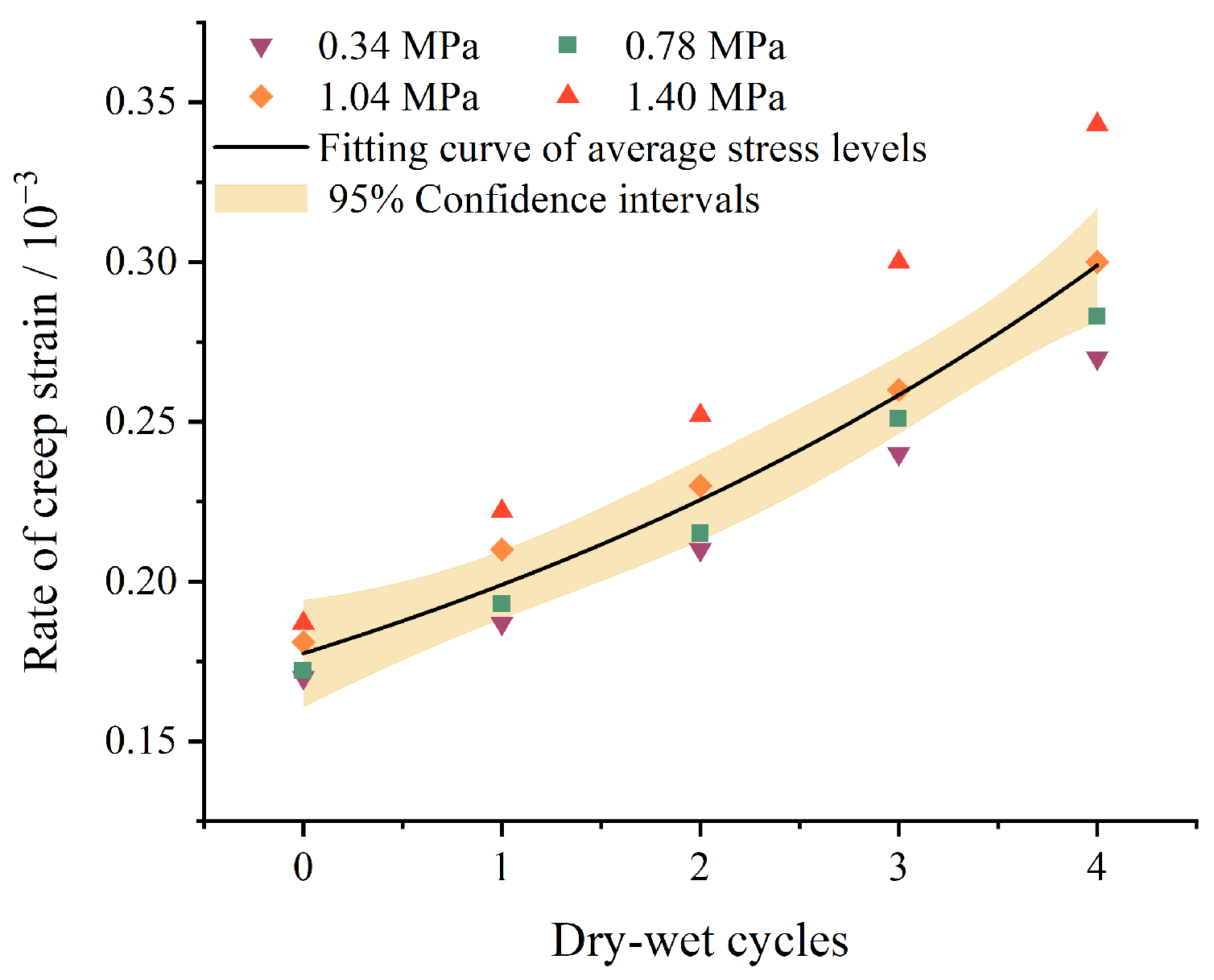
2.2.1. Creep Strain
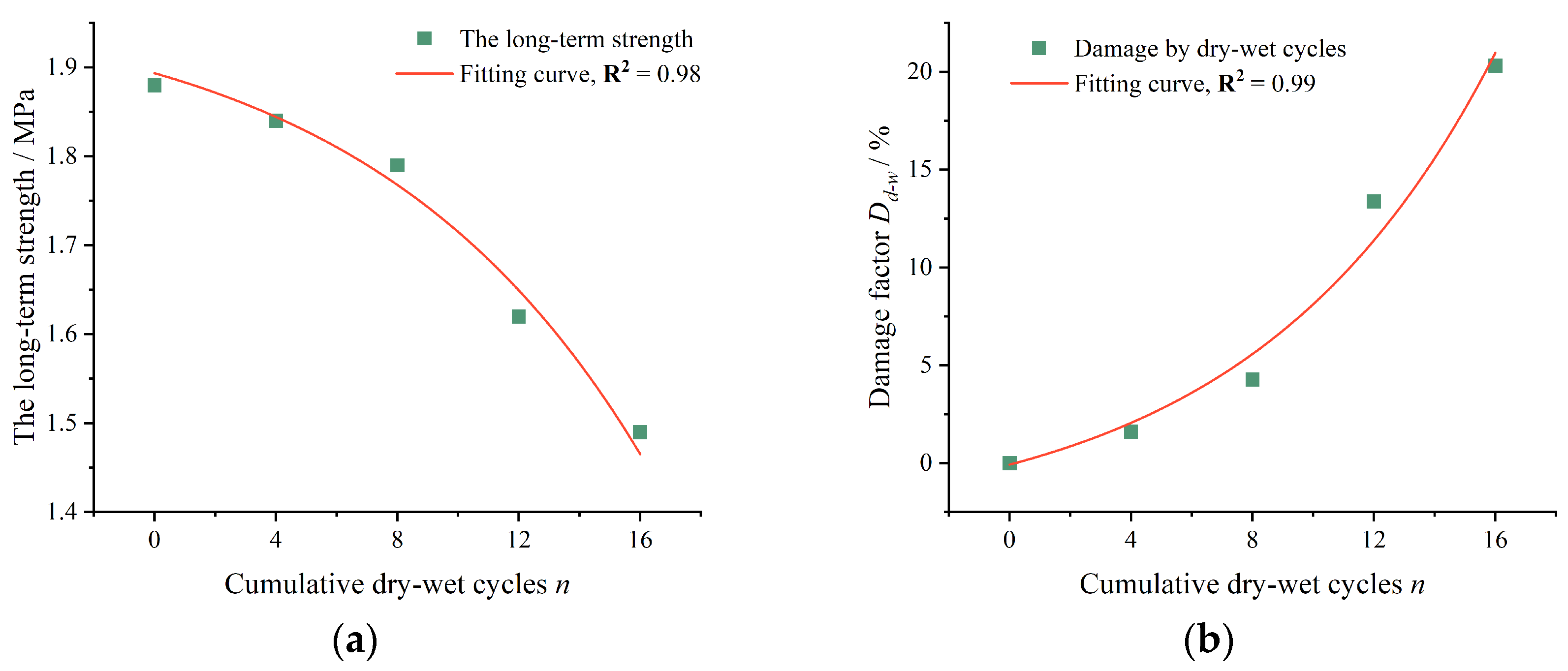
2.2.2. Long-Term Strength of Rock
2.2.3. Micro-Mechanism of Shear Damage Affected by Dry–Wet Cycles
3. Establishment of Nonlinear Creep Model
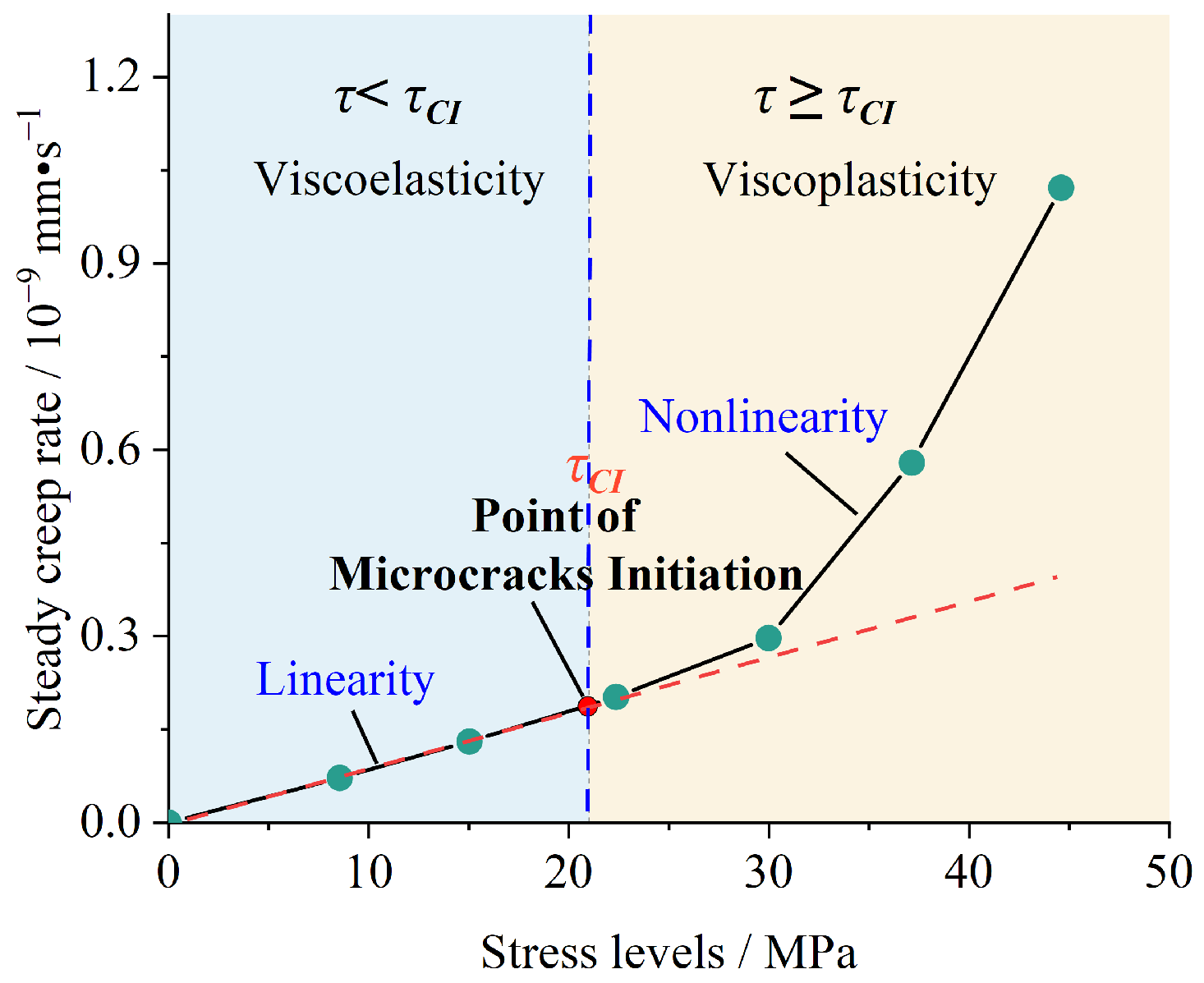
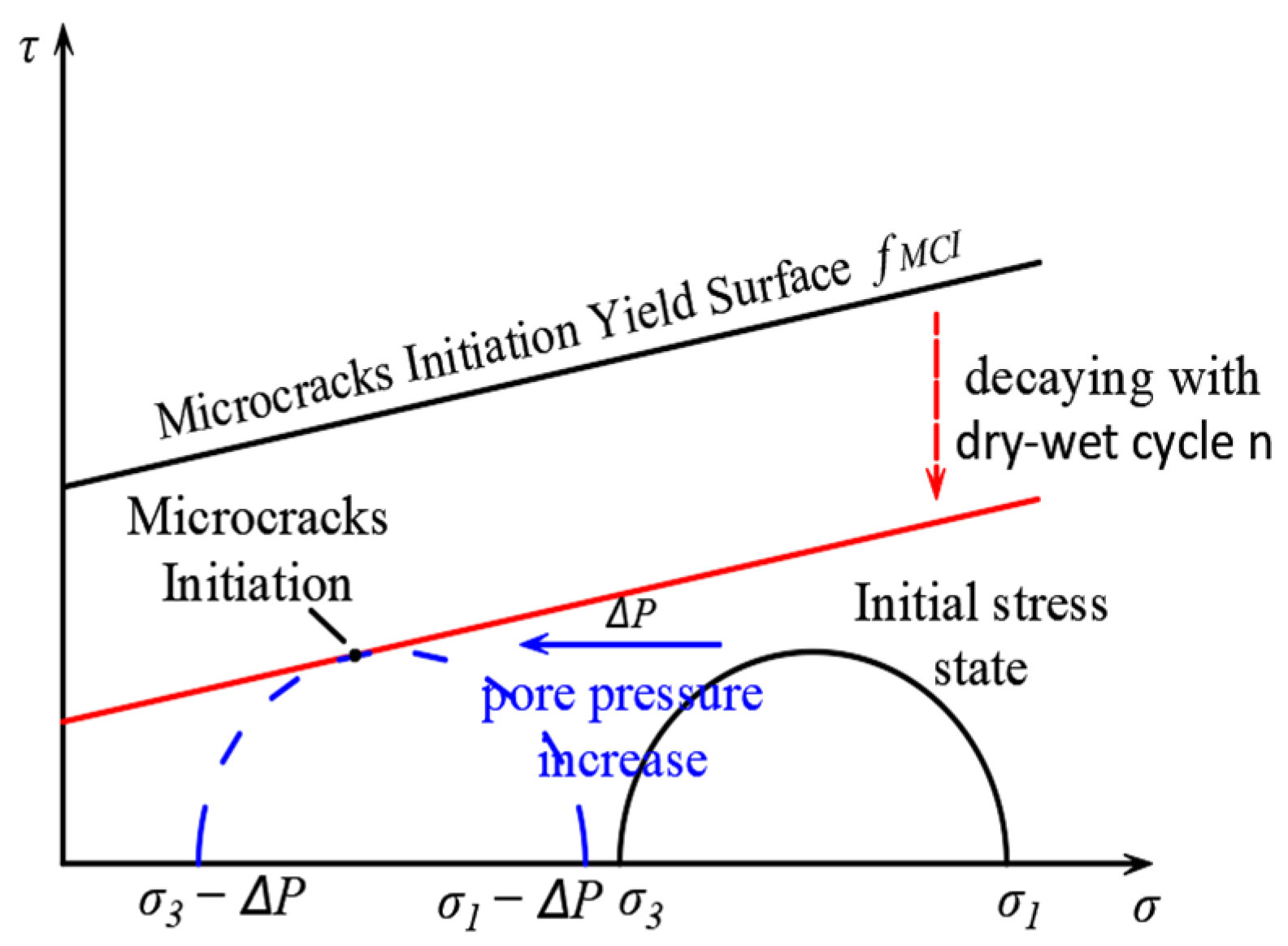
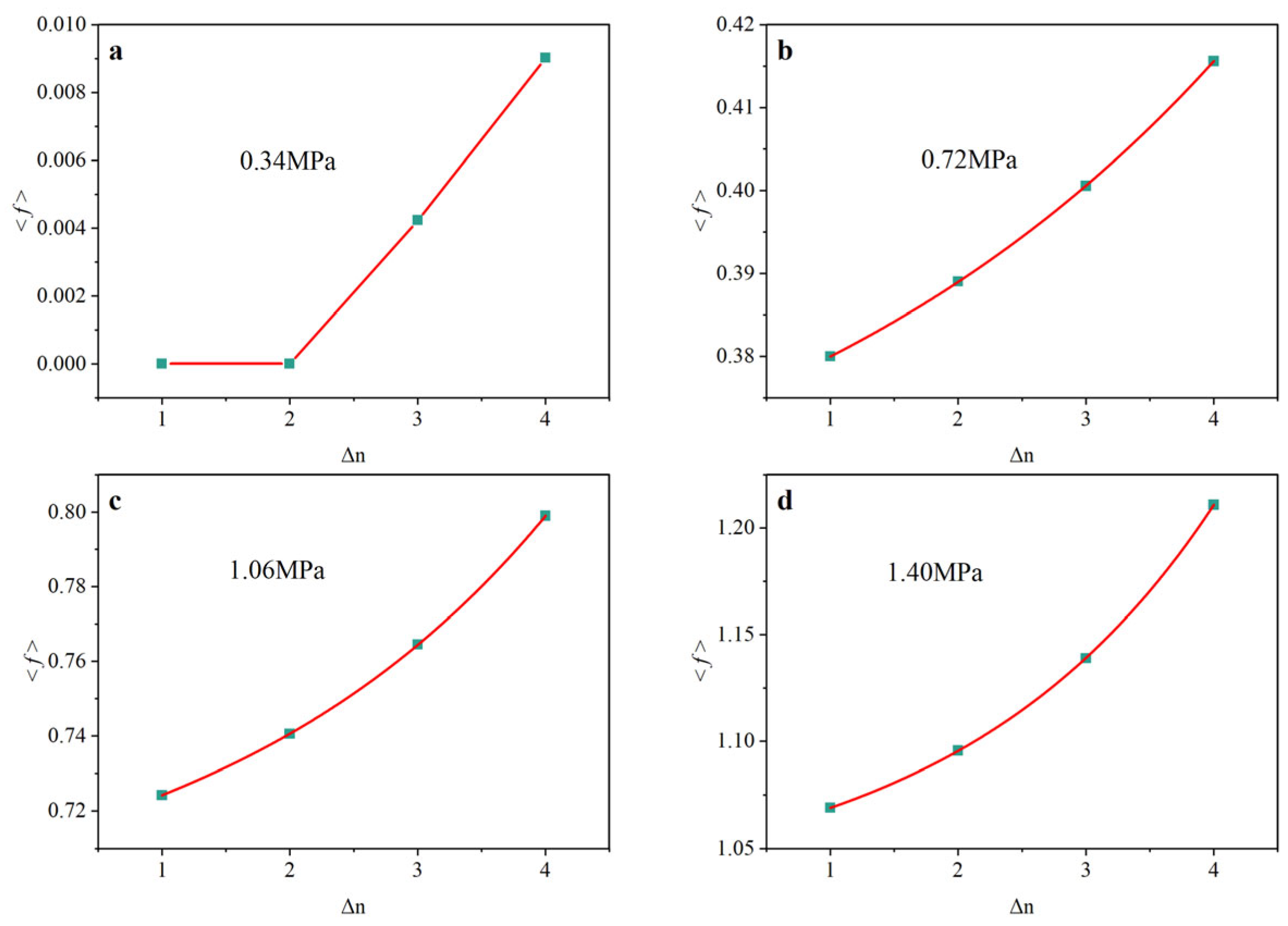
3.1. Quantification of Damage Effects
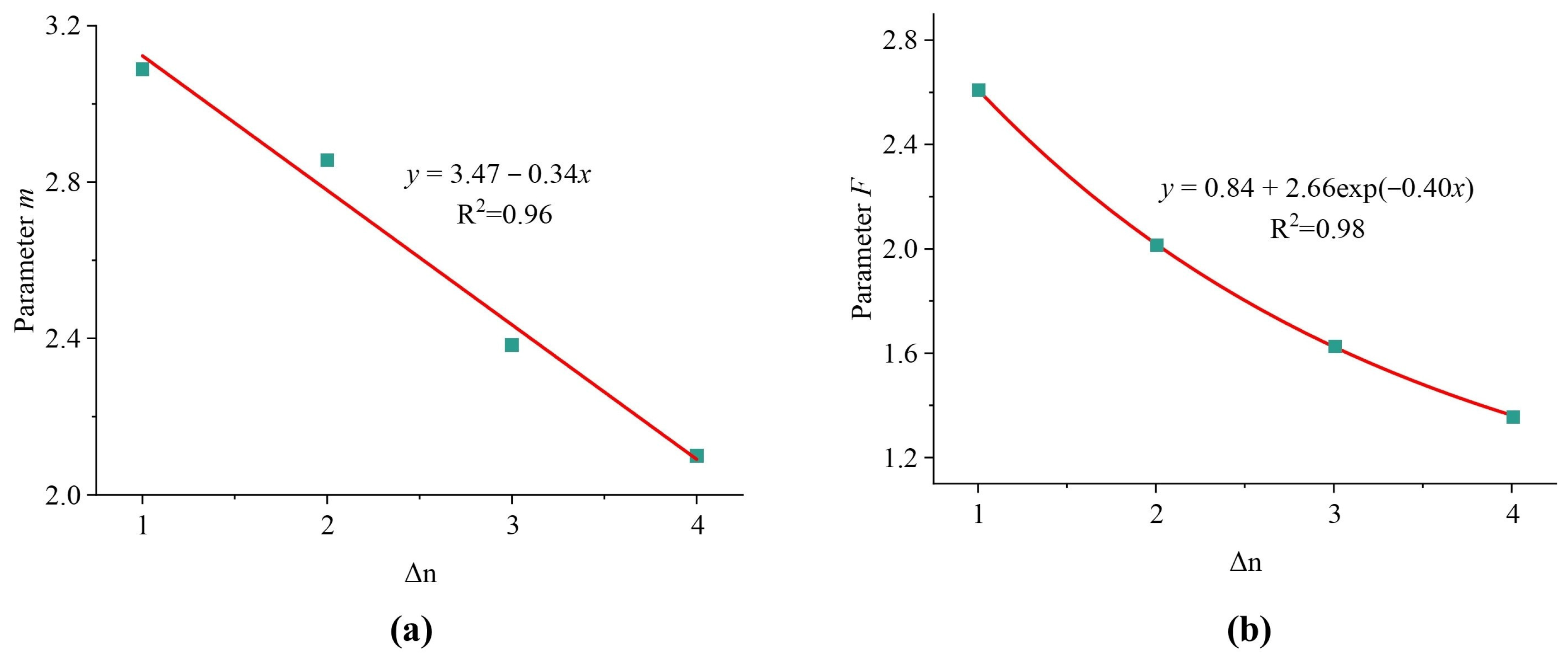
3.2. Damage Evolution Equation
3.3. Nonlinear Creep Damage Model
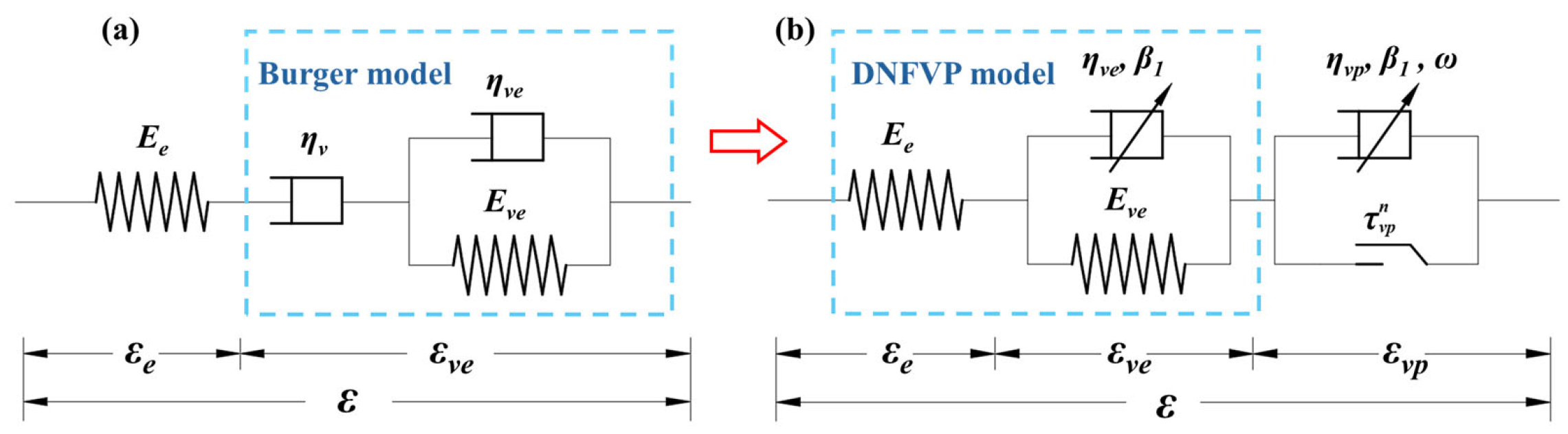
3.3.1. Fractional Derivative Component
| Yang et al. [52] | Li et al. [18] | Li et al. [33] | This Study | |
|---|---|---|---|---|
| Model name | Burger | Improved Burger model | DNFVP model | Improved DNFVP model |
| Model dimension | 1-D | 3-D | 3-D | 3-D |
| Consideration factors | Stress effect | Pore pressure effect | Effect of dry–wet cycles | Stress effect and dry–wet cycles |
| Modified components | None | Add a new damage factor | Add the fractional-order Newtonian dashpot | Add a new damage factor and a fractional derivative component |
| Damage theory | None | Kachanov–Rabotnov theory | Empirical method | Statistical theory based on the dry–wet cycle-induced damage mechanism |
| Correlation equation |
3.3.2. Time-Based Fractional Derivative Model
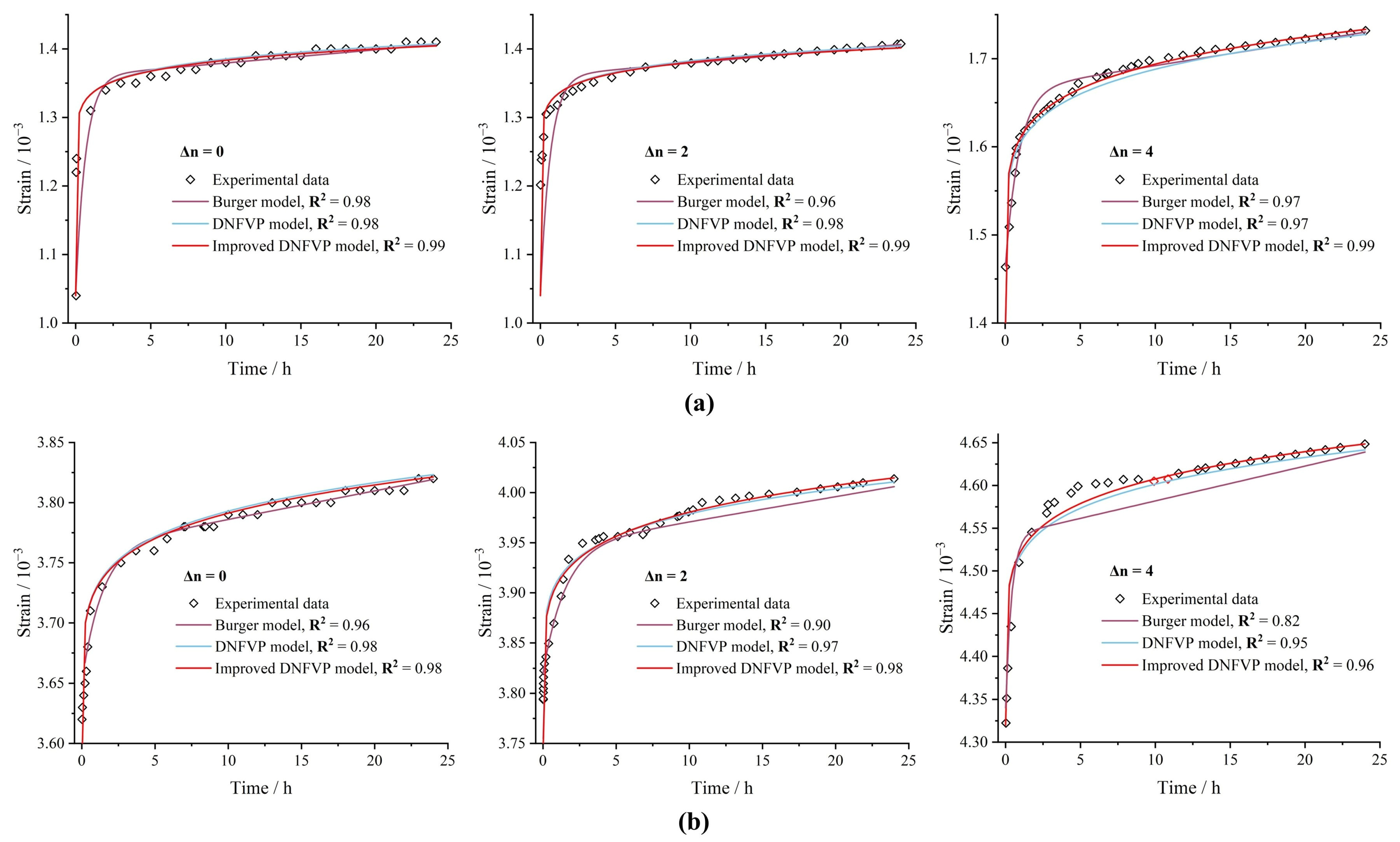
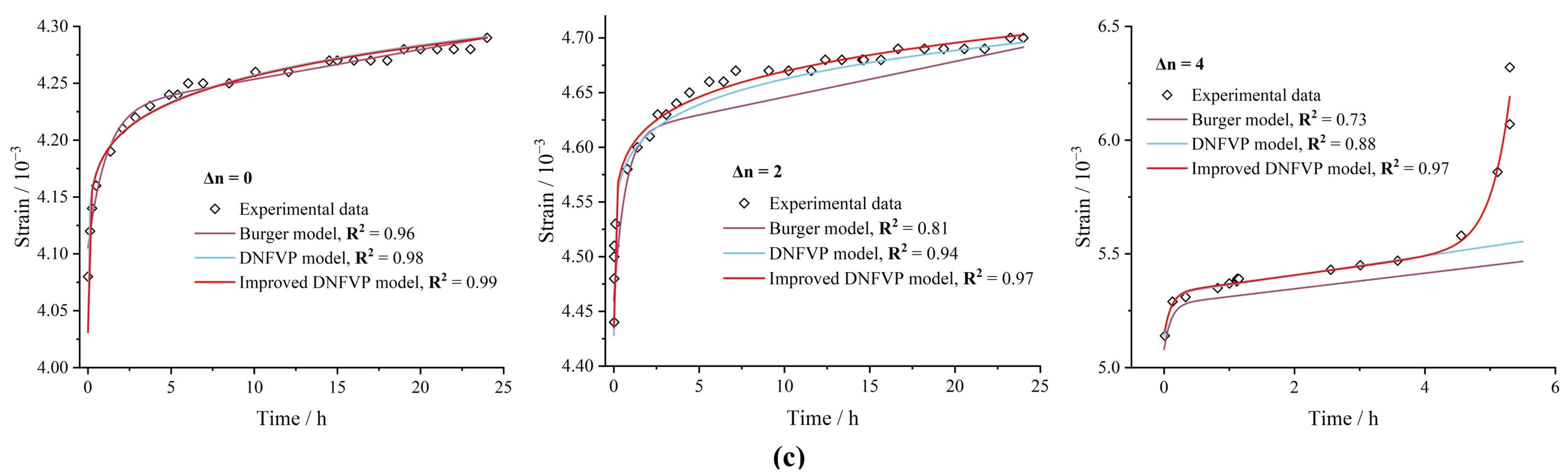
3.4. Validation of the Improved DNFVP Model
4. Discussion
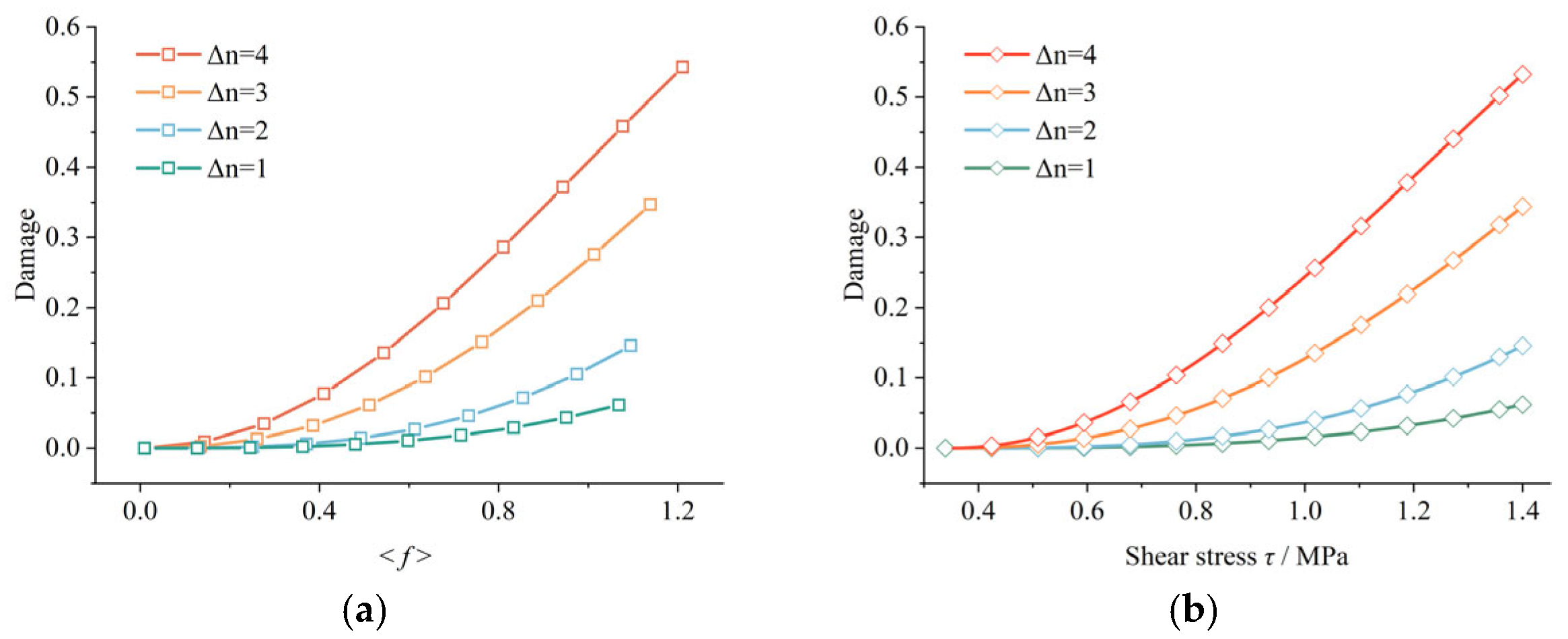
4.1. Damage Propagation Characteristics with Dry–Wet Cycles
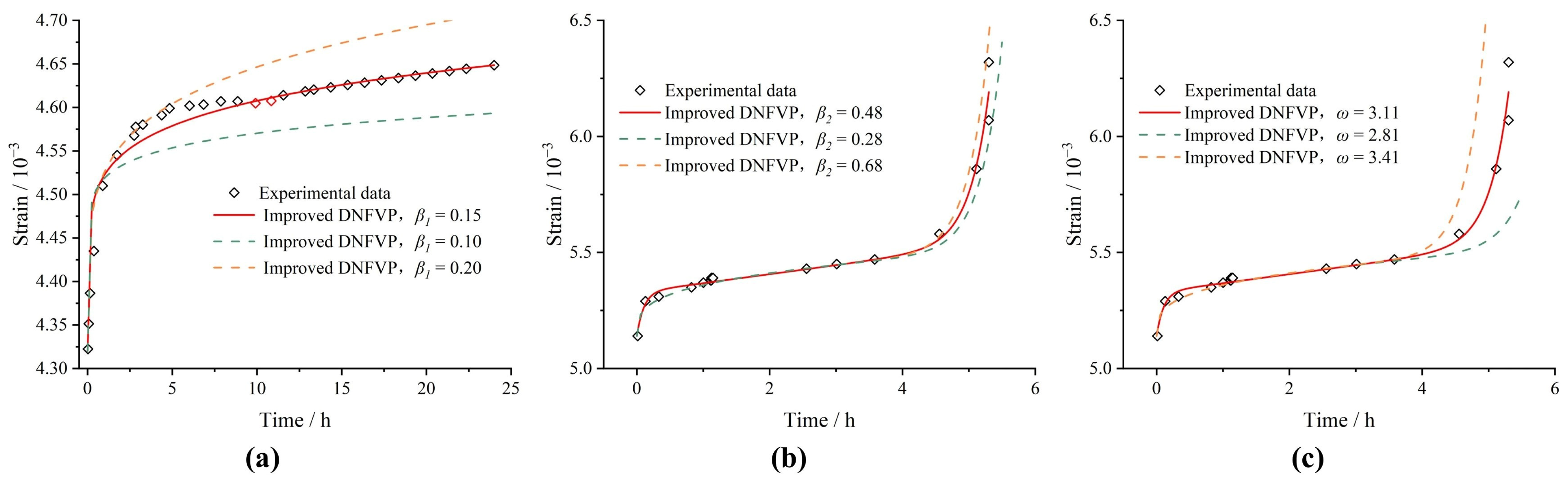
4.2. Sensitivity Analysis of the Improved DNFVP Constitutive Parameters
4.3. Limitations of This Study
5. Conclusions
- Key phenomena revealed by laboratory shear creep tests. At low deviatoric stress levels, within the viscoelastic stage, the creep deformation of the sliding zone (carbonaceous shale) exhibits a nonlinear increase with the degree of dry–wet cycles. Under dry–wet cycles, the material demonstrates significant creep strength degradation and structural damage.
- Development of the Improved DNFVP model. To account for the effects of dry–wet cycles on the creep behavior of the sliding zone (carbonaceous shale), a quantitative damage approach was introduced. The Burgers model was modified by incorporating a fractional derivative, leading to the development of the creep equation for the Improved DNFVP model. Experimental data validated the model’s reliability, demonstrating that it effectively simulates a nonlinear increase in the creep strain with increasing dry–wet cycles.
- Analysis of damage propagation characteristics with dry–wet cycles. The Weibull distribution parameters m and F decrease with increasing dry–wet cycles, reflecting the degradation of rock strength quality due to damage propagation. We demonstrated that the proposed damage evolution equation is consistent with the rock damage mechanism and possesses clear physical significance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, C.; Sun, Q.; Yang, X. A study of the factors influencing the occurrence of landslides in the Wushan area. Environ. Earth Sci. 2018, 77, 406. [Google Scholar] [CrossRef]
- Tang, H.; Wasowski, J.; Juang, C.H. Geohazards in the three Gorges Reservoir Area, China–Lessons learned from decades of research. Eng. Geol. 2019, 261, 105267. [Google Scholar] [CrossRef]
- Xu, Q.; Li, W.; Liu, H.; Tang, R.; Chen, S.; Sun, X. Hysteresis effect on the deep-seated landslide by rainfall: The case of the Kualiangzi landslide, China. In Engineering Geology for Society and Territory-Volume 2: Landslide Processes; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Sun, G.; Zheng, H.; Tang, H.; Dai, F. Huangtupo landslide stability under water level fluctuations of the Three Gorges reservoir. Landslides 2016, 13, 1167–1179. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Wu, W.; Cui, D.; Su, A.; Xiang, W. Creep properties of clastic soil in a reactivated slow-moving landslide in the Three Gorges Reservoir Region, China. Eng. Geol. 2020, 267, 105493. [Google Scholar] [CrossRef]
- Wang, X.-G.; Lian, B.-Q.; Wang, J.-D.; Feng, W.-K.; Gu, T.-F. Creep damage properties of sandstone under dry-wet cycles. J. Mt. Sci. 2020, 17, 3112–3122. [Google Scholar] [CrossRef]
- Liu, H.H.; Miao, H.B.; Chen, Z.W.; Huang, J.Y. Shear creep behaviors of sliding-zone soil of bedding landslide in Jurassic stratum in Three Gorges Reservoir area. Chin. J. Geotech. Eng. 2019, 41, 1573–1580. [Google Scholar]
- Lu, Y.; Jin, C.; Wang, Q.; Li, G.; Han, T. Deformation and failure characteristic of open-pit slope subjected to combined effects of mining blasting and rainfall infiltration. Eng. Geol. 2024, 331, 107437. [Google Scholar] [CrossRef]
- Do, T.N.; Wu, J.-H. Simulating a mining-triggered rock avalanche using DDA: A case study in Nattai North, Australia. Eng. Geol. 2020, 264, 105386. [Google Scholar] [CrossRef]
- Lian, B.; Wang, X.; Zhan, H.; Wang, J.; Peng, J.; Gu, T.; Zhu, R. Creep mechanical and microstructural insights into the failure mechanism of loess landslides induced by dry-wet cycles in the Heifangtai platform, China. Eng. Geol. 2022, 300, 106589. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, C.; Jiang, S.; Chen, Y.; Wang, Z.; Duan, S.; Xie, J. Disintegration behaviors of red clay under wet-dry cycles. J. Rock Mech. Geotech. Eng. 2024. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Peprah-Manu, D. Pore structure effects on the water retention behaviour of a compacted silty sand soil subjected to drying-wetting cycles. Eng. Geol. 2023, 313, 106963. [Google Scholar] [CrossRef]
- Zhong, Z.; Sheng, J.; Hu, B.; Li, J.; Wang, Z. Investigation of shear creep experiments and modelling of mud-shale under dry-wet cycles of rainfall. Phys. Scr. 2023, 99, 025010. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, X.; Liu, Y.; Yu, H.; Zhang, Q.; Li, X. A fractional-order damage creep model for grouting-reinforcement body under dry–wet cycle. Bull. Eng. Geol. Environ. 2023, 82, 172. [Google Scholar] [CrossRef]
- Qin, Z.; Liu, Y.; Pang, W.; Han, J.; Liu, W.; Feng, Q. A creep damage model for yellow sandstone under the action of wetting-drying cycles. Mech. Time-Depend. Mater. 2024, 28, 207–225. [Google Scholar] [CrossRef]
- Gong, F.; Yang, Y.; Li, P.; Wang, Z.; Zeng, B.; Jin, W.; Maekawa, K. Multi-physical analysis of saturation-dependent creep behavior for RC beam under sustained load and wet-dry cycles. Eng. Struct. 2024, 309, 117976. [Google Scholar] [CrossRef]
- Ye, B.; Qiu, H.; Tang, B.; Liu, Y.; Liu, Z.; Jiang, X.; Yang, D.; Ullah, M.; Zhu, Y.; Kamp, U. Creep deformation monitoring of landslides in a reservoir area. J. Hydrol. 2024, 632, 130905. [Google Scholar] [CrossRef]
- Li, Y.; Hu, X.; Zhang, H.; Zheng, H.; Xu, C. Nonlinear burgers model for sliding zone soil subjected to cyclic seepage pressure and its applications to the deformation analysis of landslide. Acta Geotech. 2025, 20, 743–763. [Google Scholar] [CrossRef]
- Shao, J.; Chau, K.; Feng, X. Modeling of anisotropic damage and creep deformation in brittle rocks. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2006, 43, 582–592. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, Y.; Shao, J. A unified elastic–plastic and viscoplastic damage model for quasi-brittle rocks. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2008, 45, 1237–1251. [Google Scholar] [CrossRef]
- Vakili, A. An improved unified constitutive model for rock material and guidelines for its application in numerical modelling. Comput. Geotech. 2016, 80, 261–282. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, A.; Yang, X. Shear creep experiments and modeling of granite under dry-wet cycling. Bull. Eng. Geol. Environ. 2021, 80, 5897–5908. [Google Scholar] [CrossRef]
- Wang, R.; Li, L.; Simon, R. A model for describing and predicting the creep strain of rocks from the primary to the tertiary stage. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2019, 123, 104087. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Al-Khaled, K.; Khan, M.I.; Haq, A.U.; Alotaibi, F.; Mousa, A.A.A.; Qayyum, S. A fractional model for the kerosene oil and water-based Casson nanofluid with inclined magnetic force. Chem. Phys. Lett. 2022, 787, 139277. [Google Scholar] [CrossRef]
- Veeresha, P. The efficient fractional order based approach to analyze chemical reaction associated with pattern formation. Chaos Solitons Fractals 2022, 165, 112862. [Google Scholar] [CrossRef]
- Zheng, Y.; Shangguan, W.-B.; Liu, X.-A. Modeling of a quasi-zero static stiffness mount fabricated with TPU materials using fractional derivative model. Mech. Syst. Signal Process. 2022, 177, 109258. [Google Scholar] [CrossRef]
- Mshary, N.; Ahmed, H.M.; Rabie, W.B. Fractional Solitons in Optical Twin-Core Couplers with Kerr Law Nonlinearity and Local M-Derivative Using Modified Extended Mapping Method. Fractal Fract. 2024, 8, 755. [Google Scholar] [CrossRef]
- Borhan, J.R.M.; Miah, M.M.; Alsharif, F.; Kanan, M. Abundant Closed-Form Soliton Solutions to the Fractional Stochastic Kraenkel–Manna–Merle System with Bifurcation, Chaotic, Sensitivity, and Modulation Instability Analysis. Fractal Fract. 2024, 8, 327. [Google Scholar] [CrossRef]
- Chen, J.; Gong, L.; Meng, R. Application of Fractional Calculus in Predicting the Temperature-Dependent Creep Behavior of Concrete. Fractal Fract. 2024, 8, 482. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, C.; Han, B.; Duan, Z. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Wang, C.; Liu, J.; Cai, Y.; Chen, L.; Wu, Z.; Liu, J. Effects of Damage and Fractional Derivative Operator on Creep Model of Fractured Rock. Rock Mech. Rock Eng. 2024, 57, 9323–9341. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the fractional order model of viscoelasticity. Mech. Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Sheng, J.; Huang, L. A Fractional-Order Creep-Damage Model for Carbonaceous Shale Describing Coupled Damage Caused by Rainfall and Blasting. Fractal Fract. 2024, 8, 459. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, W.; Zhang, H.; Zhang, J.-B.; Lu, X.-L. Study on the fatigue properties and constitutive model of siltstone under the coupled action of dry–wet cycles and cyclic loads. Soil Dyn. Earthq. Eng. 2023, 171, 107990. [Google Scholar] [CrossRef]
- Liu, J.; Chen, L.; Wang, C.; Man, K.; Wang, L.; Wang, J.; Su, R. Characterizing the mechanical tensile behavior of Beishan granite with different experimental methods. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2014, 69, 50–58. [Google Scholar] [CrossRef]
- Sun, C.; Jin, C.; Wang, L.; Ao, Y.; Zhang, J. Creep damage characteristics and local fracture time effects of deep granite. Bull. Eng. Geol. Environ. 2022, 81, 79. [Google Scholar] [CrossRef]
- Xu, T.; Zhou, G.; Heap, M.J.; Yang, S.; Konietzky, H.; Baud, P. The Modeling of Time-Dependent Deformation and Fracturing of Brittle Rocks Under Varying Confining and Pore Pressures. Rock Mech. Rock Eng. 2018, 51, 3241–3263. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Methods. Chinese Standard: Beijing, China, 2019.
- Maranini, E.; Brignoli, M. Creep behaviour of a weak rock: Experimental characterization. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1999, 36, 127–138. [Google Scholar] [CrossRef]
- Kachanov, L. Introduction to Continuum Damage Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Perzyna, P. Fundamental problems in viscoplasticity. Adv. Appl. Mech. 1966, 9, 243–377. [Google Scholar]
- Liu, H.; Liu, J.; Zhang, S.; Feng, L.; Qiu, L. Experimental study on compression characteristics of fractured soft rock and its Mohr-Coulomb criterion. Theor. Appl. Fract. Mech. 2023, 125, 103820. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, W.; Wan, W.; Tang, J. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2017, 93, 66–75. [Google Scholar] [CrossRef]
- Brantut, N.; Heap, M.; Meredith, P.; Baud, P. Time-dependent cracking and brittle creep in crustal rocks: A review. J. Struct. Geol. 2013, 52, 17–43. [Google Scholar] [CrossRef]
- Liu, H.Z.; Xie, H.Q.; He, J.D.; Xiao, M.L.; Zhuo, L. Nonlinear creep damage constitutive model for soft rocks. Mech. Time-Depend. Mater. 2017, 21, 73–96. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Yang, S. A coupled macro- and meso-mechanical model for heterogeneous coal. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2017, 94, 64–81. [Google Scholar] [CrossRef]
- Pourhosseini, O.; Shabanimashcool, M.; Sciences, M. Development of an elasto-plastic constitutive model for intact rocks. Int. J. Rock Mech. Min. Sci. 2014, 66, 1–12. [Google Scholar] [CrossRef]
- Skempton, A.W. Effective stress in soils, concrete and rocks. Sel. Pap. Soil Mech. 1984, 1032, 4–16. [Google Scholar]
- Tang, C.; Sciences, M. Numerical simulation of progressive rock failure and associated seismicity. Int. J. Rock Mech. Min. Sci. 1997, 34, 249–261. [Google Scholar] [CrossRef]
- Cai, W.; Dou, L.; Ju, Y.; Cao, W.; Yuan, S.; Si, G. A plastic strain-based damage model for heterogeneous coal using cohesion and dilation angle. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2018, 110, 151–160. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Yang, C.; Zhu, Z.; Wang, J.; Deng, H.; Huang, D.; Tang, J. Damaged creep constitutive models of rock-like materials containing multiple flaws and their relationships to those of the intact materials. Theor. Appl. Fract. Mech. 2024, 130, 104306. [Google Scholar] [CrossRef]
- Fei, W.; Jie, L.; Quanle, Z.; Cunbao, L.; Jie, C.; Renbo, G. A triaxial creep model for salt rocks based on variable-order fractional derivative. Mech. Time-Depend. Mater. 2021, 25, 101–118. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics, 2010; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Liang, C.; Liu, J.; Yang, J.; Xu, H.; Chen, Z.; Ran, L. A creep model for ultra-deep salt rock considering thermal-mechanical damage under triaxial stress conditions. J. Rock Mech. Geotech. Eng. 2024, 16, 588–596. [Google Scholar] [CrossRef]
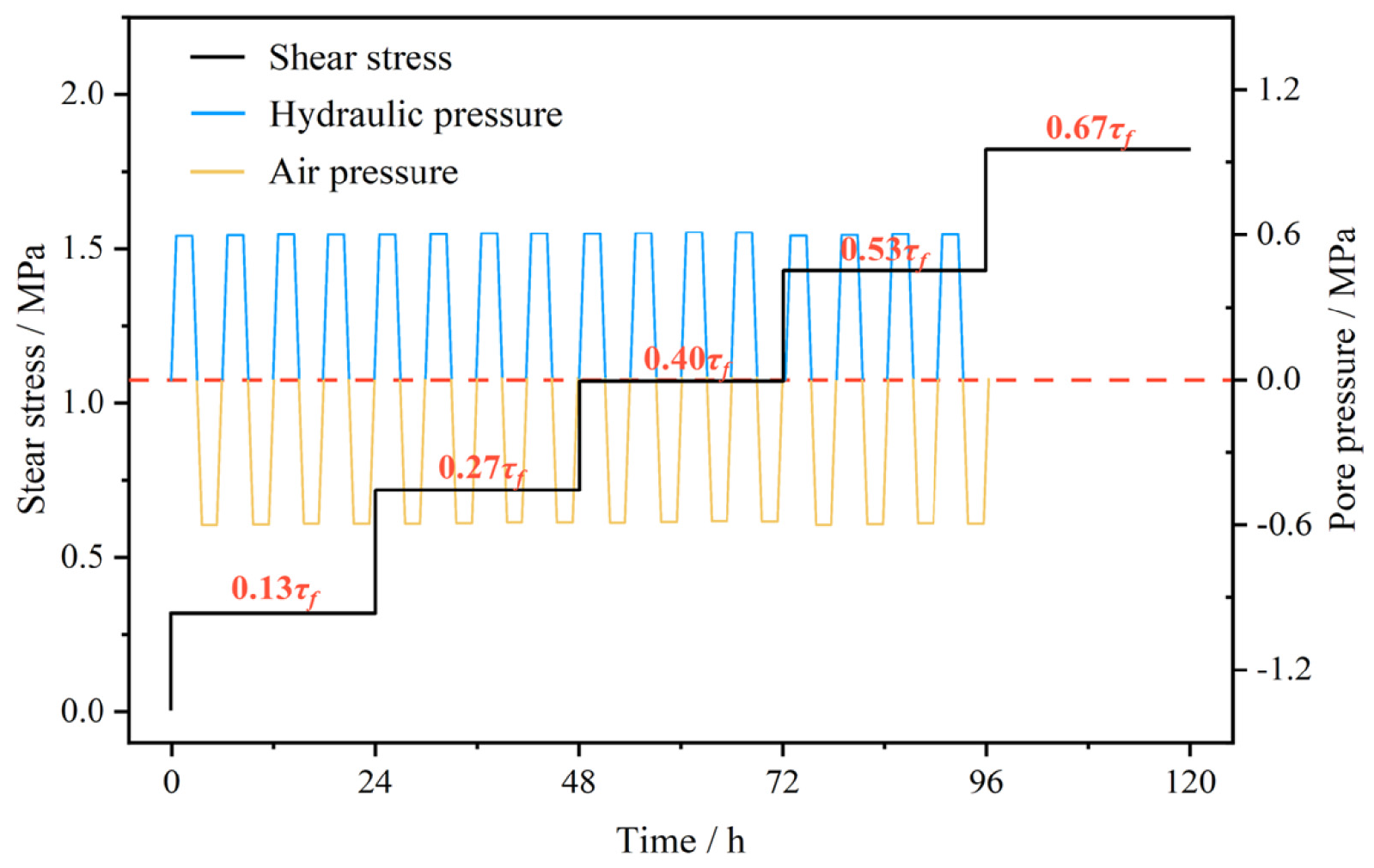

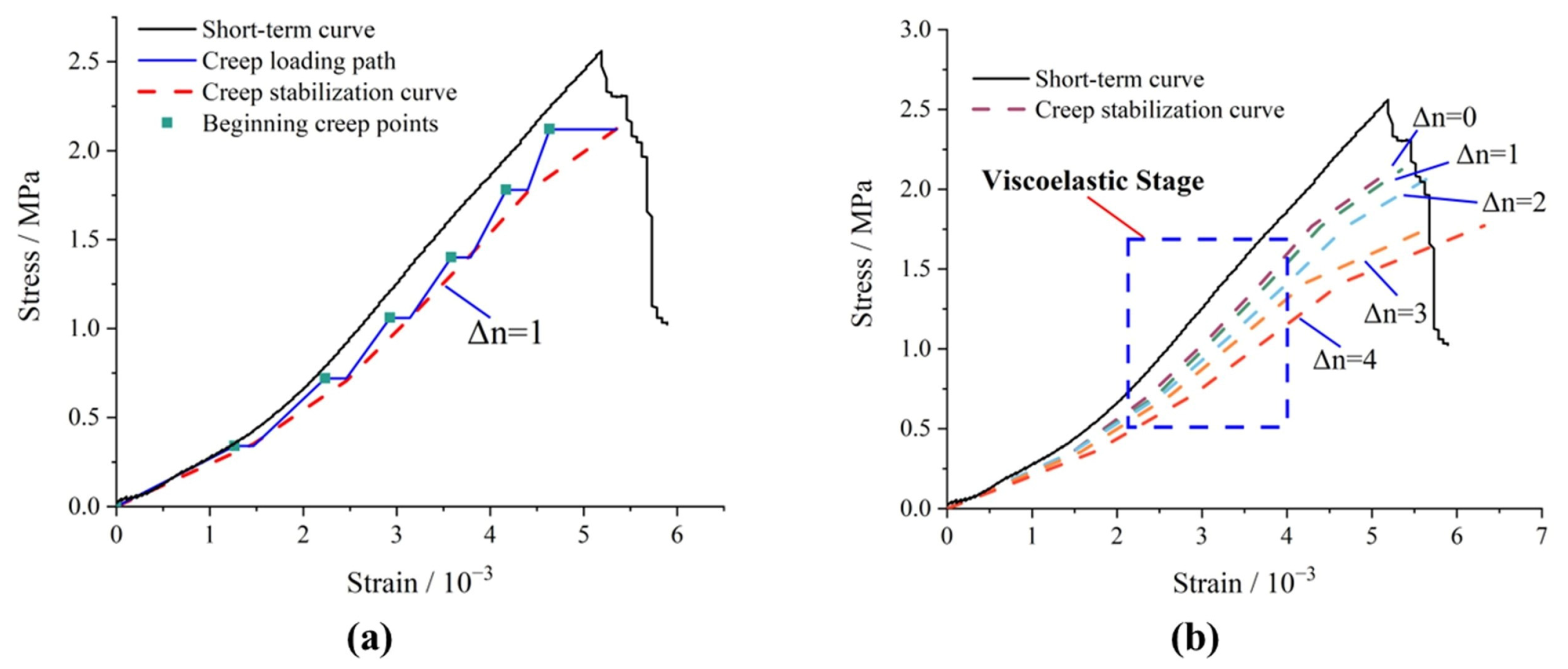


| Samples | Normal Pressure (MPa) | Shear Strength τf (MPa) | Δn 1 | Loading Shear Stress at Each Level (MPa) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0.13τf | 0.27τf | 0.40τf | 0.53τf | 0.67τf | 0.80τf | ||||
| ST-00 | 0.6 | 2.65 | 0 | 0.34 | 0.72 | 1.06 | 1.4 | 1.78 | 2.12 |
| ST-01 | 1 | ||||||||
| ST-02 | 2 | ||||||||
| ST-03 | 3 | ||||||||
| ST-04 | 4 | ||||||||
| Stress Loading Level | Deviatoric Stress (MPa) | Ee (GPa) | Eve (GPa) | ηve (GPa·hβ1) | β1 | β2 | ω | ηvp (GPa·hβ2) |
|---|---|---|---|---|---|---|---|---|
| 1st | 0.34 | 0.32 | 1.06 | 1.20 | 0.068 | / | / | / |
| 4th | 1.40 | 0.38 | 12.45 | 10.08 | 0.152 | / | / | / |
| 5th | 1.78 | 0.43 | 14.54 | 12.25 | 0.163 | 0.48 | 3.11 | 5.32 × 106 |
| Stress Loading Level | Deviatoric Stress (MPa) | Ee (GPa) | ηve (GPa·hβ1) | β1 | β2 | ω | ηvp (GPa·hβ2) |
|---|---|---|---|---|---|---|---|
| 1st | 0.34 | 0.32 | 1.20 | 0.066 | / | / | / |
| 4th | 1.40 | 0.37 | 10.08 | 0.153 | / | / | / |
| 5th | 1.78 | 0.44 | 12.25 | 0.165 | 0.50 | 3.11 | / |
| Stress Loading Level | Deviatoric Stress (MPa) | Ee (GPa) | Eve (GPa) | ηve (GPa·hβ1) | ηv (GPa·hβ1) |
|---|---|---|---|---|---|
| 1st | 0.34 | 0.32 | 1.06 | 0.69 | 176.23 |
| 4th | 1.40 | 0.38 | 12.45 | 17.07 | 591.72 |
| 5th | 1.78 | 0.43 | 14.54 | 15.89 | 2612.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Z.; Hu, B.; Li, J.; Sheng, J.; Zhang, X.; Cui, K. Modeling the Creep Behavior of Sliding Zone Carbonaceous Shale Subjected to Dry–Wet Cycles Using a Fractional Derivative Approach. Fractal Fract. 2025, 9, 236. https://doi.org/10.3390/fractalfract9040236
Zhong Z, Hu B, Li J, Sheng J, Zhang X, Cui K. Modeling the Creep Behavior of Sliding Zone Carbonaceous Shale Subjected to Dry–Wet Cycles Using a Fractional Derivative Approach. Fractal and Fractional. 2025; 9(4):236. https://doi.org/10.3390/fractalfract9040236
Chicago/Turabian StyleZhong, Zhuoxi, Bin Hu, Jing Li, Jianlong Sheng, Xiangyu Zhang, and Kai Cui. 2025. "Modeling the Creep Behavior of Sliding Zone Carbonaceous Shale Subjected to Dry–Wet Cycles Using a Fractional Derivative Approach" Fractal and Fractional 9, no. 4: 236. https://doi.org/10.3390/fractalfract9040236
APA StyleZhong, Z., Hu, B., Li, J., Sheng, J., Zhang, X., & Cui, K. (2025). Modeling the Creep Behavior of Sliding Zone Carbonaceous Shale Subjected to Dry–Wet Cycles Using a Fractional Derivative Approach. Fractal and Fractional, 9(4), 236. https://doi.org/10.3390/fractalfract9040236






