Deep Reinforcement Learning for Automated Insulin Delivery Systems: Algorithms, Applications, and Prospects
Abstract
1. Introduction
- (1)
- Non-linearity. Due to the existence of synergistic effects of human hormones as well as the complexity of biochemical reactions, the glycemic control of people with diabetes is a non-linear problem.
- (2)
- Inter- and intra-patient variability. There are significant differences in glycemic metabolism between patients, and for the same individual, the long-term and short-term glycemic performance can vary due to circadian rhythms, emotional fluctuations, external perturbations, and other factors.
- (3)
- Time lag. A time delay of up to one hour exists between making insulin infusions and the resulting BGC changes [26], necessitating adjustments in dosage calculations.
- (4)
- Uncertain disturbances. The patient’s BGC is not only determined by the insulin dose but also affected by external disturbances such as physical activities (type, intensity, and duration), emotional fluctuations, and dietary intake. Many of these factors are difficult to detect, classify, and characterize based on only CGM and insulin infusion data. They cause unknown disturbances to closed-loop AIDs, leading to high uncertainty.
- (5)
- High safety requirements. Excessive insulin may lead to severe hypoglycemic events that can be life-threatening, so safety must always be ensured in the design and operation of the control algorithm.
- (1)
- Potential resistance to perturbations. The “Agent” considers all states when evaluating the expected value, enabling the DRL algorithm to adapt to potential external perturbations of the “Environment”;
- (2)
- Inter- and intra-patient variability. People with diabetes are considered as the “Environment” in DRL, and the agent makes the appropriate decisions based on its interactions with the individualized environment, which has advantages over some fixed model-based control algorithms in adapting to the variability of the “Environment”;
- (3)
- Adaptation to time lag. The reward function in DRL calculates the cumulative reward, which can address the problem of latency in the “Environment”;
- (4)
- Adaptation to sequential decision-making tasks. The BGC control task is a sequential decision-making task, where the action at the current time step influences the subsequent state change, which in turn determines the action that needs to be made at the next time step, and DRL has a natural match with sequential decision-making tasks.
- (1)
- Low sample availability. When confronted with high-dimensional, continuous action spaces, DRL often struggles to effectively utilize sample data, leading to low learning efficiency and excessive reliance on data volume. This issue not only impacts the training speed of DRL systems but also restricts their application in the real world, as acquiring a large amount of sample data in practical environments may be limited by cost and time constraints.
- (2)
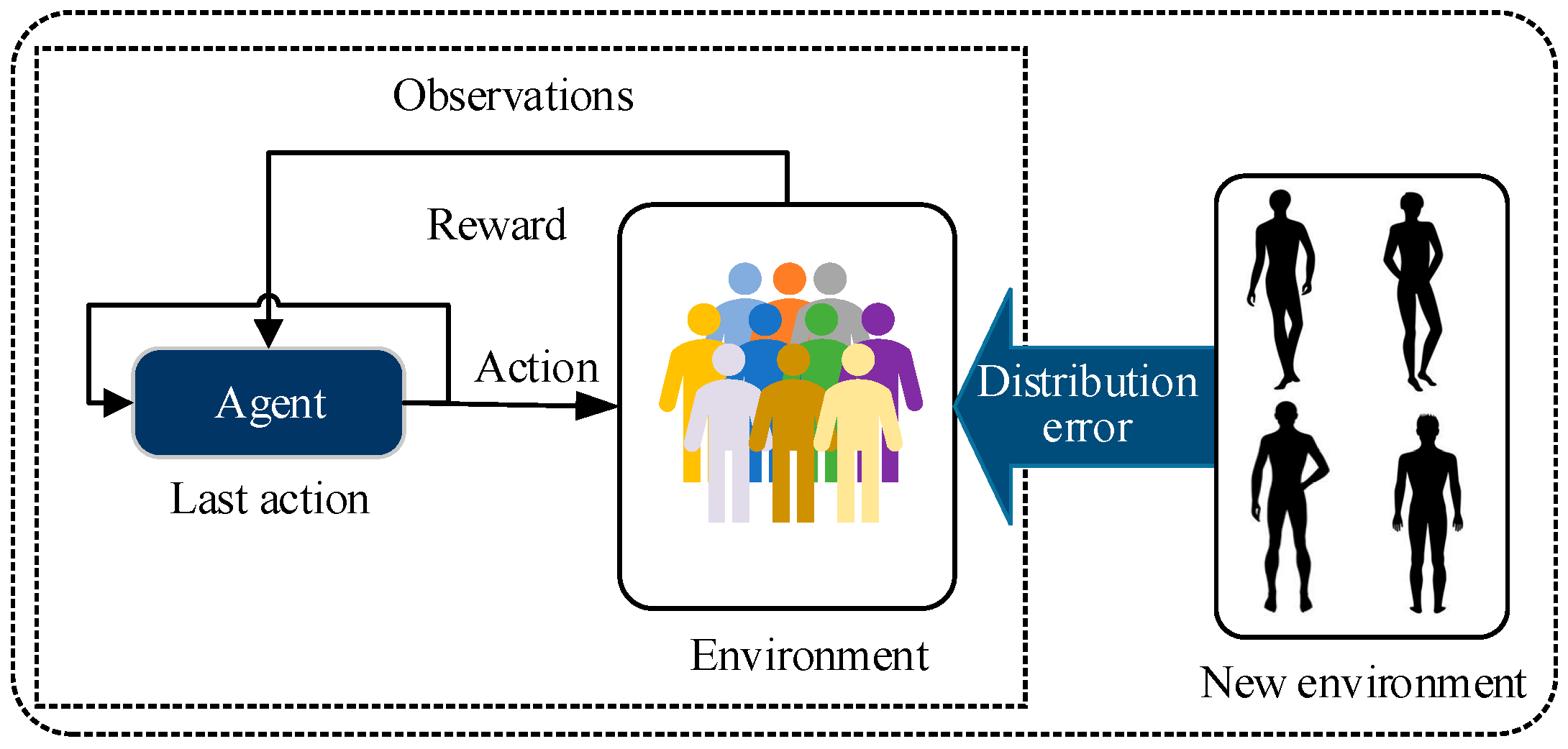
- Personalization. When an initial or pre-trained DRL controller is set to a patient, the agent encounters the challenge of distributional bias. During the training process, DRL models often only have access to local data distributions, resulting in unstable or even ineffective performance when facing different environments or unknown scenarios. Additionally, the DRL controller is required to achieve personalized control objectives due to inter-patient variability in blood glucose dynamics and individualized treatment plans.
- (3)
- Security. Since the DRL systems typically operate in dynamic and uncertain environments, their decisions may be influenced by external attacks or unexpected disturbances, leading to unexpected behaviors or outcomes.
- (1)
- To provide a well-organized overview of the methodology and applications, which includes basic concepts and detailed analysis and conclusions of DRL components applied to AIDs, focusing on discussing how DRL algorithms and AIDs can have a better match in terms of applications, including state space, action space, and reward function.
- (2)
- To classify the problems of AIDs into three key categories to illustrate the challenges of DRL in low data availability, personalization, and security.
- (3)
- To provide insights into the challenges, potential solutions, and future directions for DRL-based AIDs, with prospects for further development in terms of data requirement and computational power.
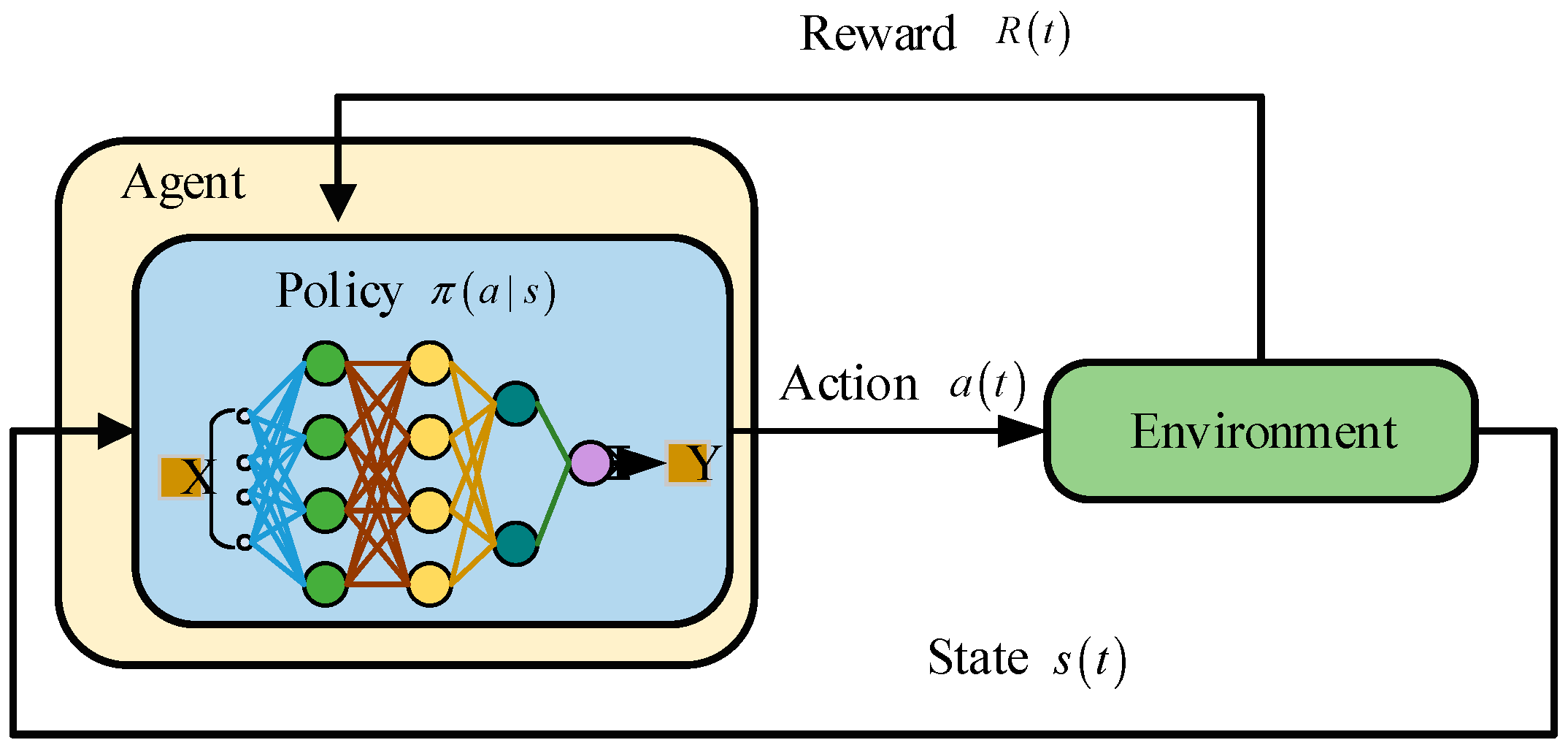
2. Overview of DRL
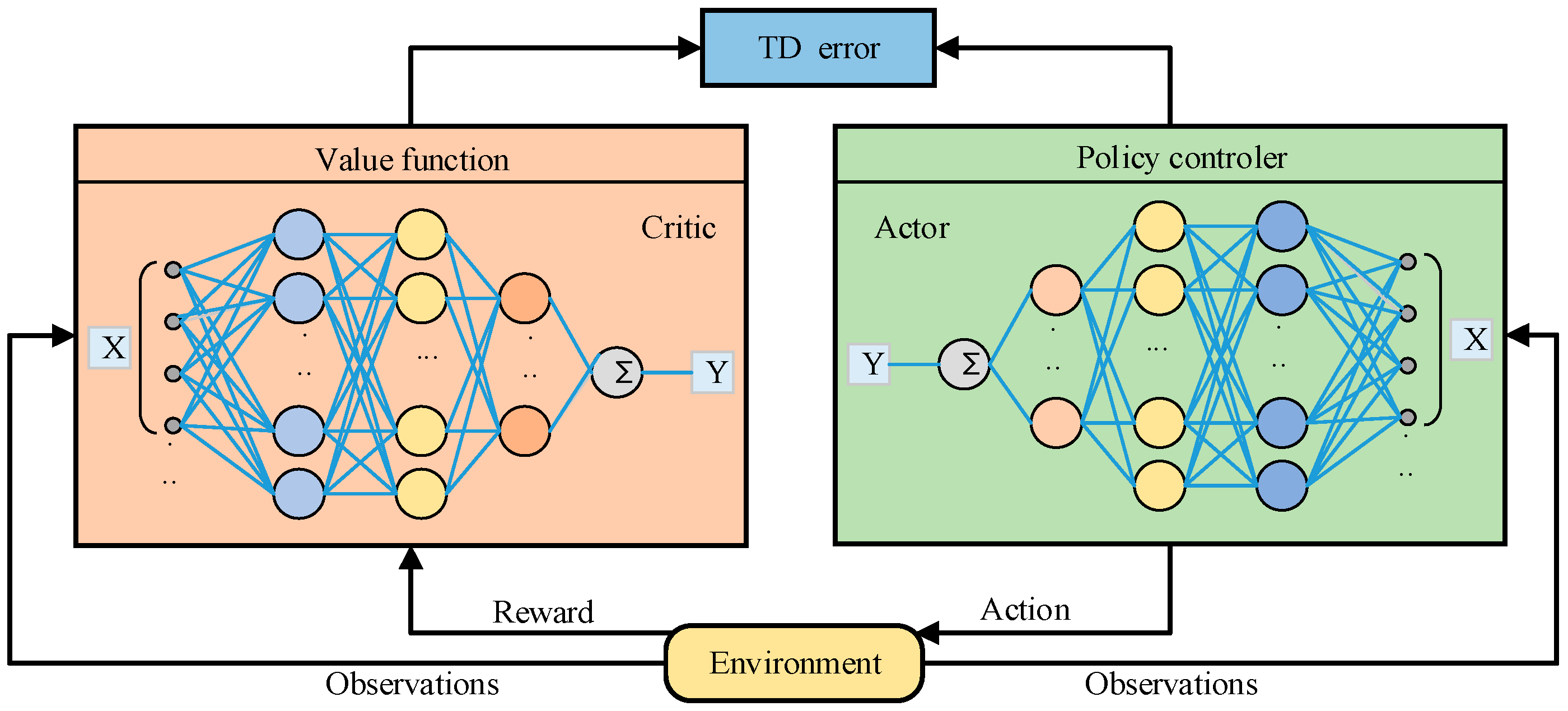
2.1. The Basic Structure of DRL
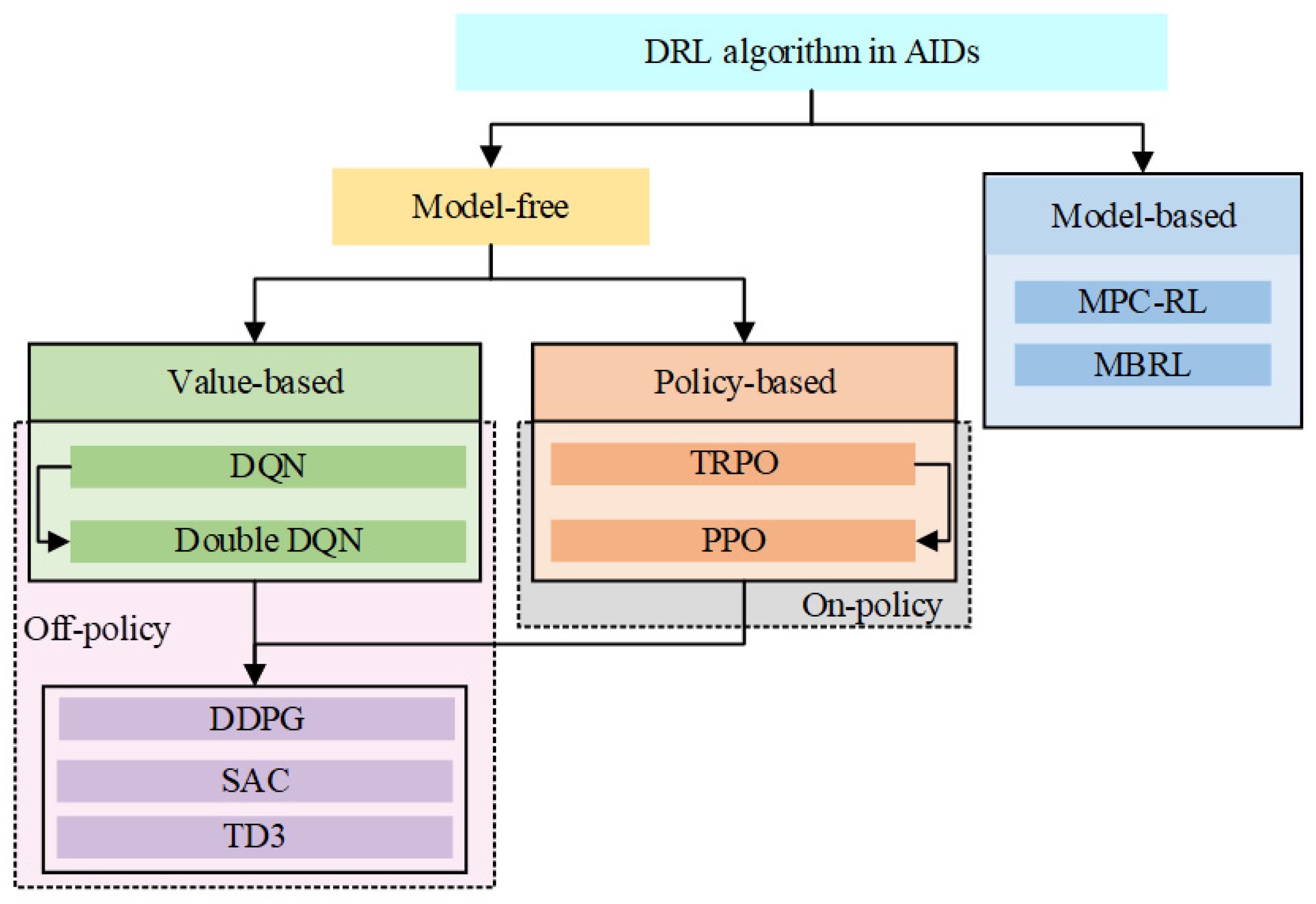
2.2. Classification of DRL and Their Characteristics
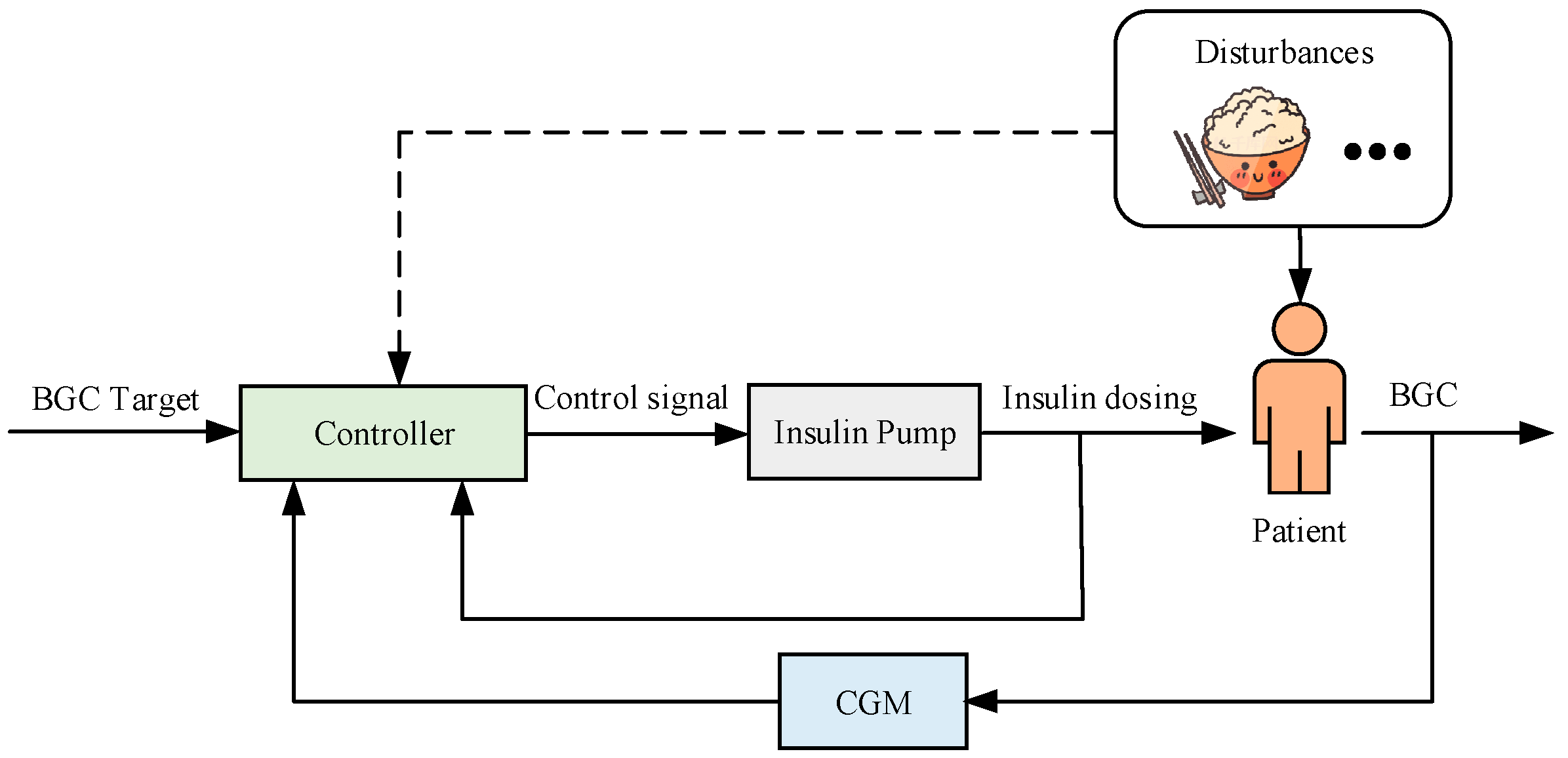
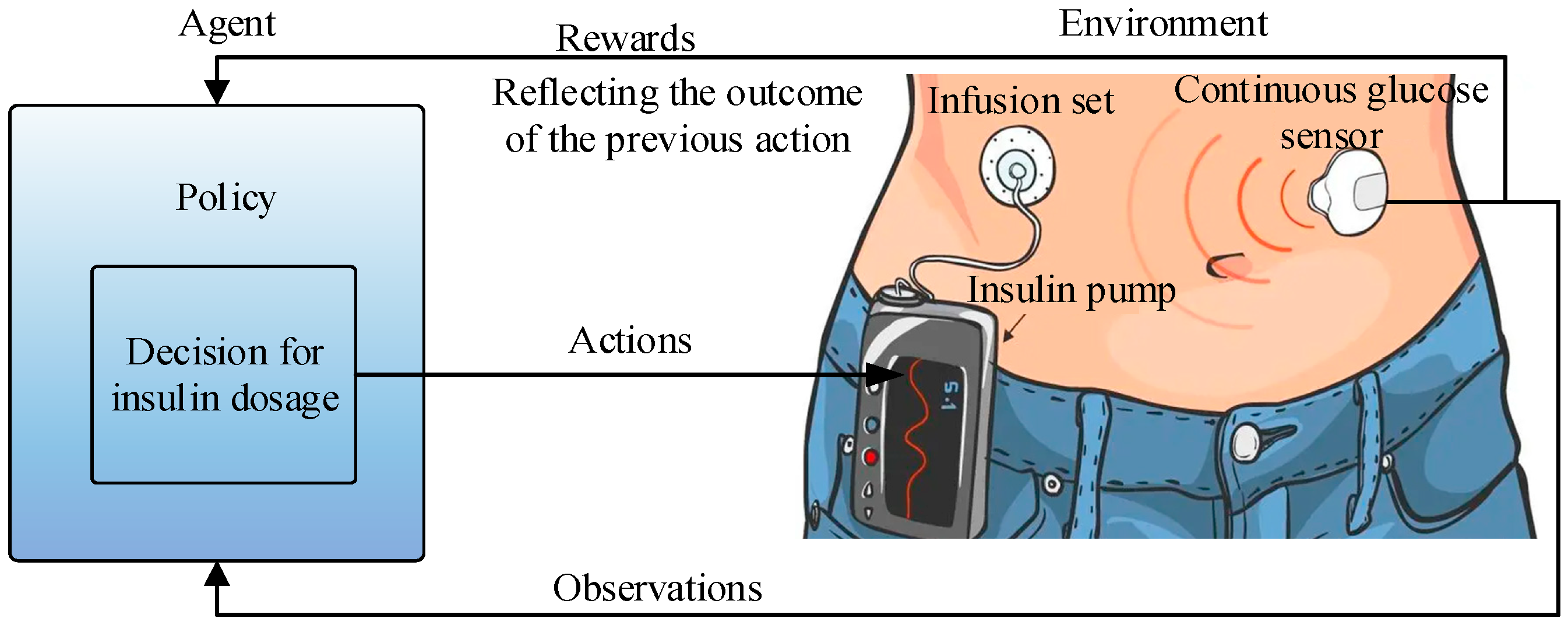
3. DRL-Based AIDs
3.1. State Space Variables Selection
3.2. Action Space Variables Selection
3.3. Reward Function Selection
4. Challenges to Be Addressed
4.1. Low Sample Availability
4.2. Personalization
4.3. Security
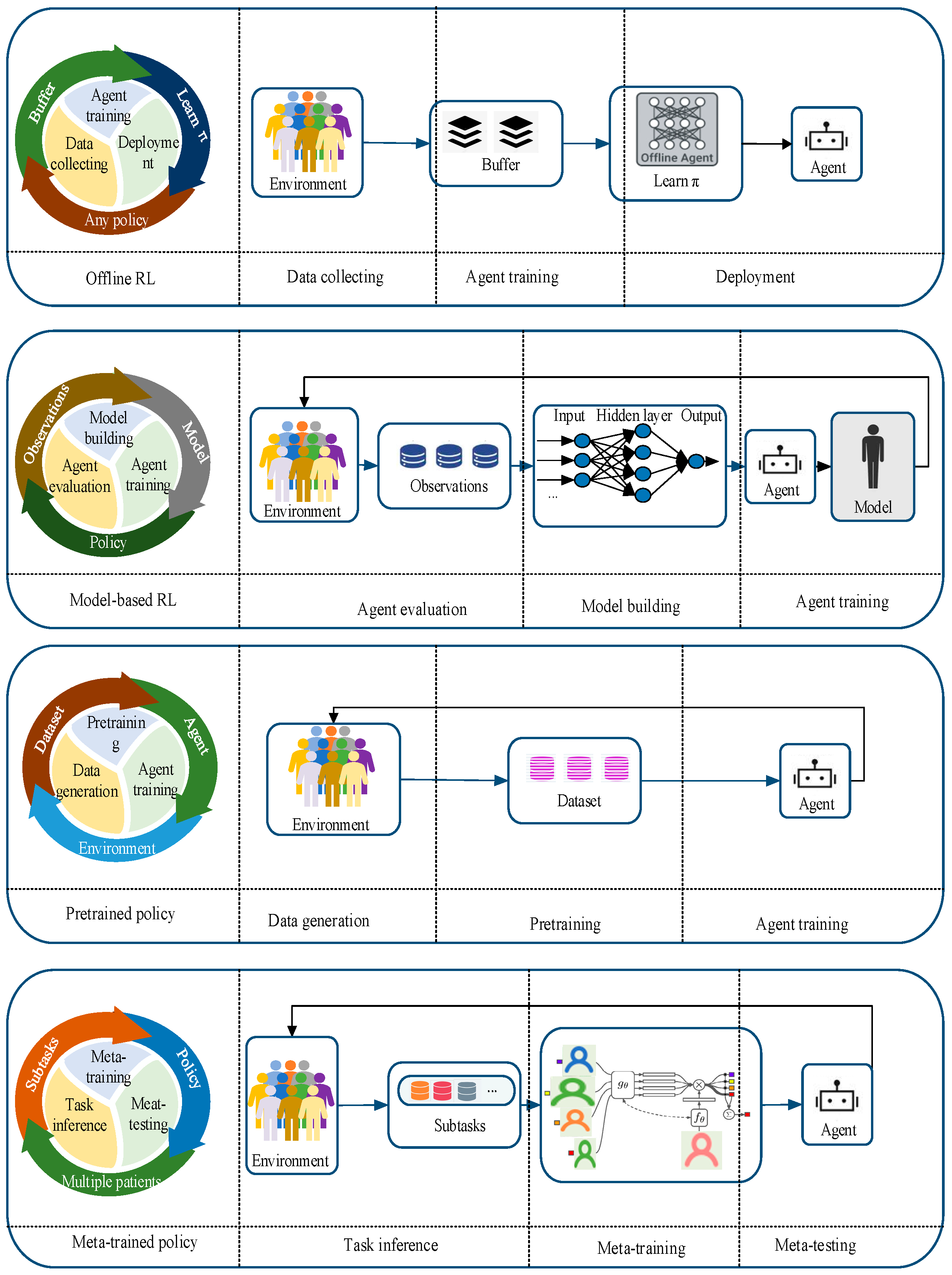
5. Practical Applications
5.1. Data
- (1)
- Collecting large amounts of clinical data is usually expensive and time-consuming [75,108], and only a few studies have made clinical validations [86,94]. The algorithms reported in Table 4 used simulated data from 5 days [76], 6 days [75], 30 days [59], 180 days [61,71], 1050 days [77] and 1000 days [48] to develop personalized dosing strategies. Whereas it is unethical to allow DRL algorithms to control patient BGC for several years in an in vivo environment without any associated safety guarantees [82], To validate the scalability of offline DRL methods in more intricate environments, algorithms should undergo training and evaluation using genuine retrospective patient data samples (e.g., data available through the OhioT1DM dataset) [83], which is why it is crucial to perform an out-of-strategy evaluation of offline algorithms [83,109].
- (2)
- Assessing algorithms in human subjects without preclinical validation or suitable safety constraints can pose risks [71]. In fact, due to the nature of DRL techniques, the use of simulated environments is particularly appropriate since the learning of the model is achieved through trial-and-error interactions with the environment, and therefore, performing such processes on virtual objects is critical to avoid dangerous situations for people with diabetes [61].
5.2. Computational Power
6. Comparison of Main Control Algorithms for AIDs
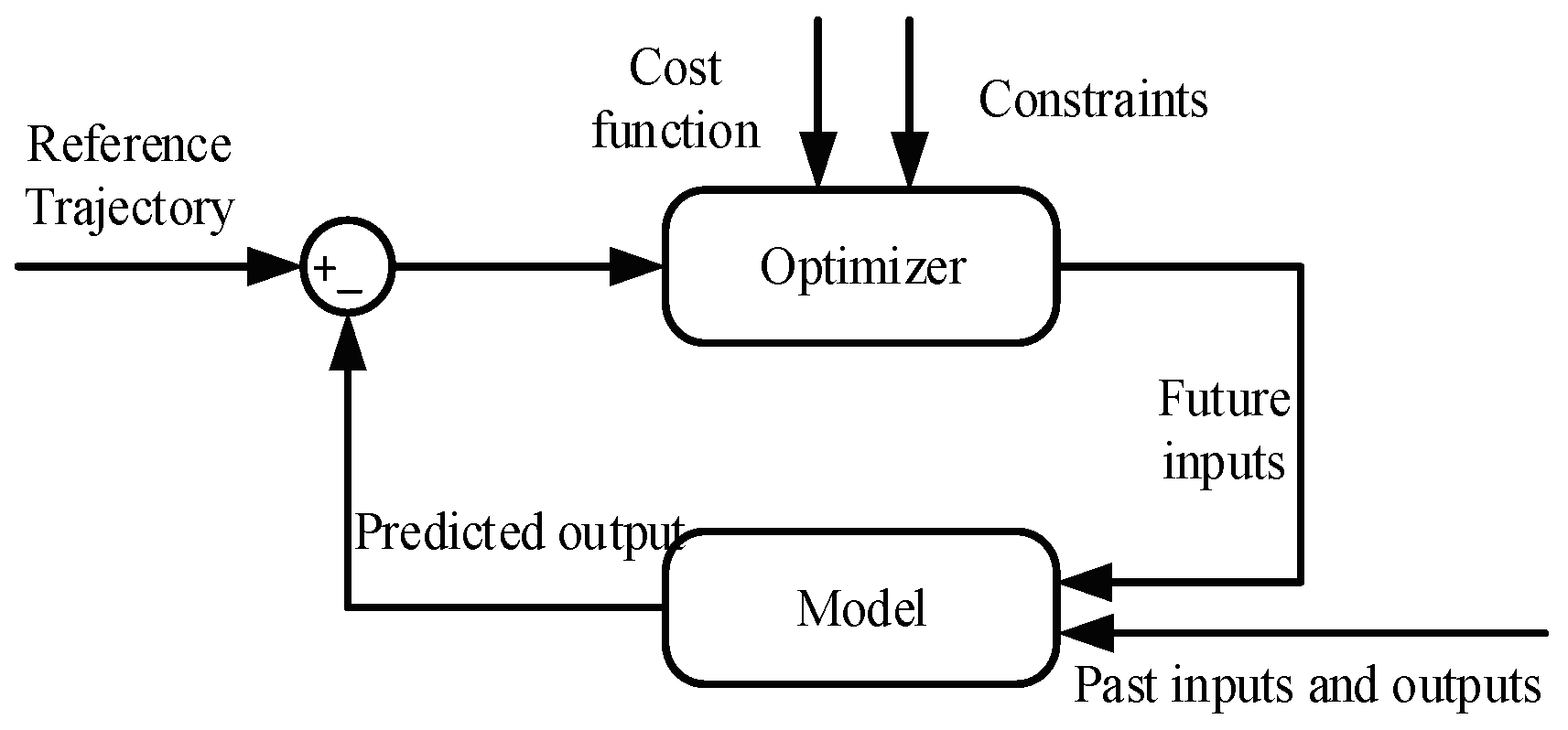
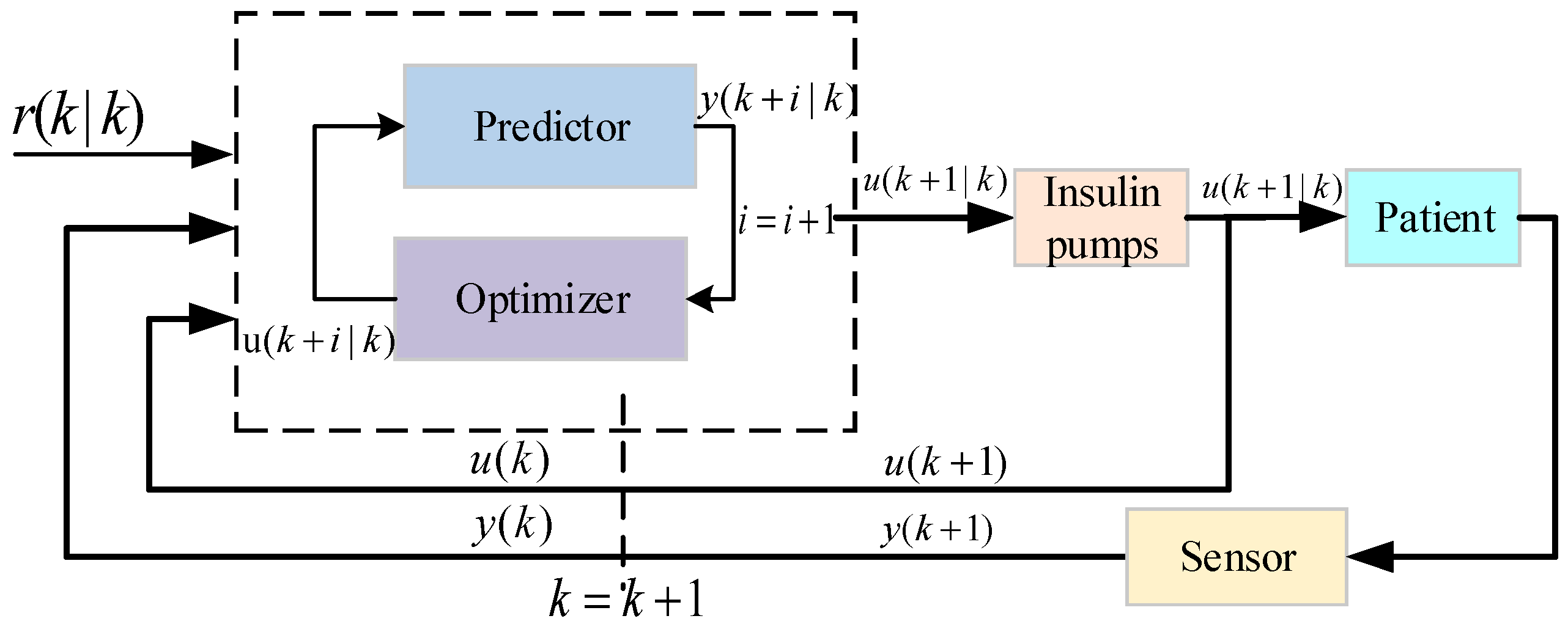
6.1. Model Predictive Control
- 1.
- Adaptation to potential perturbations
- (1)
- The model cannot adapt to uncertain perturbations because the inputs to the predictor are only factors already known to affect BGC.
- (2)
- Even with a neural network-based model, MPC still needs to solve the optimization problem at each time step (traversal solving), which can become very difficult in highly uncertain environments.
- 2.
- Responding to Patient Variability
- 3.
- Computational Efficiency
- 4.
- Exploratory Capacity
- 5.
- Adaptation to Delayed Insulin Action
6.2. Proportional Integral Derivative
6.3. Fuzzy Logic
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| AIDs | Automated insulin delivery system |
| BGC | Blood glucose concentration |
| CGM | Continuous glucose monitoring |
| CHO | Carbohydrate |
| DDPG | Deep deterministic policy gradient |
| DNN | Deep neural networks |
| Double DQN | Double deep Q-Network |
| DRL | Deep reinforcement learning |
| FL | Fuzzy logic |
| HbA1c | Hemoglobin A1c |
| IOB | Insulin on board |
| MBPO | Model-based policy optimization |
| MPC | Model predictive control |
| PID | Proportional integral derivative |
| PPO | Proximal policy optimization |
| SAC | Soft actor critic |
| SAP | Sensor augmented pump |
| TD3 | Twin delayed deep deterministic policy gradient |
| TD3-BC | Twin delayed DDPG with behavioral cloning |
| T1D | Type 1 diabetes |
| T2D | Type 2 diabetes |
| TIR | Time in range |
| TRPO | Trust region policy optimization |
References
- Association, A.D. Diagnosis and Classification of Diabetes Mellitus. Diabetes Care 2012, 36, S67–S74. [Google Scholar] [CrossRef] [PubMed]
- ElSayed, N.A.; Aleppo, G.; Aroda, V.R.; Bannuru, R.R.; Brown, F.M.; Bruemmer, D.; Collins, B.S.; Hilliard, M.E.; Isaacs, D.; Johnson, E.L.; et al. 9. Pharmacologic Approaches to Glycemic Treatment: Standards of Care in Diabetes—2023. Diabetes Care 2023, 46, S140–S157. [Google Scholar] [CrossRef] [PubMed]
- Stanford Medicine. New Research Keeps Diabetics Safer During Sleep. Available online: http://scopeblog.stanford.edu/2014/05/08/new-research-keeps-diabetics-safer-during-sleep/ (accessed on 23 October 2024).
- Phillip, M.; Nimri, R.; Bergenstal, R.M.; Barnard-Kelly, K.; Danne, T.; Hovorka, R.; Kovatchev, B.P.; Messer, L.H.; Parkin, C.G.; Ambler-Osborn, L.; et al. Consensus Recommendations for the Use of Automated Insulin Delivery Technologies in Clinical Practice. Endocr. Rev. 2023, 44, 254–280. [Google Scholar] [CrossRef]
- Oliveira, C.P.; Mitchell, B.D.; Fan, L.D.; Garey, C.; Liao, B.R.; Bispham, J.; Vint, N.; Perez-Nieves, M.; Hughes, A.; McAuliffe-Fogarty, A. Patient perspectives on the use of half-unit insulin pens by people with type 1 diabetes: A cross-sectional observational study. Curr. Med. Res. Opin. 2021, 37, 45–51. [Google Scholar] [CrossRef]
- Kamrul-Hasan, A.B.M.; Hannan, M.A.; Alam, M.S.; Rahman, M.M.; Asaduzzaman, M.; Mustari, M.; Paul, A.K.; Kabir, M.L.; Chowdhury, S.R.; Talukder, S.K.; et al. Comparison of simplicity, convenience, safety, and cost-effectiveness between use of insulin pen devices and disposable plastic syringes by patients with type 2 diabetes mellitus: A cross-sectional study from Bangladesh. BMC Endocr. Disord. 2023, 23, 37. [Google Scholar] [CrossRef]
- Machry, R.V.; Cipriani, G.F.; Pedroso, H.U.; Nunes, R.R.; Pires, T.L.S.; Ferreira, R.; Vescovi, B.; De Moura, G.P.; Rodrigues, T.C. Pens versus syringes to deliver insulin among elderly patients with type 2 diabetes: A randomized controlled clinical trial. Diabetol. Metab. Syndr. 2021, 13, 64. [Google Scholar] [CrossRef]
- ElSayed, N.A.; Aleppo, G.; Aroda, V.R.; Bannuru, R.R.; Brown, F.M.; Bruemmer, D.; Collins, B.S.; Hilliard, M.E.; Isaacs, D.; Johnson, E.L.; et al. 7. Diabetes Technology: Standards of Care in Diabetes—2023. Diabetes Care 2023, 46, S111–S127. [Google Scholar] [CrossRef]
- Chinese Society of Endocrinology. Chinese Insulin Pump Treatment Guidelines (2021 edition). Chin. J. Endocrinol. Metab. 2021, 37, 679–701. [Google Scholar]
- Tonnies, T.; Brinks, R.; Isom, S.; Dabelea, D.; Divers, J.; Mayer-Davis, E.J.; Lawrence, J.M.; Pihoker, C.; Dolan, L.; Liese, A.D.; et al. Projections of Type 1 and Type 2 Diabetes Burden in the US Population Aged <20 Years Through 2060: The SEARCH for Diabetes in Youth Study. Diabetes Care 2023, 46, 313–320. [Google Scholar] [CrossRef]
- ElSayed, N.A.; Aleppo, G.; Aroda, V.R.; Bannuru, R.R.; Brown, F.M.; Bruemmer, D.; Collins, B.S.; Hilliard, M.E.; Isaacs, D.; Johnson, E.L.; et al. 14. Children and Adolescents: Standards of Care in Diabetes—2023. Diabetes Care 2023, 46, S230–S253. [Google Scholar] [CrossRef]
- Wadwa, R.P.; Reed, Z.W.; Buckingham, B.A.; DeBoer, M.D.; Ekhlaspour, L.; Forlenza, G.P.; Schoelwer, M.; Lum, J.; Kollman, C.; Beck, R.W.; et al. Trial of Hybrid Closed-Loop Control in Young Children with Type 1 Diabetes. N. Engl. J. Med. 2023, 388, 991–1001. [Google Scholar] [CrossRef] [PubMed]
- DiMeglio, L.A.; Kanapka, L.G.; DeSalvo, D.J.; Hilliard, M.E.; Laffel, L.M.; Tamborlane, W.V.; Van Name, M.A.; Woerner, S.; Adi, S.; Albanese-O’Neill, A.; et al. A Randomized Clinical Trial Assessing Continuous Glucose Monitoring (CGM) Use with Standardized Education with or Without a Family Behavioral Intervention Compared with Fingerstick Blood Glucose Monitoring in Very Young Children with Type 1 Diabetes. Diabetes Care 2021, 44, 464–472. [Google Scholar] [CrossRef]
- Laffel, L.M.; Kanapka, L.G.; Beck, R.W.; Bergamo, K.; Clements, M.A.; Criego, A.; DeSalvo, D.J.; Goland, R.; Hood, K.; Liljenquist, D.; et al. Effect of Continuous Glucose Monitoring on Glycemic Control in Adolescents and Young Adults with Type 1 Diabetes A Randomized Clinical Trial. JAMA J. Am. Med. Assoc. 2020, 323, 2388–2396. [Google Scholar] [CrossRef] [PubMed]
- Yeh, H.C.; Brown, T.T.; Maruthur, N.; Ranasinghe, P.; Berger, Z.; Suh, Y.D.; Wilson, L.M.; Haberl, E.B.; Brick, J.; Bass, E.B.; et al. Comparative Effectiveness and Safety of Methods of Insulin Delivery and Glucose Monitoring for Diabetes Mellitus: A Systematic Review and Meta-analysis. Ann. Intern. Med. 2012, 157, 336–347. [Google Scholar] [CrossRef]
- Forlenza, G.P.; Lal, R.A. Current Status and Emerging Options for Automated Insulin Delivery Systems. Diabetes Technol. Ther. 2022, 24, 362–371. [Google Scholar] [CrossRef]
- Lal, R.A.; Ekhlaspour, L.; Hood, K.; Buckingham, B. Realizing a Closed-Loop (Artificial Pancreas) System for the Treatment of Type 1 Diabetes. Endocr. Rev. 2019, 40, 1521–1546. [Google Scholar] [CrossRef]
- Boughton, C.K.; Hovorka, R. New closed-loop insulin systems. Diabetologia 2021, 64, 1007–1015. [Google Scholar] [CrossRef]
- Karageorgiou, V.; Papaioannou, T.G.; Bellos, I.; Alexandraki, K.; Tentolouris, N.; Stefanadis, C.; Chrousos, G.P.; Tousoulis, D. Effectiveness of artificial pancreas in the non-adult population: A systematic review and network meta-analysis. Metab. Clin. Exp. 2019, 90, 20–30. [Google Scholar] [CrossRef]
- Anderson, S.M.; Buckingham, B.A.; Breton, M.D.; Robic, J.L.; Barnett, C.L.; Wakeman, C.A.; Oliveri, M.C.; Brown, S.A.; Ly, T.T.; Clinton, P.K.; et al. Hybrid Closed-Loop Control Is Safe and Effective for People with Type 1 Diabetes Who Are at Moderate to High Risk for Hypoglycemia. Diabetes Technol. Ther. 2019, 21, 356–363. [Google Scholar] [CrossRef]
- Forlenza, G.P.; Ekhlaspour, L.; Breton, M.; Maahs, D.M.; Wadwa, R.P.; DeBoer, M.; Messer, L.H.; Town, M.; Pinnata, J.; Kruse, G.; et al. Successful At-Home Use of the Tandem Control-IQ Artificial Pancreas System in Young Children During a Randomized Controlled Trial. Diabetes Technol. Ther. 2019, 21, 159–169. [Google Scholar] [CrossRef]
- Forlenza, G.P.; Pinhas-Hamiel, O.; Liljenquist, D.R.; Shulman, D.I.; Bailey, T.S.; Bode, B.W.; Wood, M.A.; Buckingham, B.A.; Kaiserman, K.B.; Shin, J.; et al. Safety Evaluation of the MiniMed 670G System in Children 7–13 Years of Age with Type 1 Diabetes. Diabetes Technol. Ther. 2019, 21, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Sherr, J.L.; Cengiz, E.; Palerm, C.C.; Clark, B.; Kurtz, N.; Roy, A.; Carria, L.; Cantwell, M.; Tamborlane, W.V.; Weinzimer, S.A. Reduced Hypoglycemia and Increased Time in Target Using Closed-Loop Insulin Delivery During Nights with or Without Antecedent Afternoon Exercise in Type 1 Diabetes. Diabetes Care 2013, 36, 2909–2914. [Google Scholar] [CrossRef] [PubMed]
- Zaharieva, D.P.; Messer, L.H.; Paldus, B.; O’Neal, D.N.; Maahs, D.M.; Riddell, M.C. Glucose Control During Physical Activity and Exercise Using Closed Loop Technology in Adults and Adolescents with Type 1 Diabetes. Can. J. Diabetes 2020, 44, 740–749. [Google Scholar] [CrossRef]
- Carlson, A.L.; Sherr, J.L.; Shulman, D.I.; Garg, S.K.; Pop-Busui, R.; Bode, B.W.; Lilenquist, D.R.; Brazg, R.L.; Kaiserman, K.B.; Kipnes, M.S.; et al. Safety and Glycemic Outcomes During the MiniMed (TM) Advanced Hybrid Closed-Loop System Pivotal Trial in Adolescents and Adults with Type 1 Diabetes. Diabetes Technol. Ther. 2022, 24, 178–189. [Google Scholar] [CrossRef]
- Bothe, M.K.; Dickens, L.; Reichel, K.; Tellmann, A.; Ellger, B.; Westphal, M.; Faisal, A.A. The use of reinforcement learning algorithms to meet the challenges of an artificial pancreas. Expert Rev. Med. Devices 2013, 10, 661–673. [Google Scholar] [CrossRef]
- Bhonsle, S.; Saxena, S. A review on control-relevant glucose-insulin dynamics models and regulation strategies. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2020, 234, 596–608. [Google Scholar] [CrossRef]
- Kovatchev, B. A Century of Diabetes Technology: Signals, Models, and Artificial Pancreas Control. Trends Endocrinol. Metab. 2019, 30, 432–444. [Google Scholar] [CrossRef]
- Quiroz, G. The evolution of control algorithms in artificial pancreas: A historical perspective. Annu. Rev. Control 2019, 48, 222–232. [Google Scholar] [CrossRef]
- Thomas, A.; Heinemann, L. Algorithm for automated insulin delivery (AID): An overview. Diabetologie 2022, 18, 862–874. [Google Scholar] [CrossRef]
- Fuchs, J.; Hovorka, R. Closed-loop control in insulin pumps for type-1 diabetes mellitus: Safety and efficacy. Expert. Rev. Med. Devices 2020, 17, 707–720. [Google Scholar] [CrossRef]
- Marchetti, G.; Barolo, M.; Jovanovic, L.; Zisser, H.; Seborg, D.E. An improved PID switching control strategy for type 1 diabetes. IEEE Trans. Biomed. Eng. 2008, 55, 857–865. [Google Scholar] [CrossRef] [PubMed]
- MohammadRidha, T.; Ait-Ahmed, M.; Chaillous, L.; Krempf, M.; Guilhem, I.; Poirier, J.Y.; Moog, C.H. Model Free iPID Control for Glycemia Regulation of Type-1 Diabetes. IEEE Trans. Biomed. Eng. 2018, 65, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Al-Hussein, A.-B.A.; Tahir, F.R.; Viet-Thanh, P. Fixed-time synergetic control for chaos suppression in endocrine glucose-insulin regulatory system. Control Eng. Pract. 2021, 108, 104723. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. Model. Identif. Control 2004, 25, 85–120. [Google Scholar] [CrossRef]
- Nath, A.; Dey, R.; Balas, V.E. Closed Loop Blood Glucose Regulation of Type 1 Diabetic Patient Using Takagi-Sugeno Fuzzy Logic Control. In Soft Computing Applications, Sofa 2016; Springer: Cham, Switzerland, 2018; Volume 634, pp. 286–296. [Google Scholar] [CrossRef]
- Yadav, J.; Rani, A.; Singh, V. Performance Analysis of Fuzzy-PID Controller for Blood Glucose Regulation in Type-1 Diabetic Patients. J. Med. Syst. 2016, 40, 254. [Google Scholar] [CrossRef]
- Bondia, J.; Romero-Vivo, S.; Ricarte, B.; Diez, J.L. Insulin Estimation and Prediction: A Review of the Estimation and Prediction of Subcutaneous Inaulin Pharmacokinetics in Closed-loop Glucose Control. IEEE Control Syst. Mag. 2018, 38, 47–66. [Google Scholar] [CrossRef]
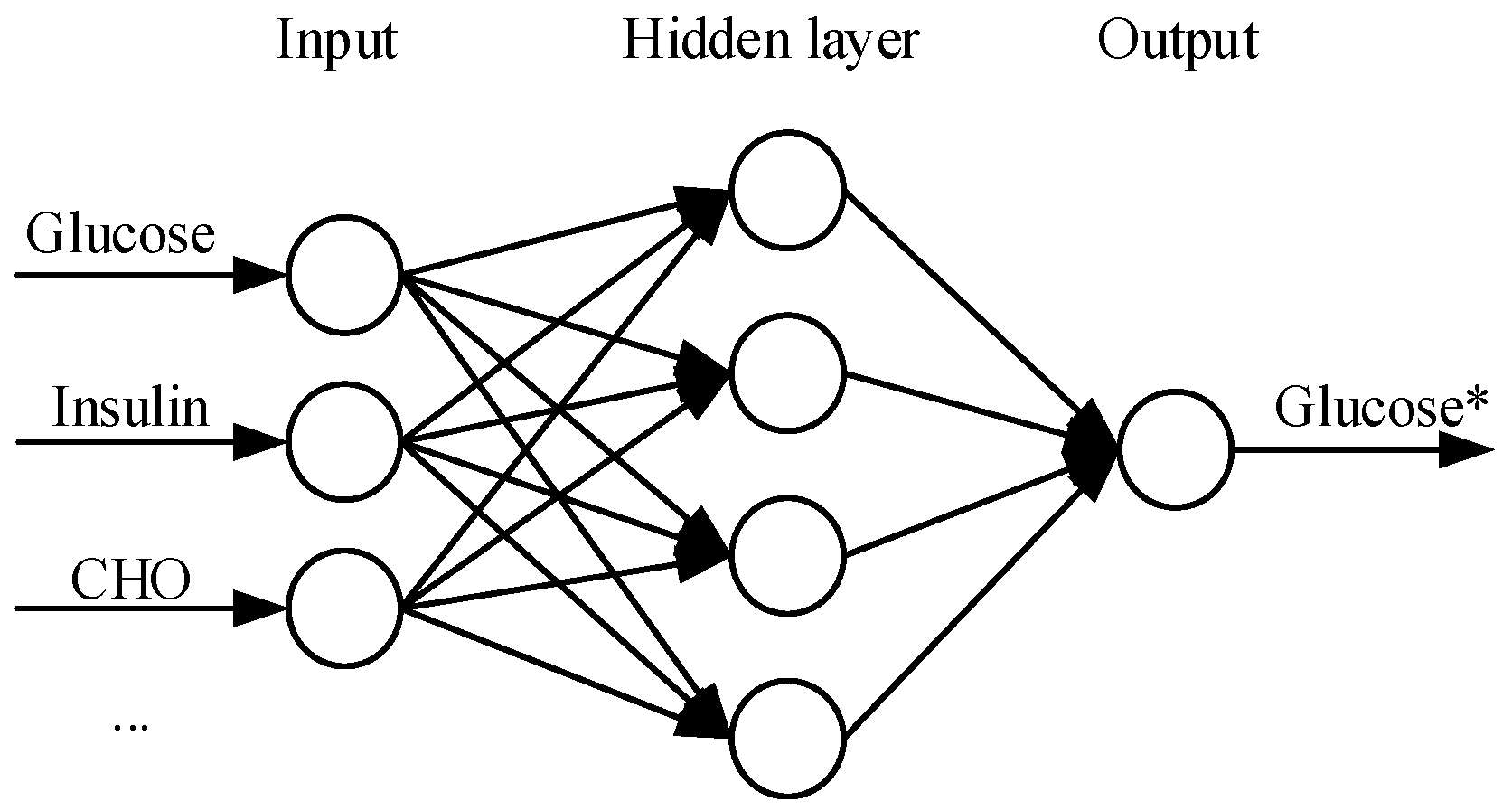
- Oviedo, S.; Vehi, J.; Calm, R.; Armengol, J. A review of personalized blood glucose prediction strategies for T1DM patients. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2833. [Google Scholar] [CrossRef]
- Gondhalekar, R.; Dassau, E.; Doyle, F.J. Velocity-weighting & velocity-penalty MPC of an artificial pancreas: Improved safety & performance. Automatica 2018, 91, 105–117. [Google Scholar] [CrossRef]
- Shi, D.W.; Dassau, E.; Doyle, F.J. Adaptive Zone Model Predictive Control of Artificial Pancreas Based on Glucose- and Velocity-Dependent Control Penalties. IEEE Trans. Biomed. Eng. 2019, 66, 1045–1054. [Google Scholar] [CrossRef]
- Birjandi, S.Z.; Sani, S.K.H.; Pariz, N. Insulin infusion rate control in type 1 diabetes patients using information-theoretic model predictive control. Biomed. Signal Process. Control 2022, 76, 103635. [Google Scholar] [CrossRef]
- Williams, G.; Drews, P.; Goldfain, B.; Rehg, J.M.; Theodorou, E.A. Information-Theoretic Model Predictive Control: Theory and Applications to Autonomous Driving. IEEE Trans. Robot. 2017, 34, 1603–1622. [Google Scholar] [CrossRef]
- Li, Y.; Yu, C.; Shahidehpour, M.; Yang, T.; Zeng, Z.; Chai, T. Deep Reinforcement Learning for Smart Grid Operations: Algorithms, Applications, and Prospects. Proc. IEEE 2023, 111, 1055–1096. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.A.; Yogamani, S.; Pérez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Nemati, S.; Ghassemi, M.M.; Clifford, G.D. Optimal medication dosing from suboptimal clinical examples: A deep reinforcement learning approach. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 2978–2981. [Google Scholar]
- Fox, I.; Lee, J.; Pop-Busui, R.; Wiens, J. Deep Reinforcement Learning for Closed-Loop Blood Glucose Control. Mach. Learn. Healthc. 2020, 126, 508–536. [Google Scholar]
- Tejedor, M.; Woldaregay, A.Z.; Godtliebsen, F. Reinforcement learning application in diabetes blood glucose control: A systematic review. Artif. Intell. Med. 2020, 104, 101836. [Google Scholar] [CrossRef]
- Sharma, R.; Singh, D.; Gaur, P.; Joshi, D. Intelligent automated drug administration and therapy: Future of healthcare. Drug Deliv. Transl. Res. 2021, 11, 1878–1902. [Google Scholar] [CrossRef]
- Toffanin, C.; Visentin, R.; Messori, M.; Palma, F.D.; Magni, L.; Cobelli, C. Toward a Run-to-Run Adaptive Artificial Pancreas: In Silico Results. IEEE Trans. Biomed. Eng. 2018, 65, 479–488. [Google Scholar] [CrossRef]
- Yau, K.-L.A.; Chong, Y.-W.; Fan, X.; Wu, C.; Saleem, Y.; Lim, P.-C. Reinforcement Learning Models and Algorithms for Diabetes Management. IEEE Access 2023, 11, 28391–28415. [Google Scholar] [CrossRef]
- Denes-Fazakas, L.; Fazakas, G.D.; Eigner, G.; Kovacs, L.; Szilagyi, L. Review of Reinforcement Learning-Based Control Algorithms in Artificial Pancreas Systems for Diabetes Mellitus Management. In Proceedings of the 18th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 23–25 May 2024; pp. 565–571. [Google Scholar] [CrossRef]
- Shin, J.; Badgwell, T.A.; Liu, K.-H.; Lee, J.H. Reinforcement Learning—Overview of recent progress and implications for process control. Comput. Chem. Eng. 2019, 127, 282–294. [Google Scholar] [CrossRef]
- Daskalaki, E.; Diem, P.; Mougiakakou, S.G. Model-Free Machine Learning in Biomedicine: Feasibility Study in Type 1 Diabetes. PLoS ONE 2016, 11, e0158722. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Gu, W. An Improved Strategy for Blood Glucose Control Using Multi-Step Deep Reinforcement Learning. arXiv 2024, arXiv:2403.07566. [Google Scholar]
- Ahmad, S.; Beneyto, A.; Zhu, T.; Contreras, I.; Georgiou, P.; Vehi, J. An automatic deep reinforcement learning bolus calculator for automated insulin delivery systems. Sci. Rep. 2024, 14, 15245. [Google Scholar] [CrossRef] [PubMed]
- Del Giorno, S.; D’Antoni, F.; Piemonte, V.; Merone, M. A New Glycemic closed-loop control based on Dyna-Q for Type-1-Diabetes. Biomed. Signal Process. Control 2023, 81, 104492. [Google Scholar] [CrossRef]
- Zhu, T.; Li, K.; Herrero, P.; Georgiou, P. Basal Glucose Control in Type 1 Diabetes Using Deep Reinforcement Learning: An In Silico Validation. IEEE J. Biomed. Health Inform. 2021, 25, 1223–1232. [Google Scholar] [CrossRef]
- Li, T.; Wang, Z.; Lu, W.; Zhang, Q.; Li, D. Electronic health records based reinforcement learning for treatment optimizing. Inf. Syst. 2022, 104, 101878. [Google Scholar] [CrossRef]
- Noaro, G.; Zhu, T.; Cappon, G.; Facchinetti, A.; Georgiou, P. A Personalized and Adaptive Insulin Bolus Calculator Based on Double Deep Q—Learning to Improve Type 1 Diabetes Management. IEEE J. Biomed. Health Inform. 2023, 27, 2536–2544. [Google Scholar] [CrossRef]
- Hettiarachchi, C.; Malagutti, N.; Nolan, C.J.; Suominen, H.; Daskalaki, E. Non-linear Continuous Action Spaces for Reinforcement Learning in Type 1 Diabetes. In Ai 2022: Advances in Artificial Intelligence; Springer: Cham, Switzerland, 2022; Volume 13728, pp. 557–570. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Park, S.W.; Jin, S.M.; Park, S.M. Toward a Fully Automated Artificial Pancreas System Using a Bioinspired Reinforcement Learning Design: In Silico Validation. IEEE J. Biomed. Health Inform. 2021, 25, 536–546. [Google Scholar] [CrossRef]
- Lehel, D.-F.; Siket, M.; Szilágyi, L.; Eigner, G.; Kovács, L. Investigation of reward functions for controlling blood glucose level using reinforcement learning. In Proceedings of the 2023 IEEE 17th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 23–26 May 2023; pp. 387–392. [Google Scholar]
- Viroonluecha, P.; Egea-Lopez, E.; Santa, J. Evaluation of blood glucose level control in type 1 diabetic patients using deep reinforcement learning. PLoS ONE 2022, 17, e0274608. [Google Scholar] [CrossRef]
- Hettiarachchi, C.; Malagutti, N.; Nolan, C.J.; Suominen, H.; Daskalaki, E. G2P2C—A modular reinforcement learning algorithm for glucose control by glucose prediction and planning in Type 1 Diabetes. Biomed. Signal Process. Control 2024, 90, 105839. [Google Scholar] [CrossRef]
- El Fathi, A.; Pryor, E.; Breton, M.D. Attention Networks for Personalized Mealtime Insulin Dosing in People with Type 1 Diabetes. IFAC-PapersOnLine 2024, 58, 245–250. [Google Scholar] [CrossRef]
- Denes-Fazakas, L.; Szilagyi, L.; Kovacs, L.; De Gaetano, A.; Eigner, G. Reinforcement Learning: A Paradigm Shift in Personalized Blood Glucose Management for Diabetes. Biomedicines 2024, 12, 2143. [Google Scholar] [CrossRef] [PubMed]
- Nordhaug Myhre, J.; Tejedor, M.; Kalervo Launonen, I.; El Fathi, A.; Godtliebsen, F. In-Silico Evaluation of Glucose Regulation Using Policy Gradient Reinforcement Learning for Patients with Type 1 Diabetes Mellitus. Appl. Sci. 2020, 10, 6350. [Google Scholar] [CrossRef]
- Di Felice, F.; Borri, A.; Di Benedetto, M.D. Deep reinforcement learning for closed-loop blood glucose control: Two approaches. IFAC Pap. 2022, 55, 115–120. [Google Scholar] [CrossRef]
- Zhu, T.; Li, K.; Kuang, L.; Herrero, P.; Georgiou, P. An Insulin Bolus Advisor for Type 1 Diabetes Using Deep Reinforcement Learning. Sensors 2020, 20, 5058. [Google Scholar] [CrossRef]
- Ellis, Z. Application of Reinforcement Learning Algorithm to Minimize the Dosage of Insulin Infusion; East Carolina University: Greenville, NC, USA, 2024; p. 59. [Google Scholar]
- Raheb, M.A.; Niazmand, V.R.; Eqra, N.; Vatankhah, R. Subcutaneous insulin administration by deep reinforcement learning for blood glucose level control of type-2 diabetic patients. Comput. Biol. Med. 2022, 148, 105860. [Google Scholar] [CrossRef]
- Lim, M.H.; Lee, W.H.; Jeon, B.; Kim, S. A Blood Glucose Control Framework Based on Reinforcement Learning With Safety and Interpretability: In Silico Validation. IEEE Access 2021, 9, 105756–105775. [Google Scholar] [CrossRef]
- Lv, W.; Wu, T.; Xiong, L.; Wu, L.; Zhou, J.; Tang, Y.; Qian, F. Hybrid Control Policy for Artificial Pancreas via Ensemble Deep Reinforcement Learning. IEEE Trans. Biomed. Eng. 2023, 72, 309–323. [Google Scholar] [CrossRef]
- Yu, X.; Guan, Y.; Yan, L.; Li, S.; Fu, X.; Jiang, J. ARLPE: A meta reinforcement learning framework for glucose regulation in type 1 diabetics. Expert Syst. Appl. 2023, 228, 120156. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, Y.; Rao, W.; Zhao, Q.; Li, J.; Wang, C. Reinforcement Learning for Diabetes Blood Glucose Control with Meal Information. Bioinform. Res. Appl. 2021, 13064, 80–91. [Google Scholar] [CrossRef]
- Jiang, J.; Shen, R.; Wang, B.; Guan, Y. Blood Glucose Control Via Pre-trained Counterfactual Invertible Neural Networks. arXiv 2024, arXiv:2405.17458. [Google Scholar]
- Chlumsky-Harttmann, M.; Ayad, A.; Schmeink, A. HypoTreat: Reducing Hypoglycemia in Artificial Pancreas Simulation. In Proceedings of the 2024 IEEE Conference on Evolving and Adaptive Intelligent Systems (EAIS), Madrid, Spain, 23–24 May 2024; pp. 56–62. [Google Scholar] [CrossRef]
- Jaloli, M.; Cescon, M. Basal-bolus advisor for type 1 diabetes (T1D) patients using multi-agent reinforcement learning (RL) methodology. Control Eng. Pract. 2024, 142, 105762. [Google Scholar] [CrossRef]
- Mackey, A.; Furey, E. Artificial Pancreas Control for Diabetes using TD3 Deep Reinforcement Learning. In Proceedings of the 2022 33rd Irish Signals and Systems Conference (ISSC), Cork, Ireland, 9–10 June 2022; pp. 1–6. [Google Scholar]
- Emerson, H.; Guy, M.; McConville, R. Offline reinforcement learning for safer blood glucose control in people with type 1 diabetes. J. Biomed. Inform. 2023, 142, 104376. [Google Scholar] [CrossRef]
- Zhu, T.; Li, K.; Georgiou, P. Offline Deep Reinforcement Learning and Off-Policy Evaluation for Personalized Basal Insulin Control in Type 1 Diabetes. IEEE J. Biomed. Health Inform. 2023, 27, 5087–5098. [Google Scholar] [CrossRef]
- Beolet, T.; Adenis, A.; Huneker, E.; Louis, M. End-to-end offline reinforcement learning for glycemia control. Artif. Intell. Med. 2024, 154, 102920. [Google Scholar] [CrossRef]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.; Abbeel, P. Trust Region Policy Optimization. Int. Conf. Mach. Learn. 2015, 37, 1889–1897. [Google Scholar]
- Wang, G.; Liu, X.; Ying, Z.; Yang, G.; Chen, Z.; Liu, Z.; Zhang, M.; Yan, H.; Lu, Y.; Gao, Y.; et al. Optimized glycemic control of type 2 diabetes with reinforcement learning: A proof-of-concept trial. Nat. Med. 2023, 29, 2633–2642. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, Z.; Tu, E.; Zhong, A.; Liu, Y.; Ding, J.; Yang, J. Reinforcement Learning-Based Insulin Injection Time And Dosages Optimization. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Unsworth, R.; Avari, P.; Lett, A.M.; Oliver, N.; Reddy, M. Adaptive bolus calculators for people with type 1 diabetes: A systematic review. Diabetes Obes. Metab. 2023, 25, 3103–3113. [Google Scholar] [CrossRef]
- Jafar, A.; Fathi, A.E.; Haidar, A. Long-term use of the hybrid artificial pancreas by adjusting carbohydrate ratios and programmed basal rate: A reinforcement learning approach. Comput. Methods Programs Biomed. 2021, 200, 105936. [Google Scholar] [CrossRef]
- Magni, L. Model Predictive Control of Type 1 Diabetes: An in Silico Trial. J. Diabetes Sci. Technol. 2007, 1, 804–812. [Google Scholar] [CrossRef]
- De Paula, M.; Acosta, G.G.; Martínez, E.C. On-line policy learning and adaptation for real-time personalization of an artificial pancreas. Expert Syst. Appl. 2015, 42, 2234–2255. [Google Scholar] [CrossRef]
- De Paula, M.; Ávila, L.O.; Martínez, E.C. Controlling blood glucose variability under uncertainty using reinforcement learning and Gaussian processes. Appl. Soft Comput. 2015, 35, 310–332. [Google Scholar] [CrossRef]
- De Paula, M.; Martinez, E. Probabilistic optimal control of blood glucose under uncertainty. In 22 European Symposium on Computer Aided Process Engineering; Elsevier: Amsterdam, The Netherlands, 2012; Volume 30, pp. 1357–1361. [Google Scholar]
- Akbari Torkestani, J.; Ghanaat Pisheh, E. A learning automata-based blood glucose regulation mechanism in type 2 diabetes. Control Eng. Pract. 2014, 26, 151–159. [Google Scholar] [CrossRef]
- Daskalaki, E.; Diem, P.; Mougiakakou, S.G. An Actor-Critic based controller for glucose regulation in type 1 diabetes. Comput. Methods Programs Biomed. 2013, 109, 116–125. [Google Scholar] [CrossRef]
- Sun, Q.; Jankovic, M.V.; Budzinski, J.; Moore, B.; Diem, P.; Stettler, C.; Mougiakakou, S.G. A Dual Mode Adaptive Basal-Bolus Advisor Based on Reinforcement Learning. IEEE J. Biomed. Health Inform. 2019, 23, 2633–2641. [Google Scholar] [CrossRef]
- Sun, Q.; Jankovic, M.V.; Mougiakakou, G.S. Reinforcement Learning-Based Adaptive Insulin Advisor for Individuals with Type 1 Diabetes Patients under Multiple Daily Injections Therapy. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 3609–3612. [Google Scholar]
- Sun, Q.; Jankovic, M.V.; Stettler, C.; Mougiakakou, S. Personalised adaptive basal-bolus algorithm using SMBG/CGM data. In Proceedings of the 11th International Conference on Advanced Technologies and Treatments for Diabetes, Vienna, Austria, 14–17 February 2018. [Google Scholar]
- Thananjeyan, B.; Balakrishna, A.; Nair, S.; Luo, M.; Srinivasan, K.; Hwang, M.; Gonzalez, J.E.; Ibarz, J.; Finn, C.; Goldberg, K. Recovery RL: Safe Reinforcement Learning With Learned Recovery Zones. IEEE Robot. Autom. Lett. 2021, 6, 4915–4922. [Google Scholar] [CrossRef]
- Yasini, S.; Naghibi-Sistani, M.B.; Karimpour, A. Agent-based simulation for blood glucose control in diabetic patients. World Acad. Sci. Eng. Technol. 2009, 33, 672–679. [Google Scholar]
- Myhre, J.N.; Launonen, I.K.; Wei, S.; Godtliebsen, F. Controlling Blood Glucose Levels in Patients with Type 1 Diabetes Using Fitted Q-Iterations and Functional Features. In Proceedings of the 2018 IEEE 28th International Workshop on Machine Learning for Signal Processing (MLSP), Aalborg, Denmark, 17–20 September 2018; pp. 1–6. [Google Scholar]
- Shifrin, M.; Siegelmann, H. Near-optimal insulin treatment for diabetes patients: A machine learning approach. Artif. Intell. Med. 2020, 107, 101917. [Google Scholar] [CrossRef]
- Shu, Y.; Cao, Z.; Gao, J.; Wang, J.; Yu, P.S.; Long, M. Omni-Training: Bridging Pre-Training and Meta-Training for Few-Shot Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 45, 15275–15291. [Google Scholar] [CrossRef]
- Reske, A.; Carius, J.; Ma, Y.; Farshidian, F.; Hutter, M. Imitation Learning from MPC for Quadrupedal Multi-Gait Control. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 5014–5020. [Google Scholar]
- Ahmad, S.; Beneyto, A.; Contreras, I.; Vehi, J. Bolus Insulin calculation without meal information. A reinforcement learning approach. Artif. Intell. Med. 2022, 134, 102436. [Google Scholar] [CrossRef]
- Brunke, L.; Greeff, M.; Hall, A.W.; Yuan, Z.; Zhou, S.; Panerati, J.; Schoellig, A.P. Safe Learning in Robotics: From Learning-Based Control to Safe Reinforcement Learning. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 411–444. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, X.; Li, D.; Ge, S.S.; Gao, B.; Chen, H.; Lee, T.H. Adaptive Safe Reinforcement Learning with Full-State Constraints and Constrained Adaptation for Autonomous Vehicles. IEEE Trans. Cybern. 2024, 54, 1907–1920. [Google Scholar] [CrossRef] [PubMed]
- Artman, W.J.; Nahum-Shani, I.; Wu, T.; McKay, J.R.; Ertefaie, A. Power analysis in a SMART design: Sample size estimation for determining the best embedded dynamic treatment regime. Biostatistics 2018, 21, 1468–4357. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Norouzi, M.; Nachum, O.; Tucker, G.; Wang, Z.; Novikov, A.; Yang, M.; Zhang, M.R.; Chen, Y.; Kumar, A.; et al. Benchmarks for Deep Off-Policy Evaluation. arXiv 2021, arXiv:2103.16596. [Google Scholar]
- Kovatchev, B.P.; Breton, M.; Dalla Man, C.; Cobelli, C. In Silico Preclinical Trials: A Proof of Concept in Closed-Loop Control of Type 1 Diabetes. J. Diabetes Sci. Technol. 2009, 3, 44–55. [Google Scholar] [CrossRef]
- Lehmann, E.D.; Deutsch, T. A physiological model of glucose-insulin interaction in type 1 diabetes mellitus. J. Biomed. Eng. 1992, 14, 235–242. [Google Scholar] [CrossRef]
- Bergman, R.N. Minimal model: Perspective from 2005. Horm. Res. 2005, 64 (Suppl. S3), 8–15. [Google Scholar] [CrossRef]
- Liu, Z.; Ji, L.; Jiang, X.; Zhao, W.; Liao, X.; Zhao, T.; Liu, S.; Sun, X.; Hu, G.; Feng, M.; et al. A Deep Reinforcement Learning Approach for Type 2 Diabetes Mellitus Treatment. In Proceedings of the 2020 IEEE International Conference on Healthcare Informatics (ICHI), Oldenburg, Germany, 30 November–3 December 2020; pp. 1–9. [Google Scholar]
- Lopez-Martinez, D.; Eschenfeldt, P.; Ostvar, S.; Ingram, M.; Hur, C.; Picard, R. Deep Reinforcement Learning for Optimal Critical Care Pain Management with Morphine using Dueling Double-Deep Q Networks. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 3960–3963. [Google Scholar]
- Weng, W.-H.; Gao, M.; He, Z.; Yan, S.; Szolovits, P. Representation and Reinforcement Learning for Personalized Glycemic Control in Septic Patients. arXiv 2017, arXiv:1712.00654. [Google Scholar]
- Fox, I.; Wiens, J. Reinforcement learning for blood glucose control: Challenges and opportunities. In Proceedings of the 2019 International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; Volume 126, pp. 508–536. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Hester, T.; Vecerik, M.; Pietquin, O.; Lanctot, M.; Schaul, T.; Piot, B.; Horgan, D.; Quan, J.; Sendonaris, A.; Osband, I.; et al. Deep Q-learning from demonstrations. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence and Thirtieth Innovative Applications of Artificial Intelligence Conference and Eighth AAAI Symposium on Educational Advances in Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; p. 394. [Google Scholar]
- Herrero, P.; El-Sharkawy, M.; Daniels, J.; Jugnee, N.; Uduku, C.N.; Reddy, M.; Oliver, N.; Georgiou, P. The Bio-inspired Artificial Pancreas for Type 1 Diabetes Control in the Home: System Architecture and Preliminary Results. J. Diabetes Sci. Technol. 2019, 13, 1017–1025. [Google Scholar] [CrossRef]
- Deshpande, S.; Pinsker, J.E.; Zavitsanou, S.; Shi, D.; Tompot, R.W.; Church, M.M.; Andre, C.C.; Doyle, F.J.; Dassau, E. Design and Clinical Evaluation of the Interoperable Artificial Pancreas System (iAPS) Smartphone App: Interoperable Components with Modular Design for Progressive Artificial Pancreas Research and Development. Diabetes Technol. Ther. 2019, 21, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Liu, C.; Zhu, T.; Herrero, P.; Georgiou, P. GluNet: A Deep Learning Framework for Accurate Glucose Forecasting. IEEE J. Biomed. Health Inform. 2020, 24, 414–423. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Daniels, J.; Liu, C.; Herrero, P.; Georgiou, P. Convolutional Recurrent Neural Networks for Glucose Prediction. IEEE J. Biomed. Health Inform. 2020, 24, 603–613. [Google Scholar] [CrossRef]
- Cobelli, C. Diabetes: Models, Signals and Control. In Proceedings of the 13th Imeko Tc1-Tc7 Joint Symposium—Without Measurement No Science, without Science No Measurement, London, UK, 1–3 September 2010; Volume 238. [Google Scholar] [CrossRef]
- Copp, D.; Gondhalekar, R.; Hespanha, J. Simultaneous model predictive control and moving horizon estimation for blood glucose regulation in Type 1 diabetes. Optim. Control Appl. Methods 2017, 39, 904–918. [Google Scholar] [CrossRef]
- Sun, X. Study on Dynamic Control of Blood Glucose in Type 1 Diabetes Mellitus Based on GPC. Master’s Thesis, Northeastern University, Boston, MA, USA, 2018. [Google Scholar]
- Babar, S.A.; Rana, I.A.; Mughal, I.S.; Khan, S.A. Terminal Synergetic and State Feedback Linearization Based Controllers for Artificial Pancreas in Type 1 Diabetic Patients. IEEE Access 2021, 9, 28012–28019. [Google Scholar] [CrossRef]
- Messori, M.; Incremona, G.P.; Cobelli, C.; Magni, L. Individualized model predictive control for the artificial pancreas: In silico evaluation of closed-loop glucose control. IEEE Control Syst. Mag. 2018, 38, 86–104. [Google Scholar] [CrossRef]
- Turksoy, K.; Bayrak, E.S.; Quinn, L.; Littlejohn, E.; Çinar, A. Multivariable adaptive closed-loop control of an artificial pancreas without meal and activity announcement. Diabetes Technol. Ther. 2013, 15, 386–400. [Google Scholar] [CrossRef]
- Turksoy, K.; Hajizadeh, I.; Hobbs, N.; Kilkus, J.; Littlejohn, E.; Samadi, S.; Feng, J.; Sevil, M.; Lazaro, C.; Ritthaler, J.; et al. Multivariable Artificial Pancreas for Various Exercise Types and Intensities. Diabetes Technol. Ther. 2018, 20, 662–671. [Google Scholar] [CrossRef]
- Hajizadeh, I.; Rashid, M.; Samadi, S.; Sevil, M.; Hobbs, N.; Brandt, R.; Cinar, A. Adaptive personalized multivariable artificial pancreas using plasma insulin estimates. J. Process Control 2019, 80, 26–40. [Google Scholar] [CrossRef]
- Hajizadeh, I.; Rashid, M.M.; Turksoy, K.; Samadi, S.; Feng, J.; Sevil, M.; Hobbs, N.; Lazaro, C.; Maloney, Z.; Littlejohn, E.; et al. Incorporating Unannounced Meals and Exercise in Adaptive Learning of Personalized Models for Multivariable Artificial Pancreas Systems. J. Diabetes Sci. Technol. 2018, 12, 953–966. [Google Scholar] [CrossRef]
- Sun, X.; Rashid, M.; Askari, M.R.; Cinar, A. Adaptive personalized prior-knowledge-informed model predictive control for type 1 diabetes. Control Eng. Pract. 2023, 131, 105386. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Rashid, M.; Hobbs, N.; Askari, M.R.; Brandt, R.; Shahidehpour, A.; Cinar, A. Prior informed regularization of recursively updated latent-variables-based models with missing observations. Control Eng. Pract. 2021, 116, 104933. [Google Scholar] [CrossRef] [PubMed]
- Castillo, A.; Villa-Tamayo, M.F.; Pryor, E.; Garcia-Tirado, J.F.; Colmegna, P.; Breton, M. Deep Neural Network Architectures for an Embedded MPC Implementation: Application to an Automated Insulin Delivery System. IFAC-Pap. 2023, 56, 11521–11526. [Google Scholar] [CrossRef]
- Steil, G.; Rebrin, K.; Mastrototaro, J.J. Metabolic modelling and the closed-loop insulin delivery problem. Diabetes Res. Clin. Pract. 2006, 74, S183–S186. [Google Scholar] [CrossRef]

| References | State Space Variables | Fully/Hybrid Closed Loop |
|---|---|---|
| Ian Fox [48], Chirath Hettiarachchi [62,66], Dénes-Fazakas Lehel [68], Senquan Wang [56], Miriam Chlumsky-Harttmann [79] | BGC, insulin | Fully |
| Seunghyun Lee [63] | BGC, rate of BGC, IOB | |
| Francesco Di Felice [70], Alan Mackey [81], Phuwadol Viroonluecha [65], Silvia Del Giorno [58], Dénes-Fazakas Lehel [64], Jingchi Jiang [78] | BGC | |
| Zackarie Ellis [72] | BGC, insulin, Error between the BGC and 4.5 mmol/L | |
| Sayyar Ahmad [57] | BGC, maximum, minimum, Area under the curve | |
| Mohammad Ali Raheb [73] | BGC, IOB | |
| Guangyu Wang [86] | BGC, demographics, diagnosis, symptom, medication, laboratory test index | |
| Jonas Nordhaug Myhre [69] | BGC, insulin, IOB | Hybrid |
| Taiyu Zhu [71] | BGC, CHO, IOB, Injection time of bolus | |
| Min Hyuk Lim [74], Jinhao Zhu [77], Mehrad Jaloli [80], Anas El Fathi [67] | BGC, insulin, CHO | |
| Zihao Wang [87] | BGC, time stamp, CHO | |
| Taiyu Zhu [59] | BGC, CHO, basal rate, bolus, glucagon | |
| Tianhao Li [60] | Dynamic and static variables in the electronic medical record | |
| Harry Emerson [82] | BGC, IOB, CHO | |
| Wenzhou Lv [75] | BGC, bolus, CHO, IOB | |
| Giulia Noaro [61] | BGC, CHO, Rate of change, Carbohydrate ratio, standard postprandial insulin dose | |
| Xuehui Yu [76] | Daily minimum and maximum BGC, posterior distribution probabilities formed from the product of the distributions of prior and individualized information (age, weight, etc.) | |
| Taiyu Zhu [83] | BGC, mean, maximum, minimum, maximum difference between adjacent measurements, percentage of high and low glucose, time stamp, number of hours to last CHO, bolus | |
| Tristan Beolet [84] | BGC, insulin, IOB, TDD, COB, time stamp, weight |
| References | Action Space Variables | Continuous/Discrete | Borderless/Bounded | ||||
|---|---|---|---|---|---|---|---|
| Basal | Bolus | Insulin Doses | Continuous | Discrete | Borderless | Bounded | |
| Ian Fox [48], Chirath Hettiarachchi [62,66], Francesco Di Felice [70], Zihao Wang [87], Taiyu Zhu [83], Guangyu Wang [86], Anas El Fathi [67], Miriam Chlumsky-Harttmann [79], Dénes-Fazakas Lehel [68] | √ | √ | √ | ||||
| Phuwadol Viroonluecha [65], Wenzhou Lv [75], Alan Mackey [81], Mehrad Jaloli [80], Tristan Beolet [84] | √ | √ | √ | ||||
| Taiyu Zhu [71], Mehrad Jaloli [80] | √ | √ | √ | ||||
| Dénes-Fazakas Lehel [64], Mohammad Ali Raheb [73], Jinhao Zhu [77], Min Hyuk Lim [74], Zackarie Ellis [72], Jingchi Jiang [78] | √ | √ | √ | ||||
| Giulia Noaro [61], Xuehui Yu [76] | √ | √ | √ | ||||
| Jonas Nordhaug Myhre [69], Harry Emerson [82], Xuehui Yu [76] | √ | √ | √ | ||||
| Silvia Del Giorno [58], Sayyar Ahmad [57] | √ | √ | √ | ||||
| Tianhao Li [60], Taiyu Zhu [59], Seunghyun Lee [63], Senquan Wang [56] | √ | √ | √ | ||||
| Log Function (Risk Function) | Gaussian Function | Power Function | Linear Function | Others |
|---|---|---|---|---|
| Ian Fox [48], Harry Emerson [82], Alan Mackey [81], Guangyu Wang [86], Chirath Hettiarachchi [66], Jinhao Zhu [77], Anas El Fathi [67], Tristan Beolet [84], Miriam Chlumsky-Harttmann [79]. e.g., where a is penalty and the value is different in different literatures | Jonas Nordhaug Myhre [69], Mehrad Jaloli [80], Min Hyuk Lim [74], Dénes-Fazakas Lehel [64,68]. e.g., where gref = 127 mg/dL | Francesco Di Felice [70], Silvia Del Giorno [58], Wenzhou Lv [75], Jingchi Jiang [78]. e.g., | Taiyu Zhu [59], Taiyu Zhu [83], Taiyu Zhu [71], Tianhao Li [60], Mohammad Ali Raheb [73], Phuwadol Viroonluecha [65], Giulia Noaro [61], Seunghyun Lee [63], Zihao Wang [87], Zackarie Ellis [72], Sayyar Ahmad [57], Senquan Wang [56]. e.g., | Xuehui Yu [76]. e.g., |
| Advantages: It quantifies the risk of BGC, which can encourage agent to pay more attention to those BGC that cause high risk, so as to effectively avoid extreme hyperglycemia and hypoglycemia events. Disadvantages: The pros and cons of BGC fluctuations are not taken into account; Different patients have a variety of BGC risks, but this function cannot make personalized reward assessments for different patients; | Advantages: It grows very quickly, so the further away from the ideal BGC, the penalty increases significantly. This helps the agent more strongly avoid extreme situations. Disadvantages: The punishment needs to be controlled by coefficient adjustment, but this adjustment can be sensitive. | Advantages: It directly penalizes deviations from the ideal blood glucose value, and the higher the value, the more severe the penalty. Disadvantages: There is the same penalty for deviations above and below ideal BGC, which is not conducive to RL differentiating the risk of hyperglycemia from hypoglycemia | Advantages: It simplifies reward calculations and clearly defines rewards or penalties for different blood glucose levels. Disadvantages: It is discontinuous at interval boundaries and can cause the agent to behave unsteadily at the boundaries; The setting of intervals may be subjective, and different individuals and different situations may require different intervals. | Advantages: It provides a more granular assessment of the pros and cons of different BGC. Disadvantages: The pros and cons of BGC fluctuations are not considered; It does not take into account the BGC assessment in different patients because the safe BGC range varies from patient to patient. |
| References | Data Source | Subjects (Patients) | Type of Patients | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Virtual Platform | Mathematical Model | Electronic Medical Records | Real | Virtual | Offline Clinical Datasets | T1DM | T2DM | No Distinction | |
| Xuehui Yu [76], Harry Emerson [82], Chirath Hettiarachchi [66], Mehrad Jaloli [80], Wenzhou Lv [75], Giulia Noaro [61], Zihao Wang [87], Ian Fox [48], Chirath Hettiarachchi [62], Jinhao Zhu [77], Seunghyun Lee [63], Alan Mackey [81], Phuwadol Viroonluecha [65], Min Hyuk Lim [74], Taiyu Zhu [83], Taiyu Zhu [59], Anas El Fathi [67], Sayyar Ahmad [57], Jingchi Jiang [78], Miriam Chlumsky-Harttmann [79], Senquan Wang [56] | √ | √ | √ | ||||||
| Taiyu Zhu [71] | √ | √ | √ | √ | |||||
| Silvia Del Giorno [58] | √ | √ | √ | ||||||
| Jonas Nordhaug Myhre [69], Francesco Di Felice [70], Dénes-Fazakas Lehel [64,68] | √ | √ | √ | ||||||
| Mohammad Ali Raheb [73] | √ | √ | √ | ||||||
| Zackarie Ellis [72] | √ | √ | √ | ||||||
| Tianhao Li [60] | √ | √ | √ | ||||||
| Tristan Beolet [84] | √ | √ | √ | ||||||
| Guangyu Wang [86] | √ | √ | √ | ||||||
| MPC | DRL | |
|---|---|---|
| Advantages |
|
|
| Disadvantages |
|
|
| Future research directions |
|
|
| PID | DRL | |
|---|---|---|
| Advantages |
|
|
| Disadvantages |
| The same as Table 5 |
| Future research directions |
| The same as Table 5 |
| FL | DRL | |
|---|---|---|
| Advantages |
|
|
| Disadvantages |
| The same as Table 5 |
| Future research directions |
| The same as Table 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Yang, Z.; Sun, X.; Liu, H.; Li, H.; Lu, J.; Zhou, J.; Cinar, A. Deep Reinforcement Learning for Automated Insulin Delivery Systems: Algorithms, Applications, and Prospects. AI 2025, 6, 87. https://doi.org/10.3390/ai6050087
Yu X, Yang Z, Sun X, Liu H, Li H, Lu J, Zhou J, Cinar A. Deep Reinforcement Learning for Automated Insulin Delivery Systems: Algorithms, Applications, and Prospects. AI. 2025; 6(5):87. https://doi.org/10.3390/ai6050087
Chicago/Turabian StyleYu, Xia, Zi Yang, Xiaoyu Sun, Hao Liu, Hongru Li, Jingyi Lu, Jian Zhou, and Ali Cinar. 2025. "Deep Reinforcement Learning for Automated Insulin Delivery Systems: Algorithms, Applications, and Prospects" AI 6, no. 5: 87. https://doi.org/10.3390/ai6050087
APA StyleYu, X., Yang, Z., Sun, X., Liu, H., Li, H., Lu, J., Zhou, J., & Cinar, A. (2025). Deep Reinforcement Learning for Automated Insulin Delivery Systems: Algorithms, Applications, and Prospects. AI, 6(5), 87. https://doi.org/10.3390/ai6050087






