Compliance-Based Determination of Fatigue Design Curves for Elastomeric Adhesive Joints
Abstract
:1. Introduction
2. Fatigue: Loading, Stiffness and Compliance
2.1. Fatigue Loading
2.2. Definition of Stiffness and Compliance
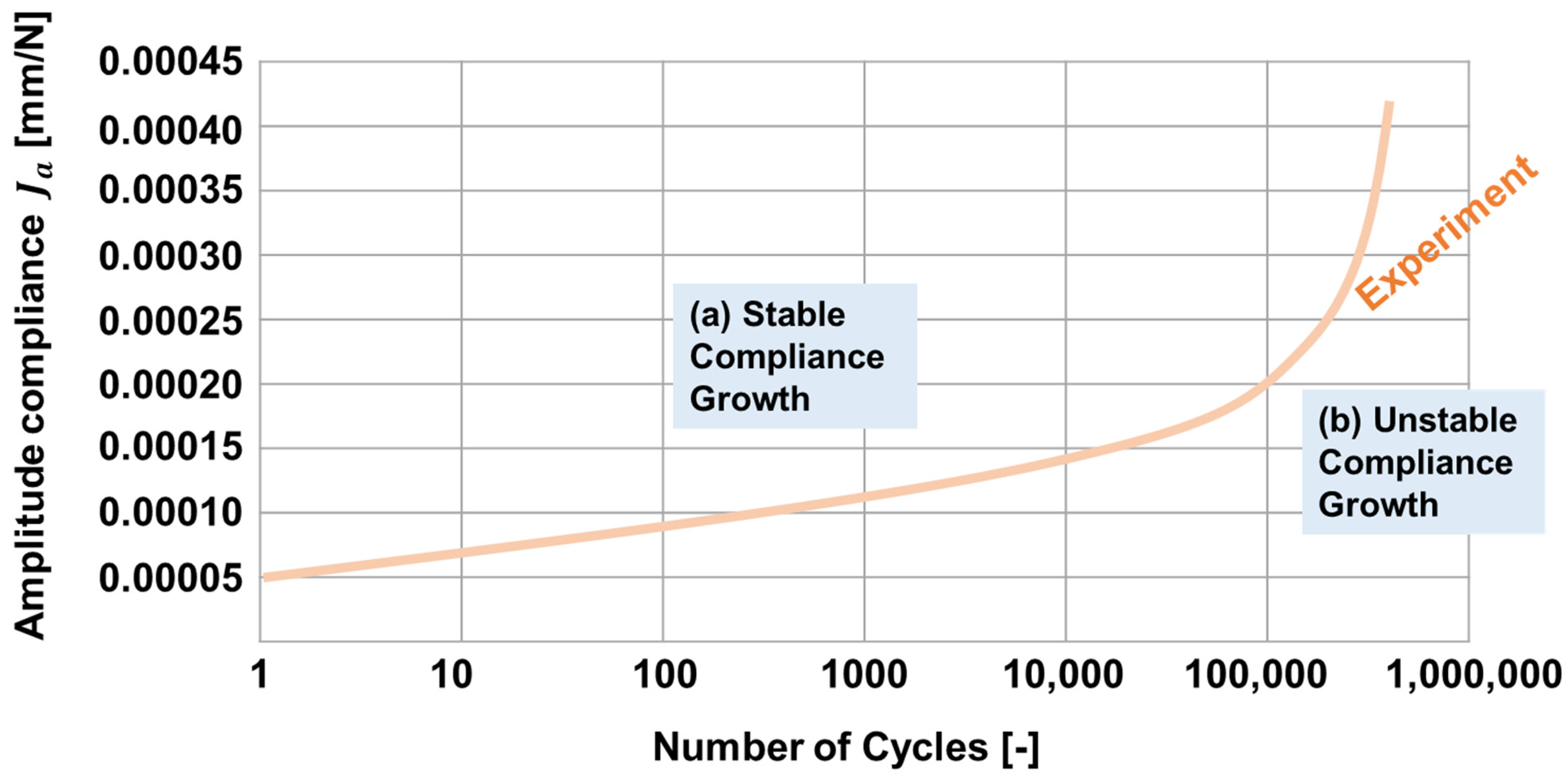
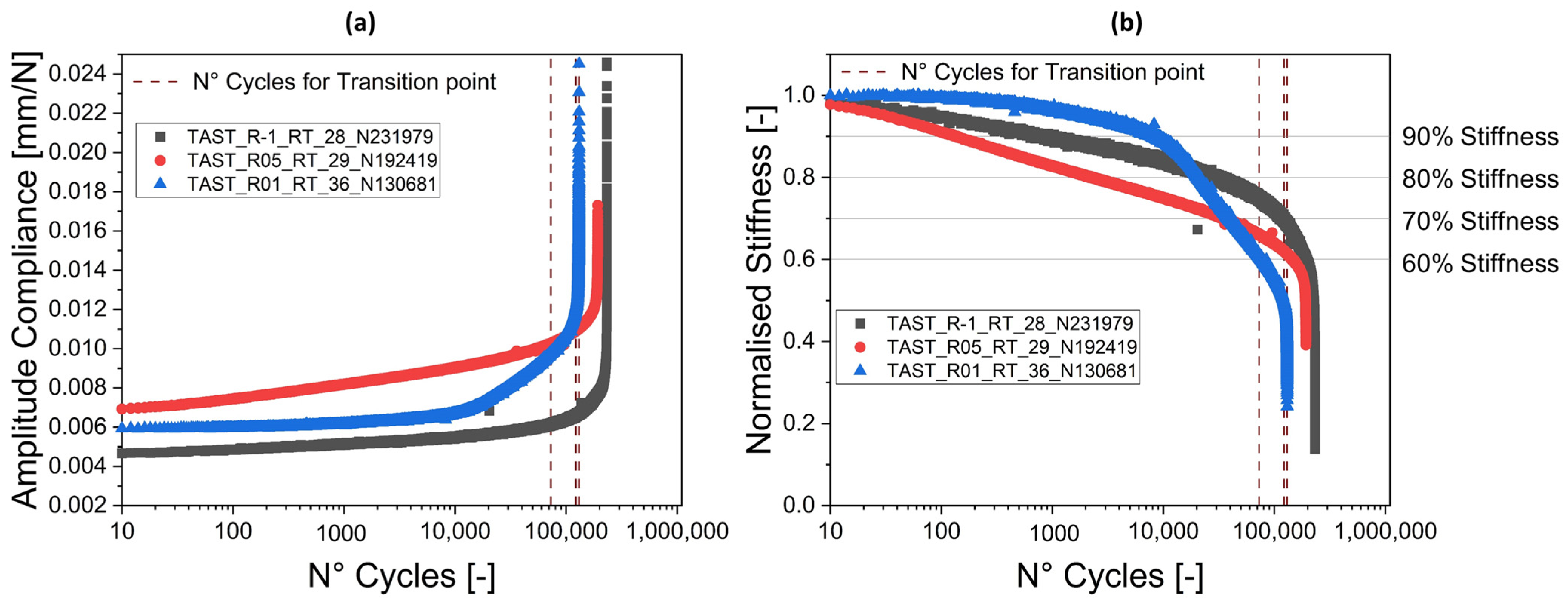
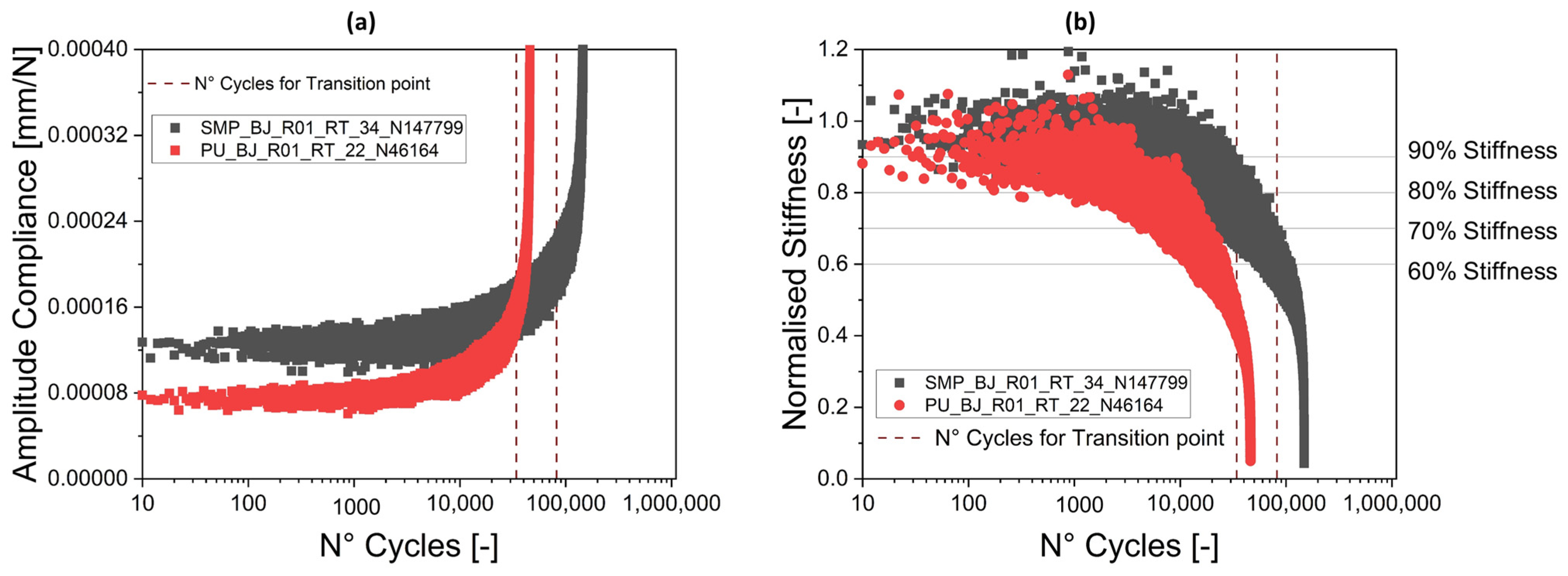
2.3. Stable versus Unstable Compliance Growth
3. Experimental Methodology
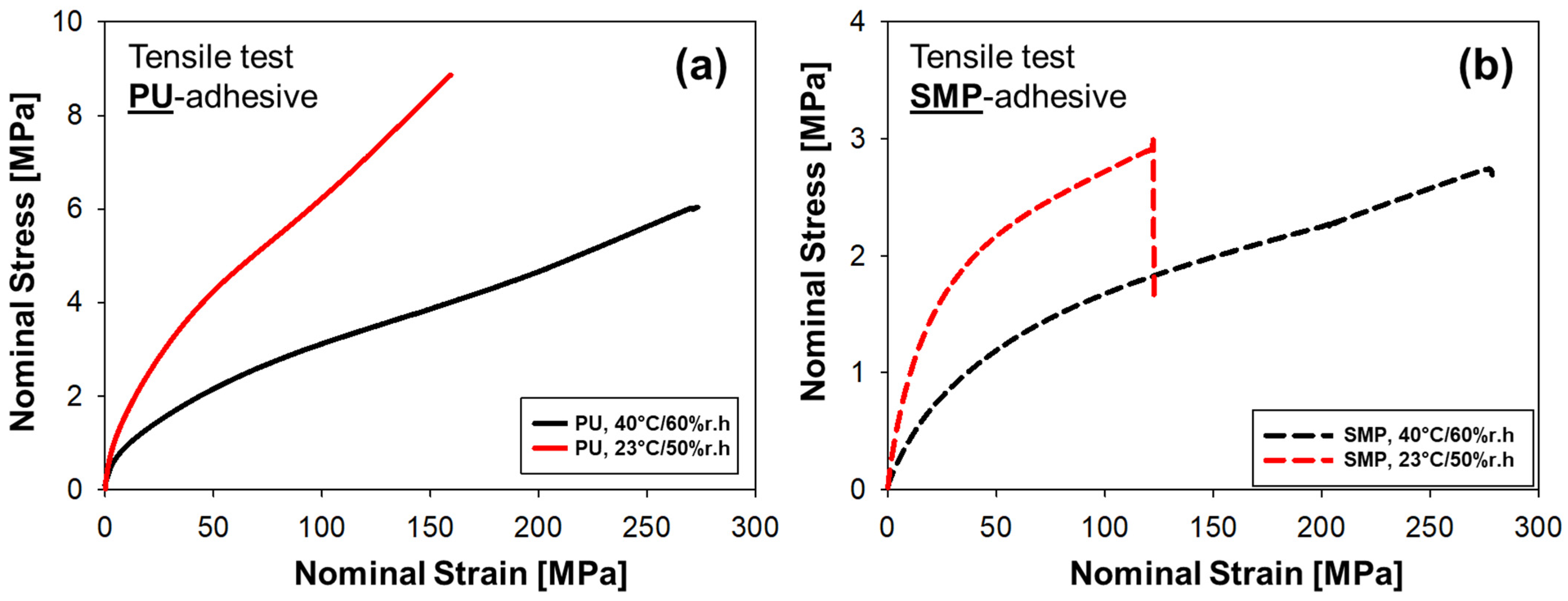
3.1. Adhesive and Joint Types
3.2. Fatigue Testing
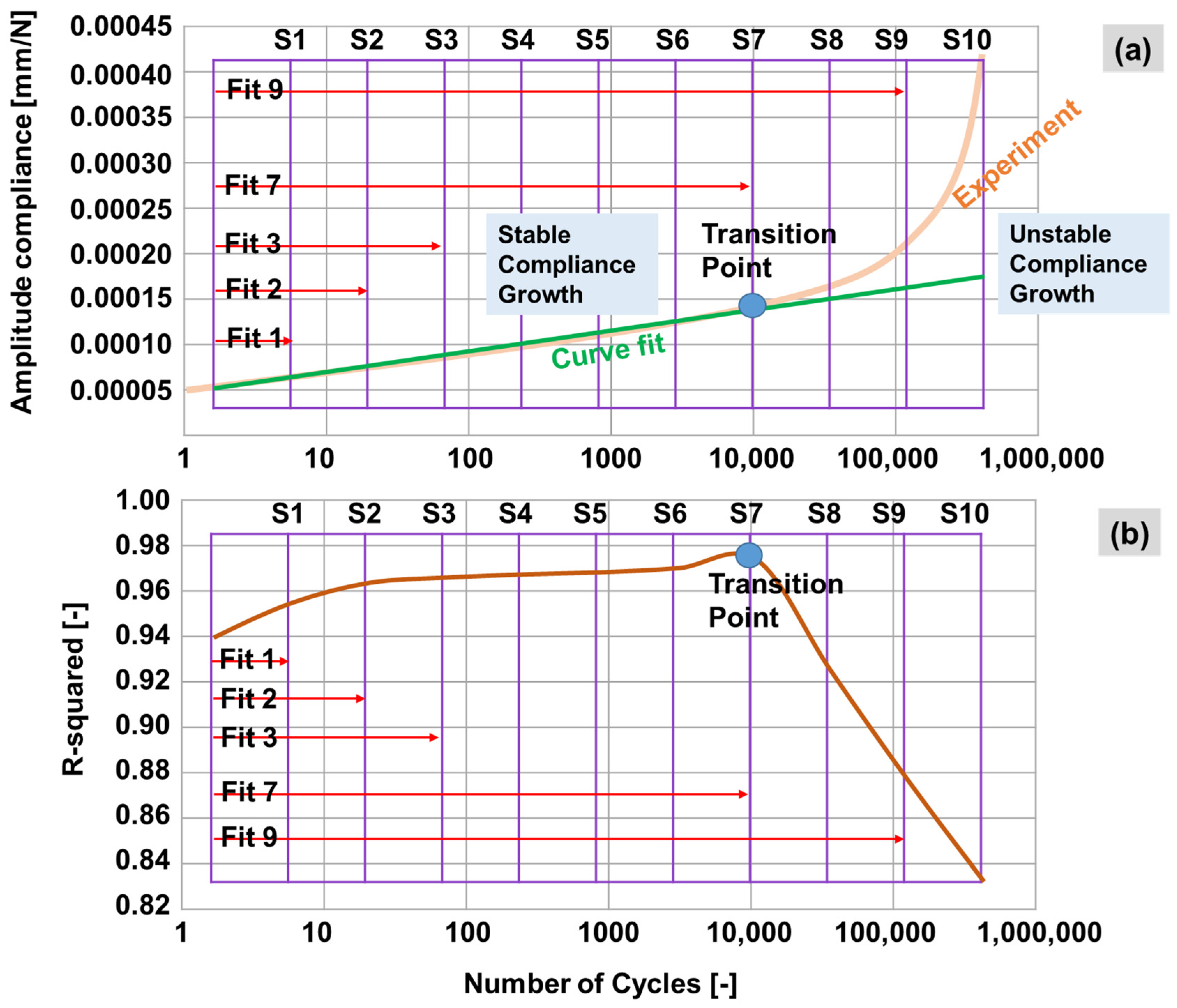
4. Proposed Method for the Determination of the Unstable Compliance Growth Region
5. Experimental Results
5.1. Implementation
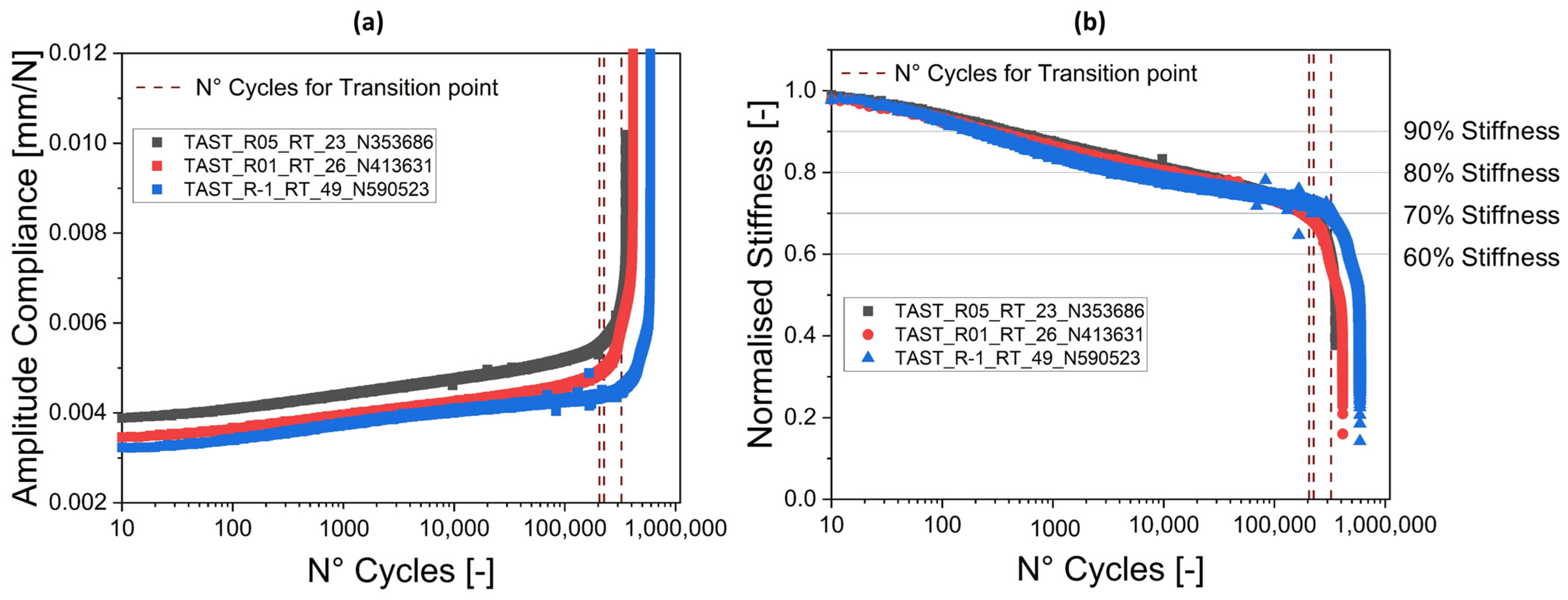
5.2. TAST Joint: Stiffness Degradation versus Picture Analysis
5.3. Butt Joint: Stiffness Degradation versus Pictures Analysis
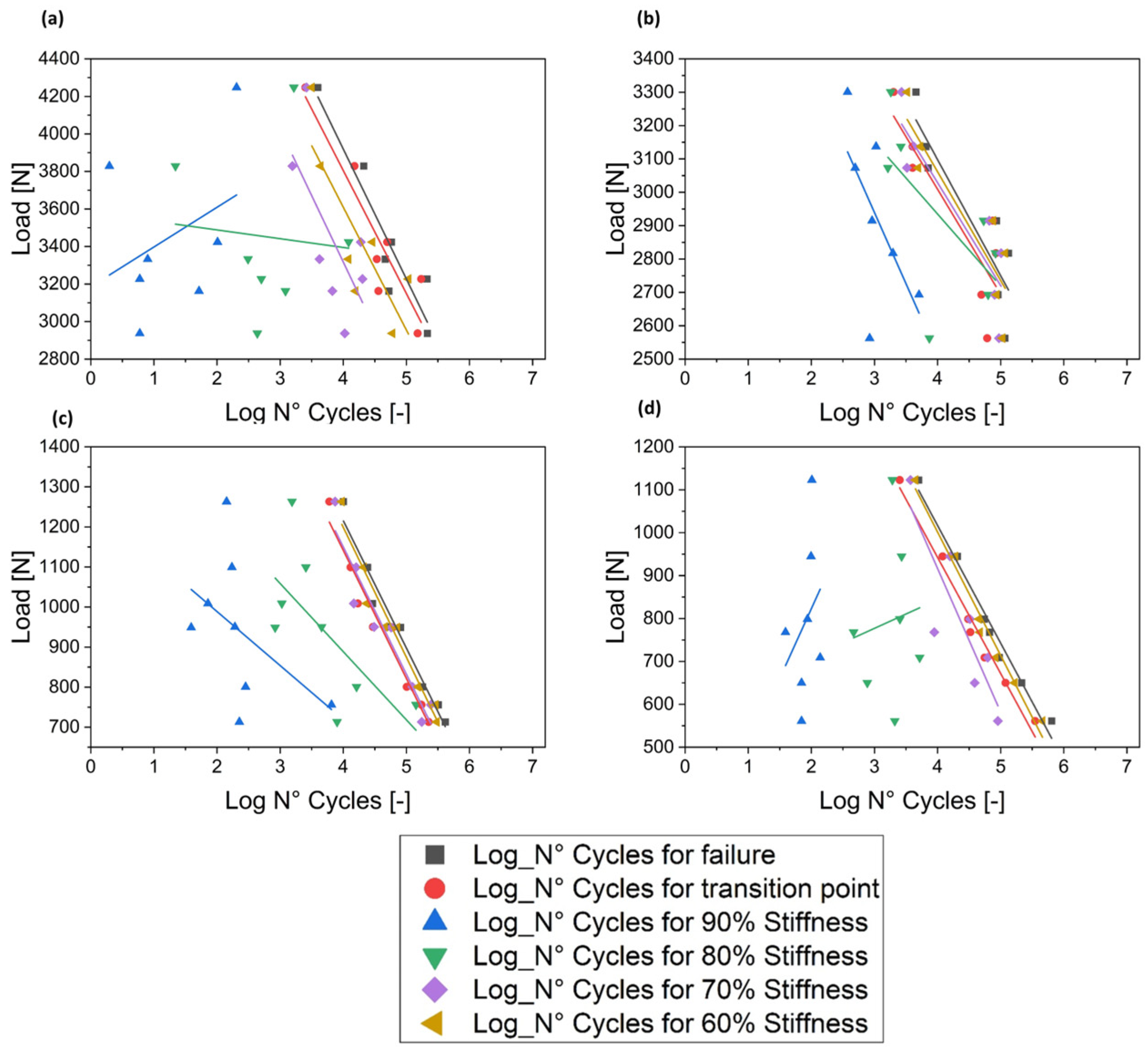
5.4. Fatigue Design Curves
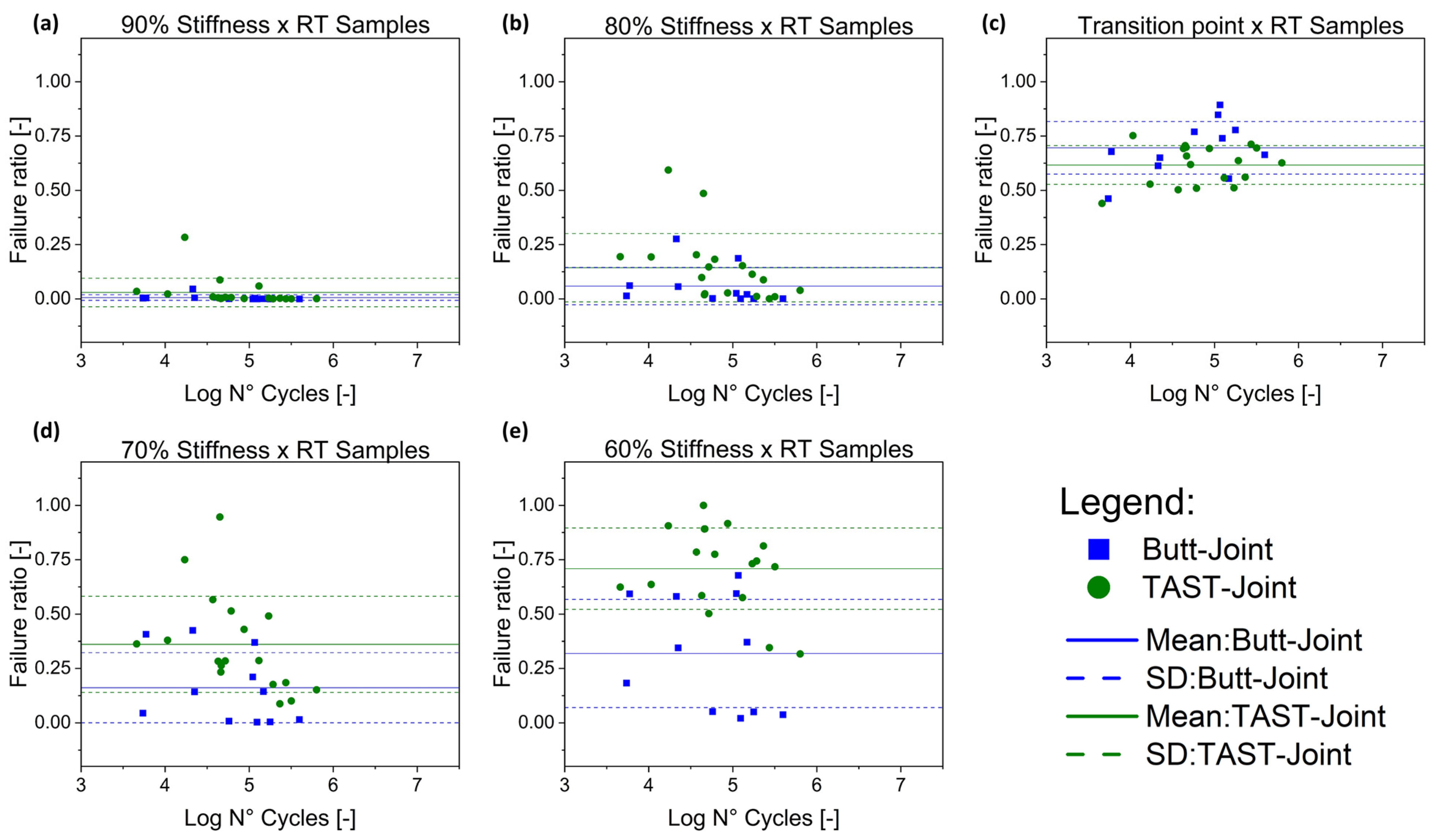
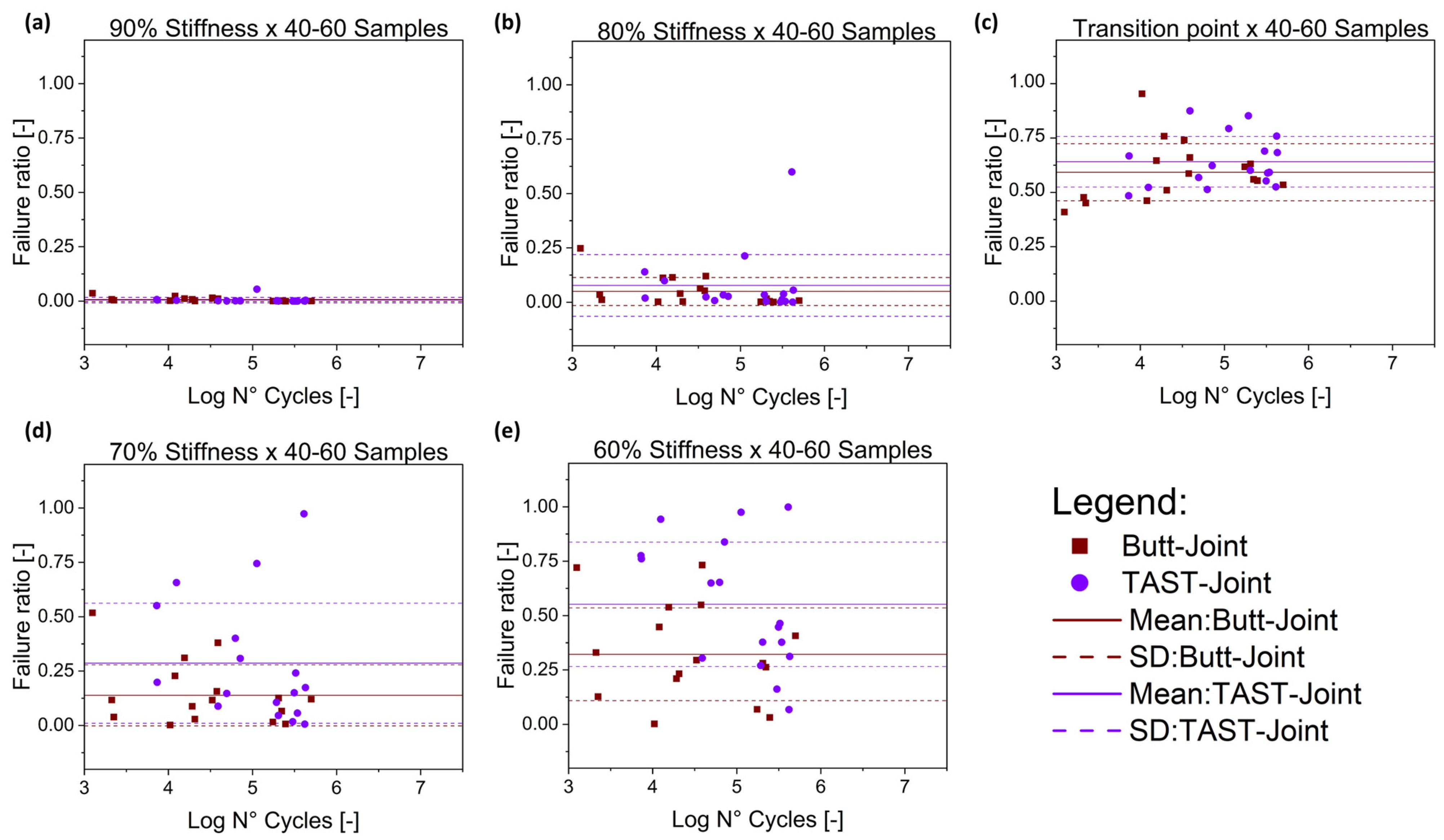
5.5. Failure Ratio
- (i)
- A high coefficient of determination (R-squared), comparable to the final failure curve;
- (ii)
- A high failure ratio, which avoids over-conservative design;
- (iii)
- Robustness, since the failure ratios for different adhesives (PU and SMP), stress ratios (R = −1, 0.1, 0.5), conditions (23 °C/50% r.h. and 40 °C/60% r.h.) and geometries (butt joint and TAST joint) are consistent.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation/Symbol | Meaning |
| N | Number of cycles |
| R | Stress ratio |
| dadh | Adhesive layer thickness |
| PU | Polyurethane |
| SMP | Silane-modified polymers |
| TAST | Thick-Adherend-Shear-Test Joint |
| r.h. | Relative humidity |
| Shear stress | |
| Tensile stress | |
| Shear stress amplitude | |
| Tensile stress amplitude | |
| Shear mean stress | |
| Tensile mean stress |
References
- Duncan, B. Developments in testing adhesive joints. In Advances in Structural Adhesive Bonding; Elsevier: Amsterdam, The Netherlands, 2010; pp. 389–436. ISBN 9781845694357. [Google Scholar]
- Burchardt, B. Advances in polyurethane structural adhesives. In Advances in Structural Adhesive Bonding; Elsevier: Amsterdam, The Netherlands, 2010; pp. 35–65. ISBN 9781845694357. [Google Scholar]
- Rosendahl, P.L. From Bulk to Structural Failure: Fracture of Hyperelastic Materials, 1st ed; Springer Fachmedien Wiesbaden; Imprint Springer Vieweg: Wiesbaden, Germany, 2021; ISBN 9783658316051. [Google Scholar]
- Adin, H.; Yildiz, B.; Adin, M.Ş. Numerical investigation of fatigue behaviours of non-patched and patched aluminium pipes. Eur. J. Tech. 2021, 11, 60–65. [Google Scholar] [CrossRef]
- Evangelista Fernandes, P.H.; Nagel, C.; Wulf, A.; Beber, V.C. Mean stress correction and fatigue failure criteria for hyperelastic adhesive joints. J. Adhes. 2023, 1–24. [Google Scholar] [CrossRef]
- Adin, H.; Sağlam, Z.; Adin, M.Ş. Numerical investigation of fatigue behavior of non-patched and patched aluminum/composite plates. Eur. Mech. Sci. 2021, 5, 168–176. [Google Scholar] [CrossRef]
- Zhang, Y.; Vassilopoulos, A.; Keller, T. Stiffness degradation and fatigue life prediction of adhesively-bonded joints for fiber-reinforced polymer composites. Int. J. Fatigue 2008, 30, 1813–1820. [Google Scholar] [CrossRef]
- Abdel Wahab, M.M. Fatigue in Adhesively Bonded Joints: A Review. ISRN Mater. Sci. 2012, 2012, 746308. [Google Scholar] [CrossRef]
- Beber, V.C.; Schneider, B. Fatigue of structural adhesives under stress concentrations: Notch effect on fatigue strength, crack initiation and damage evolution. Int. J. Fatigue 2020, 140, 105824. [Google Scholar] [CrossRef]
- Hamdi, A.; Boulenouar, A.; Benseddiq, N.; Guessasma, S. Crack propagation in elastomers subjected to cyclic loading. Proc. IMechE 2019, 233, 2301–2310. [Google Scholar] [CrossRef]
- Boutar, Y.; Naïmi, S.; Mezlini, S.; Carbas, R.J.; da Silva, L.F.; Ben Sik Ali, M. Cyclic fatigue testing: Assessment of polyurethane adhesive joints’ durability for bus structures’ aluminium assembly. J. Adv. Join. Process. 2021, 3, 100053. [Google Scholar] [CrossRef]
- Heinrich, G.; Kipscholl, R.; Stoček, R. (Eds.) Fatigue Crack Growth in Rubber Materials: Experiments and Modelling; Springer: Cham, Switzerland, 2021; ISBN 3030689190. [Google Scholar]
- Lee, S.; Pharr, M. Sideways and stable crack propagation in a silicone elastomer. Proc. Natl. Acad. Sci. USA 2019, 116, 9251–9256. [Google Scholar] [CrossRef]
- Beber, V.C.; Fernandes, P.H.E.; Wulf, A.; Nagel, C.; Koschek, K.; Mayer, B. Final Report of the Project: “Nachweisführung für die Beanspruchbarkeit von Hyperelastischen Klebverbindungen unter Betriebsrelevanten Bedingungen II”; IGF-Vorhaben Nr. 20665 N; DVS-Media: Düsseldorf, Germany, 2023. [Google Scholar]
- Varadarajan, R.; Rimnac, C.M. Compliance calibration for fatigue crack propagation testing of ultra high molecular weight polyethylene. Biomaterials 2006, 27, 4693–4697. [Google Scholar] [CrossRef]
- Çavdar, S.; Teutenberg, D.; Meschut, G.; Wulf, A.; Hesebeck, O.; Brede, M.; Mayer, B. Stress-based fatigue life prediction of adhesively bonded hybrid hyperelastic joints under multiaxial stress conditions. Int. J. Adhes. Adhes. 2020, 97, 102483. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue of Structures and Materials; Springer Netherlands: Dordrecht, The Netherlands, 2009; ISBN 9781402068089. [Google Scholar]
- Fernandes, P.H.E.; Silva, G.C.; Pitz, D.B.; Schnelle, M.; Koschek, K.; Nagel, C.; Beber, V.C. Data-Driven, Physics-Based, or Both: Fatigue Prediction of Structural Adhesive Joints by Artificial Intelligence. Appl. Mech. 2023, 4, 334–355. [Google Scholar] [CrossRef]
- Pizzi, A.; Mittal, K.L. Handbook of Adhesion Technology; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Beber, V.C.; Schneider, B.; Brede, M. Influence of Temperature on the Fatigue Behaviour of a Toughened Epoxy Adhesive. J. Adhes. 2016, 92, 778–794. [Google Scholar] [CrossRef]
- Fernandes, P.; Poggenburg-Harrach, L.; Nagel, C.; Beber, V.C. Lifetime calculation of adhesively bonded joints under proportional and non-proportional multiaxial fatigue loading: A combined critical plane and critical distance approach. J. Adhes. 2022, 98, 780–809. [Google Scholar] [CrossRef]
- Sousa, F.C.; Akhavan-Safar, A.; Goyal, R.; Da Silva, L. Fatigue life estimation of single lap adhesive joints using a critical distance criterion: An equivalent notch approach. Mech. Mater. 2021, 153, 103670. [Google Scholar] [CrossRef]
- Jeandrau, J.-P.; Peyrac, C.; Lefebvre, F.; Renard, J.; Gantchenko, V.; Patamaprohm, B.; Guinault, C. Fatigue Behaviour of Adhesive Joints. Procedia Eng. 2015, 133, 508–517. [Google Scholar] [CrossRef]
- Beber, V.C.; Brede, M. Multiaxial static and fatigue behaviour of elastic and structural adhesives for railway applications. Procedia Struct. Integr. 2020, 28, 1950–1962. [Google Scholar] [CrossRef]
- Schmandt, C.; Marzi, S. Effect of crack opening velocity on fracture behavior of hyperelastic semi-structural adhesive joints subjected to mode I loading. Procedia Struct. Integr. 2018, 13, 799–805. [Google Scholar] [CrossRef]
- Sousa, F.C.; Akhavan-Safar, A.; Goyal, R.; Silva, L.F.M. The influence of mode mixity and adhesive system on the fatigue life of adhesive joints. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 2337–2348. [Google Scholar] [CrossRef]
- Lemaitre, J. A Continuous Damage Mechanics Model for Ductile Fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Costa, J.; Vicens, J.; Blanco, N.; Rodríguez-Bellido, A. Fatigue behaviour of adhesive films and laminating resins in bonded joints for repair purposes. In Proceedings of the ICCM17–17th International Conference on Composite Materials, Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Lorenz, H.; Steinhauser, D.; Klüppel, M. Morphology and Micro-mechanics of Filled Elastomer Blends: Impact on Dynamic Crack Propagation. In Fracture Mechanics and Statistical Mechanics of Reinforced Elastomeric Blends; Grellmann, W., Heinrich, G., Kaliske, M., Klüppel, M., Schneider, K., Vilgis, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 81–128. ISBN 978-3-642-37909-3. [Google Scholar]
- Wallau, W.; Recknagel, C. Durability assessment of structural sealant glazing systems applying a performance test method. J. Adhes. 2022, 98, 464–487. [Google Scholar] [CrossRef]
- Loureiro, A.L.; da Silva, L.F.M.; Sato, C.; Figueiredo, M.A.V. Comparison of the Mechanical Behaviour Between Stiff and Flexible Adhesive Joints for the Automotive Industry. J. Adhes. 2010, 86, 765–787. [Google Scholar] [CrossRef]
- Sheikh, N.; Mirzadeh, H.; Katbab, A.A.; Salehian, P.; Daliri, M.; Amanpour, S. Isocyanate-terminated urethane prepolymer as bioadhesive material: Evaluation of bioadhesion and biocompatibility, in vitro and in vivo assays. J. Biomater. Sci. Polym. Ed. 2001, 12, 707–719. [Google Scholar] [CrossRef] [PubMed]
- Gadhave, R.V.; Gadhave, C.R.; Dhawale, P.V. Silane Terminated Prepolymers: An Alternative to Silicones and Polyurethanes. Open J. Polym. Chem. 2021, 11, 31–54. [Google Scholar] [CrossRef]
- DIN. Kleben von Schienenfahrzeugen und -Fahrzeugteilen: Teil 3: Leitfaden zur Konstruktion und Nachweisführung von Klebverbindungen im Schienenfahrzeugbau; Beuth Verlag: Berlin, Germany, 2015; pp. 6701–6703. [Google Scholar]
- Ball, J. Discontinuous equilibrium solutions and cavitation in nonlinear elasticity. Phil. Trans. R. Soc. 1982, 306, 557–611. [Google Scholar] [CrossRef]
- Lion, A.; Johlitz, M. Constitutive Models for Rubber X, Proceedings of the 10th European Conference on Constitutive Models for Rubbers X, Munich, Germany, 28–31 August 2017, 1st ed.; Taylor and Francis: Boca Raton, FL, USA, 2017; ISBN 9781315223278. [Google Scholar]
- Boutar, Y.; Naïmi, S.; Daami, T.; Mezlini, S.; da Silva, L.F.M.; Ali, M.B.S. Mode I Fracture Energy of One-Component Polyurethane Adhesive Joints as Function of Bond Thickness for the Automotive Industry. In Proceedings of the Design and Modeling of Mechanical Systems—III, Hammamet, Tunisia, 27–29 March 2017; pp. 393–403. [Google Scholar] [CrossRef]

















| Adhesive [-] | Joint [-] | Condition [°C]/[% r.h.] | R [-] |
|---|---|---|---|
| PU | Butt | 23/50 | 0.1, 0.5 |
| PU | Butt | 40/60 | −1, 0.1, 0.5 |
| PU | TAST | 23/50 | −1, 0.1, 0.5 |
| PU | TAST | 40/60 | −1, 0.1, 0.5 |
| SMP | Butt | 23/50 | 0.1, 0.5 |
| SMP | Butt | 40/60 | −1, 0.1, 0.5 |
| SMP | TAST | 23/50 | −1, 0.1, 0.5 |
| SMP | TAST | 40/60 | −1, 0.1, 0.5 |
| TAST_RT | TAST_40–60 | BJ_RT | BJ_40–60 | Average [-] | Std. Dev. [-] | |
|---|---|---|---|---|---|---|
| Failure | 0.97 | 0.98 | 0.87 | 0.81 | 0.90 | 0.06 |
| Transition p. | 0.95 | 0.98 | 0.85 | 0.75 | 0.88 | 0.08 |
| 90% Stiffness | 0.23 | 0.08 | 0.13 | 0.39 | 0.21 | 0.11 |
| 80% Stiffness | 0.46 | 0.02 | 0.01 | 0.41 | 0.22 | 0.19 |
| 70% Stiffness | 0.91 | 0.75 | 0.45 | 0.80 | 0.73 | 0.15 |
| 60% Stiffness | 0.95 | 0.98 | 0.68 | 0.81 | 0.86 | 0.11 |
| TAST_RT | TAST_40–60 | BJ_RT | BJ_40–60 | Average [-] | Std. Dev. [-] | |
|---|---|---|---|---|---|---|
| Failure | 0.98 | 0.98 | 0.93 | 0.71 | 0.90 | 0.10 |
| Transition p. | 0.99 | 0.94 | 0.93 | 0.74 | 0.90 | 0.09 |
| 90% Stiffness | 0.13 | 0.05 | 0.02 | 0.55 | 0.19 | 0.19 |
| 80% Stiffness | 0.08 | 0.58 | 0.74 | 0.88 | 0.57 | 0.27 |
| 70% Stiffness | 0.99 | 0.65 | 0.90 | 0.87 | 0.85 | 0.11 |
| 60% Stiffness | 0.98 | 0.77 | 0.93 | 0.84 | 0.88 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandes, P.H.E.; Nagel, C.; Wulf, A.; Beber, V.C.; Mayer, B. Compliance-Based Determination of Fatigue Design Curves for Elastomeric Adhesive Joints. Eng 2023, 4, 2615-2639. https://doi.org/10.3390/eng4040150
Fernandes PHE, Nagel C, Wulf A, Beber VC, Mayer B. Compliance-Based Determination of Fatigue Design Curves for Elastomeric Adhesive Joints. Eng. 2023; 4(4):2615-2639. https://doi.org/10.3390/eng4040150
Chicago/Turabian StyleFernandes, Pedro Henrique Evangelista, Christof Nagel, Andreas Wulf, Vinicius Carrillo Beber, and Bernd Mayer. 2023. "Compliance-Based Determination of Fatigue Design Curves for Elastomeric Adhesive Joints" Eng 4, no. 4: 2615-2639. https://doi.org/10.3390/eng4040150
APA StyleFernandes, P. H. E., Nagel, C., Wulf, A., Beber, V. C., & Mayer, B. (2023). Compliance-Based Determination of Fatigue Design Curves for Elastomeric Adhesive Joints. Eng, 4(4), 2615-2639. https://doi.org/10.3390/eng4040150










