Brazier Effect of Thin Angle-Section Beams under Bending
Abstract
:1. Introduction
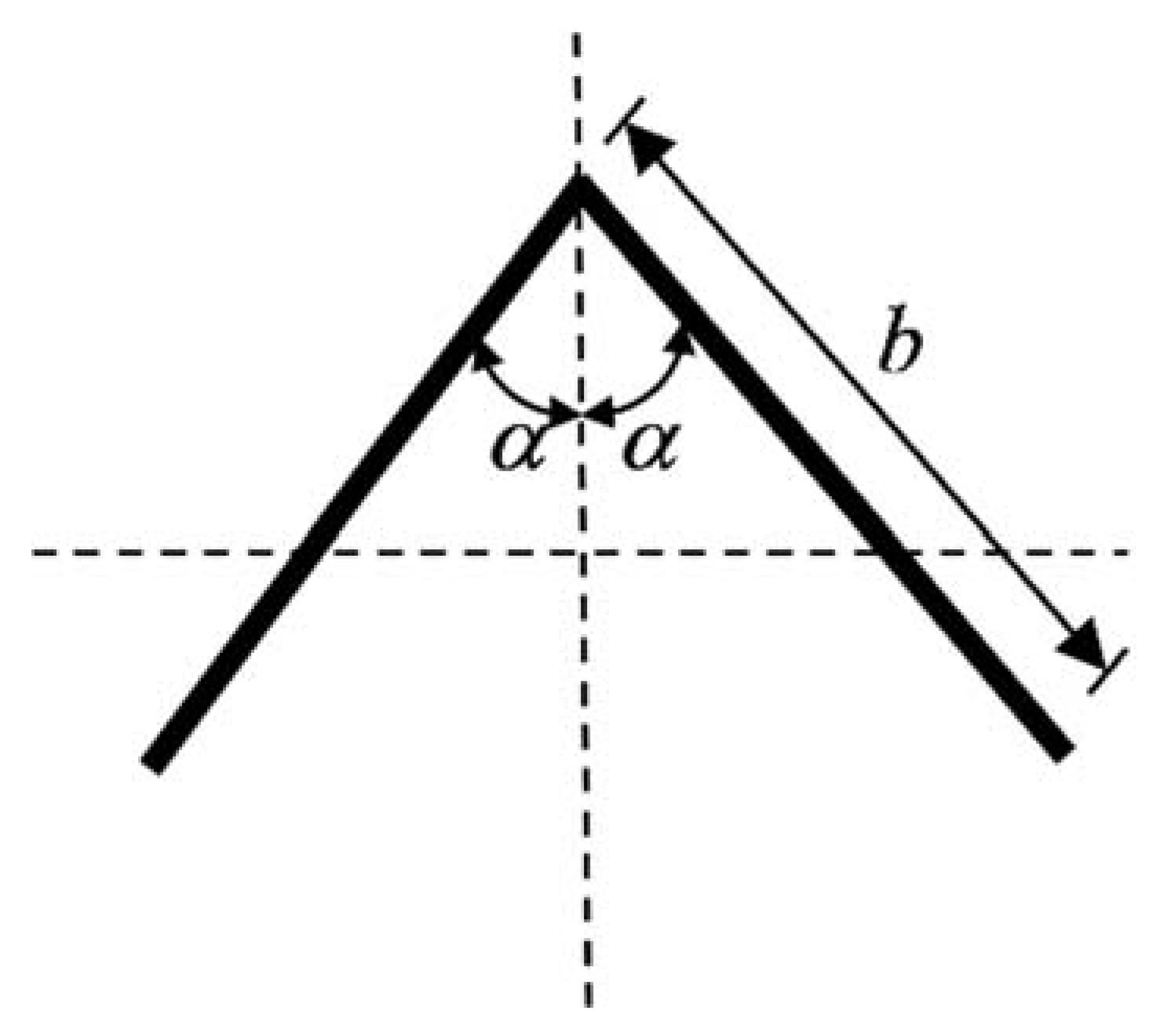
2. Theoretical Derivation
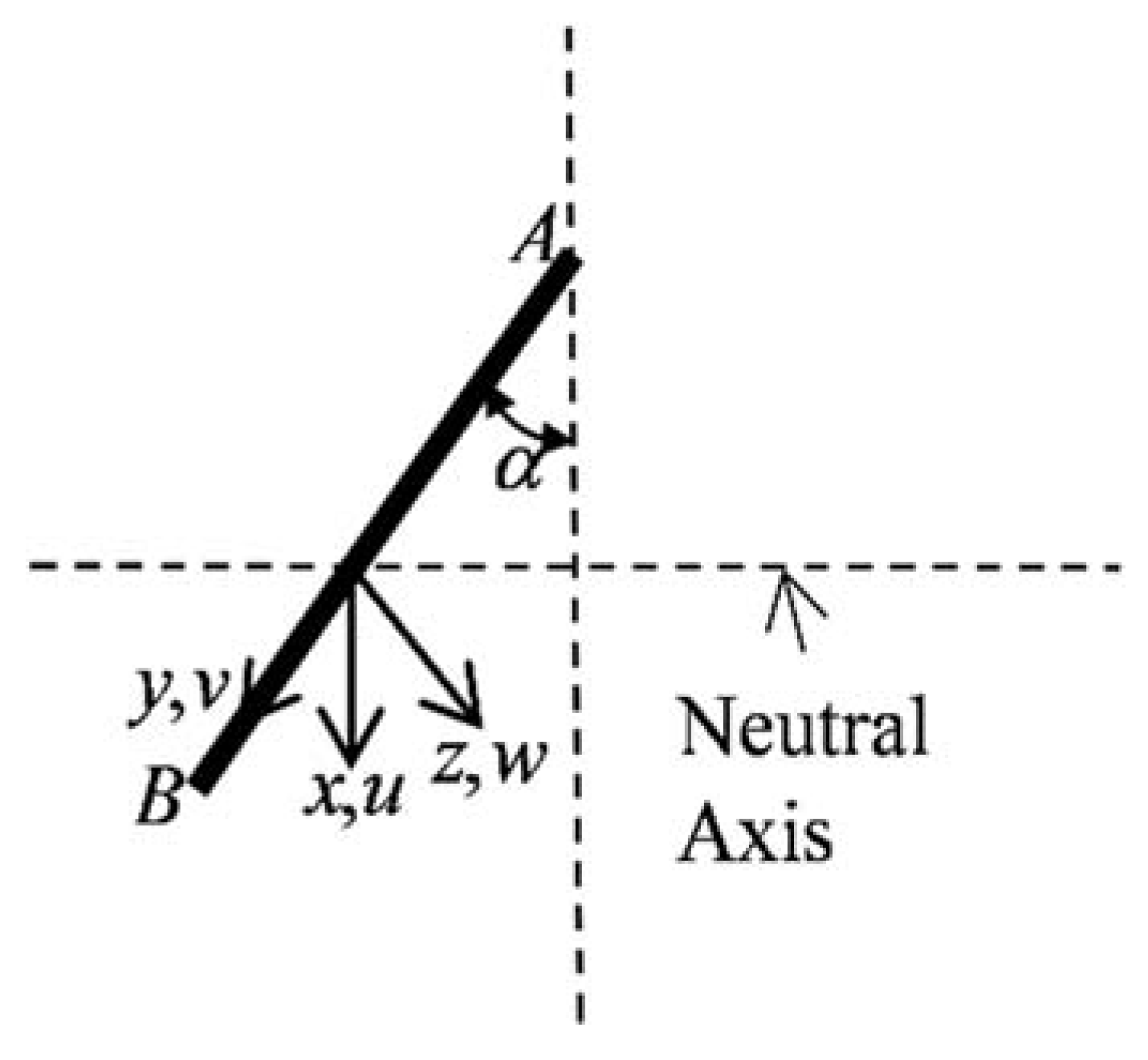
2.1. Elastic Theoretical Analysis Based on Variational Method
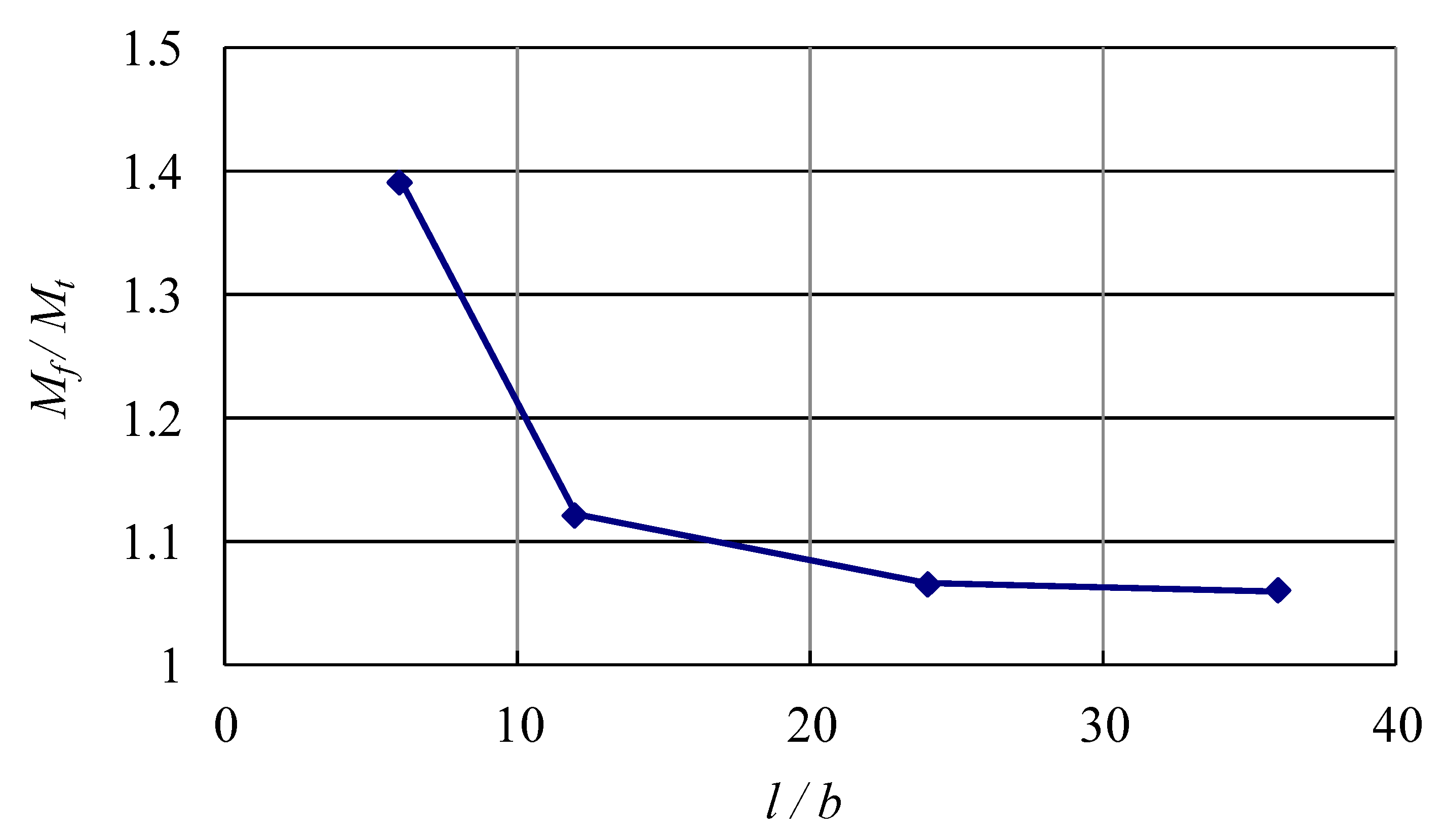
2.2. Threshold Ratio of Width to Thickness
3. Finite Element Analysis
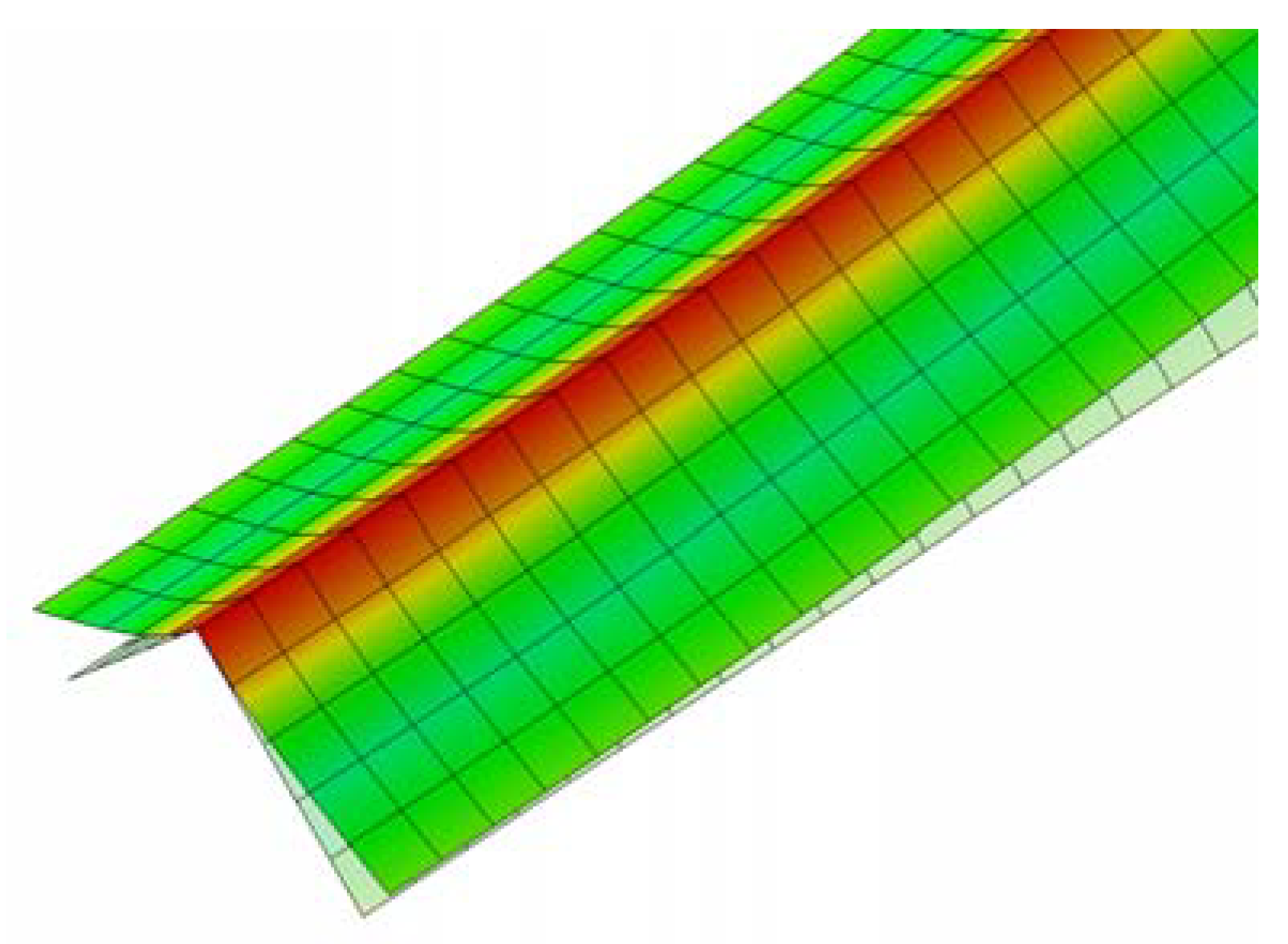
3.1. Elastic Finite Element Analysis
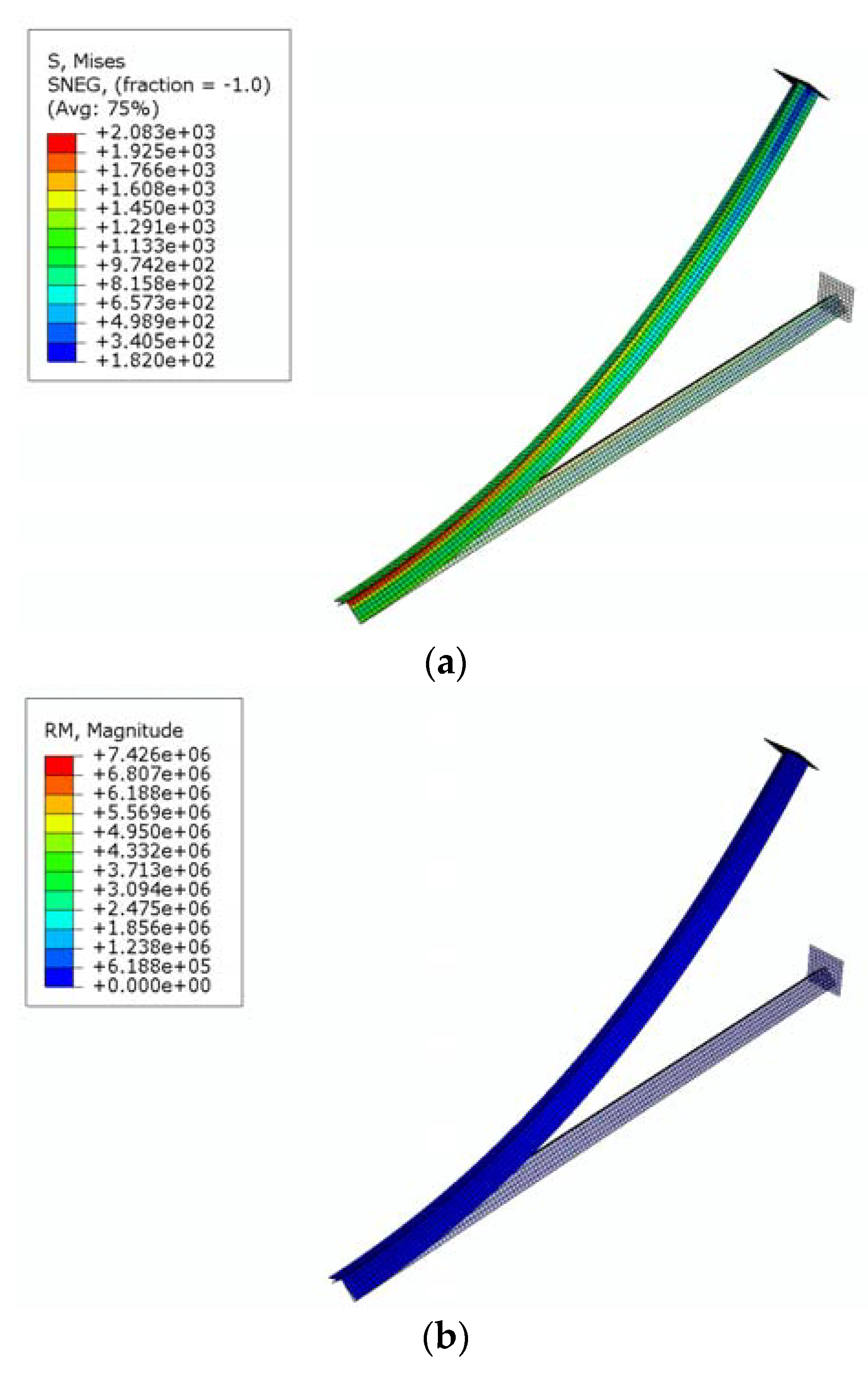
3.2. Elasto-Plastic Finite Element Analysis
4. Comparison with Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Brazier, L.G. On the flexure of thin cylindrical shells and other thin sections. Proc. R. Soc. Lond. Ser. A 1927, 116, 104–114. [Google Scholar] [CrossRef]
- Reissner, E. On finite bending of pressurized tubes. Trans. ASME 1959, 26, 386–392. [Google Scholar]
- Akselrad, E.L. Pinpointing the upper critical bending load of a pipe by calculating geometric nonlinearity. Izv. Akad. Nauk SSR. Mekh. 1965, 4, 133–139. [Google Scholar]
- Gerber, T.L. Plastic Deformation of Piping Due to Pipe-Whip Loading. 1974. Available online: http://jglobal.jst.go.jp/en/public/201002025727941512 (accessed on 22 August 2018).
- Tomasz, W.; Sinmao, M.V. A simplified model of Brazier effect in plastic bending of cylindrical tubes. Int. J. Press. Vessels Pip. 1997, 71, 19–28. [Google Scholar]
- Li, L.Y.; Kettle, R. Nonlinear bending response and buckling of ring-stiffened cylindrical shells under pure bending. Int. J. Solids. Struct. 2002, 39, 765–781. [Google Scholar] [CrossRef]
- Poonaya, S.; Teeboonma, U.; Thinvongpituk, C. Plastic collapse analysis of thin-walled circular tubes subjected to bending. Thin Wall. Struct. 2009, 47, 637–645. [Google Scholar] [CrossRef]
- Yu, T.X.; Teh, L.S. Large plastic deformation of beams of angle-section under symmetric bending. Int. J. Mech. Sci. 1997, 39, 829–839. [Google Scholar] [CrossRef]
- Huber, M.T. The Bending of Curved Tube of Elliptic Sections. In Proceedings of the Seventh International Congress for Applied Mechanics; Levy, H., Ed.; Her Majesty’s Stationery Office: London, UK, 1948; pp. 322–328. [Google Scholar]
- Rand, O. In-Plane Warping Effects in Thin-Walled Box Beams. AIAA J. 2000, 38, 542–544. [Google Scholar] [CrossRef]
- Paulsen, F.; Welo, T. Cross-Sectional Deformations of Rectangular Hollow Sections in Bending: Part II, Analytical Models. Int. J. Mech. Sci. 2001, 43, 131–152. [Google Scholar] [CrossRef]
- Cecchini, L.S.; Weaver, P.M. Brazier effect in multibay airfoil sections. AIAA J. 2005, 43, 2252–2258. [Google Scholar] [CrossRef]
- Jensen, F.M.; Weaver, P.M.; Cecchini, L.S. The Brazier effect in wind turbine blades and its influence on design. Wind Energy 2012, 15, 319–333. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D.; Scognamiglio, I. The Brazier effect for elastic pipe beams with foam cores. Thin-Wall Struct. 2018, 124, 72–80. [Google Scholar] [CrossRef]
- Sato, M.; Ishiwata, Y. Brazier effect of single- and double-walled elastic tubes under pure bending. Struct. Eng. Mech. 2015, 53, 17–26. [Google Scholar] [CrossRef]
- Shima, H.; Sato, M.; Park, S.J. Suppression of Brazier Effect in Multilayered Cylinders. Adv. Condens. Matter Phys. 2014, 10, 11–55. [Google Scholar] [CrossRef]
- Stephens, W.B.; Starnes, J.J. Collapse of long cylindrical shells under combined bending and pressure loads. AIAA J. 1975, 13, 5–20. [Google Scholar]
- Fabian, O. Collapse of cylindrical, elastic tubes under combined bending, pressure and axial loads. Int. J. Solids Struct. 1977, 13, 1257–1270. [Google Scholar] [CrossRef]
- Libai, A.; Bert, C.W. A mixed variational principle and its application to the nonlinear bending problem of orthotropic tubes-II. Application to nonlinear bending of circular cylindrical tubes. Int. J. Solids Struct. 1994, 31, 1019–1033. [Google Scholar] [CrossRef]
- Karamanos; Spyros, A. Bending instabilities of elastic tubes. Int. J. Solids Struct. 2002, 39, 2059–2085. [Google Scholar] [CrossRef]
- Tatting, B.F.; Gürdal, Z. Nonlinear shell theory solution for the bending response of orthotropic finite length cylinders including the Brazier effect. In Proceedings of the 36th Structures, Structural Dynamics and Materials Conference, New Orleans, LA, USA, 10–13 April 1995. [Google Scholar]
- Tatting, B.F.; Gürdal, Z.; Vasiliev, V.V. The Brazier effect for finite length composite cylinders under bending. Int. J. Solids Struct. 1997, 34, 1419–1440. [Google Scholar] [CrossRef]
- Makoto, W.; Gakkai, N.H. Preliminary Reconnaissance Report of the 1995 Hyogoken-Nanbu Earthquake; The Architectural Institute of Japan: Tokyo, Japan, 1995. [Google Scholar]
- Kuwamura, H. Flattening and buckling of thin angle-section beams. In Proceedings of the Fifth International Conference on “Coupled Instabilities in Metal Structures” CIMS2008, Sydney, Australia, 23–25 June 2008; pp. 101–108. [Google Scholar]





| Size | Numerical Value (N × mm) | Theoretical Value (N × mm) | Relative Difference (%) | ||
|---|---|---|---|---|---|
| b (mm) | b/t | α | |||
| 50 | 50 | 45° | 5.97 × 105 | 5.66 × 105 | +5.59 |
| 100 | 4.82 × 106 | 4.52 × 106 | +6.45 | ||
| 200 | 3.80 × 107 | 3.62 × 107 | +4.86 | ||
| 100 | 40 | 45° | 7.55 × 106 | 7.07 × 106 | +6.75 |
| 50 | 4.82 × 106 | 4.52 × 106 | +6.45 | ||
| 60 | 3.33 × 106 | 3.14 × 106 | +5.82 | ||
| 100 | 50 | 30° | 9.39 × 106 | 9.60 × 106 | −2.19 |
| 45° | 4.82 × 106 | 4.52 × 106 | +6.45 | ||
| 60° | 1.99 × 106 | 1.85 × 106 | +7.57 | ||
| Size | FEM Value (N × mm) | Elastic Theoretical Value (N × mm) | Relative Difference (%) | ||||
|---|---|---|---|---|---|---|---|
| b (mm) | b/t | α | Elastic | Elasto-Plastic | FEM Elastic | FEM Elasto-Plastic | |
| 100 | 40 | 45° | 7.55 × 106 | 2.63 × 106 | 7.07 × 106 | 6.75 | −62.80 |
| 50 | 4.82 × 106 | 2.04 × 106 | 4.52 × 106 | 6.45 | −54.88 | ||
| 60 | 3.33 × 106 | 1.65 × 106 | 3.14 × 106 | 5.82 | −47.45 | ||
| Material | Flange Thickness t (mm) | Young’s Modulus E (GPa) | Poisson’s Ratio ν | Yielding Strength σy (MPa) |
|---|---|---|---|---|
| Steel | 0.324 | 199,000 | 0.3 | 300 |
| Specimen No. | A1 | A2 | A3 | B1 | B2 | |
|---|---|---|---|---|---|---|
| Size | L (mm) | 1800 | 1800 | |||
| α | 60° | 45° | ||||
| b (mm) | 30 | 60 | ||||
| Experimental max moment (N × mm) | 1.61 × 104 | 1.60 × 104 | 1.58 × 104 | 4.83 × 104 | 5.07 × 104 | |
| Collapse mode | Brazier Flattening | Load-point crippling | Ridge-line buckling | |||
| Elastic theoretical max moment (N × mm) | 1.31 × 104 | 6.41 × 104 | ||||
| FEM max moment (N × mm) | Elastic | 1.51 × 104 | 7.84 × 104 | |||
| Elasto-plastic | 1.31 × 104 | 7.13 × 104 | ||||
| Relative difference to experimental value (%) | Theoretical value | −17.97 | 29.49 | |||
| Elastic | −5.44 | 58.38 | ||||
| Elasto-plastic | −17.97 | 44.04 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Xu, L.; Sun, C.; Xue, S. Brazier Effect of Thin Angle-Section Beams under Bending. Sustainability 2018, 10, 3047. https://doi.org/10.3390/su10093047
Zhou Z, Xu L, Sun C, Xue S. Brazier Effect of Thin Angle-Section Beams under Bending. Sustainability. 2018; 10(9):3047. https://doi.org/10.3390/su10093047
Chicago/Turabian StyleZhou, Zhiguang, Liuyun Xu, Chaoxin Sun, and Songtao Xue. 2018. "Brazier Effect of Thin Angle-Section Beams under Bending" Sustainability 10, no. 9: 3047. https://doi.org/10.3390/su10093047





