A Comprehensive Review on Finite Element Analysis of Laser Shock Peening
Abstract
1. Introduction
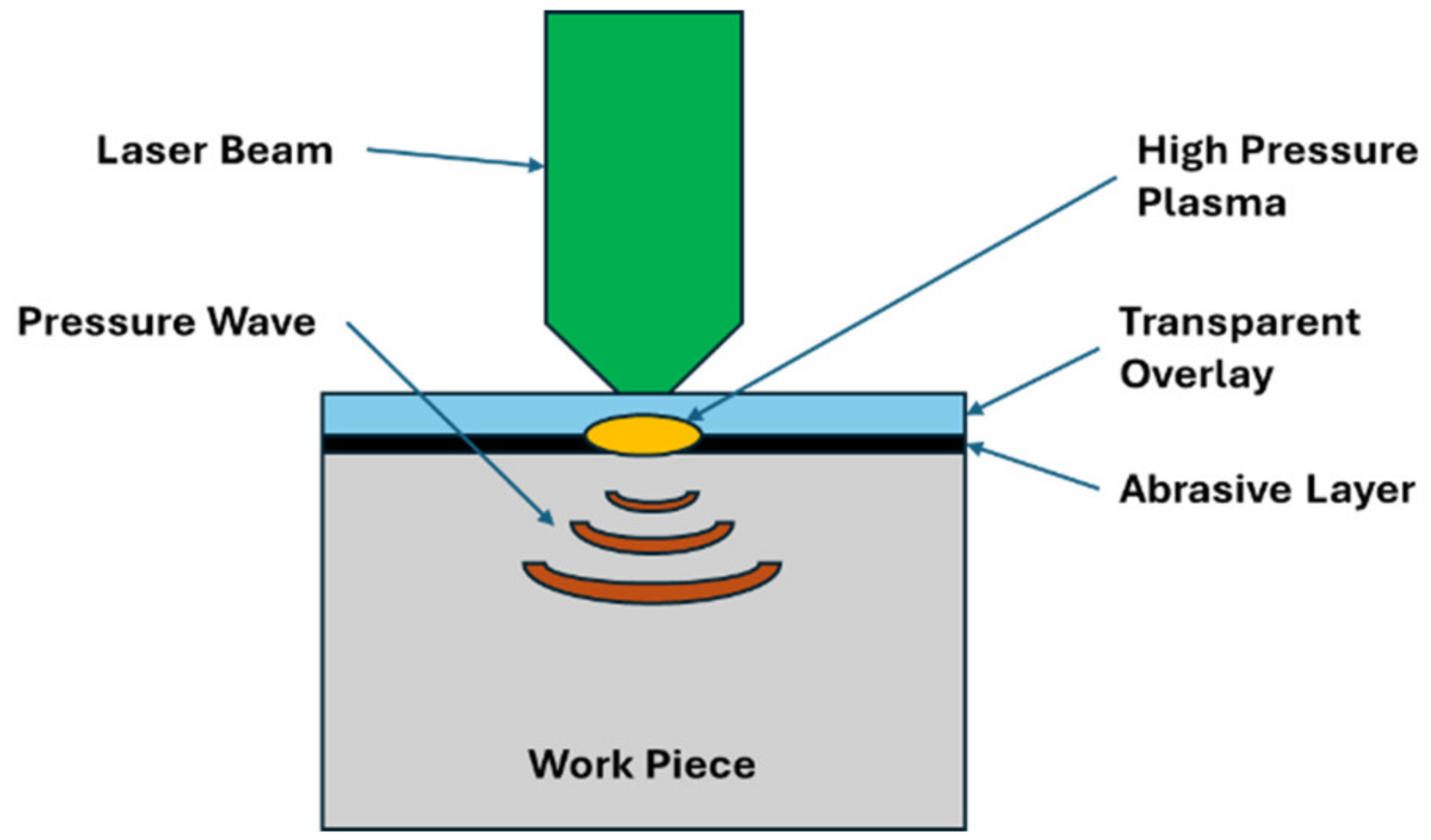
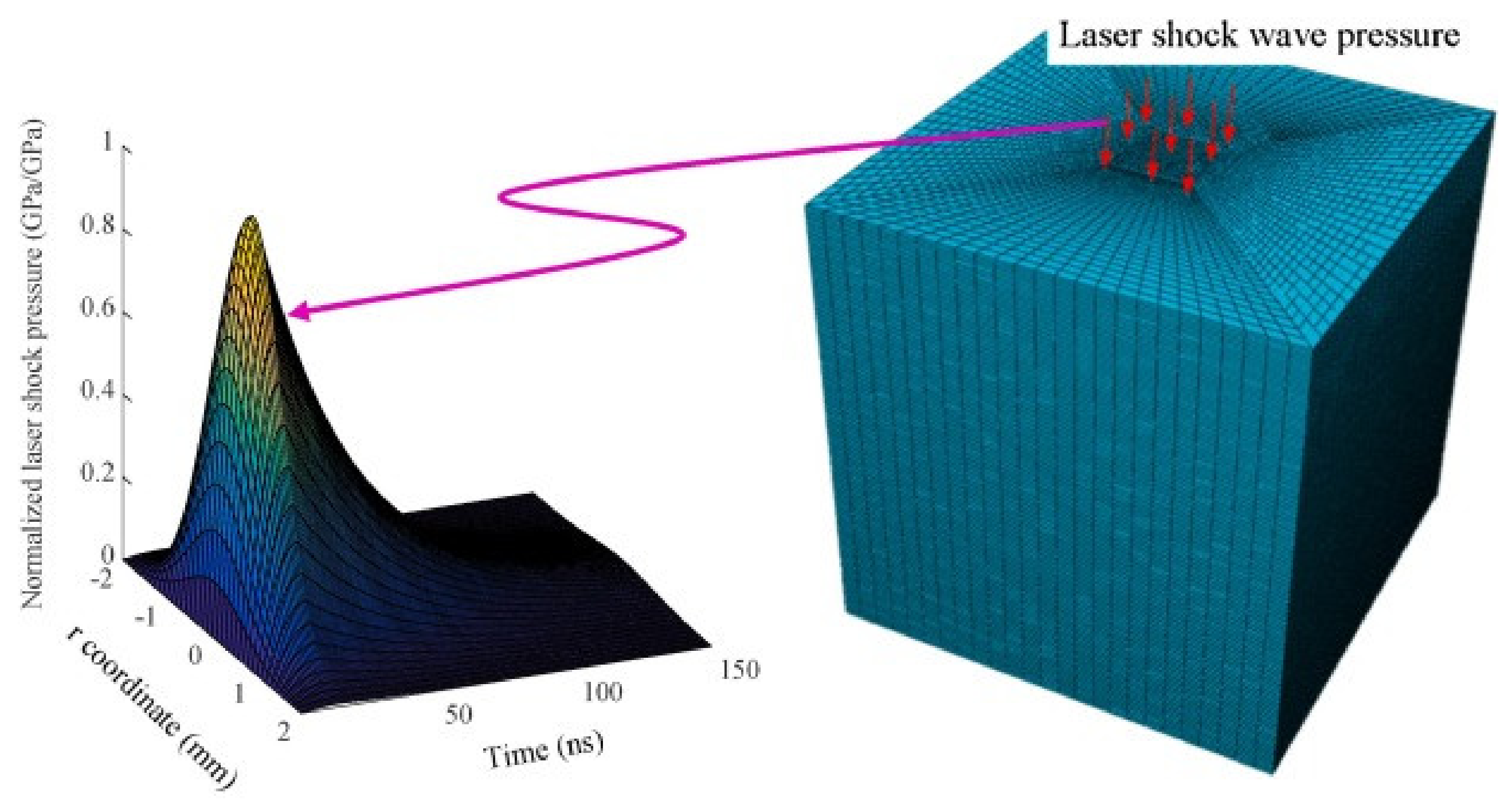
2. LSP Process
3. Key Parameters for the LSP Process
3.1. Laser Parameters
- I.
- Laser IntensityA higher laser intensity generates stronger shock waves, leading to deeper compressive residual stresses and improved fatigue resistance. This is because the increased energy density enhances the plastic deformation of the material, resulting in a more significant alteration in its microstructure. However, excessive intensity can cause surface damage or melting, which can compromise the integrity of the treated material and lead to undesirable effects such as micro-cracking or surface roughness. A lower laser intensity produces milder shock waves, which may not penetrate as deeply, resulting in less pronounced improvements in material properties. Although this can be beneficial for treating delicate or thin materials, where excessive energy might cause damage, it may not provide the same level of enhancement in fatigue resistance or hardness as higher intensities [31,32,33].
- II.
- Pulse DurationA shorter pulse duration typically results in higher peak pressures, enhancing the depth and magnitude of the compressive residual stresses. This is because shorter pulses concentrate the energy in a brief time frame, creating intense shock waves that penetrate deeper into the material. These high peak pressures can significantly improve the material’s fatigue resistance and hardness. However, very short pulses can lead to surface ablation, where the material is removed from the surface due to the high-energy density, potentially causing surface roughness or damage. A longer pulse duration generates lower peak pressures, which might reduce the effectiveness of the peening process in terms of the depth and magnitude of the compressive residual stresses. The energy is spread over a longer period, resulting in less intense shock waves. However, this can be beneficial for treating more delicate materials, as it reduces the risk of surface damage and ablation. Longer pulses can also provide a more uniform treatment over larger areas, which is advantageous for applications requiring gentle processing [34,35,36].
- III.
- Spot SizeA smaller laser spot size concentrates the energy over a limited area, resulting in a higher peak stress. This intense focus can be particularly useful for localized strengthening because it enhances material properties in specific regions. A higher energy density in a smaller spot size can lead to more significant plastic deformation and deeper compressive residual stresses. However, limited coverage means that only a small area benefits from these high stresses, which might require multiple passes to treat larger surfaces effectively. Conversely, a larger laser spot size distributes energy over a broader area, leading to a more uniform stress distribution. This can be advantageous for treating larger surfaces more evenly, reducing the likelihood of untreated areas, and ensuring consistent material properties across the entire surface. However, the peak stresses are generally lower compared to those achieved with a smaller spot size, which might result in less pronounced improvements in localized material properties. The trade-off between spot size and stress distribution is crucial for optimizing the laser treatment process based on specific applications and material requirements [37,38].
- IV.
- CoverageA higher laser coverage ensures a more uniform treatment and consistent material properties across the surface. This uniformity is crucial for enhancing the mechanical properties of the material, such as hardness and wear resistance. It can improve the overall fatigue resistance by creating a more homogeneous microstructure, which helps distribute stress more evenly and reduces the likelihood of crack initiation. Additionally, higher coverage minimizes the risk of untreated areas, which can act as stress concentrators and lead to premature failure. On the other hand, lower laser coverage may leave some areas untreated, leading to an uneven stress distribution and potentially weaker spots. These untreated areas can become focal points for stress, increasing the risk of fatigue and failure under cyclic loading. Inconsistent treatment can also result in variations in the surface hardness and wear resistance, compromising the overall performance of the material [39,40,41].
- V.
- WavelengthIn laser shock peening, shorter wavelengths are generally absorbed more efficiently by the material, leading to more effective shockwave generation. This increased absorption can enhance the peening effect, improving the surface hardness and residual stress distribution. However, the higher energy concentration associated with shorter wavelengths can also elevate the risk of surface damage, such as melting or ablation. Conversely, longer wavelengths penetrate deeper into the material, which can be beneficial for treating subsurface layers and achieving a more uniform stress distribution throughout the material. However, these longer wavelengths often require higher laser intensities to generate shock waves of strengths comparable to those produced by shorter wavelengths. This can make the process less efficient and potentially more costly due to the need for more powerful laser systems. Additionally, the choice of wavelength can influence the overall effectiveness of the peening process, depending on the specific material properties and desired outcomes. For instance, materials with higher absorption coefficients for shorter wavelengths may benefit more from their use, while those requiring deeper penetration might be better suited for longer wavelengths [32,42].
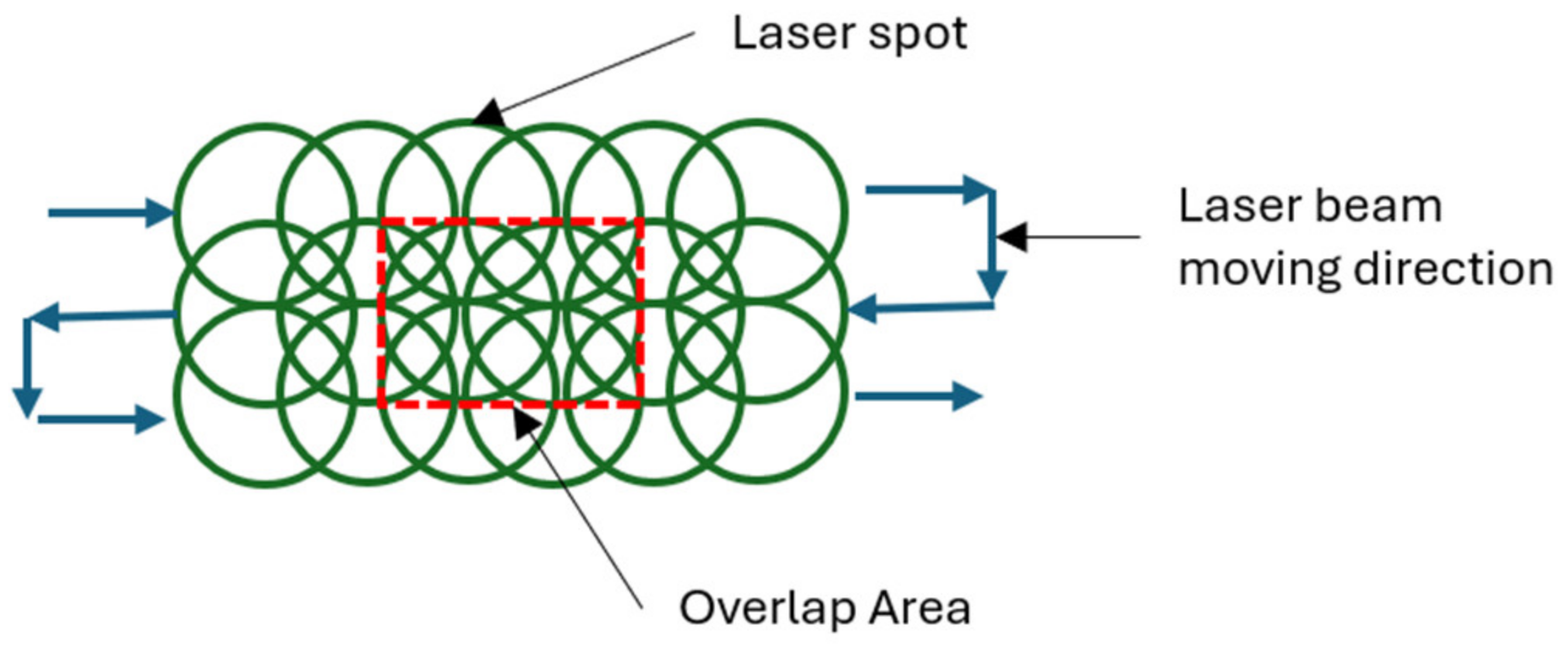
3.2. Overlapping of Laser Shots
4. Effect of LSP on Material Properties
5. Effect of LSP on Grain Refinement
6. FEA Algorithms
7. Influence of Meshing on Simulation Outcomes
8. Progressive Perspectives: Advancement in LSP FEA
9. Discussion
10. Future Direction
11. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Askar’yan, G.A.; Moroz, E.M. Pressure on Evaporation of Matter in a Radiation Beam. J. Exp. Theor. Phys. 1963, 16, 1638. [Google Scholar]
- Walz, D.R.; Lucas, L.R.; Weidner, H.A.; Vetterlein, R.J.; Seppi, E.J. Beam Dumps, Energy Slits and Collimators at SLAC--Their Final Versions and First Performance Data. IEEE Trans. Nucl. Sci. 1967, 14, 923–927. [Google Scholar] [CrossRef][Green Version]
- Banas, G.; Chu, J.; Rigsbee, J.M.; Lawrence, F.V.; Elsayed-Ali, H.E. Laser Shock Processing of Low Carbon Steel; WIT Press: Southampton, UK, 1993; Volume 2. [Google Scholar]
- Ford, S.C. Investigation of Laser Shock Processing; Flight Dynamics Laboratory, Air Force Wright Aeronautical Laboratories, Air Force Systems Command, United States Air Force: Dayton, OH, USA, 1980; Volume 2. [Google Scholar]
- Kamkarrad, H.; Narayanswamy, S. FEM of Residual Stress and Surface Displacement of a Single Shot in High Repetition Laser Shock Peening on Biodegradable Magnesium Implant. J. Mech. Sci. Technol. 2016, 30, 3265–3273. [Google Scholar] [CrossRef]
- Sakhvadze, G.Z.; Sakhvadze, G.G. Combined Model Based on the Finite Element Method and Artificial Neural Networks for Modeling Laser Shock Peening of Titanium–Niobium Implants. J. Mach. Manuf. Reliab. 2023, 52, 741–748. [Google Scholar] [CrossRef]
- John, M.; Kalvala, P.R.; Misra, M.; Menezes, P.L. Peening Techniques for Surface Modification: Processes, Properties, and Applications. Materials 2021, 14, 3841. [Google Scholar] [CrossRef]
- Pan, X.; Wang, X.; Tian, Z.; He, W.; Shi, X.; Chen, P.; Zhou, L. Effect of Dynamic Recrystallization on Texture Orientation and Grain Refinement of Ti6Al4V Titanium Alloy Subjected to Laser Shock Peening. J. Alloys Compd. 2021, 850, 156672. [Google Scholar] [CrossRef]
- Lan, L.; Jin, X.; Gao, S.; He, B.; Rong, Y. Microstructural Evolution and Stress State Related to Mechanical Properties of Electron Beam Melted Ti-6Al-4V Alloy Modified by Laser Shock Peening. J. Mater. Sci. Technol. 2020, 50, 153–161. [Google Scholar] [CrossRef]
- Rubio-González, C.; Ocaña, J.L.; Gomez-Rosas, G.; Molpeceres, C.; Paredes, M.; Banderas, A.; Porro, J.; Morales, M. Effect of Laser Shock Processing on Fatigue Crack Growth and Fracture Toughness of 6061-T6 Aluminum Alloy. Mater. Sci. Eng. A 2004, 386, 291–295. [Google Scholar] [CrossRef]
- Huang, S.; Sheng, J.; Wang, Z.; Meng, X.; Lu, J.; Hu, X.; Zhou, J. Finite Element and Experimental Analysis of Elevated-Temperature Fatigue Behavior of IN718 Alloy Subjected to Laser Peening. Int. J. Fatigue 2020, 131, 105337. [Google Scholar] [CrossRef]
- Adu-Gyamfi, S.; Ren, X.D.; Larson, E.A.; Ren, Y.; Tong, Z. The Effects of Laser Shock Peening Scanning Patterns on Residual Stress Distribution and Fatigue Life of AA2024 Aluminium Alloy. Opt. Laser Technol. 2018, 108, 177–185. [Google Scholar] [CrossRef]
- Kosaraju, S.H. Optimization of Laser Shock Peening Process Using Finite Element Modeling. Ph.D. Thesis, Graduate School of Clemson University, Clemson, SC, USA, 2018. [Google Scholar]
- Nam, T. Finite Element Analysis of Residual Stress Field Induced by Laser Shock Peening. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2002. [Google Scholar]
- Sano, Y.; Mukai, N.; Okazaki, K.; Obata, M. Residual Stress Improvement in Metal Surface by Underwater Laser Irradiation. Nucl. Instrum. Methods Phys. Res. B 1997, 121, 432–436. [Google Scholar] [CrossRef]
- Zhao, J.; Dong, Y.; Ye, C. Laser Shock Peening Induced Residual Stresses and the Effect on Crack Propagation Behavior. Int. J. Fatigue 2017, 100, 407–417. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, W.; Zhou, G. Experimental Study of the Effects of PMMA Confinement on Laser-Induced Shock Waves. Chin. J. Lasers 1997, 24, 118–122. [Google Scholar]
- Ralls, A.M.; Menezes, P.L. Revealing the fretting corrosion mechanisms of laser shock peened cold spray 316 L stainless steel. Tribol. Int. 2024, 192, 109227. [Google Scholar] [CrossRef]
- Fabbro, R.; Fournier, J.; Ballard, P.; Devaux, D.; Virmont, J. Physical Study of Laser-produced Plasma in Confined Geometry. J. Appl. Phys. 1990, 68, 775–784. [Google Scholar] [CrossRef]
- Sano, Y.; Yoda, M.; Mukai, N.; Obata, M.; Kanno, M.; Shima, S. Residual Stress Improvement Mechanism on Metal Material by Underwater Laser Irradiation. At. Energy Soc. Jpn. 2000, 42, 567–573. [Google Scholar] [CrossRef][Green Version]
- Peyre, P.; Berthe, L.; Vignal, V.; Popa, I.; Baudin, T. Analysis of Laser Shock Waves and Resulting Surface Deformations in an Al–Cu–Li Aluminum Alloy. J. Phys. D Appl. Phys. 2012, 45, 335304. [Google Scholar] [CrossRef]
- Braisted, W.; Brockman, R. Finite Element Simulation of Laser Shock Peening. Int. J. Fatigue 1999, 21, 719–724. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R.; Berthe, L.; Dubouchet, C. Laser Shock Processing of Materials, Physical Processes Involved and Examples of Applications. J. Laser Appl. 2012, 8, 135–141. [Google Scholar] [CrossRef]
- Peyre, P.; Berthe, L.; Scherpereel, X.; Fabbro, R.; Bartnicki, E. Experimental Study of Laser-Driven Shock Waves in Stainless Steels. J. Appl. Phys. 1998, 84, 5985–5992. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, J.; Sheng, J.; Meng, X.; Agyenim-Boateng, E.; Ma, D.; Li, J.; Zhou, J. Effect of Laser Peening with Different Power Densities on Vibration Fatigue Resistance of Hydrogenated TC4 Titanium Alloy. Int. J. Fatigue 2020, 131, 105335. [Google Scholar] [CrossRef]
- Pozdnyakov, V.; Keller, S.; Kashaev, N.; Klusemann, B.; Oberrath, J. Coupled Modeling Approach for Laser Shock Peening of AA2198-T3: From Plasma and Shock Wave Simulation to Residual Stress Prediction. Metals 2022, 12, 107. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Wang, C.-L.; Li, K.; Wang, X.-G. Dislocation density-based study of grain refinement induced by laser shock peening. Opt. Laser Technol. 2020, 121, 105827. [Google Scholar] [CrossRef]
- Ding, K.; Ye, L. Simulation of Multiple Laser Shock Peening of a 35CD4 Steel Alloy. J. Mater. Process. Technol. 2006, 178, 162–169. [Google Scholar] [CrossRef]
- Abhishek; Panda, S.S.; Kumar, S. Numerical Analysis on Residual Stress Hole Generation in Laser Shock Peening. Eur. Phys. J. Plus 2022, 137, 461. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R. Laser Shock Processing: A Review of the Physics and Applications. Opt. Quant. Electron. 1995, 27, 1213–1229. [Google Scholar] [CrossRef]
- Ayeb, M.; Frija, M.; Fathallah, R. Laser Peening: A Review of the Factors, Effects, Applications, Comparison with Shot Peening and State-of-the-Art. Met. Mater. Int. 2024, 30, 259–283. [Google Scholar] [CrossRef]
- Gupta, R.K.; Pant, B.K.; Kain, V.; Kaul, R.; Bindra, K.S. Laser Shock Peening and its Applications: A Review. Lasers Manuf. Mater. Process. 2019, 6, 424–463. [Google Scholar]
- Gujba, A.K.; Medraj, M. Laser Peening Process and Its Impact on Materials Properties in Comparison with Shot Peening and Ultrasonic Impact Peening. Materials 2014, 7, 7925–7974. [Google Scholar] [CrossRef]
- Li, D.; Du, K. Ultrashort Pulse Lasers. In Handbook of Laser Micro- and Nano-Engineering; Sugioka, K., Ed.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Russa, S.; Gebsa, R.; Bauera, L.; Kellera, U.; Meyera, T.; Rollera, J.; Führaa, B.; Faisstb, B. Shorter than short: How does the pulse duration influence the process efficiency of conductive materials? Lasers Manuf. Conf. 2015, 2015, 98. [Google Scholar]
- Nagl, N. Fundamentals of Ultrashort Pulse Generation. In A New Generation of Ultrafast Oscillators for Mid-Infrared Applications; Springer Theses; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Farkas, J.P.; Hoopman, J.E.; Kenkel, J.M. Five Parameters You Must Understand to Master Control of Your Laser/Light-Based Devices. Aesthetic Surg. J. 2013, 33, 1059–1064. [Google Scholar] [CrossRef]
- Guo, K.; Liu, W. Improving mechanical properties of additively manufactured H13 steel through residual stress modulation by laser shock peening. Int. J. Adv. Manuf. Technol. 2024, 132, 5289–5303. [Google Scholar] [CrossRef]
- Łach, Ł. Recent Advances in Laser Surface Hardening: Techniques, Modeling Approaches, and Industrial Applications. Crystals 2024, 14, 726. [Google Scholar] [CrossRef]
- Jeyaprakash, N.; Yang, C.H.; Kumar, D.R. Laser Surface Modification of Materials. In Practical Applications of Laser Ablation; IntechOpen: London, UK, 2020. [Google Scholar]
- Dobrzański, L.A.; Dobrzańska-Danikiewicz, A.D.; Tański, T.; Jonda, E.; Drygała, A.; Bonek, M. Laser Surface Treatment in Manufacturing. In Handbook of Manufacturing Engineering and Technology; Nee, A., Ed.; Springer: London, UK, 2015. [Google Scholar]
- Sano, T. Dry Laser Peening: Ultrashort Pulsed Laser Peening without Sacrificial Overlay Under Atmospheric Conditions. In Laser Micro-Nano-Manufacturing and 3D Microprinting; Hu, A., Ed.; Springer Series in Materials Science; Springer: Cham, Switzerland, 2020; Volume 309. [Google Scholar]
- Karbalaian, H.R.; Yousefi-Koma, A.; Karimpour, M.; Mohtasebi, S.S. Investigation on the Effect of Overlapping Laser Pulses in Laser Shock Peening with Finite Element Method. Procedia Mater. Sci. 2015, 11, 454–458. [Google Scholar] [CrossRef]
- Fang, Y.W.; Li, Y.H.; He, W.F.; Li, P.Y. Effects of Laser Shock Processing with Different Parameters and Ways on Residual Stresses Fields of a TC4 Alloy Blade. Mater. Sci. Eng. A 2013, 559, 683–692. [Google Scholar] [CrossRef]
- Xu, G.; Luo, K.Y.; Dai, F.Z.; Lu, J.Z. Effects of Scanning Path and Overlapping Rate on Residual Stress of 316L Stainless Steel Blade Subjected to Massive Laser Shock Peening Treatment with Square Spots. Appl. Surf. Sci. 2019, 481, 1053–1063. [Google Scholar] [CrossRef]
- Xiang, Y.F.; Mei, R.L.; Wang, S.P.; Azad, F.; Zhao, L.Z.; Su, S.C. Numerical Investigation of the Effect of Laser Shock Peening Parameters on the Residual Stress and Deformation Response of 7075 Aluminum Alloy. Optik 2021, 243, 167446. [Google Scholar] [CrossRef]
- Hfaiedh, N.; Peyre, P.; Song, H.; Popa, I.; Ji, V.; Vignal, V. Finite Element Analysis of Laser Shock Peening of 2050-T8 Aluminum Alloy. Int. J. Fatigue 2015, 70, 480–489. [Google Scholar] [CrossRef]
- Dong, X.; Tang, Z.; Zhang, G.; Wang, K. Research on Finite Element Simulation and Recrystallization of Laser Shock Peened Nickel-Based Single-Crystal Superalloy. J. Mater. Eng Perform 2023. [Google Scholar] [CrossRef]
- Luo, K.Y.; Liu, B.; Wu, L.J.; Yan, Z.; Lu, J.Z. Tensile Properties, Residual Stress Distribution and Grain Arrangement as a Function of Sheet Thickness of Mg–Al–Mn Alloy Subjected to Two-Sided and Simultaneous LSP Impacts. Appl. Surf. Sci. 2016, 369, 366–376. [Google Scholar] [CrossRef]
- Yan, H.; Qin, Z.; Zhang, W.; Ming, A.; Wang, X.; Chu, F. Dynamic Analysis of Laser Shock Response: Experimental and Numerical Studies. Aerosp. Sci. Technol. 2019, 94, 105430. [Google Scholar] [CrossRef]
- Golabi, S.; Vakil, M.R.; Amirsalari, B. Multi-Objective Optimization of Residual Stress and Cost in Laser Shock Peening Process Using Finite Element Analysis and PSO Algorithm. Lasers Manuf. Mater. Process. 2019, 6, 398–423. [Google Scholar] [CrossRef]
- Keller, S.; Chupakhin, S.; Staron, P.; Maawad, E.; Kashaev, N.; Klusemann, B. Experimental and Numerical Investigation of Residual Stresses in Laser Shock Peened AA2198. J. Mater. Process. Technol. 2018, 255, 294–307. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, Z.; Hu, J. 3-D FEM Simulation of Laser Shock Processing. Surf. Coat. Technol. 2006, 201, 1426–1435. [Google Scholar] [CrossRef]
- Warren, A.W.; Guo, Y.B.; Chen, S.C. Massive Parallel Laser Shock Peening: Simulation, Analysis, and Validation. Int. J. Fatigue 2008, 30, 188–197. [Google Scholar] [CrossRef]
- Kashaev, N.; Ventzke, V.; Horstmann, M.; Chupakhin, S.; Riekehr, S.; Falck, R.; Maawad, E.; Staron, P.; Schell, N.; Huber, N. Effects of Laser Shock Peening on the Microstructure and Fatigue Crack Propagation Behaviour of Thin AA2024 Specimens. Int. J. Fatigue 2017, 98, 223–233. [Google Scholar] [CrossRef]
- Bikdeloo, R.; Farrahi, G.H.; Mehmanparast, A.; Mahdavi, S.M. Multiple Laser Shock Peening Effects on Residual Stress Distribution and Fatigue Crack Growth Behaviour of 316L Stainless Steel. Theor. Appl. Fract. Mech. 2020, 105, 102429. [Google Scholar] [CrossRef]
- Tan, Y.; Wu, G.; Yang, J.-M.; Pan, T. Laser Shock Peening on Fatigue Crack Growth Behaviour of Aluminium Alloy. Fatigue Fract. Eng. Mater. Struct. 2004, 27, 649–656. [Google Scholar] [CrossRef]
- ASTM Standard E647-11; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM International: West Conshohocken, PA, USA, 2003.
- Granados-Alejo, V.; Rubio-González, C.; Vázquez-Jiménez, C.A.; Banderas, J.A.; Gómez-Rosas, G. Influence of Specimen Thickness on the Fatigue Behavior of Notched Steel Plates Subjected to Laser Shock Peening. Opt. Laser Technol. 2018, 101, 531–544. [Google Scholar] [CrossRef]
- Wang, M.; Wang, C.; Tao, X.; Zhou, Y. Numerical Study on Laser Shock Peening of Pure Al Correlating with Laser Shock Wave. Materials 2022, 15, 7051. [Google Scholar] [CrossRef]
- Zhou, Z.; Gill, A.S.; Qian, D.; Mannava, S.R.; Langer, K.; Wen, Y.; Vasudevan, V.K. A Finite Element Study of Thermal Relaxation of Residual Stress in Laser Shock Peened IN718 Superalloy. Int. J. Impact Eng. 2011, 38, 590–596. [Google Scholar] [CrossRef]
- Lou, S.; Li, Y.; Zhou, L.; Nie, X.; He, G.; Li, Y.; He, W. Surface Nanocrystallization of Metallic Alloys with Different Stacking Fault Energy Induced by Laser Shock Processing. Mater. Des. 2016, 104, 320–326. [Google Scholar] [CrossRef]
- Zhu, L.; Ruan, H.; Chen, A.; Guo, X.; Lu, J. Microstructures-Based Constitutive Analysis for Mechanical Properties of Gradient-Nanostructured 304 Stainless Steels. Acta Mater. 2017, 128, 375–390. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Wu, X.; Soh, A.K. A Physical Model Revealing Strong Strain Hardening in Nano-Grained Metals Induced by Grain Size Gradient Structure. Mater. Sci. Eng. A 2015, 620, 16–21. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, Z.; Panicaud, B. Constitutive Modeling of TWIP/TRIP Steels and Numerical Simulation of Single Impact during Surface Mechanical Attrition Treatment. Mech. Mater. 2018, 122, 69–75. [Google Scholar] [CrossRef]
- Hassani-Gangaraj, S.M.; Cho, K.S.; Voigt, H.-J.L.; Guagliano, M.; Schuh, C.A. Experimental Assessment and Simulation of Surface Nanocrystallization by Severe Shot Peening. Acta Mater. 2015, 97, 105–115. [Google Scholar] [CrossRef]
- Lin, Q.; Liu, H.; Zhu, C.; Chen, D.; Zhou, S. Effects of Different Shot Peening Parameters on Residual Stress, Surface Roughness and Cell Size. Surf. Coat. Technol. 2020, 398, 126054. [Google Scholar] [CrossRef]
- Kamkarrad, H. High Repetition Rate Laser Shock Peening on Biodegradable Magnesium Alloys. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2016. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture Characteristics of Three Metals Subjected to Various Strains, Strain Rates, Temperatures and Pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Wei, X.L.; Ling, X. Numerical Modeling of Residual Stress Induced by Laser Shock Processing. Appl. Surf. Sci. 2014, 301, 557–563. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, Z. Numerical Simulation and Experimentation of Overlapping Laser Shock Processing with Symmetry Cell. Int. J. Mach. Tools Manuf. 2008, 48, 152–162. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Khan, A.S.; Sung Suh, Y.; Kazmi, R. Quasi-Static and Dynamic Loading Responses and Constitutive Modeling of Titanium Alloys. Int. J. Plast. 2004, 20, 2233–2248. [Google Scholar] [CrossRef]
- Kim, R.; Suh, J.; Shin, D.; Lee, K.-H.; Bae, S.-H.; Cho, D.-W.; Yi, W.-G. FE Analysis of Laser Shock Peening on STS304 and the Effect of Static Damping on the Solution. Metals 2021, 11, 1516. [Google Scholar] [CrossRef]
- Coratella, S.; Sticchi, M.; Toparli, M.B.; Fitzpatrick, M.E.; Kashaev, N. Application of the Eigenstrain Approach to Predict the Residual Stress Distribution in Laser Shock Peened AA7050-T7451 Samples. Surf. Coat. Technol. 2015, 273, 39–49. [Google Scholar] [CrossRef]
- Sakhvadze, G.Z. Finite Element Modeling of the Technology of Multiple Laser Shock Processing of Materials Using the Eigenstrain Method. J. Mach. Manuf. Reliab. 2018, 47, 473–478. [Google Scholar] [CrossRef]
- Luo, M.; Li, X.; Liu, F.; Tan, J. Investigating the Applicability of the Layered Average Eigenstrain Method in Laser Shock Peening. Mater. Today Commun. 2023, 36, 106699. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, Y. An Iterative Approach Combined with Multi-Dimensional Fitting of Limited Measured Stress Points to Reconstruct Residual Stress Field Generated by Laser Shock Peening. Surf. Coat. Technol. 2022, 436, 128237. [Google Scholar] [CrossRef]
- Sun, J.; Li, J.; Chen, X.; Xu, Z.; Lin, Y.; Jiang, Q.; Chen, J.; Li, Y. Optimizing Parameters with FEM Model for 20CrMnTi Laser Shocking. Materials 2023, 16, 3288. [Google Scholar] [CrossRef]
- Li, X.; He, W.; Luo, S.; Nie, X.; Tian, L.; Feng, X.; Li, R. Simulation and Experimental Study on Residual Stress Distribution in Titanium Alloy Treated by Laser Shock Peening with Flat-Top and Gaussian Laser Beams. Materials 2019, 12, 1343. [Google Scholar] [CrossRef]
- Zhang, X.; She, J.; Li, S.; Duan, S.; Zhou, Y.; Yu, X.; Zheng, R.; Zhang, B. Simulation on Deforming Progress and Stress Evolution during Laser Shock Forming with Finite Element Method. J. Mater. Process. Technol. 2015, 220, 27–35. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, J.S.; Kim, Y.J.; Bae, H.Y.; Kim, J.S. Effects of Simulation Parameters on Residual Stresses of Inconel Alloy 600 in Finite Element Laser Shock Peening Analysis. In Proceedings of the ASME 2012 Pressure Vessels and Piping Conference. Volume 6: Materials and Fabrication, Parts A and B, Toronto, ON, Canada, 15–19 July 2012; pp. 1157–1163. [Google Scholar]
- Kumar, G.R.; Rajyalakshmi, G. FE Simulation for Stress Distribution and Surface Deformation in Ti-6Al-4V Induced by Interaction of Multi Scale Laser Shock Peening Parameters. Optik 2020, 206, 164280. [Google Scholar]
- Kostina, A.; Zhelnin, M.; Gachegova, E.; Prokhorov, A.; Vshivkov, A.; Plekhov, O.; Swaroop, S. Finite-Element Study of Residual Stress Distribution in Ti-6Al-4V Alloy Treated by Laser Shock Peening with Varying Parameters. Frat. Ed Integrità Strutt. 2022, 16, 419–436. [Google Scholar] [CrossRef]
- Qiao, H.; Sun, B.; Zhao, J.; Lu, Y.; Cao, Z. Numerical Modeling of Residual Stress Field for Linear Polarized Laser Oblique Shock Peening. Optik 2019, 186, 52–62. [Google Scholar] [CrossRef]
- Sun, R.; Li, L.; Zhu, Y.; Zhang, L.; Guo, W.; Peng, P.; Li, B.; Guo, C.; Liu, L.; Che, Z.; et al. Dynamic Response and Residual Stress Fields of Ti6Al4V Alloy under Shock Wave Induced by Laser Shock Peening. Modelling Simul. Mater. Sci. Eng. 2017, 25, 065016. [Google Scholar]
- Mylavarapu, P.; Bhat, C.; Perla, M.K.R.; Banerjee, K.; Gopinath, K.; Jayakumar, T. Identification of Critical Material Thickness for Eliminating Back Reflected Shockwaves in Laser Shock Peening–A Numerical Study. Opt. Laser Technol. 2021, 142, 107217. [Google Scholar] [CrossRef]
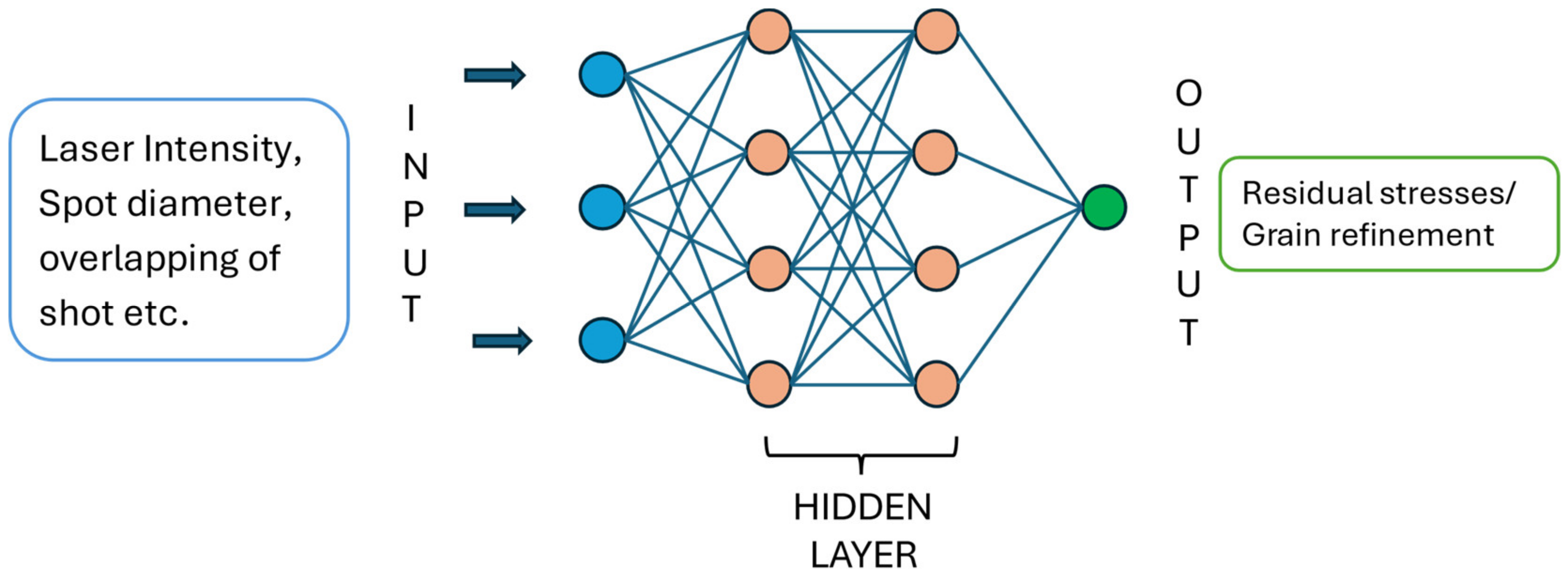
- Ayeb, M.; Frija, M.; Fathallah, R. Prediction of Residual Stress Profile and Optimization of Surface Conditions Induced by Laser Shock Peening Process Using Artificial Neural Networks. Int. J. Adv. Manuf. Technol. 2019, 100, 2455–2471. [Google Scholar] [CrossRef]
- Sung, A. Ranking Importance of Input Parameters of Neural Networks. Expert Syst. Appl. 1998, 15, 405–411. [Google Scholar] [CrossRef]
- Wu, J.; Liu, X.; Qiao, H.; Zhao, Y.; Hu, X.; Yang, Y.; Zhao, J. Using an Artificial Neural Network to Predict the Residual Stress Induced by Laser Shock Processing. Appl. Opt. AO 2021, 60, 3114–3121. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, R.; Li, G.; Du, Z.; Li, Z.; Lin, Y.; He, W. Deep Learning-Based Monitoring of Surface Residual Stress and Efficient Sensing of AE for Laser Shock Peening. J. Mater. Process. Technol. 2022, 303, 117515. [Google Scholar] [CrossRef]
- Wang, C.; Li, K.; Hu, X.; Yang, H.; Zhou, Y. Numerical Study on Laser Shock Peening of TC4 Titanium Alloy Based on the Plate and Blade Model. Opt. Laser Technol. 2021, 142, 107163. [Google Scholar] [CrossRef]
- Socha, K.; Blum, C. An Ant Colony Optimization Algorithm for Continuous Optimization: Application to Feed-Forward Neural Network Training. Neural Comput. Appl. 2007, 16, 235–247. [Google Scholar] [CrossRef]
- Tserpes, K.; Kormpos, P. Detailed Finite Element Models for the Simulation of the Laser Shock Wave Response of 3D Woven Composites. J. Compos. Sci. 2024, 8, 83. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, J.; Ji, Z.; Zhang, H.; Lu, G.; Zhang, C. Crystal Plasticity–Based Finite Element Modeling and Experimental Study for High Strain Rate Microscale Laser Shock Clinching of Copper Foil. Int. J. Adv. Manuf. Technol. 2023, 128, 3427–3439. [Google Scholar] [CrossRef]
- Leung, F.H.F.; Lam, H.K.; Ling, S.H.; Tam, P.K.S. Tuning of the Structure and Parameters of a Neural Network Using an Improved Genetic Algorithm. IEEE Trans. Neural Netw. 2003, 14, 79–88. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, X.; Xia, Q.; Yan, C. Strengthening Effect of Laser Shock Peening on 7075-T6 Aviation Aluminum Alloy. Adv. Mech. Eng. 2020, 12, 1687814020952177. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, e931256. [Google Scholar] [CrossRef]
- Langer, K.; Spradlin, T.J.; Fitzpatrick, M.E. Finite Element Analysis of Laser Peening of Thin Aluminum Structures. Metals 2020, 10, 93. [Google Scholar] [CrossRef]
- Mao, B.; Siddaiah, A.; Menezes, P.L.; Liao, Y. Surface texturing by indirect laser shock surface patterning for manipulated friction coefficient. J. Mater. Process. Technol. 2018, 257, 227–233. [Google Scholar] [CrossRef]
- Siddaiah, A.; Mao, B.; Liao, Y.; Menezes, P.L. Surface characterization and tribological performance of laser shock peened steel surfaces. Surf. Coat. Technol. 2018, 351, 188–197. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, B.; Siddaiah, A.; Menezes, P.L.; Liao, Y. Direct laser shock surface patterning of an AZ31B magnesium alloy: Microstructure evolution and friction performance. J. Mech. Work. Technol. 2020, 275, 116333. [Google Scholar] [CrossRef]
- Siddaiah, A.; Mao, B.; Liao, Y.; Menezes, P.L. Effect of Laser Shock Peening on the Wear–Corrosion Synergistic Behavior of an AZ31B Magnesium Alloy. ASME J. Tribol. 2020, 142, 041701. [Google Scholar] [CrossRef]
- John, M.; Ralls, A.M.; Kuruveri, U.B.; Menezes, P.L. Tribological, Corrosion, and Microstructural Features of Laser-Shock-Peened Steels. Metals 2023, 13, 397. [Google Scholar] [CrossRef]
- Ralls, A.M.; Mao, B.; Menezes, P.L. Tribological Performance of Laser Shock Peened Cold Spray Additive Manufactured 316L Stainless Steel. ASME J. Tribol. 2023, 145, 071702. [Google Scholar] [CrossRef]
- John, M.; Ralls, A.M.; Misra, M.; Menezes, P.L. Understanding the Mechanism of Stress Corrosion Cracking Resistance in Stainless Steel Welds Subjected to Laser Shock Peening without Coating for Nuclear Canister Applications. J. Mater. Eng. Perform. 2024, 33, 3957–3977. [Google Scholar] [CrossRef]
- John, M.; Islam, M.S.; Misra, M.; Menezes, P.L. Understanding the stress corrosion cracking resistance of laser shock surface patterned austenitic stainless-steel weld joints. Int. J. Adv. Manuf. Technol. 2024, 131, 4089–4105. [Google Scholar] [CrossRef]
- Ralls, A.M.; Frizell, J.; Menezes, P.L. Understanding the Tribocorrosion Synergism of Laser Shock Peened Steel Deposited by Cold-Spray Additive Manufacturing. ASME J. Tribol. 2024, 146, 094201. [Google Scholar] [CrossRef]

| Laser Parameter | Material | Effect on Material Properties | Reference |
|---|---|---|---|
| Laser Energy (Joule) | Inconel 718 Super-alloy | - Increased high-temperature fatigue resistance - Enhanced creep resistance | [51] |
| Pulse Duration (ns) | AA2198-T3 AA2198-T8 | - Improved resistance to crack initiation - Increased surface hardness | [52] |
| Spot Size (mm) | AA2198-T8 AA2198-T8 | - Enhanced fatigue performance - Improved stress corrosion resistance | [52] |
| Number of Pulses | IN718 Alloy (Inconel 718) | - Increased resistance to fretting fatigue - Enhanced creep resistance | [51] |
| Laser Wavelength (nm) | 7075 Aluminum Alloy | - Improved resistance to crack initiation - Enhanced material toughness | [46] |
| Laser Intensity (GW/cm2) | AA2198-T3 AA2198-T8 | - Enhanced tensile strength - Reduced surface roughness | [52] |
| Aspect | Simulation Results | Experimental Results | Comparison | Reference |
|---|---|---|---|---|
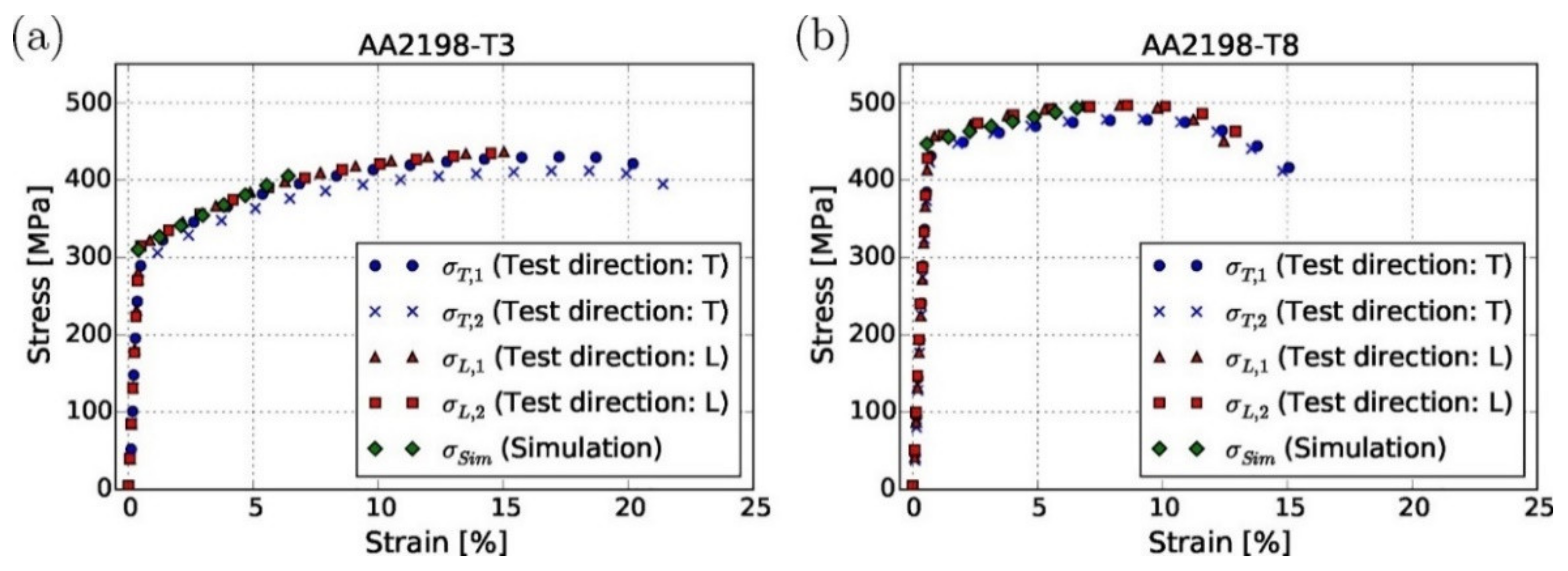
| Residual Stress Profile | Predicts compressive residual stresses to a depth of 1 mm | Measured residual stresses show similar depth but vary in magnitude | Simulation predicts trends accurately; slight magnitude differences may suggest refinement in material modeling needed. | [52] |
| Plastic Deformation Depth | Predicted plastic zone depth: 1 mm | Measured plastic zone depth: 2 mm | Good agreement; validates the accuracy of the simulation model. | [52] |
| Temperature Rise | In most work, LSP is assumed to be a purely mechanical process. Therefore, the influence of the temperature is assumed to be negligible. | Experimental temperature increases up to 48 °C | Close match; confirms thermal aspects of simulation. | [52] |
| Crack Formation/Propagation | Predicts reduced crack propagation rate due to compressive stresses | Experiment confirms reduced crack growth but at a slower rate than predicted [10]. | Simulation trends confirmed; rate differences highlight possible factors like microstructural effects not fully captured. | [10,52] |
| Process Efficiency | Simulated process efficiency under optimal conditions | Experiment shows efficiency slightly lower than predicted | Efficiency loss in real conditions may be due to unmodeled factors like energy losses. | [52] |
| Effect of Transparent Overlays & Absorbent Coatings | FE model shows enhanced shock response (SRS amplitude) with minimal impact on SRS slope. | Experimental tests confirm increased SRS amplitude and negligible effect on SRS slope. | Both methods confirm that coatings improve shock response amplitude, validating the FE model’s accuracy. | [50] |
| Capacity to Simulate Transient Response | FE model accurately simulates the transient response of the aluminum alloy plate under laser shock. | Experimental data supports the model, showing consistent transient response characteristics. | Strong correlation indicates the FE model’s reliability in predicting transient dynamics. | [50] |
| Shock Response Spectrum (SRS) Amplitude | FE model predicts SRS amplitude reaching hundreds of g, with a high and broadband frequency range. | Experimental results confirm high SRS amplitudes and similar frequency characteristics. | The FE model effectively captures the high SRS amplitude and frequency behavior observed experimentally. | [50] |
| Relationship Between Laser Parameters and Response | Simulated response increases linearly with peak pressure and shows a quadratic relationship with laser power density. | Experimental data corroborates the linear increase with peak pressure and quadratic correlation with power density. | Both approaches demonstrate the same trends, validating the predictive capability of the FE model. | [50] |
| Effect of Pulse Duration and Spot Size on Response | FE model shows enhanced response with longer pulse durations and larger spot sizes, with complex trends between 100 Hz and 10,000 Hz. | Experiments confirm enhancement at extreme frequencies and complex, non-monotonous behavior in the mid-frequency range. | The FE model accurately reflects the experimental trends, although complexities in mid-frequency behavior warrant further study. | [50] |
| Effect on SRS Slope | FE model indicates that laser pulse duration significantly affects SRS slope, while spot size has minimal impact. | Experimental results support the significant effect of pulse duration on SRS slope, with little influence from spot size. | Consistent findings across both methods affirm the FE model’s precision in capturing the effects on SRS slope. | [50] |
| Material | Software’s Used | Variable Parameters Considered | Reference |
|---|---|---|---|
| Ti-6Al-4V alloy | Abaqus | The effect of the spot size and shape, the pulse energy, the number of peen layers, overlapping of spots, and temporal variation of the mechanical pressure induced by plasma is considered and analyzed | [84] |
| Inconel 718 super-alloy | Abacus Explicit and Implicit PSO technique with Python coding | Laser power, Laser beam shape, Scan Pitch, Scan Pattern | [51] |
| TC4 alloy | Abaqus Explicit and Standard | Shock angle, laser polarization state | [85] |
| Ti6Al4V titanium alloy | Abaqus Standard | Laser power, Impact times, Pulse duration, Spot size | [86] |
| AA2198-T3 AA2198-T8 | Abaqus Explicit and Standard | Laser power, square laser beam dimension, Temperature, Thickness | [52] |
| 7075 aluminum alloy | Abaqus/Explicit | Scanning patterns, Overlapping rate, Spot shape (Square and Circle). | [46] |
| STS304 | ANSYS Autodyn | Number of shots, Damping value | [74] |
| Pure Al | Abaqus/CAE FEM | Material thickness, Spot diameter, Laser power | [87] |
| IN718 alloy | Abaqus and MSC.Patran | Laser power, Temperature | [12] |
| Method | Description | References |
|---|---|---|
| Detailed FE Models | Models the geometry and material properties in detail, allowing for accurate simulation of shock wave propagation. | [94] |
| Homogenized FE Models | Uses averaged material properties to simplify the model and reduce computational time, though with less accuracy. | [94] |
| Crystal Plasticity-Based FE Models | Incorporates crystal plasticity theories to simulate deformation mechanisms at the grain level. | [95] |
| Explicit FE Analysis with LS-Dyna | Employs explicit dynamics software like LS-Dyna to simulate high-strain-rate behaviors and shock responses. | [94] |
| Residual Stress Analysis | Focuses on analyzing and mitigating residual stresses induced by laser peening in thin structures. | [96] |
| Progressive Damage Models | Applies damage mechanics to predict initiation and propagation of cracks and other failures in the material. | [94] |
| Thermo-Mechanical Coupled Analysis | Considers both thermal and mechanical effects simultaneously to capture the complex interactions during shock. | [96] |
| High-Fidelity 3D Woven Composite Models | Utilizes high-fidelity models to represent the complex architecture of woven composites for more accurate results. | [94] |
| Simulation of Plasma Expansion Effects | Models the expansion of plasma created by laser interaction to understand its impact on material deformation. | [94] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wakchaure, M.B.; Misra, M.; Menezes, P.L. A Comprehensive Review on Finite Element Analysis of Laser Shock Peening. Materials 2024, 17, 4174. https://doi.org/10.3390/ma17174174
Wakchaure MB, Misra M, Menezes PL. A Comprehensive Review on Finite Element Analysis of Laser Shock Peening. Materials. 2024; 17(17):4174. https://doi.org/10.3390/ma17174174
Chicago/Turabian StyleWakchaure, Mayur B., Manoranjan Misra, and Pradeep L. Menezes. 2024. "A Comprehensive Review on Finite Element Analysis of Laser Shock Peening" Materials 17, no. 17: 4174. https://doi.org/10.3390/ma17174174
APA StyleWakchaure, M. B., Misra, M., & Menezes, P. L. (2024). A Comprehensive Review on Finite Element Analysis of Laser Shock Peening. Materials, 17(17), 4174. https://doi.org/10.3390/ma17174174








