An Experimental Study of a Bottom-Hinged Wave Energy Converter with a Reflection Wall in Regular Waves—Focusing on Behavioral Characteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Description
2.2. Reflection Coefficient
2.3. Estimation of Power Generation Efficiency
3. Results and Discussions
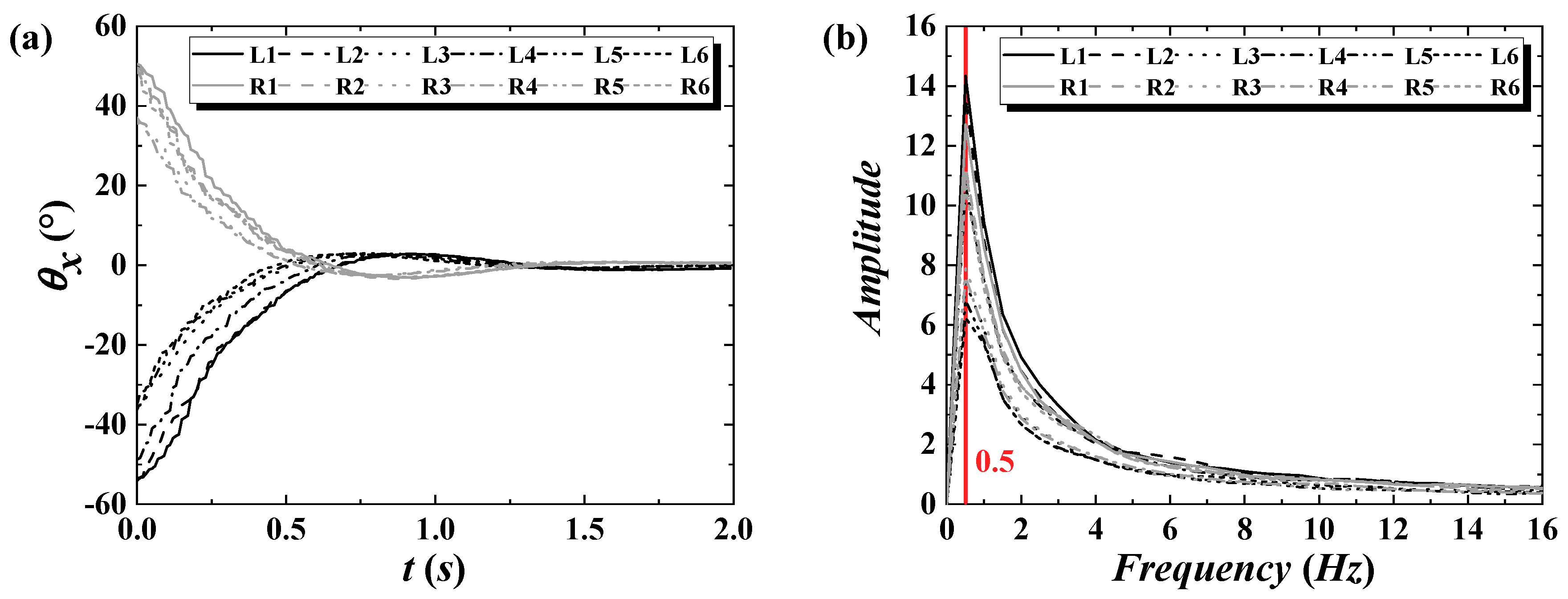
3.1. Natural Frequency of the Flap
3.2. Behavioral Characteristics of the Flap
- Pattern A (stable, 108 cases): the flap rotated stably with incident waves.
- Pattern B (fluctuation, 66 cases): the flap behavior changed with time.
- Pattern C (unstable, 40 cases): the behavior of the flap changed randomly during the experiment.
- Pattern D (loss, 65 cases): the flap did not return to its original position after moving several times so that the flap lost its restoring force and remained stationary in the water.
- Pattern E (PWEC = 0, 49 cases): the flap did not move during experiments.
3.3. Power Generation Characteristics
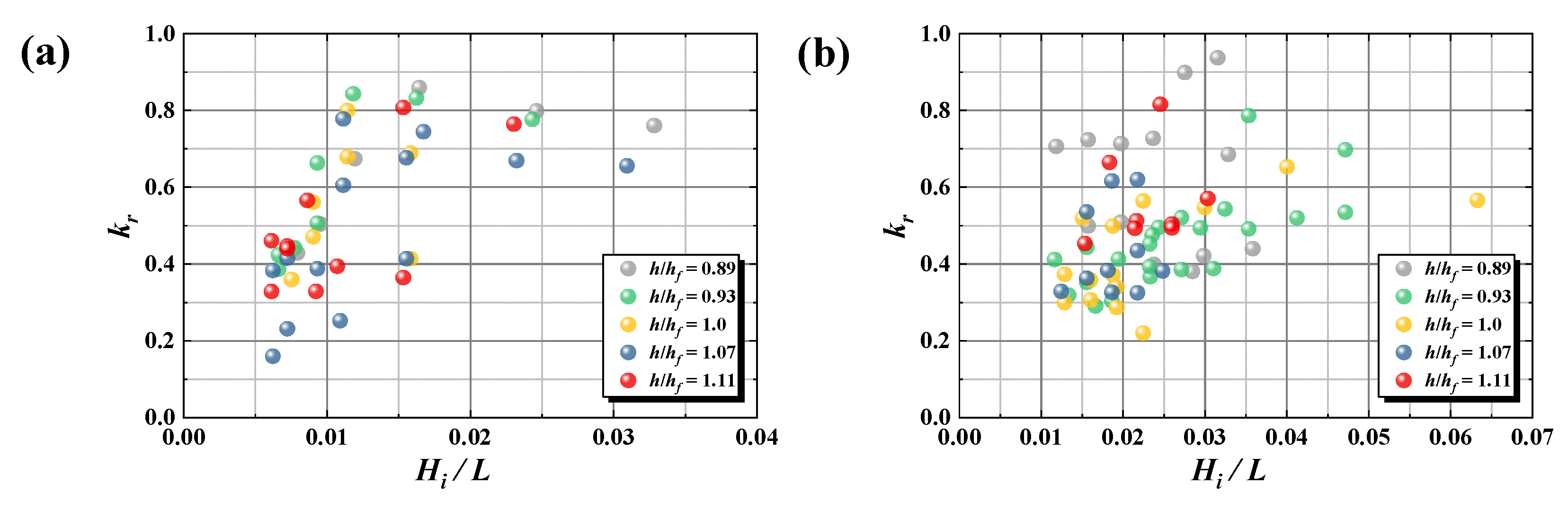
3.4. Reflection Characteristics
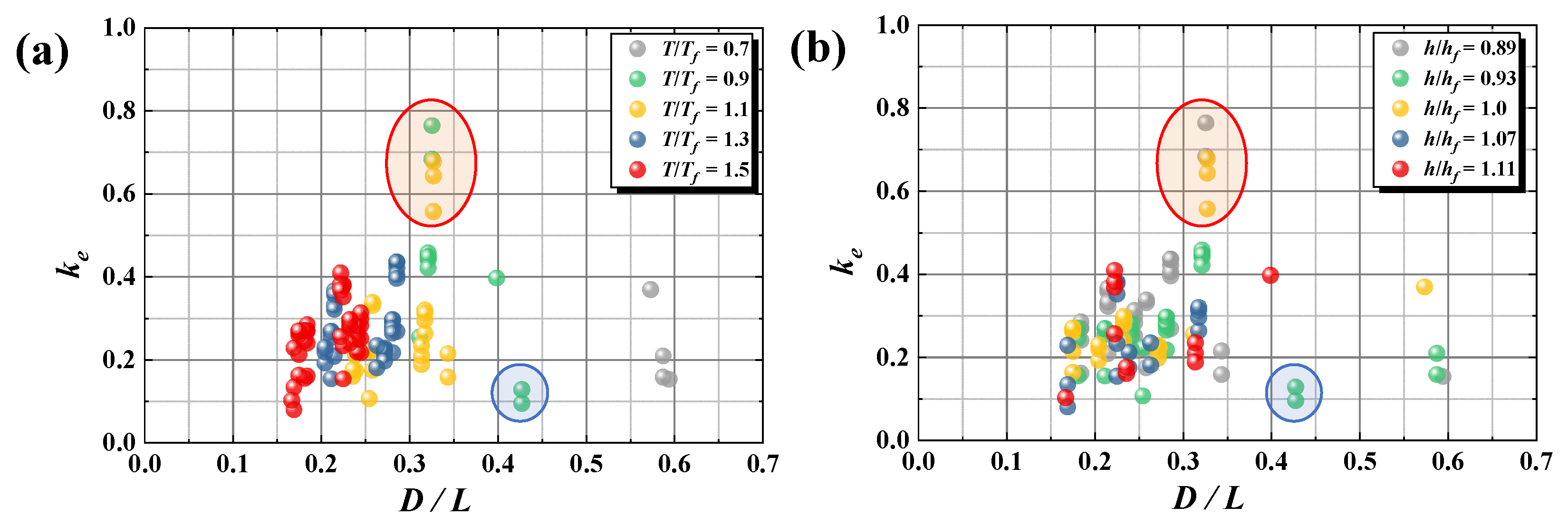
3.5. Effects of T/Tf and h/hf on PWEC
3.6. Behavior Characteristics of the Flap
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IEA. World Energy Outlook 2019: Executive Summary 2019. Available online: https://webstore.iea.org/world-energy-outlook-2019 (accessed on 15 January 2020).
- EIA. International Energy Outlook; EIA: Washington, DC, USA, 2019. [Google Scholar]
- López, I.; Andreu, J.; Ceballos, S.; De Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Mørk, G.; Barstow, S.; Kabuth, A.; Pontes, M. Assessing the global wave energy potential. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 3, pp. 447–454. [Google Scholar]
- Takahashi, S.; Adachi, T. A study on wave power around Japan and its utilization. Coast. Eng. Proc. JSCE 1989, 3, 874–878. [Google Scholar] [CrossRef] [Green Version]
- CIA. World Factbook. Available online: https://www.cia.gov/library/publications/the-world-factbook/geos/ja.html (accessed on 15 January 2020).
- Pelc, R.; Fujita, R.M. Renewable energy from the ocean. Mar. Policy 2002, 26, 471–479. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.; Sahinkaya, M. A review of wave energy converter technology. Proc. Inst. Mech. Eng. A 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Greaves, D.; Iglesias, G. Wave and Tidal Energy; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Ibarra-Berastegi, G.; Sáenz, J.; Ulazia, A.; Serras, P.; Esnaola, G.; Garcia-Soto, C. Electricity production, capacity factor, and plant efficiency index at the Mutriku wave farm (2014–2016). Ocean Eng. 2018, 147, 20–29. [Google Scholar] [CrossRef] [Green Version]
- Boccotti, P. On a new wave energy absorber. Ocean. Eng. 2003, 30, 1191–1200. [Google Scholar] [CrossRef]
- Boccotti, P. Caisson breakwaters embodying an OWC with a small opening—Part I: Theory. Ocean. Eng. 2007, 34, 806–819. [Google Scholar] [CrossRef]
- Boccotti, P.; Filianoti, P.; Fiamma, V.; Arena, F. Caisson breakwaters embodying an OWC with a small opening—Part II: A small-scale field experiment. Ocean. Eng. 2007, 34, 820–841. [Google Scholar] [CrossRef]
- Folley, M.; Curran, R.; Whittaker, T. Comparison of LIMPET contra-rotating wells turbine with theoretical and model test predictions. Ocean. Eng. 2006, 33, 1056–1069. [Google Scholar] [CrossRef]
- Bruschi, D.; Fernandes, J.C.S.; Falcão, A.; Bergmann, C.P. Analysis of the degradation in the Wells turbine blades of the Pico oscillating-water-column wave energy plant. Renew. Sustain. Energy Rev. 2019, 115, 109368. [Google Scholar] [CrossRef]
- Falcão, A. The shoreline OWC wave power plant at the Azores. In Proceedings of the 4th European Wave Energy Conference, Aalborg, Denmark, 4–6 December 2000; Danish Technological Institute: Taastrup, Denmark, 2000; pp. 44–48. [Google Scholar]
- Falcão, A.; Sarmento, A.J.; Gato, L.; Brito-Melo, A. The Pico OWC wave power plant: Its lifetime from conception to closure 1986–2018. Appl. Ocean. Res. 2020, 98, 102104. [Google Scholar] [CrossRef]
- Whittaker, T.; Collier, D.; Folley, M.; Osterried, M.; Henry, A.; Crowley, M. The development of Oyster—A shallow water surging wave energy converter. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007; pp. 11–14. [Google Scholar]
- Mäki, T.; Mucha, T.; Vuorinen, M. WaveRoller—One of the leading technologies for wave energy conversion. In Proceedings of the 5th International Conference on Ocean Energy, Halifax, NS, Canada, 4–6 November 2014; ICOE: El Centro, CA, USA, 2014. [Google Scholar]
- Marquis, L.; Kramer, M.; Kringelum, J.; Chozas, J.; Helstrup, N. Introduction of Wavestar Wave Energy Converters at the Danish offshore wind power plant Horns Rev 2. In Proceedings of the 4th International Conference on Ocean Energy, Dublin, Ireland, 17–19 October 2012; ICOE: El Centro, CA, USA, 2012. [Google Scholar]
- Weber, J.; Mouwen, F.; Parish, A.; Robertson, D. Wavebob—Research & development network and tolls in the context of systems engineering. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009; pp. 416–420. [Google Scholar]
- Chozas, J.; Soerensen, H. State of the art of wave energy in Spain. In Proceedings of the 2009 IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 22–23 October 2009; pp. 1–6. [Google Scholar]
- Retzler, C. Measurements of the slow drift dynamics of a model Pelamis wave energy converter. Renew. Energy 2006, 31, 257–269. [Google Scholar] [CrossRef]
- Kofoed, J. Wave Overtopping of Marine Structures: Utilization of Wave Energy. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2002. [Google Scholar]
- Vicinanza, D.; Margheritini, L.; Kofoed, J.P.; Buccino, M. The SSG wave energy converter: Performance, status and recent developments. Energies 2012, 5, 193–226. [Google Scholar] [CrossRef] [Green Version]
- Babarit, A.; Hals, J.; Muliawan, M.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]
- Falcão, A. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Washio, Y.; Osawa, Y.; Nagata, F.; Fujii, F.; Furuyama, H.; Fujita, T. The offshore floating type wave power device ‘Mighty Whale’: Open sea tests. In Proceedings of the 10th International Offshore and Polar Engineering Conference (ISOPE), Seattle, WA, USA, 28 May–2 June 2000. [Google Scholar]
- Watabe, T.; Yokouchi, H.; Kondo, H.; Inoya, M.; Kudo, M. Installation of the new Pendulor for the 2nd stage sea test. In Proceedings of the 9th International Offshore and Polar Engineering Conference (ISOPE), Brest, France, 30 May–4 June 1999. [Google Scholar]
- Kanki, H.; Arii, S.; Furusawa, T.; Otoyo, T. Development of advanced wave power generation system by applying gyroscopic moment. In Proceedings of the 8th European Wave and Tidal energy Conference (EWTEC), Uppsala, Sweden, 7–10 September 2009. [Google Scholar]
- Vicinanza, D.; Di Lauro, E.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of Innovative Harbor Breakwaters for Wave-Energy Conversion. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 03119001. [Google Scholar] [CrossRef]
- Takahashi, S.; Nakada, H.; Ohneda, H.; Shikamori, M. Wave power conversion by a prototype wave power extracting caisson in Sakata port. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 3440–3453. [Google Scholar]
- Raju, V.S.; Neelamani, S. Concrete caisson for a 150KW wave energy pilot plant: Design, construction, and installation aspects. In Proceedings of the 2nd International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 14–19 June 1992; pp. 584–591. [Google Scholar]
- Schoolderman, J.; Reedijk, B.; Vrijling, H.; Molenaar, W.; Oever, E.T.; Zijlema, M. Generating electricity at a breakwater in a moderate wave climate. Coast. Eng. Proc. 2011, 1, 63. [Google Scholar] [CrossRef]
- Kim, J.S.; Nam, B.W.; Kim, K.H.; Park, S.; Shin, S.H.; Hong, K. A numerical study on hydrodynamic performance of an inclined OWC wave energy converter with nonlinear turbine–chamber interaction based on 3D potential flow. J. Mar. Sci. Eng. 2020, 8, 176. [Google Scholar] [CrossRef] [Green Version]
- Vicinanza, D.; Contestabile, P.; Nørgaard, J.Q.H.; Andersen, T.L. Innovative rubble mound breakwaters for overtopping wave energy conversion. Coast. Eng. 2014, 88, 154–170. [Google Scholar] [CrossRef]
- Kralli, V.E.; Theodossiou, N.; Karambas, T. Optimal design of overtopping breakwater for energy conversion (OBREC) systems using the harmony search algorithm. Front. Energy Res. 2019, 7, 80. [Google Scholar] [CrossRef] [Green Version]
- Iuppa, C.; Cavallaro, L.; Musumeci, R.E.; Vicinanza, D.; Foti, E. Empirical overtopping volume statistics at an OBREC. Coast. Eng. 2019, 152, 103524. [Google Scholar] [CrossRef]
- Sarkar, D.; Renzi, E.; Dias, F. Effect of a straight coast on the hydrodynamics and performance of the Oscillating Wave Surge Converter. Ocean Eng. 2015, 105, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, D.; Dias, F. Performance enhancement of the oscillating wave surge converter by a breakwater. J. Ocean Wind Energy 2015, 2, 73–80. [Google Scholar] [CrossRef]
- Liu, Y.; Cavalier, G.; Pastor, J.; Viera, R.J.; Guillory, C.; Judice, K.; Guiberteau, K.; Kozman, T.A. Design and construction of a wave generation system to model ocean conditions in the Gulf of Mexico. Int. J. Energy Technol. 2012, 4, 1–7. [Google Scholar]
- Liu, Y.; Pastor, J.; Viera, R.J. Establishment of a wave energy and technology lab to promote the experimental study of ocean and wave energy, IMECE2013-62968. In Proceedings of the ASME 2013 International Mechanical Engineering Congress & Exposition, San Diego, CA, USA, 15–21 November 2013; pp. 13–21. [Google Scholar]
- Morimoto, Y.; Mizutani, N. Development of wave energy conversion system using bottom-hinged pendulum and evaluation of its performance. J. Jpn. Soc. Civ. Eng. Ser. B3 Ocean. Eng. 2013, 69, 132–137. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.Y.; Huang, C.J. Decomposition of incident and reflected higher harmonic waves using four wave gauges. Coast. Eng. 2004, 51, 395–406. [Google Scholar] [CrossRef]
- Mansard, E.; Funke, E. The measurement of incident and reflected spectra using a least squares method. Coast. Eng. Proc. 1980, 1, 154–172. [Google Scholar]
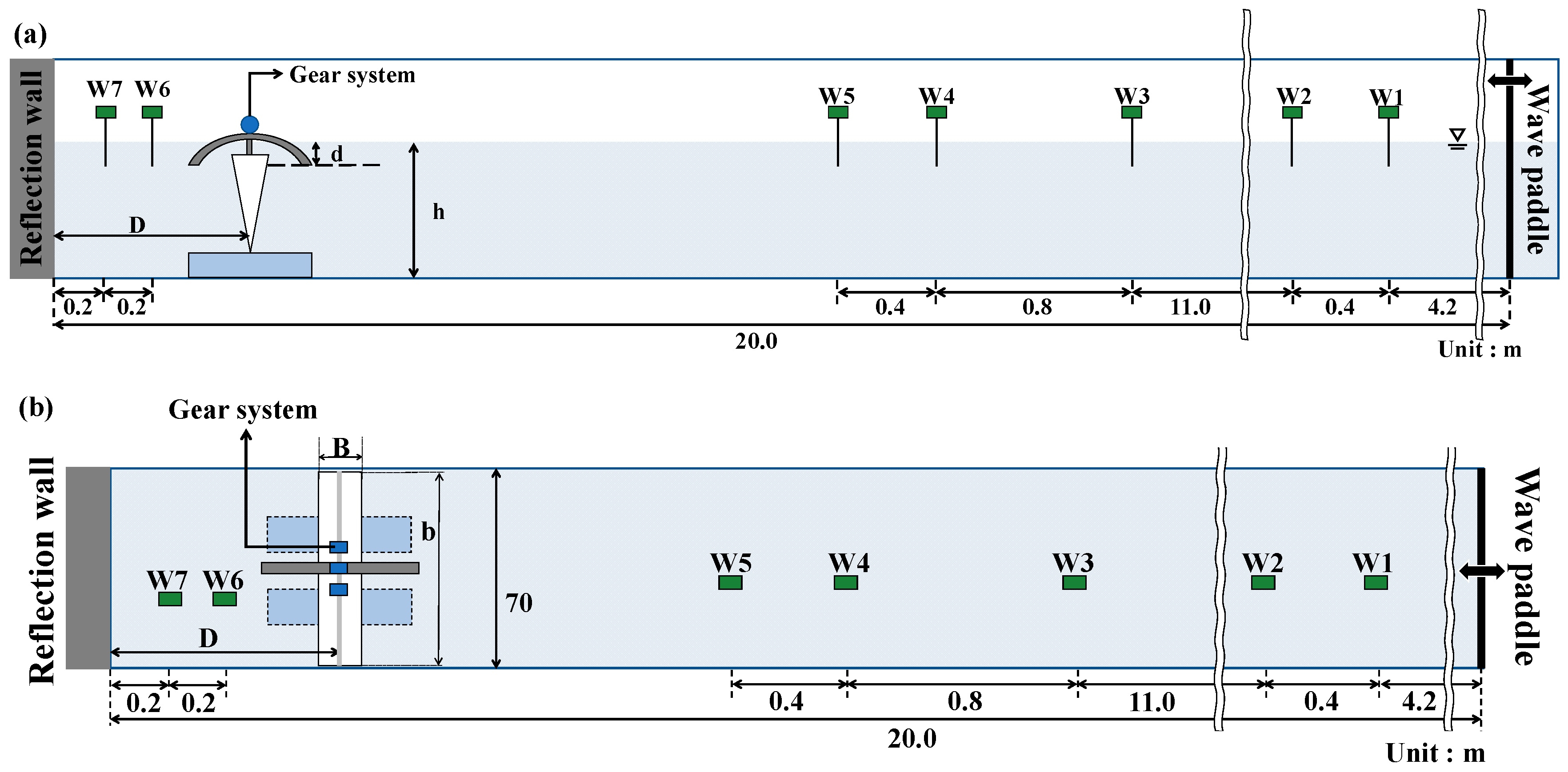
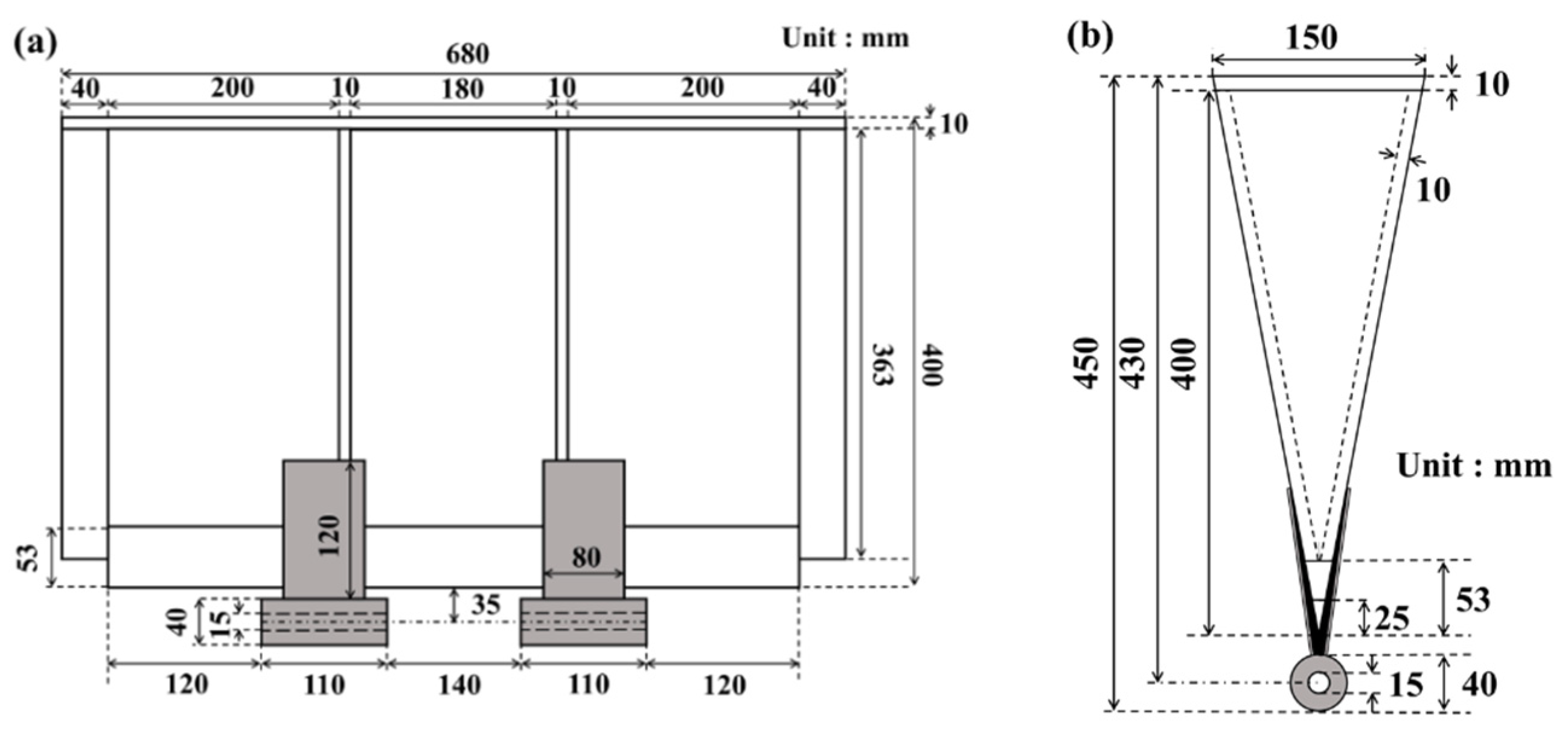

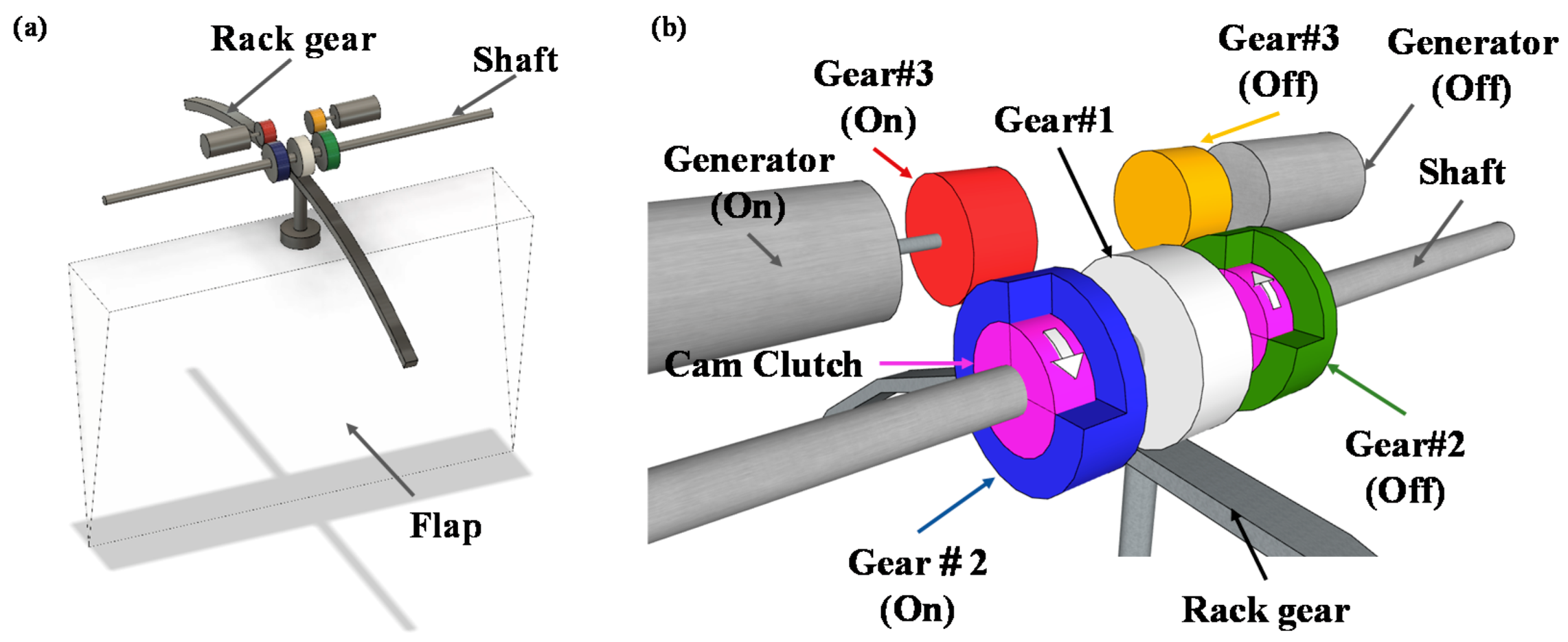
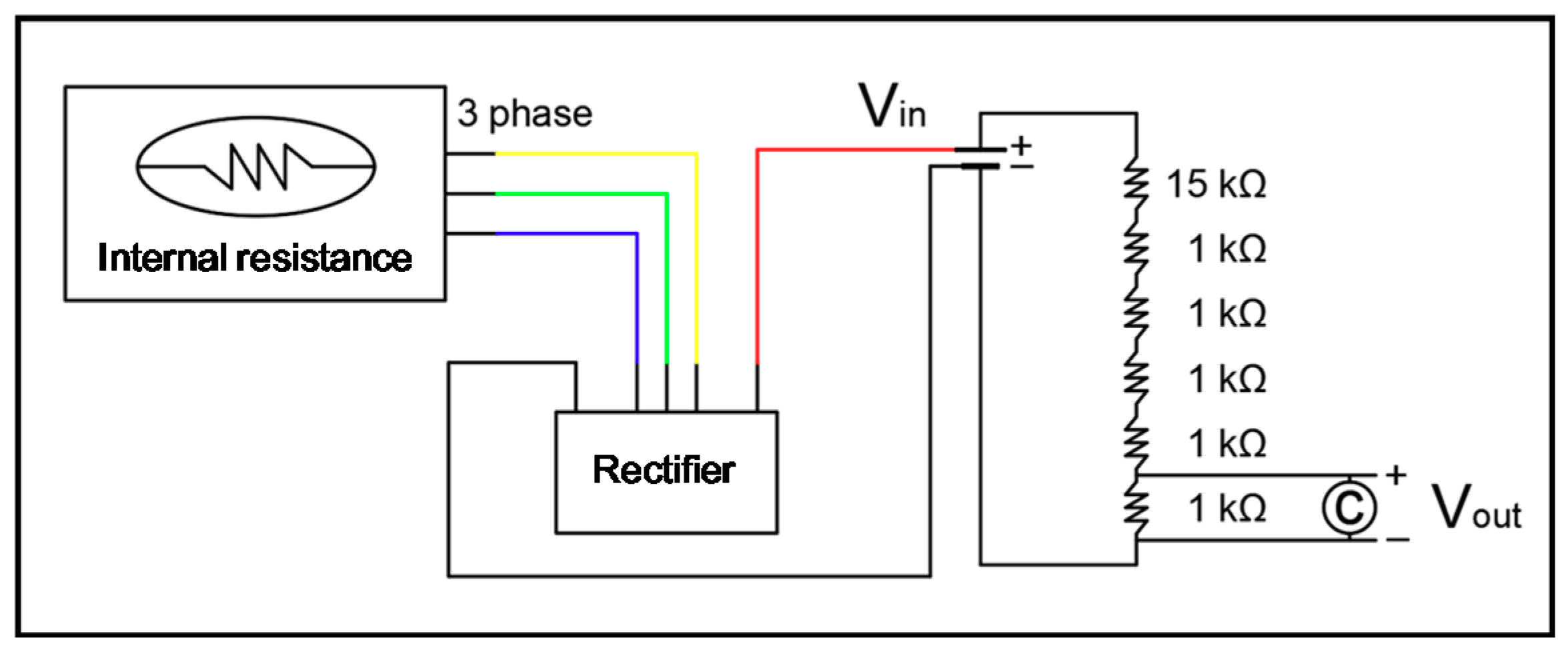













| Case No. | Distance to the Reflection Wall D (m) | Water Depth h (m) (Submergence Depth d (m)) | Wave Period T (s) | Wave Height H (m) |
|---|---|---|---|---|
| 1–328 | 1.09 | 0.425 (−0.05) | 1.4 | 0.04 |
| 0.06 | ||||
| 0.440 (−0.035) | 1.8 | 0.08 | ||
| 2.2 | 0.10 | |||
| 2.6 | 0.12 | |||
| 0.14 | ||||
| 0.475 (0.0) | 3.0 | 0.16 | ||
| 0.510 (+0.035) | ||||
| 1.45 | 0.525 (+0.05) |
| Internal Diameter (mm) | External Diameter (mm) | Width (mm) | Number of Teeth | Total Length (mm) | |
|---|---|---|---|---|---|
| Rack gear | - | - | 5 | - | 560 |
| Gear1 | 15 | 60 | 10 | 60 | - |
| Gear2 | 35 | 60 | 60 | - | |
| Cam Clutch | 15 | 35 | - | - | |
| Gear3 | 6 | 18 | 18 | - | |
| Shaft | - | - | - | - | 600 |
| Model | Rated Voltage V0 (V) | No-Load Speed (rpm) | No-Load Current Iidle (A) | Rated Load Speed (rpm) | Rated-Load Current Istall (A) |
|---|---|---|---|---|---|
| 24J36SBLA2 | 24 | 4200 | 0.12 | 3600 | 0.3 |
| Pattern | h/hf | T/Tf = 0.7 | T/Tf = 0.9 | T/Tf = 1.1 | T/Tf = 1.3 | T/Tf = 1.5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Total No. | No. | Total No. | No. | Total No. | No. | Total No. | No. | Total No. | ||
| A | 1.11 | 0 (0.0) | 4 (6.1) | 1 (9.1) | 11 (16.9) | 5 (22.7) | 22 (34.9) | 0 (0.0) | 31 (46.3) | 5 (12.5) | 40 (60.0) |
| 1.07 | 0 (0.0) | 0 (0.0) | 6 (27.3) | 2 (6.4) | 8 (20.0) | ||||||
| 1.0 | 1 (25.0) | 1 (9.1) | 3 (13.6) | 8 (25.8) | 10 (25.0) | ||||||
| 0.93 | 2 (50.0) | 7 (63.6) | 2 (9.1) | 10 (32.3) | 7 (17.5) | ||||||
| 0.89 | 1 (25.0) | 2 (18.2) | 6 (27.3) | 11 (35.5) | 10 (25.0) | ||||||
| B | 1.11 | 0 (0.0) | 18 (27.3) | 4 (19.1) | 21 (32.3) | 0 (0.0) | 15 (23.8) | 3 (37.5) | 8 (11.9) | 0 (0.0) | 4 (6.0) |
| 1.07 | 0 (0.0) | 4 (19.1) | 1 (6.7) | 5 (62.5) | 0 (0.0) | ||||||
| 1.0 | 4 (22.2) | 3 (14.3) | 3 (20.0) | 0 (0.0) | 0 (0.0) | ||||||
| 0.93 | 8 (44.4) | 4 (19.1) | 8 (53.3) | 0 (0.0) | 3 (75.0) | ||||||
| 0.89 | 6 (33.3) | 6 (28.6) | 3 (20.0) | 0 (0.0) | 1 (25.0) | ||||||
| C | 1.11 | 0 (0.00) | 3 (4.6) | 3 (21.4) | 14 (21.5) | 3 (37.5) | 8 (12.7) | 3 (33.3) | 9 (13.4) | 2 (33.3) | 6 (9.0) |
| 1.07 | 0 (0.00) | 3 (21.4) | 1 (12.5) | 2 (22.2) | 0 (0.0) | ||||||
| 1.0 | 1 (33.3) | 3 (21.4) | 1 (12.5) | 3 (33.3) | 1 (16.7) | ||||||
| 0.93 | 1 (33.3) | 1 (7.1) | 0 (0.0) | 1 (11.1) | 2 (33.3) | ||||||
| 0.89 | 1 (33.3) | 4 (28.6) | 3 (37.5) | 0 (0.0) | 1 (16.7) | ||||||
| D | 1.11 | 9 (33.3) | 27 (40.9) | 2 (22.2) | 9 (13.9) | 3 (25.0) | 12 (19.1) | 3 (30.0) | 10 (14.9) | 2 (28.6) | 7 (10.5) |
| 1.07 | 8 (29.6) | 2 (22.2) | 4 (33.3) | 1 (10.0) | 2 (28.6) | ||||||
| 1.0 | 6 (22.2) | 4 (44.4) | 2 (16.7) | 2 (20.0) | 3 (42.9) | ||||||
| 0.93 | 1 (3.7) | 1 (1.1) | 2 (16.7) | 2 (20.0) | 0 (0.0) | ||||||
| 0.89 | 3 (11.1) | 0 (0.0) | 1 (8.3) | 2 (20.0) | 0 (0.0) | ||||||
| E | 1.11 | 3 (21.4) | 14 (21.2) | 2 (20.0) | 10 (15.4) | 1 (16.7) | 6 (9.5) | 3 (33.3) | 9 (13.4) | 3 (30.0) | 10 (14.9) |
| 1.07 | 4 (28.6) | 3 (30.0) | 0 (0.0) | 3 (33.3) | 3 (4.5) | ||||||
| 1.0 | 2 (14.3) | 2 (20.0) | 2 (33.3) | 1 (11.1) | 0 (0.0) | ||||||
| 0.93 | 2 (14.3) | 1 (10.0) | 2 (33.3) | 1 (11.1) | 2 (20.0) | ||||||
| 0.89 | 3 (21.4) | 2 (20.0) | 1 (16.7) | 1 (11.1) | 2 (20.0) | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, Y.-H.; Nakamura, T.; Mizutani, N.; Lee, K.-H. An Experimental Study of a Bottom-Hinged Wave Energy Converter with a Reflection Wall in Regular Waves—Focusing on Behavioral Characteristics. Appl. Sci. 2020, 10, 6734. https://doi.org/10.3390/app10196734
Cho Y-H, Nakamura T, Mizutani N, Lee K-H. An Experimental Study of a Bottom-Hinged Wave Energy Converter with a Reflection Wall in Regular Waves—Focusing on Behavioral Characteristics. Applied Sciences. 2020; 10(19):6734. https://doi.org/10.3390/app10196734
Chicago/Turabian StyleCho, Yong-Hwan, Tomoaki Nakamura, Norimi Mizutani, and Kwang-Ho Lee. 2020. "An Experimental Study of a Bottom-Hinged Wave Energy Converter with a Reflection Wall in Regular Waves—Focusing on Behavioral Characteristics" Applied Sciences 10, no. 19: 6734. https://doi.org/10.3390/app10196734
APA StyleCho, Y.-H., Nakamura, T., Mizutani, N., & Lee, K.-H. (2020). An Experimental Study of a Bottom-Hinged Wave Energy Converter with a Reflection Wall in Regular Waves—Focusing on Behavioral Characteristics. Applied Sciences, 10(19), 6734. https://doi.org/10.3390/app10196734





