Compositional Modeling of Dimethyl Ether–CO₂ Mixed Solvent for Enhanced Oil Recovery

Abstract

Dimethyl ether (DME) is a compound first introduced by Shell as a chemical solvent for enhanced oil recovery (EOR). This study aims to investigate the efficiency of EOR using the minimum miscible pressure (MMP) and viscous gravity number when a mixed solvent of CO₂ and DME is injected. Adding DME to the CO₂ water-alternating-gas process reduces the MMP and viscous gravity number. Reduction in MMP results in miscible conditions at lower pressures, which has a favorable effect on oil swelling and viscosity reduction, leading to improved mobility of the oil. In addition, the viscous gravity number decreases, increasing the sweep efficiency by 26.6%. Numerical studies were conducted through a series of multi-phase, multi-component simulations. At a DME content of 25%, the MMP decreased by 30.1% and the viscous gravity number decreased by 66.4% compared with the injection of CO₂ only. As a result, the maximum oil recovery rate increased by 31% with simultaneous injection of DME and CO₂ compared with only using CO₂.

1. Introduction

As the discovery of new oil fields becomes increasingly difficult, most oil companies are focusing on maintaining economic oil prices through enhanced oil recovery (EOR) technology to maximize the recovery from oil fields [1]. Solvent injection is a mature EOR method [2]. CO₂ and hydrocarbon gas are widely used as injection fluids [3], wherein their contact with reservoir fluid causes viscosity reduction and oil swelling. The effect is greater under miscible conditions than immiscible conditions [4]. Research using hydrocarbon gas or CO₂ as a solvent has been conducted, from the laboratory to the field, for decades [3,5,6]. Additionally, research is being conducted to improve oil recovery and economic efficiency using a mixed solvent of CO₂ and hydrocarbon gas or a surfactant [7,8,9,10]. In particular, according to previous studies that added liquefied petroleum gas (LPG) to CO₂ flooding, LPG increases the displacement efficiency by reducing the minimum miscible pressure (MMP), which accelerates the effects of oil viscosity reduction, interfacial tension (IFT) reduction, and oil swelling, resulting in an increase in oil recovery [6,11,12]. Dimethyl ether (DME), an industrial chemical used as a fuel additive and aerosol propellant, is being investigated as a solvent for EOR. Recently, DME was mixed with LPG and used as fuel for transportation as well as for cooking and heating fuel [13,14]. As a solvent, DME has the advantage of being soluble in both water and oil. DME can be mixed nearly ideally in the oleic phase and is partially soluble in water because of its slight polarity [15]. These properties enable a unique and improved oil recovery mechanism. DME remaining near the injection well is extracted by the chasing water, which acts as a DME carrier, improving the oil mobility near the production well [13]. Additionally, DME can be extracted from the produced fluid and reused through distillation and adsorption processes [14]. DME was first introduced as a solvent for EOR by Shell [15,16,17,18], and this method has proven effectiveness in improving oil recovery [14,15,16,19,20,21]. Recent research on DME in the field of EOR has focused on modeling and experiments of the DME–water–oil phase behavior or studies modeling the core scale [15,16,21,22,23,24,25]. Additionally, most of the EOR using DME has been studied for the DME-enhanced water flood method, and to the best of our knowledge, no studies have been reported on a CO₂–DME mixed solvent. Though DME has been proven as an effective solvent in improving oil recovery, it is an expensive solvent around $565/m³ [26]. Therefore, the optimum amount of DME into the CO₂ flood should be determined through extensive compositional simulations to improve the economics of the project. Therefore, this study evaluated the use of a mixed solvent to reduce DME and increase the oil recovery rate by adding DME to the CO₂ flooding. In addition, the amount of DME that was recovered by chased water was examined with compositional analysis of the produced fluid. In this study, a compositional model was developed to investigate oil recovery when injecting a CO₂–DME mixed solvent under the WAG scenario. Based on the results from simulations, the sweep efficiency and displacement efficiency by WAG using a CO₂–DME mixed solvent were analyzed in terms of oil viscosity, viscous gravity number, and MMP.

2. Materials and Methods

2.1. Fluid Modeling

Fluid modeling was performed using the properties of Weyburn W3 fluid. The components of the Weyburn W3 fluid and the parameters of the equation of state (EOS) for fluid modeling are listed in

Table 1. Oil components and properties of each component for equation of state (EOS) calculation.

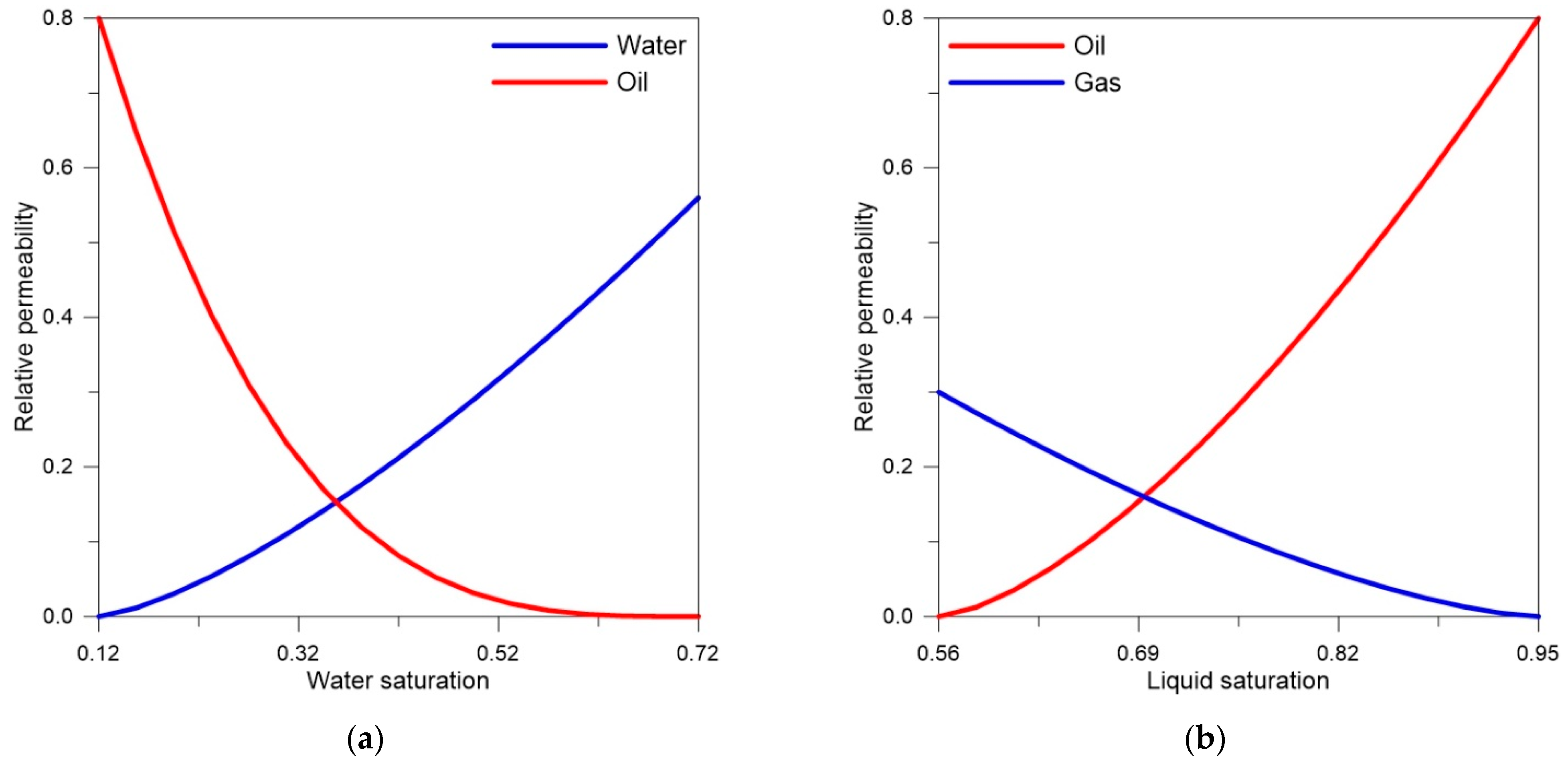
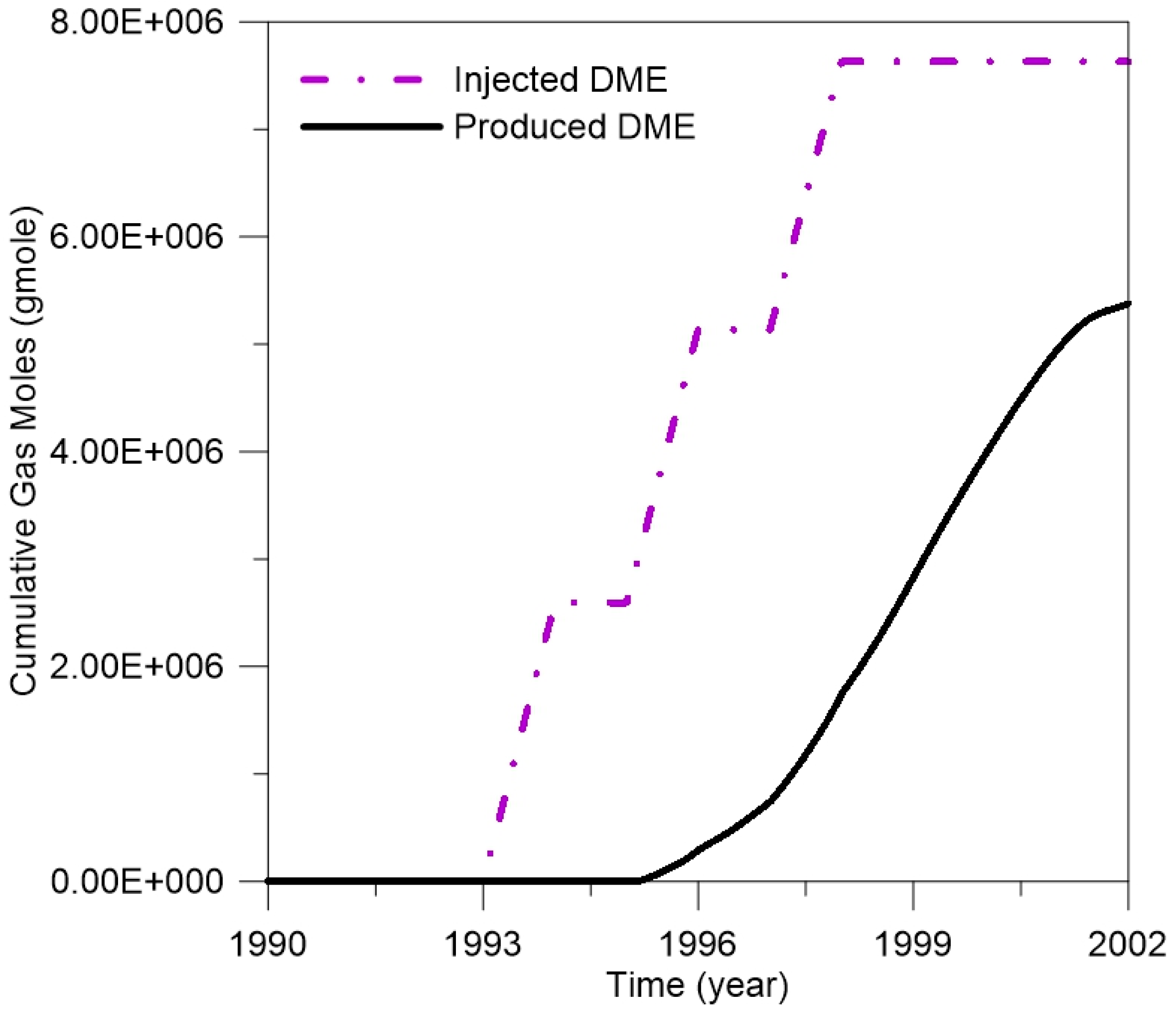
Component	Composition	Critical Pressure (kPa)	Critical Temperature (K)	Parachor	Acentric Factor	Molecular Weight (g/gmol)
N2	0.0207	3394.4	126.2	41	0.04	28.01
CO2	0.0074	7376.5	304.2	78	0.225	44.01
H2S	0.0012	8936.9	373.2	80	0.1	34.08
C1	0.0749	4600.2	190.6	77	0.008	16.04
C2	0.0422	4883.9	305.4	108	0.098	30.07
C3	0.0785	4245.5	369.8	150	0.152	44.09
DME	0.0001	5442.2	400.3	132	0.2	46.07
C4	0.0655	3722.7	416.5	185	0.1845	58.12
C5	0.0459	3379.4	464.9	228	0.239	72.15
C6-9	0.2155	3019.6	556.4	296	0.331	102.5
C10-17	0.2202	2017.5	692.3	505	0.584	184
C18-27	0.1027	1327.0	808.4	768	0.893	306.2
C28+	0.1252	1155.1	915.5	1001	1.1	585.61

[27]. The acentric factor was proposed by Pitzer [28] as a comprehensive expression of the boiling point, molecular weight and polarity characteristics of pure ingredients. Parachor is a material-specific value that relates surface tension to chemical structure.

Regression matching is promoted using the experimental data of the Weyburn W3 fluid. Results from the fluid model adequately matched the experimental data and confirmed the reliability for composition simulation. The data values compared with the modeling fluid are shown in

Table 2. Comparison of the fluid model and experimental data for Weyburn W3 fluid.

Parameters	Fluid Model	Experimental Data
Saturation Pressure (kPa)	4784.95	4920
Oil density at psat (kg/m3)	805.73	806.4
Oil viscosity at psat (mPa·s)	1.75	1.76
Formation volume factor	1.11	1.12
API (°)	34.8	31

.

The Winprop software, developed by the Computer Modeling Group (CMG), was used for fluid modeling. The Peng–Robinson EOS (PR EOS) [29,30] was used to calculate the fugacity of a component in the oil and gas phases. The concept of fugacity is usually used for multi-component equilibrium involving solid, liquid and gas phases. It is used to determine the amount of ingredients in each stage of a multi-component mixture at various temperatures and pressures [31]. Therefore, the Peng–Robinson equation was used to predict the phase behavior of the mixed fluid and to tune the experimental values. The PR EOS is as follows:

$$p=\frac{RT}{v-b}-\frac{a}{v\left(v+b\right)+b\left(v-b\right)}$$

(1)

or, in terms of the Z factor:

$$Z^3-\left(1-B\right)Z^2+\left(A-3B^2-2B\right)Z-\left(AB-B^2-B^3\right)=0$$

(2)

where a is the attraction parameter, b is the repulsion parameter, p is the pressure (Pa), T is the temperature (K), v is the volume ($\frac{{\mathrm{m}}^3}{\mathrm{mol}}$), and R is the universal gas constant ($\frac{{\mathrm{m}}^3·\mathrm{Pa}}{\mathrm{K}·\mathrm{mol}}$). The EOS constants for pure components are given by:

$$A=a\frac{p}{{\left(RT\right)}^2}$$

(3)

$$B=b\frac{p}{RT}$$

(4)

$$a={\mathsf{\Omega }}_a^0\frac{R^2{T}_c^2}{p_c}\alpha$$

(5)

$$b={\mathsf{\Omega }}_b^0\frac{R{T}_c}{p_c}$$

(6)

$$\alpha ={\left[1+m\left(1-\sqrt{T_r}\right)\right]}^2$$

(7)

where $\alpha$ is a parameter for temperature, $p_c$ is the critical pressure, $T_c$ is the critical temperature, and $T_r$ is the reduced temperature. Additionally, values of the constants are given as follows:

$$\alpha ={\left[1+m\left(1-\sqrt{T_r}\right)\right]}^2 \alpha ={\left[1+m\left(1-\sqrt{T_r}\right)\right]}^2$$

(8)

The parameter m is expressed as a function of the acentric factor $\omega$:

$$m=0.37464+1.54226\omega -0.26992{\omega }^2$$

(9)

Robinson and Peng [30] proposed a modified expression for m for heavier components ($\omega >0.49$):

$$m=0.3796+1.485\omega -0.1644{\omega }^2+0.01667{\omega }^3$$

(10)

In PR EOS, the fugacity of component i of the hydrocarbon mixture, ${\mathsf{\Phi }}_i$, is expressed through the following equation:

$$\ln {\mathsf{\Phi }}_i=\frac{B_i}{B}\left(Z-1\right)-\ln \left(Z-B\right)+\frac{A}{2\sqrt{2}B}\left(\frac{B_i}{B}-\frac{2}{A}{\displaystyle \sum }_{j=1}^N{y}_j{A}_{ij}\right)\ln \left[\frac{Z+\left(1+\sqrt{2}\right)B}{Z-\left(1-\sqrt{2}\right)B}\right]$$

(11)

where $y_j$ is the gas mole fraction of component i. The mixing rules for expressing multi-component fugacity are as follows:

$$A={\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N{y}_i{y}_j{A}_{ij}$$

(12)

$$B={\displaystyle \sum }_{i=1}^N{y}_i{B}_i$$

(13)

$$A_{ij}=\left(1-K_{ij}\right)\sqrt{A_i{A}_j}$$

(14)

where $K_{ij}$ is the binary interaction parameter.

The parameters of DME used in PR EOS were obtained from literature (

Table 3. Binary interaction coefficients between DME and each component.

	N2	CO2	H2S	C1	C2	C3	DME	C4	C5	C6-9	C10–17	C18–27	C28+
N2	0.00	-	-	-	-	-	-	-	-	-	-	-	-
CO2	0.00	0.00	-	-	-	-	-	-	-	-	-	-	-
H2S	0.13	0.14	0.00	-	-	-	-	-	-	-	-	-	-
C1	0.25	0.11	0.07	0.00	-	-	-	-	-	-	-	-	-
C2	0.01	0.13	0.09	0.00	0.00	-	-	-	-	-	-	-	-
C3	0.09	0.13	0.08	0.01	0.00	0.00	-	-	-	-	-	-	-
DME	0.10	0.00	0.00	0.29	0.25	0.25	0.00	-	-	-	-	-	-
C4	0.10	0.12	0.08	0.02	0.01	0.00	0.25	0.00	-	-	-	-	-
C5	0.10	0.12	0.07	0.02	0.01	0.00	0.25	0.00	0.00	-	-	-	-
C6-9	0.11	0.12	0.05	0.03	0.02	0.01	0.20	0.00	0.00	0.00	-	-	-
C10-17	0.11	0.12	0.05	0.06	0.04	0.02	0.08	0.02	0.01	0.01	0.00	-	-
C18-27	0.11	0.12	0.05	0.09	0.06	0.05	0.08	0.03	0.03	0.02	0.00	0.00	-
C28+	0.11	0.12	0.05	0.12	0.09	0.07	0.08	0.05	0.05	0.03	0.01	0.00	0.00

) [13,32].

DME is also soluble in the aqueous phase, and Henry’s law was used to determine the fugacity in the aqueous phase. The phase of the gas that dissolves in the water is obtained through Henry’s law as [33]:

$$f_{iw}=y_{iw}{H}_i,i=1,\dots .,n_c$$

(15)

where $H_i$ is Henry’s constant of component i and $y_{iw}$ is the mole fraction in the aqueous phase of component i. Henry’s constant for the pressure change is calculated by:

$$\ln H_i=\ln H_i^{*}+\frac{\overline{v_i}\left(p-p^{*}\right)}{RT}$$

(16)

where $H_i^{*}$ is Henry’s constant of component i at a reference pressure (Pa) and temperature (K) $p^{*}, T$ and $\overline{v_i}$ is the molar volume of component i. The values of the solubility properties of DME in the aqueous phase were obtained from literature [34]. The phase behavior and solubility in the aqueous solution were determined through fugacity obtained by PR EOS and Henry’s law.

2.2. Reservoir Modeling

The GEM compositional simulator developed by CMG was used for numerical simulation. In this paper, the 2D homogenous cross-sectional reservoir model was designed to analyze the sweep efficiency change according to the DME mole fraction. The properties of the reservoir were obtained from the literature (

Table 4. Classification of cases according to DME content.

Case	Injection Gas Contents
1	100% CO2 + 0% DME
2	90% CO2 + 10% DME
3	85% CO2 + 15% DME
4	75% CO2 + 25% DME

) [31]. In oil-wet system, water flooding is not effective for enhancing oil recovery [35]. Therefore, the oil-wet system was chosen to show the improved performance of DME-CO₂ mixed solvent. The end point values and crossover saturation of relative permeability are measures of wettability [36]. The relative permeability obtained from the literature is shown in Figure 1 [37]. The relative permeability of water is quite high at residual oil saturation and crossover saturation is less than 0.5, which are good qualitative indications of oil wet conditions.

The size of the reservoir was designed as 52 × 1 × 20 grids and each grid block was 3 m × 3 m × 1.5 m. In this paper, WAG was applied to enhance the oil recovery. The total injection process was conducted for 12 years: 3 years for the secondary water flooding, 6 years for WAG (1:1.5 WAG ratio), and 3 years for the water flooding to produce the residual DME (Figure 2).

Four WAG cases depending on the mole fraction of DME (0% to 25%) were analyzed (Table 4).

Other properties, including production pressure, were maintained to examine the effect of the injection fluid. Reservoir properties and the operation conditions are shown in

Table 5. Reservoir initial conditions and operating conditions.

Properties	Values
Initial Pressure (kPa)	13,789
Initial oil saturation	0.88
Porosity (%)	30
Permeability (m2)	4.9 × 10−14
Producing pressure (kPa)	11,031
Total injection (PV)	1.5

.

2.3. Viscous Gravity Number (N_gv)

Since the density of the gas used in the WAG was less than that of the reservoir fluid, the difference between the density and gravity causes an override in which the injected gas moves to the upper layer, which reduces the vertical sweep efficiency. The vertical sweep efficiency was affected by the relationship between the viscosity and gravity. The change in the vertical sweep efficiency with the addition of DME was quantitatively investigated using the viscous gravitational number (N_gv), which can be expressed by [38]:

$$N_{gv}=\frac{\mathrm{time}\mathrm{for}\mathrm{horizontal}\mathrm{flow}}{\mathrm{time}\mathrm{for}\mathrm{vertical}\mathrm{flow}}=\frac{k_v{k}_{rs}\Delta \rho g\cos \alpha AL}{q_s{\mu }_{s}h}$$

(17)

where $k_v$ is vertical permeability, $k_{rs}$ is relative permeability, $\Delta \rho$ is density difference between injected and reservoir fluids, $g$ is gravitational acceleration, $A$ is cross sectional area, $L$ is length of the reservoir, $q_s$ is flow rate of the solvent, ${\mu }_s$ is solvent viscosity and $h$ is height of the reservoir.

If N_gv = 10, horizontal flow takes ten times longer than vertical flow. The guidelines for determining which gravity or viscous force dominates are as follows:

$$\begin{gathered} N_{gv}<0.1: \mathrm{Viscous}\mathrm{forces}\mathrm{dominate}; \\ 0.1 < N_{gv} <10: \mathrm{Intermediate}; \\ {N}_{gv}>10:\mathrm{Gravity}\mathrm{dominate}. \end{gathered}$$

2.4. Minimum Miscible Pressure

The MMP is the minimum pressure at which the injected gas and oil can be mixed under a specific reservoir temperature condition. If the reservoir pressure is less than the MMP, the immiscible flooding process is applied. Conversely, if the reservoir pressure is greater than the MMP, the miscible flooding process is applied. Though the main mechanism of the effect of oil expansion and oil viscosity reduction in immiscible flooding and miscible flooding is similar, the effect is greater in miscible flooding [39]. In addition, in the case of miscible flooding, the displacement efficiency increases because of the decrease in IFT between gas and oil [40]. In this study, the MMP between oil and gas according to DME addition was investigated. The slim tube test is recognized to be the most accurate experimental method for determining MMP. However, the slim tube test is expensive and takes a long time to measure MMP [41]. To overcome the limitations, slim tube test simulation has been widely used. Since slim tube test simulation is a cost-effective method providing an accurate prediction [42]. Therefore, we used slim tube simulation in this study.

3. Results

3.1. Effects of DME Injection on Oil Recovery

3.1.1. Vertical Sweep Efficiency

The vertical sweep efficiency according to the mole fraction of DME was compared using 2D reservoir modeling. The front of the sweep area was confirmed through the change in the viscosity of the oil in contact with the injected gas. The steeper the slope of the front contact in the sweep area, the more the injected gas contacts the fluid under the reservoir. Figure 3 shows the oil viscosity when 0.5 PV was injected. When comparing the slope of the front of sweep area, Cases 1, 2, 3 and 4 were 5, 3.75, 5, and 8, respectively. The sweep efficiency increased with the addition of DME, as confirmed by the slope comparison. The contact area at breakthrough and the viscous gravity values were compared to confirm the increase in sweep efficiency. When comparing the area of the swept grids when the breakthrough occurred, Cases 1, 2, 3, and 4 were 6372 m³, 6867.6 m³, 7235.8 m³ and 8071.2 m³, respectively. Case 4 was 26.6% greater than Case 1.

Table 6. Comparison of the viscous gravity number.

Case	Viscous Gravity Number (Ngv)
1	5.06
2	3.94
3	3.26
4	1.70

shows the viscous gravity number of all cases. In Case 1, the viscous gravity number decreased by as much as 66.4% when DME was added. Decreasing the viscous gravity number increases the viscous forces. The addition of DME is more advantageous to sweep the lower reservoir fluid. As a result, the vertical sweep efficiency was significantly improved by the addition of DME.

3.1.2. Displacement Efficiency

Oil saturation, oil viscosity, and MMP were compared to confirm the displacement efficiency. Figure 4 shows the oil saturation at the end of the WAG cycle. After three WAG cycles, the oil saturation in Case 1 remains relatively greater than Case 4. As the content of DME increases, the MMP between the injection gas and oil decreases, which has a greater effect on reducing the oil viscosity and IFT, both of which are advantageous for oil flow. Figure 5 shows the oil viscosity after 0.6 PV injection. When the initial oil viscosity was 2 mPa s, it decreased to 0.56 mPa s in Case 1 and to 0.36 mPa s in Case 4. For Case 4, the lowest oil viscosity value was 35% less than that for Case 1. In addition, in Case 4, the deep blue area, in which oil viscosity was less than 0.5 mPa s, was more widespread. The deep blue area in Case 4 was 2902.8 m³, and in Case 1, the deep blue area did not exist. The values at the middle of the reservoir were compared to evaluate the fluid properties and residual oil component after displacement. As shown in Figure 6, after some point, the oil viscosity of Case 4 was greater than that of Case 1 because the intermediate component was displaced (Figure 7a). The mole fraction of the heavy component (C₂₈₊) increases (Figure 7b) because the heavy component remains behind the flood front. MMP was measured using a slim tube (

Table 7. Minimum miscible pressure (MMP) for each case calculated using a slim tube.

Case	MMP (kPa)
1	14,127
2	13,065
3	12,079
4	9866

). Figure 8 shows the IFT of the swept area in the middle of the reservoir for the cases, where the IFT value of Case 4 is less than that of Case 1. The lowest IFT value of Case 4 was 0.012 mM/m. The values for Cases 1, 2, and 3 were 0.054 mM/m, 0.115 mM/m, 0.485 mM/m, which were 350%, 858%, and 3941% greater than Case 4.

3.2. Recovery

The oil recovery factor (RF) can be expressed as follows:

$$\mathrm{RF}=E_D{E}_v{E}_A$$

(18)

where, E_D is displacement efficiency, E_v is vertical sweep efficiency and E_A is areal sweep efficiency. Since is not considered in 2D cross-sectional system, oil recovery can be increased by improving E_D and E_v. In Section 3.1.1 and Section 3.1.2, it was confirmed that both E_D and E_v increased with the addition of DME. Figure 9 shows the oil recovery for each case according to the DME content. For Case 1, the maximum oil recovery was 55%. Cases 2, 3, and 4 showed recoveries of 60%, 64%, and 72%, respectively. As the mole fraction of DME increased, the oil recovery increased. In Case 4, the recovery increased by 31% compared with Case 1 because the displacement efficiency and sweep efficiency increased as the mole fraction of DME increased. In addition, as DME is easily dissolved in water, it is recovered with the production fluid. To improve the economics of the process, the produced DME can be recovered through distillation and adsorption processes. Figure 10 compares the cumulative amount of injected DME and produced DME in Case 4. It can be confirmed that about 70% of the injected amount has been recovered and can be reused.

4. Conclusions

A model using a mixed solvent of CO₂–DME was developed to explain the change in oil recovery when CO₂ WAG and DME were added. To evaluate the reliability of the compositional simulation, results from fluid modeling were matched with experimental data from real Weyburn W3 fluids. A cross-sectional 2D model was designed to examine the sweep efficiency considering the gravity override phenomenon during WAG. Since DME is an expensive solvent, a mixed solvent of DME and CO₂ was used and the effect was analyzed. Four cases with different DME addition ratios were modeled and the oil recovery was analyzed through changes in the sweep efficiency and displacement efficiency. DME in CO₂ decreases the IFT and MMP, which increases the displacement efficiency. Adding DME to the CO₂ flood also increases the vertical sweep efficiency. The developed compositional model illustrated that DME increases the sweep efficiency and displacement efficiency. In addition, the vertical sweep efficiency and displacement efficiency was presented quantitatively with viscous gravitational numbers, MMP, and IFT. When the DME content was 25%, the oil recovery was 72%, a 31% increase over CO₂ only. This study confirmed the favorable effect of DME addition into the CO₂ WAG process over simple CO₂ flooding. Since DME is an expensive solvent, the optimum design with an integrative techno-economical model is required for successful field implementation of the process. In addition, a full 3D model is required to analyze the effect of vertical and areal reservoir heterogeneities on the oil recovery from actual fields.