Computational Design of a Broadband In-Line Coaxial-to-Rectangular Waveguide Transition

Abstract

This Communication presents a computational design approach for a broadband in-line coaxial-to-rectangular waveguide transition having a 2.83:1 bandwidth. Existing designs have a bandwidth ranging from 1.36:1 to 2:1. The proposed transition consists of a four-step ridge transformer and three sections of the rectangular waveguide. The proposed design approach extends the bandwidth of the transition by a theory-based design of the width and height of the three-section waveguides and by a computer-aided optimization of the stepped-ridge transformer. The dimensions of the three waveguide sections are determined such that the transition operates from very close to the TE₁₀-mode cutoff to slightly less than the TE₃₀-mode cutoff. A four-step ridge transformer was computer-optimized for a low reflection coefficient over a broad bandwidth. The proposed design approach was applied to the design of a coaxial-to-WR75 transition whose reflection coefficient is less than −22.6 dB at 8.14–23.00 GHz (2.83:1 bandwidth). The dimensions of the proposed transition were obtained using an electromagnetic simulation tool. The increased bandwidth of the transition can be very useful, especially in measurement applications.

1. Introduction

Rectangular waveguide-to-coaxial transitions are commonly used in communication and measurement systems to convert the coaxial TEM-mode signal into the rectangular waveguide TE₁₀-mode wave and vice versa. In the fields of advanced multi-system radars, radio telescopes, near-field measurements, and material dielectric constant measurements, broadband operation is often required to cover a standard waveguide band and its adjacent ones. For example, using the WR75 waveguide (10.0–15.0 GHz), one can cover WR90 (8.2–12.4 GHz), WR62 (12.4–18.0 GHz), and WR51 (15.00–22.00 GHz) bands if higher-order modes are suppressed. A coaxial-to-rectangular waveguide transition can be either of right-angle type or in-line type. For some applications, in-line transitions are more convenient. Commercial products are available in either type.

Research on the coaxial-to-waveguide transition is believed to have started during World War II. Volume 9 (1948) of the MIT Radiation Laboratory Series describes the design of the coaxial-to-rectangular waveguide transition in a significant number of pages [1]. This volume deals with transitions employing a right-angle probe of circular cylindrical or wine glass or hemispherical shape along with various matching structures such as a coaxial stub, a symmetrical probe gap, a dielectric cylinder around the probe, and a cross bar. In [1], wideband right-angle or in-line transitions are also presented where a single or dual continuously curved-ridge transformer is employed. The book also describes narrow-band in-line transition designs with E- or H-plane loop coupling or resonant-slot coupling.

A journal paper on the coaxial-to-waveguide transition dates back to a 1947 work by S. B. Cohn [2], where various designs of the right-angle transition were presented along with a design theory that includes the transmission line and the characteristic impedance. As one of the fundamental high-frequency devices, the enduring importance of the coaxial transition can be seen in its continued research interest nowadays [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

The in-line coaxial transition has been investigated from the early days of microwave technology developments [1,2,3,4,5,6,7,8,9], when the engineering designs were carried out by experiments guided by an elementary theory. Theoretical analysis has been restricted to transitions constructed with a simple rectangular loop mode converter [6,8]. A right-angle transition employing a single or double continuously tapered ridge was already known in the 1940s [1,2].

G. J. Wheeler appears to be the first engineer to employ a stepped TEM-TE₁₀ mode transformer in the design of an in-line coaxial-to-rectangular waveguide transition [3]. In 1957, he achieved a VSWR of less than 1.10 at 2.6–3.8 GHz and a VSWR of less than 1.19 at 4.8–6.5 GHz with his transition. In 1963, Dix used a three-step ridge transformer plus a coaxial quarter-wave transformer to design and test an in-line transition operating at 2.5–4.1 GHz (1.64:1 bandwidth) with a VSWR < 1.22 or a reflection coefficient < −20.1 dB [4]. Das and co-workers presented the theoretical analysis and the design of an in-line transition employing an inverted-L shaped loop probe [5]. Their transition showed a narrow bandwidth. It appears that Deshpande, Das, and Sanyal are the ones who presented a rigorous theoretical analysis of the inverted-L shape end launcher assuming a sinusoidal current distribution on the inverted-L probe wire [6]. Later, Saad improved the theory of Deshpande, Das, and Sanyal to include more general cases [7]. Gangadharan used a stepped wire loop to experimentally design an in-line transition operating at 8.2–12.0 GHz (1.46:1 bandwidth) with a VSWR < 1.25 or a reflection coefficient < −19.1 dB [8].

Chan and co-workers employed a dual stepped-ridge transformer along with a rectangular coaxial matching section for the theoretical design of an in-line transition operating at 0.85–1.16 GHz (1.36:1 bandwidth) with a reflection coefficient < −32.3 dB [9]. They analyzed the transition using the mode-matching method. Levy and Hendrick used an equivalent-circuit method and an in-house computer program to theoretically design an in-line transition with a three-step ridge transformer [10]. Their transition showed a reflection coefficient < −30.0 dB at 3.05–4.60 GHz (1.51:1 bandwidth). Durga and co-workers [11] and Carmel and co-workers [12] used a stepped-ridge transformer in their design of an in-line transition. Their transition showed performance similar to that in the preceding works.

Cano and Mediavilla achieved a 2:1 bandwidth in an in-line rectangular waveguide-to-coaxial transition [13] using oversized mode conversion and a stepped-ridge transformer. Subsequent works [14,15,16,17,18,19] on the in-line transition were not targeted for extending the bandwidth beyond 2:1. In [14], a two-step ridge transformer was employed in a transition working at 9.5–10.8 GHz with a reflection coefficient of less than −20 dB. Ye and co-workers used a single waveguide and a three-step ridge transformer to design an in-line transition operating at 11.5–19.0 GHz (1.65:1 bandwidth) with a reflection coefficient < −20.0 dB [15]. Bilik employed a two-step ridge transformer in a high-power in-line transition design working at 2.4–2.5 GHz with a reflection coefficient of less than −25 dB [16]. In [17], a triple-stepped probe extended out of a coaxial cable was used to design an in-line transition working at 7.6–12.2 GHz (1.61:1 bandwidth) with a VSWR of less than 1.5 (reflection coefficient < −14.0 dB).

Simone and co-workers realized a five-step ridge transition operating at 33–50 GHz (1.52:1 bandwidth) with a reflection coefficient < −25.0 dB [18]. Shu and co-workers used a four-step ridge transformer to realize WR28, WR22, and WR19 transitions operating at 26.5–40.0 GHz (1.51:1 bandwidth), at 33–50 GHz (1.52:1 bandwidth), and at 40–60 GHz (1.50:1 bandwidth) with a reflection coefficient of less than −23.0 dB, −28.0 dB, and −25.0 dB, respectively [19]. A patent for an in-line coaxial-to-rectangular waveguide transition was granted as early as in 1973 [20]. In [20], a four-step ridge transformer was employed to design a transition working at 7.0–11.0 GHz (1.57:1 bandwidth) with a VSWR of less than 1.28 or a reflection coefficient < −18.2 dB.

A comprehensive literature survey shows that the concept of the stepped-ridge transformer and the stepped waveguide height transformer has been applied to the design of the broadband right-angle coaxial-to-rectangular waveguide transitions [21,22,23,24,25,26,27]. In [26], a double stepped-ridge transformer was used. Study of the literature shows that the stepped-ridge transformer has been a preferred choice in the design of broadband coaxial-to-rectangular waveguide transitions.

In this Communication, we present a design approach for the broadband in-line coaxial-to-rectangular waveguide transition and two design examples having a bandwidth exceeding 2.8:1. The proposed transition employs a stepped-ridge transformer for the conversion of the coaxial TEM mode into the rectangular waveguide TE₁₀ mode. The transformer was placed in a converter waveguide whose broad-wall width is slightly larger than that of the output waveguide. The narrow-wall height of the converter waveguide was reduced from a standard height (one-half of the broad-wall width) so that the TE₁₁-mode cutoff coincided with the TE₃₀-mode cutoff in the converter waveguide. A matching waveguide was placed between the converter waveguide and the output waveguide to reduce reflections from a step discontinuity in the waveguide broad wall.

Using the powerful capability of a modern electromagnetic simulation tool—CST Studio Suite^TM V2023, a widely used simulation tool in the antenna and RF community—the dimensions of the proposed transition were optimized for a reflection coefficient < −20 dB over a bandwidth approaching the theoretical maximum of 3:1.

In many papers, authors present a design with experimental validation. In others, a design method is validated with computer simulation [9,11,18,28,29,30,31,32,33]. We believe that the accuracy of the simulation tool used in this Communication is sufficient to prove the proposed design approach. All the dimensions of the design examples are given, and anyone can verify the results presented in this paper.

The construction of this Communication is as follows. In Section 2, we review the performance of a representative commercial in-line coaxial-to-rectangular transition to show the state of the art in practice. It is followed by the concept and the equations of the proposed design approach. In Section 3, two design examples are presented: one for a WR75 waveguide with a reduced narrow-wall height and the other for a standard WR75 waveguide. Finally, in Section 4, we draw conclusions and suggest possible future research topics.

2. Design Approach

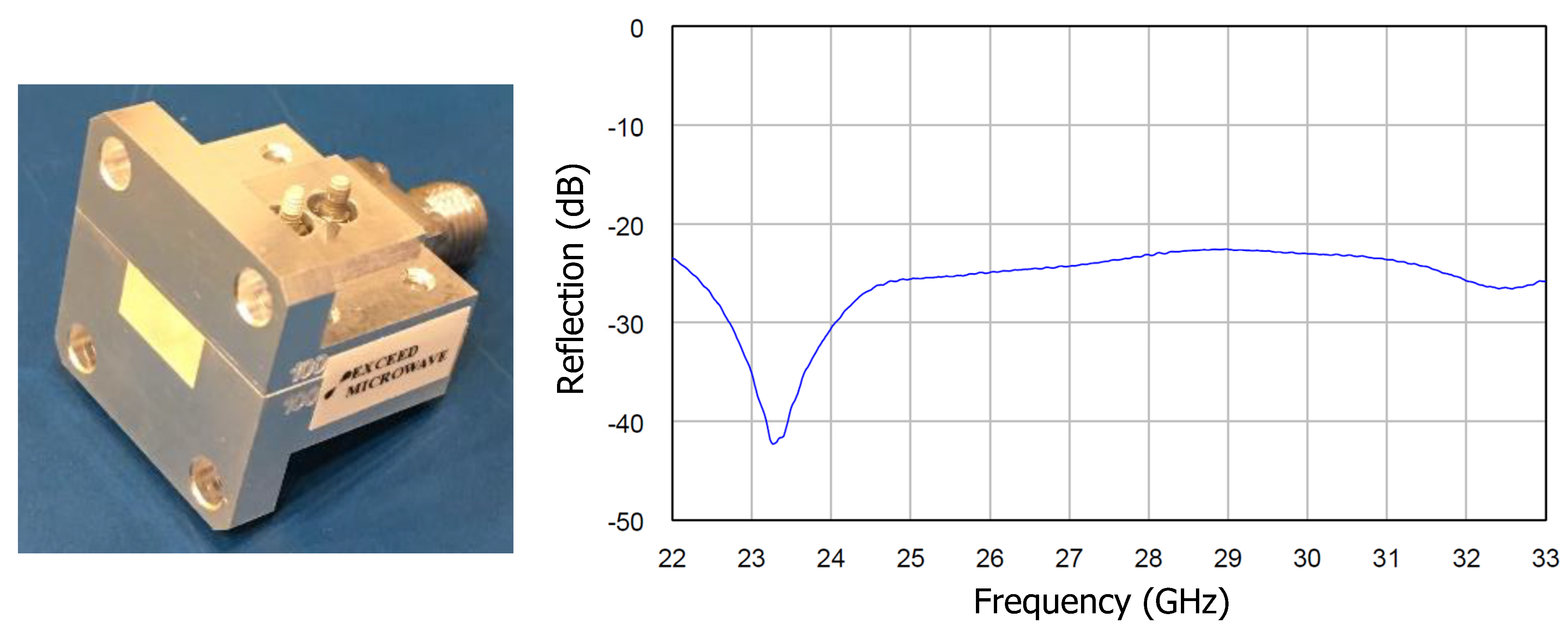
There are many commercial products of the coaxial-to-rectangular waveguide transitions either of right-angle type or of in-line type. Figure 1 shows a commercial in-line coaxial transition in a WR34 waveguide [28]. By approximately extrapolating the manufacturer’s reflection coefficient data, it can be seen that the transition operates with a reflection coefficient < −22.7 dB from about 21 GHz to about 34 GHz. The start and end frequencies (21 and 34 GHz) are 1.21 and 1.96 times the fundamental TE₁₀-mode cutoff frequency, respectively (1.62:1 bandwidth). If one can extend the bandwidth close to 3:1, it will be very useful in many applications. Especially in measurement applications, it will reduce the number of measurement accessories and the measurement time.

Figure 2 shows the waveguide wall structure in the proposed design approach. The symbols W, W₁, and W₂ denote the output waveguide, the impedance matching waveguide, and the TEM-TE₁₀ mode converter waveguide, respectively; a, a₁, and a₂ their broad-wall width, respectively; b, b₁, and b₂ their narrow-wall height, respectively. A stepped-ridge transformer is placed in the mode-converter waveguide W₂.

In a rectangular waveguide, the TE_mn/TM_mn-mode cutoff occurs at the following:

f_mn = (c/2) [(m/a)² + (n/b)²]^1/2

(1)

where c is the speed of light, a is the waveguide broad-wall width, and b is the narrow-wall height. From now on, we will use the TE modes to mean the TM modes as well since their cutoff frequencies are the same.

In a standard output waveguide W, where b is equal to a/2, the cutoff frequency of the TE₁₀, TE₂₀, TE₁₁, and TE₃₀ modes is given by the following:

f₁₀ = c/(2a)

(2a)

f₂₀ = 2c/(2a) = 2f₁₀

(2b)

f₁₁ = √5c/(2a) = 2.24f₁₀

(2c)

f₃₀ = 3c/(2a) = 3f₁₀

(2d)

Since the stepped-ridge transformer is symmetric in the H plane of the mode-converter waveguide W₂, the antisymmetric TE₂₀ mode is not excited in W₂, and the next higher-order mode will be the TE₁₁ or TE₃₀ mode. In a standard rectangular waveguide, the TE₁₁-mode cutoff frequency is 2.24 times the fundamental TE₁₀-mode cutoff frequency. Thus, the bandwidth limit of a transition constructed using a standard rectangular waveguide is 2.24:1. The achieved bandwidth, however, is about 90% of the theoretical maximum or 2:1 since it is difficult to operate a transition at very close to the cutoff of the TE₁₀ and TE₁₁ modes.

At frequencies above the cutoff, the TE₃₀ mode can be generated in W₂ along with the fundamental TE₁₀ mode and subsequently transmitted to the output waveguide W. One can make a transition operate approximately from the TE₁₀ cutoff to the TE₃₀ cutoff in the output waveguide (about 3:1 bandwidth) if the TE₁₁ mode is suppressed in the waveguides W, W₁, and W₂. If the discontinuity effect is small between W₂ and W, the generation of the TE₁₁ mode will be minimized.

This can be achieved by reducing the narrow-wall height of the mode-converter waveguide W₂ so that the TE₁₁ cutoff of W₂ coincides with the TE₃₀ cutoff of W₂:

f₁₁ = f₃₀

(3)

Then, the narrow-wall height b₂ of W₂ can be obtained from the following:

(c/2) [(1/a₂)² + (1/b₂)²]^1/2 = 3c/(2a₂)

(4)

or

b₂ = a₂/√8 = 0.354a₂

(5)

With a given waveguide broad-wall width a₂, the TE₃₀-mode cutoff frequency f₃₀ is fixed, and the TE₁₁-mode cutoff frequency f₁₁ can be increased by reducing the waveguide narrow-wall height b₂. Making f₁₁ larger than f₃₀ offers no gain since the frequency upper limit will still be f₃₀, and the height difference between the output and converter waveguides will be increased, resulting in an increased mismatch between W₂ and W.

The broad-wall width of the converter waveguide is chosen to satisfy the following condition:

a₂ = (1 + Δ)a

(6)

where Δ is a design parameter in the range of 0.04–0.08, and a is the broad-wall width of the output waveguide W. Equation (6) ensures a transition to operate close to the TE₁₀-mode cutoff of the output waveguide. The larger Δ, the closer to the TE₁₀ cutoff the start frequency of operation. Large values of Δ will increase the reflection at the waveguide width step discontinuity, and more than one section of the matching waveguide may be required.

From the foregoing discussion, we find that the proposed transition will work in the following frequency range:

f₁ < f < f₂

(7)

where

f₁ = max(f_{10_}o, f_{10_}m, f_{10_}c)

(8)

The 10 symbol in the subscript denotes the cutoff frequency of the fundamental TE₁₀ mode. The symbols o, m, and c refer to the output, matching, and converter waveguides, respectively. The frequency upper limit f₂ is determined by the level of the higher-order TE₁₁ and TE₃₀ modes generated in the transition. The frequency f₂ is more or less determined by the cutoff frequency of TE₁₁ and TE₃₀ modes in the waveguides W, W₁, and W₂. Of course, the bandwidth of the transition is also influenced by the performance of the TEM-to-TE₁₀ mode transformer, which is a stepped-ridge transformer in our case.

The impedance matching waveguide W₁ is employed to match the impedance of W with that of W₂. The broad-wall width a₁ of W₁ is between a and a₂. The width a₁, height b₁, and length L₁ of W₁ are determined using an automatic optimization function of the simulation tool. The difference in the height of W and W₂ can be matched in the form of a single- or multi-step transformer or in the form of a continuously tapered transformer.

It is important to note that the TE₁₁ mode should not be generated in the region between the output waveguide W and the converter waveguide W₂ in the operating frequency range of the transition. In fact, during the parametric analysis and the optimization, we observed that the TE₁₁ mode can be generated in the converter waveguide W₂ due to the presence of the stepped-ridge transformer, indicating that a careful design is required. In the next section, we apply the foregoing design approach to the design of two coaxial-to-WR75 transitions having a bandwidth exceeding 2.8:1.

3. Design Examples

Figure 3 shows the structure of an in-line coaxial-to-rectangular waveguide transition to be designed according the approach proposed in this Communication. The output waveguide W is a standard waveguide with broad-wall width a and narrow-wall height b (b = a/2 in most of the standard waveguides). The converter waveguide W₂ has broad-wall width a₂ slightly larger than a (as given by Equation (6)) and narrow-wall height b₂ smaller than b (as given by Equation (5)).

The matching waveguide W₁ is used to ensure a broadband impedance matching between the converter waveguide W₂ and output waveguides W, which have different broad-wall widths. A linear taper T in the narrow-wall height is used in the waveguides W₁ and W for design simplicity and for a smooth change in the narrow-wall height from b₂ to b. One may use a stepped waveguide transformer, in which case there will be more parameters to be optimized. If necessary, the linear taper may have a zero slope or a negative slope to make the height of the output waveguide W₁ less than or equal to that of the converter waveguide W₂.

A stepped-ridge transformer S converts the TEM mode of the coaxial connector X to the TE₁₀ mode of the converter waveguide W₂. The coaxial probe P is connected to the stepped-ridge transformer S across a cavity C through a probe hole H in the back short B. The four-step ridge transformer S plays an important role, as it is crucial in determining the level of the reflection coefficient and the degree of the higher-order mode generation. A stepped-ridge transformer seems to be better in achieving a low reflection coefficient over a broad bandwidth than a continuously tapered transformer since it has more control parameters. The number of steps in the ridge transformer is important for broadband operation. It has been found that four steps are sufficient for our transition design. The edges of the first ridge—the one connected to the coaxial probe P—are rounded in the circular shape of radius R for better impedance matching. In addition to S, the cavity C and the probe hole H play a role in achieving a low reflection coefficient over a broad frequency range.

Figure 4 shows the dimensional parameters of the transition. With the given dimensions a and b of the output waveguide W, the design of the transition starts with determining a₂ and b₂ of the converter waveguide W₂, which was explained in the previous section. The height b₂ of the converter waveguide W₂ is held constant throughout its length to suppress the generation of the TE₁₁ mode. The length (L₂ + L₃ in Figure 4) of the converter waveguide W₂ is one of the optimization parameters.

The width a₁ and the length L₁ of the matching waveguide are among the parameters to be optimized. The length of a linear taper T is the sum of the output waveguide length L and the matching waveguide length L₁, which is optimized for a reflection coefficient < −20 dB, especially at the start frequency in the operating bandwidth.

The dimensions of the four-step ridge transformer S, the cavity C, and the probe hole H can be optimized by using a powerful modern simulation tool such as CST Studio Suite^TM V2023. The ridge-edge-rounding radius R is held at a constant value. It is virtually impossible to obtain a low reflection coefficient over a broad frequency range by an analytical method since the calculation of the reflection coefficient is extremely complicated if not impossible. An experimental approach is not suitable either because there are too many parameters to be optimized.

Prior to the design of a WR75 transition, a transition with a linear taper T of zero slope (b = b₁ = b₂) was designed. This aided in estimating the increased level of higher-order modes due to in the linear taper T of nonzero slope. In the final design of the WR75 transition, a linear taper with a slope was added, and dimensions were re-adjusted. Figure 5 shows the structure of a transition with a linear taper T of zero slope whose dimensions are listed in

Table 1. Dimensions of the designed transition with a linear taper of zero slope.

Parameter	Value (mm)	Parameter	Value (mm)
a, b, L	19.05, 6.57, 21.27	F, D	2.33, 4.59
a1, b1, L1	19.47, 6.57, 16.92	t, G, R	1.59, 0.79, 0.90
a2, b2, L2, L3	19.89, 6.57, 2.89, 23.78	Ridge width/height	3.55/0.91, 1.99, 3.75, 5.27
Coaxial connector	1.27/4.11, εr = 2.1 (SMA)	Probe hole	Dia. = 2.95, Len. = 1.59

. An SMA connector was used for the coaxial input port. Figure 6 shows the reflection and transmission coefficients of the designed transition in both a decibel scale and a natural scale. The reflection coefficient is less than −24 dB at 8.00–22.54 GHz (2.82:1 bandwidth). A resonance spike was generated at 21.24 GHz, causing the reflection coefficient to increase from −30 dB to −24 dB.

Figure 7 shows the transmission coefficient of the higher-order modes from the coaxial port to the output waveguide port. In the operating frequency range of 8.00–22.54 GHz, the TE₁₁ and TE₃₀ modes are predominant the highest ranging from −70.0 dB to −40.2 dB. The TM₁₁ mode is the next-highest one with a maximum level of −72 dB at 22.54 GHz. The TE₃₁ and TM₃₁ modes are in the level of −130 dB, −150 dB, respectively.

After confirming the performance of a transition with a linear taper of zero slope, the slope of the linear taper T was adjusted for the WR75 output waveguide, and the transition was optimized. Starting with initial dimensions, we used the “Trust Region Framework” optimization in CST Studio Suite^TM V2023 to obtain a final WR75 transition, whose dimensions are given in

Table 2. Dimensions of the designed WR75 transition.

Parameter	Value (mm)	Parameter	Value (mm)
a, b, L	19.05, 8.06–9.53, 15.01	F, D	2.17, 5.60
a1, b1, L1	19.47, 6.57–8.06, 15.25	t, G, R	1.81, 1.21, 0.90
a2, b2, L2, L3	20.58, 6.57, 1.89, 20.05	Ridge width/height	3.23/0.37, 1.98, 3.86, 5.31
Coaxial connector	1.27/4.11, εr = 2.1 (SMA)	Probe hole	Dia. = 2.95, Len. = 1.81

. An SMA connector was used for the coaxial input port. All the dimensional parameters except the port dimensions of the coaxial connector and the output WR75 waveguide were optimized. The range of the parameter values to be set in the optimization was obtained from the parametric analysis carried out prior to the optimization.

Figure 8 shows the reflection coefficients during an optimization of the designed WR75 transition, where the curve in red is the reflection coefficient of the final design. In Figure 8, we observe that the reflection coefficient rapidly approaches −20 dB level and that many more iterations are required to lower the reflection coefficient below −20 dB. Over 200 simulations of the transition’s reflection coefficient were carried out before obtaining the final design.

In the final optimized reflection coefficient, in Figure 8, we observe small ripples at 17–20 GHz, larger ripples in at 20–23 GHz, and a spike at 23.15 GHz. This is caused by higher-order modes excited in the mode-converter waveguide W₂, where the stepped-ridge transformer acts as an obstacle giving rise to higher-order modes. This can more clearly be understood with the help of Figure 9, where the transmission coefficients of higher-order modes are plotted. At 17–20 GHz, the higher-order mode level is about −50 dB, while at 20–23 GHz, it steadily increases from −50 dB to −20 dB. At 23.15 GHz, all three higher-order modes, namely TM₁₁, TE₃₀, and TE₁₁ have a local peak, causing a large spike in the reflection coefficient of the TE₁₁ mode.

Figure 9 shows the transmission coefficient between the coaxial TEM mode and the rectangular waveguide high-order modes. Analysis of the higher-order modes is important in the design of the proposed transition. In

Table 3. Waveguide modes and their cutoff frequencies in the designed WR75 transition.

Waveguide	Dimension a × b (mm)	TE10-Mode Cutoff Frequency f10 (GHz)	TE30-Mode Cutoff Frequency f30 (GHz)	TE11/TM11-Mode Cutoff Frequency f11 (GHz)
Output Waveguide W	19.05 × (8.06–9.53)	7.87	23.61	17.59–20.18
Matching Waveguide W1	19.47 × (6.57–8.06)	7.70	23.10	20.13–24.08
Converter Waveguide W2	20.58 × 6.57	7.28	21.85	23.95

, we show the cutoff frequency of the TE₁₀, TE₃₀, and TE₁₁ modes in the designed WR75 transition. The lower frequency limit of the transition is determined by the TE₁₀ cutoff frequency 7.87 GHz (f₁₀) of the output waveguide W. In Figure 9, the spikes at 23.10 GHz are at the −13.7 dB level caused by the TM₁₁ mode, at the −17.1 dB level due to the TE₃₀ mode, and at the −20.0 dB level due to the TE₁₁ mode. We note that the cutoff of the TE₁₁, TM₁₁, and TE₃₀ modes occurs at the same frequency of 23.10 GHz, as predicted by the design theory.

We note in Figure 9 that at 8.14–19.40 GHz, the TE₁₂ mode is the highest, ranging from −51.0 dB to −41.4 dB except for a TM₁₁-mode spike of −44.6 dB at 17.7 GHz. At 19.40– 23.00 GHz, the TM₁₁ mode is the largest (−51.0 dB to −25.0 dB). In Figure 10, we also observe that the TE₁₁, TM₁₁, and TE₃₀ modes steadily increase at 20–23 GHz from about −50 dB to −25 dB. This is in contrast to the transition without a linear taper, where the higher-order mode level is less than −47.4 dB in the operating frequency range.

Figure 10 shows the simulated performance of the designed WR75 transition in a decibel scale and in a natural scale as well. The reflection coefficient of the TE₁₀ mode is plotted along with the transmission coefficient between the coaxial TEM mode and the output waveguide TE₁₀ mode. The reflection coefficient (|Γ|) is less than −22.6 dB at 8.14–23.0 GHz (2.83:1 bandwidth). The transmission coefficient is determined via the relationship 1 − |Γ|².

In Figure 10a, the start frequency for the reflection coefficient < −20 dB is 8.09 GHz (=1.028f₁₀). The transition maintains a reflection coefficient < −22.6 dB from 8.14 GHz to 23.00 GHz (=0.974f₃₀). The theoretical upper frequency limit of the transition is determined by the level of the higher-order TE₁₁ and TE₃₀ modes generated in the waveguides W, W₁, and W₂. A spike in the reflection coefficient is generated at 23.1 GHz, where the TE₁₁, TM₁₁, and TE₃₀ modes have a transmission peak all at the same time, as shown in Figure 9. The transition operates from slightly above the TE₁₀ mode cutoff to slightly below the TE₃₀ cutoff. The resultant bandwidth is 2.83:1 or 94.3% of the theoretical limit of 3:1.

In Table 3, we note that the cutoff frequency of the TE₁₁, TM₁₁ and TE₃₀ modes ranges from 20.13 GHz to 24.08 GHz in the matching waveguide W₁ and from 17.59 GHz to 23.61 GHz in the output waveguide W. In Figure 10, there are low-level spikes in the higher-order mode transmission coefficients: −44.5 dB at 17.7 GHz due to the TM₁₁ mode, −42.4 dB at 20.4 GHz due to the TM₁₁ mode, and −46.1 dB at 20.5 GHz due to the TE₁₁ mode. These spike frequencies closely correlate with the cutoff frequency of the TE₁₁ and TM₁₁ modes in the matching and output waveguides.

During the optimization of the WR75 transition, we observed that the resonance spikes of the TE₁₁ and TM₁₁ modes can be generated between 20 GHz and 22 GHz. It was found that this is not caused by the steps in the waveguide broad wall. This can be checked by analyzing the structure with the waveguides W, W₁, and W₂ only (i.e., with the structure with S, B, P, and X in Figure 3 removed). It is caused by the stepped-ridge transformer S in the converter waveguide W₂.

Careful efforts are required for a transition design having a bandwidth approaching the theoretical limit of 3:1. It is because the TE₁₁ and TM₁₁ modes can be generated by the stepped-ridge transformer in the converter waveguide and then transmitted to the matching and output waveguides. Thus, the design effort should be focused on the suppression of the TE₁₁ and TM₁₁ modes while achieving a low reflection coefficient over a broad frequency range. The designed WR75 transition was obtained by simultaneously optimizing for both the low reflection coefficient and the low level of higher-order modes.

To achieve a much smaller reflection coefficient in the range of −30 dB with the proposed transition, a further investigation is necessary that involves a re-design of the stepped-ridge transformer, including an increase in the number of steps. On the other hand, it may even require a different approach to the TEM-to-TE₁₀ mode transformer design. A literature survey revealed that a design with a reflection coefficient in the level of −30 dB over such a broad bandwidth seems to be rare if not impossible. The problem of designing a very-low-reflection broadband transition is left as a future research topic.

To ascertain the validity of the computational design, we compared the time- and frequency-domain simulations of the WR75 transition in Figure 11. The agreement between the two simulation methods is excellent.

In

Table 4. Comparison with previous works.

Work	Year	Feature	Frequency (GHz)/ Ratio Bandwidth	Reflection Coefficient (dB)
[4]	1957	Three-step ridge and coaxial quarter-wave transformer	2.5–4.1/1.64:1	−20.1
[8]	1979	Stepped wire loop	8.2–12.0/1.46:1	−19.1
[9]	1990	Dual stepped ridge	0.85–1.16/1.36:1	−32.3
[10]	1998	Three-step ridge	3.05–4.60/1.51:1	−30.0
[13]	2017	Oversized mode conversion and four-step ridge	10.0–20.0/2.00:1	−30.0
[15]	2018	Three-step ridge	11.5–19.0/1.65:1	−20.0
[18]	2021	Five-step ridge	33–50/1.52:1	−25.0
[19]	2021	Four-step ridge	40–60/1.50:1	−25.0
[28]	In production	Commercial product	21–34/1.62:1	−22.7
This work	2023	Four-step ridge and linear taper	8.14–23.00/2.83:1	−22.6

, we compare the proposed transition design with previous works. We performed a thorough literature search for comparison and listed in Table 4 only those previous works that are worthy of comparison in this paper. For completeness, we include a commercial transition by Exceed Microwave [28], which is shown in Figure 1 along with its reflection coefficient graph. Compared with the bandwidth of 1.36:1 to 2.00:1 in the previous works, the design approach presented in this Communication achieves a 2.83:1 bandwidth, a great increase from existing results. The proposed transition uses a WR75 waveguide and operates from 8.14 GHz to 23.00 GHz, fully covering the WR90, WR62, and WR51 waveguide bands.

4. Conclusions

The design approach proposed in this paper enables a realization of an in-line rectangular waveguide-to-coaxial transition with a bandwidth close to the theoretical limit of 3:1. The maximum bandwidth in previous works was 2:1. The proposed design approach employs three waveguides—output, matching, and converter waveguides. A standard waveguide was used at the output, and a mode-converter waveguide was used at the input. A matching waveguide was placed between the input and the output. Making the broad-wall width of the converter waveguide slightly larger than that of the output waveguide ensured an operation close the TE₁₀-mode cutoff. The narrow-wall height of the converter waveguide was reduced such that the TE₁₁-mode cutoff frequency was the same as the TE₃₀-mode cutoff frequency. For low reflection over a broad frequency range, a four-step ridge transformer was used for the coaxial TEM to waveguide TE₁₀ mode conversion. With the proposed scheme, a transition can operate with a maximum bandwidth of 3:1. It was found that the discontinuity-induced generation of the unwanted higher-order modes should be suppressed by a careful optimization of the stepped-ridge transformer. A WR75 transition designed according to the proposed approach showed a 2.83:1 bandwidth, close to the theoretical limit of 3:1 with a reflection coefficient < −22.6 dB. We expect that the proposed design approach will pave the way for a significant extension in the bandwidth of microwave devices and antennas that employ coaxial-to-rectangular waveguide transitions. Possible future research topic may include (1) reduction of the transition’s reflection coefficient to −30 dB level, (2) further extension of the transition’s bandwidth by suppressing higher-order modes, and (3) design integration of the proposed transition in such devices as near-field antenna measurement probes and materials measurement fixtures.