Water Pipeline Leakage Detection Based on Coherent φ-OTDR and Deep Learning Technology
Abstract
:1. Introduction
2. Sensing Principle of φ-OTDR
3. Data Collection and Preprocessing
3.1. Experimental Setup
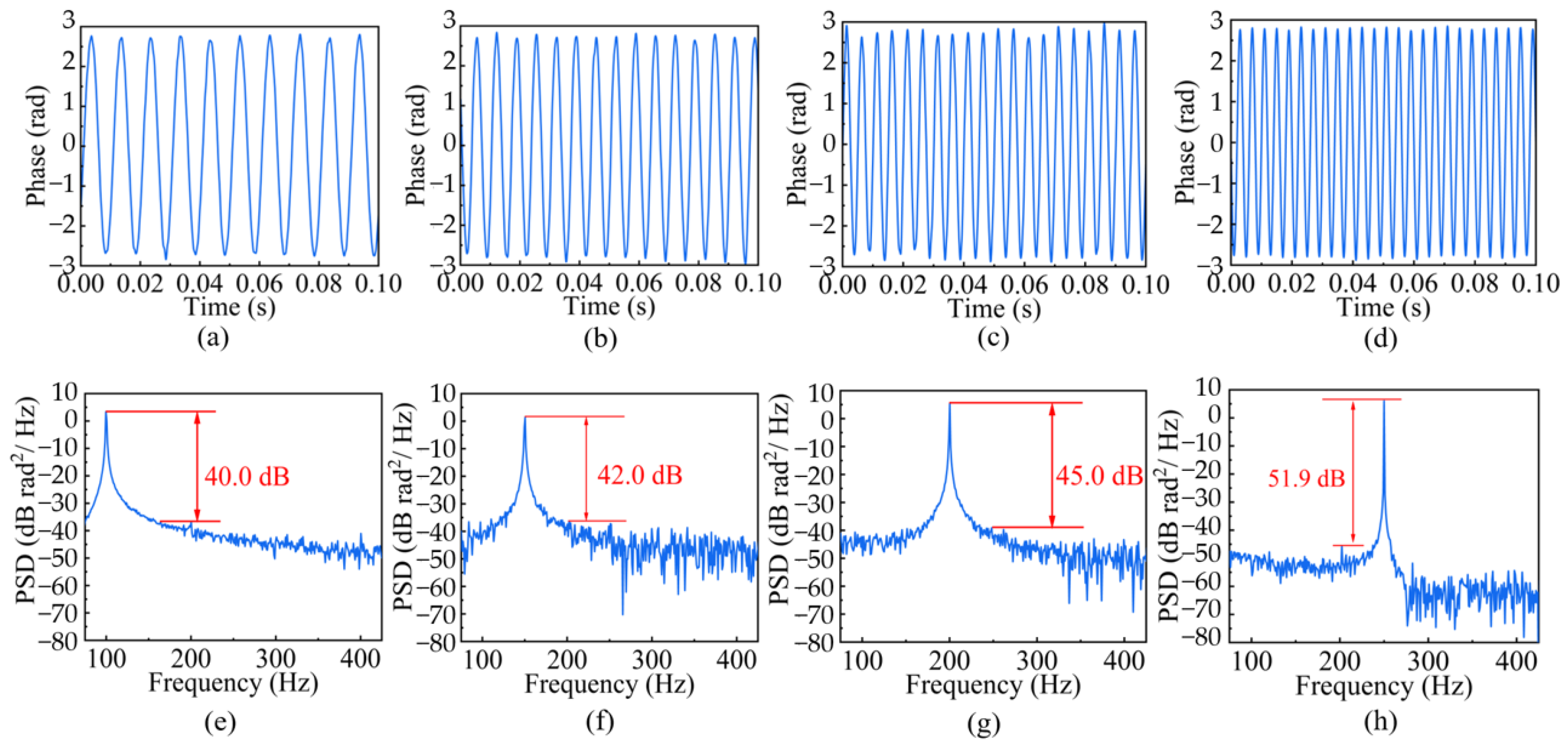
3.2. Sensing Characteristic
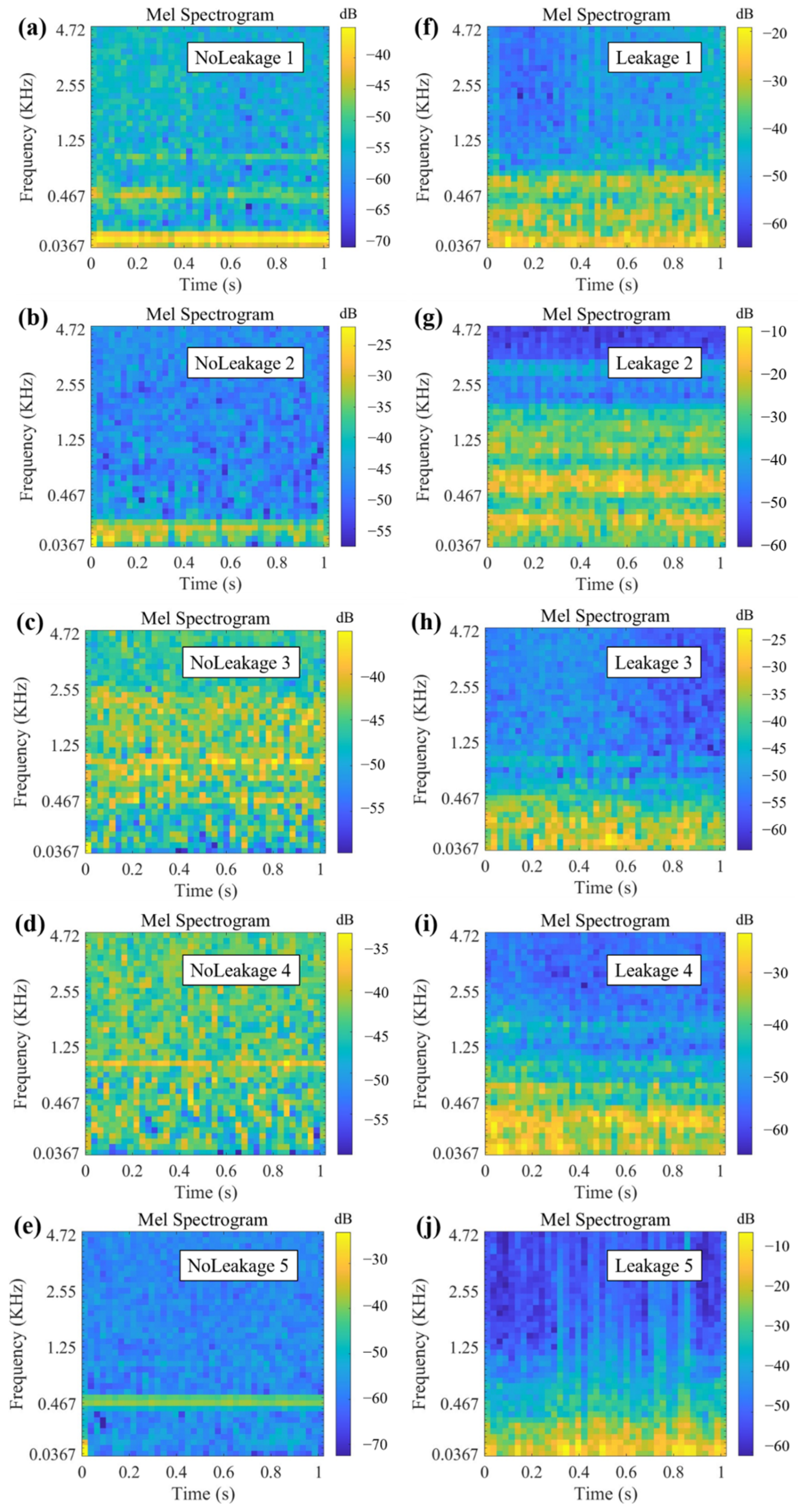
3.3. Dataset Production
4. Deep Learning Training
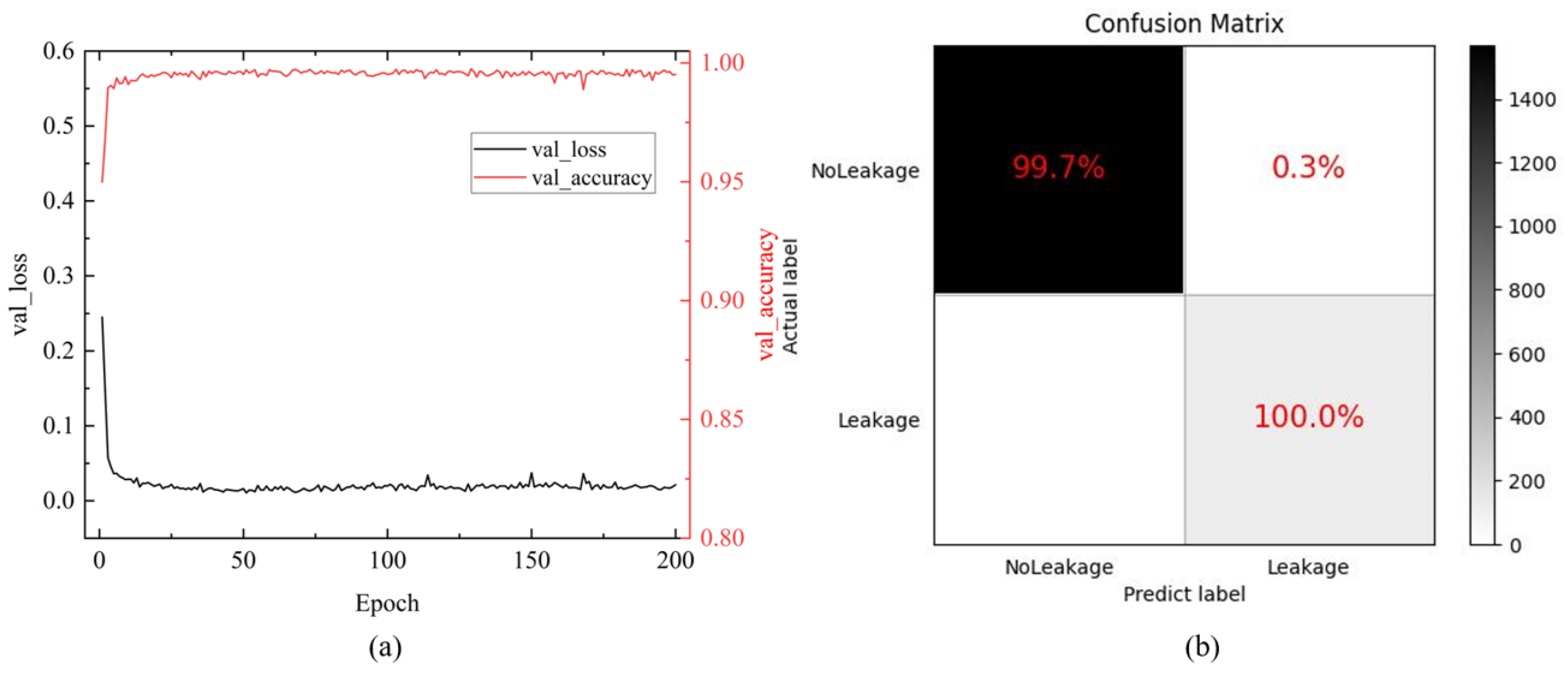
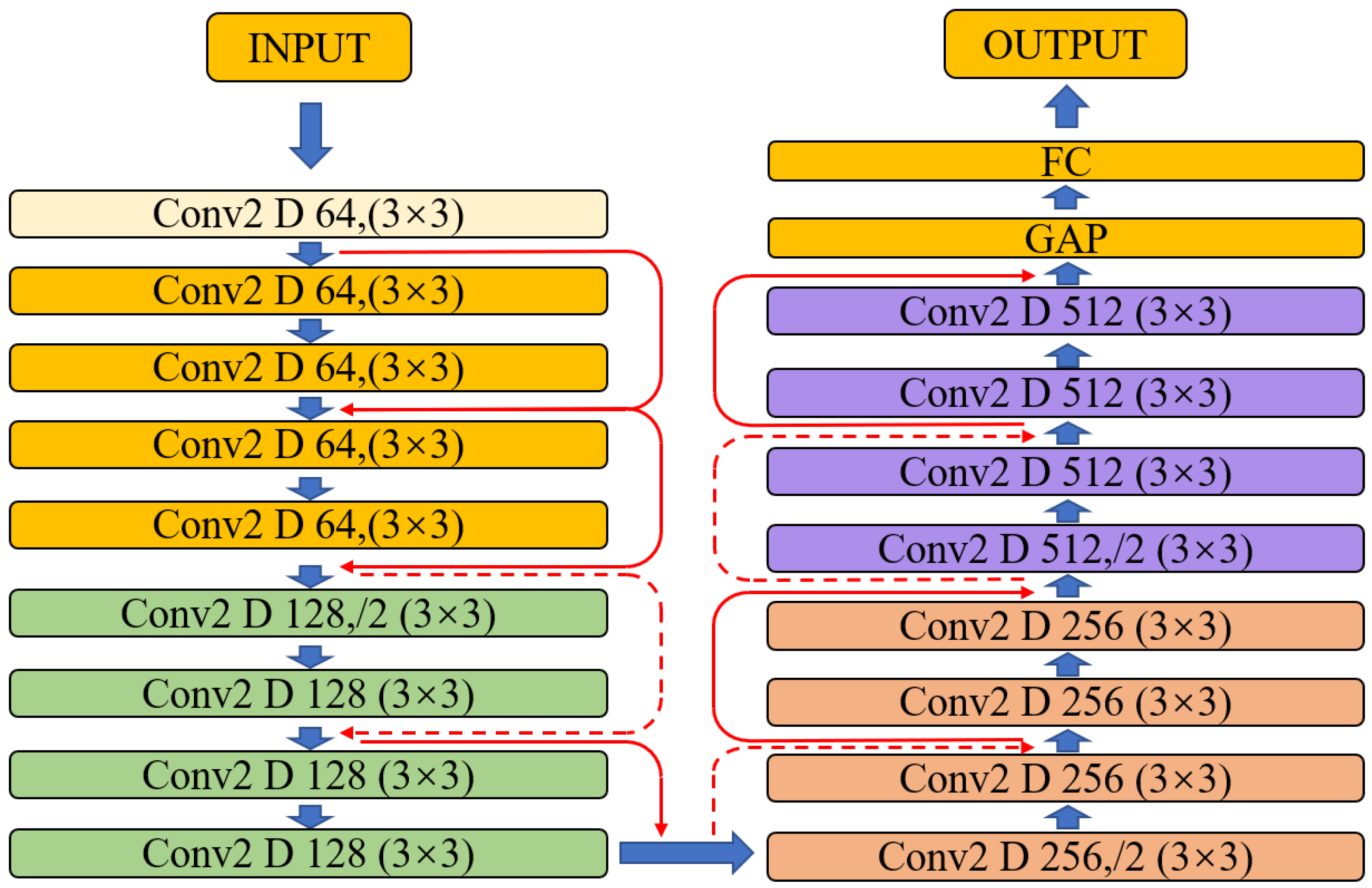
4.1. CNN with Mel Spectrograms as Input
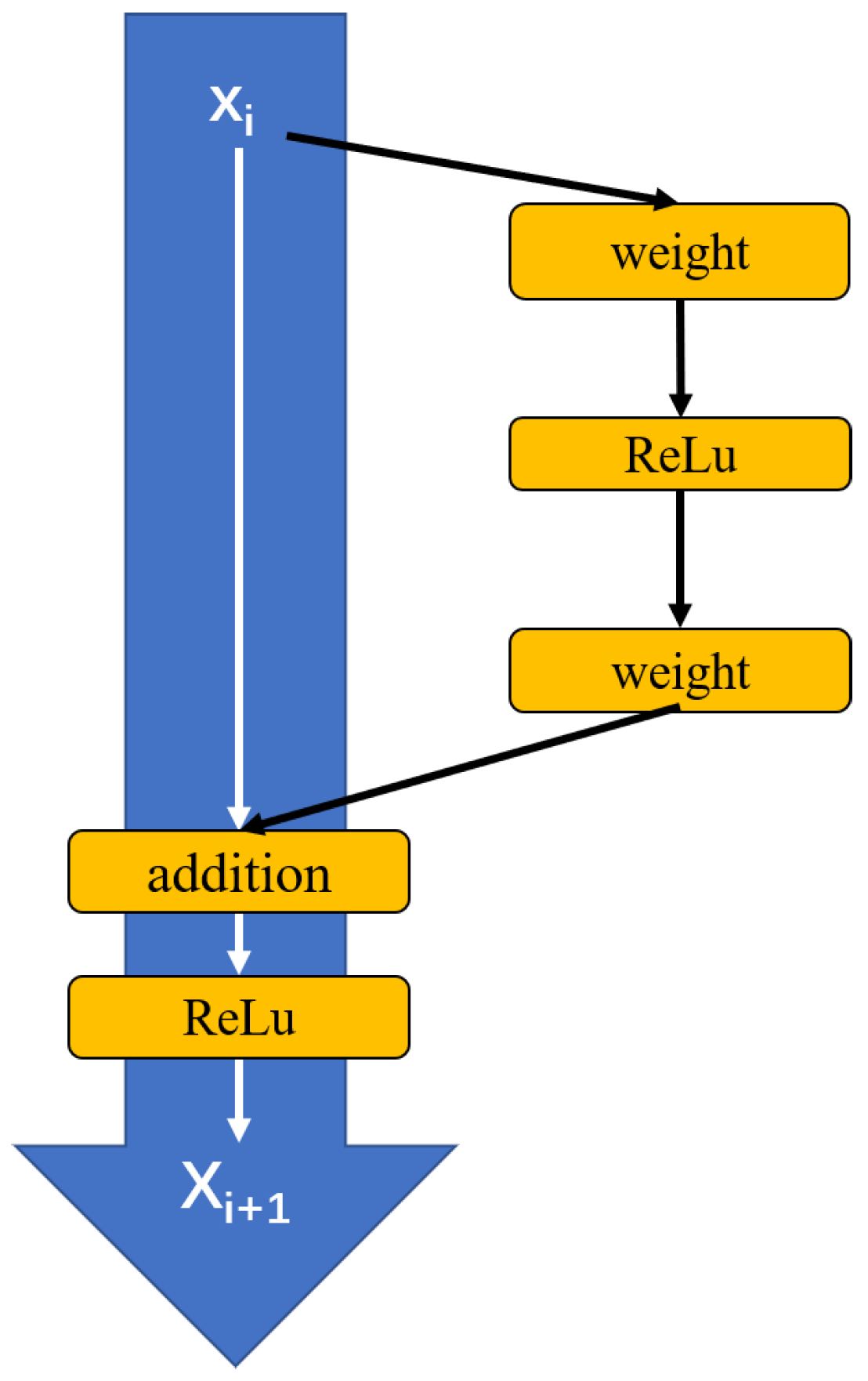
4.2. ResNet18 with Mel Spectrograms as Input
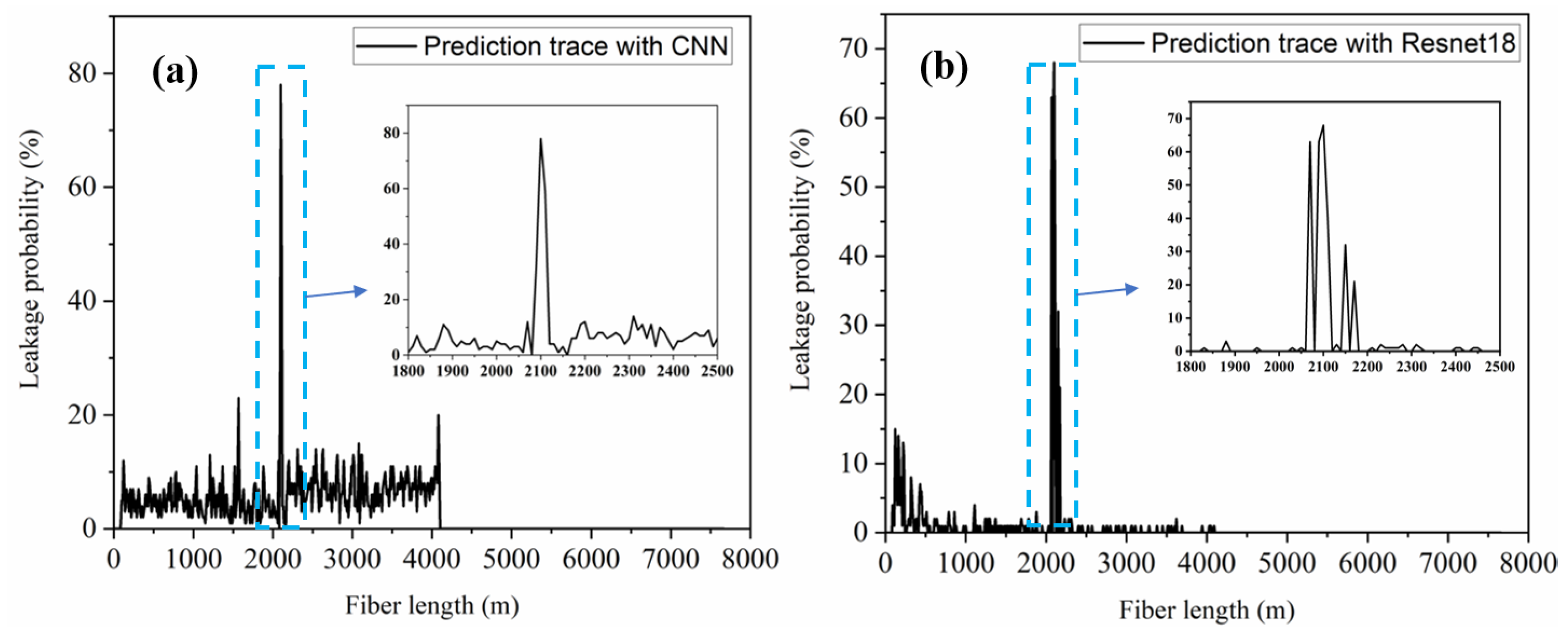
4.3. Multi-Leakage Point Detection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhuo, L.; Feng, B.; Wu, P. Water Footprint Study Review for Understanding and Resolving Water Issues in China. Water 2020, 12, 2988. [Google Scholar] [CrossRef]
- Momeni, A.; Piratla, K.R. A Proof-of-Concept Study for Hydraulic Model-Based Leakage Detection in Water Pipelines Using Pressure Monitoring Data. Front. Water 2021, 3, 648622. [Google Scholar] [CrossRef]
- Korlapati, N.V.S.; Khan, F.; Noor, Q.; Mirza, S.; Vaddiraju, S. Review and Analysis of Pipeline Leak Detection Methods. J. Pipeline Sci. Eng. 2022, 2, 100074. [Google Scholar] [CrossRef]
- Sousa, D.P.; Du, R.; Mairton Barros da Silva, J., Jr.; Cavalcante, C.C.; Fischione, C. Leakage Detection in Water Distribution Networks Using Machine-Learning Strategies. Water Supply 2023, 23, 1115–1126. [Google Scholar] [CrossRef]
- Peng, L.; Huang, S.; Wang, S.; Zhao, W. A Simplified Lift-Off Correction for Three Components of the Magnetic Flux Leakage Signal for Defect Detection. IEEE Trans. Instrum. Meas. 2021, 70, 6005109. [Google Scholar] [CrossRef]
- Wu, D.; Chatzigeorgiou, D.; Youcef-Toumi, K.; Mekid, S.; Ben-Mansour, R. Channel-Aware Relay Node Placement in Wireless Sensor Networks for Pipeline Inspection. IEEE Trans. Wirel. Commun. 2014, 13, 3510–3523. [Google Scholar] [CrossRef]
- Wu, D.; Chatzigeorgiou, D.; Youcef-Toumi, K.; Ben-Mansour, R. Node Localization in Robotic Sensor Networks for Pipeline Inspection. IEEE Trans. Ind. Inform. 2016, 12, 809–819. [Google Scholar] [CrossRef]
- Mashford, J.; De Silva, D.; Marney, D.; Burn, S. An Approach to Leak Detection in Pipe Networks Using Analysis of Monitored Pressure Values by Support Vector Machine. In Proceedings of the 2009 Third International Conference on Network and System Security, Gold Coast, QLD, Australia, 19–21 October 2009; pp. 534–539. [Google Scholar]
- Leu, S.-S.; Nha, B. Leak Prediction Model for Water Distribution Networks Created Using a Bayesian Network Learning Approach. Water Resour. Manag. 2016, 30, 2719–2733. [Google Scholar] [CrossRef]
- Wu, H.; Sun, Z.; Qian, Y.; Zhang, T.; Rao, Y. A Hydrostatic Leak Test for Water Pipeline by Using Distributed Optical Fiber Vibration Sensing System. In Proceedings of the Fifth Asia-Pacific Optical Sensors Conference, Jeju, Republic of Korea, 20–22 May 2015; Lee, B., Lee, S.-B., Rao, Y., Eds.; SPIE: Bellingham, WA, USA, 2015; p. 965543. [Google Scholar]
- Fu, S.; Zhang, D.; Peng, Y.; Shi, B.; Yedili, N.; Ma, Z. A Simulation of Gas Pipeline Leakage Monitoring Based on Distributed Acoustic Sensing. Meas. Sci. Technol. 2022, 33, 095108. [Google Scholar] [CrossRef]
- Zhu, H.; Pan, C.; Sun, X. Vibration Pattern Recognition and Classification in OTDR Based Distributed Optical-Fiber Vibration Sensing System. Proc. SPIE-Int. Soc. Opt. Eng. 2014, 9062, 906205. [Google Scholar] [CrossRef]
- Jiang, F.; Li, H.; Zhang, Z.; Zhang, Y.; Zhang, X. Localization and Discrimination of the Perturbation Signals in Fiber Distributed Acoustic Sensing Systems Using Spatial Average Kurtosis. Sensors 2018, 18, 2839. [Google Scholar] [CrossRef] [PubMed]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Jia, H.; Liang, S.; Lou, S.; Sheng, X. A k-Nearest Neighbor Algorithm-Based Near Category Support Vector Machine Method for Event Identification of φ-OTDR. IEEE Sens. J. 2019, 19, 3683–3689. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y.; Chen, J.; Song, Y.; Zhang, J.; Wang, M. Event Detection Method Comparison for Distributed Acoustic Sensors Using φ-OTDR. Opt. Fiber Technol. 2019, 52, 101980. [Google Scholar] [CrossRef]
- Pan, Z.; Liang, K.; Ye, Q.; Cai, H.; Qu, R.; Fang, Z. Phase-Sensitive OTDR System Based on Digital Coherent Detection. In Proceedings of the 2011 Asia Communications and Photonics Conference and Exhibition (ACP), Shanghai, China, 13–16 November 2011; pp. 1–6. [Google Scholar]







| Dataset | No Leakage | Leakage |
|---|---|---|
| Training set | 13,699 | 1951 |
| Test set | 1574 | 120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xiong, Z.; Ji, B.; Li, N.; Yu, Z.; Wu, S.; He, S. Water Pipeline Leakage Detection Based on Coherent φ-OTDR and Deep Learning Technology. Appl. Sci. 2024, 14, 3814. https://doi.org/10.3390/app14093814
Zhang S, Xiong Z, Ji B, Li N, Yu Z, Wu S, He S. Water Pipeline Leakage Detection Based on Coherent φ-OTDR and Deep Learning Technology. Applied Sciences. 2024; 14(9):3814. https://doi.org/10.3390/app14093814
Chicago/Turabian StyleZhang, Shuo, Zijian Xiong, Boyuan Ji, Nan Li, Zhangwei Yu, Shengnan Wu, and Sailing He. 2024. "Water Pipeline Leakage Detection Based on Coherent φ-OTDR and Deep Learning Technology" Applied Sciences 14, no. 9: 3814. https://doi.org/10.3390/app14093814
APA StyleZhang, S., Xiong, Z., Ji, B., Li, N., Yu, Z., Wu, S., & He, S. (2024). Water Pipeline Leakage Detection Based on Coherent φ-OTDR and Deep Learning Technology. Applied Sciences, 14(9), 3814. https://doi.org/10.3390/app14093814







